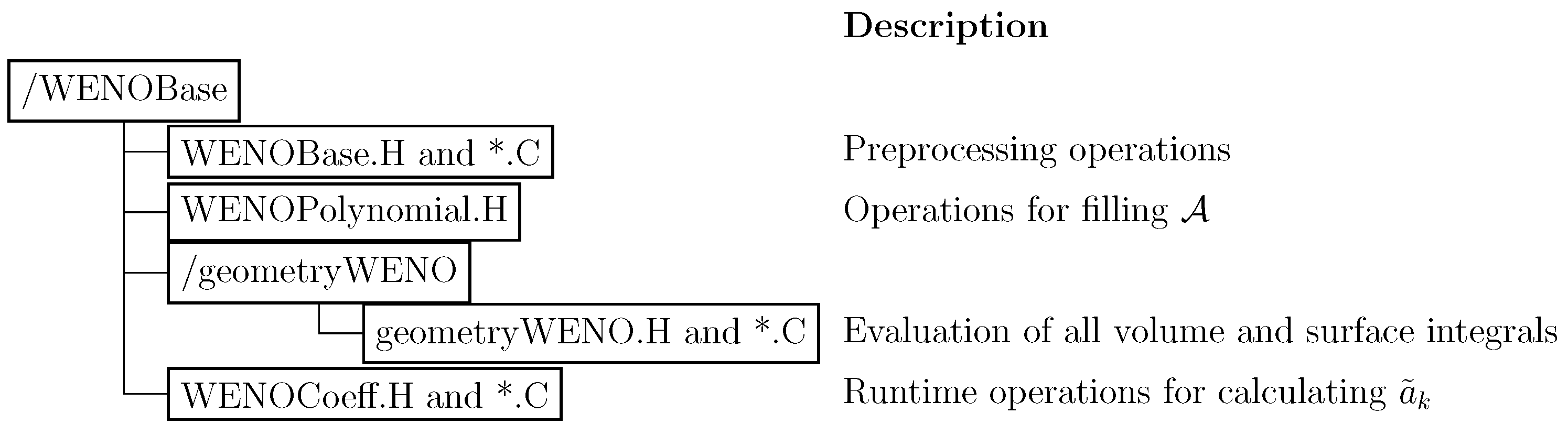
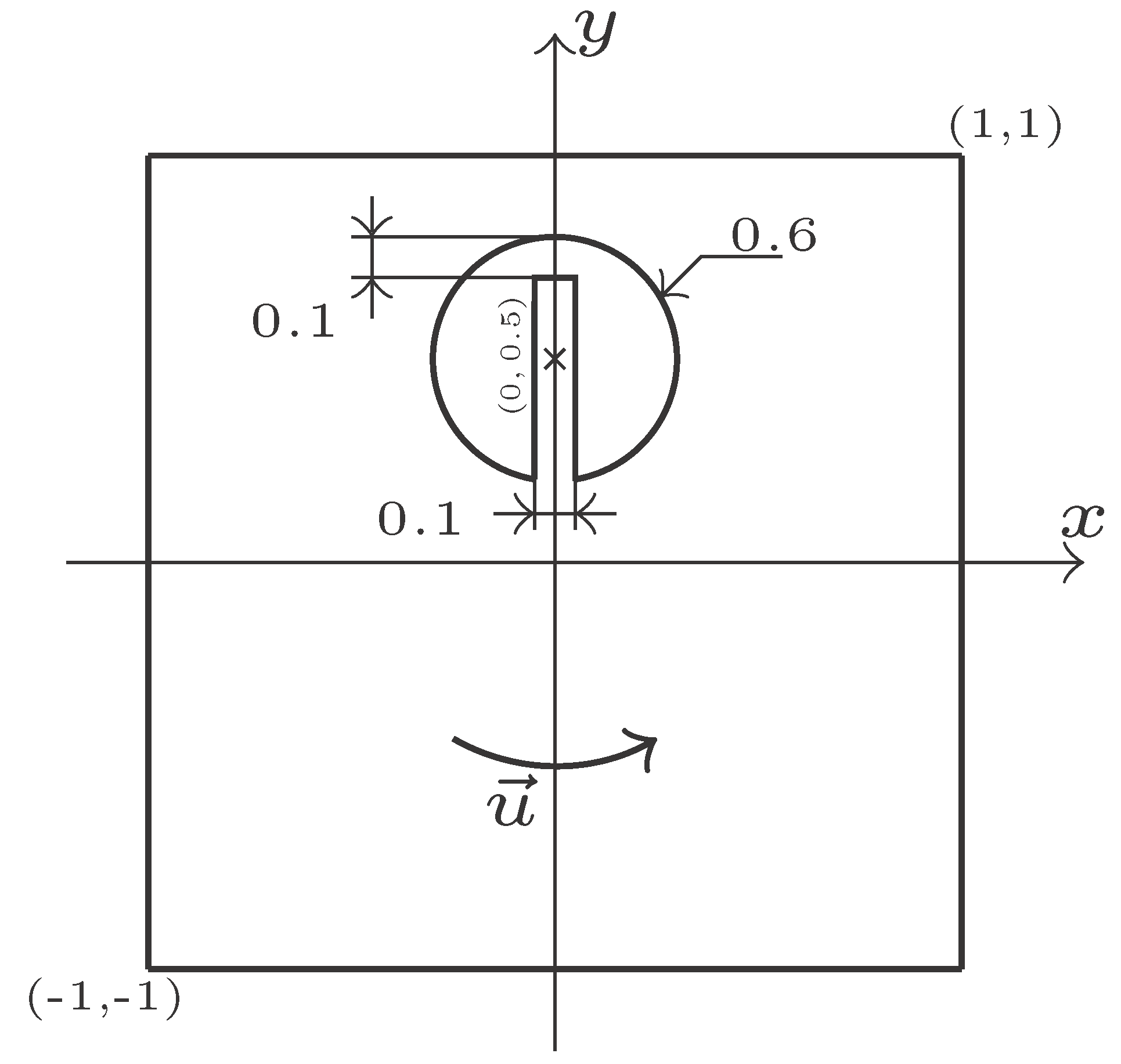
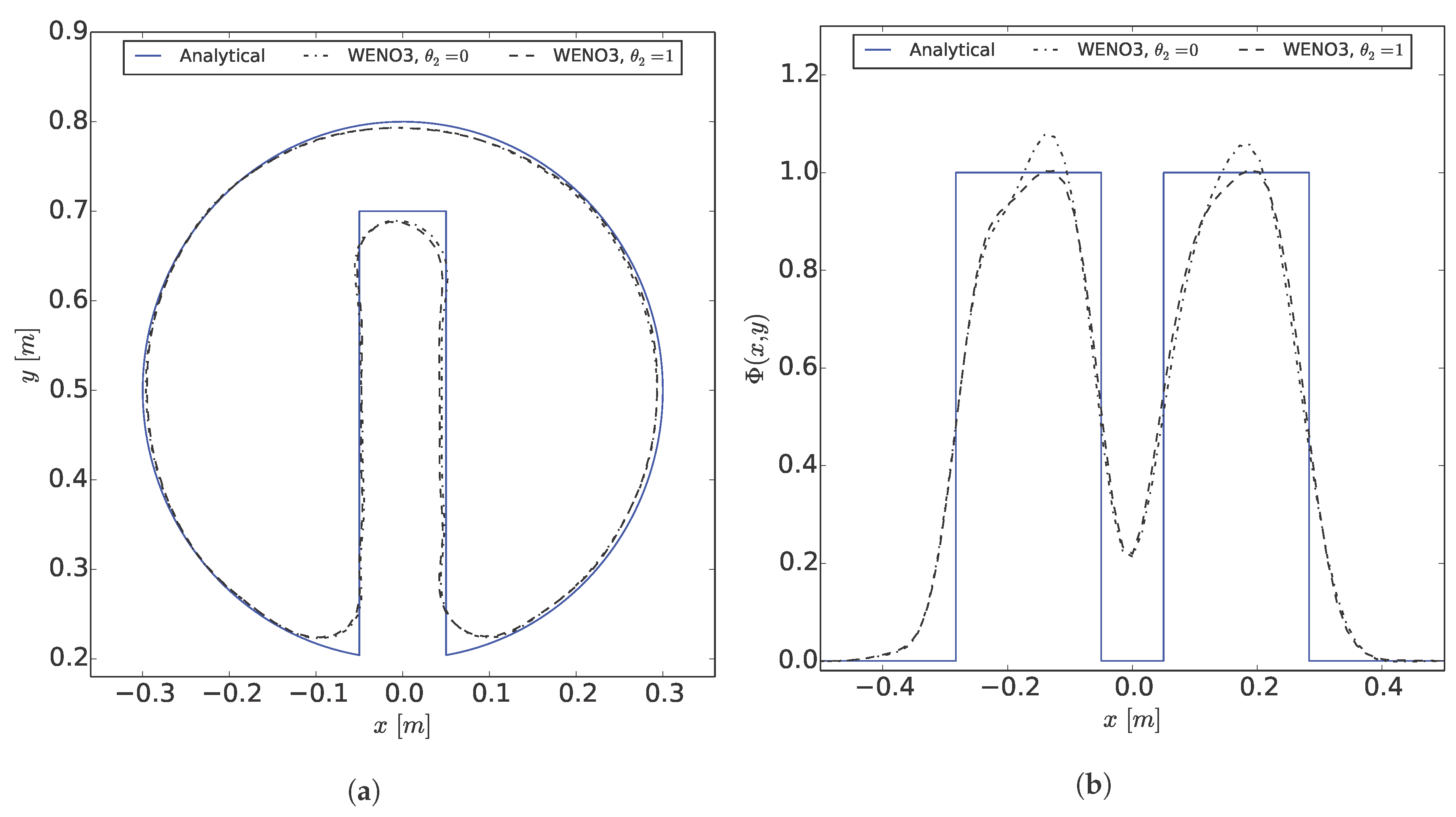
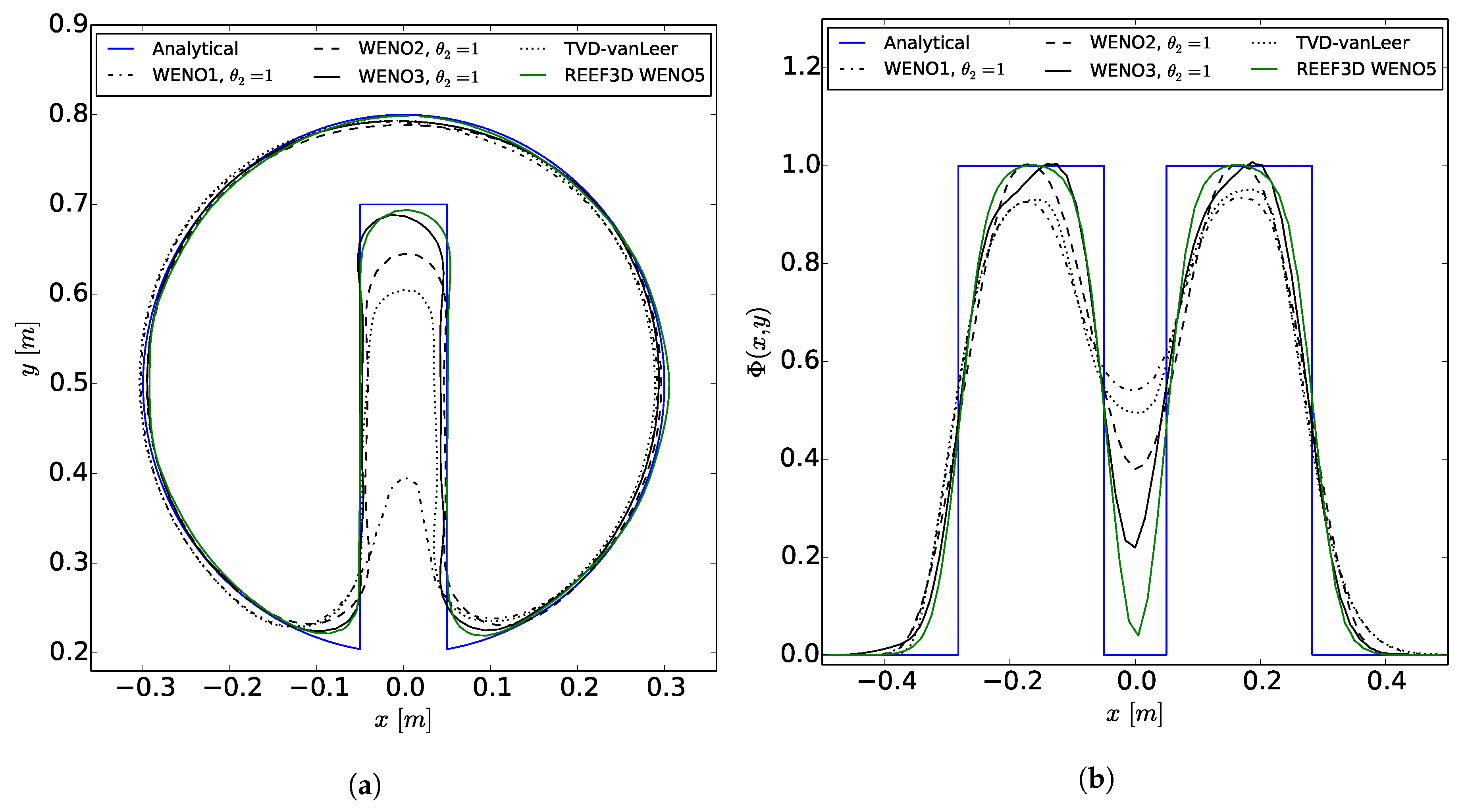
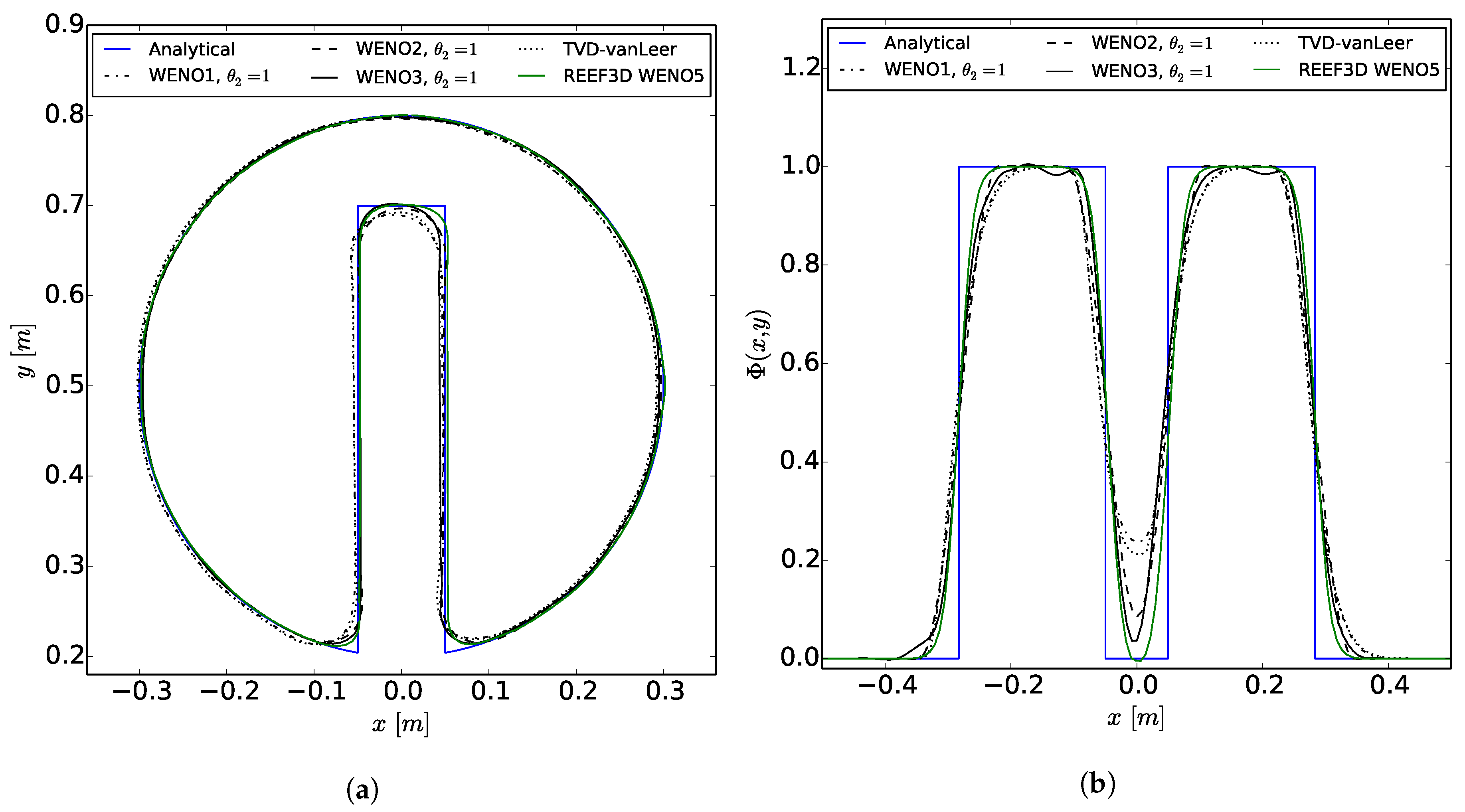
1. Introduction
In recent years, open source Computational Fluid Dynamics (CFD) codes experienced an increased influence not only on ongoing science but also on the industry. It is caused by providing a suitable environment for a wide range of new developments as well as different solvers for multiple applications at no charge. Among others, the Finite Volume Method (FVM)-based open source C++ library OpenFOAM
® gained popularity in the recent past since it can handle unstructured grids with polyhedral cells and provides a high-level programming platform for applying new solvers easily. Unstructured meshes are currently in the focus of operators due to their increased versatility in the application CFD methods in complex geometries [
1] and the reduced generation time. However, the irregular structure of the grid prevents most codes such as OpenFOAM
® to reach more than second order of accuracy. Further, the commonly applied second-order methods such as total variation diminishing (TVD) schemes are derived for structured grids. This might cause unbounded solutions on unstructured grids dependent on the chosen gradient scheme.
High-order methods would be preferable especially for the challenging task of discretising convective terms. Related to turbulence flows, high-order methods increase the accuracy of simulating mixing by reducing numerical diffusion significantly. At the same time, convection dominant flows, resulting in an appearance of hyperbolic aspects in the underlying equations, require monotonic schemes to assure stability [
2]. Such challenging tasks arise e.g., in flows with discontinuities such as shocks or free surfaces. A suitable scheme has to be chosen which copes with the formation of large gradients in front propagating problems and preserve the sharpness of the interface without creating spurious oscillations near discontinuities at the interface [
3]. This Gibbs-like phenomenon generates
spurious oscillations at points of discontinuity, proportional to the size of the jump [
4].
Linear schemes with such monotone behaviour are restricted to first-order accuracy according to Godunov [
5]. Therefore, non-linear schemes were developed such as TVD schemes which are based on limiters derived from corresponding conditions of Sweby [
6]. Their main drawbacks are the degeneration to first-order accuracy near extrema regardless of a smooth peak or discontinuity and at most second-order accuracy. This led to the development of (weighted) essentially non-oscillatory ((W)ENO) schemes. They introduce non-linear weighting for preventing oscillations near discontinuities and simultaneously reach an arbitrary order of accuracy in smooth regions. However, the solution is not strictly bounded leading to the eventual necessity of additional limiting [
7].
The first ENO scheme based on adaptive stencils was developed by Harten et al. [
4]. Their scheme searches for the most suitable cells in a dynamic manner in order to obtain a stencil with the smoothest solution in each time step. The application on unstructured grids was provided by Abgrall [
8] for the first time. The drawbacks of ENO methods are the prevention of convergence in the case of frequent switching of the stencil from one time step to another and costly operations at runtime reducing the overall performance [
9]. An alternative scheme, named Quasi-ENO, was introduced by Ollivier-Gooch [
9] to overcome these drawbacks. In contrast to classical ENO schemes, it is based on a high-order least-squares reconstruction which fulfils the ENO-property by a pointwise data-dependent weighting in one fixed, central stencil [
10]. Classical least-squares reconstructions are able to reach high-orders in smooth regions but fail near discontinuities. A common way of eliminating this problem is introducing a limiter as Wang [
11] and McDonald [
12] demonstrated. However, the underlying mathematical problem is the inclusion of the data from cells behind a discontinuity into the reconstruction. The Quasi-ENO scheme solves this problem in a more efficient way than the classical ENO scheme and furthermore, offers the possibility of excluding cells of poor quality from the reconstruction. It has been shown by the authors [
13] that the Quasi-ENO approach provides accurate solutions as long as the topology allows compact stencils without scaling effects. However, the solutions of the systems of equations often have to be calculated from ill-conditioned matrices, particularly in case of higher order polynomials. The common way of improving the condition numbers by applying preconditioning fails for the ENO weighted reconstruction matrices. Further, the stencils may lose too much information for reaching the nominal order of accuracy near discontinuities which results in a reduction of the order similar to TVD schemes [
14].
In contrast to ENO, WENO schemes compute the solution on several fixed stencils and combine them by a non-linear weighting in order to obtain a final smooth solution. The weights are calculated from an evaluation of the smoothness in each stencil. This theoretically leads up to
th order of accuracy by using a polynomial of
rth-order [
10]. Further, they yield better convergence due to smoother numerical fluxes [
15]. In return, they need the preparation of several stencils which is computationally quite expensive in preprocessing especially on unstructured meshes in three dimensions [
16]. Besides, the reconstruction may fail near critical points, on very coarse grids or if not enough smooth data is provided [
17]. The first WENO scheme was introduced by Liu et al. [
18] and Jiang and Shu [
19] on regular grids. Later, Friedrich [
20] extended it to two-dimensional, unstructured grids. In the recent past, Dumbser and Käser [
16] and Tsoutsanis et al. [
1] accomplished that finite volume WENO schemes are applicable on three-dimensional, unstructured grids with arbitrary order of accuracy. Pringuey [
3] successfully extended their approach to non-uniform cells and sketched the possibility to implement WENO schemes in OpenFOAM
®. However, in his work, he restricted the usage to explicit convection terms in hyperbolic equations and provided less information about the implementation into the code itself.
The presented research, therefore, aims firstly at a derivation and detailed verification of a WENO reconstruction method fully embedded in the existing code structure of OpenFOAM
® using a similar approach to [
3]. This provides high-order reconstructions on unstructured grids to a huge group of researchers and enables these developments to a broad scope of applications for the first time. The method is mainly based on the approach of Dumbser and Käser [
16] and Tsoutsanis et al. [
1]. Hence, the scheme operates in a reference space without scaling effects in order to prevent ill-conditioned matrices and improve the accuracy on irregular grids. All mesh types are handled automatically which is in accordance to OpenFOAM
®. On these general grids, finite volume WENO schemes were usually applied to convection terms in an explicit manner. As an exceptional example, implicit discontinuous Galerkin methods based on hierarchical WENO reconstructions might be of interest to the reader [
21]. The possibility to build a semi-implicit finite volume WENO convection scheme arises by including the reconstruction in OpenFOAM
® due to existing code structures for such an implementation. It results in a more stable reconstruction for larger time steps and an utilization of high-order convection schemes in common semi-implicit solution algorithms such as SIMPLE or PISO (Pressure-Implicit with Splitting of Operators). However, the theoretical accuracy limitation of these algorithms can of course not be affected.
In
Section 2, the derivation of the basic reconstruction method is presented. Here, especially the parallelisation process within the 0-halo approach of OpenFOAM
® is described in detail. Afterwards, the derivations of semi-implicit WENO convection schemes (
Section 3) and different gradient schemes (
Section 4) are given. It follows
Section 5 with implementation and application details.
Section 6 is dedicated to the verification process of the schemes, whereas
Section 7 shows several test cases including an efficiency comparison. A conclusion completes this article in
Section 8.
2. Numerical Approach of WENO Reconstruction Methods
The spatial domain is taken in its discretised form of
N cells with the volumes
, and the data of any scalar variable
is stored in the cell centres
represented by the cell averaged values
. In case of a vector or tensor field, each component is evaluated separately because of the later introduced weighting. With the aid of a least-squares reconstruction,
is replaced by a polynomial representation
in each cell
with the constraint of conservation of the mean value within
. Scaling effects are prevented by mapping the reconstruction process from the physical space
into a reference space
using an affine transformation
and its inversion
, respectively. The affinity of the transformation conserves the conservation condition which results in
with
the mapped cell
in its reference space. The polynomials
are expressed by an expansion over local polynomial basis functions
[
1]
The number of degrees of freedom
K relates to the order of the polynomial
r in three dimensions according to
respectively in two dimensions to
The basis functions
have to be chosen with the constraint of satisfying (
1), equivalent to a zero mean value over
. The condition can be satisfied analytically by an appropriate definition of the basis functions
with arbitrary orthogonal polynomial basis functions
. In accordance with Ollivier-Gooch [
9] and Friedrich [
20], a Taylor series expansion around the centre of
is applied and defined as
where
k corresponds to one combination of
such that
.
The degrees of freedom
are evaluated on a set of stencils
for each cell
in comparison to the single, central stencil of classical least-squares reconstructions. By definition, the stencil
is the central stencil. The number of sector stencils
depends on the cell shape and its closeness to boundaries. For each
, appropriate neighbouring cells
in the reference space of
are collected. The necessary number if cells
is an important parameter which is discussed in
Section 2.1. By definition,
corresponds to the target cell
. A polynomial
is formulated for each
using (
2). Afterwards, the WENO reconstructed polynomial of each cell is obtained by a non-linear combination of several
according to [
16]
with the non-linear weights
and
defined as
with
to prevent the denominator from becoming zero and
as discussed in [
22]. The linear weights
are defined as
for
and 1 else in accordance with Dumbser and Käser [
16]. The weights (
8) have to determine to what extend the solution in a stencil provides a qualitative contribution to a smooth solution of the polynomial reconstruction in the target cell. Here, the key element is the smoothness indicator
, which represents the smoothness indicator of the solution in the stencil
. It diminishes in case of smooth solutions and, thus, the corresponding weight
increases. The matrix expression for
is given by [
3]
where
is an element of the mesh-independent oscillation indicator matrix
. The aim of the indicator is the minimization of the total variation of the sum of the
-norms of all derivatives of the polynomial, which is comparable to the TVD property of other convection schemes [
19]. This property has to be satisfied by
which is, therefore, defined as
with
and
r the polynomial order. As can be seen from (
11), the matrix is solution independent and may be precomputed. Additionally, it is mesh independent through the calculation in the reference space. Under consideration of the definitions for the basis Function (
5), Equation (
11) can be further simplified to
The monomials are expressed by their orthogonal basis functions as
with the condition
and
. Applying the partial derivatives to (
13), Equation (
12) yields
with [
3]
The evaluation of the volume integrals in (
14) is carried out as described below.
The final WENO polynomial arises in the form of (
2) by substituting (
2) in (
7) and considering the partition of unity through the weights
Here,
are denominated as modified degrees of freedom. A system of equations can be computed with the aim of preserving the averaged values
in all cells
of the stencil
by the corresponding cell averages of
. It can be expressed by (compare (
1))
Substituting (
2) in (
17) yields the final system of equations
where
can be calculated under consideration of (
2), (
5) and (
18) as
The volume integrals evaluation of each combination
is avoided by transforming the Taylor series appropriate, e.g.,
by
with
the cell centre of
. Inserting these expressions in (
20), the final computation of
gets [
9]
The volume integrations in (
21) have to be computed for each cell and its appropriate stencil separately due to the dependency of
on the coordinate system of
. For this purpose, the volume integrals are transformed into surface integrals by using the divergence theorem [
23]. Denoting
as the outward unit normal vector in the reference space, it yields
The right-hand side can be further written as a sum of surface integrals over the
faces
of
. Here, the unit normal vector of each face
is constant and can be taken out of the integrals. The desired volume integrals of the monomials are obtained from (
22) by integrating
analytically over one of the coordinates. Under consideration of the definition of
in (
6), the evaluation can be written as
The surface integrals are computed by decomposing the faces into triangles, transforming each of them to a standard triangle using linear mapping [
24] and using a fifth-order Gaussian quadrature rule for the standard triangle [
24].
The system of Equation (19) provides a solution if the matrix
is at least squared resulting in the condition
. As Tsoutsanis et al. [
1] state, choosing
leads to unstable solutions or eventually ill-conditioned systems. Therefore,
should be approximately 2 K for three-dimensional problems and 1.5 K in 2D for the sake of robustness. This results in an overdetermined, linear least-squares problem. Physically, it corresponds to the minimization of the
-norm of the error in predicting the averaged values of the polynomial in all cells of the stencil [
10]
with
a the solution vector containing the degrees of freedom and calculated as
with
the Moore-Penrose pseudoinverse. The pseudoinverses have to be computed for each stencil in preprocessing once since
is solution independent. In each time step,
can be inserted in (
25) for calculating
a. It is obtained using singular value decomposition (SVD) [
25,
26], here. A detailed discussion of other methods for calculating
can be found in [
13,
27]. Further, it might be noticed that rank-deficient matrices may occur caused by nearly linear-dependent lines in
. They arise if several cells of a stencil lie on a straight line on structured grids [
16].
2.1. Stencil Collection Algorithm
The modified degrees of freedom are calculated from weighted solutions in several stencils. These solutions are evaluated in one central and several sectoral stencils which cover all spatial directions of the target cell. In the case of cells near boundaries, some stencils could be too small and have to be discarded. In contrast to classical ENO schemes, WENO reconstruction computes the solutions on time-invariant stencils. Thus, the time-consuming collection part simplifies and has to be executed just once during the preprocessing step. The most important requirement for stencils to obtain an accurate solution is compactness. On isotropic, uniform meshes it is simply preserved by adding the nearest neighbours iteratively. However, on unstructured meshes and in regions with highly anisotropic cells this procedure cannot ensure compactness. The selection of the stencils in physical space may lead to a loss of information near walls and along the boundary layer region, in particular. Therefore, the stencil is transformed to a reference system
where no scaling effects from increasing grid resolution or deformed cells occur. Detailed descriptions of the applied mapping can be found in [
3,
16,
27].
As the starting point of the collection algorithm, one big, central stencil is gathered. On arbitrary mapped meshes, the most compact stencil could be collected by using point-neighbour information. On the contrary, the use of face-neighbours extends the dependent data further into the mesh which reduces the redundancy of data on anisotropic, structured meshes [
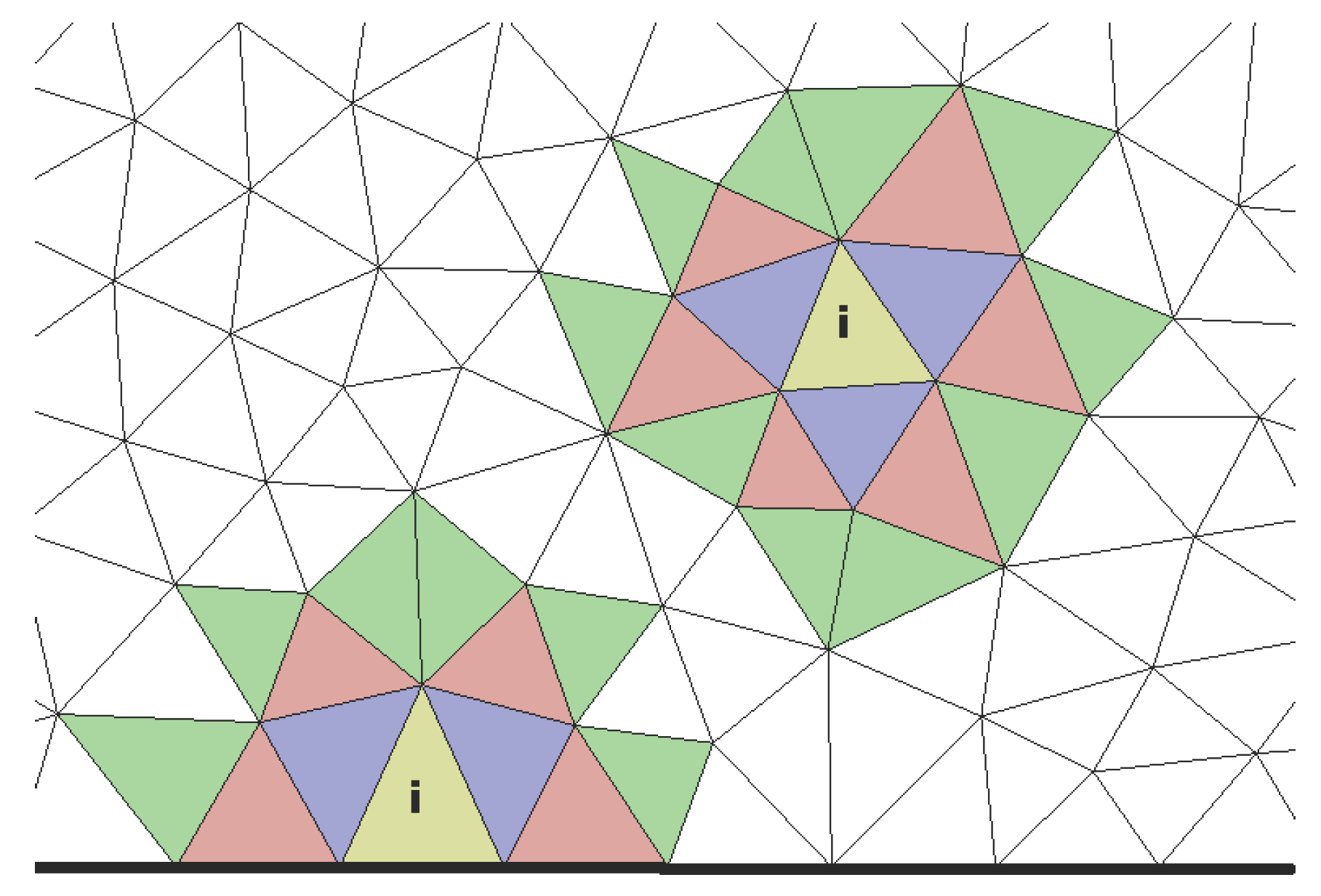
3]. The affine transformation preserves the principal connections between the cells for which reason the gathering can be performed using existing owner-neighbour lists. The most efficient way of collecting cells on unstructured meshes is based on adding the neighbours of the target cell iteratively until each stencil has the sought size. By collecting a surplus of possible stencil cells, the algorithm is independent of the starting point of an iteration and provides complete layers of new neighbours at a time as it is shown in
Figure 1. The necessary size of the list
relates to the number of internal faces of the target cell
according to
which offers a small surplus due to the described collection of layers and in case of convoluted boundaries. After the selection of sectoral stencils, the central stencil is simply obtained by cutting it to the necessary size
. In general, the number of sectors equals the number of internal faces of
. However, if some sector does not provide enough cells it is not taken into account for the runtime operations. It may happen that more layers have to be considered until the necessary size is reached near boundaries. At this point, the iterative implementation is straightforward and advantageous. Once the lists are completed, all candidates are sorted by the centre to centre distances to the target cell in
and the nearest
cells are stored.
As the next step, sectoral stencils are constructed under consideration of the on condition that they are not allowed to share another cell than the target cell [
3]. For this purpose, each sector is spanned as a cone with the cell centre of the target cell
as the apex and the contour of the related face as the base. The
cells are assigned to the sectors according to the position of their cell centres which results in a distribution as can be seen in
Figure 2. In order to check the assignment of the cells, each sector is mapped to the first octant of another transformation space
where the relevant cell centres have positive coordinates (see [
3] for details). The cell centre of each of the
cells is transformed to
of every sectoral stencil and added to its list if
All coordinates in the reference space are positive.
The cell is not already a member of another stencil which may happen on Cartesian grids where the centre lies on the boundary of two adjunct sectors.
The target stencil list contains no more than cells.
The first and last condition are simple requests while the second condition is prevented by using a dynamic list from which cells are removed after being assigned to a sector. The obtained stencils are compact by itself since the central lists are presorted and scanned from the nearest to the farthest cells.
2.2. Parallelisation
In this section, details of the parallelisation of the code are given. It is a crucial step due to the time-consuming reconstruction process at runtime. By default, OpenFOAM® is based on a 0-halo approach which divides the domain into several non-overlapping regions and Message Passing Interface (MPI) to transmit the information between the inter-processor boundaries. This leads to at best second-order accurate solutions at such boundaries. In contrast, the stencils of a high-order (W)ENO scheme near processor patches need the geometrical and physical data from several layers of the neighbouring domain. Consequently, a n-halo approach with several overlapping sub-domains would be the proper choice. The implicit handling of the Navier-Stokes equations leads to algebraic systems of equations which are solved by linear, iterative solvers in OpenFOAM®. Since these solvers only work for 0-halo approaches, a n-halo approach is discarded. Instead, the solution is the virtual extension of the sub-domains by collecting halo cells from neighbouring processors in additional lists. Then, the field values of the halo cells are updated at the beginning of each runtime step which is computed on non-overlapping domains.
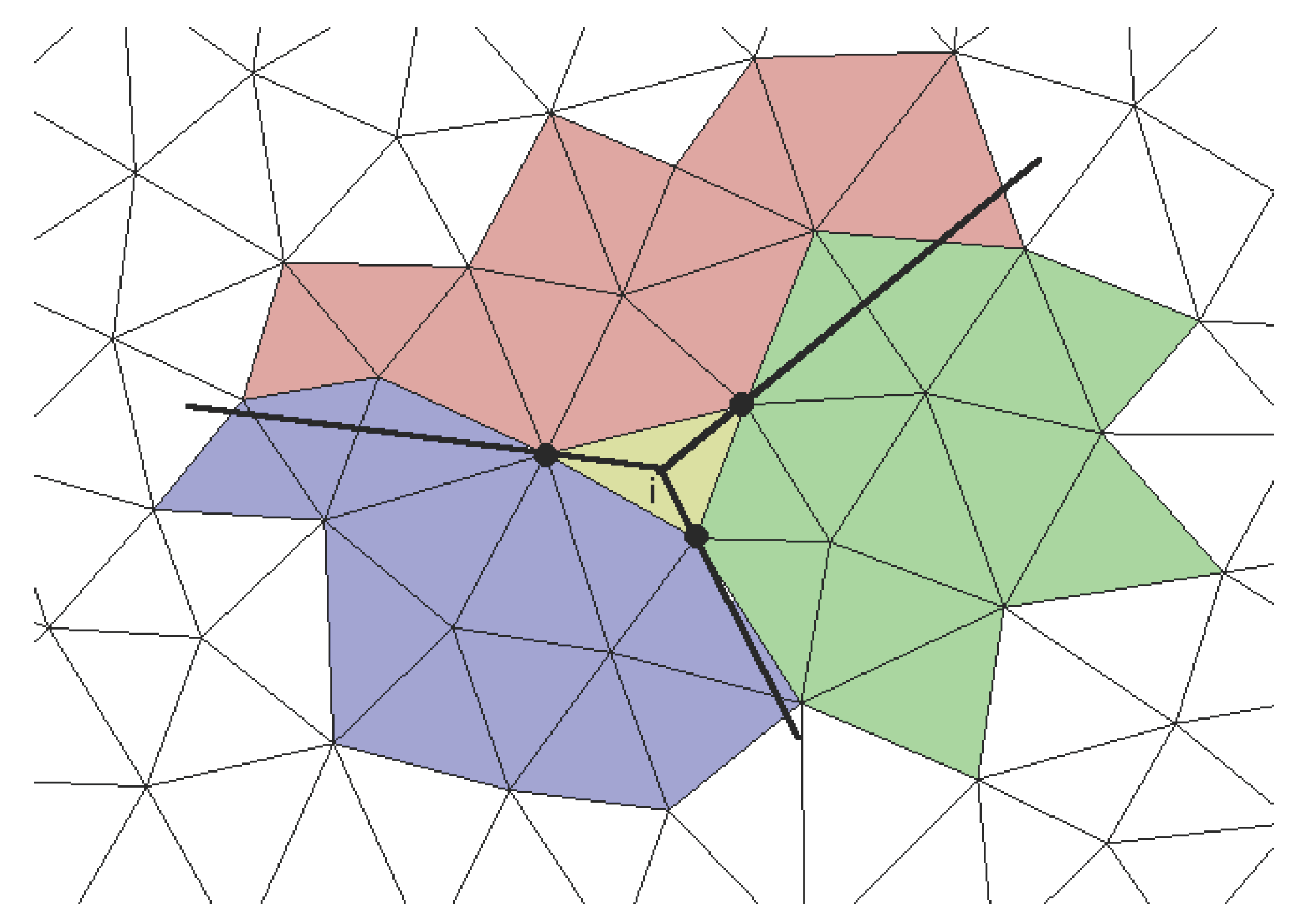
The initialization of parallelisation starts in the preprocessing step after the local stencils are collected. At this point, several stencils with a deformed shape exist near processor boundaries such as the blue framed stencil in
Figure 3a. Appropriate halo cells from other processors provide the necessary correction of the stencils. It is noticeable that all possible stencils with a deformed shape and therefore, acceptors for halo cells, are included in the stencils of target cells next to processor boundaries. It implies that these acceptor cells are vice versa the only possible halo cells for stencils of other processors. Hence, the halo cells do not have to be collected separately but can just be taken from the prepared local stencil lists. This leads to the following modification of the central stencil collection algorithm (
Section 2.1) in the case of using several processors:
For each sub-domain
, all cells from the stencils of target cells next to a processor boundary are gathered in a list of halo cells together with the information of the target processor. Beyond, the stencils of these cells are marked as possible acceptors for halo cells from other sub-domains. In
Figure 3a, acceptor cells of the sub-domain
are coloured green while its halo cells from sub-domain
are coloured red and vice versa the green cells are the halo cells from sub-domain
for the red acceptor cells of
.
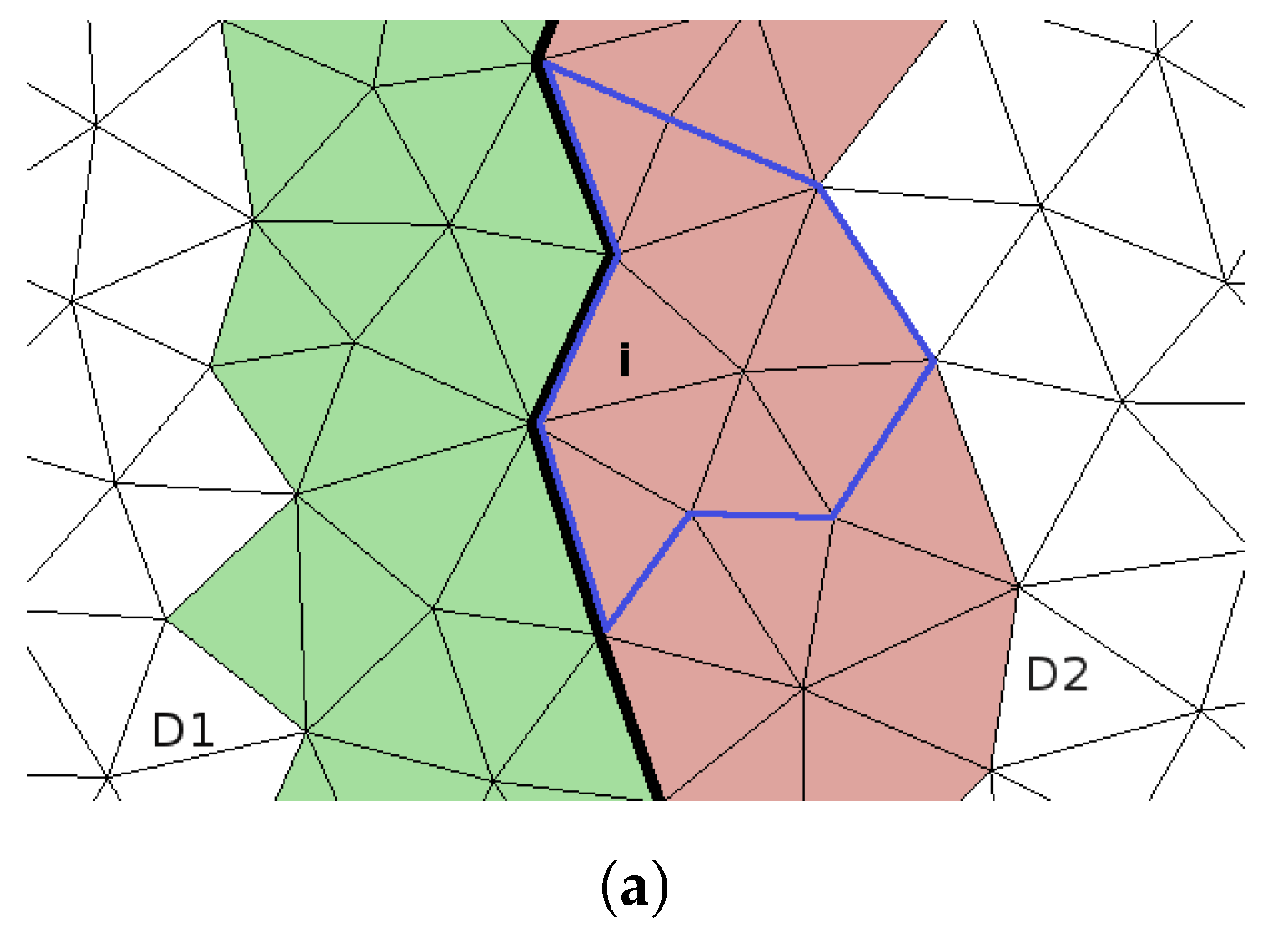
The lists of halo cells are further prepared by assigning them a new ID and additionally, storing their cell centre coordinates and the coordinates of the triangles from the triangulation of the cell’s boundaries. Afterwards, the lists are transmitted to the appropriate target processor using MPI.
The required halo cells for each marked central stencil
are determined by a geometrical selection due to missing face neighbour information beyond processor boundaries. For this purpose, a sphere is spanned around the target cell
of
with the distance from the centre of
to the outermost cell centre in the local stencil as the radius. All halo cells whose cell centres are located within this sphere are added to a new global stencil. In
Figure 3b, this geometrical selection results in the yellow coloured global stencil for the blue framed stencil in
Figure 3a.
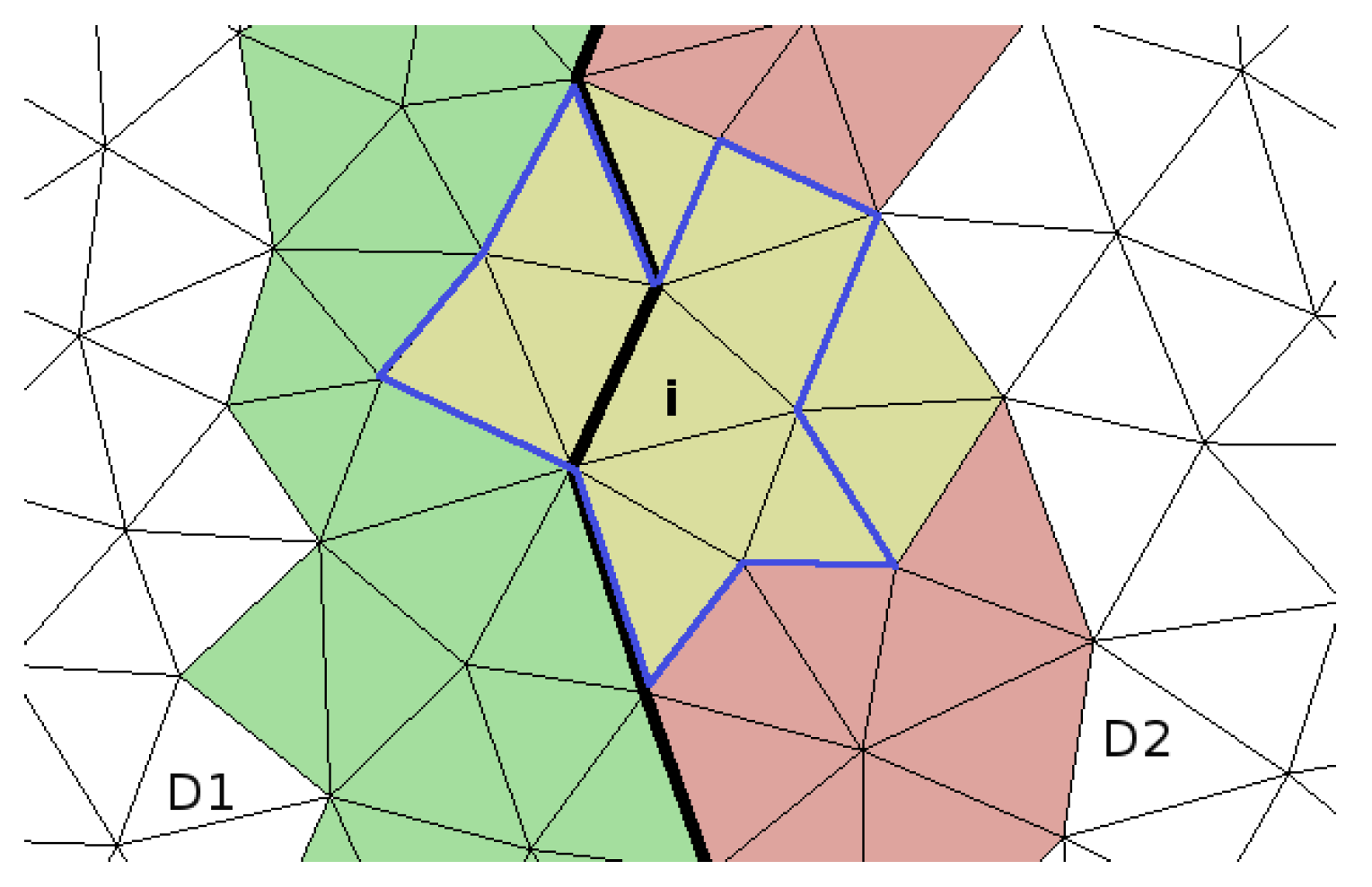
The final stencils are attained from sorting the global stencils by distance and pick the nearest
cells. In
Figure 3b, the new stencil is framed in blue.
Additional lists with the information of the origin processor of each cell in a stencil are generated in order to transmit the field data between processors before the local reconstruction starts in each runtime step. It might be noticed that the results of a reconstruction on multiple processors are minimally different to results of serial calculations due to the slightly different stencils [
13]. The stencil collecting algorithm through processor boundaries uses geometrical searching while on a single processor just the face neighbours are gathered.
3. Derivation of Semi-Implicit WENO-based Convection Schemes
The reconstruction of any function in multiple dimensions and on unstructured meshes can be computed using the above presented WENO reconstruction method. In the following sections, possible discretisation schemes are derived which are all generally applicable in the high-level use of OpenFOAM® (The presented interpolations are, however, limited to the surface interpolation class of OpenFOAM® which stands in contrast to the point interpolation class).
In FVM, any convective term is discretised applying volume integration over each cell and Gauss’s theorem for transforming the arising volume integrals in a sum of surface integrals over all faces
of cell
,
In case of a high-order scheme, the integrals in (
27) have to be evaluated with a Gaussian integration of higher order, too. The velocity at the face are taken out of the integration since (
27) is always treated in a linearised form here. Inserting the polynomial expressions of
(
16) in (
27) yields at any face
of
with
the volumetric flow rate (Since the common gaussian integration of OpenFOAM
® is limited to second order of accuracy, the basis classes multiply the results of the interpolation by the face areas. Therefore, we neglect the surface area in (
28) in the implementation in order stay consistent). The remaining surface integrals in (
28) are solution independent and can be precomputed. Under consideration of (
5), they are expressed as
The volume integrals in (
29) are already computed during the reconstruction procedure. The surface integrals over the basis functions are evaluated in a similar way by decomposing the faces into triangles and using Gaussian quadrature rules of appropriate order. Hence, the evaluation of linearised convective terms reduces to a sum of scalar products at runtime, at which the considered polynomials depend on the chosen flux evaluation procedure.
The flux evaluation of linearised convective terms can be interpreted as the flux solution of the Riemann problem for the linear advection equation which is defined as [
28]
under consideration of an incompressible fluid. Its finite volume formulation arises similar to (
27) as
with the numerical flux
Toro [
28] showed that the flux evaluation in (
31) can be executed in the normal direction of each face
due to its rotational invariance. Thereby, it is represented at each face by the one-dimensional equation
resulting in the Riemann problem [
28]
with the initial data
representing the values of
from the adjacent cells at one point of the considered face. Taking the exact solution of (
34) [
28] into account, the flux yields at the face (
) at any time
These fluxes result in an unconditional stable solution for which reason the Riemann solver (
35) is appropriate for creating high-order interpolation methods based on WENO reconstructions. As proposed by Toro [
29], we extend Godunov’s first-order version, which is based on cell centre values of
, by higher-order terms of the reconstruction; the so-called WENOUpwindFit arises as a high-order non-oscillatory upwind scheme. For this purpose, the two reconstructed face values
and
are recalled from above (compare (
16))
Here, the index
i represents the owner and
represents the neighbour cell of the face. The correlating reference spaces are denoted by
. The sought fluxes can be evaluated from (
27) and (
35) as
with the polynomials (
36) instead of
. The surface integrals are evaluated using (
28) in the proper reference space.
So far, most WENO schemes were used explicitly. However, the presented method can also be applied as a deferred correction method [
30] which combines an implicit first-order upwind scheme with an explicit high-order correction term. The first-order part ensures convergence due to its monotonicity and diagonal dominance. The required subdivision is already available as can be seen in (
36). This semi-implicit WENO scheme fits in the most solution algorithms of OpenFOAM
® such as SIMPLE or PISO. Unfortunately, as it is shown in [
31], WENO schemes are not strictly bounded. The explicit correction term can, therefore, be unbounded and still influence the solution’s physical reliability.
In order to overcome possible issues with unbounded solutions, the limiting strategy of Zhang and Shu [
7], which can be applied to any high-order finite volume scheme in order to satisfy the maximum-principle for scalar conservation laws, is adapted to the presented scheme . The property implies that a time step’s solution is bounded by the cell centred values of the previous step. Hence, it is important for the convergence to the entropy solution. It might be noticed, that all monotone and TVD schemes fulfil the maximum-principle but lose accuracy at smooth extrema due to the measuring of the total variation using the cell centred values. In contrast, the new limiter is evaluated from the maximum and minimum of the reconstruction polynomials in each cell which preserves the accuracy. I was shown [
7] that the limited WENO polynomial
fulfils the maximum-principle by applying a linear scaling limiter
to the polynomial
of cell
in accordance to
Here,
M and
m are defined as the upper and lower global bounds of
. The local minimum and maximum is calculated as [
7]
The values in (
39) should be evaluated from the polynomials at all Gaussian points at runtime. In the presented interpolation scheme, the surface integration is precomputed for which reason this handling would be inefficient. It is, therefore, decided to take the surface integrated values of
into account instead. This decision is towards the underlying mathematics, but on the other hand, the values of
M and
m are also just available at the cell centres in OpenFOAM
®. Hence, Equation (
39) is evaluated as
By limiting the integrated polynomials, the interpolation scheme can be rewritten as a sum of a first-order upwind scheme and a limited high-order correction. For the sake of practicability, another user specified parameter
is introduced which provides the switch between a limited (
) and unlimited (
) computation. Hence, the final fluxes of the WENOUpwindFit scheme become (compare (
28))
As an alternative, WENO reconstructions can also be used for the implementation of central schemes which evaluate the fluxes as follows
with
from (
36) and
the central differencing weights. Analogue to the upwind scheme, this scheme is the combination of an implicit central-differencing discretisation and a central high-order correction term. The scheme is not monotone and may lead to divergence of the solution in case of convection dominant flows [
32] and hyperbolic equations, respectively, due to the negligence of characteristic curves. More stable centred schemes can generally be build from WENO reconstructions but are not in the scope of this research (see e.g., in [
33,
34,
35]).
4. Derivation of a WENO Gradient Scheme
The calculation of gradients in the cell centres is a frequent operation in FVM. Besides the standard discretisation using Gauss’s theorem and linear interpolation, OpenFOAM® offers a least-squares-based gradient scheme whose stencils are however limited to the first neighbours. On the contrary, the presented scheme takes a larger stencil into account and avoids spurious oscillations at the same time. Alternatively, the WENO weighting could also be skipped in order to get a high-order version of the existing least-squares method.
The starting point of the gradient calculation in the cell centre of
is its finite volume formulation
The volume integral in (
43) can be evaluated with a high-order accuracy in two ways. One opportunity is the transformation into surface integrals and a high-order interpolation of
to the boundaries using e.g., the central WENO scheme. This method is applicable without any further derivations and superior to linear interpolation due to the mesh independence. A more efficient computation is the direct evaluation of the volume integral by replacing the gradient of
by its polynomial representation using WENO reconstructions. Here, the difficulty is the correct definition of the Gaussian points in arbitrary shaped volumes which could be obtained by decomposing each cell in tetrahedra where the Gaussian points are known. The coordinates and weights could be stored in the preprocessing resulting in higher efficiency in runtime. However, the additional tetrahedralization is a time-consuming computation and should be avoided. If the non-oscillatory behaviour of the scheme is in the first place and the theoretical order of accuracy is less important, a more efficient gradient scheme can be derived by replacing the gradient of
by its polynomial representation and evaluating the volume integral with second order of accuracy. It corresponds to the evaluation of the gradient at the centre
of
according to
The resulting gradients are a compromise between accuracy, stability and efficiency due to its simple evaluation without any integrations. They have to be further transformed into the reference space in accordance with the polynomials of the WENO reconstruction. As given in [
3], the gradient at
yields then
due to the affine transformation.
represents the gradients in the principal directions of the reference space. Next,
is replaced by its polynomial Formulation (
16), derivatives are taken and
is inserted. The formula can then be simplified due to the cell centred orthogonal basis functions (see [
27] for details). The remaining non-zero terms are related to the coefficients of the first-order terms of the polynomial, so that the final expression reads as follows
The inverse Jacobian matrices are already calculated in the mapping process during the preprocessing. The resulting gradient scheme, called WENOGrad, can be applied to any gradient computation in OpenFOAM® due to its explicit treatment in any case.
8. Conclusions
The basis for the developed high-order convection and gradient schemes is a WENO reconstruction method. It is derived from the approaches of Dumbser and Käser [
16] and Tsoutsanis et al. [
1], and handles two- and three-dimensional polyhedral meshes in parallel. Most computational work is moved to the preprocessing in order to receive more efficient schemes in runtime. The implementations are integrated into the given interpolation and gradient classes of OpenFOAM
® which simplifies further working with the code in high-level programming and allows the development of a wider range of high-order convection and gradient schemes. Further, the reconstruction process can be taken as the basis of high-order Riemann solver which extends the possible scope of OpenFOAM
® significantly.
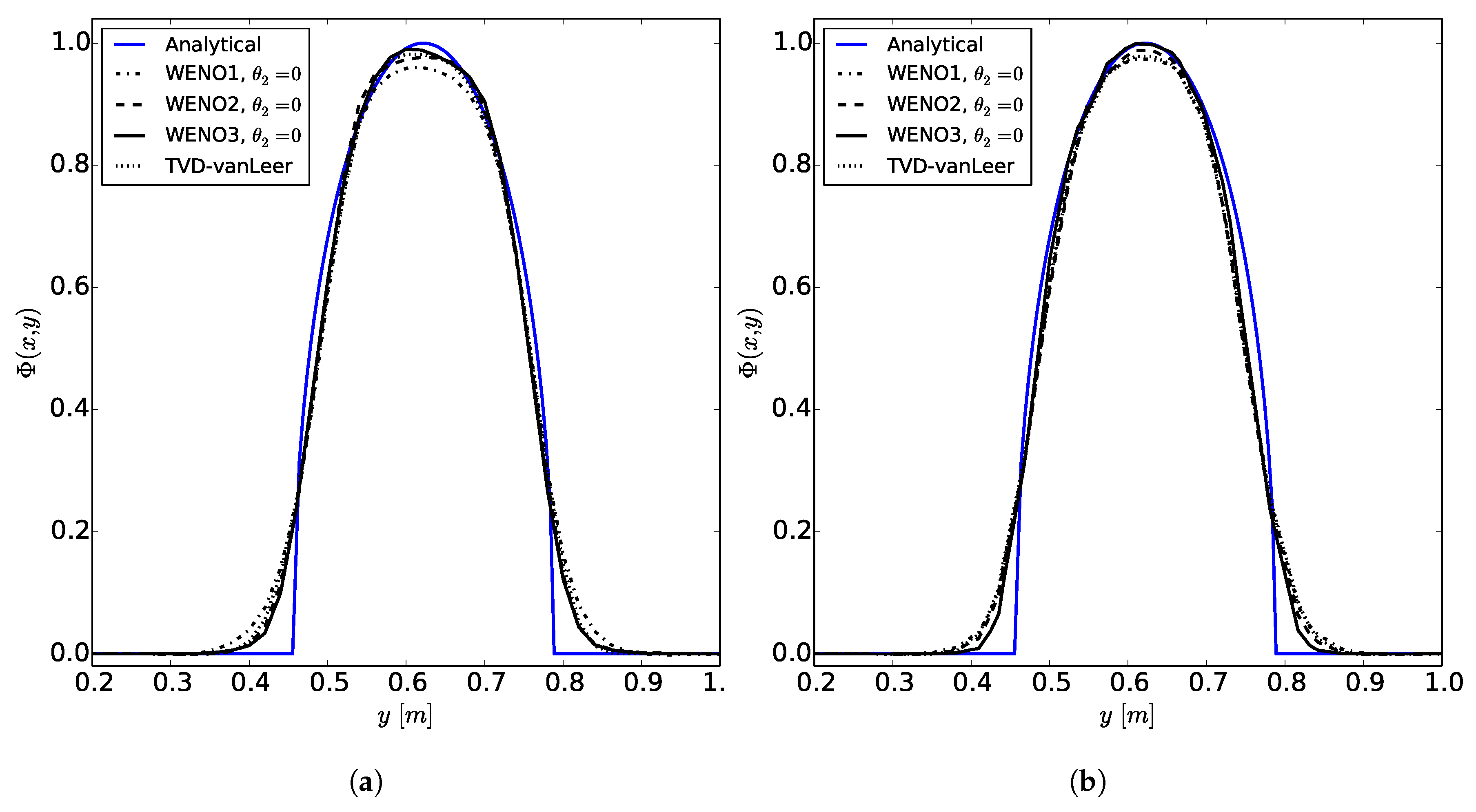
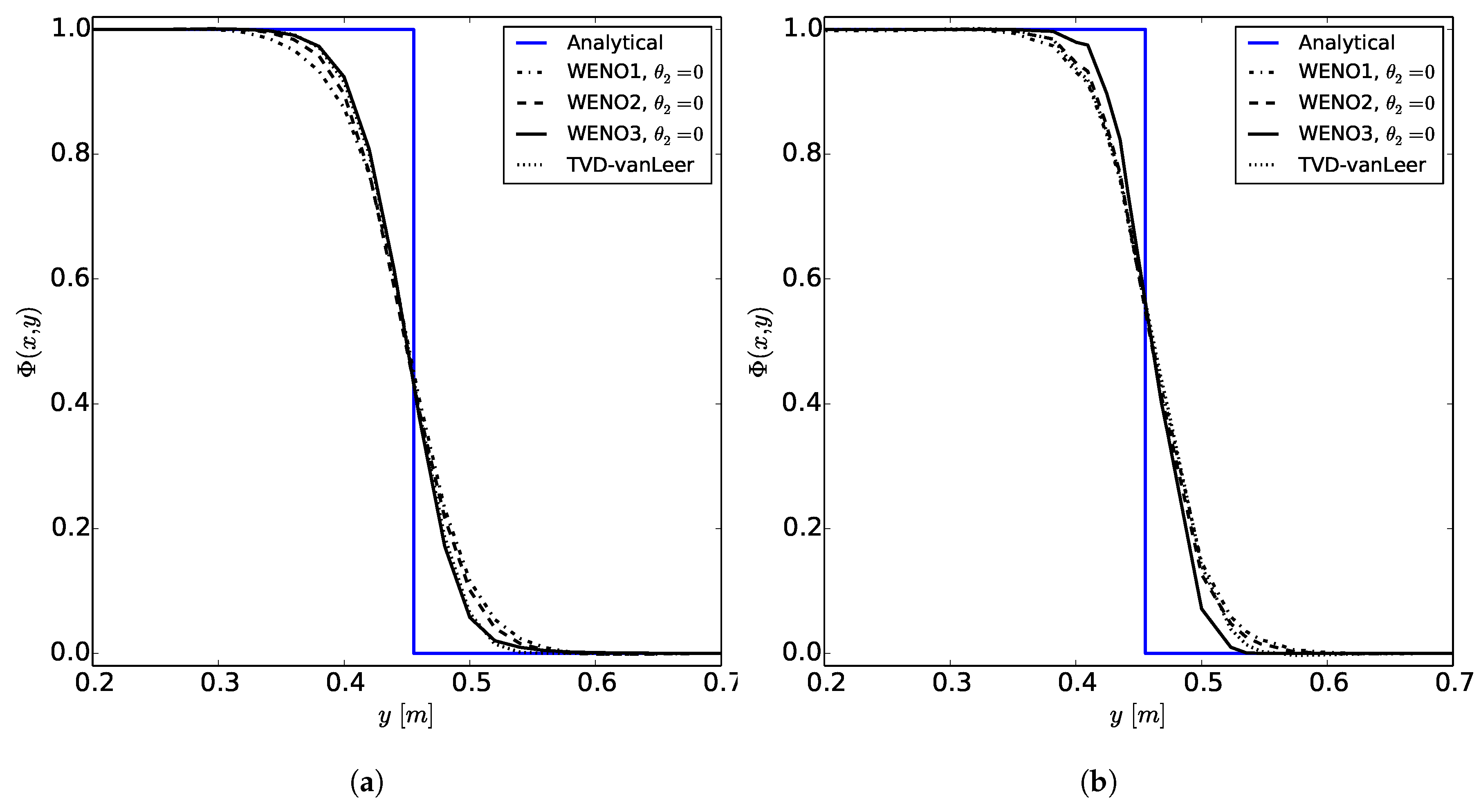
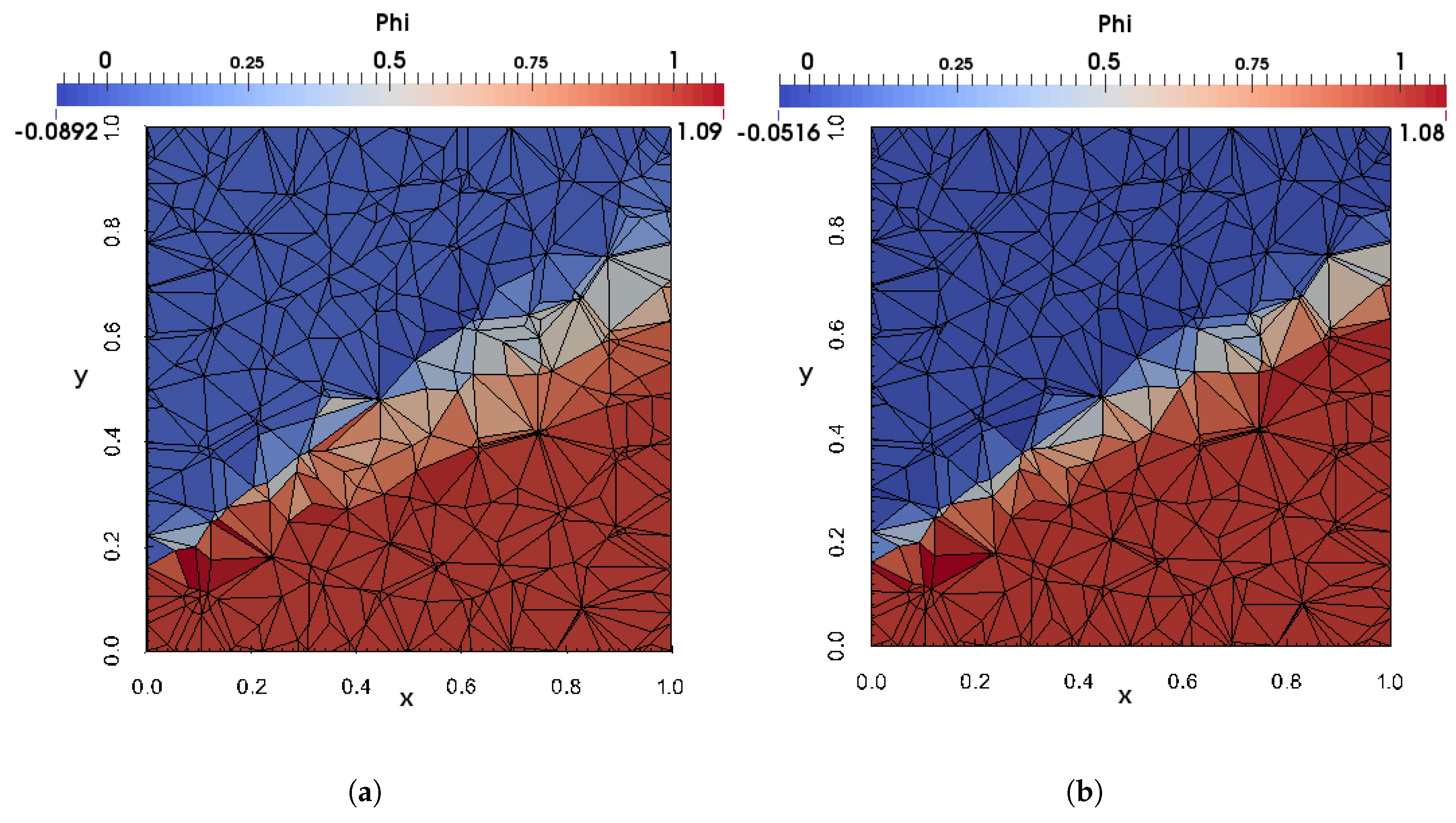
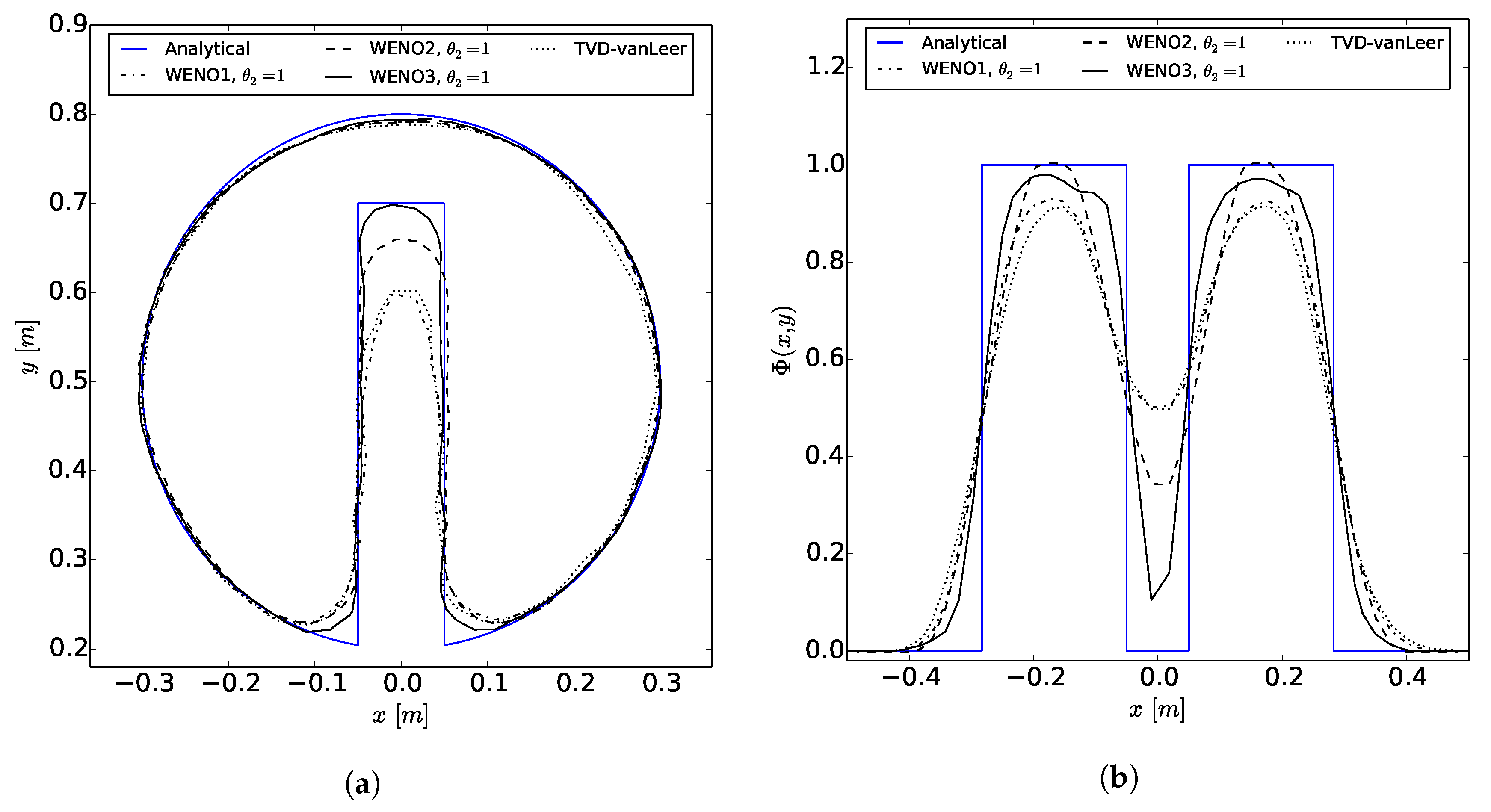
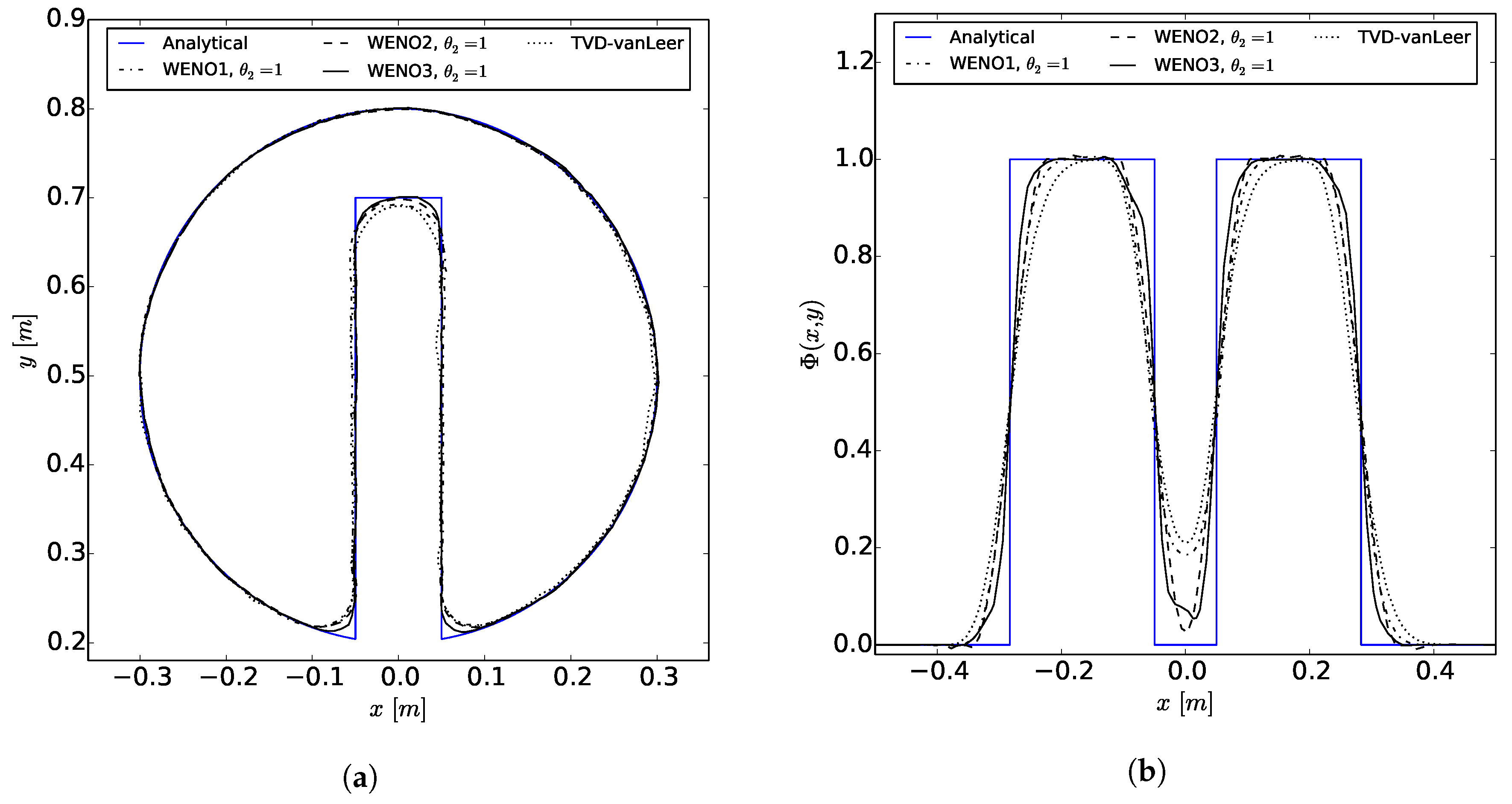
The WENOUpwindFit scheme extends the class of high-order upwind schemes and shows superior results for the scalar advection equation and in convection dominated, incompressible flows. It has been shown that the advanced handling of unstructured meshes reduces potential problems of common TVD schemes regarding accuracy and boundedness. Additionally, the stability of the simulations using the semi-implicit implementation was demonstrated. In perspective, a blending of upwind and downwind fluxes would be preferable for improving large eddy simulations or increase the accuracy of front propagating problems by avoiding MULES.
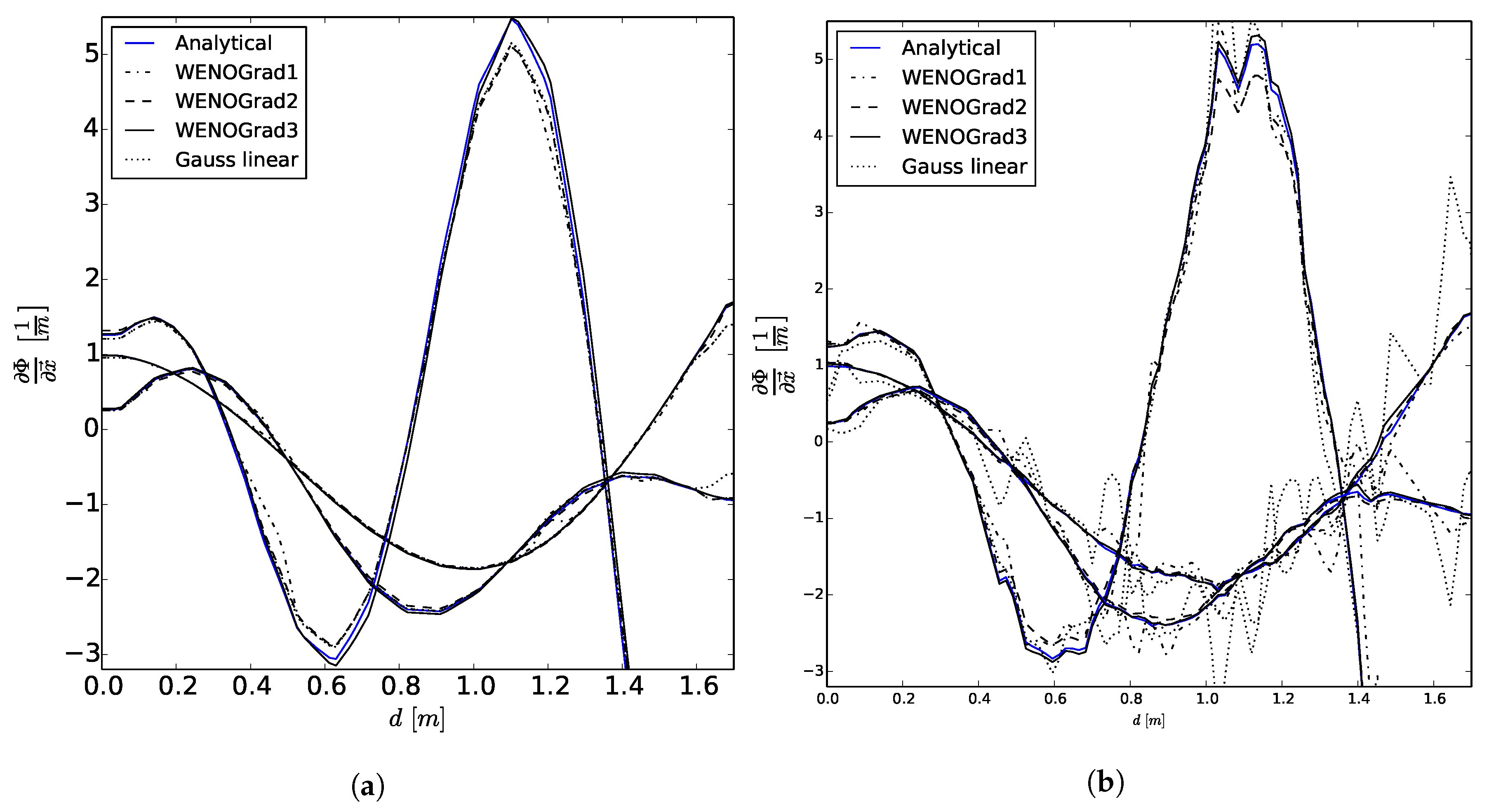
The derived gradient scheme WENOGrad represents a compromise between accuracy and efficiency, but still outperforms the standard linear gradient scheme. This class of schemes can easily be adapted to other operations in the code as the calculation of surface normal gradients (see [
27] for the derivation).
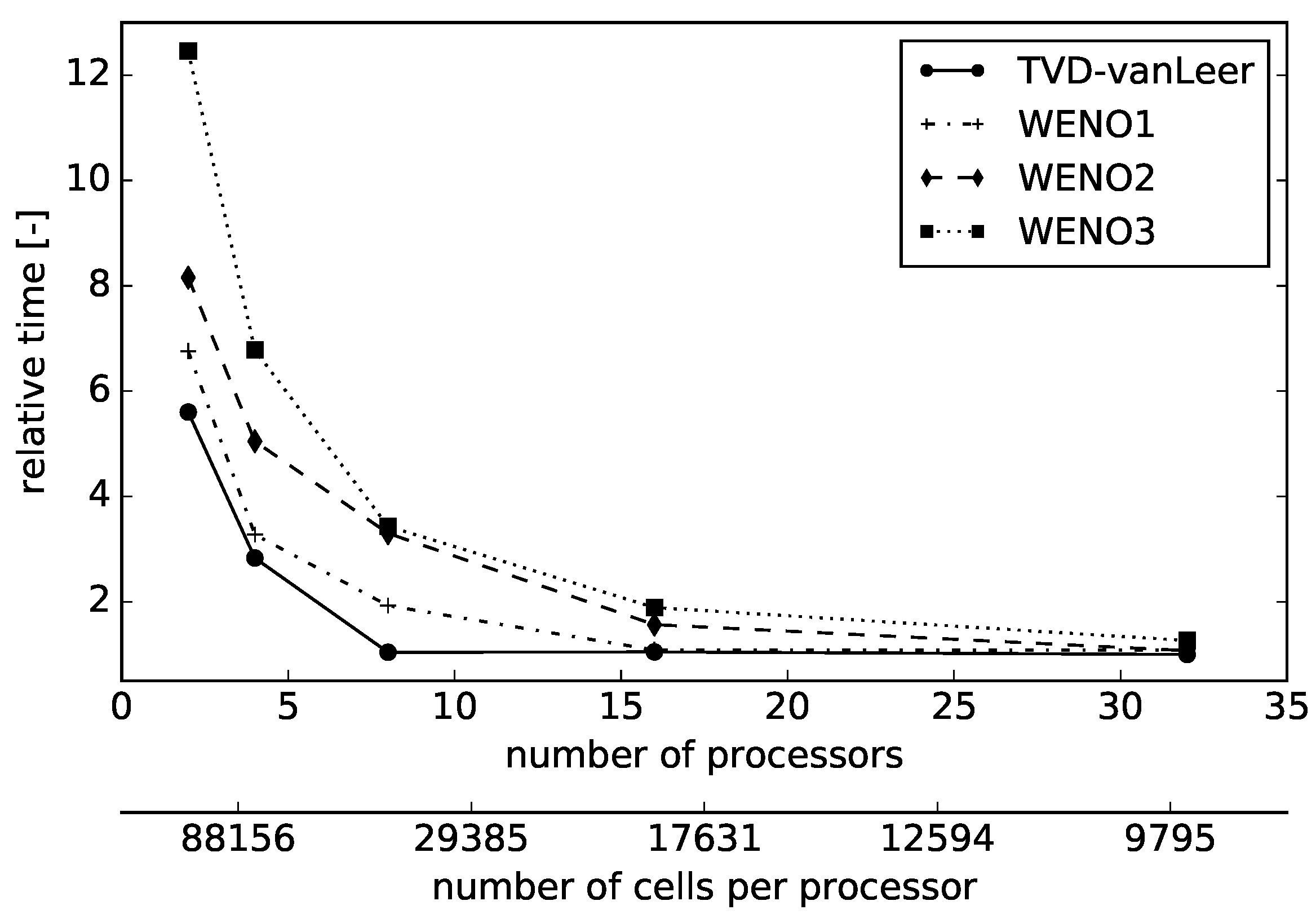
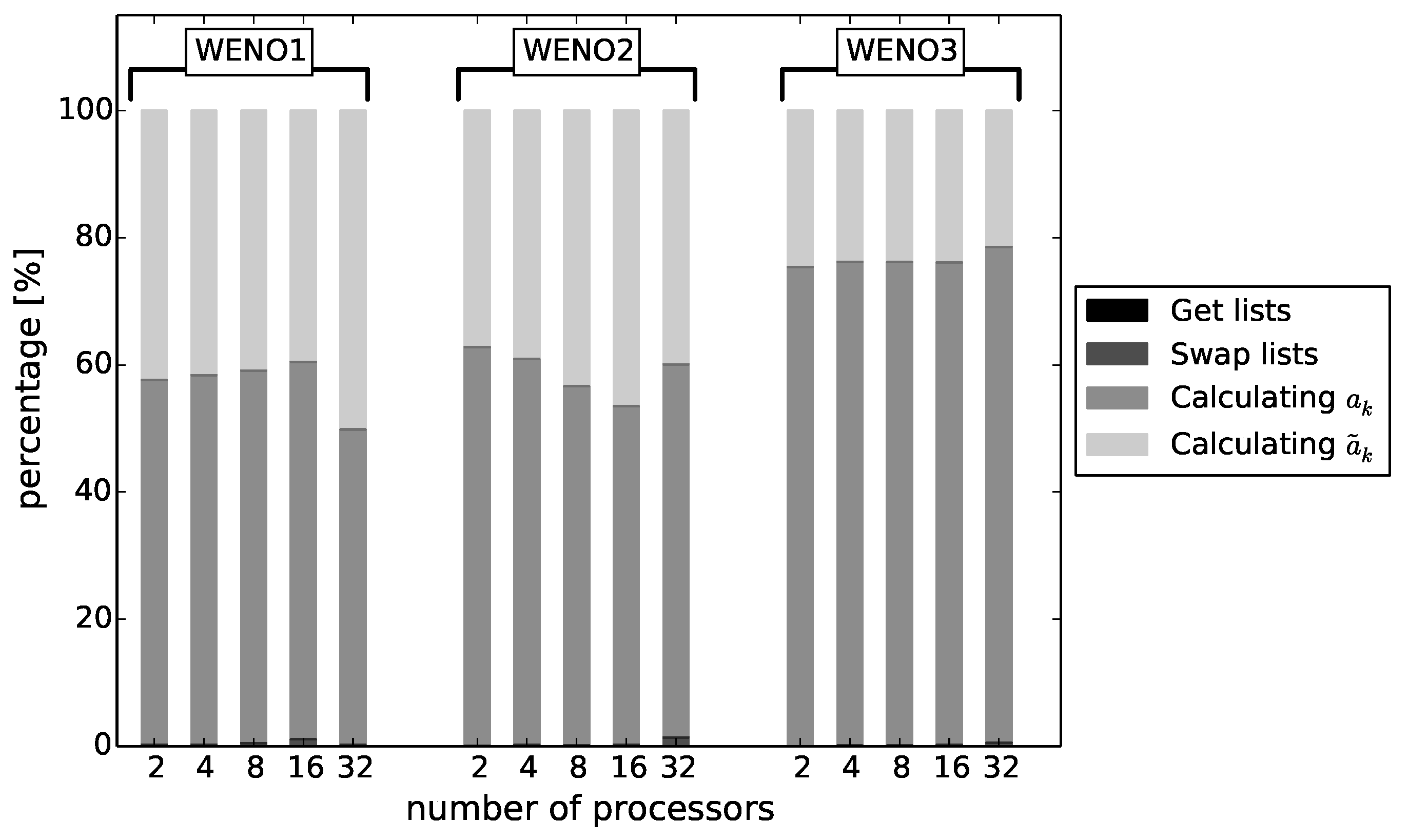
The presented efficiency analysis exposes the obvious increase at runtime during increasing the order of accuracy but also shows the possibility to reach similar computational time by increasing the number of processors. Both the preprocessing and runtime efficiency could be increased by modifying specific parameters of the reconstruction. Single test cases showed little effect of a reduced stencil expansion (compare (
26)) in a reasonable range. This leads to a smaller initial stencil and less inter-processor communications in the preprocessing. The final stencil sizes are also reasonable parameters which would especially affect the runtime performance. In addition, the order of the Gaussian integration is currently fixed but could be adapted to the chosen order of the polynomials in order so save preprocessing time. Further, several approaches should be noticed which would improve the efficiency of a high-order convection scheme. The limited least-squares scheme proposed by Michalak and Ollivier-Gooch [
46] is based on a single, central stencil and avoids weighting of the coefficients. The limiter could be implemented within the interpolation class similar to the presented one. Hence, the final degrees of freedom would be calculated faster than using WENO reconstructions. However, the proposed limiter is restricted to third-order of accuracy and results were just shown for the Euler equations in 2D. As an alternative approach, the adaptive WENO scheme of Costa and Don [
47] might be interesting. It diminishes to a low-order upwind scheme in smooth regions and applies WENO in regions of high gradients. Thereby, a fast algorithm could be developed especially for steady-state two-phase flows where the influence of surfaces is just active in a narrow band of the domain. The difficulties are the definition of a proper criterion to distinguish between the different regions and the preservation of the accuracy of the scheme. In this connection, it is though suggested to extend the indicated performance evaluation and compute weak and strong scaling tests on the basis of a suitable benchmark test before further adjustments for performance reasons are considered.