1. Introduction
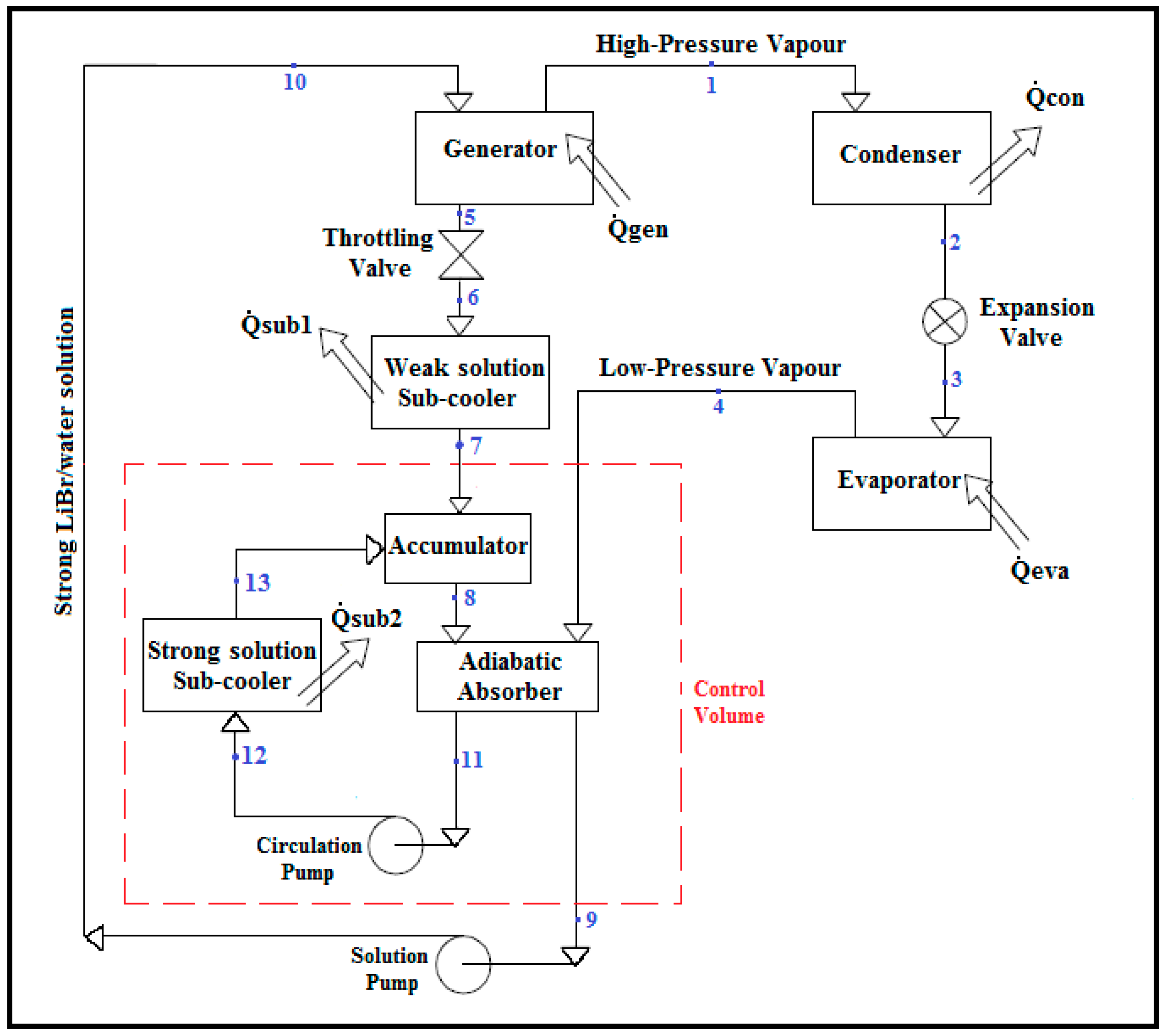
The absorption refrigeration cycle is similar to the conventional compression refrigeration cycle, having the compressor replaced by an absorber, pump, and generator. The compression refrigeration cycle is described as a work-operated cycle, since work input at the compressor is required to lift the refrigerant from the low side pressure to high side pressure. On the other hand, the lifting process of the vapor refrigerant pressure in the absorption refrigeration system is accomplished by three steps; absorbing vapor refrigerant in weak LiBr/water solution while removing heat in the absorber, elevating the pressure of the strong LiBr/water solution resulting from the absorption process and delivering it to the generator at high pressure using a pump, and driving off vapor refrigerant by applying heat in a generator. For this reason, the absorption refrigeration cycle is better known as a heat-operated cycle [
1]. In some applications, where a compact absorber is needed, solution sub-coolers are added to the cycle, in order to extract the heat of the absorption process from the LiBr/water solution, as shown in
Figure 1. The flow of the solutions are driven by solution and circulation pumps. This type of system is known as the LiBr/water absorption refrigeration system equipped with an adiabatic absorber [
2,
3].
Many published mathematical models and experimental studies of the absorption refrigeration systems show that the COP (coefficient of performance) of the absorption system is greatly influenced by the system temperatures [
4,
5,
6,
7]. The effect of the parameters, like the generator, absorber, condenser, and evaporator temperature, on the COP of the absorption refrigeration system have been experimentally studied by Eisa and Holland [
4], and the result shows that the most significant parameter affecting the COP of the cycle is the generator temperature, where an increase in generator temperature increases the COP. Another experimental study by Eisa et al. [
5] shows that an increase in the difference between the temperatures of the absorber and condenser decreases the cooling effect and COP of the absorption refrigeration system. Also, a theoretical study by Micallef and Micallef [
6] shows that the COP of the absorption refrigeration cycle increases when the generator temperature increases or the absorber temperature decreases.
According to Samanta and Basu [
7], the optimum generator temperature can be identified for each combination of condenser and evaporator temperatures and, in the case of a solar powered absorption system, the optimum generator temperature is 75 °C when the condenser and evaporator temperatures are 40 °C and 15 °C, respectively. The design and performance study of an absorption system by Sharma et al. [
8] concludes that a decrease in the exit concentration of the LiBr/water solution at the absorber, or an increase in the evaporator pressure, leads to an increase in the COP of the cycle; however, an increase in the condenser pressure decreases the COP of the cycle. A new method for COP optimization of single and double LiBr/water absorption machines by Marcos et al. [
9] shows that an increase in the difference between the LiBr mass concentrations of the strong and weak LiBr/water solutions (∆C) increases the COPs of the cycles up to certain values; above these values, the COPs are only slightly affected by any increase in ∆C, and then any further increase in ∆C leads to crystallization of the LiBr/water solution. Additionally, this study concludes that using water as the cooling medium to cool the components of the absorption system provides a better margin against crystallization problems than would be the case with air, and excludes the effect of the ambient temperature on the COP of the cycle [
9].
A falling column adiabatic LiBr/water absorption refrigeration unit, where heat and mass transfer can be separated, was experimentally investigated by Jingyuan et al. [
10]. Their results showed that the absorption rate of LiBr/water solution inside the absorber was strongly dependent on the initial solution properties, which are the temperature and LiBr mass concentration of the solution entering the adiabatic absorber. However, the absorption rate is less dependent on the mass flow rate of LiBr/water solution entering the adiabatic absorber and pressure difference between the absorber and evaporator.
Zacarías et al. [
11], investigated the dispersion method of the solution inside the adiabatic absorber using a full cone nozzle. Their results show that the absorption process inside the adiabatic absorber is not significantly affected by the height of the nozzle, but the degree of sub-cooling for LiBr/water solution entering the adiabatic absorber has potentially an effect on the absorption mass transfer.
Experimental results taken from an absorption test rig equipped with an adiabatic absorber were presented by Gutierrez-Urueta et al. [
3]. They concluded that the absorption rate and cooling capacity of the system increase when the generator temperature, recirculation ratio of the strong solution to the recirculated solution, and the mass flow rate of weak LiBr/water solution increase. They also observed that the average loss in cooling capacity due to the overflow of refrigerant from the evaporator to the solution reservoir was about 52% of total cooling capacity rate.
Fengmin et al. [
12] developed an improved analytical Newman model considering the absorption heat effect. The model was used to study the absorption characteristics of the LiBr/water solution in an adiabatic spray absorber, in which the absorption fluid is dispersed into fine droplets with diameters ranging from 100 μm to 500 μm, resulting in immense absorption surface area of LiBr/water solution exposed to the vapor refrigerant. Their results show that the absorption heat released from phase change of vapor refrigerant significantly decreased absorption mass transfer in the adiabatic spray absorber, and when the droplet radius was reduced, the absorption rate was improved and the maximum absorption time was reduced.
Experimental results on a direct air-cooled LiBr/water absorption machine were presented by González-Gil et al. [
13]. The distribution of the LiBr/water solution inside the absorber was in flat-fan sheets style, which allowed for a compact design of the absorber. Generally, the numerical model predictions were in agreement with experimental results to within 10%. It was concluded that, for an absorber equipped with 18 flat-fan sheet injectors, for a 4.5 kW single-effect system the cooling air flow rate required was 1.6 kg/s, and for a 7 kW double-effect system the cooling air flow rate required was 2.2 kg/s. According to the authors, due to heat transfer limitations, there was a higher risk of crystallization when using air-cooled absorbers compared to water-cooled absorbers.
An air-cooled adiabatic absorption refrigeration system with a falling film absorber was theoretically investigated and developed by Wang et al. [
14] to improve the performance of the conventional air-cooled absorption refrigeration systems. Low-temperature and high-temperature heat exchangers were added to the cycle in order to conserve energy and boost the COP. The exothermic heat due to the absorption process was rejected using an air-cooled heat exchanger. The results showed that both mass transfer in the adiabatic absorber and heat transfer in the air cooler could be effectively enhanced at the same time. Moreover, numerical results indicated that low solution distribution ratio in the adiabatic absorber enhanced the operation of the cycle in a vacuum state and increased the COP of the cycle, but it also increased the risk of crystallization in the high-temperature heat exchanger.
This paper presents a mathematical model of an LiBr/water absorption refrigeration system equipped with an adiabatic absorber. An efficient mathematical method of solving the mathematical model is also presented. Furthermore, the effect of key parameters, such as the generator and adiabatic absorber temperatures and the LiBr mass concentrations of the weak and strong LiBr/water solutions, on the COP of a LiBr/water absorption refrigeration system equipped with an adiabatic absorber having a cooling capacity of 1 kW, is analyzed.
2. System Description
With reference to the numbering system shown in
Figure 1, at point (1) the superheated refrigerant vapor flows to the condenser, where it is condensed. Heat (
) is rejected to an external sink in the condenser. The condensed liquid refrigerant at point (2) flows through the expansion valve to point (3), where it enters the evaporator. In the evaporator, the refrigerant is evaporated by gaining heat from the surroundings, producing a cooling effect (
). The evaporated refrigerant at point (4) is absorbed by the LiBr/water solution entering into the adiabatic absorber, producing a strong LiBr/water solution.
A small portion of the refrigerant may leave the evaporator as liquid spillover into the absorber via an overflow pipe. This portion is not included in the calculation because of its small effect on the result; thereby it is neglected. The strong LiBr/water solution produced in the adiabatic absorber flows in two separate streams; one stream is pumped from the adiabatic absorber to the generator through the solution pump (path 9–10), while another stream is pumped from the adiabatic absorber to the strong solution sub-cooler through the circulation pump (path 11–12). In the strong solution sub-cooler, the heat generated by the exothermic absorption process in the adiabatic absorber is rejected to the external sink ().
In the absorption refrigeration system, the pump work is negligible compared to heat input at the generator, and therefore it is neglected in this analysis. In the generator, heat energy () is supplied to boil the refrigerant out of the strong LiBr/water solution at the generator, thus producing a refrigerant vapor at point (1) and a weak LiBr/water solution at point (5). This weak LiBr/water solution flows back to the adiabatic absorber through the following components: a throttling valve, where the pressure of the weak LiBr/water solution at point (5) is reduced to the adiabatic absorber pressure at point (6), followed by the weak solution sub-cooler, where the temperature of the weak LiBr/water solution at point (6) is dropped to the adiabatic absorber temperature () at point (7) while rejecting heat () to the external sink, and then the accumulator, where the weak LiBr/water solution at point (7) is mixed adiabatically with the strong LiBr/water solution at point (13), producing a mixture of LiBr/water solutions at point (8). This mixture is the sorbent LiBr/water solution entering the adiabatic absorber at a temperature below the adiabatic absorber temperature and with a LiBr mass concentration higher than the strong LiBr/water solution at point (11) and lower than the weak LiBr/water solution at point (7), depending on the circulation flow rate.
The input thermal energy in the generator is equal to both the energy required for the refrigerant to change from a liquid phase to a vapor phase, and the energy required to break the intermolecular bonds formed between the refrigerant and the strong solution. Therefore, the total thermal energy input in the generator, which is required to separate the refrigerant from the solution, is around 15% more than the thermal energy required to boil the refrigerant alone, and this additional energy is known as the heat of mixing [
15]. As a result, the refrigerant vapor produced in the generator is in a superheated vapor state rather than in a saturated vapor state.
To establish the design parameters and to simplify the modeling of an LiBr/water absorption refrigeration system equipped with an adiabatic absorber, the following assumptions were made:
The refrigerant at the exit of the evaporator is saturated vapor (no liquid spillover).
The solutions which leave the adiabatic absorber and the generator are saturated liquid at the units’ temperatures.
The adiabatic absorber pressure is equal to the evaporator pressure and the generator pressure is equal to the condenser pressure.
The solution entering the generator is at the generator pressure.
The throttling and pumping processes are adiabatic.
The solution and circulation pumps’ work are negligible.
The solution leaving the weak solution sub-cooler is at the adiabatic absorber temperature.
The adiabatic absorber and the accumulator are insulated well.
The mathematical model of the absorption refrigeration system is based on the equilibrium of the pressure between the LiBr/water solution in the absorber and the refrigerant in the evaporator, and the equilibrium of the pressure between the LiBr/water solution in the generator and the refrigerant in the condenser [
1]. This is reflected in assumption 3. Additionally, it is assumed that the inlet and outlet temperatures of the LiBr/water solutions crossing the control volume are equal at points (7) & (9), as a result of which, only the amount of heat generated by the exothermic absorption process in the adiabatic absorber is rejected at the strong solution sub-cooler, and this is reflected in assumption 7.
In reality, there are slight differences in pressures between the absorber and the evaporator and also between the generator and the condenser. The solution vapor pressure in the generator is slightly higher than the refrigerant vapor pressure in the condenser. This pressure difference is the driving force of refrigerant flow from the generator to the condenser. Also, the refrigerant vapor pressure in the evaporator is slightly higher than the solution vapor pressure in the absorber; thereby, the absorption process takes place [
16].
The LiBr/water absorption refrigeration system equipped with an adiabatic absorber was analyzed based on the following specification:
A cooling capacity () at the evaporator of 1 kW.
The temperature of the condenser () was set to 35 °C, which is a suitable temperature for the external sink to the condenser.
The evaporator temperature () was set to 10 °C, which is a suitable temperature when using water as refrigerant.
The range of temperatures of the generator () considered was 65–90 °C.
The range of temperatures of the absorber () considered was 25–50 °C.
The ratio (X) of the solution mass flow rate at the circulation pump to that at the solution pump was set to 25.
The LiBr mass concentration and specific enthalpy of the LiBr/water solutions were estimated using correlations available from the ASHRAE Handbook [
17]. Most of the absorption systems use solutions with a concentration of less than 65% by mass of lithium-bromide in solution, to avoid crystallization problems [
18]. Consequently, the concentration of the weak LiBr/water solutions was kept below 65% in this thermodynamic analyses. The specific enthalpy of water and vapor refrigerant was determined using a steam liberary for water and steam properties according to IAPWS IF-97 [
19].
3. Mathematical Model
The following equations mathematically describe the LiBr/water absorption refrigeration system equipped with an adiabatic absorber:
Throttling process between stations 2 & 3 and between stations 5 & 6; applying the steady state energy equation across the throttling and expansion valves:
Pumping process between stations 9 & 10 and between stations 11 & 12; applying the steady state energy equation across the solution and circulation pumps (neglecting pumps’ work):
Refrigerant circuit between stations 1, 2, 3, & 4; applying the mass conservation equation:
Evaporation process between stations 3 & 4; applying the steady state energy equation across the evaporator:
Condensation process between stations 1 & 2; applying the steady state energy equation across the condenser:
Lithium-bromide mass balance between stations 5, 6, & 7 yields:
Lithium-bromide mass balance between stations 9 & 10 yields:
Lithium-bromide mass balance between stations 11, 12, & 13 yields:
where
is the specific enthalpy (kJ/kg),
is the mass flow rate (kg/s),
is the cooling capacity at the evaporator (kW),
is the heat reject at the condenser (kW), and
is the LiBr mass concentration of LiBr/water solution (%).
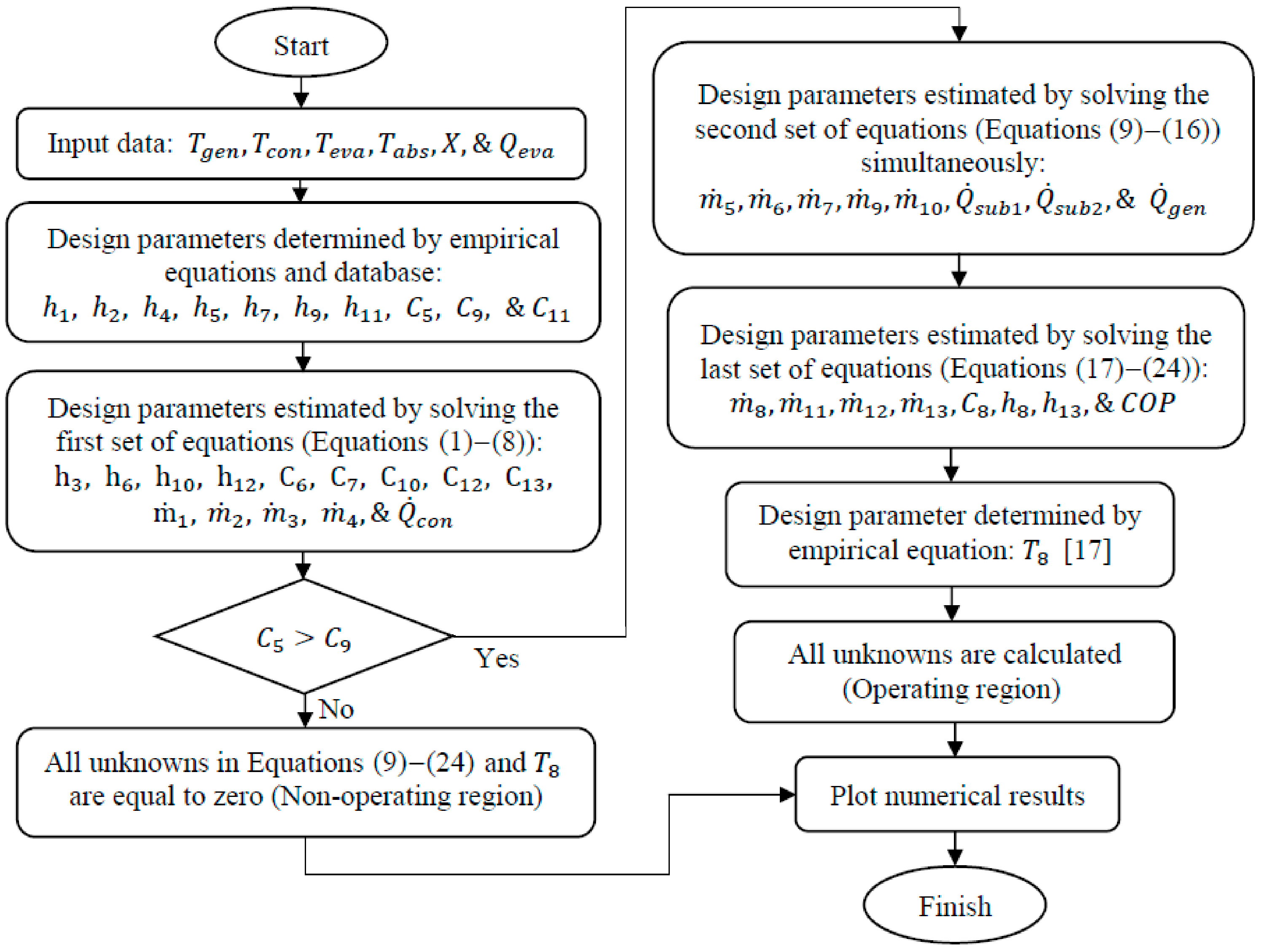
In order to perform the thermodynamic analysis of the LiBr/water absorption refrigeration system equipped with an adiabatic absorber, three groups of equations need to be solved (Equations (1)–(8), Equations (9)–(16), & Equations (17)–(24)). The first group of eight equations (Equations (1)–(8)) relate to the refrigeration section (branches 1, 2, 3, & 4), lithium-bromide mass balance, and the energy balance at the throttling and expansion valves and at the solution and circulation pumps. The unknowns in Equations (1)–(8) may be evaluated directly from system and fluids properties. The next set of eight equations (Equations (9)–(16)) relate to the mass and energy balances at the generator, the mass balance at the throttling valve and solution pump, the energy balance at the weak solution sub-cooler, and the mass and energy balances across the control volume. These equations need to be solved simultaneously in order to evaluate the eight unknown variables.
Applying the mass and LiBr mass conservation equations and the steady state energy equation across the generator:
Applying the mass conservation equation across the throttling valve:
Applying the mass conservation equation across the solution pump:
Applying the steady state energy equation across the weak solution sub-cooler:
Applying the mass conservation equation and the steady state energy equation across the control volume shown in
Figure 1:
where
is the heat input at the generator,
is the heat reject at the weak solution sub-cooler, and
is the heat reject at the strong solution sub-cooler.
The last set of equations (Equations (17)–(24)) refers to the circulation pump mass balance, strong solution sub-cooler mass and energy balances, accumulator mass, LiBr mass, and energy balances, and calculating of the COP. The unknown variables in Equations (17)–(24) may be evaluated directly.
From the ratio (X) of the solution mass flow rate at the circulation pump to that at the solution pump:
Applying the mass conservation equation across the circulation pump:
Applying the mass conservation equation and the steady state energy equation across the strong solution sub-cooler:
Applying the mass and LiBr mass conservation equations and the steady state energy equation across the accumulator:
The coefficient of performance (COP) of a LiBr/water absorption refrigeration cycle is defined as:
5. Numerical Results
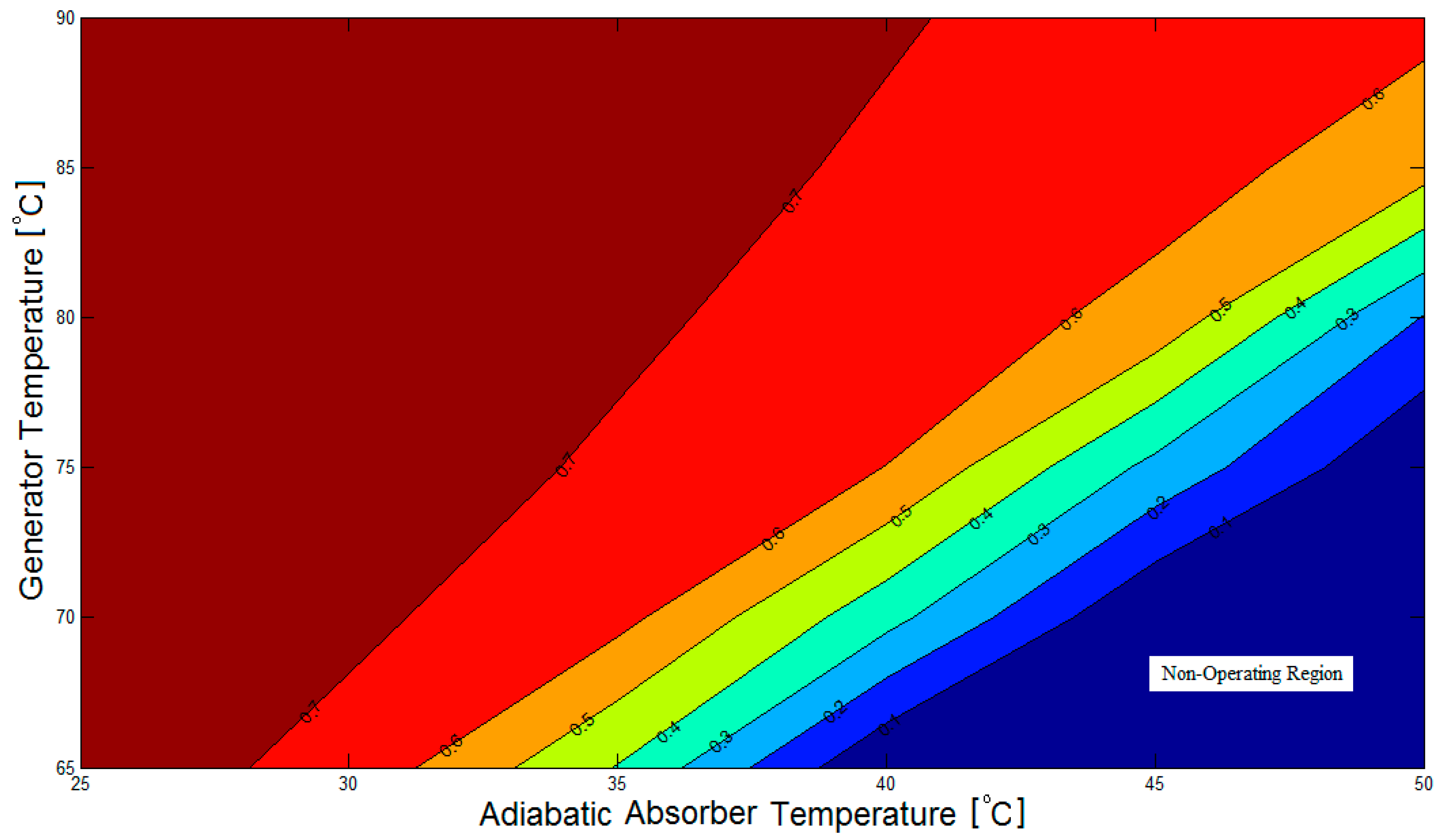
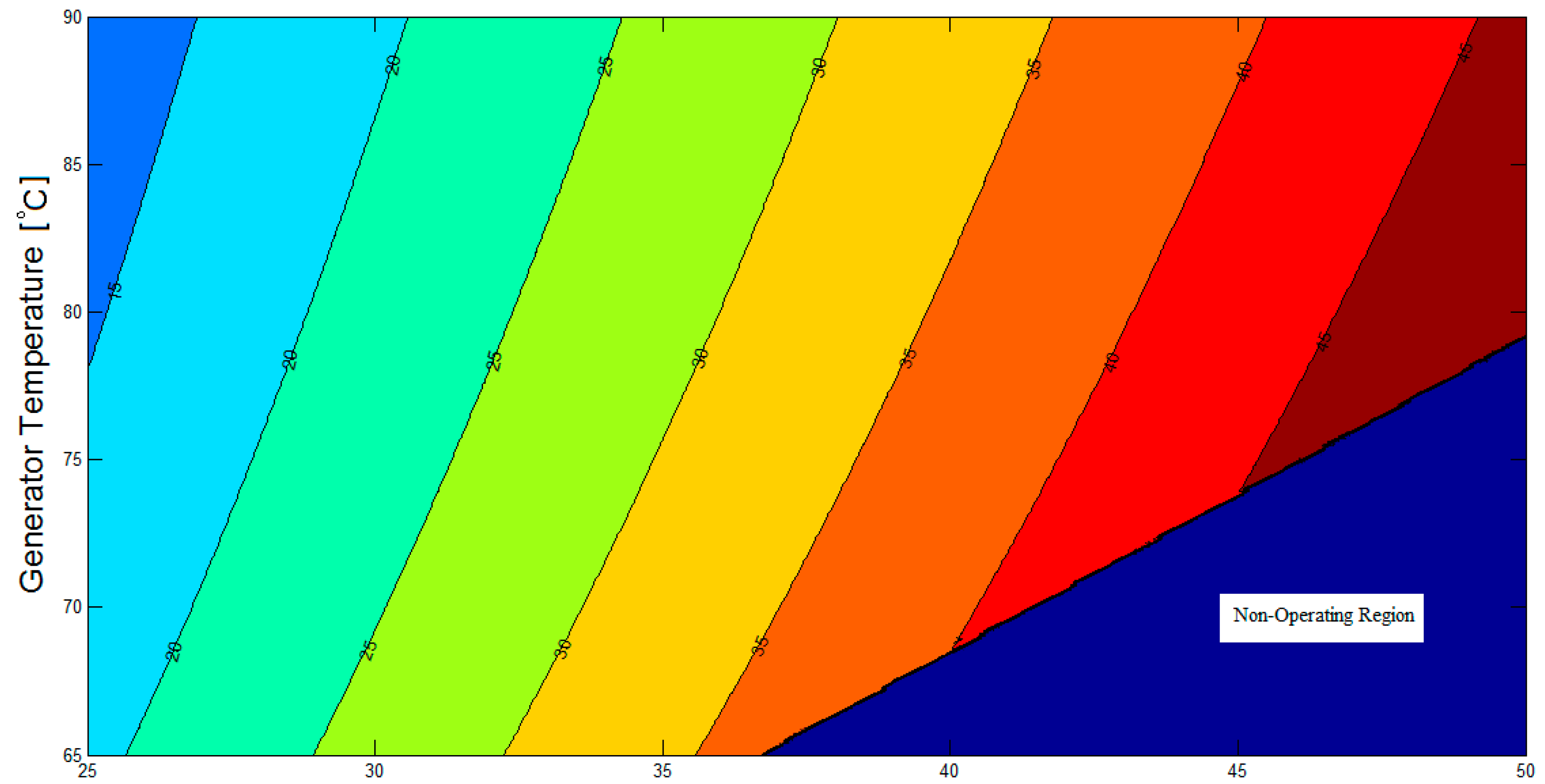
Figure 3 illustrates the contour plot of the coefficient of performance of the LiBr/water absorption refrigeration system equipped with an adiabatic absorber against generator temperature (
) and adiabatic absorber temperature (
) when the condenser temperature (
) and evaporator temperature (
) are fixed at 35 °C and 10 °C, respectively.
In
Figure 3, there are both operating and non-operating regions. The values of the COP ranges between 0.1 up to 0.77 for the operating region. However, by default, the COP value is zero for the non-operational region. In order for the absorption refrigeration system to operate successfully, the LiBr mass concentration of the solution flowing from the generator to the adiabatic absorber must be larger than that of the solution flowing from the adiabatic absorber to the generator. When this is not the case, the system is said to be non-operational.
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
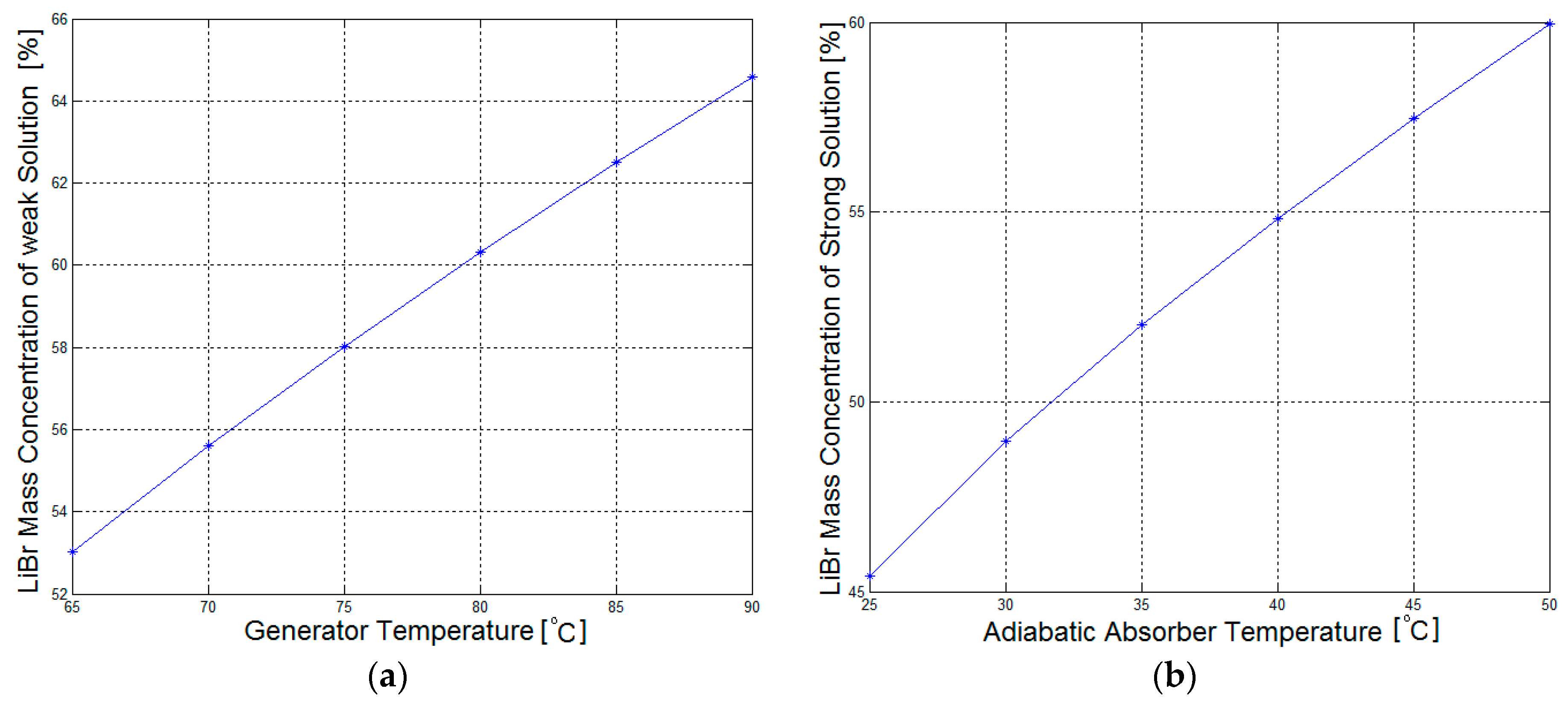
Figure 10 show other numerical results from this mathematical model. As shown in
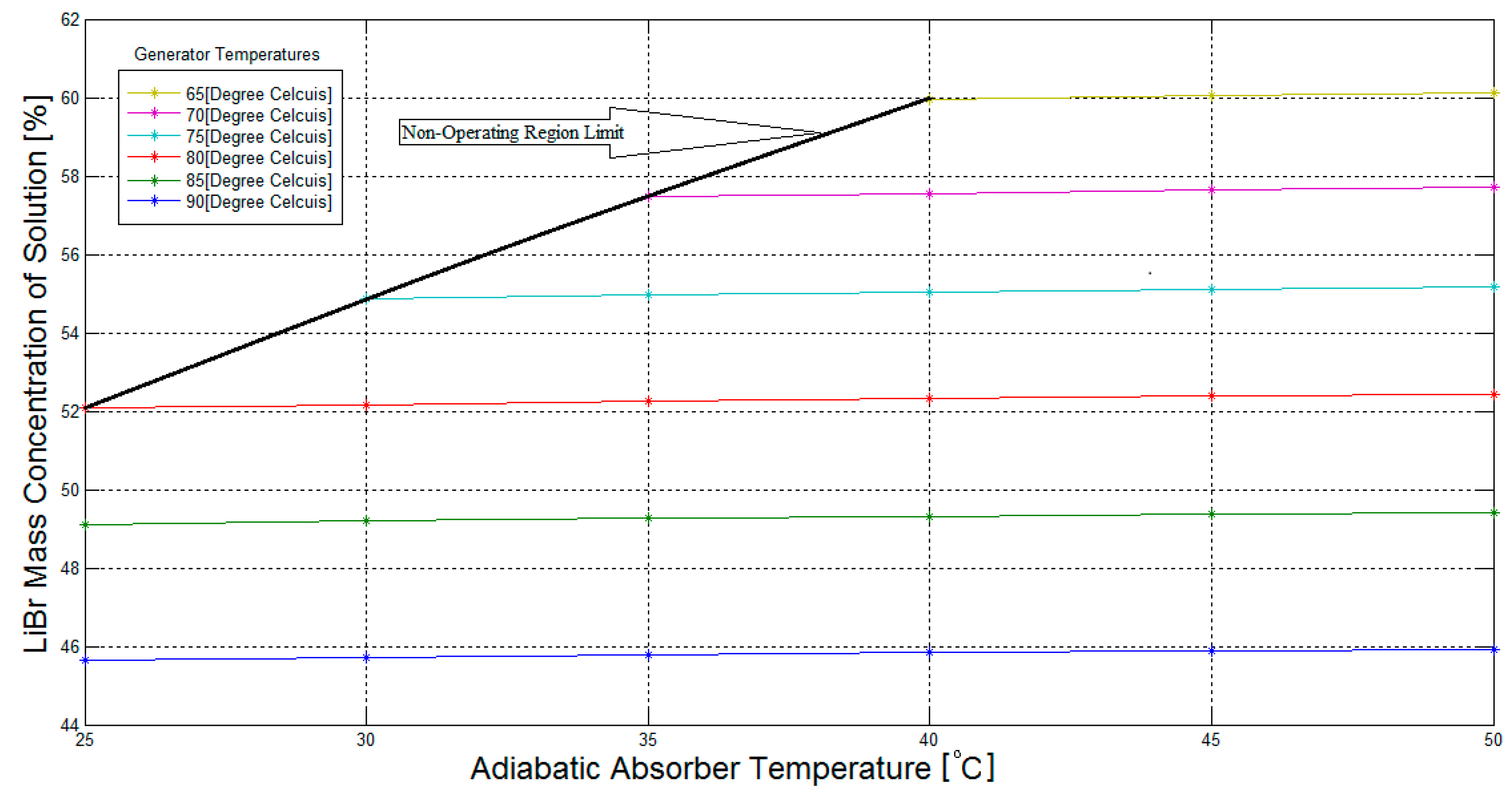
Figure 4a, the LiBr mass concentration of the weak solution in the generator increases with increasing generator temperatures, and is independent of the adiabatic absorber temperature.
A similar trend can be seen in
Figure 4b, where the LiBr mass concentration of the strong solution increases with increasing adiabatic absorber temperature, and is independent of the generator temperature. The relations between the LiBr mass concentration of the solutions and the associated temperatures of the components are almost linear.
However,
Figure 5 shows that the LiBr mass concentration of the solution entering the adiabatic absorber (point (8)
Figure 1) is more sensitive to the generator temperature than to the adiabatic absorber temperature. Also,
Figure 4a shows that the LiBr mass concentration of the weak solution is approximately 65% when the generator temperature is 90 °C. As previously stated, the absorption refrigeration system should limit the maximum LiBr mass concentration of the solution to 65% in order to avoid crystallization problems [
18]. Consequently, the maximum generator temperature must be slightly below 90 °C for an absorption refrigeration system with a cooling capacity of 1 kW, and this temperature may be set at 80 °C to give a better margin of safety against crystallization.
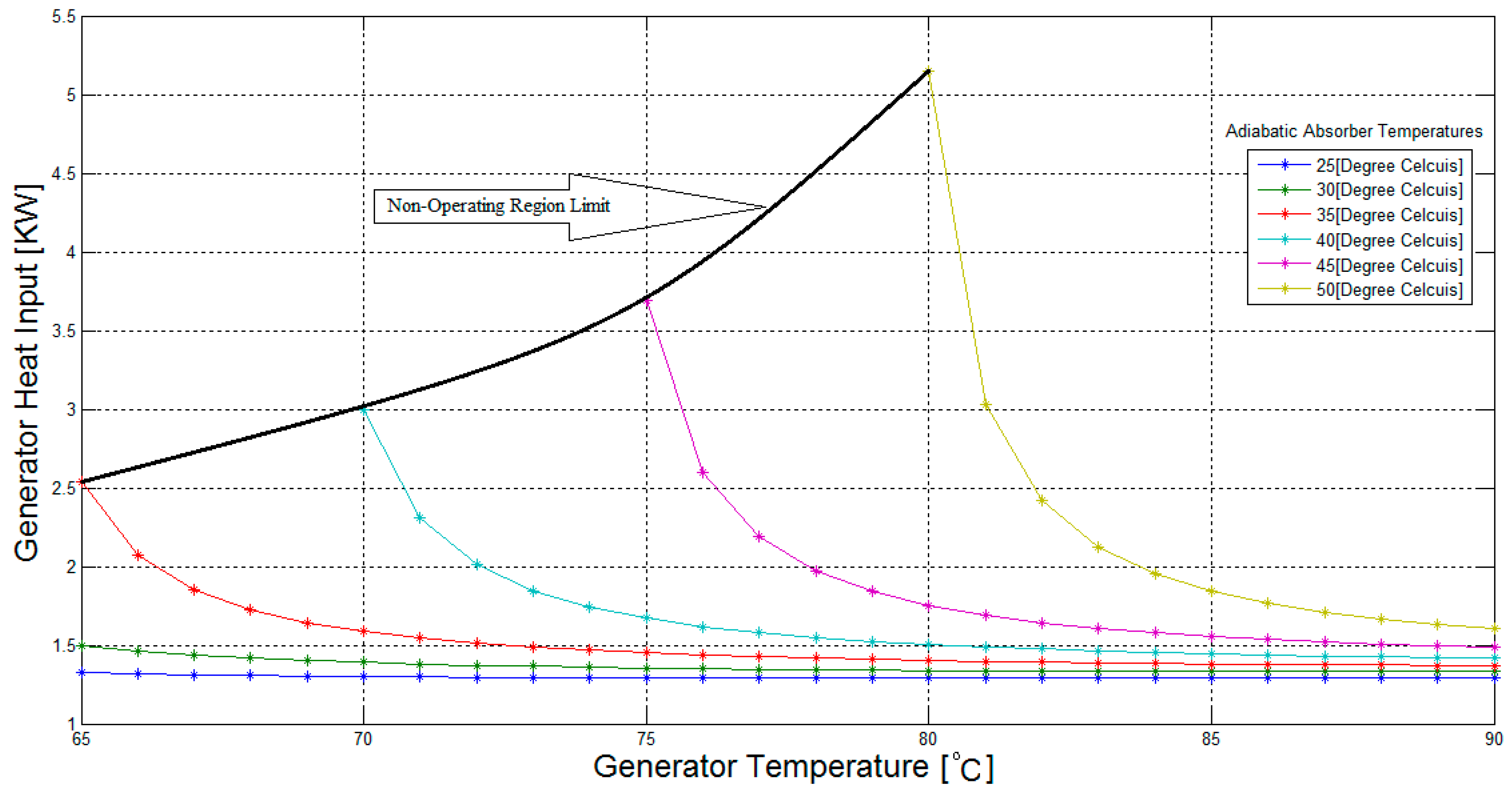
Figure 6 shows a rapid increase in the generator heat input for the adiabatic absorber temperatures of 35 °C, 40 °C, 45 °C, and 50 °C, when the generator temperatures are below 70 °C, 75 °C, 80 °C, and 85 °C, respectively. Also,
Figure 7 shows a similar rapid increase in the case of the weak solution sub-cooler heat rejection, for generator temperatures of 65 °C, 70 °C, 75 °C, and 80 °C, when the adiabatic absorber temperatures are above 30 °C, 35 °C, 40 °C, and 45 °C, respectively. These areas are synonymous with reduced COP values, as shown in
Figure 3, and thus should be avoided.
The variation of the strong solution sub-cooler heat rejection with generator temperature and adiabatic absorber temperature is shown in
Figure 8, while
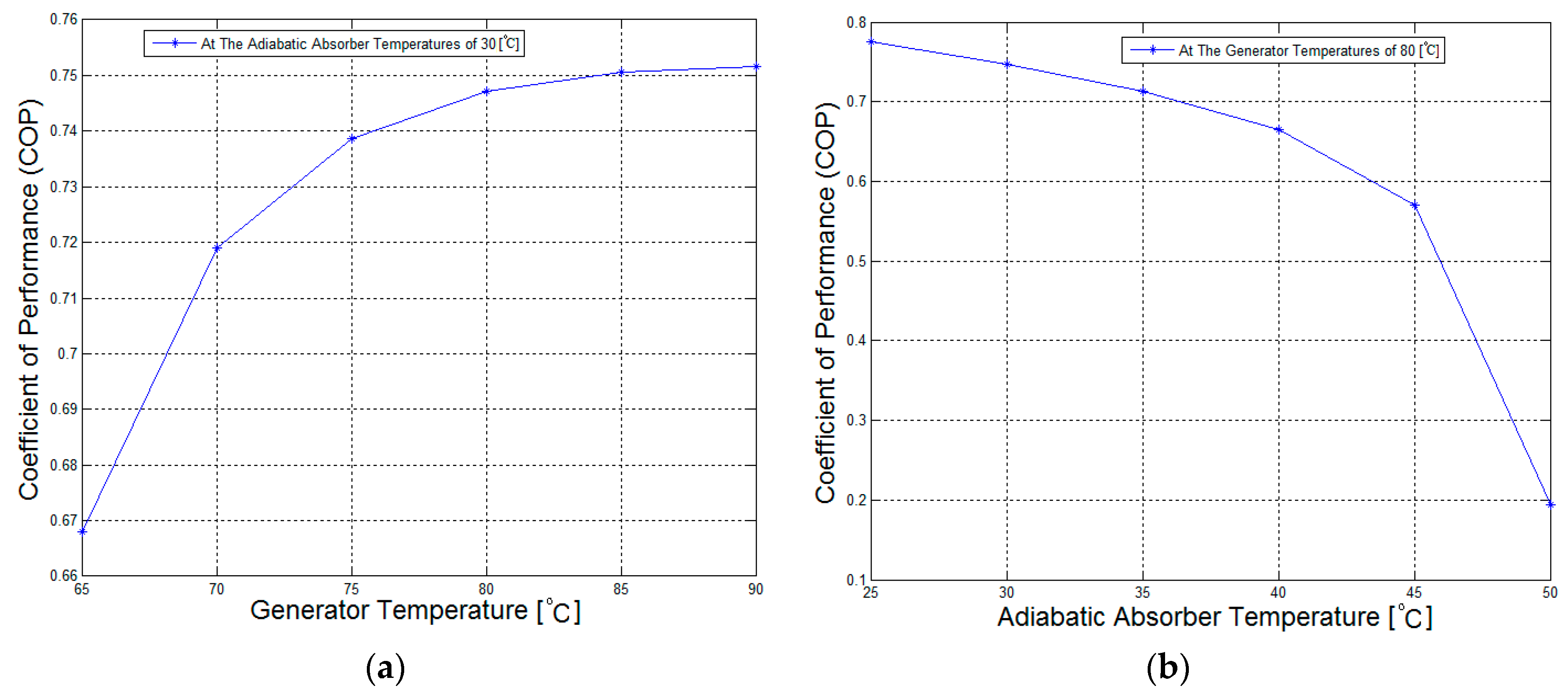
Figure 9 shows the influence of the generator temperature and adiabatic absorber temperature on the COP of the LiBr/water absorption refrigeration system equipped with an adiabatic absorber. It can be observed that, as the generator temperature increases, the system COP value increases. From a generator temperature of 65 °C–90 °C, the COP increases rapidly. In contrast, the system COP value increases as the adiabatic absorber temperature decreases.
Figure 10 illustrates the contour plot of the temperature of the LiBr/water solution entering the adiabatic absorber against the generator and adiabatic absorber temperatures. As can be seen in
Figure 10, the temperature of the LiBr/water solution entering the adiabatic absorber is more sensitive to the adiabatic absorber temperature than to the generator temperature.
As a result of this thermodynamic analysis, the temperature of the adiabatic absorber may be set at 40 °C when the generator temperature is above 75 °C, for a good margin of safety against the non-operating region, as shown in
Figure 3 and
Figure 10. Consequently, the temperature of LiBr/water solution leaving the strong solution sub-cooler is 35 °C, which can be reached easily using the same external cooling fluid that is used in the condenser. It can be noted that if, in order to optimize further the COP of the system, a lower adiabatic absorber temperature is chosen, a negligible useful refrigerating effect will result, since the cooling fluid required would be close to the evaporator temperature.
Table 1 and
Table 2 show the summary of the thermodynamic analysis of the system for the optimal temperatures of the design components. The chosen temperatures of the generator, condenser, adiabatic absorber, and evaporator were 80 °C, 35 °C, 40 °C, and 10 °C, respectively. This summary can be used to size the heat exchangers of a new LiBr/water absorption refrigeration system equipped with an adiabatic absorber. With reference to the numbering system shown in
Figure 1, the specific enthalpy, temperature, pressure, mass flow rate, LiBr mass concentration, and fluid state have been determined and indicated for each point in the system, as shown in
Table 1.
Also,
Table 2 shows the heat transfer in each component in the LiBr/water absorption refrigeration system equipped with an adiabatic absorber, and the COP of the system. As indicated in
Table 2, the COP of the absorption refrigeration cycle is apparently lower than that of the vapor-compression refrigeration cycle. However, the comparison of the two COPs should not be to the detrimental judgement of the absorption refrigeration cycle, because the two COPs are defined in different ways. The COP of the vapor-compression refrigeration cycle is defined as a ratio of the refrigeration rate to the mechanical work supplied to the compressor. In contrast, the COP of the absorption refrigeration system is defined as a combination of power cycle and refrigeration cycle [
1].
6. Conclusions
A mathematical model for an LiBr/water absorption refrigeration system equipped with an adiabatic absorber has been presented. It has been shown that the generator temperature is an important factor in designing the absorption refrigeration system, taking into consideration the crystallization problem of the LiBr/water solution. The COP, the LiBr mass concentration of the solutions, and heat transfer in each component in the system were analyzed for specific input design parameters. The results show that an increase in generator temperature or decrease in the adiabatic absorber temperature increases the COP. Additionally, this analysis made it possible to determine the recommended generator and adiabatic absorber temperatures, which were 80 °C and 40 °C respectively, of such an absorption refrigeration system.
Due to the fact that the LiBr/water absorption refrigeration system equipped with an adiabatic absorber is influenced by many key parameters, and that it is difficult to investigate each one individually, the condenser temperature, evaporator temperature, cooling capacity, and ratio of the solution mass flow rate at the circulation pump to that at the solution pump, were kept constant at suitable values throughout this analysis. In future, this model can be used in combination with experimental data for validation purposes of the LiBr/water absorption refrigeration system equipped with an adiabatic absorber. Since the system shows a high value of COP at a low generator temperature of 80 °C, which can be reached using a solar collector, this makes it a promising application in the field of solar-powered absorption refrigeration systems. Furthermore, to improve the efficiency of the LiBr/water absorption refrigeration cycle equipped with an adiabatic absorber, the weak solution sub-cooler can be replaced by a solution heat exchanger between the adiabatic absorber and the generator without changing the operation process. This heat exchanger recuperates heat from the weak LiBr/water solution and delivers it to the strong LiBr/water solution before entering the generator.