Ab Initio Research on a New Type of Half-Metallic Double Perovskites, A2CrMO6 (A = IVA Group Elements; M = Mo, Re and W)
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussions
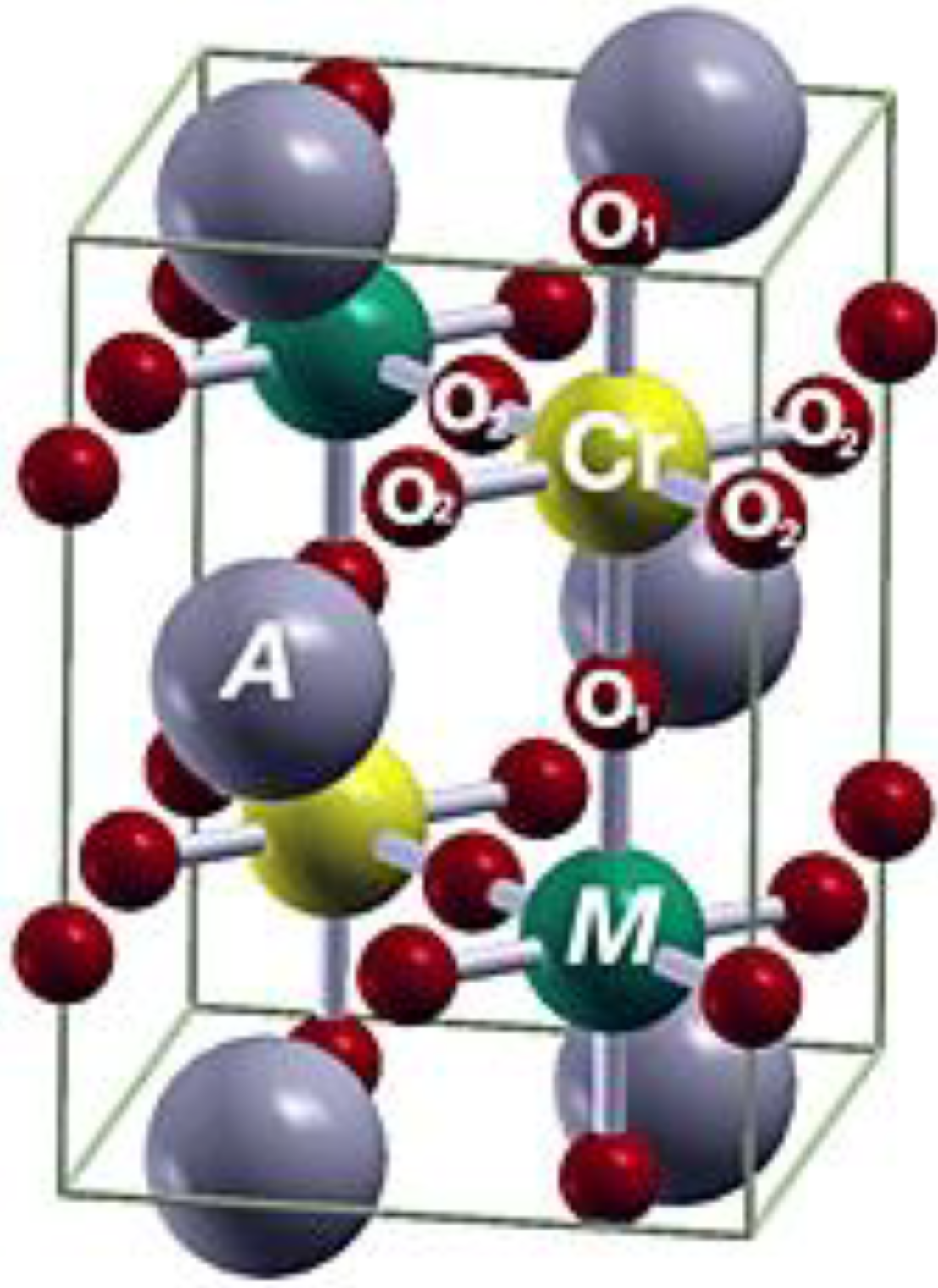
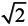 , shows that the symmetry reduction is minor. Although some compounds remained in the ideal cubic structure (Fm3m, no. 255) during full structural optimization, the O1 and O2 are equivalent to the c/a ratio,
, shows that the symmetry reduction is minor. Although some compounds remained in the ideal cubic structure (Fm3m, no. 255) during full structural optimization, the O1 and O2 are equivalent to the c/a ratio, 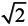 . In the AF state, the tetragonal structure (P4/mmm, no. 123) remains the same in the full structural optimization.
. In the AF state, the tetragonal structure (P4/mmm, no. 123) remains the same in the full structural optimization. | Materials | U (Cr, M) | Spin magnetic moment (μB/f.u.) | d Orbital electrons ↑/↓ | N (EF) | Band gap | Spin-polarization | ΔE = FM − AF | |||
|---|---|---|---|---|---|---|---|---|---|---|
| A2Cr[M]O6 | MCr | MM | mtot | Cr | M | states/eV/f.u. | eV | N((↑ − ↓)/(↑ + ↓)) (%) | meV/f.u. | |
| Si[Mo] | (0, 0) | 2.297 | −0.407 | 2.004 | 3.333/1.069 | 1.934/2.320 | ↑0.152/↓2.739 | −89.5 | −27.9 | |
| (3, 2) | 2.618 | −0.701 | 2.000 | 3.479/0.898 | 1.764/2.442 | ↓3.620 | ↑0.925 | −100.0 | −197.9 | |
| Ge[Mo] | (0, 0) | 2.318 | −0.439 | 2.000 | 3.336/1.051 | 1.914/2.332 | ↓3.108 | ↑0.150 | −100.0 | −63.1 |
| (3, 2) | 2.267 | −0.729 | 2.000 | 3.474/0.885 | 1.746/2.451 | ↓3.592 | ↑1.100 | −100.0 | −109.3 | |
| Sn[Mo] | (0, 0) | 2.370 | −0.503 | 2.000 | 3.328/0.992 | 1.864/2.344 | ↓2.759 | ↑0.675 | −100.0 | −117.3 |
| (3, 2) | 2.656 | −0.806 | 2.000 | 3.447/0.829 | 1.690/2.471 | ↓3.143 | ↑1.675 | −100.0 | −118.1 | |
| Pb[Mo] | (0, 0) | 2.381 | −0.513 | 2.000 | 3.324/0.977 | 1.850/2.340 | ↓2.767 | ↑0.700 | −100.0 | −123.7 |
| (3, 2) | 2.659 | −0.806 | 2.000 | 3.439/0.818 | 1.680/2.461 | ↓3.160 | ↑1.825 | −100.0 | −120.8 | |
| Si[Re] | (0, 0) | 2.294 | −0.958 | 1.095 | 3.319/1.059 | 1.659/2.593 | ↑0.541/↓2.357 | −62.7 | −158.1 | |
| (3, 2) | 2.624 | −1.364 | 1.000 | 3.463/0.877 | 1.446/2.783 | ↓2.243 | ↑1.125 | −100.0 | −176.3 | |
| Ge[Re] | (0, 0) | 2.314 | −1.030 | 1.042 | 3.323/1.043 | 1.623/2.628 | ↑0.338/↓4.108 | −84.8 | −253.9 | |
| (3, 2) | 2.631 | −1.399 | 1.000 | 3.458/0.865 | 1.427/2.798 | ↓2.303 | ↑1.300 | −100.0 | −292.9 | |
| Sn[Re] | (0, 0) | 2.360 | −1.125 | 1.000 | 3.317/0.992 | 1.568/2.666 | ↓2.772 | ↑0.800 | −100.0 | −301.9 |
| (3, 2) | 2.652 | −1.469 | 1.000 | 3.433/0.819 | 1.384/2.824 | ↓2.842 | ↑1.850 | −100.0 | −276.3 | |
| Pb[Re] | (0, 0) | 2.372 | −1.143 | 1.000 | 3.314/0.977 | 1.553/2.669 | ↓2.865 | ↑0.875 | −100.0 | −308.7 |
| (3, 2) | 2.656 | −1.473 | 1.000 | 3.426/0.808 | 1.376/2.282 | ↓2.875 | ↑1.825 | −100.0 | −273.9 | |
| Si[W] | (0, 0) | 2.377 | −0.268 | 2.617 | 3.359/1.015 | 1.951/2.199 | ↑0.545/↓2.226 | −60.7 | −28.9 | |
| (3, 2) | 2.640 | −0.429 | 2.165 | 3.464/0.861 | 1.826/2.235 | ↑0.550/↓2.300 | −61.4 | −53.6 | ||
| Ge[W] | (0, 0) | 2.374 | −0.311 | 2.131 | 3.355/1.014 | 1.925/2.215 | ↑0.473/↓2.273 | −65.5 | −70.6 | |
| (3, 2) | 2.635 | −0.496 | 2.119 | 3.458/0.859 | 1.790/2.625 | ↑0.438/↓2.449 | −69.7 | −85.6 | ||
| Sn[W] | (0, 0) | 2.349 | −0.454 | 2.000 | 3.320/1.004 | 1.842/2.273 | ↓3.149 | ↑0.825 | −100.0 | −166.2 |
| (3, 2) | 2.623 | −0.703 | 2.000 | 3.422/0.834 | 1.683/2.360 | ↓3.177 | ↑1.900 | −100.0 | −143.2 | |
| Pb[W] | (0, 0) | 2.352 | −0.464 | 2.000 | 3.313/0.993 | 1.831/2.271 | ↓2.890 | ↑1.025 | −100.0 | −180.2 |
| (3, 2) | 2.622 | −0.716 | 2.000 | 3.411/0.825 | 1.671/2.360 | ↓3.099 | ↑2.725 | −100.0 | −151.9 | |
| A2Cr[M]O6 | a | c/a | V0 (Å3/f.u.) | O1z | O2x | O2y |
|---|---|---|---|---|---|---|
| Si[Mo] | 5.4616 | 1.4138 | 115.17 | 0.24755 | 0.25238 | 0.25238 |
| Ge[Mo] | 5.4816 | 1.4135 | 116.41 | 0.24779 | 0.25210 | 0.25210 |
| Sn[Mo] * | 5.5653 | 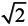 | 121.89 | 0.24896 | 0.24896 | 0.24896 |
| Pb[Mo] | 5.5879 | 1.4146 | 123.41 | 0.24923 | 0.25077 | 0.25077 |
| Si[Re] | 5.4561 | 1.4134 | 114.78 | 0.24926 | 0.25075 | 0.25075 |
| Ge[Re] | 5.4768 | 1.4136 | 116.11 | 0.24931 | 0.25071 | 0.25071 |
| Sn[Re] | 5.5614 | 1.3920 | 119.72 | 0.24974 | 0.25025 | 0.25025 |
| Pb[Re] * | 5.5837 | 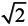 | 123.10 | 0.25000 | 0.25000 | 0.25000 |
| Si[W] | 5.4719 | 1.4137 | 115.80 | 0.24951 | 0.25047 | 0.25047 |
| Ge[W] | 5.4892 | 1.4147 | 116.99 | 0.24966 | 0.25038 | 0.25038 |
| Sn[W] * | 5.5721 | 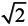 | 122.33 | 0.25059 | 0.25059 | 0.25059 |
| Pb[W] | 5.5952 | 1.4147 | 123.90 | 0.25109 | 0.24884 | 0.24884 |
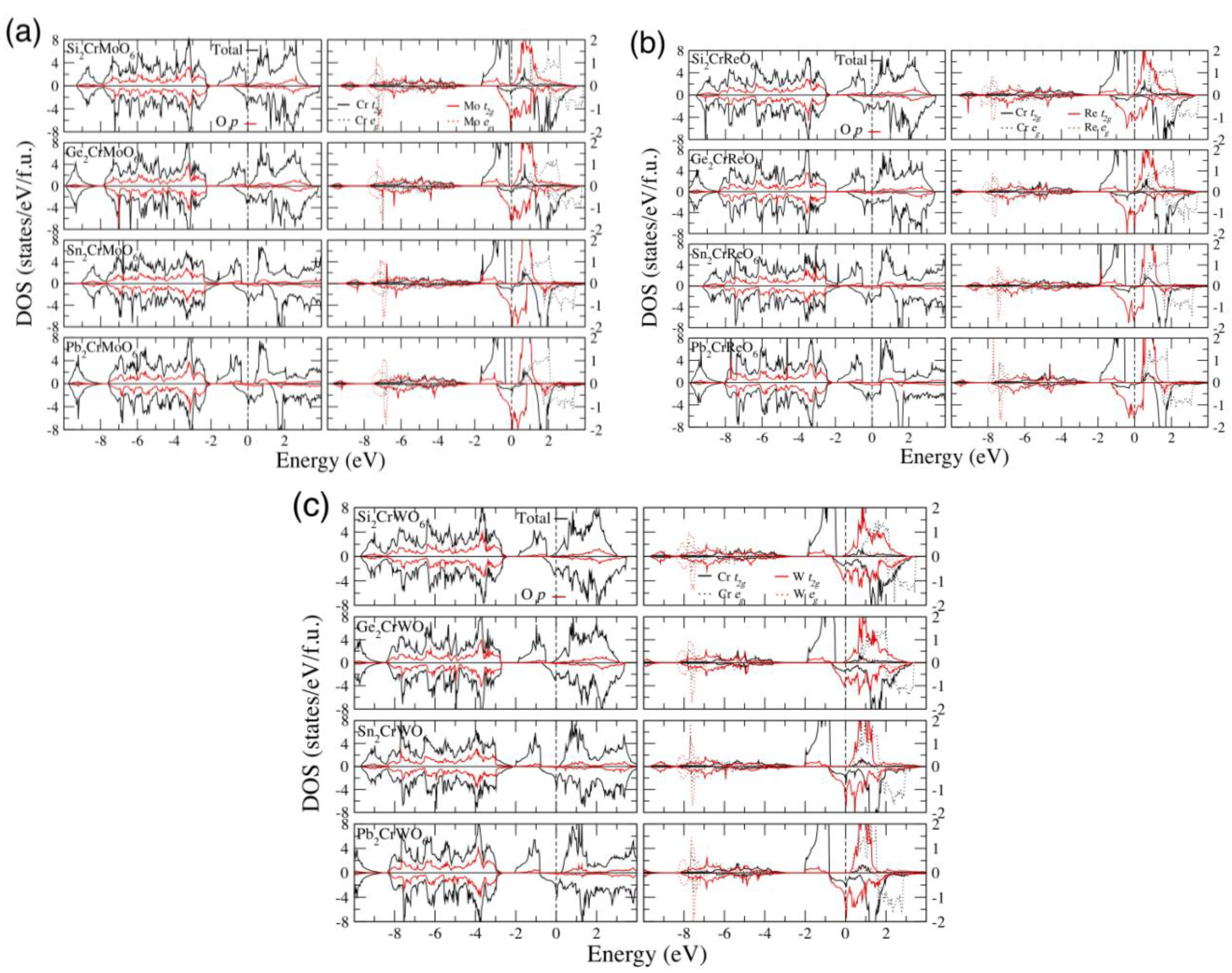
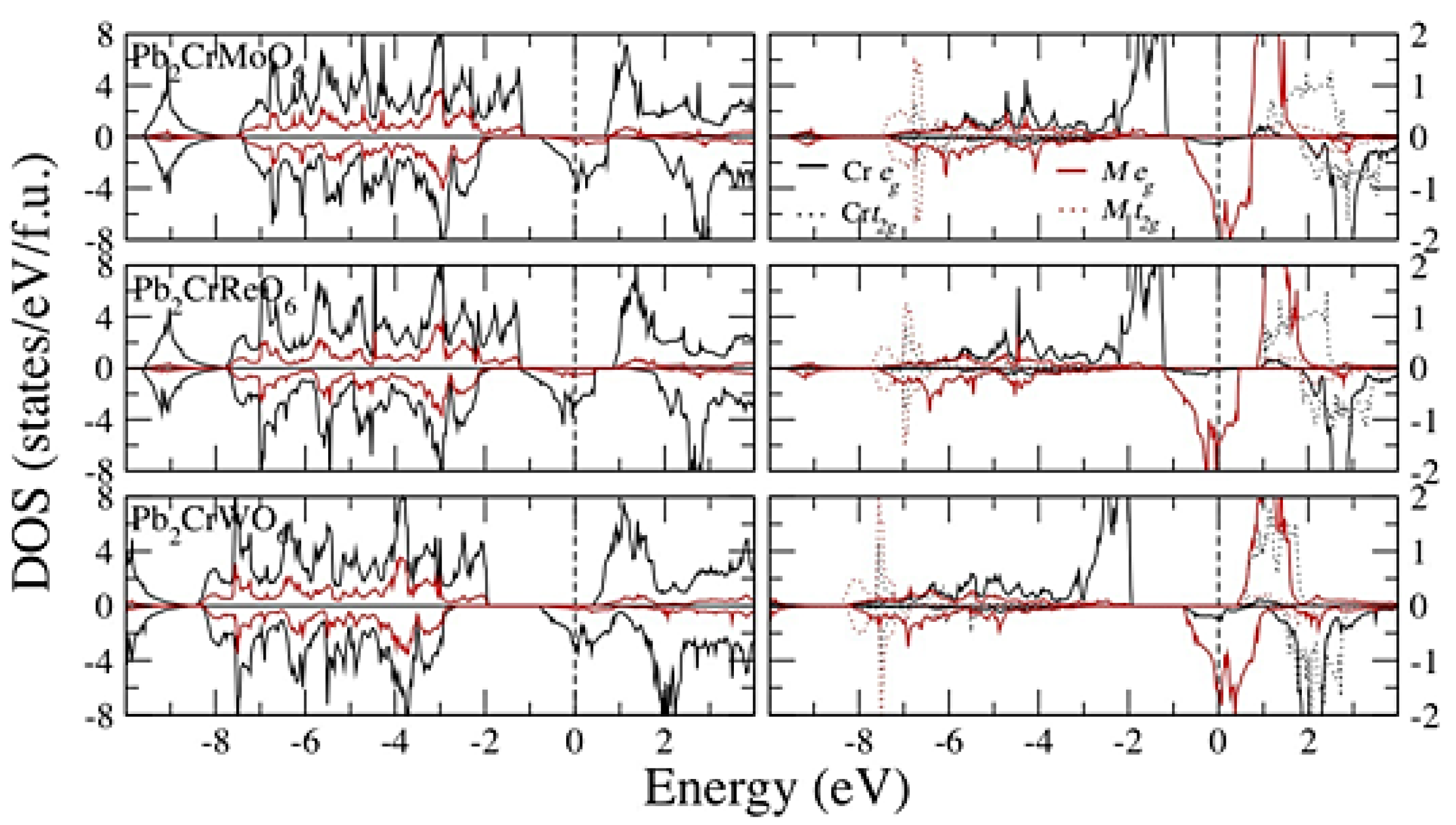
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Longo, J.M.; Ward, R. Compounds of heptavalent rhenium with the perovskite structure. J. Am. Chem. Soc. 1961, 83, 1088–1090. [Google Scholar] [CrossRef]
- Garcia-Landa, B.; Ritter, C.; Ibarra, M.R.; Blasco, J.; Algarabel, P.A.; Mahendiran, R.; Garcia, J. Magnetic and magnetotransport properties of the ordered perovskite Sr2FeMoO6. Solid State Commun. 1999, 110, 435–438. [Google Scholar] [CrossRef]
- Jin, S.; Teifel, T.H.; McCormack, M.; Fastacht, R.A.; Ramesh, R.; Chen, L.H. Thousandfold change in resistivity in magnetoresistive La-Ca-Mn-O films. Science 1994, 264, 413–415. [Google Scholar]
- Kobayashi, K.I.; Kimura, T.; Sawada, H.; Terakura, K.; Tokura, Y. Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure. Nature 1998, 395, 677–680. [Google Scholar] [CrossRef]
- Kobayashi, K.I.; Kimura, T.; Tomioka, Y.; Sawada, H.; Terakura, K.; Tokura, Y. Intergrain tunneling magnetoresistance in polycrystals of the ordered double perovskite Sr2FeReO6. Phys. Rev. B 1999, 59, 11159. [Google Scholar] [CrossRef]
- Chan, T.S.; Liu, R.S.; Guo, G.Y.; Hu, S.F.; Lin, J.G.; Chen, J.M.; Chang, C.-R. Effects of B'-site transition metal on the properties of double perovskites Sr2FeMO6 (M = Mo, W): B' 4d–5d system. Solid State Commun. 2005, 133, 265–270. [Google Scholar] [CrossRef]
- Moritomo, Y.; Kusura, H.; Akimoto, T.; Machida, A. Room-Temperature Magnetoresistance in Fe-Site-Substituted Sr2FeMoO6. Jpn. J. Appl. Phys. 2000, 39, L360–L362. [Google Scholar]
- Itoh, M.; Ohta, I.; Inaguma, Y. Cooperative interaction of oxygen octahedra for dielectric properties in the perovskite-related layered compounds Srn+1TinO3n+1, Can+1 TinO3n+1 and Srn+1(Ti0.5Sn0.5)nO3n+1 (n = 1,2,3 and ∞). Mater. Sci. Eng. B 1996, 41, 50–54. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, Z.Q. Electronic structures of double perovskites Ba2MnMO6 (M = W and Re) from first-principles studies. Phys. Status. Solidi B 2006, 243, 1151–1158. [Google Scholar] [CrossRef]
- Gray, B.; Lee, H.N.; Liu, J.; Chakhalian, J.; Freeland, W. Local electronic and magnetic studies of an artificial La2FeCrO6 double perovskite. Appl. Phys.Lett. 2010, 97, 013105. [Google Scholar] [CrossRef]
- Tang, C.Q.; Zang, Y.; Dai, J. Electronic and magnetic structure studies of double perovskite Sr2CrReO6 by first-principles calculations. Solid State. Commun. 2005, 133, 219–222. [Google Scholar] [CrossRef]
- Wu, H. Electronic structure study of double perovskites A2FeReO6 (A = Ba,Sr,Ca) and Sr2MMoO6 (M = Cr,Mn,Fe,Co) by LSDA and LSDA + U. Phys. Rev. B 2001, 64, 125126. [Google Scholar] [CrossRef]
- Sarma, D.D.; Mahadevan, P.; Dasgupta, T.S.; Ray, S.; Kumar, A. Electronic structure of Sr2FeMoO6. Phys. Rev. Lett. 2000, 85, 2549–2554. [Google Scholar] [CrossRef]
- Jeng, H.T.; Guo, G.Y. First-principles investigations of orbital magnetic moments and electronic structures of the double perovskites Sr2FeMoO6, Sr2FeReO6, and Sr2CrWO6. Phys. Rev. B 2003, 67, 1–4. [Google Scholar]
- Kato, H.; Okuda, T.; Okimoto, Y.; Tomioka, Y. Structural and electronic properties of the ordered double perovskites A2MReO6 (A = Sr, Ca; M = Mg, Sc, Cr, Mn, Fe, Co, N. Phys. Rev. B 2004, 69, 184412. [Google Scholar] [CrossRef]
- Solovyev, I.V. On the competition between ferromagnetic and antiferromagnetic states in Sr2MnMoO6. J. Magn. Magn. Mater. 2004, 268, 194–197. [Google Scholar] [CrossRef]
- Song, W.; Wang, J.; Wu, Z. Half metallic properties of Sr2CuOsO6. Chem. Phys. Lett. 2009, 482, 246–248. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Wu, Z. First principles investigations on the half metallic properties of Sr2MOsO6 (M = V, Mn, Fe, Co). Chem. Phys. Lett. 2011, 501, 324–329. [Google Scholar] [CrossRef]
- Yousif, S.E.A.; Yassin, O.A. The electronic and magnetic properties of Sr2MnNbO6, Sr2FeMoO6 and Sr2NiRuO6 double perovskites: An LSDA + U + SOC study. J. Alloys Compd. 2010, 506, 456–460. [Google Scholar] [CrossRef]
- Bannikov, V.V.; Shein, I.R.; Kozhevnikov, V.L.; Ivanovsky, A.L. Electronic structure and magnetic properties of double perovskites Sr2FeMO6 (M = Sc, Ti, ..., Ni, Cu) according to the data of FLAPW-GGA band structure calculations. J. Struct. Chem. 2008, 49, 781–787. [Google Scholar] [CrossRef]
- Bonilla, C.M.; Landínez Téllez, D.A.; Arbey Rodríguez, J.; Vera López, E.; Roa-Rojas, J. Half-metallic behavior and electronic structure of Sr2CrMoO6 magnetic system. Phys. B 2007, 398, 208–211. [Google Scholar] [CrossRef]
- Philipp, J.B.; Majewski, P.; Alff, L.; Erb, A.; Gross, R.; Graf, T.; Brandt, M.S.; Simon, J.; Walther, T.; Mader, W.; et al. Structural and doping effects in the half-metallic double perovskite A2CrWO6 (A = Sr, Ba, and Ca). Phys. Rev. B 2003, 68, 144431. [Google Scholar] [CrossRef]
- Liu, Y.P.; Fuh, H.R.; Wang, Y.K. First-principles study of half-metallic materials in double-perovskite A2FeMO6 (M = Mo, Re, and W) with IVA group elements set on the A-site position. J. Phys. Chem. C 2012, 116, 18032–18037. [Google Scholar] [CrossRef]
- Cardona, R.; Landínez Téllez, D.A.; Arbey Rodríguez M., J.; Fajardo, F.; Roa-Rojas, J. Structural and magnetic properties of double-perovskite Ba2MnMoO6 by density functional theory. J. Magn. Magn. Mater. 2008, 320, e85–e87. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomegeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef]
- Lichtenstein, A.I.; Anisimov, V.I.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Aryasetiawan, F.; Lichtenstein, A.I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA + U method. J. Phys 1997, 9, 767. [Google Scholar]
- Jeng, H.T.; Guo, G.Y.; Huang, D.J. Charge-orbital ordering and verwey transition in magnetite. Phys. Rev. Lett. 2004, 93, 156403. [Google Scholar] [CrossRef]
- Jiang, X.; Guo, G.Y. Electronic structure and exchange interactions in BaVS3. Phys. Rev. B 2004, 70, 035110. [Google Scholar] [CrossRef]
- Solovyev, I.V.; Dederichs, P.H.; Anisimov, V.I. Corrected atomic limit in the local-density approximation and the electronic structure of d impurities in Rb. Phys. Rev. B 1994, 50, 16861. [Google Scholar] [CrossRef]
- Wang, Y.K.; Lee, P.H.; Guo, G.Y. Half-metallic antiferromagnetic nature of La2VTcO6 and La2VCuO6 from ab initio calculations. Phys. Rev. B 2009, 80, 224418. [Google Scholar] [CrossRef]
- Terakura, K.; Fang, Z.; Kanamori, J. High pressure phase transition and elastic properties of cerium chalcogenides and pnictides. J. Phys. Chem. Solids 2002, 63, 907–912. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, Y.-P.; Fuh, H.-R.; Wang, Y.-K. Ab Initio Research on a New Type of Half-Metallic Double Perovskites, A2CrMO6 (A = IVA Group Elements; M = Mo, Re and W). Computation 2014, 2, 12-22. https://doi.org/10.3390/computation2010012
Liu Y-P, Fuh H-R, Wang Y-K. Ab Initio Research on a New Type of Half-Metallic Double Perovskites, A2CrMO6 (A = IVA Group Elements; M = Mo, Re and W). Computation. 2014; 2(1):12-22. https://doi.org/10.3390/computation2010012
Chicago/Turabian StyleLiu, Yun-Ping, Huei-Ru Fuh, and Yin-Kuo Wang. 2014. "Ab Initio Research on a New Type of Half-Metallic Double Perovskites, A2CrMO6 (A = IVA Group Elements; M = Mo, Re and W)" Computation 2, no. 1: 12-22. https://doi.org/10.3390/computation2010012
APA StyleLiu, Y.-P., Fuh, H.-R., & Wang, Y.-K. (2014). Ab Initio Research on a New Type of Half-Metallic Double Perovskites, A2CrMO6 (A = IVA Group Elements; M = Mo, Re and W). Computation, 2(1), 12-22. https://doi.org/10.3390/computation2010012




