Comparative Analysis of Wavelet Bases for Solving First-Kind Fredholm Integral Equations
Abstract
1. Introduction
2. Materials and Methods
2.1. Bubnov–Galerkin Method
2.2. Alpert Wavelets
- They are defined on the interval .
- They form an orthonormal set
- These functions generate the space of polynomials up to degree .
2.2.1. Alpert Wavelet Function Spaces
2.2.2. Definition of Functions
- is a polynomial of degree at most on ;
- on the interval it is continued as an even or odd function depending on the parity of ;
- wavelets satisfy orthonormality
- wavelets satisfy the moment annihilation conditions
2.3. Chebyshev Wavelets
2.4. Hermite Wavelets
2.5. Laguerre Wavelets
2.6. Legendre Wavelets
2.7. CAS Wavelets
3. Results and Discussion
3.1. Computational Experiment for Test Problem 1
3.2. Computational Experiment for Test Problem 2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kabanikhin, S.I.; Shishlenin, M.A. Theory and Numerical Methods for Solving Inverse and Ill-Posed Problems. J. Inverse Ill-Posed Probl. 2019, 27, 453–456. [Google Scholar] [CrossRef]
- Bitsadze, A.V. Integral Equations of First Kind, 1st ed.; World Scientific: Singapore, 1995; Volume 7. [Google Scholar]
- Krisch, A. An Introduction to the Mathematical Theory of Inverse Problems, 1st ed.; Springer: New York, NY, USA, 1996; pp. 1–300. [Google Scholar] [CrossRef]
- Baker, C.T.H. The Numerical Treatment of Integral Equations, 1st ed.; Clarendon Press: Oxford, UK, 1977; pp. 1–250. [Google Scholar]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; pp. 1–350. [Google Scholar] [CrossRef]
- Weese, J. A Reliable and Fast Method for the Solution of Fredholm Integral Equations of the First Kind Based on Tikhonov Regularization. Comput. Phys. Commun. 1992, 69, 99–111. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Shishlenin, M.A.; Nurseitov, D.B.; Nurseitova, A.T.; Kasenov, S.E. Comparative Analysis of Methods for Regularizing an Initial Boundary Value Problem for the Helmholtz Equation. J. Appl. Math. 2014, 2014, 786326. [Google Scholar] [CrossRef]
- Altürk, A.; Cosgun, T. The Use of Lavrentiev Regularization Method in Fredholm Integral Equations of the First Kind. Int. J. Adv. Appl. Math. Mech. 2019, 7, 70–79. [Google Scholar]
- Hanson, R.J. A Numerical Method for Solving Fredholm Integral Equations of the First Kind Using Singular Values. SIAM J. Numer. Anal. 1971, 8, 616–622. [Google Scholar] [CrossRef]
- Luo, X.; Hu, W.; Xiong, L.; Li, F. Multilevel Jacobi and Gauss–Seidel Type Iteration Methods for Solving Ill-Posed Integral Equations. J. Inverse Ill-Posed Probl. 2015, 23, 477–490. [Google Scholar] [CrossRef]
- Landweber, L. An Iteration Formula for Fredholm Integral Equations of the First Kind. Am. J. Math. 1951, 73, 615–624. [Google Scholar] [CrossRef]
- Marchuk, G.I. Conjugate Equations: A Course of Lectures, 1st ed.; IVM RAS: Moscow, Russia, 2000; p. 335. (In Russian) [Google Scholar]
- Temirbekov, N.; Temirbekova, L. Using the Conjugate Equations Method for Solving Inverse Problems of Mathematical Geophysics and Mathematical Epidemiology. AIP Conf. Proc. 2021, 2325, 020023. [Google Scholar] [CrossRef]
- Temirbekov, N.M.; Temirbekova, L.N.; Nurmangaliyeva, M.B. Numerical Solution of the First Kind Fredholm Integral Equations by Projection Methods with Wavelets as Basis Functions. TWMS J. Pure Appl. Math. 2022, 13, 105–118. [Google Scholar] [CrossRef]
- Atkinson, K.E. The Numerical Solution of Integral Equations of the Second Kind, 1st ed.; Cambridge University Press: Cambridge, UK, 1997; pp. 1–300. [Google Scholar] [CrossRef]
- Maleknejad, K.; Aghazadeh, N.; Mollapourasl, R. Numerical Solution of Fredholm Integral Equation of the First Kind with Collocation Method and Estimation of Error Bound. Appl. Math. Comput. 2006, 179, 352–359. [Google Scholar] [CrossRef]
- Polozhiy, G.N. On a Method for Solving Integral Equations. Izv. USSR Acad. Sci. Ser. Math. 1959, 23, 295–312. [Google Scholar]
- Twomey, S. On the Numerical Solution of Fredholm Integral Equations of the First Kind by the Inversion of the Linear System Produced by Quadrature. J. ACM 1963, 10, 97–101. [Google Scholar] [CrossRef]
- Maleknejad, K.; Sohrabi, S. Numerical Solution of Fredholm Integral Equations of the First Kind by Using Legendre Wavelets. Appl. Math. Comput. 2007, 186, 836–843. [Google Scholar] [CrossRef]
- Tamabay, D.; Temirbekov, N.; Zhumagulov, B. Approximate Solution of Nonlinear Integral Hammerstein Equations by Projection Method Using Multiwavelets. AIP Conf. Proc. 2023, 2879, 040012. [Google Scholar] [CrossRef]
- Shang, X.; Han, D. Numerical Solution of Fredholm Integral Equations of the First Kind by Using Linear Legendre Multi-Wavelets. Appl. Math. Comput. 2007, 191, 440–444. [Google Scholar] [CrossRef]
- Bahmanpour, M.; Fariborzi Araghi, M.A. A Method for Solving Fredholm Integral Equations of the First Kind Based on Chebyshev Wavelets. Anal. Theory Appl. 2013, 29, 197–207. [Google Scholar] [CrossRef]
- Adibi, H.; Assari, P. Chebyshev Wavelet Method for Numerical Solution of Fredholm Integral Equations of the First Kind. Math. Probl. Eng. 2010, 2010, 138408. [Google Scholar] [CrossRef]
- Turan Dincel, A.; Tural Polat, S.N.; Sahin, P. Hermite Wavelet Method for Nonlinear Fractional Differential Equations. Fractal Fract. 2023, 7, 346. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Angadi, L.M.; Kumbinarasaiah, S. Laguerre Wavelet-Galerkin Method for the Numerical Solution of One Dimensional Partial Differential Equations. RN 2018, 55, 7. [Google Scholar]
- Alpert, B.K. A class of bases in L2 for the sparse representation of integral. SIAM J. Sci. Comput. 1993, 14, 159–184. [Google Scholar] [CrossRef]
- Maleknejad, K.; Karami, M. Numerical Solution of Non-Linear Fredholm Integral Equations by Using Multiwavelets in the Petrov–Galerkin Method. Appl. Math. Comput. 2005, 168, 102–110. [Google Scholar] [CrossRef]
- Yousefi, S.; Banifatemi, A. Numerical Solution of Fredholm Integral Equations by Using CAS Wavelets. Appl. Math. Comput. 2006, 183, 458–463. [Google Scholar] [CrossRef]
- Saeedi, H.; Moghadam, M.M. Numerical Solution of Nonlinear Volterra Integro-Differential Equations of Arbitrary Order by CAS Wavelets. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1216–1226. [Google Scholar] [CrossRef]
- Yuan, D.; Zhang, X. An Overview of Numerical Methods for the First Kind Fredholm Integral Equation. SN Appl. Sci. 2019, 1, 1178. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, X. Numerical Solution of the Convection Diffusion Equations by the Second Kind Chebyshev Wavelets. Appl. Math. Comput. 2014, 247, 353–367. [Google Scholar] [CrossRef]
- Ghasemi, M.; Kajani, M.T. Numerical Solution of Time-Varying Delay Systems by Chebyshev Wavelets. Appl. Math. Model. 2011, 35, 5235–5244. [Google Scholar] [CrossRef]
- Kumar, S.; Ghosh, S.; Kumar, R.; Jleli, M. A Fractional Model for Population Dynamics of Two Interacting Species by Using Spectral and Hermite Wavelets Methods. Numer. Methods Partial Differ. Equ. 2021, 37, 1652–1672. [Google Scholar] [CrossRef]
- Saeed, U.; ur Rehman, M. Hermite Wavelet Method for Fractional Delay Differential Equations. J. Differ. Equ. 2014, 2014, 359093. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, X. Numerical Solutions for the Linear and Nonlinear Singular Boundary Value Problems Using Laguerre Wavelets. Alderremy, A.A.; Shah, R.; Shah, N.A.; Aly, S.; Nonlaopon, K. Evaluation of Fractional-Order Pantograph Delay Differential Equation via Modified Laguerre Wavelet Method. Symmetry 2022, 14, 2356. [Google Scholar] [CrossRef]
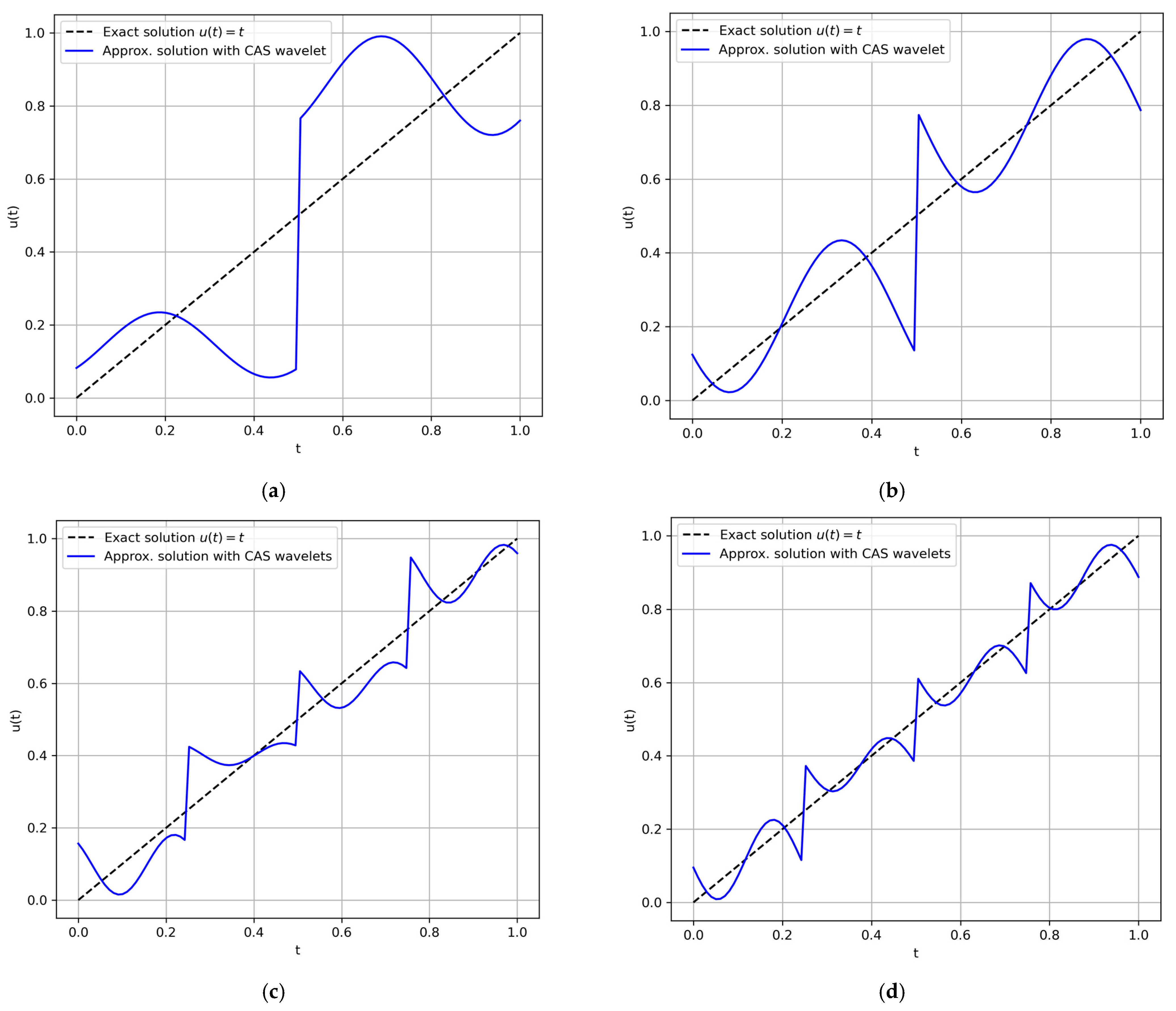
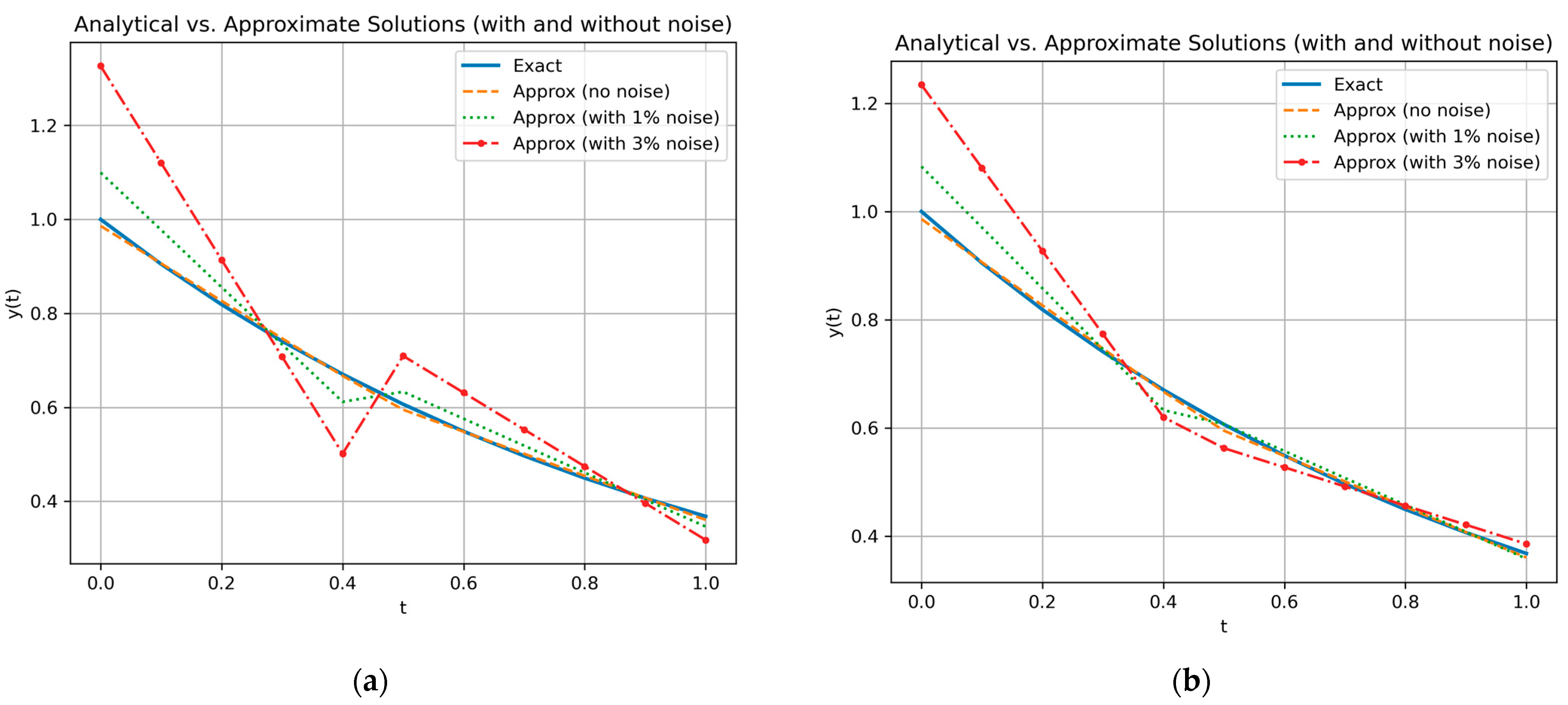
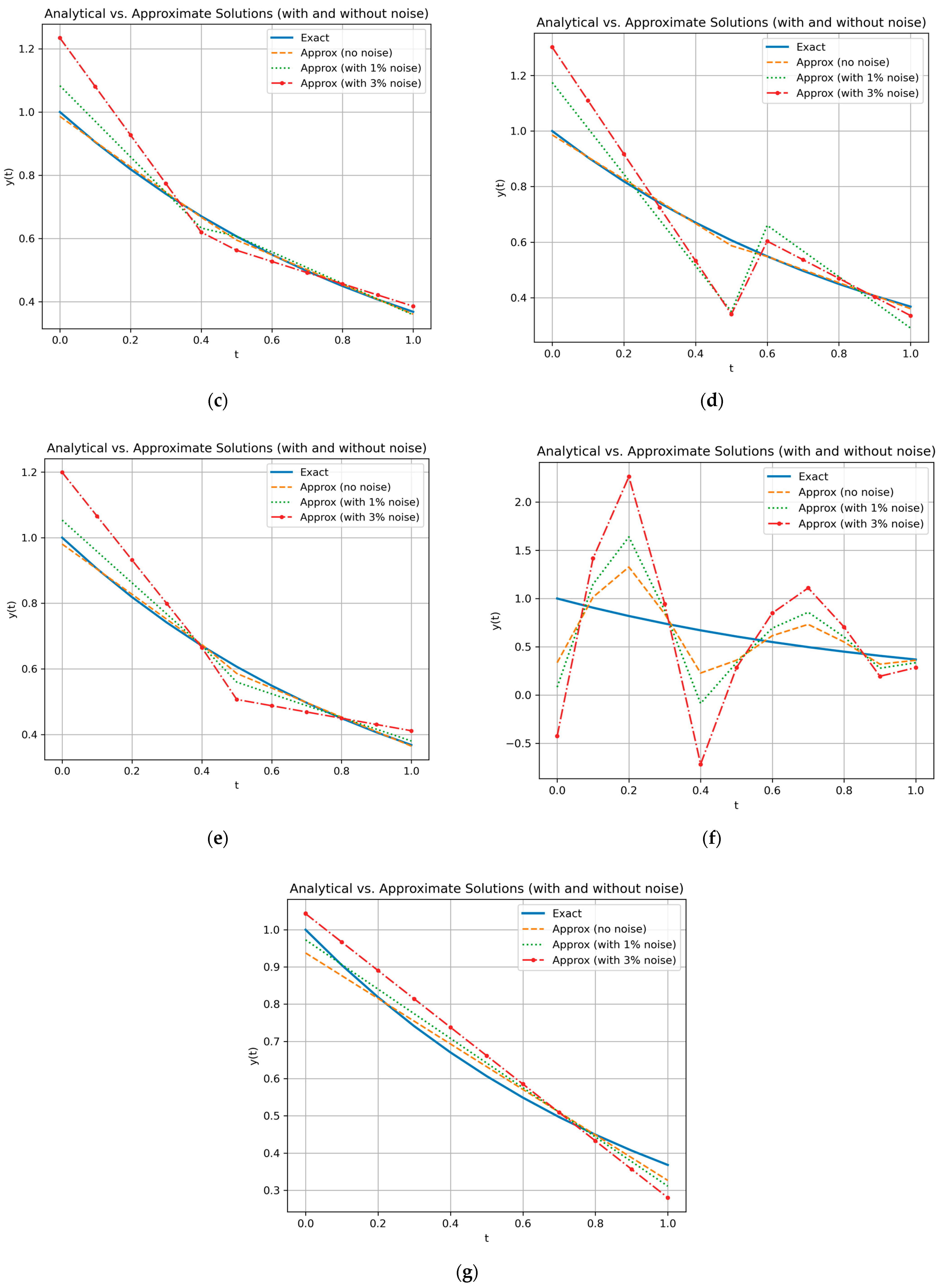
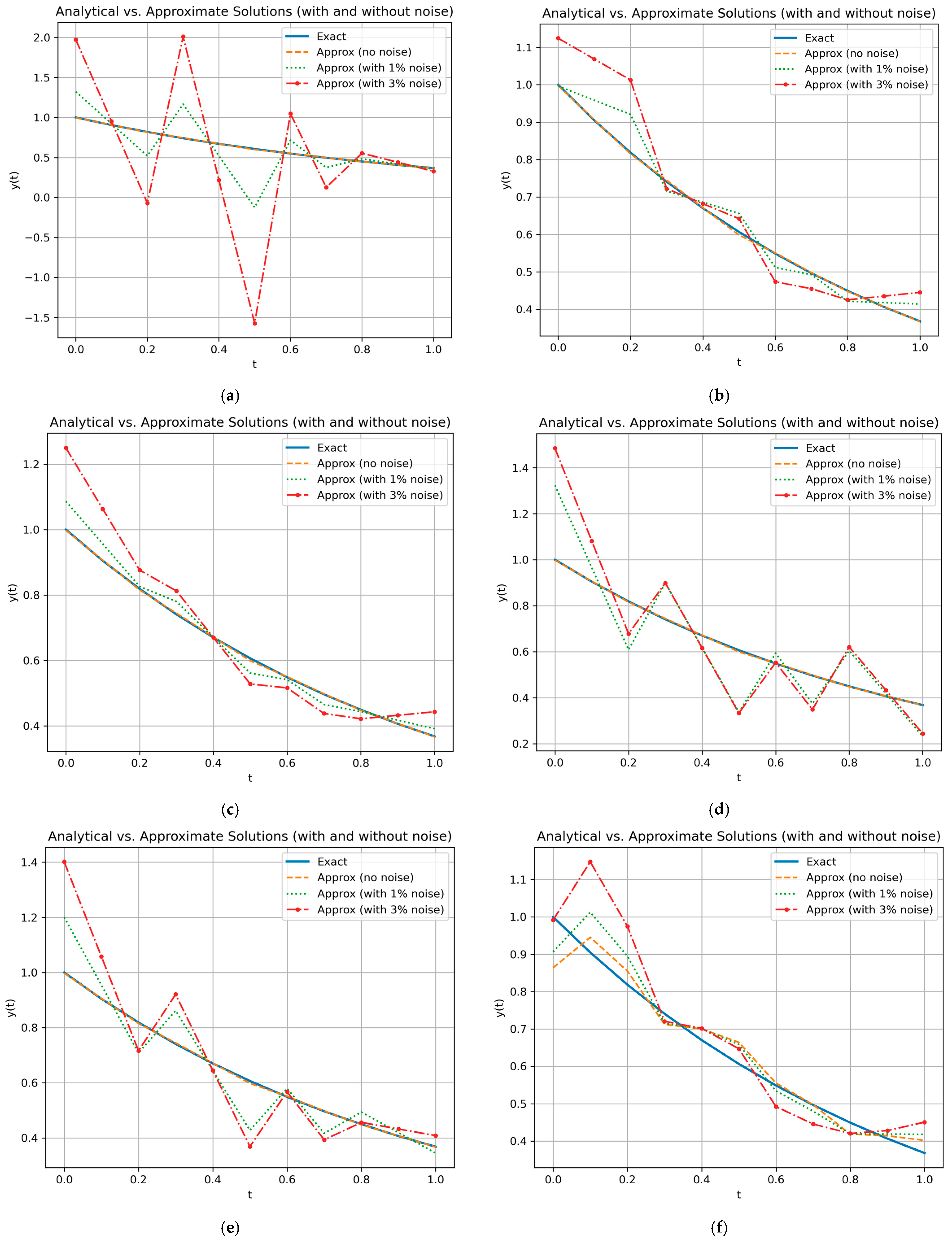
| Wavelets | k = 2, M = 2 | k = 2, M = 3 |
|---|---|---|
| Alpert wavelets | ||
| Chebyshev wavelets | ||
| Hermite wavelets | ||
| Laguerre wavelets | ||
| Legendre wavelets | ||
| CAS wavelets | ||
| Alpert | Chebyshev | Hermite | Laguerre | Legendre | CAS | Polynomial Basis | |
|---|---|---|---|---|---|---|---|
| 0.00 | |||||||
| 0.10 | |||||||
| 0.20 | |||||||
| 0.30 | |||||||
| 0.40 | |||||||
| 0.50 | |||||||
| 0.60 | |||||||
| 0.70 | |||||||
| 0.80 | |||||||
| 0.90 | |||||||
| 1.00 |
| Alpert | Chebyshev | Hermite | Laguerre | Legendre | CAS | Polynomial Basis | |
|---|---|---|---|---|---|---|---|
| 0.00 | |||||||
| 0.10 | |||||||
| 0.20 | |||||||
| 0.30 | |||||||
| 0.40 | |||||||
| 0.50 | |||||||
| 0.60 | |||||||
| 0.70 | |||||||
| 0.80 | |||||||
| 0.90 | |||||||
| 1.00 |
| Alpert | Chebyshev | Hermite | Laguerre | Legendre | CAS | Polynomial Basis | |
|---|---|---|---|---|---|---|---|
| 0.00 | |||||||
| 0.10 | |||||||
| 0.20 | |||||||
| 0.30 | |||||||
| 0.40 | |||||||
| 0.50 | |||||||
| 0.60 | |||||||
| 0.70 | |||||||
| 0.80 | |||||||
| 0.90 | |||||||
| 1.00 |
| Alpert | Chebyshev | Hermite | Laguerre | Legendre | CAS | Polynomial Basis | |
|---|---|---|---|---|---|---|---|
| 0.00 | |||||||
| 0.10 | |||||||
| 0.20 | |||||||
| 0.30 | |||||||
| 0.40 | |||||||
| 0.50 | |||||||
| 0.60 | |||||||
| 0.70 | |||||||
| 0.80 | |||||||
| 0.90 | |||||||
| 1.00 |
| Alpert | Chebyshev | Hermite | Laguerre | Legendre | CAS | Polynomial Basis | |
|---|---|---|---|---|---|---|---|
| 0.00 | |||||||
| 0.10 | |||||||
| 0.20 | |||||||
| 0.30 | |||||||
| 0.40 | |||||||
| 0.50 | |||||||
| 0.60 | |||||||
| 0.70 | |||||||
| 0.80 | |||||||
| 0.90 | |||||||
| 1.00 |
| Wavelet Basis | Error at 1% | Error at 3% | Increase | Growth Factor |
|---|---|---|---|---|
| Wavelets | Alpert | Chebyshev | Hermite | Laguerre | Legendre | CAS | Polynomial Basis |
|---|---|---|---|---|---|---|---|
| Time (s) | 0.0820 | 0.0847 | 0.0850 | 0.0769 | 0.0899 | 0.2793 | 0.0040 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Temirbekov, N.; Tamabay, D.; Tleulesova, A.; Mukhanova, T. Comparative Analysis of Wavelet Bases for Solving First-Kind Fredholm Integral Equations. Computation 2025, 13, 199. https://doi.org/10.3390/computation13080199
Temirbekov N, Tamabay D, Tleulesova A, Mukhanova T. Comparative Analysis of Wavelet Bases for Solving First-Kind Fredholm Integral Equations. Computation. 2025; 13(8):199. https://doi.org/10.3390/computation13080199
Chicago/Turabian StyleTemirbekov, Nurlan, Dinara Tamabay, Aigerim Tleulesova, and Tomiris Mukhanova. 2025. "Comparative Analysis of Wavelet Bases for Solving First-Kind Fredholm Integral Equations" Computation 13, no. 8: 199. https://doi.org/10.3390/computation13080199
APA StyleTemirbekov, N., Tamabay, D., Tleulesova, A., & Mukhanova, T. (2025). Comparative Analysis of Wavelet Bases for Solving First-Kind Fredholm Integral Equations. Computation, 13(8), 199. https://doi.org/10.3390/computation13080199





