Mathematical Modeling of Regional Infectious Disease Dynamics Based on Extended Compartmental Models

Abstract

This study presents an extended approach to compartmental modeling of infectious disease spread, focusing on regional heterogeneity within affected areas. Using classical SIS, SIR, and SEIR frameworks, we simulate the dynamics of COVID-19 across two major regions of Ukraine—Dnipropetrovsk and Kharkiv—during the period 2020–2024. The proposed mathematical model incorporates regionally distributed subpopulations and applies a system of differential equations solved using the classical fourth-order Runge–Kutta method. The simulations are validated against real-world epidemiological data from national and international sources. The SEIR model demonstrated superior performance, achieving maximum relative errors of 4.81% and 5.60% in the Kharkiv and Dnipropetrovsk regions, respectively, outperforming the SIS and SIR models. Despite limited mobility and social contact data, the regionally adapted models achieved acceptable accuracy for medium-term forecasting. This validates the practical applicability of extended compartmental models in public health planning, particularly in settings with constrained data availability. The results further support the use of these models for estimating critical epidemiological indicators such as infection peaks and hospital resource demands. The proposed framework offers a scalable and computationally efficient tool for regional epidemic forecasting, with potential applications to future outbreaks in geographically heterogeneous environments.

1. Introduction

Infectious diseases have consistently posed significant threats to global public health, leading to numerous regional epidemics and global pandemics with profound societal and economic impacts. Historical data reveal infection counts ranging from thousands to hundreds of millions, with mortality rates spanning from hundreds to tens of millions. The SARS-CoV-2 pandemic (2020–2025), which infected billions and resulted in millions of deaths worldwide, underscored the devastating consequences of infectious diseases and the urgent need for effective forecasting tools. Variations in infection dynamics across countries—shaped by factors such as population density, healthcare infrastructure, mobility patterns, and public health interventions—highlight the complexity of epidemic management.

Mathematical modeling has become a cornerstone of epidemiology, enabling researchers and policymakers to predict infection dynamics, peak incidence, and temporal trends. Accurate forecasts allow healthcare systems to prepare for surges, optimize resource allocation, and implement timely interventions, such as lockdowns or vaccination campaigns, to mitigate disease spread and reduce mortality. Compartmental models like SIS (Susceptible–Infected–Susceptible), SIR (Susceptible–Infected–Removed), and SEIR (Susceptible–Exposed–Infected–Recovered) have been extensively used to simulate disease transmission and inform public health strategies. These models provide valuable insights into the temporal evolution of epidemics, capturing key parameters such as infection rates, recovery rates, and basic reproduction numbers.

However, a critical limitation of classical compartmental models is their assumption of spatial homogeneity, which overlooks the geographic variability inherent in disease spread. Factors such as population density, transportation networks, urban versus rural settings, and the localized impact of anti-epidemic measures significantly influence transmission patterns. For instance, densely populated urban areas may experience faster disease spread due to high contact rates, while rural regions may face delays in healthcare access. Similarly, mobility patterns, such as interregional travel, and the effectiveness of containment measures, such as quarantine zones, vary across geographic areas. These spatial factors are particularly relevant in large, diverse regions like Ukraine’s Dnipropetrovsk and Kharkiv regions, each with a population exceeding 3 million and distinct demographic and infrastructural characteristics.

The SARS-CoV-2 pandemic demonstrated the need for models that account for spatial heterogeneity to improve forecasting accuracy and support region-specific interventions. While classical models have been effective for broad-scale predictions, their inability to incorporate spatial dynamics limits their applicability in scenarios where geographic variability drives transmission. Addressing this gap is essential for developing robust tools that can guide public health responses in diverse settings, from densely populated cities to remote rural areas.

This study introduces an advanced mathematical model that extends classical SIS, SIR, and SEIR frameworks by integrating regional heterogeneity through spatial differentiation and stratified parameterization. Using epidemiological data from the 2020–2025 SARS-CoV-2 pandemic in Ukraine’s Dnipropetrovsk and Kharkiv regions, the model captures region-specific transmission patterns, accounting for population density, mobility flows, and localized interventions. By addressing the limitations of spatial homogeneity in traditional models, this approach offers improved predictive accuracy and practical utility for modern epidemiological forecasting and public health decision-making.

Although the model uses data from more than 50 municipalities, the simulations are conducted at the regional level, with no explicit modeling of inter-settlement transmission. To avoid misinterpretation, we refer to this approach as regional epidemic modeling rather than spatial epidemic modeling in the strict mathematical sense.

2. Background

Mathematical modeling of infectious disease dynamics has been a focal point for both domestic and international researchers, particularly in the context of the COVID-19 pandemic caused by SARS-CoV-2. These efforts have traditionally leveraged classical compartmental models such as SIS, SIR, and SEIR to simulate epidemic progression and inform public health strategies. Such models, by dividing the population into compartments based on disease status, provide an analytically tractable framework to understand epidemic thresholds, reproduction numbers, and potential outbreak sizes [1,2,3]. However, despite their utility, these classical models often assume homogeneous mixing and lack spatial or behavioral granularity, which limits their accuracy in capturing real-world epidemic complexity.

Recognizing these limitations, recent studies have extended classical frameworks to incorporate additional features such as time delays, behavioral responses, and spatial heterogeneity. For instance, dynamic models with delays account for incubation periods and latency effects critical for diseases like COVID-19 [4,5,6,7]. Cellular automata and multi-agent simulations have been utilized to model localized interactions and heterogeneous contact patterns, enabling more realistic exploration of intervention strategies [4,8]. These approaches bridge epidemiology with complex system dynamics seen in ecological modeling, highlighting shared challenges in predicting nonlinear phenomena.

Spatial structure has become a central focus in epidemic modeling, especially for capturing disease diffusion across geographically heterogeneous territories. A spatially distributed SIR model integrating population behavior demonstrates how local density, mobility, and immunity levels impact transmission dynamics [9]. Such spatially explicit models improve predictive accuracy over homogeneous models by accounting for region-specific factors and enabling targeted public health responses such as localized lockdowns or vaccination campaigns [9,10]. Similar approaches applied to Ebola outbreaks underscore how healthcare access and population distribution modulate epidemic outcomes [11].

Within this broader trend, regional epidemic modeling has emerged as a practically oriented subclass of spatial models, where the geographic domain corresponds to administrative units (e.g., regions, provinces, municipalities) with available epidemiological and organizational data. These models offer actionable insights for regional authorities by linking infection dynamics to healthcare resource planning, containment strategies, and logistical coordination. Regional models also enable retrospective validation against granular data and support simulation of scenarios under limited data availability—an important feature in countries with uneven surveillance infrastructure. Beyond spatial considerations, recent advances emphasize the integration of temporal dynamics, stochasticity, and network theory. Reviews highlight that classical models must evolve by incorporating branching processes, time-varying parameters, and data-driven machine learning techniques to refine forecasts and parameter estimations [12,13]. Bayesian frameworks, in particular, offer robust handling of uncertainty and heterogeneous data sources, improving both numerical and qualitative model outputs [14]. Hybrid models combining SEIR compartments with Cox regression or other survival models further enhance analytical depth, particularly when age-specific or contact pattern data are available [15].

The practical application of epidemic models depends heavily on their calibration and validation using real-world data. Retrospective analyses comparing model forecasts with observed epidemiological statistics reinforce the need for iterative model refinement and caution in interpretation [16,17]. Incorporating mobility data, social contact matrices, and dynamic parameter estimation enhances the adaptability of models to changing epidemic conditions, such as emergence of new variants or shifts in public behavior [18,19]. Furthermore, metapopulation and regionally structured models, dividing populations into epidemiologically distinct subgroups, capture heterogeneities critical for accurate predictions, especially in diverse urban–rural contexts [20].

Despite these advances, simple models remain valuable tools. Parsimonious models can effectively describe epidemic phases and intervention impacts with fewer parameters, facilitating analytical insights and computational efficiency [21]. Comparative studies also demonstrate that mathematical models often outperform expert opinion in estimating outbreak dynamics, underscoring their role in data-driven decision-making [22].

A significant contemporary challenge is the dynamic nature of epidemic data, driven by factors such as emerging viral variants, vaccination campaigns, and changing human behavior. This requires models to be not only spatially and behaviorally informed but also dynamically adaptable. Techniques from machine learning and data assimilation are increasingly integrated into epidemic modeling frameworks to enable real-time parameter updates and improve forecast accuracy [12,18,23]. Such hybrid approaches combine mechanistic understanding with empirical data, offering a powerful paradigm for epidemic forecasting and control.

Overall, the literature points to a clear trajectory: epidemic modeling is progressively becoming more spatially aware, behaviorally informed, computationally sophisticated, and data-adaptive. The integration of spatial diffusion mechanisms within classical compartmental frameworks, supported by real-time data assimilation and validated through comprehensive retrospective studies, exemplifies this trend [5,6,7,8,9,18,23,24]. Regional epidemic modeling represents a practical and scalable realization of this trajectory, tailored to the decision-making needs of local health authorities.

In this work, we contribute to this progression by developing a spatially and regionally adapted extension of the SIS/SIR/SEIR family of models, calibrated for epidemic forecasting in two Ukrainian regions—Dnipropetrovsk and Kharkiv. Our model incorporates heterogeneous population interactions, mobility patterns, and behavioral responses, with application to the Dnipropetrovsk and Kharkiv regions during the SARS-CoV-2 pandemic. By bridging classical theory with spatial and behavioral realism and embedding data-adaptive components, this study aims to improve predictive performance and offer actionable insights for localized epidemic control.

3. Materials and Methods

Mathematical modeling of infectious disease dynamics has become a fundamental tool in epidemiology, enabling researchers and policymakers to forecast outbreaks and evaluate control strategies. One of the most widely adopted frameworks is the SIR model, which divides the population into three compartments:

• S (Susceptible): individuals who can contract the disease;
• I (Infected): individuals capable of transmitting the disease;
• R (Removed): individuals who are no longer infectious, having either recovered with immunity or died.

The dynamics of this model are governed by the following system of ordinary differential equations [25]:

$$\left\{\begin{array}{l}\dot{S}=-\beta \cdot {\displaystyle \frac{S\cdot I}{N}}\\ \dot{I}=\beta \cdot {\displaystyle \frac{S\cdot I}{N}}-\gamma \cdot I\\ \dot{R}=\gamma \cdot I\end{array}\right.$$

(1)

where $N=S+I+R$ is the total population, $\beta$ is the infection rate, and $\gamma$ is the recovery rate.

While the SIR model provides a simple yet powerful abstraction of disease progression, it makes several limiting assumptions: homogeneity of the population, instantaneous disease transitions, and the impossibility of reinfection. Furthermore, the SIR model is inherently “point-based”, assuming the population is concentrated in a single location and neglecting spatial effects [25].

To address these shortcomings, various extensions have been proposed. One notable example is the SEIR model, which introduces an Exposed (E) compartment to account for the incubation period during which individuals are infected but not yet infectious [26]:

$$\left\{\begin{array}{l}{\displaystyle \frac{dS}{dt}}=-\beta \cdot {\displaystyle \frac{S\cdot I}{N}}\\ {\displaystyle \frac{dE}{dt}}=\beta \cdot {\displaystyle \frac{S\cdot I}{N}}-\alpha \cdot E\\ {\displaystyle \frac{dI}{dt}}=\alpha \cdot E-\gamma \cdot I\\ {\displaystyle \frac{dR}{dt}}=\gamma \cdot I\end{array}\right.$$

(2)

where $\alpha$ is the rate at which exposed individuals become infectious.

Although the SEIR model improves the realism of epidemic dynamics by introducing a latent stage, it still relies on the assumption of a homogeneous population and does not address individual variability in disease progression or contact patterns. To overcome these limitations, numerous extensions of the classical models have been developed.

These extensions fall into several broad categories:

• quarantine-based models (e.g., SIQR) [27], which introduce compartments for isolated individuals;
• models with waning immunity (e.g., SIRS) [28] allowing recovered individuals to become susceptible again;
• risk-stratified models [29] dividing the population into groups with varying infection and recovery rates;
• metapopulation or spatial models that account for region-specific dynamics and mobility between regions.

However, many of these remain compartmental in nature and struggle to incorporate both spatial heterogeneity and individual-level variability in susceptibility and disease duration. To address these gaps, we propose a model that decomposes the infected population into a finite set of heterogeneous subgroups.

The proposed model aims to improve upon classical compartmental approaches by capturing variability in infection dynamics across heterogeneous subgroups.

Let us define our terms as follows:

p is the number of subgroups with distinct infection and recovery characteristics;

$I_j$ is the number of infected individuals in the j-th subgroup;

${\beta }_j$ is the infection probability for individuals in subgroup j;

${\gamma }_j$ is the recovery probability for subgroup j;

$N=S+{\displaystyle \sum _{j=1}^p{I}_j}+R$ is the total metapopulation.

We have the following system of differential equations:

$$\left\{\begin{array}{l}{\displaystyle \frac{dS}{dt}}=-{\displaystyle \frac{S}{N}}{\displaystyle \sum _{j=1}^p{\beta }_j}\cdot {\displaystyle \sum _{j=1}^p{I}_j}\\ {\displaystyle \frac{d{I}_1}{dt}}={\displaystyle \frac{S}{N}}{\beta }_1{\displaystyle \sum _{j=1}^p{I}_j}-{\gamma }_1\cdot I_1\\ {\displaystyle \frac{d{I}_2}{dt}}={\displaystyle \frac{S}{N}}{\beta }_2{\displaystyle \sum _{j=1}^p{I}_j}-{\gamma }_2\cdot I_2\\ \dots \\ {\displaystyle \frac{d{I}_p}{dt}}={\displaystyle \frac{S}{N}}{\beta }_p{\displaystyle \sum _{j=1}^p{I}_j}-{\gamma }_p\cdot I_p\\ {\displaystyle \frac{dR}{dt}}={\displaystyle \sum _{j=1}^p{\gamma }_j\cdot I_j}\end{array}\right.$$

(3)

The core idea is that not all infected individuals contribute equally to disease spread. Some subgroups may recover quickly or exhibit mild symptoms, while others remain infectious for extended periods, exerting disproportionate influence on transmission. Such heterogeneity can arise from differences in immune response, spatial localization, presence or absence of preventive measures, and policy-driven isolation or exposure levels.

This distinction is crucial since individuals who stay infectious longer can sustain chains of transmission even if the average infection rate is low. This paradox mirrors effects observed in cellular automata models, where lower transmission probabilities may prolong the overall duration of the epidemic and delay full recovery of the system [30].

The mathematical model developed in this work is calibrated using detailed regional-level data on the progression of the COVID-19 epidemic in two large administrative regions of Ukraine. Each region covers an area of over 30,000 square kilometers, with the first having a population exceeding 3 million people and the second over 2 million. While the model is not spatial in the strict sense of modeling inter-settlement transmission, its structure reflects important geographic and demographic heterogeneities across the regions. Model calibration was based on high-resolution epidemiological data collected from more than 50 cities and towns, and key parameters were identified with consideration of critical regional features such as population density, passenger transport flows, and other socio-demographic indicators.

A key feature of the proposed model is the division of the infected population into subgroups exhibiting different temporal profiles of disease progression. While some individuals recover rapidly and have limited impact on overall transmission dynamics, others remain infectious for significantly longer periods and thus have a disproportionately strong influence on epidemic persistence and spread. This structure allows the model to better capture regional transmission dynamics and to account for realistic behavioral and biological heterogeneity. A more detailed theoretical formulation of the model can be found in [19], while the present study emphasizes the numerical results and their practical interpretation in the context of regional epidemic control.

The described effect shares similarities with the well-known model of infectious dis-ease spread in cellular automata theory. Although this model is discrete, which imposes certain limitations on input data, model structure, and simulation outcomes, it produces a comparable paradox: a reduction in the probability of infection can prolong the overall duration of the disease within the affected area or even lead to the system’s inability to achieve full recovery, resulting in chaotic migration of the infection across the spatial domain.

From an applied perspective, this effect can be explained by the fact that a low probability of infection, while slowing the disease’s progression across the area, hinders the formation of an immune barrier between infected and healthy individuals.

Figure 1 demonstrates the result of a simulation of infectious disease spread using a cellular automaton model. In a discrete spatial simulation on a 100 × 100 grid with a step size of 0.1 and varying infection probabilities, we observed that a lower probability of infection can sometimes lead to longer disease persistence and the emergence of spatial chaotic patterns. In the illustration, white cells represent healthy individuals, black cells represent removed individuals (recovered or deceased), and a green gradient indicates infected individuals at various stages of disease progression.

The model’s key parameters include the probability of infection of neighboring cells and the neighborhood structure used to define possible infectious contacts—either Moore or von Neumann neighborhoods [31]. These features capture the spatial distribution of individuals and generate two notable effects, which may not be intuitively obvious.

From an applied standpoint, this implies that control measures aimed solely at reducing infection probability may be insufficient or counterproductive in the long run unless accompanied by targeted isolation of highly infectious subgroups or spatial segregation measures.

First, a decrease in the infection probability does not necessarily increase the likelihood of disease eradication. On the contrary, a lower infection probability can hinder the formation of immune “barriers” and lead to prolonged, chaotic infection dynamics. For instance, in a scenario where the infection probability is 100%, the infected area evolves into an expanding square with a stable outer “belt” of removed individuals. This belt prevents reinfection of the center, effectively containing the epidemic. However, when the infection probability drops below 0.5, as shown in Figure 1, this barrier may not form, resulting in continuous circulation of the infection throughout the domain.

Second, the choice of neighborhood significantly affects the model’s behavior. The Moore neighborhood doubles the infection potential compared to the von Neumann neighborhood. Consequently, when using a von Neumann configuration, edge propagation is delayed by one step, and chaotic infection dynamics become more likely unless the infection probability exceeds 80%.

In summary, while cellular automata offer a convenient and intuitive tool for visualizing the dynamics of SIR-like models, they are highly sensitive to key parameters and incorporate a strong stochastic component. Therefore, despite their illustrative value, they may not be suitable for practical applications involving realistic spatial domains, transportation networks, and individual behavioral differences.

4. Results

In this section, the proposed epidemiological models are applied to simulate the spread of COVID-19 in two Ukrainian regions: Dnipropetrovsk and Kharkiv. The primary objective is to evaluate how well the models replicate real-world infection dynamics based on data collected between 2020 and 2024.

Numerical simulations were performed by solving the system of differential equations (Equation (3)) using the classical fourth-order Runge–Kutta method. This method provides a good balance between computational accuracy and efficiency, making it well-suited for modeling nonlinear epidemiological processes. A time step of 0.1 days was chosen to ensure numerical stability and minimize cumulative errors over the extended simulation period.

It is important to note that the development of this mathematical model was initiated at the request of the regional Emergency Anti-Epidemic Commission tasked with combating COVID-19. The results obtained from these simulations were subsequently used to formulate recommendations and implement both epidemiological and organizational restrictive measures in the studied regions.

The simulation outcomes for each region are presented below.

4.1. Modeling COVID-19 Spread in the Dnipropetrovsk Region

Model inputs were based on publicly available epidemiological data from the following sources:

• Ministry of Health of Ukraine. Official website of the Ministry. Available online: https://moz.gov.ua/ (accessed on 31 July 2025);
• Public Health Center of Ukraine. Official site of UPHC, Ministry of Health Ukraine. Available online: https://phc.org.ua/ (accessed on 31 July 2025);
• State Statistics Service of Ukraine. Official statistics portal of Ukraine. Available online: https://stat.gov.ua/en (accessed on 31 July 2025) https://eurohealthobservatory.who.int (accessed on 31 July 2025);
• Johns Hopkins University. COVID-19 Dashboard. Available online: https://coronavirus.jhu.edu/map.html (accessed on 31 July 2025) https://eurohealthobservatory.who.int (accessed on 31 July 2025);
• World Health Organization (WHO). Coronavirus Disease (COVID-19) Pandemic. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 31 July 2025) https://eurohealthobservatory.who.int (accessed on 31 July 2025);
• Our World in Data. Coronavirus (COVID-19) Pandemic Data Explorer. Available online: https://ourworldindata.org/coronavirus (accessed on 31 July 2025).

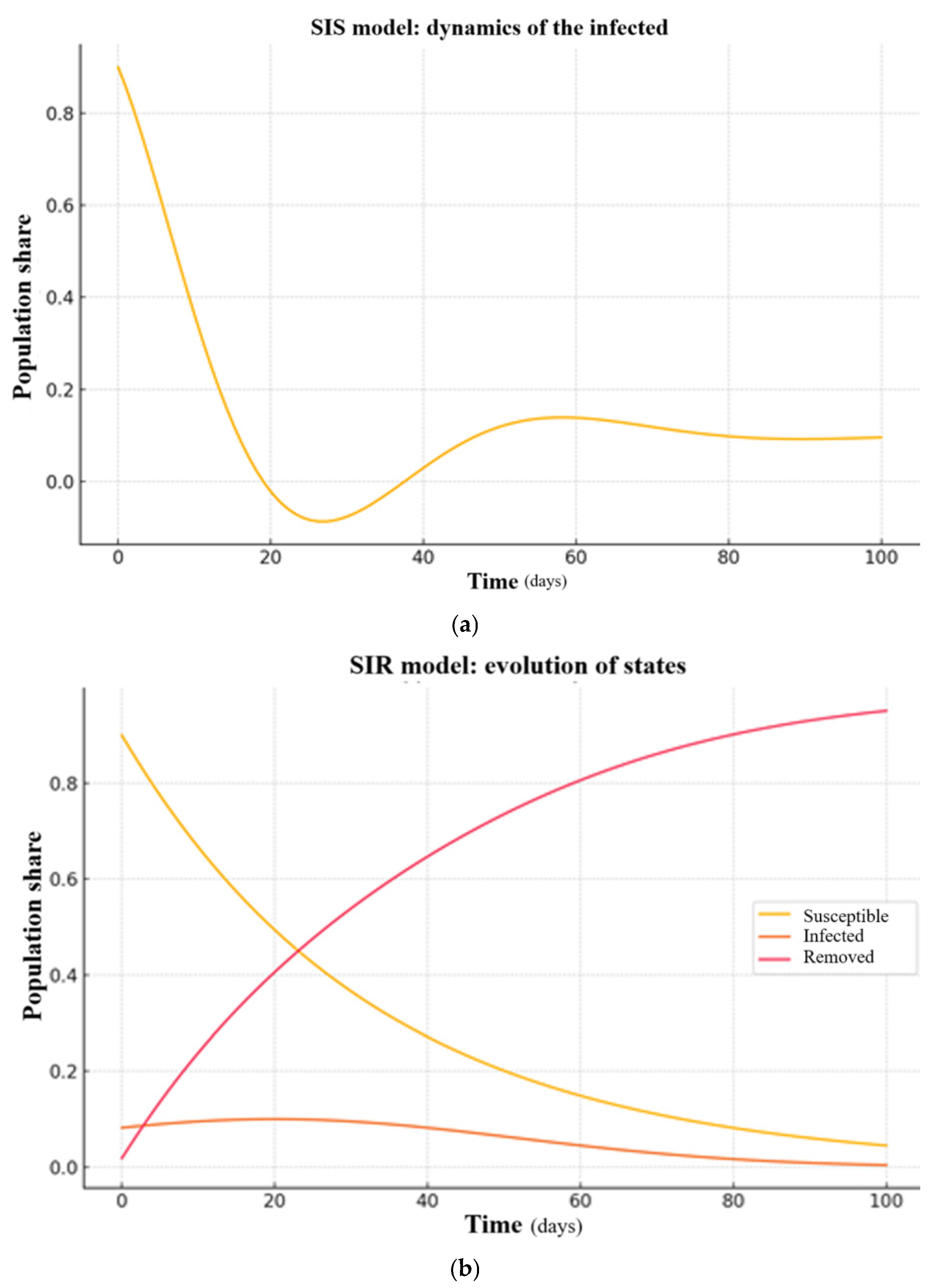
Figure 2 presents the results of numerical simulations for the Dnipropetrovsk region during the period 2020–2024. The simulation was performed using the SIS and SIR models, where the x-axis denotes time and the y-axis represents the proportion of infected individuals relative to the region’s total population (3.1 million).

The models were parameterized using observed case data, with initial conditions derived from official infection counts.

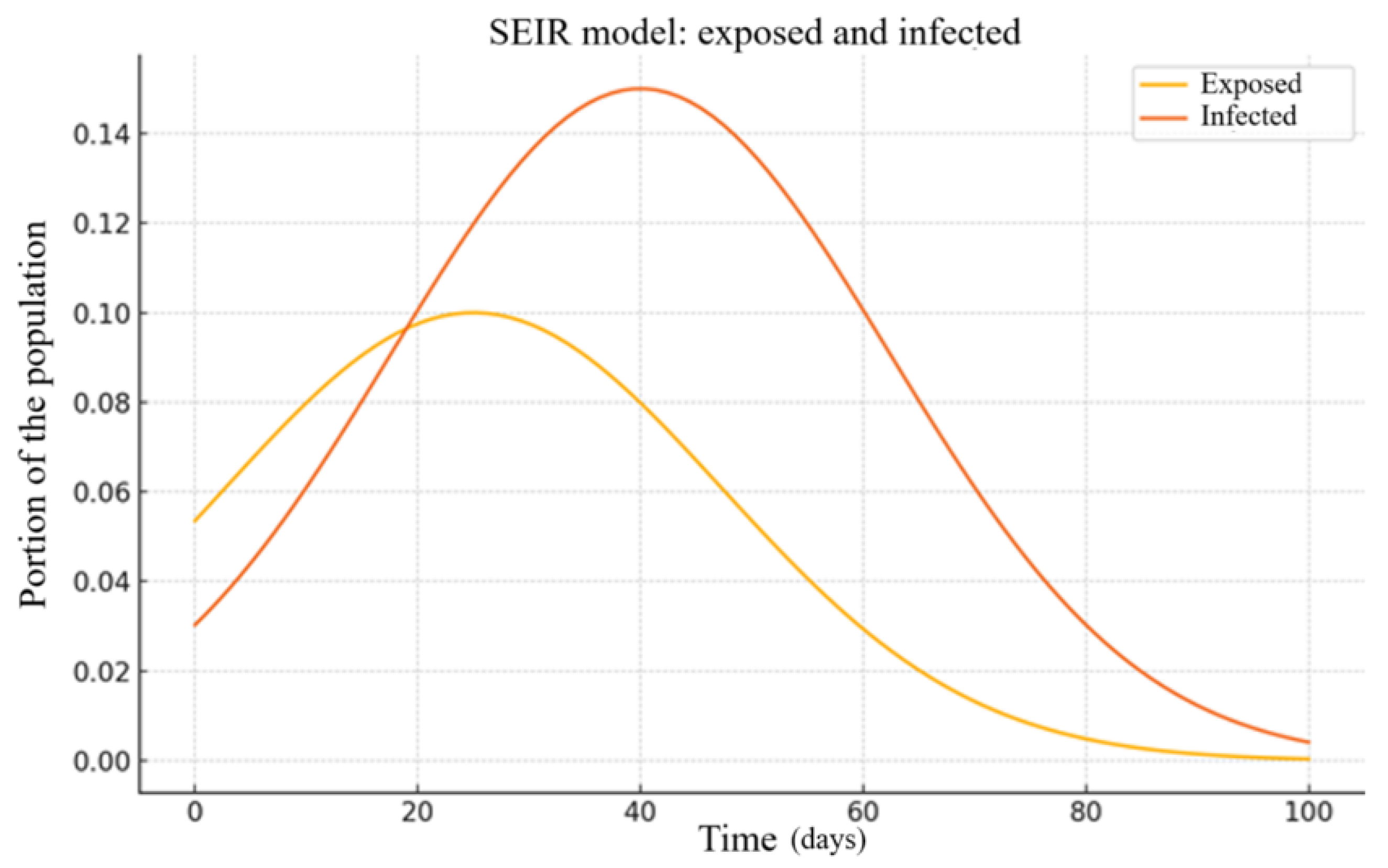
Figure 3 shows the simulation results obtained using the SEIR model for the same region and period.

Quantitative accuracy of the models was assessed by calculating the relative error between the predicted and actual infection levels.

Table 1. Relative error (%) of the SIS, SIR, and SEIR models for the Dnipropetrovsk region (2020–2024).

Period	SIS	SIR	SEIR
04.2020–06.2020	6.54%	2.88%	4.69%
07.2020–09.2020	6.92%	3.60%	3.79%
10.2020–12.2020	4.16%	7.34%	2.02%
01.2021–03.2021	3.57%	7.49%	3.61%
…	…	…	…
10.2024–12.2024	5.78%	5.86%	4.30%
Maximum error	7.64%	7.89%	5.60%

summarizes the quarterly relative error (%) for each model over the entire simulation period.

4.2. Modeling COVID-19 Spread in the Kharkiv Region

The same modeling approach was applied to the Kharkiv region using data from national and international sources mentioned above.

The total population of the Kharkiv region was estimated at approximately 2.658 million. Figure 4 shows the SIS and SIR model simulation results for the period from 2020 to 2024.

Figure 5 displays the results obtained using the SEIR model for the same region and time frame.

The quarterly relative error (%) for each model over the entire simulation period is presented in

Table 2. Relative error (%) of the SIS, SIR, and SEIR models for the Kharkiv region (2020–2024).

Period	SIS	SIR	SEIR
04.2020–06.2020	6.75%	4.99%	3.65%
07.2020–09.2020	3.71%	4.39%	4.74%
10.2020–12.2020	2.92%	2.75%	2.64%
…	…	…	…
10.2024–12.2024	2.26%	2.32%	2.37%
Maximum error	7.77%	7.50%	4.81%

.

The simulations were implemented with initial values and parameters calibrated to regional data. Although the model is continuous, rounding was avoided at each step to minimize numerical accumulation of error, especially when dealing with daily infection counts above 1000 cases.

Across both the Dnipropetrovsk and Kharkiv regions, all three compartmental models (SIS, SIR, and SEIR) were able to approximate the observed infection trends with reasonable accuracy. The SEIR model generally achieved the lowest relative errors, with values under 5.6% in Dnipropetrovsk and 4.81% in Kharkiv. These results suggest that even simplified epidemiological models can offer reliable short- and medium-term projections when properly calibrated to regional data. A more detailed interpretation of these findings is provided in the Section 5.

5. Discussion

This study extends classical compartmental models—SIS, SIR, and SEIR—to incorporate regional heterogeneity in modeling the spread of COVID-19 in the Dnipropetrovsk and Kharkiv regions of Ukraine over the period 2020–2024. By integrating region-specific epidemiological data, the models achieved acceptable predictive accuracy, with maximum relative errors of 7.64–7.89% for the SIS and SIR models and 4.81–5.60% for the SEIR model, as detailed in Table 1. These results confirm that even simplified compartmental frameworks, when calibrated with high-quality data, can effectively capture regional infection dynamics, supporting their use in public health planning.

In the Dnipropetrovsk region, both the SIS and SIR models successfully captured the general infection trends, with a maximum relative error not exceeding 8%. These models were further used to estimate healthcare needs, such as hospital capacity during peak infection periods, providing valuable inputs for local health authorities.

A similar outcome was observed in the Kharkiv region, where the SIS and SIR models also maintained acceptable predictive accuracy, and the SEIR model again proved superior with a maximum relative error of 4.81%. The simulation results were used to forecast potential surges in hospital visits and to assist in planning for regional healthcare resource allocation.

A key contribution of this research lies in adapting compartmental models to account for spatial distribution, addressing a critical limitation of point-based models that assume a homogeneous population. The proposed model, described in Equation (3), divides regions into subregions with distinct infection dynamics, reflecting factors such as population density centers and transportation flows. This approach proved particularly relevant for the Dnipropetrovsk and Kharkiv regions, where urban concentration and interregional connectivity accelerated infection spread. The numerical experiments demonstrated that the SEIR model, with its incorporation of an incubation period, consistently outperformed the SIS and SIR models, achieving lower errors (up to 5.6% in Dnipropetrovsk) due to its ability to model latent infections.

The parameter identification algorithms developed in this study were robust across diverse datasets, enabling accurate estimation of critical epidemiological quantities, such as the timing of infection peaks and hospital capacity requirements. For the Dnipropetrovsk region, daily data updates from the Regional Laboratory Center facilitated real-time model calibration, supporting forecasts over one-week to six-month horizons. In the Kharkiv region, open-source data from reputable institutions (e.g., Ministry of Health of Ukraine, World Health Organization) provided a comparable foundation for modeling. Despite challenges like underreporting—due to untested cases or home recoveries—the models maintained acceptable accuracy, underscoring their resilience to data limitations.

However, the models did not explicitly incorporate complex factors such as interregional transportation networks, road topology, or social connectivity patterns, which are known to influence infection dynamics. Surprisingly, the results remained robust, with errors below 8% for all models, suggesting that simplified compartmental frameworks can still provide valuable insights when spatial data are limited. This finding highlights the trade-off between model complexity and practical applicability: while detailed mobility data could enhance accuracy, the computational cost and data requirements may outweigh the benefits for regional forecasting.

The study also addressed practical challenges in epidemiological modeling. For instance, the identification of infection control center locations in Dnipropetrovsk was optimized based on capacity constraints and proximity, demonstrating the models’ utility for resource allocation. However, factors such as unreported cases and variable testing rates introduced uncertainties, particularly for long-term forecasts. These limitations underscore the need for comprehensive data collection and standardized reporting to improve model performance.

6. Conclusions

This study validates the efficacy of spatially adapted compartmental models (SIS, SIR, SEIR) for forecasting the spread of COVID-19 in the Dnipropetrovsk and Kharkiv regions of Ukraine. The results, supported by numerical experiments and error analyses, confirm that these models achieve sufficient accuracy (errors below 8%) for medium-term epidemiological forecasting, even without detailed mobility or social connectivity data. The SEIR model’s superior performance, with errors as low as 4.81%, highlights the importance of incorporating incubation periods in disease modeling.

Theoretically, the research demonstrates that classical compartmental frameworks can be extended to capture spatial heterogeneity, offering insights into regional infection dynamics. Practically, the models supported critical public health objectives, including forecasting hospital visits, optimizing control center locations, and informing socioeconomic response strategies. The robustness of the parameter identification algorithms, tested on high-quality regional data, further affirms their applicability for real-world scenarios.

Key contributions of this work include the following:

• Development of a novel compartmental model for simulating the spatial dynamics of infectious diseases;
• Execution of numerical simulations that closely match the real-world dynamics and consequences of COVID-19 spread in two large Ukrainian regions;
• Retrospective validation confirming the accuracy and adequacy of the proposed modeling approach;
• Formulation of practical recommendations based on simulation results, including both epidemiological and organizational restrictions for regional implementation.

Future work should focus on integrating interregional transportation and social connectivity data to enhance model accuracy, particularly for long-term forecasts. Additionally, addressing data limitations, such as underreporting, through improved testing and surveillance systems will strengthen predictive capabilities. The proposed modeling framework offers a scalable tool for managing infectious disease outbreaks at the regional level, with potential applications to future epidemics and other spatially heterogeneous environments.