Abstract
Small- and medium-sized enterprises (SMEs) face dynamic and competitive environments where resilience and data-driven decision-making are critical. Despite the potential benefits of artificial intelligence (AI), machine learning (ML), and optimization techniques, SMEs often struggle to adopt these tools due to high costs, limited training, and restricted hardware access. This study reviews how SMEs can employ heuristics, metaheuristics, ML, and hybrid approaches to support strategic decisions under uncertainty and resource constraints. Using bibliometric mapping with UMAP and BERTopic, 82 key works are identified and clustered into 11 thematic areas. From this, the study develops a practical framework for implementing and evaluating optimization strategies tailored to SMEs’ limitations. The results highlight critical application areas, adoption barriers, and success factors, showing that heuristics and hybrid methods are especially effective for multi-objective optimization with lower computational demands. The study also outlines research gaps and proposes future directions to foster digital transformation in SMEs. Unlike prior reviews focused on specific industries or methods, this work offers a cross-sectoral perspective, emphasizing how these technologies can strengthen SME resilience and strategic planning.
1. Introduction
According to the European Commission, SMEs account for of European businesses (https://single-market-economy.ec.europa.eu/smes_en) and play a central role in innovation and entrepreneurship, which are important drivers of economic activity. However, the use of AI remains difficult for many SMEs, even though it can generate new opportunities. According to the 2025 Organisation for Economic Co-operation and Development (OECD) Survey (https://www.oecd.org/digital), AI adoption among SMEs rose to , up from in 2024. Despite this increase, only half of the surveyed SMEs showed a “competent” or higher level of digital maturity [1]. Generative AI is now the most commonly used form, with of SMEs adopting it to support productivity and innovation, up from in 2024. The main barriers to broader adoption remain maintenance costs (), lack of time for training (), and hardware costs (), showing that resource constraints are a key issue in many OECD countries.
Globalization intensifies competition and increases the difficulty of accurate demand forecasting. Human decision-making is often affected by cognitive biases. As shown by Kahneman [2], people tend to rely on intuition instead of analytical reasoning, which can lead to systematic errors. SMEs operate in competitive environments where they face pressure from fast innovation cycles, price competition, and high customer turnover. These conditions make long-term planning difficult. SMEs need to identify products that offer a competitive advantage and shift resources from less productive areas without adding extra cost or effort [3]. Sustainability is another factor that influences consumer preferences. There is growing evidence that many consumers are willing to change their buying behavior based on environmental and social performance [4]. These challenges make it necessary for SMEs to adopt tools that can improve decision-making and efficiency. Heuristics, metaheuristics, ML, and hybrid optimization approaches are well-suited to deal with such problems. These methods are effective when solving complex, large-scale, and multi-objective problems, especially when the parameters are uncertain and resources are limited [5]. They are used in different areas. In supply chain management, they help to optimize production processes, distribution plans, and supplier selection [6,7]. In human resources, they support better hiring practices and help to identify causes of employee turnover [8,9]. In finance and project management, they improve portfolio allocation, project scheduling, and credit risk assessment [10]. By applying these techniques, SMEs can improve competitiveness and develop more efficient and sustainable decision-making processes [11].
This study examines how SMEs can apply these methods to support strategic decisions. It addresses three questions. First, what has been the impact of heuristics and ML on strategic decision-making in SMEs? Second, what strategies can SMEs follow to make use of these tools to gain a competitive advantage? Third, how can these techniques be adapted to fit the needs of SMEs given their specific limitations and differences from large firms? To address these questions, we adopt a cross-sectoral perspective that moves beyond isolated case studies or industry-specific applications, aiming instead to integrate insights from diverse domains. This broader view is necessary given the fragmentation of the existing literature and the limited generalizability of many prior findings. By mapping the current landscape of heuristic and machine learning applications, our goal is to bridge the gap between theoretical developments and practical implementation, providing context-aware and transferable guidance for SMEs operating under resource constraints.
The manuscript reviews the recent research on heuristics, metaheuristics, ML, and hybrid optimization approaches used by SMEs. It provides an overview of their main applications, benefits, and limitations. It also identifies the key challenges and gaps in the existing literature. In addition, it outlines future directions for research to improve the design and implementation of these methods in SME contexts. The structure of the manuscript is as follows. Section 2 presents an introduction to the optimization methods under study. Section 3 explains the research methodology, including the bibliometric analysis used to identify 11 research clusters. Section 4 analyzes these clusters and discusses key patterns and adoption trends. Section 5 presents a practical framework for SMEs to implement and evaluate optimization strategies by (i) outlining the key approaches identified in the literature; (ii) illustrating potential business impacts and suggesting new KPIs; (iii) assessing the implementation feasibility and common barriers; and (iv) offering targeted recommendations to overcome those obstacles. Section 6 concludes the paper.
2. Integrating Heuristics and Machine Learning
Linear programming (LP) and integer programming (IP) are fundamental Operations Research (OR) techniques for solving structured deterministic optimization problems. These methods efficiently handle linear objective functions and constraints, often yielding optimal solutions in polynomial time. However, their effectiveness declines in nonlinear or dynamic environments with complex constraints, non-convexity, or numerous integer variables. LP and IP struggle to model nonlinear relationships or adapt to changing parameters, limiting their applicability in real-world scenarios requiring flexibility and scalability [12]. The following subsections provide a brief overview of the main techniques used in this study. A more detailed review of the literature is presented in Section 4 and Section 5.
2.1. Heuristics and Metaheuristics
Heuristics and metaheuristics provide flexible alternatives to exact methods to address complex optimization challenges. Traditional heuristics make decision-making easier using rule-based strategies, helping to tackle uncertain situations efficiently when little information is available. Greedy algorithms, for instance, approximate solutions by following problem-specific rules. However, heuristics can lead to systematic errors when applied broadly, particularly in strategic planning, due to cognitive biases. While they offer stability, they often lack adaptability to dynamic business conditions compared to advanced decision algorithms [13]. Managers often avoid taking risks because they fear the adverse effects of their decisions. In SMEs, limited resources can affect decision-making heavily. This leads managers to focus on reducing risks rather than seeking long-term growth opportunities. This bias, identified by Kahneman and Tversky [14], can result in overly cautious decision-making, especially when managers relate their judgments on current financial performance. Consequently, opportunities for expansion or market entry may be missed as psychological barriers distort the evaluation of future potential, reinforcing conservative strategies [15].
Unlike heuristics, metaheuristics offer systematic iterative approaches for solving complex nonlinear optimization problems. Techniques such as genetic algorithms (GAs) and particle swarm optimization (PSO) balance exploration and exploitation to refine solutions, although they do not guarantee a global optimum [16]. Their ability to manage trade-offs between short-term risks and long-term gains makes them valuable for SMEs, where exact methods are impractical. By reducing cognitive biases like loss aversion, metaheuristics assist managers in making better decisions. This improvement helps them to optimize strategic choices for sustainable growth [17].
2.2. Machine Learning
ML has become a powerful tool for decision-making, offering the ability to uncover hidden patterns, model complex relationships, and adapt to dynamic environments. ML techniques, particularly deep learning (DL) and reinforcement learning (RL), have demonstrated significant advantages over traditional approaches by efficiently handling intricate scenarios, reducing computational time, and exploring solution spaces more effectively [18]. Unlike some traditional methods, DL provides a robust framework for tackling optimization problems involving nonlinear relationships, high-dimensional spaces, and real-time data. Deep neural networks, for example, have been successfully applied to resource allocation, portfolio selection, and dynamic decision-making, where variable relationships are complex and evolving [19]. RL further improves optimization by facilitating continuous learning and adaptability in real-time decision-making. Algorithms like Q-learning and policy gradient methods perform well when decisions need to adapt to changing conditions. A key application is resource allocation in cloud computing, where RL efficiently distributes resources based on usage patterns and system performance [20].
While traditional optimization methods remain effective for well-structured deterministic problems, they often struggle with real-world challenges that involve nonlinearity, uncertainty, and dynamic constraints. ML approaches are more flexible than traditional methods because they can model complex relationships without strict mathematical rules. Moreover, DL models excel in managing large-scale high-dimensional datasets, improving predictive accuracy and scalability, making them particularly well-suited for modern optimization challenges [21].
2.3. Hybrid Approaches
As real-world optimization problems grow increasingly complex, hybrid approaches that integrate traditional heuristics with ML have gained prominence [22,23]. Heuristics are particularly effective at quickly identifying good solutions in NP-hard combinatorial problems, making them valuable for tackling computationally intensive tasks. However, they often suffer from premature convergence to local optima and rely heavily on problem-specific rules, limiting generalization [24]. To address these limitations, ML components can be incorporated to introduce adaptability and learning capabilities to guide the search process. By doing so, hybrid methodologies can combine the strengths of heuristics and ML. In GAs, ML changes mutation rates and crossover strategies as the fitness landscape evolves. This helps to increase search efficiency in real time. Additionally, ML models can predict how good the solutions from heuristics are, allowing algorithms to prioritize promising areas while discarding less effective ones. This integration finds reasonable solutions faster and improves the chances of achieving the best solution [25].
RL has also been successfully integrated with heuristics, enabling RL agents to optimize decision rules dynamically. In scenarios like the traveling salesperson problem (TSP), RL enhances heuristics by adjusting decision strategies based on problem-specific characteristics, improving solution quality and avoiding local optima [12]. Similarly, metaheuristic techniques such as PSO and ant colony optimization (ACO) can improve from ML-driven parameter tuning. By using DL models, these algorithms can adjust their settings based on ongoing feedback, which helps to make their search processes more efficient [26]. Several case studies highlight the effectiveness of hybrid approaches in complex optimization tasks. In supply chain optimization, hybrid models combining GAs with neural networks (NNs) have enhanced decision-making by learning from historical data. The NN identifies patterns that guide the GA’s search, leading to better trade-offs between competing objectives [27]. Similarly, in industrial scheduling, tabu search augmented with ML has improved production planning. ML predicts configurations likely to cause bottlenecks, enabling the search algorithm to avoid inefficiencies [28].
3. Research Methodology: Exploring Heuristics and Machine Learning for Optimization
The literature review is based on articles retrieved from the Scopus database, which has a wide range of peer-reviewed journals, conference papers, and academic resources across multiple disciplines. Moreover, we decided to rely solely on Scopus because it provides broad and interdisciplinary coverage, especially in the fields relevant to this study (e.g., engineering, computer science, and decision sciences). The initial search yielded close to 100,000 documents, which we consider offering a sufficiently comprehensive landscape of the field, capturing a wide range of perspectives and contributions. Given this volume and diversity, we believe that incorporating additional databases would not substantially change the insights or representativeness of the dataset, while it would increase redundancy and complexity.
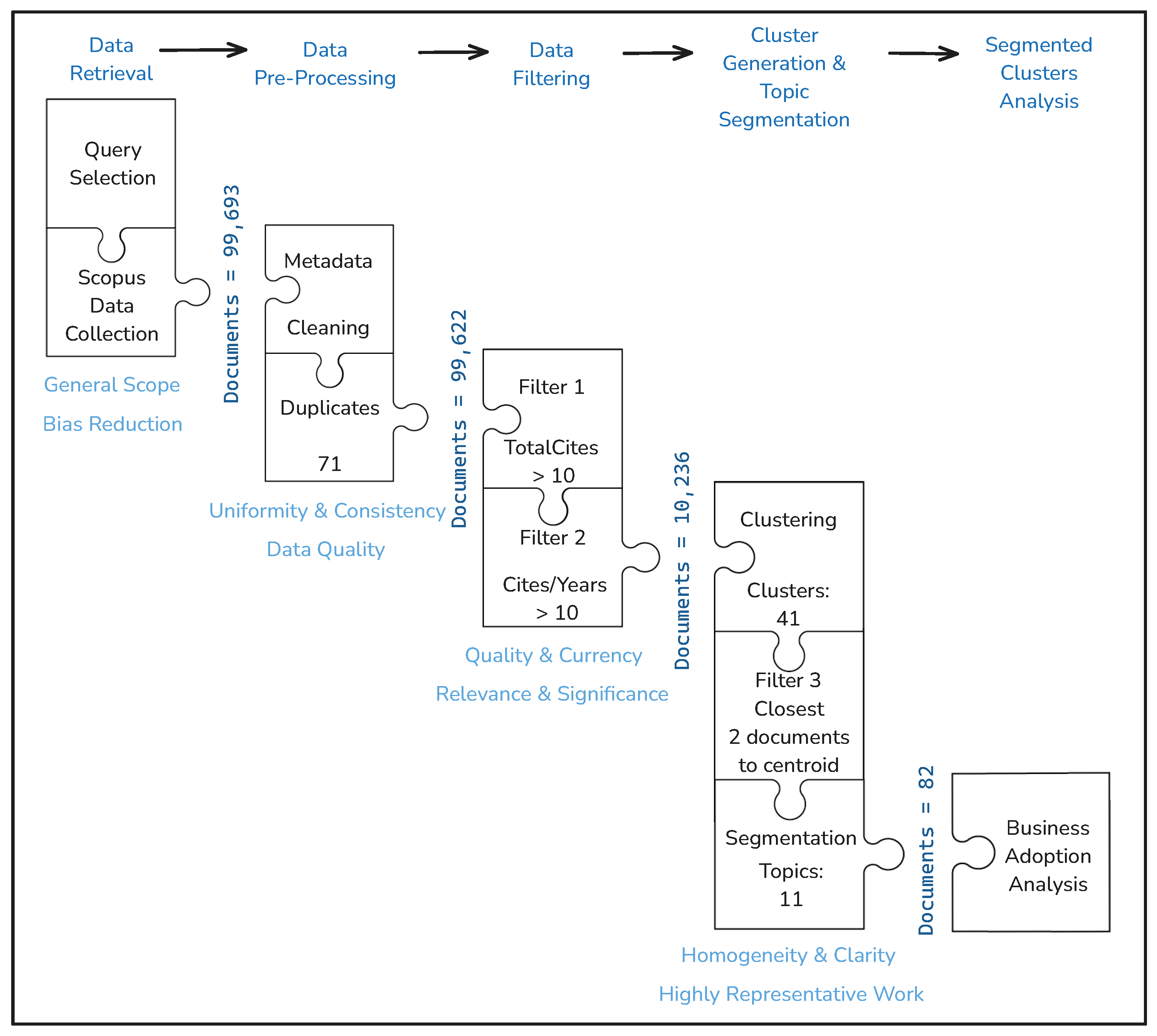
The first step was to gather articles broadly to obtain a balanced view of the research area, reduce bias, and include different perspectives. The search targeted titles, abstracts, and keywords containing terms such as “heuristic”, “optimization”, “machine learning”, or “hybrid”, alongside strategic or complexity-related terms like “strategic”, “multi-objective”, “multi-criteria”, “combinatorial”, “NP-hard”, or “uncertainty.” The query focused on English-language articles published between 2014 and 2024 within Engineering, Computer Science, and Mathematics. Figure 1 shows that the search retrieved 99,693 documents. During preprocessing, metadata was cleaned and standardized, and duplicate removal identified 71 redundant papers (), resulting in a final dataset of 99,622. Next, a filtering phase ensured that the selected studies met the relevance, significance, quality, and currency criteria. The first filter excluded articles cited fewer than 10 times. A second filter required an average of more than 10 citations per year (using 2024 as the reference year) to ensure the inclusion of recent influential studies and long-standing foundational works. After filtering, 10,236 articles remained.
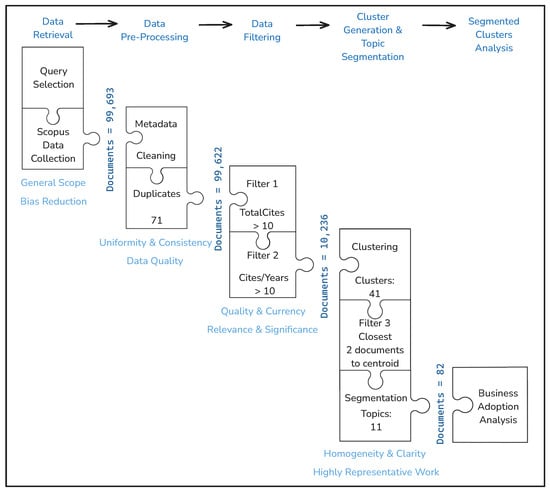
Figure 1.
Analysis process: steps to filter and refine the dataset for SME adoption analysis.
Following filtering, clustering and topic segmentation were conducted to enhance thematic coherence and organization. Grouping similar clusters into segments ensured clarity and representation, while selecting the closest two articles to each cluster centroid identified the most representative studies. The bibliographic data was processed using DuckDB [29]. Uniform Manifold Approximation and Projection (UMAP) was applied to reduce dimensionality while preserving structural information. The reduced data was then clustered using BERTopic [30], with the SentenceTransformer model generating dense vector representations of abstracts. BERTopic applied probabilistic topic modeling, identifying 41 clusters and improving document distribution understanding. To refine semantic relationships, BERTopic combined UMAP [31] for dimensionality reduction with Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN) for clustering. UMAP preserved local structures, enabling meaningful pattern recognition in high-dimensional data. HDBSCAN can find clusters of different sizes and densities, which makes it great for understanding topics. Unlike traditional methods, HDBSCAN can identify topics even when there is noise or clusters vary in size. It also provides probabilistic topic assignments that show the detailed nature of document content. This helps to improve the accuracy of grouping documents and identifying topics. The clustering pipeline produced a robust segmentation outcome. An additional cluster, Cluster , representing 3136 outlier publications, was excluded. After cluster identification, centroids were determined, and a third filter was applied to select the two closest documents per cluster as representative studies. All in all, we identified 11 main groupings or topics, leading to a final selection of 82 representative documents for further analysis in the next section.
4. Exploring Cluster Grouping: Patterns and Insights
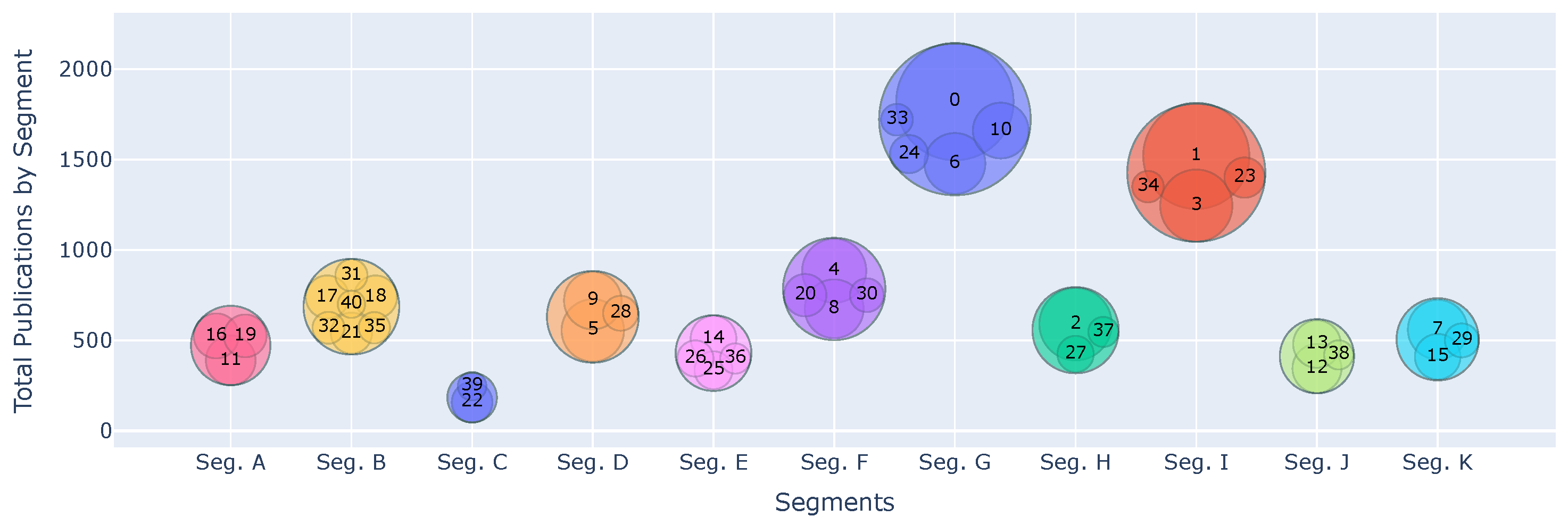
Figure 2 provides a visual synthesis of the aggregated size of each cluster group.
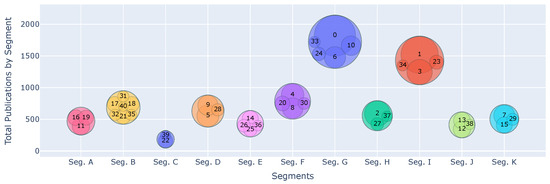
Figure 2.
Total publications by segment (large bubbles), with cluster numbers indicated.
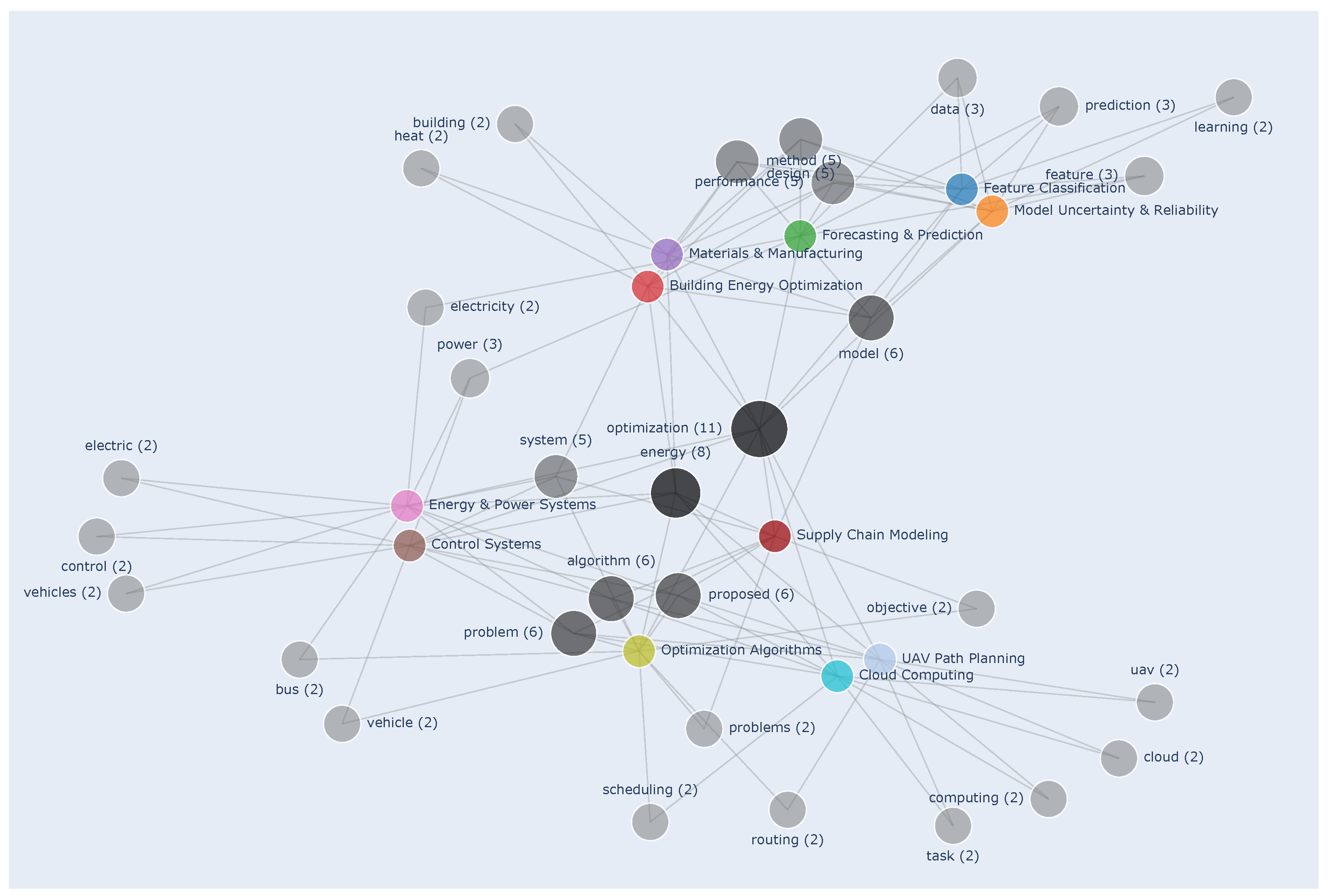
The relationships between these clusters and their associated keywords are visualized in Figure 3. This visualization displays the connections between clusters of publications and their most important associated keywords. Only keywords appearing in at least two segments are shown. The frequency of each keyword across different segments is represented by the intensity of the color, with more frequent keywords in darker shades, and the node size, which increases with higher frequency.
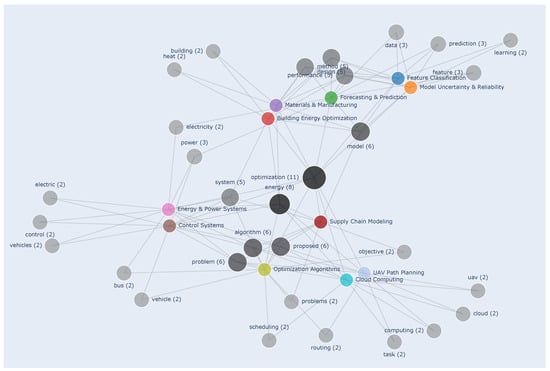
Figure 3.
Keyword frequency across segments (keywords are sized and shaded by frequency, with segments color-coded; frequencies are in parentheses). This plot shows which keywords, identified as most relevant by the clustering model, are distinctive to specific clusters and which act as semantic bridges across segments.
4.1. Segment A: Multi-Domain Feature Engineering and Uncertainty Quantification
This segment focuses on optimizing model performance through data-driven feature engineering and ML techniques, applied across various domains, such as computer vision and decision systems. Cluster 16 combines fuzzy logic with structured criteria sets to manage uncertainty in decision-making processes. Ashraf et al. [32] introduced spherical fuzzy sets with Dombi operations, improving uncertainty modeling and aggregation in multi-criteria decision-making. Akram and Martino [33] expanded this by developing generalized hybrid frameworks that incorporate picture, spherical, and t-spherical fuzzy soft rough sets to address complexities and inconsistencies, showing greater modeling robustness compared to traditional fuzzy approaches. Cluster 19 focuses on optimal feature selection to enhance model accuracy using techniques such as dimensionality reduction and feature scoring. Zhang et al. [34] proposed a particle swarm optimization-based feature selection method that balances accuracy with feature costs. Additionally, Wang et al. [35] introduced a differential evolution approach to eliminate irrelevant features, improving classification performance and offering greater diversity in feature selection.
Cluster 11 integrates image segmentation with ML techniques for tasks like object detection. Zhang et al. [36] presented an uncertainty-guided framework for semi-supervised medical image segmentation. Xiao et al. [37] enhanced magnetic resonance (MR) image segmentation by combining limited labeled data with synergy between convolutional neural networks (CNNs) and transformer models, achieving improved segmentation results.
4.2. Segment B: Data-Driven Modeling and Uncertainty Management—Cross-Domain Applications
This segment explores data-driven methodologies for modeling complex systems while addressing uncertainty by focusing on domains such as molecular learning, physics-based reliability, geo-technical modeling, and battery state estimation. Cluster 21 applies ML to chemical and molecular systems for drug design and molecular modeling. Gao and Coley [38] investigated generative models for molecular discovery, highlighting challenges related to synthesizability. Similarly, Abbasi et al. [39] introduced a feedback Generative Adversarial Network (GAN) with an encoder–decoder framework, incorporating stereo-chemical information to enhance drug design and generate tailored drug-like molecules. Clusters 17, 31, and 32 focus on physics-informed models, Bayesian methods, and structural reliability techniques to predict damage, fatigue, and system reliability under uncertainty. In Cluster 17, Wang et al. [40] presented a reliability-based optimization model for thermal structure design, using random, interval, and fuzzy variables to address uncertainties, improving computational efficiency with a sub-interval vertex method. Yoo et al. [41] proposed a multi-fidelity probabilistic optimization framework for composite structures, enhancing early-stage design accuracy while reducing computational time through reliability analysis methods validated by engineering examples. Cluster 31 addresses physics-based Bayesian methods for uncertainty quantification. Xiao et al. [42] introduced a data-driven physics-informed Bayesian framework to quantify and reduce model-form uncertainties in Reynolds-averaged Navier–Stokes (RANS) simulations, incorporating empirical priors and physical constraints. Geneva and Zabaras [43] proposed a framework that uses Bayesian deep neural networks to model Reynolds stress tensors and Monte Carlo simulations for uncertainty propagation, improving RANS simulation accuracy in turbulence modeling.
Cluster 32 explores structural damage identification techniques. Bandara et al. [44] introduced a neural network-based method using frequency response function data, focusing on feature selection and optimal sensor placement to improve damage detection in noisy environments. Yin et al. [45] proposed a physics-guided deep neural network for identifying bridge damage caused by moving vehicle loads, showing its effectiveness through simulations and field tests for real-world bridge monitoring applications. Clusters 18 and 40 address geo-technical and hydrological challenges. In Cluster 18, Ahmed et al. [46] evaluated six ML algorithms for daily river water level prediction, finding that Gaussian process regression provides superior accuracy for flood risk management. Wang et al. [47] presented a weight-based feature selection approach for water quality prediction, demonstrating the effectiveness of support vector machines (SVMs) and long short-term memory networks in achieving high prediction accuracy.
Cluster 40 focuses on geo-technical challenges in tunneling. Liu et al. [48] introduced a multi-objective optimization method for tunnel boring machine parameters, incorporating rock–machine interaction and muck information to enhance excavation efficiency. Liu et al. [49] developed a hybrid data-driven model that combines deep neural networks with physical knowledge to predict tunnel-induced ground settlement and quantify risks under uncertain conditions. Lastly, Cluster 35 addresses state-of-charge (SOC) estimation for lithium-ion batteries. Mohammadi [50] presented an improved Coulomb-counting algorithm for SOC estimation, achieving a maximum error over a ten-year period. Wu et al. [51] proposed a PCA–PSO–BPNN (Principal Component Analysis–PSO–back–propagation neural network) method for state-of-health (SOH) estimation, optimizing battery energy management and lifespan under varying conditions.
4.3. Segment C: Energy Demand and Wind Power Forecasting
This segment examines different aspects of the energy supply–demand equation, focusing on electricity demand prediction and wind power forecasting. Within this scope, Cluster 39 addresses electricity demand forecasting. Wang et al. [52] developed a hybrid model optimized through a multi-objective ant lion algorithm, significantly improving accuracy and stability in annual electricity consumption predictions across China. Expanding on this, Wu et al. [53] introduced a modified generalized regression neural network, incorporating a non-dominated sorting-based multi-objective cuckoo search to enhance short-term load forecasting, balancing predictive accuracy and operational stability for power system management. Cluster 22 focuses on wind power forecasting, emphasizing precision and robustness. Liu et al. [54] presented a hybrid model that outperforms conventional approaches in both accuracy and stability across multiple locations, with sensitivity analysis confirming its reliability. In a complementary study, Nie et al. [55] proposed a bi-forecasting system designed for simultaneous point and interval wind speed predictions. This system integrates the multi-objective multi-verse optimization (MOMVO) algorithm for weight optimization alongside Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) for time-series preprocessing, demonstrating improved forecasting performance.
4.4. Segment D: Energy Efficiency and Thermal Performance in Building Systems
Segment D focuses on energy optimization in building systems, addressing energy-efficient design, exergy-based efficiency improvements, and heat transfer mechanisms. Within this segment, Cluster 9 prioritizes energy-efficient building design and resident comfort. Yu et al. [56] developed a multi-objective optimization model that integrates the Non-dominated Sorting Genetic Algorithm II (NSGA-II) with simulation-based back-propagation networks to balance energy consumption and indoor thermal performance in green building design. Expanding on this approach, Li et al. [57] introduced a simulation-based energy–comfort optimization model for green retrofits, identifying key building parameters and generating optimal solutions, which are validated through a case study on a school building in Wuhan, China. Cluster 5 examines exergy cycle efficiency improvements. Behzadi et al. [58] optimized a waste-to-energy plant utilizing an organic Rankine cycle, identifying R123 as the most efficient working fluid to enhance system efficiency and reduce costs. Complementing this, Zhang et al. [59] proposed an integrated compressed carbon dioxide energy storage and organic Rankine cycle system, optimizing power output and exergy efficiency through thermodynamic and exergoeconomic analyses. Cluster 28 explores thermal transfer and pressure system optimization. Arie et al. [60] enhanced the performance of manifold–microchannel plate heat exchangers by developing a hybrid numerical modeling method to improve heat transfer efficiency while minimizing pressure drop. In a related study, Attarzadeh et al. [61] integrated triply periodic minimal surfaces into heat exchanger designs to facilitate efficient waste heat recovery, employing a GA to optimize thermal performance and key design variables.
4.5. Segment E: Advanced Materials and Manufacturing
Segment E covers topics in materials science and manufacturing. It includes how to make concrete, the steps involved in machining, designing structures for safety, and improving electric motors. Within this segment, Cluster 26 focuses on optimizing concrete composition for high-strength applications. Behnood and Golafshani [62] examined the use of silica fume to enhance mechanical properties and reduce environmental impact, employing artificial neural networks (ANNs) combined with a multi-objective optimization method to predict and simplify compressive strength modeling. In a related study, Amiri et al. [63] investigated the incorporation of coal waste as a sustainable alternative in concrete mixtures, optimizing material proportions to maximize compressive strength while minimizing water absorption. Cluster 14 examines machining and cutting process optimization. Younas et al. [64] applied gray relational analysis to optimize the machining parameters for Ti6Al4V alloy, enhancing energy efficiency, tool lifespan, and surface integrity. Similarly, Khan et al. [65] employed a Taguchi–gray integrated approach to improve sustainability, productivity, and efficiency in machining by optimizing tool wear, surface roughness, and specific cutting energy. Cluster 25 addresses crashworthiness and energy absorption in structural design. Wu et al. [66] optimized multi-cell thin-wall structures, demonstrating the influence of cell number and topology on energy absorption through simulation and finite element analysis. Expanding on this, Chen et al. [67] introduced novel design methods for thin-walled hybrid multi-cell structures, revealing superior energy absorption performance through experimental testing and numerical analysis. Cluster 36 focuses on the optimization of permanent magnet motor designs. Xiang et al. [68] developed a brushless flux-switching motor for hybrid electric vehicles, applying multilevel optimization techniques to enhance torque, reduce ripple, and minimize magnetic coupling. In a complementary study, Zheng et al. [69] designed multi-permanent magnet motors to increase torque output while reducing dependence on rare-earth materials, integrating low-cost ferrite magnets to maintain competitive pricing despite manufacturing challenges.
4.6. Segment F: Control Strategies for Energy Systems and Autonomous Vehicles
Segment F explores optimization and control strategies across energy systems and autonomous vehicles. Within this segment, Cluster 8 focuses on Proportional–Integral–Derivative (PID)-based frequency control in power systems. Lu et al. [70] introduced a robust Proportional–Integral (PI) controller using constrained population extremal optimization for multi-area load frequency control, demonstrating superior performance under various disturbances compared to conventional methods. Similarly, Annamraju and Nandiraju [71] proposed an adaptive fractional-order fuzzy-PID controller for load frequency control in renewable energy-integrated systems, achieving enhanced dynamic performance metrics. Cluster 4 examines nonlinear control strategies under uncertainties. Kang et al. [72] presented an event-triggered model-predictive control approach with learning terminal cost for robotic manipulators, effectively balancing computational efficiency and performance in the presence of model uncertainties. In a related study, Chen and Dong [73] introduced an approximate optimal tracking control framework that leverages adaptive neural networks and prescribed performance control to address both partially known and unknown system dynamics. Cluster 30 investigates traffic control for autonomous vehicles. Shao and Sun [74] developed a robust optimization-based vehicle control strategy for intersections, optimizing fuel efficiency and safety while maintaining computational efficiency. Expanding on this, Li et al. [75] proposed a deep reinforcement learning-based eco-driving strategy for automated hybrid electric vehicles, co-optimizing fuel economy, safety, and efficiency in connected traffic environments with signalized intersections. Cluster 20 focuses on energy management strategies for electric vehicles (EVs). Yang et al. [76] introduced a model-predictive-control-based energy management system (EMS) for plug-in hybrid electric vehicles, optimizing fuel economy and safety in vehicle-following scenarios. Similarly, Yuan et al. [77] developed a real-time EMS for fuel cell hybrid vehicles, minimizing hydrogen consumption and optimizing battery usage while ensuring fuel cell efficiency under diverse driving conditions.
4.7. Segment G: Management of Renewable Energy Systems
Segment G covers different parts of renewable energy systems, including electric vehicle charging, power distribution, and managing energy in homes. Within this segment, Cluster 10 focuses on the optimization of electric vehicle charging systems and infrastructure. In this context, Li et al. [78] explored vehicle-to-grid integration, emphasizing the role of aggregators in optimizing contract capacity and reducing charging costs through chance-constrained programming. A study by An et al. [79] presented a charging model designed to reduce charging time and improve efficiency in cities. This model meets the need for better scheduling tools. Cluster 6 examines power distribution networks, particularly voltage regulation. Biswas et al. [80] employed a multi-objective evolutionary algorithm based on decomposition (MOEA/D) to optimize the placement of distributed generators and shunt capacitors, reducing power losses and improving system reliability. In a complementary approach, Wu et al. [81] introduced a random fuzzy theory framework to manage uncertainties in renewable energy generation, focusing on power loss reduction and voltage stability in distribution network reconfiguration. Cluster 0 explores the broader optimization of renewable energy systems and their integration into power grids. Sedighizadeh et al. [82] optimized residential microgrid scheduling by integrating combined cooling, heating, and power systems with plug-in hybrid vehicles and energy storage, employing scenario-based methods to manage uncertainties. In a similar way, Shen et al. [83] developed an energy storage optimization method for multi-energy microgrids, minimizing costs and emissions through a multi-objective optimization approach coupled with demand response strategies. Cluster 24 focuses on the optimization of residential energy consumption. Khalid et al. [84] introduced an advanced appliance scheduling framework using the Generalized Weighted Cooperative Search Optimization (GWCSO) algorithm to optimize electricity costs, user comfort, and the peak-to-average ratio under real-time pricing signals. Regarding this approach, Waseem et al. [85] proposed a load-shifting strategy for smart homes, leveraging hybrid optimization techniques to minimize costs and peak-to-average ratio while maintaining user comfort through day-ahead and real-time appliance coordination. Finally, Cluster 33 addresses power system resilience and recovery from disruptive events. Sang et al. [86] presented a framework for optimizing restoration sequences and skeleton-network reconfiguration in coupled power and gas systems, emphasizing the role of resources and repair modes in enhancing resilience. In a related study, Xu et al. [87] developed a two-stage stochastic model for post-disaster restoration of interdependent infrastructures, highlighting the importance of system interdependencies in improving resilience.
4.8. Segment H: Supply Chain and Logistics Management
Segment H incorporates three clusters focused on applying optimization techniques to various aspects of supply chain management, logistics, and emergency response. Cluster 37 addresses maritime logistics optimization. Ma et al. [88] developed a multi-objective model for optimizing ship routes, speed, and fleet size, employing an improved genetic algorithm to reduce costs, time, and emissions. Elmi et al. [89] proposed a multi-objective model for ship schedule recovery, minimizing late arrivals and profit loss due to disruptions in liner shipping. Cluster 2 focuses on sustainable supply chain management. Sadeghi Rad and Nahavandi [90] developed an integrated model for a closed-loop green supply chain, optimizing supplier selection with quantity discounts to reduce costs and emissions while maximizing customer satisfaction. Mohebalizadehgashti et al. [91] proposed a multi-objective model for green meat supply chains, minimizing costs and emissions while maximizing capacity utilization, thus integrating environmental concerns into logistics management. Cluster 27 addresses optimization in emergency response and disaster management. Bozorgi-Amiri and Khorsi [92] developed a multi-objective stochastic model for humanitarian relief logistics, minimizing shortages, travel time, and costs during pre- and post-disaster operations. Liu et al. [93] proposed a robust optimization model for post-disaster relief logistics, focusing on supply mobilization and helicopter deployment under uncertainties related to demand and transportation.
4.9. Segment I: Algorithms for Complex Operational Problems
Segment I contains four clusters collectively addressing optimization challenges in different operational contexts, from evolutionary algorithm development to specific applications in manufacturing, logistics, and public transportation. Cluster 1 addresses evolutionary algorithms for optimization. Cheng et al. [94] developed a method for creating test problems for large-scale multi/many-objective optimization, enhancing variable-objective correlations. Qu et al. [95] introduced a grid-guided particle swarm optimizer for multi-modal and multi-objective problems, improving search efficiency and diversity through a grid-based approach, outperforming existing methods on benchmark functions. Cluster 3 addresses production scheduling optimization. Dai et al. [96] proposed a multi-objective model for flexible job shop scheduling, minimizing energy consumption and makespan using an enhanced genetic algorithm. Jiang et al. [97] developed an energy-efficient scheduling model for aerospace components, optimizing energy consumption, makespan, and costs in flexible job shops through a novel algorithm enhancing efficiency and resource utilization. Cluster 23 addresses vehicle routing and logistics optimization. Guo et al. [98] developed a robust dynamic multi-objective method optimizing carbon emissions, waiting times, and vehicle numbers, incorporating dynamic demands and hard time windows. Hu et al. [99] proposed a robust optimization model and two-stage algorithm for vehicle routing with hard time windows under demand and travel time uncertainty, balancing customer requirements with cost and distance minimization. Cluster 34 addresses public transit optimization. Lu et al. [100] proposed a joint optimization approach for passenger flow control and train timetabling on congested metro lines, using integer linear programming models for both deterministic and uncertain demand scenarios. Hu et al. [101] developed a collaborative optimization model integrating timetable scheduling, passenger flow control, and skip-stop patterns, employing robust optimization to balance service levels and costs in congested metro systems.
4.10. Segment J: Cloud and Edge Computing for Internet of Things (IoT) and Mobile Systems
Segment J incorporates three clusters addressing optimization challenges in distributed computing paradigms, from cloud-based workflow management to fog computing for Internet of Things (IoT) and mobile edge computing for mobile devices. Cluster 13 addresses cloud workflow scheduling optimization. Mohammadzadeh et al. [102] proposed a multi-objective approach combining Antlion and Grasshopper Optimization algorithms with chaos theory to minimize makespan, cost, and energy consumption in scientific workflows. Alsadie [103] introduced a Metaheuristic-based Dynamic Virtual Machine Allocation (MDVMA) framework and task scheduling using NSGA-II, optimizing energy usage, makespan, and cost simultaneously in cloud environments. Cluster 38 addresses fog computing for IoT optimization. Liu et al. [104] proposed a framework integrating cloud–fog control middleware to optimize IoT service placement, using a cuckoo search algorithm for multi-objective optimization of resource utilization and Quality of Service (QoS). Mahboubeh Salimian and Shahidinejad [105] developed a fog–cloud middleware framework for IoT service placement, focusing on reducing latency and improving resource management for real-time applications in fog environments. Cluster 12 addresses mobile edge computing optimization. Ning et al. [106] proposed an iterative heuristic resource allocation algorithm (IHRA) for optimizing computation offloading in IoT applications, addressing single- and multi-user scenarios across cloud and edge computing. You and Tang [107] developed a particle swarm optimization-based task offloading strategy for mobile edge computing, focusing on managing computing-intensive and delay-sensitive tasks to optimize energy consumption and reduce delay.
4.11. Segment K: Unmanned Aerial Vehicle (UAV) and Wireless Sensor Networks
Segment K includes three clusters addressing optimization challenges in aerial and ground-based wireless networks, focusing on communication efficiency, path planning, and network routing. Cluster 15 addresses beamforming and channel optimization for UAV communications. Zhang et al. [108] proposed a robust Non-Orthogonal Multiple Access (NOMA) beamforming design for Multiple-Input Single-Output (MISO) channels, maximizing worst-case sum rate under channel uncertainties. Pan et al. [109] developed a dual-based iterative algorithm for power control and channel assignment in Device-to-Device NOMA (D2D-NOMA) networks, optimizing D2D sum rate while meeting cellular user requirements. Cluster 7 addresses UAV path planning optimization. Fu et al. [110] developed a framework for multi-UAV task allocation, optimizing energy efficiency and addressing flight safety and network security. Zhu et al. [111] proposed a deep reinforcement learning algorithm for UAV path planning in cellular networks, incorporating prioritized experience replay and game theory to enhance learning and solve various subproblems in UAV-assisted networks. Cluster 29 addresses wireless sensor network routing optimization. Rao et al. [112] proposed a PSO-Enhanced Colliding Hill Strategy (PSO-ECHS) algorithm for energy-efficient cluster head selection, considering intra-cluster distance, sink distance, and residual energy. Mosavvar and Ghaffari [113] developed a firefly algorithm-based method for optimizing cluster head selection and data aggregation, improving network lifetime and efficiency compared to the Low-Energy Adaptive Clustering Hierarchy (LEACH) and Shuffled Frog Algorithm (SFA) methods.
5. Optimization in SMEs: Optimization Strategy Implementation and Impact Assessment
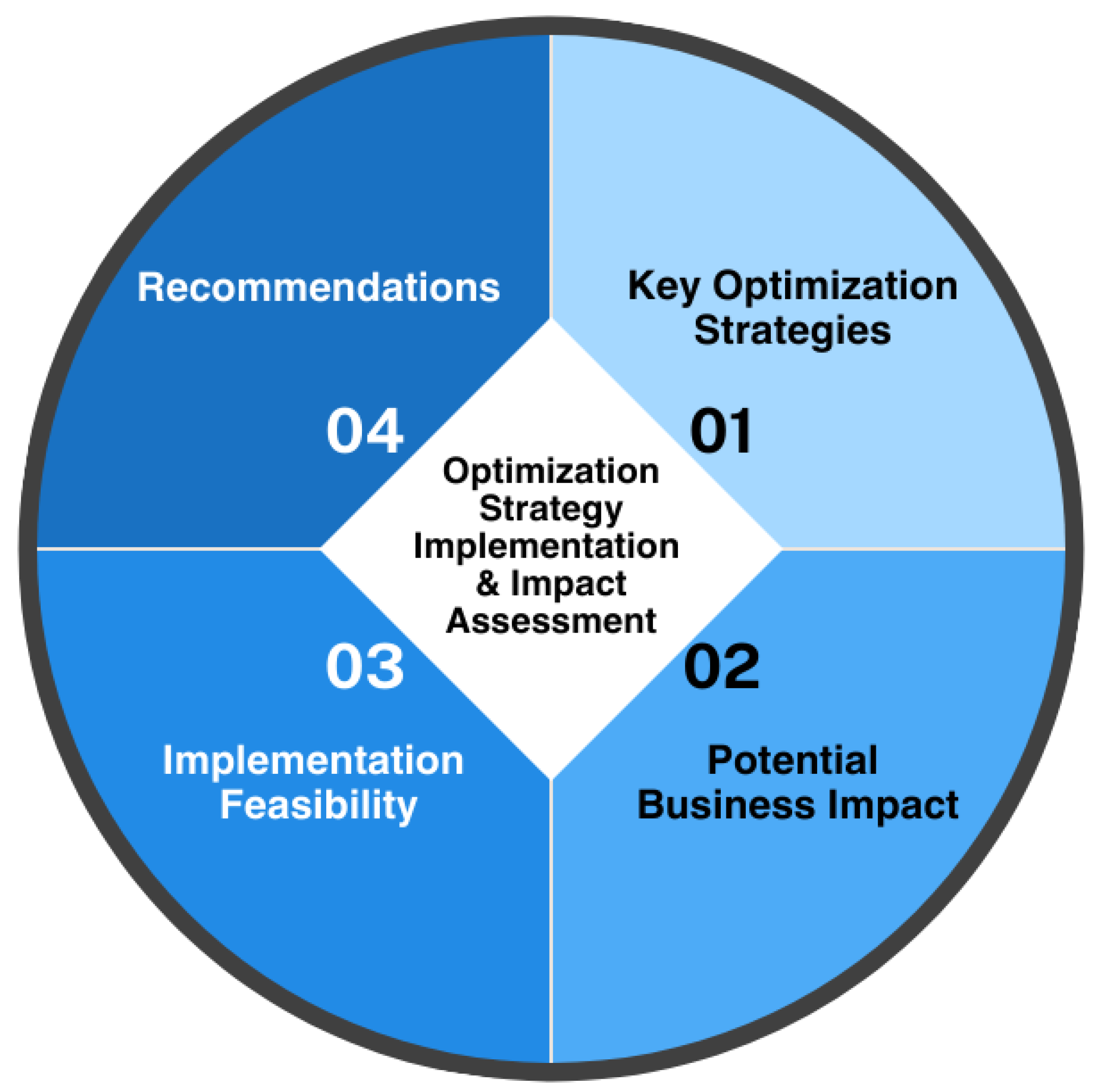
This section describes a framework for implementing optimization strategies and assessing their impact on SMEs. Figure 4 shows the sequential steps in constructing the framework. It could also be followed as an iterative process.
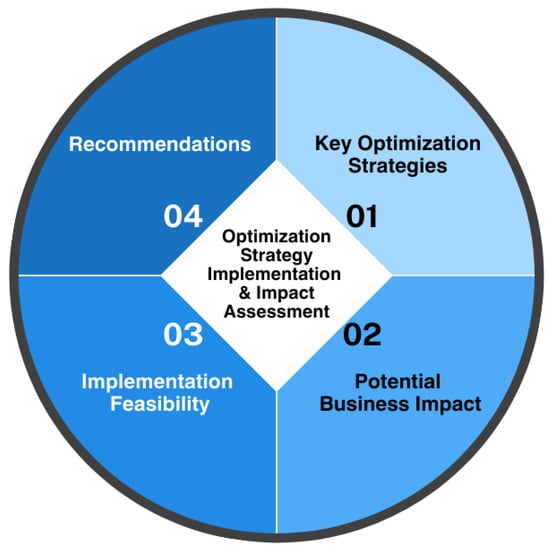
Figure 4.
Optimization in SMEs: optimization strategy implementation and impact assessment.
5.1. Key Optimization Strategies
Evolutionary and swarm-intelligence algorithms, particularly GA and PSO with multi-objective extensions such as NSGA-II, are most frequently highlighted for their flexibility, global search capabilities, and ability to balance cost, efficiency, and quality trade-offs [53,59,61]. Complementary bio-inspired methods like the ant lion optimizer and gray wolf optimizer provide additional robustness in nonlinear or constrained scenarios, while hybrid frameworks that integrate metaheuristics with surrogate-based approaches accelerate convergence and reduce expensive evaluations [52,65]. Parameter-light algorithms such as teaching–learning-based optimization minimize the need for expert tuning [71], and recent ML-driven auto-tuning techniques, stochastic gradient descent and grid search for hyper-parameters, streamline model selection and parameter optimization for resource-constrained SMEs [36]. The complete analysis is summarized in Table A1.
5.2. Potential Business Impact
The literature consistently emphasizes the importance of aligning business objectives with quantifiable performance indicators to support decision-making and operational improvement, particularly within SMEs. Common objectives such as cost reduction, quality enhancement, risk mitigation, efficiency, and sustainability are frequently addressed through a variety of KPIs, including error metrics like Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE), as well as industry-specific measures such as exergy efficiency in energy systems or network lifetime in wireless networks [35,59,82,112]. Multi-objective optimization frameworks are widely employed to manage trade-offs among conflicting goals, using tools like Pareto optimality and hypervolume to evaluate solution quality and diversity [34,97]. These approaches, when adapted to the resource constraints and strategic needs of SMEs, enable more targeted data-driven management by offering interpretable benchmarks for performance evaluation and guiding resource allocation decisions [51,90,102,104]. The complete analysis is summarized in Table A2.
5.3. Implementation Feasibility
The success of optimization strategies in SMEs depends on several key factors. Firstly, having access to high-quality data is essential. Secondly, sufficient computing power is necessary. These factors are particularly important for ML applications, where a lack of data and limited hardware often limit possibilities [35,46]. Reliable optimization also depends on the proper definition of operational parameters and constraints [49,83], as well as the integration of domain expertise to ensure model interpretability and effective parameter selection [47]. However, SMEs’ barriers include high computational and annotation costs, limited access to labeled data, and the challenges of working with noisy real-world datasets [36,104]. These constraints are compounded by organizational limitations, such as a lack of technical expertise and resistance to change adopting complex multi-objective models [34,43]. Conflicting objectives (particularly between cost, performance, and safety) further complicate decision-making processes [58,83]. To address these challenges, SMEs are encouraged to adopt strategic objectives that include investing in scalable infrastructure, improving employee skills, and selecting interpretable context-sensitive optimization tools that support transparent trade-offs and adaptation to uncertainty [37,105]. The complete analysis is summarized in Table A3.
5.4. Recommendations and Managerial Insights
The reviewed literature identifies several methodological approaches that are particularly valuable for SMEs in terms of attempting to enhance decision-making under uncertainty and optimize with limited resources. Multi-objective and hybrid metaheuristics, such as GAs and PSO, are frequently recommended due to their flexibility and effectiveness in multi-criteria environments [40,80]. A growing trend is focusing on combining physical models with data-driven techniques, such as neural networks or ensemble learning, to balance expert knowledge and predictive power, especially under dynamic or uncertain conditions [37,43,44,45]. Robust modeling frameworks and uncertainty quantification are also highlighted as critical for ensuring reliable performance in variable and dynamic contexts [42,99]. For SMEs, methods involving fuzzy logic and decision aggregation offer accessible ways to manage incomplete or ambiguous data [32,33], while heuristic and surrogate-based strategies enable low-cost near-real-time applications [60,66]. Across these contributions, practical concerns, such as integration into existing systems, scalability, and affordability, are consistently prioritized, with approaches like modular design, adaptive scheduling, and rule-based energy management proving particularly well-suited to SME contexts [63,78]. The complete analysis is summarized in Table A4.
6. Conclusions
This review examined how optimization methods are used in SMEs, focusing on four key questions: which optimization goals and techniques are relevant, how they are applied in real use cases, which business indicators are used and how, and what conditions support or prevent implementation. The findings show that SMEs use optimization to improve cost, quality, and risk management. Multi-objective methods, such as genetic algorithms and particle swarm optimization, are commonly used to handle trade-offs, such as balancing cost and performance. These methods are suitable for SMEs as they can operate with limited data and adapt to changing conditions. SMEs apply these methods in areas like manufacturing, logistics, and energy. Success largely depends on how well the models align with real-world conditions, including constraints in scheduling, resource use, and safety. Some studies combine data-driven models with expert knowledge or rules to improve model performance, especially when data is incomplete or noisy.
The manuscript also examined how SMEs measure progress. Indicators like RMSE, MAPE, and latency are commonly used. SMEs should select indicators that are relevant to their specific industry, and these indicators must be simple and understandable to guide business decisions. Barriers to applying these methods include poor data, insufficient computing resources, a lack of technical expertise, and resistance to new technologies. These challenges can be addressed by improving digital infrastructure, training staff, and opting for simpler models that are easy to understand and apply. Using flexible small-scale tools can be particularly beneficial for SMEs. Furthermore, the paper highlighted that implementing optimization strategies in SMEs requires overcoming several challenges. High-quality data, sufficient computational power, and clear operational parameters are relevant for successful implementation. However, SMEs often face issues such as limited data, high computational costs, and a lack of technical expertise. To address these, SMEs should invest in scalable data infrastructure, train personnel, and adopt modular interpretable tools that are easy to implement. Additionally, balancing conflicting objectives, such as cost and safety, requires transparent optimization approaches that align with business goals. Adjusting optimization tools to the specific needs and constraints of SMEs can make these methods more practical and effective in real-world applications.
Future research should focus on developing optimization models that can handle limited, incomplete, or noisy data as many SMEs lack large clean datasets. Combining expert knowledge with machine learning could help to bridge data gaps and improve model reliability. To address the lack of high-quality datasets, especially common in SMEs, one practical approach involves combining expert-validated rules with techniques such as transfer learning or synthetic data generation. For instance, expert knowledge can be encoded as constraints, helping to guide model behavior in data-sparse environments. Additionally, external sources such as open data repositories, publicly available industry reports, or web scraping from competitor websites can serve as valuable inputs. Establishing data partnerships with academic institutions, government agencies, or sectoral organizations can also offer access to richer datasets while preserving confidentiality.
Another promising area for future work is the use of digital twins and low-cost simulation tools, which can assist SMEs in testing and planning new strategies. These tools could help SMEs to experiment with approaches in areas like production planning, energy management, and service delivery before making real-world changes. Moreover, there is potential in hybridizing intelligent algorithms, such as heuristics and metaheuristics, with machine learning and generative AI techniques. These hybrid approaches can combine the strengths of both heuristics and metaheuristics for optimizing decision processes in uncertain or complex environments, and machine learning for predictive modeling and learning from data. Such hybrid models can be particularly useful in real-world applications where SMEs face dynamic and unpredictable environments.
Generative AI and large language models (LLMs) offer SMEs unprecedented opportunities to transform how they analyze data, generate strategic insights, and navigate complex decision-making scenarios. Beyond merely summarizing information, these technologies can power systems of specialized virtual agents capable of offering perspectives tailored to different business contexts and strategic challenges. Such agents can also learn from historical data and adapt their recommendations dynamically, supporting SMEs in proactively identifying risks and opportunities as markets evolve. Nevertheless, these advances introduce significant challenges and risks, including the danger of over-reliance on algorithmic suggestions, biases rooted in training data, and critical ethical considerations related to transparency, fairness, and accountability. For many SMEs, addressing these issues may prove especially difficult if a data-driven culture is lacking or organizational barriers hinder the adoption of AI-based solutions. Explainable AI can help to mitigate some of these concerns by making the inner workings of models more understandable to human users. However, it remains essential to go further: integrating these systems into organizational processes in ways that align with natural human cognitive patterns. Drawing on insights from fields such as psychology and neuroscience, future developments should ensure that AI tools adapt to human decision-making dynamics rather than forcing humans to adapt to the logic of machines, ultimately fostering more natural and effective collaboration between people and technology.
Author Contributions
Conceptualization, L.C., D.R. and A.A.J.; methodology, G.M.-A.; investigation, G.M.-A.; writing—original draft preparation, G.M.-A.; writing—review and editing, L.C., A.A.J. and D.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partially supported by the Spanish Ministry of Science and the Spanish Research Agency (PID2022- 138860NB-I00 and RED2022-134703-T).
Data Availability Statement
All data employed in this paper is contained in the main text or the included references.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
What are the main optimization strategies commonly referenced in the documents? Which specific algorithms are most prominently highlighted and particularly advantageous for SMEs?
Table A1.
What are the main optimization strategies commonly referenced in the documents? Which specific algorithms are most prominently highlighted and particularly advantageous for SMEs?
| Strategy | Key Algorithms | Advantages for SMEs |
|---|---|---|
| Evolutionary and Multi-Objective Optimization | Genetic Algorithm (GA), NSGA-II, NSGA-III [53,61] | Flexible and robust for multi-objective problems and handles large nonlinear decision spaces [59] |
| Swarm Intelligence | Particle Swarm Optimization (PSO) and variants [80,112] | Fast convergence, Minimal fine-tuning required, and low computational cost [81] |
| Other Bio-inspired Metaheuristics | Ant Lion Optimizer (ALO), Grey Wolf Optimizer (GWO), Cuckoo Search (CS), Firefly Algorithm [52,113] | Manages nonlinear, high-dimensional, or constrained problems, and robust under complex constraints [54] |
| Hybrid and Surrogate-based Methods | Metaheuristics, Kriging, grid search, and Mathematical programming [63,65,67] | Balances exploration and exploitation; improves convergence rates and reduces expensive objective calls |
| Parameter-Light Algorithms | Teaching–Learning-Based Optimization (TLBO) [71] | Minimal dependence on algorithm-specific parameters and quick to implement without deep prior expertise |
| ML-Integrated/Auto-tuning Approaches | Stochastic Gradient Descent (SGD); grid search for hyper-parameters and Metaheuristics with ML modules [35,36] | Automates model selection and parameter tuning and lowers barriers to entry for resource-constrained SMEs |

Table A2.
What business objectives and key performance indicators are commonly utilized and assessed in the literature, and how can these be effectively applied to SMEs? Source: author’s own work.
Table A2.
What business objectives and key performance indicators are commonly utilized and assessed in the literature, and how can these be effectively applied to SMEs? Source: author’s own work.
| Aspect and Description | Examples from the Literature | Implications for SMEs |
|---|---|---|
| Common business objectives: Performance goals aimed at improving operations and decision quality. | Cost reduction, quality enhancement, risk mitigation, efficiency, sustainability, customer satisfaction | Focus on objectives that are measurable, strategic, and aligned with core SME needs. |
| Key performance indicators (KPIs): Metrics used to evaluate progress toward goals. | MAE, RMSE, MAPE, F1 score, Dice coefficient, exergy efficiency, network lifetime | Prioritize interpretable and actionable KPIs to enable process optimization |
| Optimization frameworks: Structures for balancing conflicting business goals through multi-objective analysis. | Pareto front analysis, hypervolume indicators, solution convergence/diversity | Clarifies trade-offs and supports transparent decision-making. |
| Domain-specific KPIs: Tailored metrics that reflect industry-specific operations and constraints. | Exergy efficiency (energy), Dice/Jaccard (image analysis), makespan/energy (scheduling), latency/lifetime (cyber–physical systems) | Choose KPIs aligned with the SME’s sector and operational focus. |
| Application benefits: Strategic advantages gained from the structured use of objectives and KPIs. | Better decisions, goal alignment, performance benchmarking, financial discipline | Fosters agility, continuous improvement, and competitiveness. |
| Strategic recommendations: Key practices for effective use of metrics and goals in SMEs. | Prioritize profitability-related goals, standardize metrics, use multi-objective approaches | Enables scalable, cost-effective optimization initiatives. |

Table A3.
What are the most common conditions and potential barriers for implementing optimization strategies, and how can these be utilized as strategic objectives for SMEs?
Table A3.
What are the most common conditions and potential barriers for implementing optimization strategies, and how can these be utilized as strategic objectives for SMEs?
| Aspect | Details | References |
|---|---|---|
| Common Conditions | High-quality comprehensive data essential for model reliability and training, particularly in ML-based optimization. Robust computational resources required to manage high-dimensional and real-time problems. Clear operational parameters and boundary conditions are foundational for effective and safe optimization, especially in industrial contexts. Alignment of domain expertise and algorithmic models improves interpretability and parameter tuning. | [35,36,46,47,49,83,105] |
| Potential Barriers | High computational and annotation costs and lack of infrastructure challenge feasibility and scalability. Data that is scarce, noisy, or redundant can hurt how accurate and stable a model is. Limited technical expertise and organizational resistance slow adoption of optimization approaches. Complexity and opacity of models reduce managerial trust and hinder implementation. Conflicting objectives such as cost vs. safety complicate optimization. | [34,36,43,58,83,104] |
| Strategic Objectives for SMEs | Invest in high-quality data infrastructure to enable accurate and adaptable models. Upskill personnel to bridge domain knowledge and advanced modeling. Adopt modular, interpretable, and scalable tools, tailored to SME constraints. Address trade-offs with multi-objective frameworks, ensuring transparency and alignment with strategic goals. Design resource-adaptive systems for uncertain and dynamic contexts. | [37,105] |

Table A4.
What are the most common recommendations or alternative approaches identified in the analysis, and which of these could be particularly beneficial for SMEs?
Table A4.
What are the most common recommendations or alternative approaches identified in the analysis, and which of these could be particularly beneficial for SMEs?
| Recommendations | Benefit for SMEs | References |
|---|---|---|
| Multi-objective and hybrid optimization strategies: Application of metaheuristics (e.g., Genetic Algorithms or Particle Swarm Optimization) to address complex decision-making with multiple competing objectives. | Versatile and effective across diverse decision contexts with limited resources. | [40,80] |
| Model-based and data-driven integration: Combining physical expert models with ML (e.g., neural networks or ensembles) for improved accuracy and adaptability. | Improves predictive power under uncertainty; supports informed decisions with limited historical data. | [37,43,44,45] |
| Uncertainty quantification and robust modeling: Developing solutions that remain reliable under variability and incomplete knowledge. | Promotes resilience and reduces risk in dynamic or volatile environments. | [37,43,44,45] |
| Advanced decision aggregation and fuzzy logic: Use of fuzzy systems and aggregation operators to handle ambiguity and partial information in decision processes. | Provides accessible interpretable decision support for non-expert users. | [32,33] |
| Heuristic and surrogate-assisted methods: Use of simplified or approximate models to reduce computational cost while maintaining solution quality. | Enables faster resource-efficient optimization, suitable for SMEs with limited computational capacity. | [60,66] |
| Implementation-oriented design: Emphasis on modular, rule-based, and low-complexity systems for cost-effective deployment. | Ensures practical applicability, ease of integration, and short learning curves in SME environments. | [63,78] |
References
- Bianchini, M.; Sancho, M.L. SME Digitalisation for Competitiveness: The 2025 OECD D4SME Survey; Technical Report 68; OECD Publishing: Paris, France, 2025. [Google Scholar] [CrossRef]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Naradda Gamage, S.K.; Ekanayake, E.M.S.; Abeyrathne, G.; Prasanna, R.; Jayasundara, J.; Rajapakshe, P.S.K. A Review of Global Challenges and Survival Strategies of Small and Medium Enterprises (SMEs). Economies 2020, 8, 79. [Google Scholar] [CrossRef]
- Frey, S.; Am, J.B.; Doshi, V.; Malik, A.; Noble, S. Consumers Care About Sustainability—And Back It up with Their Wallets; Mckinsey and Company: New York, NY, USA, 2023. [Google Scholar]
- Juan, A.A.; Keenan, P.; Martí, R.; McGarraghy, S.; Panadero, J.; Carroll, P.; Oliva, D. A review of the role of heuristics in stochastic optimisation: From metaheuristics to learnheuristics. Ann. Oper. Res. 2023, 320, 831–861. [Google Scholar] [CrossRef]
- Guzmán-Ortiz, B.E.; Poler, R.; Andres, B. A matheuristic approach combining genetic algorithm and mixed integer linear programming model for production and distribution planning in the supply chain. Adv. Prod. Eng. Manag. 2023, 18, 19–31. [Google Scholar] [CrossRef]
- Arabsheybani, A.; Paydar, M.M.; Safaei, A.S. Sustainable supplier selection and order allocation applying metaheuristic algorithms. Int. J. Supply Oper. Manag. 2020, 7, 164–177. [Google Scholar]
- Pourkhodabakhsh, N.; Mamoudan, M.M.; Bozorgi-Amiri, A. Effective machine learning, meta-heuristic algorithms and multi-criteria decision making to minimizing human resource turnover. Appl. Intell. 2023, 53, 16309–16331. [Google Scholar] [CrossRef]
- Anju, K.; Avanish, K. An advanced approach to the employee recruitment process through genetic algorithm. Int. J. Inf. Technol. 2021, 13, 313–319. [Google Scholar] [CrossRef]
- Doering, J.; Kizys, R.; Juan, A.A.; Fito, A.; Polat, O. Metaheuristics for rich portfolio optimisation and risk management: Current state and future trends. Oper. Res. Perspect. 2019, 6, 100121. [Google Scholar] [CrossRef]
- Hadjinicolaou, N.; Kader, M.; Abdallah, I. Strategic innovation, foresight and the deployment of project portfolio management under mid-range planning conditions in medium-sized firms. Sustainability 2021, 14, 80. [Google Scholar] [CrossRef]
- Karimi-Mamaghan, M.; Mohammadi, M.; Meyer, P.; Karimi-Mamaghan, A.M.; Talbi, E.G. Machine learning at the service of meta-heuristics for solving combinatorial optimization problems: A state-of-the-art. Eur. J. Oper. Res. 2022, 296, 393–422. [Google Scholar] [CrossRef]
- Artinger, F.M.; Petersen, M.; Gigerenzer, G.; Weibler, J. Heuristics as adaptive decision strategies in management. J. Organ. Behav. 2015, 36, S33–S52. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision Under Risk. In Handbook of the Fundamentals of Financial Decision Making; Econometrica: New Haven, CT, USA, 1979; Chapter 6; pp. 99–127. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in Prospect Theory: Cumulative Representation of Uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Monteiro, A.C.B.; França, R.P.; Arthur, R.; Iano, Y. The fundamentals and potential of heuristics and metaheuristics for multiobjective combinatorial optimization problems and solution methods. Multi-Object. Comb. Optim. Probl. Solut. Methods 2022, 9–29. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Li, H.; Wen, Y.; Han, Z. Reinforcement learning-based resource allocation for cloud native applications. In Proceedings of the Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1383–1391. [Google Scholar]
- Moody, J.; Saffell, M. Reinforcement learning for trading. In Proceedings of the Conference on Advances in Neural Information Processing Systems, Denver, CO, USA, 30 November–5 December 1998; pp. 917–923. [Google Scholar]
- Calvet, L.; de Armas, J.; Masip, D.; Juan, A.A. Learnheuristics: Hybridizing metaheuristics with machine learning for optimization with dynamic inputs. Open Math. 2017, 15, 261–280. [Google Scholar] [CrossRef]
- Azevedo, B.F.; Rocha, A.M.A.; Pereira, A.I. Hybrid approaches to optimization and machine learning methods: A systematic literature review. Mach. Learn. 2024, 113, 4055–4097. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Mitchell, M. Genetic Algorithms and Simulated Annealing; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Zhang, Z.; Zhang, Y.; Zhao, C. Deep Reinforcement Learning for Optimization: A Comprehensive Survey. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3561–3578. [Google Scholar]
- Prasanna, R.M.; Bhat, M.K.; Raghunathan, S. Supply Chain Optimization Using Hybrid Genetic Algorithm. Oper. Res. Perspect. 2017, 4, 109–119. [Google Scholar]
- Oliner, S.J.; Kauffman, R.J.; Wei, K. Machine Learning for Scheduling in Production Systems. IEEE Trans. Autom. Sci. Eng. 2015, 12, 778–785. [Google Scholar]
- Mühleisen, H.; Raasveldt, M. duckdb: DBI Package for the DuckDB Database Management System. R Package Version 1.2.0.9000. 2025. Available online: https://github.com/duckdb/duckdb-r (accessed on 16 July 2025).
- Grootendorst, M. BERTopic: Neural topic modeling with a class-based TF-IDF procedure. arXiv 2022, arXiv:2203.05794. [Google Scholar]
- Healy, J.; McInnes, L. Uniform manifold approximation and projection. Nat. Rev. Methods Prim. 2024, 4, 82. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Mahmood, T. Spherical fuzzy Dombi aggregation operators and their application in group decision making problems. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 2731–2749. [Google Scholar] [CrossRef]
- Akram, M.; Martino, A. Multi-attribute group decision making based on T-spherical fuzzy soft rough average aggregation operators. Granul. Comput. 2023, 8, 171–207. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.w.; Cheng, J. Multi-Objective Particle Swarm Optimization Approach for Cost-Based Feature Selection in Classification. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xue, B.; Liang, J.; Zhang, M. Feature Selection Using Diversity-Based Multi-objective Binary Differential Evolution. Inf. Sci. 2023, 626, 586–606. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, R.; Liao, Q.; Li, D.; Zhang, J. Uncertainty-guided mutual consistency learning for semi-supervised medical image segmentation. Artif. Intell. Med. 2023, 138, 102476. [Google Scholar] [CrossRef]
- Xiao, Z.; Su, Y.; Deng, Z.; Zhang, W. Efficient Combination of CNN and Transformer for Dual-Teacher Uncertainty-guided Semi-supervised Medical Image Segmentation. Comput. Methods Programs Biomed. 2022, 226, 107099. [Google Scholar] [CrossRef]
- Gao, W.; Coley, C.W. The Synthesizability of Molecules Proposed by Generative Models. J. Chem. Inf. Model. 2020, 60, 5714–5723. [Google Scholar] [CrossRef]
- Abbasi, M.; Santos, B.P.; Pereira, T.C.; Sofia, R.; Monteiro, N.R.C.; Simões, C.J.V.; Brito, R.; Ribeiro, B.; Oliveira, J.L.; Arrais, J.P. Designing optimized drug candidates with Generative Adversarial Network. J. Cheminform. 2022, 14, 40. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z.; Xu, M.; Li, Y. Novel reliability-based optimization method for thermal structure with hybrid random, interval and fuzzy parameters. Appl. Math. Model. 2017, 47, 573–586. [Google Scholar] [CrossRef]
- Yoo, K.; Bacarreza, O.; Aliabadi, M.H.F. A novel multi-fidelity modelling-based framework for reliability-based design optimisation of composite structures. Eng. Comput. 2022, 38, 595–608. [Google Scholar] [CrossRef]
- Xiao, H.; Wu, J.L.; Wang, J.X.; Sun, R.; Roy, C. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier–Stokes simulations: A data-driven, physics-informed Bayesian approach. J. Comput. Phys. 2016, 324, 115–136. [Google Scholar] [CrossRef]
- Geneva, N.; Zabaras, N. Quantifying model form uncertainty in Reynolds-averaged turbulence models with Bayesian deep neural networks. J. Comput. Phys. 2019, 383, 125–147. [Google Scholar] [CrossRef]
- Bandara, R.P.; Chan, T.H.; Thambiratnam, D.P. Frequency response function based damage identification using principal component analysis and pattern recognition technique. Eng. Struct. 2014, 66, 116–128. [Google Scholar] [CrossRef]
- Yin, X.; Huang, Z.; Liu, Y. Bridge damage identification under the moving vehicle loads based on the method of physics-guided deep neural networks. Mech. Syst. Signal Process. 2023, 190, 110123. [Google Scholar] [CrossRef]
- Ahmed, A.N.; Yafouz, A.; Birima, A.H.; Kisi, O.; Huang, Y.F.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Water level prediction using various machine learning algorithms: A case study of Durian Tunggal river, Malaysia. Eng. Appl. Comput. Fluid Mech. 2022, 16, 422–440. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Qiao, Q.; Tavares, A.; Liang, Y. Water Quality Prediction Based on Machine Learning and Comprehensive Weighting Methods. Entropy 2023, 25, 1186. [Google Scholar] [CrossRef]
- Liu, B.; Wang, Y.; Zhao, G.; Yang, B.; Wang, R.; Huang, D.; Xiang, B. Intelligent decision method for main control parameters of tunnel boring machine based on multi-objective optimization of excavation efficiency and cost. Tunn. Undergr. Space Technol. 2021, 116, 104054. [Google Scholar] [CrossRef]
- Liu, W.; Li, A.; Fang, W.; Love, P.E.; Hartmann, T.; Luo, H. A hybrid data-driven model for geotechnical reliability analysis. Reliab. Eng. Syst. Saf. 2023, 231, 108985. [Google Scholar] [CrossRef]
- Mohammadi, F. Lithium-ion battery State-of-Charge estimation based on an improved Coulomb-Counting algorithm and uncertainty evaluation. J. Energy Storage 2022, 48, 104061. [Google Scholar] [CrossRef]
- Wu, M.; Zhong, Y.; Wu, J.; Wang, Y.; Wang, L. State of health estimation of the lithium-ion power battery based on the principal component analysis-particle swarm optimization-back propagation neural network. Energy 2023, 283, 129061. [Google Scholar] [CrossRef]
- Wang, J.; Du, P.; Lu, H.; Yang, W.; Niu, T. An improved grey model optimized by multi-objective ant lion optimization algorithm for annual electricity consumption forecasting. Appl. Soft Comput. 2018, 72, 321–337. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, X.; Ma, Y.; Zhao, X. A hybrid model based on modified multi-objective cuckoo search algorithm for short-term load forecasting. Appl. Energy 2019, 237, 896–909. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, P.; Zhang, L.; Niu, X. A combined forecasting model for time series: Application to short-term wind speed forecasting. Appl. Energy 2020, 259, 114137. [Google Scholar] [CrossRef]
- Nie, Y.; Liang, N.; Wang, J. Ultra-short-term wind-speed bi-forecasting system via artificial intelligence and a double-forecasting scheme. Appl. Energy 2021, 301, 117452. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.; Jia, H.; Zhang, M.; Wang, D. Application of multi-objective genetic algorithm to optimize energy efficiency and thermal comfort in building design. Energy Build. 2015, 88, 135–143. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, L.; Zhang, L.; Wu, X. Optimizing energy efficiency and thermal comfort in building green retrofit. Energy 2021, 237, 121509. [Google Scholar] [CrossRef]
- Behzadi, A.; Gholamian, E.; Houshfar, E.; Habibollahzade, A. Multi-objective optimization and exergoeconomic analysis of waste heat recovery from Tehran’s waste-to-energy plant integrated with an ORC unit. Energy 2018, 160, 1055–1068. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, T.; Yang, K. An integrated energy storage system consisting of Compressed Carbon dioxide energy storage and Organic Rankine Cycle: Exergoeconomic evaluation and multi-objective optimization. Energy 2022, 247, 123566. [Google Scholar] [CrossRef]
- Arie, M.; Shooshtari, A.; Dessiatoun, S.; Al-Hajri, E.; Ohadi, M. Numerical modeling and thermal optimization of a single-phase flow manifold-microchannel plate heat exchanger. Int. J. Heat Mass Transf. 2015, 81, 478–489. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Attarzadeh-Niaki, S.H.; Duwig, C. Multi-objective optimization of TPMS-based heat exchangers for low-temperature waste heat recovery. Appl. Therm. Eng. 2022, 212, 118448. [Google Scholar] [CrossRef]
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 202, 54–64. [Google Scholar] [CrossRef]
- Amiri, H.; Azadi, S.; Karimaei, M.; Sadeghi, H.; Dabbaghi, F. Multi-objective optimization of coal waste recycling in concrete using response surface methodology. J. Build. Eng. 2022, 45, 103472. [Google Scholar] [CrossRef]
- Younas, M.; Jaffery, S.H.I.; Khan, M.; Khan, M.A.; Ahmad, R.; Mubashar, A.; Ali, L. Multi-objective optimization for sustainable turning Ti6Al4V alloy using grey relational analysis (GRA) based on analytic hierarchy process (AHP). Int. J. Adv. Manuf. Technol. 2019, 105, 1175–1188. [Google Scholar] [CrossRef]
- Khan, M.A.; Jaffery, S.H.I.; Khan, M.; Younas, M.; Butt, S.I.; Ahmad, R.; Warsi, S.S. Multi-objective optimization of turning titanium-based alloy Ti-6Al-4V under dry, wet, and cryogenic conditions using gray relational analysis (GRA). Int. J. Adv. Manuf. Technol. 2020, 106, 3897–3911. [Google Scholar] [CrossRef]
- Wu, S.; Zheng, G.; Sun, G.; Liu, Q.; Li, G.; Li, Q. On design of multi-cell thin-wall structures for crashworthiness. Int. J. Impact Eng. 2016, 88, 102–117. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Y.; Lin, J.; Lu, Y. Theoretical analysis and crashworthiness optimization of hybrid multi-cell structures. Thin-Walled Struct. 2019, 142, 116–131. [Google Scholar] [CrossRef]
- Xiang, Z.; Zhu, X.; Quan, L.; Du, Y.; Zhang, C.; Fan, D. Multilevel Design Optimization and Operation of a Brushless Double Mechanical Port Flux-Switching Permanent-Magnet Motor. IEEE Trans. Ind. Electron. 2016, 63, 6042–6054. [Google Scholar] [CrossRef]
- Zheng, S.; Zhu, X.; Xu, L.; Xiang, Z.; Quan, L.; Yu, B. Multi-Objective Optimization Design of a Multi-Permanent-Magnet Motor Considering Magnet Characteristic Variation Effects. IEEE Trans. Ind. Electron. 2022, 69, 3428–3438. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Zheng, Y. Constrained population extremal optimization-based robust load frequency control of multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2019, 105, 249–271. [Google Scholar] [CrossRef]
- Annamraju, A.; Nandiraju, S. Robust frequency control in a renewable penetrated power system: An adaptive fractional order-fuzzy approach. Prot. Control Mod. Power Syst. 2019, 4, 16. [Google Scholar] [CrossRef]
- Kang, E.; Qiao, H.; Chen, Z.; Gao, J. Tracking of Uncertain Robotic Manipulators Using Event-Triggered Model Predictive Control With Learning Terminal Cost. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2801–2815. [Google Scholar] [CrossRef]
- Chen, G.; Dong, J. Approximate Optimal Adaptive Prescribed Performance Control for Uncertain Nonlinear Systems With Feature Information. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2298–2308. [Google Scholar] [CrossRef]
- Shao, Y.; Sun, Z. Eco-Approach with Traffic Prediction and Experimental Validation for Connected and Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 1562–1572. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Xu, M.; Liu, Y. Deep reinforcement learning and reward shaping based eco-driving control for automated HEVs among signalized intersections. Energy 2022, 251, 123924. [Google Scholar] [CrossRef]
- Yang, C.; Wang, M.; Wang, W.; Pu, Z.; Ma, M. An efficient vehicle-following predictive energy management strategy for PHEV based on improved sequential quadratic programming algorithm. Energy 2021, 219, 119595. [Google Scholar] [CrossRef]
- Yuan, H.B.; Zou, W.J.; Jung, S.; Kim, Y.B. A Real-Time Rule-Based Energy Management Strategy with Multi-Objective Optimization for a Fuel Cell Hybrid Electric Vehicle. IEEE Access 2022, 10, 102618–102628. [Google Scholar] [CrossRef]
- Li, D.; Zouma, A.; Liao, J.T.; Yang, H.T. An energy management strategy with renewable energy and energy storage system for a large electric vehicle charging station. eTransportation 2020, 6, 100076. [Google Scholar] [CrossRef]
- An, Y.; Gao, Y.; Wu, N.; Zhu, J.; Li, H.; Yang, J. Optimal scheduling of electric vehicle charging operations considering real-time traffic condition and travel distance. Expert Syst. Appl. 2023, 213, 118941. [Google Scholar] [CrossRef]
- Biswas, P.P.; Mallipeddi, R.; Suganthan, P.; Amaratunga, G.A. A multiobjective approach for optimal placement and sizing of distributed generators and capacitors in distribution network. Appl. Soft Comput. 2017, 60, 268–280. [Google Scholar] [CrossRef]
- Wu, H.; Dong, P.; Liu, M. Distribution Network Reconfiguration for Loss Reduction and Voltage Stability with Random Fuzzy Uncertainties of Renewable Energy Generation and Load. IEEE Trans. Ind. Inform. 2020, 16, 5655–5666. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Esmaili, M.; Mohammadkhani, N. Stochastic multi-objective energy management in residential microgrids with combined cooling, heating, and power units considering battery energy storage systems and plug-in hybrid electric vehicles. J. Clean. Prod. 2018, 195, 301–317. [Google Scholar] [CrossRef]
- Shen, Y.; Hu, W.; Liu, M.; Yang, F.; Kong, X. Energy storage optimization method for microgrid considering multi-energy coupling demand response. J. Energy Storage 2022, 45, 103521. [Google Scholar] [CrossRef]
- Khalid, A.; Javaid, N.; Guizani, M.; Alhussein, M.; Aurangzeb, K.; Ilahi, M. Towards Dynamic Coordination Among Home Appliances Using Multi-Objective Energy Optimization for Demand Side Management in Smart Buildings. IEEE Access 2018, 6, 19509–19529. [Google Scholar] [CrossRef]
- Waseem, M.; Lin, Z.; Liu, S.; Sajjad, I.A.; Aziz, T. Optimal GWCSO-based home appliances scheduling for demand response considering end-users comfort. Electr. Power Syst. Res. 2020, 187, 106477. [Google Scholar] [CrossRef]
- Sang, M.; Ding, Y.; Bao, M.; Li, S.; Ye, C.; Fang, Y. Resilience-based restoration strategy optimization for interdependent gas and power networks. Appl. Energy 2021, 302, 117560. [Google Scholar] [CrossRef]
- Xu, M.; Li, G.; Chen, A. Resilience-driven post-disaster restoration of interdependent infrastructure systems under different decision-making environments. Reliab. Eng. Syst. Saf. 2024, 241, 109599. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, J.; Han, Y.; Zheng, H.; Ma, D.; Chen, M. A chaos-coupled multi-objective scheduling decision method for liner shipping based on the NSGA-III algorithm. Comput. Ind. Eng. 2022, 174, 108732. [Google Scholar] [CrossRef]
- Elmi, Z.; Li, B.; Liang, B.; yip Lau, Y.; Borowska-Stefańska, M.; Wiśniewski, S.; Dulebenets, M.A. An epsilon-constraint-based exact multi-objective optimization approach for the ship schedule recovery problem in liner shipping. Comput. Ind. Eng. 2023, 183, 109472. [Google Scholar] [CrossRef]
- Sadeghi Rad, R.; Nahavandi, N. A novel multi-objective optimization model for integrated problem of green closed loop supply chain network design and quantity discount. J. Clean. Prod. 2018, 196, 1549–1565. [Google Scholar] [CrossRef]
- Mohebalizadehgashti, F.; Zolfagharinia, H.; Amin, S.H. Designing a green meat supply chain network: A multi-objective approach. Int. J. Prod. Econ. 2020, 219, 312–327. [Google Scholar] [CrossRef]
- Bozorgi-Amiri, A.; Khorsi, M. A dynamic multi-objective location–routing model for relief logistic planning under uncertainty on demand, travel time, and cost parameters. Int. J. Adv. Manuf. Technol. 2016, 85, 1633–1648. [Google Scholar] [CrossRef]
- Liu, Y.; Lei, H.; Zhang, D.; Wu, Z. Robust optimization for relief logistics planning under uncertainties in demand and transportation time. Appl. Math. Model. 2018, 55, 262–280. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. Test Problems for Large-Scale Multiobjective and Many-Objective Optimization. IEEE Trans. Cybern. 2017, 47, 4108–4121. [Google Scholar] [CrossRef]
- Qu, B.; Li, G.; Yan, L.; Liang, J.; Yue, C.; Yu, K.; Crisalle, O.D. A grid-guided particle swarm optimizer for multimodal multi-objective problems. Appl. Soft Comput. 2022, 117, 108381. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A. Multi-objective optimization for energy-efficient flexible job shop scheduling problem with transportation constraints. Robot.-Comput.-Integr. Manuf. 2019, 59, 143–157. [Google Scholar] [CrossRef]
- Jiang, X.; Tian, Z.; Liu, W.; Suo, Y.; Chen, K.; Xu, X.; Li, Z. Energy-efficient scheduling of flexible job shops with complex processes: A case study for the aerospace industry complex components in China. J. Ind. Inf. Integr. 2022, 27, 100293. [Google Scholar] [CrossRef]
- Guo, Y.N.; Cheng, J.; Luo, S.; Gong, D.; Xue, Y. Robust Dynamic Multi-Objective Vehicle Routing Optimization Method. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 1891–1903. [Google Scholar] [CrossRef]
- Hu, C.; Lu, J.; Liu, X.; Zhang, G. Robust vehicle routing problem with hard time windows under demand and travel time uncertainty. Comput. Oper. Res. 2018, 94, 139–153. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, L.; Yang, H.; Zhou, H.; Gao, Z. Robust collaborative passenger flow control on a congested metro line: A joint optimization with train timetabling. Transp. Res. Part B Methodol. 2023, 168, 27–55. [Google Scholar] [CrossRef]
- Hu, Y.; Li, S.; Wang, Y.; Zhang, H.; Wei, Y.; Yang, L. Robust metro train scheduling integrated with skip-stop pattern and passenger flow control strategy under uncertain passenger demands. Comput. Oper. Res. 2023, 151, 106116. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Masdari, M.; Gharehchopogh, F.S. Energy and Cost-Aware Workflow Scheduling in Cloud Computing Data Centers Using a Multi-objective Optimization Algorithm. J. Netw. Syst. Manag. 2021, 29, 31. [Google Scholar] [CrossRef]
- Alsadie, D. A Metaheuristic Framework for Dynamic Virtual Machine Allocation With Optimized Task Scheduling in Cloud Data Centers. IEEE Access 2021, 9, 74218–74233. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Zhou, L.; Rezaeipanah, A. Solving the Multi-Objective Problem of IoT Service Placement in Fog Computing Using Cuckoo Search Algorithm. Neural Process. Lett. 2022, 54, 1823–1854. [Google Scholar] [CrossRef]
- Mahboubeh Salimian, M.G.A.; Shahidinejad, A. An Evolutionary Multi-objective Optimization Technique to Deploy the IoT Services in Fog-enabled Networks: An Autonomous Approach. Appl. Artif. Intell. 2022, 36, 2008149. [Google Scholar] [CrossRef]
- Ning, Z.; Dong, P.; Kong, X.; Xia, F. A Cooperative Partial Computation Offloading Scheme for Mobile Edge Computing Enabled Internet of Things. IEEE Internet Things J. 2019, 6, 4804–4814. [Google Scholar] [CrossRef]
- You, Q.; Tang, B. Efficient task offloading using particle swarm optimization algorithm in edge computing for industrial internet of things. J. Cloud Comput. 2021, 10, 41. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Q.; Qin, J. Robust Beamforming for Nonorthogonal Multiple-Access Systems in MISO Channels. IEEE Trans. Veh. Technol. 2016, 65, 10231–10236. [Google Scholar] [CrossRef]
- Pan, Y.; Pan, C.; Yang, Z.; Chen, M. Resource Allocation for D2D Communications Underlaying a NOMA-Based Cellular Network. IEEE Wirel. Commun. Lett. 2018, 7, 130–133. [Google Scholar] [CrossRef]
- Fu, Z.; Mao, Y.; He, D.; Yu, J.; Xie, G. Secure Multi-UAV Collaborative Task Allocation. IEEE Access 2019, 7, 35579–35587. [Google Scholar] [CrossRef]
- Zhu, S.; Gui, L.; Cheng, N.; Sun, F.; Zhang, Q. Joint Design of Access Point Selection and Path Planning for UAV-Assisted Cellular Networks. IEEE Internet Things J. 2020, 7, 220–233. [Google Scholar] [CrossRef]
- Rao, P.C.S.; Jana, P.K.; Banka, H. A particle swarm optimization based energy efficient cluster head selection algorithm for wireless sensor networks. Wirel. Netw. 2017, 23, 2005–2020. [Google Scholar] [CrossRef]
- Mosavvar, I.; Ghaffari, A. Data Aggregation in Wireless Sensor Networks Using Firefly Algorithm. Wirel. Pers. Commun. 2019, 104, 307–324. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).