Lattice Boltzmann Framework for Multiphase Flows by Eulerian–Eulerian Navier–Stokes Equations

Abstract

Although the lattice Boltzmann method (LBM) is relatively straightforward, it demands a well-crafted framework to handle the complex partial differential equations involved in multiphase flow simulations. For the first time to our knowledge, this work proposes a novel LBM framework to solve Eulerian–Eulerian multiphase flow equations without any finite difference correction, including very-large-density ratios and also a realistic relation for the drag coefficient. The proposed methodology and all reported LBM formulas can be applied to any dimension. This opens a promising venue for simulating multiphase flows in large High Performance Computing (HPC) facilities and on novel parallel hardware. This LBM framework consists of six coupled LBM schemes—running on the same lattice—ensuring an efficient implementation in large codes with minimum effort. The preliminary numeral results agree in an excellent way with the reference numerical solution obtained by a traditional finite difference solver.

1. Introduction

The computational fluid dynamics (CFD) of multiphase flows is crucial in the energy sector, particularly in oil and gas, as it enables the detailed simulation and optimization of complex fluid interactions, such as those in bubble column reactors. These reactors are used extensively in refining processes, gas treatment, and chemical synthesis, where accurate modeling of gas–liquid interactions can lead to improved efficiency, reduced energy consumption, and enhanced safety. Using CFD, industry can better understand the flow dynamics, optimize reactor designs, and ultimately reduce costs and emissions, making it a vital tool for the advancement of sustainable energy solutions.

A multiphase flow system consists of the simultaneous flow of materials with different phases or states of matter in regions bounded by moving interfaces. The lattice Boltzmann method (LBM) has garnered significant interest for modeling multiphase flows, particularly because its inherent parallelism makes it ideal for high-performance computing applications when dealing with large domains. Notably, diffuse interface approaches have become well-established for simulating such flows without relying on Lagrangian meshes and immersed boundaries [1]. Among these, “color gradient” LBM techniques have proven to be particularly effective for modeling multiphase flows in porous media and microchannels [2]. The color-gradient method assigns different “colors” to each fluid and uses recoloring algorithms to maintain immiscibility and model surface tension. It is known for robustness and numerical stability, accommodating moderate-density ratios (up to ∼100). Various strategies have been developed to incorporate surface tension into LBMs. For example, pseudo-potential models, originally introduced by Shan and Chen, simulate surface tension through pairwise molecular interactions [3,4]. They introduce phase separation through a density-dependent interparticle force. They are widely used due to their simplicity and and work best for moderate-density ratios (typically up to ∼100, or ∼1000 with advanced forcing schemes). The free-energy method employs a Ginzburg–Landau-type free energy functional to model interfacial dynamics and control surface tension precisely. It is suitable for capturing diffuse interfaces but is typically limited to lower-density ratios (∼10–20) [5]. Furthermore, phase-field models solve a coupled Cahn–Hilliard equation to evolve an order parameter representing phase concentration. It shares many features with the free-energy approach, including good interface capturing and limited-density-ratio capabilities [6]. However, all these lattice Boltzmann methods are generally formulated to solve a single-fluid set of equations with a diffuse interface or interfacial force rather than separate momentum equations for each phase. This means they do not directly solve two separate Eulerian momentum equations coupled with drag. Instead, they treat the multiphase system as a single effective fluid with an internal interface. Accurately capturing phase interfaces becomes particularly difficult in complex systems, such as a swarm of bubbles like those seen in the bubble column reactors. Furthermore, these models often introduce an artificial dependence of surface tension on viscosity, leading to numerical instabilities and artifacts at fluid interfaces [7]. A possible approach to modeling multiphase flows without simulating the interface is the mixture approach, which essentially treats the multiphase system as a single mixture with properties that are weighted averages of the different phases [8]. Instead of solving separate momentum equations for each phase, a single momentum equation is solved for the mixture. For this reason, it is a simple and computationally convenient approach but with a lower detail level because a proper model must be provided for the velocity difference between the two phases. It needs small relative velocities, so it is more suitable for closely coupled phases moving together (slurry, sediment) [9].

This work, on the other hand, focuses on developing an Eulerian–Eulerian lattice Boltzmann method (LBM) to simulate multiphase flows. It has the advantage of not solving the interface between the phases, simulating the two fluids as if they interpenetrate and solving separate volume-averaged Navier–Stokes equations for each phase. This frees its applicability from any extensional constraints regarding the number of dispersed phase elements, making it optimal for cases where there are swarms of bubbles/particles. This implies the application of a volume-averaging procedure to both the continuity and momentum equation for every phase, and it requires us to define a volume fraction as follows:

$${\alpha }_{\phi }={\displaystyle \frac{V_{\phi }}{V}},\sum _{\phi =1}^P{\alpha }_{\phi }=1,$$

(1)

where V is the volume under consideration, the subscript $\phi$ stays for a generic phase, and P is used for the total number of phases. In the following, for the sake of simplicity and without loss of generality, let us focus on two phases, namely, $P=2$, where two phases are identified by l for the liquid phase and g for the gas phase, respectively. In case $P=2$, if $\phi$ stays for a generic phase, then $\overline{\phi }$ stays for the other one. Writing down the governing equation for both phases constitutes the Eulerian–Eulerian approach (or two-fluid approach) and is a framework used to model multiphase flows where each phase is treated as a continuum, and separate sets of equations are solved for each phase in the same Eulerian (fixed) reference frame. They are used in fluid dynamics to describe the motion of a fluid while accounting for the effects of spatial variations over a finite region [10]. Let us start by recalling the original Eulerian–Eulerian Navier–Stokes equations for multiphase flows in the isothermal limiting case, used in traditional CFD for both phases [11]:

$${\displaystyle \frac{𝜕\left({\rho }_l{\alpha }_l\right)}{𝜕t}}+\nabla ·\left({\alpha }_l{\rho }_l{\mathit{u}}_l\right)=0,$$

(2)

$${\displaystyle \frac{𝜕\left({\rho }_l{\alpha }_l{\mathit{u}}_l\right)}{𝜕t}}+\nabla ·\left({\alpha }_l{\rho }_l{\mathit{u}}_l{\mathit{u}}_l\right)=-{\alpha }_l\nabla p+{\rho }_l{\alpha }_l\mathit{g}+\nabla ·\left({\alpha }_l{\rho }_l{\mathbf{\sigma }}_l\right)+{\mathit{F}}_{lg}+{\mathit{F}}_l,$$

(3)

$${\displaystyle \frac{𝜕\left({\rho }_g{\alpha }_g\right)}{𝜕t}}+\nabla ·\left({\alpha }_g{\rho }_g{\mathit{u}}_g\right)=0,$$

(4)

$${\displaystyle \frac{𝜕\left({\rho }_g{\alpha }_g{\mathit{u}}_g\right)}{𝜕t}}+\nabla ·\left({\alpha }_g{\rho }_g{\mathit{u}}_g{\mathit{u}}_g\right)=-{\alpha }_g\nabla p+{\rho }_g{\alpha }_g\mathit{g}+\nabla ·\left({\alpha }_g{\rho }_g{\mathbf{\sigma }}_g\right)+{\mathit{F}}_{gl}+{\mathit{F}}_g.$$

(5)

For each phase (the subscript $\phi$ can be either l or g), ${\alpha }_{\phi }$ is the previously mentioned volume fraction, ${\rho }_{\phi }$ is the density, ${\mathit{u}}_{\phi }$ the velocity vector, ${\mathbf{\sigma }}_{\phi }$ the viscous stress tensor per unit volume, p the common pressure, ${\mathit{F}}_{gl}=-{\mathit{F}}_{lg}$ is the interphase momentum exchange term, which is a cumulative force resulting from the summation of the single interfacial forces acting between the two phases (drag force, lift force, wall lubrication, virtual mass, etc.) per unit volume, and ${\mathit{F}}_{\phi }$ is the force per unit volume of the specific phase $\phi$. Concerning the interphase momentum exchange, let us limit the following discussion to the drag contribution only, which can be formulated as

$${\mathit{F}}_{gl}={\rho }_g{K}_I\parallel {\mathit{u}}_l-{\mathit{u}}_g\parallel \left({\mathit{u}}_l-{\mathit{u}}_g\right)=-{\mathit{F}}_{lg},$$

(6)

where $K_I$ is the effective drag coefficient and is evaluated from empirical or semi-empirical correlations. The viscous stress tensor per unit volume is defined as follows:

$${\mathbf{\sigma }}_{\phi }={\nu }_{\phi }\left(\nabla {\mathit{u}}_{\phi }+\nabla {\mathit{u}}_{\phi }^T\right)+\left({\xi }_{\phi }-{\displaystyle \frac{2}{3}}{\nu }_{\phi }\right)(\nabla ·{\mathit{u}}_{\phi })\mathit{I},$$

(7)

where ${\nu }_{\phi }$ is the effective kinematic viscosity for the generic phase, defined as the ratio between dynamic viscosity and density, i.e., ${\nu }_{\phi }={\mu }_{\phi }/{\rho }_{\phi }$, and ${\xi }_{\phi }$ is the effective kinematic bulk viscosity. In general, the effective kinematic viscosity should also include turbulent effects. It is important to realize that in multiphase flows, even under the incompressible limit which we will discuss in the following, $\nabla ·{\mathit{u}}_{\phi }$ for the individual phase can be different from zero in general.

The previous equations define a proper system of equations for the following variables: ${\alpha }_g$, p, ${\mathit{u}}_g$ and ${\mathit{u}}_l$, as far as the equation of state for the dispersed phase, i.e., ${\rho }_g={\rho }_g\left(p\right)$, and the equation of state for the liquid phase, i.e., ${\rho }_l={\rho }_l\left(p\right)$ in the isothermal limiting case, are provided.

In case of the incompressible limit (i.e., low Mach number limit), one can assume the following equations of state: ${\rho }_g={\rho }_g\left(p\right)={\rho }_g^0$ and ${\rho }_l={\rho }_l\left(p\right)={\rho }_l^0$, where ${\rho }_g^0$, and ${\rho }_l^0$ are proper constants consisting in the average density of each phase. In this case, the previous equations reduce to the following:

$${\displaystyle \frac{𝜕{\alpha }_l}{𝜕t}}+\nabla ·\left({\alpha }_l{\mathit{u}}_l\right)=0,$$

(8)

$${\displaystyle \frac{𝜕\left({\alpha }_l{\mathit{u}}_l\right)}{𝜕t}}+\nabla ·\left({\alpha }_l{\mathit{u}}_l{\mathit{u}}_l\right)=-{\displaystyle \frac{{\alpha }_l}{{\rho }_l^0}}\nabla p+{\alpha }_l\mathit{g}+\nabla ·\left({\alpha }_l{\mathbf{\sigma }}_l\right)+{\displaystyle \frac{1}{{\rho }_l^0}}\left({\mathit{F}}_{lg}+{\mathit{F}}_l\right),$$

(9)

$${\displaystyle \frac{𝜕{\alpha }_g}{𝜕t}}+\nabla ·\left({\alpha }_g{\mathit{u}}_g\right)=0,$$

(10)

$${\displaystyle \frac{𝜕\left({\alpha }_g{\mathit{u}}_g\right)}{𝜕t}}+\nabla ·\left({\alpha }_g{\mathit{u}}_g{\mathit{u}}_g\right)=-{\displaystyle \frac{{\alpha }_g}{{\rho }_g^0}}\nabla p+{\alpha }_g\mathit{g}+\nabla ·\left({\alpha }_g{\mathbf{\sigma }}_g\right)+{\displaystyle \frac{1}{{\rho }_g^0}}\left({\mathit{F}}_{gl}+{\mathit{F}}_g\right).$$

(11)

From the numerical point of view, the previous formulation is not convenient and it is better to derive an equivalent system of equations. Summing up continuity equations for both phases in the incompressible limit yields

$$\nabla ·({\alpha }_g{\mathit{u}}_g+{\alpha }_l{\mathit{u}}_l)=0.$$

(12)

Summing up momentum equations for both phases in the incompressible limit yields

$$\begin{array}{c}{\displaystyle \frac{𝜕({\alpha }_g{\mathit{u}}_g+{\alpha }_l{\mathit{u}}_l)}{𝜕t}}+\nabla ·({\alpha }_g{\mathit{u}}_g{\mathit{u}}_g+{\alpha }_l{\mathit{u}}_l{\mathit{u}}_l)=-\left({\displaystyle \frac{{\alpha }_g}{{\rho }_g^0}}+{\displaystyle \frac{{\alpha }_l}{{\rho }_l^0}}\right)\nabla p+\mathit{G}+\dots \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\dots +\nabla ·\left({\alpha }_g{\mathbf{\sigma }}_g\right)+\nabla ·\left({\alpha }_l{\mathbf{\sigma }}_l\right)+{\displaystyle \frac{1}{{\rho }_g^0}}\left({\mathit{F}}_{gl}+{\mathit{F}}_g\right)+{\displaystyle \frac{1}{{\rho }_l^0}}\left({\mathit{F}}_{lg}+{\mathit{F}}_l\right).\end{array}$$

(13)

Applying the divergence operator to both sides of the equation and swapping the order of the derivatives in the first term yields

$$\begin{array}{c}{\displaystyle \frac{𝜕}{𝜕t}}\left[\nabla ·({\alpha }_g{\mathit{u}}_g+{\alpha }_l{\mathit{u}}_l)\right]+\nabla ·\nabla ·({\alpha }_g{\mathit{u}}_g{\mathit{u}}_g+{\alpha }_l{\mathit{u}}_l{\mathit{u}}_l)=-\nabla ·\left[\left({\displaystyle \frac{{\alpha }_g}{{\rho }_g^0}}+{\displaystyle \frac{{\alpha }_l}{{\rho }_l^0}}\right)\nabla p\right]\dots \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\nabla ·\left[\nabla ·\left({\alpha }_g{\mathbf{\sigma }}_g\right)+\nabla ·\left({\alpha }_l{\mathbf{\sigma }}_l\right)+{\displaystyle \frac{1}{{\rho }_g^0}}\left({\mathit{F}}_{gl}+{\mathit{F}}_g\right)+{\displaystyle \frac{1}{{\rho }_l^0}}\left({\mathit{F}}_{lg}+{\mathit{F}}_l\right)\right].\end{array}$$

(14)

Applying Equation (12), it is possible to derive the Poisson equation, which is typically solved for computing the common pressure field p, namely,

$$\begin{array}{c}\nabla ·\nabla ·({\alpha }_g{\mathit{u}}_g{\mathit{u}}_g+{\alpha }_l{\mathit{u}}_l{\mathit{u}}_l)=-\nabla ·\left[\left({\displaystyle \frac{{\alpha }_g}{{\rho }_g^0}}+{\displaystyle \frac{{\alpha }_l}{{\rho }_l^0}}\right)\nabla p\right]\dots \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\nabla ·\left[\nabla ·\left({\alpha }_g{\mathbf{\sigma }}_g\right)+\nabla ·\left({\alpha }_l{\mathbf{\sigma }}_l\right)+{\displaystyle \frac{1}{{\rho }_g^0}}\left({\mathit{F}}_{gl}+{\mathit{F}}_g\right)+{\displaystyle \frac{1}{{\rho }_l^0}}\left({\mathit{F}}_{lg}+{\mathit{F}}_l\right)\right].\end{array}$$

(15)

From the numerical point of view, it is better to reformulate the momentum equations in the incompressible limit. This is performed by expanding the derivatives in the left-hand side of the equations and applying Equations (8) and (10) to the momentum equation of the liquid and dispersed phases, respectively:

$${\displaystyle \frac{𝜕{\mathit{u}}_g}{𝜕t}}+{\mathit{u}}_g·\nabla {\mathit{u}}_g=-{\displaystyle \frac{1}{{\rho }_g^0}}\nabla p+\mathit{G}+{\displaystyle \frac{1}{{\alpha }_g}}\nabla ·\left({\alpha }_g{\mathbf{\sigma }}_g\right)+{\displaystyle \frac{1}{{\alpha }_g{\rho }_g^0}}\left({\mathit{F}}_{gl}+{\mathit{F}}_g\right),$$

(16)

$${\displaystyle \frac{𝜕{\mathit{u}}_l}{𝜕t}}+{\mathit{u}}_l·\nabla {\mathit{u}}_l=-{\displaystyle \frac{1}{{\rho }_l^0}}\nabla p+\mathit{G}+{\displaystyle \frac{1}{{\alpha }_l}}\nabla ·\left({\alpha }_l{\mathbf{\sigma }}_l\right)+{\displaystyle \frac{1}{{\alpha }_l{\rho }_l^0}}\left({\mathit{F}}_{lg}+{\mathit{F}}_l\right).$$

(17)

The singularity of the forces depend on the terms $\nabla ln\left({\alpha }_{\phi }\right)$ (where $\phi$ can be either g or l). There are well-established techniques in standard computational fluid dynamics for multiphase flows to handle exactly this kind of term [12]. For this term to be well-behaved as ${\alpha }_{\phi }\to 0$, it is necessary for the gradient $\nabla {\alpha }_{\phi }$ to approach zero faster than ${\alpha }_{\phi }$. Numerically, in standard CFD methods, it is straightforward to discretize this term in a way that prevents division by zero: this can be achieved by representing ${\alpha }_{\phi }$ in the denominator using a proper volumetric average and/or by applying a proper slope limiter [13].

The system of equations defined by Equations (10) and (15)–(17) in terms of quantities ${\alpha }_g$, p, ${\mathit{u}}_g$, and ${\mathit{u}}_l$ represents a promising starting point for numerics in most of the existing software for solving multiphase flows by the Eulerian–Eulerian approach (e.g., OpenFOAM).

In spite of the existence of feasible numerical methods, there are remaining complexities of the Eulerian–Eulerian approach which must be faced. The solution of the multifluid set of equations presents many challenges:

• Possible singularities of the phase momentum equations;
• Coupling between the phases, which could lead to instabilities in the numerical procedure;
• Phase volume fraction needs to be bounded between 0 and 1;
• Sharp profiles of phase volume fractions;
• Extension of iterative solution procedures to the co-located grid arrangement for avoiding checkerboard instability patterns.

For example, the open-source code OpenFOAM implements a numerical iterative solution procedure proposed by Passalacqua et al. [14], originally developed for fluid-particle flows. It consists in a finite volume method (FVM) discretizing the Navier–Stokes equations Equations (10) and (15)–(17). It uses face fluxes and velocity fluxes to overcome the problems described above along with deriving the pressure equation and the dispersed phase continuity equation. Despite its effectiveness in FVM, this procedure is clearly unfeasible for LBM, e.g., because LBM cannot easily solve Equation (15) and cannot straightforwardly impose the same pressure gradient $\nabla p$ to both phases.

2. Materials and Methods: Eulerian–Eulerian Lattice Boltzmann Method (LBM) to Simulate Multiphase Flows

The lattice Boltzmann method (LBM) is highly promising for simulating multiphase flows on High Performance Computing (HPC) systems due to its unique computational structure, which is naturally parallel and localized. Unlike conventional CFD methods that rely on solving the Navier–Stokes equations through techniques like finite difference (FD), the finite volume method (FVM), or the finite element method (FEM), LBM simulates fluid flows by modeling the fluid as discrete particles moving and colliding on a lattice [15]. This approach enables LBM to perform computations locally at each grid point, making it well-suited for parallel execution across HPC platforms.

For LBM to fully exploit HPC capabilities, it is essential to maintain the standard, unmodified LBM formulation, avoiding FD corrections or other modifications that introduce non-local dependencies. These corrections, sometimes used to address stability or accuracy, create dependencies that disrupt the purely local and independent computations that are a key advantage of LBM. Such non-local adjustments increase computational costs, reduce parallel efficiency, and complicate memory access patterns, which diminishes the performance of LBM on large HPC systems.

Therefore, adhering closely to the standard LBM formulation preserves its localized computation advantage, reducing communication overhead and allowing efficient scaling across numerous computational nodes. This efficiency enables the simulation of high-resolution, large-domain multiphase flows crucial for energy sector applications, like bubble column reactors in oil and gas, where detailed fluid dynamics insights are essential for optimizing processes.

This paper aims to derive an LBM framework to simulate Eulerian–Eulerian equations for multiphase flows. The overall scheme consists of six LBM schemes for the two phases, as follows:

• Two LBM schemes for artificially compressible continuity equations and momentum equations, in terms of particle distribution functions $f_g$ and $f_l$;
• Two LBM schemes for phase volume fractions, in terms of $f_{\alpha g}$ and $f_{\alpha l}$;
• Two LBM schemes for phase continuity sources, in terms of $f_{\beta g}$ and $f_{\beta l}$.

The proposed LBM framework is derived and analyzed in the rest of this section in a general, way which does not pose any constraint on the physical dimensionality, while the following section reports a preliminary numerical validation.

2.1. The Key Point: Artificially Compressible Continuity Equation and Momentum Equation for Each Phase

The LBM uses the artificial compressibility concept [16] and hence it cannot solve Equation (15) directly. Hence a pseudo-compressible system of equations for each phase is needed as a starting point for deriving the Eulerian–Eulerian LBM framework to simulate multiphase flows. Applying the artificial compressibility concept requires a system of equations made of (a) a momentum equation and (b) an artificially compressible continuity equation, which is obviously missing in the incompressible formulation, for each phase. Let us start with the dispersed phase and let us start by modifying Equation (12) in the following way:

$${\displaystyle \frac{𝜕{ϵ}_g}{𝜕t}}+\nabla ·({\alpha }_g{\mathit{u}}_g+{\alpha }_l{\mathit{u}}_l)=0,$$

(18)

where ${ϵ}_g$ is a function computed by flow quantities. If the artificial compressibility is used as a shortcut to find out only the steady-state solution, then it is enough that $𝜕{ϵ}_g/𝜕t$ is small enough with regard to the other terms. However, in this work, the idea is to recover the right incompressible dynamics as well, and hence, $𝜕{ϵ}_g/𝜕t$ must be asymptotically small during the entire dynamics, according to the order of convergence of the numerical scheme. For example, this term could be $𝜕{ϵ}_g/𝜕t=O\left(h^2\right)$ in the case of a second-order method, where h is the mesh spacing. The last condition can be recovered by a proper scaling, namely, a proper choice of the simulation parameters during mesh refinement. We will enforce this condition in the following, after discussing the asymptotic analysis of the proposed methodology. Let us manipulate the previous equation as follows:

$${\displaystyle \frac{𝜕{ϵ}_g}{𝜕t}}+\nabla ·{\mathit{u}}_g=\nabla ·\left[{\alpha }_l({\mathit{u}}_g-{\mathit{u}}_l)\right]\equiv S_g.$$

(19)

The previous equation is an artificially compressible continuity equation designed for the dispersed-phase velocity field ${\mathit{u}}_g$. We have to derive a similar equation for the liquid-phase velocity field ${\mathit{u}}_l$. Hence, this time, let us modify Equation (12) as follows:

$${\displaystyle \frac{𝜕{ϵ}_l}{𝜕t}}+\nabla ·{\mathit{u}}_l=\nabla ·\left[{\alpha }_g({\mathit{u}}_l-{\mathit{u}}_g)\right]\equiv S_l.$$

(20)

Different strategies are possible in choosing the pair of functions ${ϵ}_g$ and ${ϵ}_l$:

• Because both previous equations are derived from the same Equation (12), then one could assume ${ϵ}_g={ϵ}_l=ϵ\left(p\right)$. The simplest choice would be $ϵ\left(p\right)=p$, or by looking at the Poisson equation for the mixture velocity given by Equation (15), one could use instead $ϵ\left(p\right)=({\alpha }_g/{\rho }_g^0+{\alpha }_l/{\rho }_l^0)p$, introducing a further dependence on the volume fraction in the pseudo-compressibility.
• The problem with the previous approach is that it forces both phases not only to have the same asymptotic target given by Equation (12) but also to have the same approaching dynamics. Because the two phases are subject to different forces, this could lead to over-constraining. Hence, one could assume instead two independent functions ${ϵ}_g={ϵ}_g\left(p\right)$ and ${ϵ}_l={ϵ}_l\left(p\right)$. In this work, we choose this second approach. The explicit expressions of these functions will be provided in the following.

Concerning the momentum equations, let us manipulate Equations (16) and (17) as follows:

$${\displaystyle \frac{𝜕{\mathit{u}}_g}{𝜕t}}+\nabla ·\left({\mathit{u}}_g{\mathit{u}}_g\right)-{\mathit{u}}_g\nabla ·{\mathit{u}}_g=-{\displaystyle \frac{1}{{\rho }_g^0}}\nabla p+\mathit{g}+{\displaystyle \frac{1}{{\alpha }_g}}\nabla ·\left({\alpha }_g{\mathbf{\sigma }}_g\right)+{\displaystyle \frac{1}{{\alpha }_g{\rho }_g^0}}\left({\mathit{F}}_{gl}+{\mathit{F}}_g\right),$$

(21)

$${\displaystyle \frac{𝜕{\mathit{u}}_l}{𝜕t}}+\nabla ·\left({\mathit{u}}_l{\mathit{u}}_l\right)-{\mathit{u}}_l\nabla ·{\mathit{u}}_l=-{\displaystyle \frac{1}{{\rho }_l^0}}\nabla p+\mathit{g}+{\displaystyle \frac{1}{{\alpha }_l}}\nabla ·\left({\alpha }_l{\mathbf{\sigma }}_l\right)+{\displaystyle \frac{1}{{\alpha }_l{\rho }_l^0}}\left({\mathit{F}}_{lg}+{\mathit{F}}_l\right).$$

(22)

Using Equations (19) and (20) coherently with the artificial compressibility approach, $\nabla ·{\mathit{u}}_g=S_g+O\left(h^2\right)$ and $\nabla ·{\mathit{u}}_l=S_l+O\left(h^2\right)$. Let us assume that $\nabla ·{\mathit{u}}_g\approx S_g$ and $\nabla ·{\mathit{u}}_l\approx S_l$, which can be used to simplify the previous equations. For the dispersed phase, this yields

$${\displaystyle \frac{𝜕{\mathit{u}}_g}{𝜕t}}+\nabla ·\left({\mathit{u}}_g{\mathit{u}}_g\right)=-\nabla \left({\displaystyle \frac{p}{{\rho }_g^0}}\right)+\nabla ·{\mathbf{\sigma }}_g+{\mathit{G}}_g,$$

(23)

where

$${\mathit{G}}_g\equiv S_g{\mathit{u}}_g+{\displaystyle \frac{1}{{\alpha }_g}}{\mathbf{\sigma }}_g·\nabla {\alpha }_g+\mathit{g}+{\displaystyle \frac{1}{{\alpha }_g{\rho }_g^0}}({\mathit{F}}_{gl}+{\mathit{F}}_g).$$

(24)

Similarly, it holds that

$${\displaystyle \frac{𝜕{\mathit{u}}_l}{𝜕t}}+\nabla ·\left({\mathit{u}}_l{\mathit{u}}_l\right)=-\nabla \left({\displaystyle \frac{p}{{\rho }_l^0}}\right)+\nabla ·{\mathbf{\sigma }}_l+{\mathit{G}}_l,$$

(25)

where

$${\mathit{G}}_l\equiv S_l{\mathit{u}}_l+{\displaystyle \frac{1}{{\alpha }_l}}{\mathbf{\sigma }}_l·\nabla {\alpha }_l+\mathit{g}+{\displaystyle \frac{1}{{\alpha }_l{\rho }_l^0}}({\mathit{F}}_{lg}+{\mathit{F}}_l).$$

(26)

For a given dispersed-phase volume fraction ${\alpha }_g$, Equations (19) and (23) may be target equations for an LBM scheme for the dispersed phase. Similarly, Equations (20) and (25) may be target equations for an LBM scheme for the liquid phase. However, it is important to highlight the following peculiarity: Equations (19) and (20) are driven by the same pressure time derivative because ${𝜕}_t{ϵ}_g=(𝜕{ϵ}_g/𝜕p){𝜕}_{t}p$ and ${𝜕}_t{ϵ}_l=(𝜕{ϵ}_l/𝜕p){𝜕}_{t}p$ (time pressure coupling), and moreover, Equations (23) and (25) are coupled by the same pressure gradient $\nabla p$ (space pressure coupling). It is important to remind at this point that the system of equations for both phases can be closed only by providing the additional equation for ${\alpha }_g$ (which is discussed in the following sections).

Before entering into the details of the LBM schemes, it is worth discussing first both the time and the space pressure coupling, mentioned above, in the LBM context. Let us recall first some preliminaries about LBM. Let us define $ϵ$ as the zeroth order moment of the distribution function, namely, $ϵ={\sum }_{q}f\left(q\right)$, where q identifies the probability distribution function $f\left(q\right)$ corresponding to the lattice velocity ${\mathit{v}}_q\in \mathbb{L}$ in the velocity lattice/set $\mathbb{L}$, designed for the D-dimensional physical space and for the Q-dimensional velocity space. In the LBM framework, as will be clearer in the following, it is possible to impose an equation of state where the pressure is $p=c_s^2\varphi \rho ϵ$, where $c_s\sqrt{\varphi }$ is the (artificial) sound speed and $\varphi$ is a tunable function (close to 1 for stability reasons). Let us now assume that Equations (19) and (23) are solved by an LBM scheme in terms of $f_g$, and for the sake of simplicity, let us assume ${\varphi }_g=1$. This allows one to identify the pressure p as

$$p\equiv c_s^2{\rho }_g^0{ϵ}_g,$$

(27)

where ${ϵ}_g={\sum }_q{f}_g\left(q\right)$ or equivalently

$${ϵ}_g\left(p\right)={\displaystyle \frac{p}{c_s^2{\rho }_g^0}},$$

(28)

which identifies the first function appearing in Equation (19).

Let us now assume that Equations (20) and (25) are solved by another LBM scheme in terms of $f_l$ and that this time ${\varphi }_l\ne 1$, which requires a specific equilibrium distribution function. Because Equations (23) and (25) are coupled, one has to ensure that the same pressure gradient (space pressure coupling) will drive also the evolution of this second LBM scheme for the liquid phase as well. The target Equation (25) involves the following term, which is ruled by the generalized equation of state, namely,

$$\nabla \left({\displaystyle \frac{p}{{\rho }_l^0}}\right)=\nabla \left({\varphi }_l{c}_s^2{ϵ}_l\right),$$

(29)

where ${ϵ}_l={\sum }_l{f}_l\left(q\right)$. Substituting Equation (27) into the previous one yields

$$\nabla \left({\varphi }_l{ϵ}_l\right)={\displaystyle \frac{1}{R}}\nabla {ϵ}_g,$$

(30)

where $R={\rho }_l^0/{\rho }_g^0>1$. Solving the previous equations yields

$${\varphi }_l{ϵ}_l={\displaystyle \frac{1}{R}}{ϵ}_g+k,$$

(31)

where k is an arbitrary constant. In order to choose the proper constant k, let us remember that ${ϵ}_{\phi }={\sum }_q{f}_{\phi }\left(q\right)$ is close to 1 in the incompressible limit and that one wants ${\varphi }_l$ to be close to 1 for stability reasons. Assuming $k=-1/R+1$ yields

$${\varphi }_l=\varphi \equiv {\displaystyle \frac{1}{{ϵ}_l}}\left[1+{\displaystyle \frac{1}{R}}\left({ϵ}_g-1\right)\right],$$

(32)

or equivalently

$${ϵ}_l\left(p\right)={\displaystyle \frac{1}{\varphi }}\left[1+{\displaystyle \frac{1}{R}}\left({\displaystyle \frac{p}{c_s^2{\rho }_g^0}}-1\right)\right],$$

(33)

which identifies the second function appearing in Equation (20). Clearly, ${ϵ}_g\left(p\right)$ given by Equation (28) and ${ϵ}_l\left(p\right)$ given by Equation (33) are driven by the same pressure dynamics (time pressure coupling), but they are different functions.

Let us recap the work performed so far. Equation (19) with source $S_g$ and Equation (23) with force ${\mathit{G}}_g$ can be solved by an LBM scheme in terms of $f_g$ with a standard equation of state given by Equation (27). On the other hand, Equation (20) with source $S_l$ and Equation (25) with force ${\mathit{G}}_l$ can be solved by an LBM scheme in terms of $f_l$ with a generalized equation of state, i.e., with ${\varphi }_l$ given by Equation (32). In the next section, we will discuss the complete LBM schemes proposed for solving these equations.

2.1.1. LBM Schemes for Solving the Key Equations

Let us consider the following two LBM schemes for solving the artificially compressible continuity equations and the momentum equations for the two phases, formulated in terms of the corresponding particle distribution functions $f_g$ and $f_l$, namely,

$$f_g(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)=f_g\left(q\right)+{\widehat{\mathsf{\Omega }}}_g\left(q\right)+{\widehat{\mathsf{\Omega }}}_g^F\left(q\right),$$

(34)

$$f_l(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)=f_l\left(q\right)+{\widehat{\mathsf{\Omega }}}_l\left(q\right)+{\widehat{\mathsf{\Omega }}}_l^F\left(q\right),$$

(35)

where all functions in the right-hand side are computed in $(\widehat{\mathit{x}},\widehat{t})$ locally, $\widehat{\mathit{x}}$ is the space coordinate divided by the distance $\lambda$ between two neighboring lattices nodes (mean free path), $\widehat{t}$ is the physical time divided by the time $\tau$ between two consecutive lattice collisions (mean collision time), and ${\mathit{v}}_q$ is the generic particle velocity divided by the average particle velocity $c=\lambda /\tau$ in the velocity lattice/set $\mathbb{L}$ designed for the D-dimensional physical space and for the Q-dimensional velocity space. These normalizations are consistent with the usual Boltzmann scaling adopted in the LBM numerical codes, which will be denoted by the hat notation $\widehat{·}$ from here on in order to simplify the discussion about how to tune the simulation parameters for solving the target equations. In the following, we discuss the terms ${\widehat{\mathsf{\Omega }}}_{\phi }$ and ${\widehat{\mathsf{\Omega }}}_{\phi }^F$.

The term ${\widehat{\mathsf{\Omega }}}_{\phi }$ is the collisional operator, defined as

$${\widehat{\mathsf{\Omega }}}_{\phi }\left(q\right)={\omega }_{\phi }\left[f_{\phi }^{eq}\left(q\right)-f_{\phi }\left(q\right)\right],$$

(36)

where ${\omega }_{\phi }$ is the relaxation frequency divided by the frequency $1/\tau$ for the phase $\phi$, which drives the relaxation of the distribution function towards the equilibrium $f_{\phi }^{eq}$. The equilibrium $f_{\phi }^{eq}$ is defined by means of the so-called incompressible equilibrium $f_I^e(\varphi ,\widehat{ϵ},\widehat{\mathit{u}})$. This equilibrium is called incompressible because all terms of the equilibrium moments which depend on the velocity $\widehat{\mathit{u}}$ do not depend on the zeroth order moment $\widehat{ϵ}$, e.g., ${\sum }_q{\mathit{v}}_q{f}_I^e(\varphi ,\widehat{ϵ},\widehat{\mathit{u}},q)=\widehat{\mathit{u}}$. The equilibrium distribution is different for the two phases even though it is formulated by means of the same functional form in the incompressible limit [1], namely,

$$f_I^{eq}(\varphi ,\widehat{ϵ},\widehat{\mathit{u}},q)=w_q\left[\widehat{ϵ}{\eta }_q\left(\varphi \right)+{\displaystyle \frac{{\mathit{v}}_q·\widehat{\mathit{u}}}{c_s^2}}+{\displaystyle \frac{({\mathit{v}}_q{\mathit{v}}_q-c_s^2\mathit{I}):\widehat{\mathit{u}}\widehat{\mathit{u}}}{2c_s^4}}\right],$$

(37)

where

$${\eta }_q\left(\varphi \right)={\delta }_q\left[1+{\displaystyle \frac{(1-w_0)}{w_0}}(1-\varphi )\right]+(1-{\delta }_q)\varphi ,$$

(38)

and

$${\delta }_q=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}q=0,\hfill \\ 0,\hfill & \mathrm{if}q\ne 0.\hfill \end{array}\right.$$

(39)

The two equilibrium distributions differ from each other because $f_g^{eq}\equiv f_I^{eq}(1,{\widehat{ϵ}}_g,{\widehat{\mathit{u}}}_g)$ for the dispersed phase, while $f_l^{eq}\equiv f_I^{eq}(\varphi ,{\widehat{ϵ}}_l,{\widehat{\mathit{u}}}_l)$ for the liquid phase, where $\varphi$ is given by Equation (32). The quantities ${\widehat{ϵ}}_{\phi }$ and ${\widehat{\mathit{u}}}_{\phi }$ can be computed by the function $f_{\phi }$, which acts as an auxiliary vector, namely,

$${\widehat{ϵ}}_{\phi }=\sum _{q=0}^{Q-1}{f}_{\phi }\left(q\right),$$

(40)

$${\widehat{\mathit{u}}}_{\phi }=\sum _{q=0}^{Q-1}{\mathit{v}}_q{f}_{\phi }\left(q\right).$$

(41)

It is important to highlight the difference between ${\widehat{\mathit{u}}}_{\phi }$ and ${\mathit{u}}_{\phi }$ discussed in the previous sections. The former is the velocity field normalized by the characteristic flow speed $U=L/T$, where $L\gg \lambda$ is the characteristic length scale of the flow field and $T\gg \tau$ is the characteristic time scale of the flow field. Hence, the following relation holds: ${\widehat{\mathit{u}}}_{\phi }={\mathit{u}}_{\phi }(L/\lambda )(\tau /T)$. Hence it is not granted that the code output ${\widehat{\mathit{u}}}_{\phi }$ converges to the physical solution ${\mathit{u}}_{\phi }$ when the mesh is refined, namely, when $\lambda /L\to 0$. The strategy for tuning the code parameters such that this convergence is enforced is called the scaling. Typically, the acoustic scaling, i.e., $\tau /T=\lambda /L$, and the diffusive scaling, i.e., $\tau /T={(\lambda /L)}^2$, are the two most popular examples. Similar considerations hold also for ${\widehat{ϵ}}_{\phi }$, but they require us to proceed with the formal asymptotic expansion, which is performed in the following.

The term ${\widehat{\mathsf{\Omega }}}_{\phi }^F$ is the forcing operator and it can be defined by the same linearized functional form, namely,

$${\widehat{\mathsf{\Omega }}}_{\phi }^F({\psi }_{\phi },{\widehat{S}}_{\phi },{\widehat{\mathit{G}}}_{\phi },q)\equiv f_L^{eq}({\psi }_{\phi },{\widehat{S}}_{\phi },{\widehat{\mathit{G}}}_{\phi },q)=w_q\left[{\widehat{S}}_{\phi }\eta \left({\psi }_{\phi }\right)+{\displaystyle \frac{{\mathit{v}}_q·{\widehat{\mathit{G}}}_{\phi }}{c_s^2}}\right].$$

(42)

In general, ${\psi }_g$ is different from ${\psi }_l$ and is different from $\varphi$. Intuitively, ${\widehat{S}}_{\phi }$ and ${\widehat{\mathit{G}}}_{\phi }$ are the expressions computed using ${\widehat{\mathit{u}}}_{\phi }$ (Boltzmann scaling) in the code.

2.1.2. Asymptotic Analysis by the Equivalent Moment System

Equations (34) and (35) do not solve directly the target fluid equations, in the sense that the computed quantities, indicated with the hat notation $\widehat{·}$, do not converge automatically to the target fluid quantities if a proper scaling is not provided. The scaling is the set of rules used to update the input parameters once the mesh is refined. Hence, an asymptotic analysis is needed in order to find out under which conditions these equations at least approximate the target fluid equations. Here we use the asymptotic method based on the equivalent moment system [17], inspired by the moment method, which was first introduced to gas kinetic theory by H. Grad. The previous equations share the same structure, namely,

$$f_{\phi }(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)=f_{\phi }\left(q\right)+{\widehat{\mathsf{\Omega }}}_{\phi }\left(q\right)+{\widehat{\mathsf{\Omega }}}_{\phi }^F\left(q\right).$$

(43)

Let us apply a Taylor expansion, namely,

$$f_{\phi }(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)-f_{\phi }(\widehat{\mathit{x}},\widehat{t},q)={\displaystyle \frac{𝜕f_{\phi }}{𝜕\widehat{t}}}+{\mathit{v}}_q·\widehat{\nabla }{f}_{\phi }+{\displaystyle \frac{1}{2}}{({\mathit{v}}_q·\widehat{\nabla })}^2{f}_{\phi }+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{𝜕}^2{f}_{\phi }}{𝜕{\widehat{t}}^2}}+\dots .$$

(44)

In the previous equation, the unit of the space coordinate is the distance $\lambda$ between two neighboring lattice nodes (mean free path) and the unit of the time evolution is the time $\tau$ between two consecutive lattice collisions (mean collision time). Obviously, they are not appropriate as the characteristic scales for the flow field in the continuum limit, namely, L and T. Let us introduce the parameter $\epsilon =\lambda /L\ll 1$ (mesh spacing) and let us reduce the corresponding time step quadratically, namely, $\tau /T={\epsilon }^2$ (diffusive scaling), which increases quadratically the number of time steps, as well as the computational time needed to solve the problem. By using these assumptions, the relations $\widehat{t}=t/{\epsilon }^2$ and $\widehat{\mathit{x}}=x/\epsilon$ hold, which lead to

$$f_{\phi }(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)-f_{\phi }(\widehat{\mathit{x}},\widehat{t},q)=\epsilon {\mathit{v}}_q·\nabla f_{\phi }+{\displaystyle \frac{{\epsilon }^2}{2}}{({\mathit{v}}_q·\nabla )}^2{f}_{\phi }+{\epsilon }^2{\displaystyle \frac{𝜕f_{\phi }}{𝜕t}}+O\left({\epsilon }^3\right).$$

(45)

Neglecting terms $O\left({\epsilon }^3\right)$ yields

$${\epsilon }^2{\displaystyle \frac{𝜕f_{\phi }}{𝜕t}}+\epsilon {\mathit{v}}_q·\nabla f_{\phi }+{\displaystyle \frac{{\epsilon }^2}{2}}{({\mathit{v}}_q·\nabla )}^2{f}_{\phi }={\widehat{\mathsf{\Omega }}}_{\phi }\left(q\right)+{\widehat{\mathsf{\Omega }}}_{\phi }^F\left(q\right).$$

(46)

Taking the zeroth-order, first-order, and second-order moments of the previous equations yields

$${\epsilon }^2{\displaystyle \frac{𝜕{\widehat{ϵ}}_{\phi }}{𝜕t}}+\epsilon \nabla ·{\widehat{\mathit{u}}}_{\phi }+{\displaystyle \frac{{\epsilon }^2}{2}}\nabla ·\nabla ·{\widehat{\mathbf{\Pi }}}_{\phi }={\widehat{S}}_{\phi },$$

(47)

$${\epsilon }^2{\displaystyle \frac{𝜕{\widehat{\mathit{u}}}_{\phi }}{𝜕t}}+\epsilon \nabla ·{\widehat{\mathbf{\Pi }}}_{\phi }+{\displaystyle \frac{{\epsilon }^2}{2}}\nabla ·\nabla ·{\widehat{\mathbf{\Phi }}}_{\phi }={\widehat{\mathit{G}}}_{\phi },$$

(48)

$${\epsilon }^2{\displaystyle \frac{𝜕{\widehat{\mathbf{\Pi }}}_{\phi }}{𝜕t}}+\epsilon \nabla ·{\widehat{\mathbf{\Phi }}}_{\phi }+{\displaystyle \frac{{\epsilon }^2}{2}}\nabla ·\nabla ·\sum _q{\mathit{v}}_q{\mathit{v}}_q{\mathit{v}}_q{\mathit{v}}_q{f}_{\phi }\left(q\right)={\omega }_{\phi }({\widehat{\mathbf{\Pi }}}_{\phi }^{eq}-{\widehat{\mathbf{\Pi }}}_{\phi })+{\psi }_{\phi }{c}_s^2{\widehat{S}}_{\phi }\mathit{I},$$

(49)

where ${\widehat{\mathbf{\Pi }}}_{\phi }={\sum }_{q=0}^{Q-1}{\mathit{v}}_q{\mathit{v}}_q{f}_{\phi }\left(q\right)$ is the second-order tensor of the distribution function and ${\widehat{\mathbf{\Phi }}}_{\phi }={\sum }_{q=0}^{Q-1}{\mathit{v}}_q{\mathit{v}}_q{\mathit{v}}_q{f}_{\phi }\left(q\right)$ is the third-order tensor. Moreover, by the definition given by Equation (37), it is possible to compute

$${\widehat{\mathbf{\Pi }}}_{\phi }^{eq}={\widehat{\varphi }}_{\phi }{c}_s^2{\widehat{ϵ}}_{\phi }\mathit{I}+{\widehat{\mathit{u}}}_{\phi }{\widehat{\mathit{u}}}_{\phi },$$

(50)

and

$${\left({\widehat{\mathbf{\Phi }}}_{\phi }^{eq}\right)}_{ijk}=c_s^2\left({\widehat{u}}_{\phi i}{\delta }_{jk}+{\widehat{u}}_{\phi j}{\delta }_{ik}+{\widehat{u}}_{\phi k}{\delta }_{ij}\right).$$

(51)

In order to analyze this system of equations, it is now time to understand the impact of the previous assumptions on the scaling of the moments, namely, how changing the mesh spacing impacts the numerical values of the lattice moments (in Boltzmann scaling) computed by the code. The relation ${\widehat{\mathit{u}}}_{\phi }={\mathit{u}}_{\phi }(L/\lambda )(\tau /T)$ becomes ${\widehat{\mathit{u}}}_{\phi }=\epsilon {\mathit{u}}_{\phi }$. Consequently, ${\widehat{S}}_{\phi }={\epsilon }^2{S}_{\phi }$ because the source is the divergence of a velocity vector combination. Recalling the definitions given by Equations (24) and (26), there are four terms in ${\widehat{\mathit{G}}}_{\phi }$. According to the previous scaling, ${\widehat{S}}_{\phi }{\widehat{\mathit{u}}}_{\phi }$ and ${\widehat{\mathbf{\sigma }}}_{\phi }·\widehat{\nabla }{\alpha }_g$ are automatically $O\left({\epsilon }^3\right)$. Hence it makes sense to scale in the same way also the two remaining terms. Adopting $\widehat{\mathit{g}}={\epsilon }^3\mathit{g}$ means that if $\epsilon$ becomes half, then $\widehat{\mathit{g}}$ must become $1/2^3$ of the original value. Similarly, we adopt ${\widehat{\mathit{F}}}_{\phi \overline{\phi }}={\epsilon }^3{\mathit{F}}_{\phi \overline{\phi }}$, where $\overline{\phi }$ is the other phase in relation with phase $\phi$, and ${\widehat{\mathit{F}}}_{\phi }={\epsilon }^3{\mathit{F}}_{\phi }$. The first decision implies ${\widehat{K}}_I=\epsilon K_I$ because in Equation (6) there is already a quadratic dependence on some velocity. Putting together all these assumptions yields ${\widehat{\mathit{G}}}_{\phi }={\epsilon }^3{\mathit{G}}_{\phi }$, which is consistent with the fact that a force induces an acceleration, namely, ${\widehat{\mathit{G}}}_{\phi }\propto 𝜕{\widehat{\mathit{u}}}_{\phi }/𝜕\widehat{t}={\epsilon }^3𝜕{\mathit{u}}_{\phi }/𝜕t$.

A system of moments can be truncated if we have some expectations about the high-order moments. Actually, on a discrete lattice, the system of moments is automatically truncated because of the limited number of independent degrees of freedoms (typically up to some components of the fourth-order moment) [17]. Let us now imagine the equation for the third-order moment ${\widehat{\mathbf{\Phi }}}_{\phi }$, which is very similar to the previous equations. On the left-hand side of this equation, there is a term which is proportional to ${\epsilon }^2$ multiplied by the double divergence of the fifth-order moment, which is “odd” with regard to the power of ${\mathit{v}}_q$, and hence it scales as ${\widehat{\mathit{u}}}_{\phi }=\epsilon {\mathit{u}}_{\phi }$: altogether this term on the left-hand side scales as $O\left({\epsilon }^3\right)$. On the right-hand side, we have ${\widehat{\mathbf{\Phi }}}_{\phi }^{eq}-{\widehat{\mathbf{\Phi }}}_{\phi }$ and the third-order moment of the forcing operator, which is proportional to ${\epsilon }^3{\mathit{G}}_{\phi }$ and hence again $O\left({\epsilon }^3\right)$. Putting the pieces together, the equation for the third-order moment looks like ${\widehat{\mathbf{\Phi }}}_{\phi }={\widehat{\mathbf{\Phi }}}_{\phi }^{eq}+O\left({\epsilon }^3\right)$. It is clear from Equation (51) that ${\widehat{\mathbf{\Phi }}}_{\phi }^{eq}=\epsilon {\mathbf{\Phi }}_{\phi }^{eq}$ and consequently

$${\mathbf{\Phi }}_{\phi }={\mathbf{\Phi }}_{\phi }^{eq}+O\left({\epsilon }^2\right).$$

(52)

Substituting these considerations in Equation (48) yields

$${\epsilon }^3{\displaystyle \frac{𝜕{\mathit{u}}_{\phi }}{𝜕t}}+\epsilon \nabla ·{\widehat{\mathbf{\Pi }}}_{\phi }+{\displaystyle \frac{{\epsilon }^3}{2}}\nabla ·\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}={\epsilon }^3{\mathit{G}}_{\phi }+O\left({\epsilon }^5\right),$$

(53)

which implies $\nabla ·{\widehat{\mathbf{\Pi }}}_{\phi }={\epsilon }^2\nabla ·{\mathbf{\Pi }}_{\phi }$. Consequently,

$${\displaystyle \frac{𝜕{\mathit{u}}_{\phi }}{𝜕t}}+\nabla ·{\mathbf{\Pi }}_{\phi }+{\displaystyle \frac{1}{2}}\nabla ·\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}={\mathit{G}}_{\phi }+O\left({\epsilon }^2\right).$$

(54)

Similarly, the equation for the second-order moment looks like ${\widehat{\mathbf{\Pi }}}_{\phi }={\widehat{\mathbf{\Pi }}}_{\phi }^{eq}+O\left({\epsilon }^2\right)={\widehat{\varphi }}_{\phi }{c}_s^2{\widehat{ϵ}}_{\phi }\mathit{I}+O\left({\epsilon }^2\right)$. Using again the last relation implies $\nabla ·{\widehat{\mathbf{\Pi }}}_{\phi }={\epsilon }^2\nabla ·{\mathbf{\Pi }}_{\phi }=O\left({\epsilon }^2\right)$ and then $\nabla \left({\widehat{\varphi }}_{\phi }{c}_s^2{\widehat{ϵ}}_{\phi }\right)=O\left({\epsilon }^2\right)$ and equivalently $\nabla \left({\widehat{\varphi }}_{\phi }{\widehat{ϵ}}_{\phi }\right)=O\left({\epsilon }^2\right)$. Moreover, let us assume that in some portion of the domain boundary (typically the outflow), namely, for $x\in {\mathsf{\Omega }}_B$, the following boundary conditions hold: ${\widehat{ϵ}}_g{|}_B=1$, ${\widehat{ϵ}}_l{|}_B=1$ and consequently $\widehat{\varphi }{|}_B=1$. These boundary conditions allow one to integrate the previous relation, which yields

$${\widehat{ϵ}}_g=1+{\epsilon }^2{ϵ}_g,$$

(55)

$$\widehat{\varphi }{\widehat{ϵ}}_l=1+(1/R)\left({\widehat{ϵ}}_g-1\right)=1+{\epsilon }^2{ϵ}_g/R.$$

(56)

Assuming ${\varphi }_g=1$ and ${\varphi }_l=\left({ϵ}_g/{ϵ}_l\right)/R$, the relations given by Equations (55) and (56) can be expressed by one unique formula, namely,

$${\widehat{\varphi }}_{\phi }{\widehat{ϵ}}_{\phi }=1+{\epsilon }^2{\varphi }_{\phi }{ϵ}_{\phi }.$$

(57)

Concerning ${\widehat{ϵ}}_l$, introducing the relation $\nabla ·{\widehat{\mathbf{\Pi }}}_l=O\left({\epsilon }^2\right)$ into Equation (47) implies that $𝜕{\widehat{ϵ}}_l/𝜕t=O\left(1\right)$ or $𝜕{\widehat{ϵ}}_l/𝜕t=O\left({\epsilon }^2\right)$. Let us focus on the second case by assuming that the boundary conditions change smoothly in time. Taking into account the boundary condition ${\widehat{ϵ}}_l{|}_B=1$ and integrating the relation $𝜕{\widehat{ϵ}}_l/𝜕t=O\left({\epsilon }^2\right)$ yields

$${\widehat{ϵ}}_l=1+{\epsilon }^2{ϵ}_l,$$

(58)

and consequently

$$\widehat{\varphi }={\displaystyle \frac{1+{\epsilon }^2{ϵ}_g/R}{1+{\epsilon }^2{ϵ}_l}}=1+{\epsilon }^2\left({ϵ}_g/R-{ϵ}_l\right)+O\left({\epsilon }^4\right).$$

(59)

Introducing Equations (55), (57) and (58) into Equation (47) yields

$$\nabla ·{\mathit{u}}_{\phi }=S_{\phi }+O\left({\epsilon }^2\right).$$

(60)

Equations (54) and (60) prove that the proposed scaling converges asymptotically with the second order of convergence to some equations, but we still have to prove that they coincide with the target equations. First of all, we search for an approximation of ${\mathbf{\Pi }}_{\phi }$. Recalling Equation (49), taking into account that the term with a sequence of divergences of the fourth-order moment scales as ${\epsilon }^2\nabla \left({\widehat{\varphi }}_{\phi }{\widehat{ϵ}}_{\phi }\right)=O\left({\epsilon }^4\right)$, because of Equation (57) and recalling Equation (60), it follows that

$${\epsilon }^2\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}={\omega }_{\phi }({\widehat{\mathbf{\Pi }}}_{\phi }^{eq}-{\widehat{\mathbf{\Pi }}}_{\phi })+{\epsilon }^2{\psi }_{\phi }{c}_s^2\nabla ·{\mathit{u}}_{\phi }\mathit{I}+O\left({\epsilon }^4\right).$$

(61)

Recalling that $\nabla ·{\widehat{\mathbf{\Pi }}}_{\phi }={\epsilon }^2\nabla ·{\mathbf{\Pi }}_{\phi }$ yields

$$\nabla ·{\mathbf{\Pi }}_{\phi }=\nabla ·{\mathbf{\Pi }}_{\phi }^{eq}-\nabla ·\left[{\displaystyle \frac{1}{{\omega }_{\phi }}}\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}-{\displaystyle \frac{c_s^2{\psi }_{\phi }}{{\omega }_{\phi }}}\nabla ·{\mathit{u}}_{\phi }\mathit{I}\right]+O\left({\epsilon }^2\right).$$

(62)

Substituting Equation (62) into Equation (54) yields

$${\displaystyle \frac{𝜕{\mathit{u}}_{\phi }}{𝜕t}}+\nabla ·{\mathbf{\Pi }}_{\phi }^{eq}=\nabla ·\left[\left({\displaystyle \frac{1}{{\omega }_{\phi }}}-{\displaystyle \frac{1}{2}}\right)\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}-{\displaystyle \frac{c_s^2{\psi }_{\phi }}{{\omega }_{\phi }}}\nabla ·{\mathit{u}}_{\phi }\mathit{I}\right]+{\mathit{G}}_{\phi }+O\left({\epsilon }^2\right).$$

(63)

From the definition given by Equation (51), it is possible to prove that

$$\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}=c_s^2\left(\nabla {\mathit{u}}_{\phi }+\nabla {\mathit{u}}_{\phi }^T+\nabla ·{\mathit{u}}_{\phi }\mathit{I}\right).$$

(64)

Let us add another ingredient by defining the kinematic viscosity as

$${\nu }_{\phi }=c_s^2\left({\displaystyle \frac{1}{{\omega }_{\phi }}}-{\displaystyle \frac{1}{2}}\right),$$

(65)

and by choosing the tunable parameter ${\psi }_{\phi }$ in order to recover the right kinematic bulk viscosity ${\xi }_{\phi }$ as

$${\psi }_{\phi }={\displaystyle \frac{{\omega }_{\phi }}{c_s^2}}\left({\displaystyle \frac{5}{3}}{\nu }_{\phi }-{\xi }_{\phi }\right).$$

(66)

It is important to note that both previous viscosity coefficients are normalized by the characteristic scales for the flow field in the continuum limit, namely, by $L^2/T$ (in other words, the viscosity coefficients are the inverses of the corresponding Reynolds numbers). Substituting the previous expression into Equation (63) yields

$${\displaystyle \frac{𝜕{\mathit{u}}_{\phi }}{𝜕t}}+\nabla ·{\mathbf{\Pi }}_{\phi }^{eq}=\nabla ·{\mathbf{\sigma }}_{\phi }+{\mathit{G}}_{\phi }+O\left({\epsilon }^2\right).$$

(67)

Clearly, Equations (60) and (67) approach the solution of the target equations in the asymptotic limit of $\epsilon \to 0$ with second-order accuracy, thanks to the adopted diffusive scaling.

These LBM schemes are not only useful to recover an approximated solution of the target equations but they can also be used to compute relevant quantities which will be used in the following. For example, it is possible to compute the viscous stress tensor per unit volume without further computational efforts. Comparing Equations (63) and (67), it is possible to derive

$${\mathbf{\sigma }}_{\phi }=\left({\displaystyle \frac{1}{{\omega }_{\phi }}}-{\displaystyle \frac{1}{2}}\right)\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}-{\displaystyle \frac{c_s^2{\psi }_{\phi }}{{\omega }_{\phi }}}\nabla ·{\mathit{u}}_{\phi }\mathit{I}+O\left({\epsilon }^2\right).$$

(68)

From the numerical point of view, it is possible to compute $\nabla ·{\mathbf{\Phi }}_{\phi }^{eq}$ by Equation (61) and $\nabla ·{\mathit{u}}_{\phi }$ by Equation (60), namely,

$${\mathbf{\sigma }}_{\phi }=\left({\displaystyle \frac{1}{{\omega }_{\phi }}}-{\displaystyle \frac{1}{2}}\right)\left[{\omega }_{\phi }\left({\mathbf{\Pi }}_{\phi }^{eq}-{\mathbf{\Pi }}_{\phi }\right)+{\psi }_{\phi }{c}_s^2{S}_{\phi }\mathit{I}\right]-{\displaystyle \frac{c_s^2{\psi }_{\phi }}{{\omega }_{\phi }}}{S}_{\phi }\mathit{I}+O\left({\epsilon }^2\right),$$

(69)

or equivalently,

$${\mathbf{\sigma }}_{\phi }=\left({\displaystyle \frac{1}{{\omega }_{\phi }}}-{\displaystyle \frac{1}{2}}\right){\omega }_{\phi }\left({\mathbf{\Pi }}_{\phi }^{eq}-{\mathbf{\Pi }}_{\phi }\right)-{\displaystyle \frac{c_s^2{\psi }_{\phi }}{2}}{S}_{\phi }\mathit{I}+O\left({\epsilon }^2\right),$$

(70)

which do not require us to compute explicitly additional space derivatives.

2.2. LBM Schemes for Solving the Volume Fraction Equation for Each Phase and Their Asymptotic Analysis

In addition of the two LBM schemes discussed above for the momentum equations, one needs to solve the equation for the volume fraction but must ensure that the volume fraction is bounded between zero and one, namely, $0\le {\alpha }_{\phi }\le 1$. There are many advanced numerical techniques to ensure this condition. One simple alternative may be that proposed by Spalding [18]. Essentially, the idea is to solve both Equations (8) and (10) for ${\alpha }_g$ and ${\alpha }_l$, and then perform a proper renormalization. In the LBM context, let us consider the following two LBM schemes for solving the volume fraction equations given by Equations (8) and (10), formulated in terms of the corresponding particle distribution functions $f_{\alpha g}$ and $f_{\alpha l}$, namely,

$$f_{\alpha \phi }(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)=f_{\alpha \phi }\left(q\right)+{\widehat{\omega }}_{\alpha \phi }\left[f_{\alpha \phi }^{eq}\left(q\right)-f_{\alpha \phi }\right],$$

(71)

where ${\widehat{\omega }}_{\alpha \phi }$ (for the volume phase fraction ${\alpha }_{\phi }$) is the relaxation frequency, divided by the frequency $1/\tau$, which drives the relaxation of the distribution function towards the equilibrium $f_{\alpha \phi }^{eq}$. The fact that we report the relaxation frequency ${\widehat{\omega }}_{\alpha \phi }$ with the hat notation $\widehat{·}$ means that we allow the possibility of adjusting the relaxation frequency during the mesh refinement according the adopted scaling. The equilibrium distribution is formulated by means of the same functional form, namely, $f_{\alpha \phi }^{eq}\equiv f^{eq}({\widehat{\alpha }}_{\phi },{\widehat{\mathit{u}}}_{\phi })$, where

$$f^{eq}(\widehat{\alpha },\widehat{\mathit{u}},q)=w_q\widehat{\alpha }\left[1+{\displaystyle \frac{{\mathit{v}}_q·\widehat{\mathit{u}}}{c_s^2}}+{\displaystyle \frac{({\mathit{v}}_q{\mathit{v}}_q-c_s^2\mathit{I}):\widehat{\mathit{u}}\widehat{\mathit{u}}}{2c_s^4}}\right],$$

(72)

and

$${\widehat{\alpha }}_{\phi }=\sum _{q=0}^{Q-1}{f}_{\alpha \phi }\left(q\right).$$

(73)

It is very important to highlight that the velocity field ${\widehat{\mathit{u}}}_{\phi }$ is computed by the LBM schemes discussed in the previous section, and hence the first-order moment ${\widehat{\alpha }}_{\phi }{\widehat{\mathbf{\upsilon }}}_{\phi }$ of the distribution $f_{\alpha \phi }$ is not conserved, namely,

$${\widehat{\mathit{u}}}_{\phi }=\sum _{q=0}^{Q-1}{\mathit{v}}_q{f}_{\phi }\left(q\right)\ne \sum _{q=0}^{Q-1}{\mathit{v}}_q{f}_{\alpha \phi }\left(q\right)={\widehat{\alpha }}_{\phi }{\widehat{\mathbf{\upsilon }}}_{\phi }.$$

(74)

As discussed in the previous section, an asymptotic analysis is needed in order to find out under which conditions these equations at least approximate the target volume fraction equations. Again we use here the asymptotic method based on the equivalent moment system [17]. Let us apply a Taylor expansion and let us assume a diffusive scaling, namely, $\widehat{t}=t/{\epsilon }^2$ and $\widehat{\mathit{x}}=x/\epsilon$, which leads to

$$f_{\alpha \phi }(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)-f_{\alpha \phi }(\widehat{\mathit{x}},\widehat{t},q)=\epsilon {\mathit{v}}_q·\nabla f_{\alpha \phi }+{\displaystyle \frac{{\epsilon }^2}{2}}{({\mathit{v}}_q·\nabla )}^2{f}_{\alpha \phi }+{\epsilon }^2{\displaystyle \frac{𝜕f_{\alpha \phi }}{𝜕t}}+O\left({\epsilon }^3\right).$$

(75)

Neglecting terms $O\left({\epsilon }^3\right)$ yields

$${\epsilon }^2{\displaystyle \frac{𝜕f_{\alpha \phi }}{𝜕t}}+\epsilon {\mathit{v}}_q·\nabla f_{\alpha \phi }+{\displaystyle \frac{{\epsilon }^2}{2}}{({\mathit{v}}_q·\nabla )}^2{f}_{\alpha \phi }={\widehat{\omega }}_{\alpha \phi }\left[f_{\alpha \phi }^{eq}\left(q\right)-f_{\alpha \phi }\right].$$

(76)

Taking the zeroth-order, first-order, and second-order moments of the previous equations yields

$${\epsilon }^2{\displaystyle \frac{𝜕{\widehat{\alpha }}_{\phi }}{𝜕t}}+\epsilon \nabla ·\left({\widehat{\alpha }}_{\phi }{\widehat{\mathbf{\upsilon }}}_{\phi }\right)+{\displaystyle \frac{{\epsilon }^2}{2}}\nabla ·\nabla ·{\widehat{\mathbf{\Pi }}}_{\alpha \phi }=0,$$

(77)

$${\epsilon }^2{\displaystyle \frac{𝜕\left({\widehat{\alpha }}_{\phi }{\widehat{\mathbf{\upsilon }}}_{\phi }\right)}{𝜕t}}+\epsilon \nabla ·{\widehat{\mathbf{\Pi }}}_{\alpha \phi }+{\displaystyle \frac{{\epsilon }^2}{2}}\nabla ·\nabla ·{\widehat{\mathbf{\Phi }}}_{\alpha \phi }={\widehat{\omega }}_{\alpha \phi }{\widehat{\alpha }}_{\phi }\left({\widehat{\mathit{u}}}_{\phi }-{\widehat{\mathbf{\upsilon }}}_{\phi }\right),$$

(78)

$${\epsilon }^2{\displaystyle \frac{𝜕{\widehat{\mathbf{\Pi }}}_{\alpha \phi }}{𝜕t}}+\epsilon \nabla ·{\widehat{\mathbf{\Phi }}}_{\alpha \phi }+O\left({\epsilon }^2\right)={\widehat{\omega }}_{\alpha \phi }({\widehat{\mathbf{\Pi }}}_{\alpha \phi }^{eq}-{\widehat{\mathbf{\Pi }}}_{\alpha \phi }),$$

(79)

where ${\widehat{\mathbf{\Pi }}}_{\alpha \phi }={\sum }_{q=0}^{Q-1}{\mathit{v}}_q{\mathit{v}}_q{f}_{\alpha \phi }\left(q\right)$ is the second-order tensor of the distribution function and ${\widehat{\mathbf{\Phi }}}_{\alpha \phi }={\sum }_{q=0}^{Q-1}{\mathit{v}}_q{\mathit{v}}_q{\mathit{v}}_q{f}_{\alpha \phi }\left(q\right)$ is the third-order tensor. Moreover, by the definition given by Equation (72), it is possible to compute

$${\widehat{\mathbf{\Pi }}}_{\alpha \phi }^{eq}=c_s^2{\widehat{\alpha }}_{\phi }\mathit{I}+{\widehat{\alpha }}_{\phi }{\widehat{\mathit{u}}}_{\phi }{\widehat{\mathit{u}}}_{\phi },$$

(80)

and

$${\left({\widehat{\mathbf{\Phi }}}_{\alpha \phi }^{eq}\right)}_{ijk}=c_s^2{\widehat{\alpha }}_{\phi }\left({\widehat{u}}_{\phi i}{\delta }_{jk}+{\widehat{u}}_{\phi j}{\delta }_{ik}+{\widehat{u}}_{\phi k}{\delta }_{ij}\right).$$

(81)

As discussed in the previous section, in order to analyze this system of equations, one needs to understand the impact of the diffusive scaling on the scaling of the moments. Let us suppose we do not scale the volume fraction, namely, ${\widehat{\alpha }}_{\phi }={\alpha }_{\phi }$, which has an impact on all even moments of the distribution function. On the other hand, let us keep the same scaling as before for the odd moments, because they depend on the imposed velocity ${\widehat{\mathit{u}}}_{\phi }=\epsilon {\mathit{u}}_{\phi }$. This implies

$${\widehat{\mathbf{\Pi }}}_{\alpha \phi }^{eq}=c_s^2{\alpha }_{\phi }\mathit{I}+{\epsilon }^2{\alpha }_{\phi }{\mathit{u}}_{\phi }{\mathit{u}}_{\phi },$$

(82)

and

$${\left({\widehat{\mathbf{\Phi }}}_{\alpha \phi }^{eq}\right)}_{ijk}=\epsilon c_s^2{\alpha }_{\phi }\left(u_{\phi i}{\delta }_{jk}+u_{\phi j}{\delta }_{ik}+u_{\phi k}{\delta }_{ij}\right).$$

(83)

A system of moments can be truncated if we have some expectations about the high-order moments. Let us now imagine the equation for the third-order moment ${\widehat{\mathbf{\Phi }}}_{\alpha \phi }$, which can be analyzed with very similar arguments discussed in the previous section. These arguments lead to conclude that the equation for the third-order moment looks like ${\widehat{\mathbf{\Phi }}}_{\alpha \phi }={\widehat{\mathbf{\Phi }}}_{\alpha \phi }^{eq}+O\left({\epsilon }^3\right)$ and consequently ${\widehat{\mathbf{\Phi }}}_{\alpha \phi }=\epsilon {\mathbf{\Phi }}_{\alpha \phi }^{eq}+O\left({\epsilon }^3\right)$, because of Equation (83). Substituting the last result in Equation (79) and taking into account Equation (82) yields

$$O\left({\epsilon }^2\right)-{\widehat{\omega }}_{\alpha \phi }{\epsilon }^2{\alpha }_{\phi }{\mathit{u}}_{\phi }{\mathit{u}}_{\phi }={\widehat{\omega }}_{\alpha \phi }\left(c_s^2{\alpha }_{\phi }\mathit{I}-{\widehat{\mathbf{\Pi }}}_{\alpha \phi }\right),$$

(84)

or equivalently, ${\widehat{\mathbf{\Pi }}}_{\alpha \phi }=c_s^2{\alpha }_{\phi }\mathit{I}+O\left({\epsilon }^2\right)$. Substituting this result in Equation (77) yields

$${\epsilon }^2{\displaystyle \frac{𝜕{\widehat{\alpha }}_{\phi }}{𝜕t}}+\epsilon \nabla ·\left({\widehat{\alpha }}_{\phi }{\widehat{\mathbf{\upsilon }}}_{\phi }\right)+{\displaystyle \frac{{\epsilon }^2}{2}}{c}_s^2{\nabla }^2{\alpha }_{\phi }=O\left({\epsilon }^4\right),$$

(85)

which proves that ${\widehat{\mathbf{\upsilon }}}_{\phi }=\epsilon {\mathbf{\upsilon }}_{\phi }$. Substituting this result into Equation (78) yields

$$c_s^2\nabla {\alpha }_{\phi }={\widehat{\omega }}_{\alpha \phi }{\alpha }_{\phi }\left({\mathit{u}}_{\phi }-{\mathbf{\upsilon }}_{\phi }\right)+O\left({\epsilon }^2\right).$$

(86)

Substituting the previous equation into Equation (85) yields

$${\displaystyle \frac{𝜕{\alpha }_{\phi }}{𝜕t}}+\nabla ·\left({\alpha }_{\phi }{\mathit{u}}_{\phi }\right)={\widehat{\chi }}_{\alpha \phi }{\nabla }^2{\alpha }_{\phi }+O\left({\epsilon }^2\right),$$

(87)

where

$${\widehat{\chi }}_{\alpha \phi }=c_s^2\left({\displaystyle \frac{1}{{\widehat{\omega }}_{\alpha \phi }}}-{\displaystyle \frac{1}{2}}\right).$$

(88)

Adopting the following scaling

$${\widehat{\omega }}_{\alpha \phi }={\displaystyle \frac{2}{1+2{\epsilon }^2{\chi }_{\alpha \phi }/c_s^2}},$$

(89)

implies ${\widehat{\chi }}_{\alpha \phi }={\epsilon }^2{\chi }_{\alpha \phi }$ and consequently

$${\displaystyle \frac{𝜕{\alpha }_{\phi }}{𝜕t}}+\nabla ·\left({\alpha }_{\phi }{\mathit{u}}_{\phi }\right)=O\left({\epsilon }^2\right).$$

(90)

Clearly, the previous equation approaches the solution of the target equations given by Equations (8) and (10) in the asymptotic limit of $\epsilon \to 0$ with second-order accuracy, thanks to the adopted diffusive scaling.

These LBM schemes are not only useful to recover an approximated solution of the target equations but they can also be used to compute other relevant quantities. For example, it is possible to compute the volume fraction gradient without further computational efforts using Equation (86), namely,

$${\displaystyle \frac{1}{{\alpha }_{\phi }}}\nabla {\alpha }_{\phi }={\displaystyle \frac{{\widehat{\omega }}_{\alpha \phi }}{c_s^2}}\left({\mathit{u}}_{\phi }-{\mathbf{\upsilon }}_{\phi }\right)+O\left({\epsilon }^2\right).$$

(91)

In particular, Equations (70) and (91) can be used to compute the second term of the force ${\mathit{G}}_g$ given by Equation (24) as well as the second term of the force ${\mathit{G}}_l$ given by Equation (26), namely,

$${\displaystyle \frac{1}{{\alpha }_{\phi }}}{\mathbf{\sigma }}_{\phi }·\nabla {\alpha }_{\phi }={\displaystyle \frac{{\widehat{\omega }}_{\alpha \phi }}{c_s^2}}\left[\left(1-{\displaystyle \frac{{\omega }_{\phi }}{2}}\right)\left({\mathbf{\Pi }}_{\phi }^{eq}-{\mathbf{\Pi }}_{\phi }\right)-{\displaystyle \frac{c_s^2{\psi }_{\phi }}{2}}{S}_{\phi }\mathit{I}\right]·\left({\mathit{u}}_{\phi }-{\mathbf{\upsilon }}_{\phi }\right).$$

(92)

One last remark is about the need for ensuring that volume fraction ${\alpha }_{\phi }$ is bounded between zero and one, namely, $0\le {\alpha }_{\phi }\le 1$. Among many available numerical techniques to ensure this condition, we follow here that proposed by Spalding [18]. Essentially, the idea is to solve both Equations (8) and (10) by the discussed LBM schemes for $f_{\alpha \phi }$, compute the raw volume fraction ${\alpha }_{\phi }={\sum }_{q=0}^{Q-1}{f}_{\alpha \phi }\left(q\right)$, and then perform the following renormalization at the beginning of every collision and streaming cycle:

$${\alpha }_{\phi }^B\equiv {\displaystyle \frac{B\left({\alpha }_{\phi }\right)}{B\left({\alpha }_g\right)+B\left({\alpha }_l\right)}},$$

(93)

where $B\left(x\right)=xH\left(x\right)H(1-x)+H(x-1)$ and $H\left(x\right)$ is the Heaviside step function. Of course, ${\alpha }_l^B=1-{\alpha }_g^B$.

Similarly, we propose a second correction for ensuring that $\nabla {\alpha }_g=-\nabla {\alpha }_l$, when using Equation (91). Let us suppose that the vector $\mathit{\delta }=\nabla {\alpha }_g+\nabla {\alpha }_l$ has a non-zero modulus, i.e., $\parallel \mathit{\delta }\parallel \ne 0$. In this case, the second Spalding-like correction is

$$\nabla {\alpha }_{\phi }^G\equiv \nabla {\alpha }_{\phi }-\mathit{\delta }/2.$$

(94)

Of course, $\nabla {\alpha }_l^G+\nabla {\alpha }_g^G=0$. In the following, we will drop the superscript B in Equation (93) as well as the superscript G in Equation (94) for the sake of simplicity and without risk of confusion.

2.3. LBM Schemes for Solving the Phase Continuity Source for Each Phase and Their Asymptotic Analysis

In addition to the two LBM schemes discussed above for the momentum equations and the two LBM schemes for the volume fractions, one needs to compute the phase continuity sources, namely, $S_g$ in Equation (19) and $S_l$ in Equation (20). Let us consider the following two schemes for computing the phase continuity sources, formulated in terms of the corresponding particle distribution functions $f_{\beta g}$ and $f_{\beta l}$, namely,

$$f_{\beta \phi }(\widehat{\mathit{x}}+{\mathit{v}}_q,\widehat{t}+1,q)=f_{\beta \phi }^{eq}(\widehat{\mathit{x}},\widehat{t},q),$$

(95)

where $f_{\beta \phi }^{eq}\equiv f^{eq}({\widehat{\beta }}_{\phi },{\widehat{\mathit{c}}}_{\phi })$ and $f^{eq}$ is the functional form given by Equation (72). The zero-order moment ${\widehat{\beta }}_{\phi }$ is given by

$${\widehat{\beta }}_{\phi }=\sum _{q=0}^{Q-1}{f}_{\beta \phi }\left(q\right)=\sum _{q=0}^{Q-1}{f}_{\beta \phi }^{eq}\left(q\right),$$

(96)

and the imposed velocity field is given by

$${\widehat{\mathit{c}}}_{\phi }={\displaystyle \frac{1}{{\widehat{\beta }}_{\phi }}}{\widehat{\alpha }}_{\overline{\phi }}\left({\widehat{\mathit{u}}}_{\phi }-{\widehat{\mathit{u}}}_{\overline{\phi }}\right).$$

(97)

The velocity field ${\widehat{\mathit{c}}}_{\phi }$ is computed by the LBM schemes discussed in the previous sections and, by definition, the following relation holds:

$$\sum _{q=0}^{Q-1}{\mathit{v}}_q{f}_{\alpha \phi }^{eq}\left(q\right)={\widehat{\beta }}_{\phi }{\widehat{\mathit{c}}}_{\phi }={\widehat{\alpha }}_{\overline{\phi }}\left({\widehat{\mathit{u}}}_{\phi }-{\widehat{\mathit{u}}}_{\overline{\phi }}\right).$$

(98)

It is worth noting that the continuity sources which we are trying to compute are related to the fluxes ${\widehat{\beta }}_{\phi }{\widehat{\mathit{c}}}_{\phi }$, namely, ${\widehat{S}}_{\phi }=\widehat{\nabla }·\left({\widehat{\beta }}_{\phi }{\widehat{\mathit{c}}}_{\phi }\right)=\widehat{\nabla }·\left[{\widehat{\alpha }}_{\overline{\phi }}\left({\widehat{\mathit{u}}}_{\phi }-{\widehat{\mathit{u}}}_{\overline{\phi }}\right)\right]$.

Equation (95) is the lattice kinetic scheme (LKS) [19] and is a particular case of the link-wise artificial compressibility method (link-wise ACM) [20]. As in LBM schemes, a link-wise ACM scheme also proceeds by a sequence of collision and streaming cycles. Equation (95) assumes collision first and then streaming, but the scheme can also be rationalized by inverting this order, namely,

$$f_{\beta \phi }(\widehat{\mathit{x}},\widehat{t}+1,q)=f_{\beta \phi }^{eq}(\widehat{\mathit{x}}-{\mathit{v}}_q,\widehat{t},q).$$

(99)

Let us apply the Taylor expansion to the previous expression, namely,

$$f_{\beta \phi }(\widehat{\mathit{x}},\widehat{t}+1,q)-f_{\beta \phi }^{eq}(\widehat{\mathit{x}},\widehat{t},q)=-\epsilon {\mathit{v}}_q·\nabla f_{\beta \phi }^{eq}+{\displaystyle \frac{{\epsilon }^2}{2}}{({\mathit{v}}_q·\nabla )}^2{f}_{\beta \phi }^{eq}-{\displaystyle \frac{{\epsilon }^3}{6}}{({\mathit{v}}_q·\nabla )}^3{f}_{\beta \phi }^{eq}+O\left({\epsilon }^4\right).$$

(100)

Computing the zeroth-order moment of the previous expression and applying the scaling to the known quantities yields

$${\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t}+1)-{\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t})=-{\epsilon }^2{S}_{\phi }+{\displaystyle \frac{{\epsilon }^2}{2}}\nabla ·\nabla ·{\widehat{\mathbf{\Pi }}}_{\beta \phi }^{eq}-{\displaystyle \frac{{\epsilon }^3}{6}}\nabla ·\nabla ·\nabla ·{\widehat{\mathbf{\Phi }}}_{\beta \phi }^{eq}+O\left({\epsilon }^4\right),$$

(101)

where

$${\widehat{\mathbf{\Pi }}}_{\beta \phi }^{eq}={\widehat{\beta }}_{\phi }\left(c_s^2\mathit{I}+{\epsilon }^2{\mathit{u}}_{\phi }{\mathit{u}}_{\phi }\right)={\widehat{\beta }}_{\phi }{c}_s^2\mathit{I}+O\left({\epsilon }^2\right),$$

(102)

and

$${\left({\widehat{\mathbf{\Phi }}}_{\beta \phi }^{eq}\right)}_{ijk}=\epsilon c_s^2{\widehat{\beta }}_{\phi }\left(u_{\phi i}{\delta }_{jk}+u_{\phi j}{\delta }_{ik}+u_{\phi k}{\delta }_{ij}\right).$$

(103)

Substituting the previous expressions into Equation (101) yields

$${\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t}+1)-{\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t})=-{\epsilon }^2{S}_{\phi }+{\epsilon }^2{\displaystyle \frac{c_s^2}{2}}{\nabla }^2{\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t})+O\left({\epsilon }^4\right).$$

(104)

It is important to remind that ${\widehat{\beta }}_{\phi }$ are just auxiliary functions without physical interest, with the exception of their derivatives, as will be clarified in the following. Assuming ${\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t})=1$ at the beginning of every time step yields

$${\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t}+1)-1=-{\epsilon }^2{S}_{\phi }+O\left({\epsilon }^4\right),$$

(105)

or equivalently,

$${\displaystyle \frac{𝜕{\widehat{\beta }}_{\phi }}{𝜕t}}=-S_{\phi }+O\left({\epsilon }^2\right).$$

(106)

In particular, Equation (105) can be reformulated as

$${\widehat{S}}_{\phi }=1-{\widehat{\beta }}_{\phi }(\widehat{\mathit{x}},\widehat{t}+1)+O\left({\epsilon }^4\right),$$

(107)

which is particularly useful in this context because it allows one to compute ${\widehat{S}}_{\phi }$ as coded into the LBM schemes, without explicit finite difference formulas.

3. Results: Numerical Validation

3.1. One-Dimensional Test Case

We consider a one-dimensional vertical tube with a generic two-phase flow as a test case to validate the proposed computational methodology. Although simplified, the one-dimensional vertical tube offers a foundational model for analyzing multiphase flow behavior in systems such as bubble column reactors, where gas–liquid interactions are key to reactor performance. Additionally, this configuration is pertinent for studying flow dynamics in natural circulation loops driven by gas injection, a mechanism critical in systems like molten salt nuclear reactors. This test case provides a controlled yet insightful context, enabling us to investigate flow patterns, pressure gradients, and phase interactions relevant to both chemical and nuclear reactor environments [21].

Let us suppose that the vertical tube is aligned with the axis identified by the unit vector ${\mathbf{e}}_x$, where $\parallel {\mathbf{e}}_x\parallel =1$. In this case, the gravitational acceleration field is $\mathit{g}=-g{\mathit{e}}_x$, where g is the standard acceleration of gravity. It is sometimes convenient to remove the hydrostatic pressure from the pressure in order to make the buoyancy effect explicit by defining a new quantity

$$p^{\prime }=p+{\rho }_l^{0}gx,$$

(108)

where x is the coordinate along the unit vector ${\mathbf{e}}_x$. Let us introduce the kinematic pressure $p_k$, defined as

$$p_k={\displaystyle \frac{p^{\prime }}{{\rho }_g^0}}={\displaystyle \frac{p+{\rho }_l^{0}gx}{{\rho }_g^0}}={\displaystyle \frac{p}{{\rho }_g^0}}+Rgx,$$

(109)

and consequently

$${\displaystyle \frac{1}{R}}{p}_k={\displaystyle \frac{p}{{\rho }_l^0}}+gx.$$

(110)

The previous definitions lead to $-{𝜕}_x(p/{\rho }_g^0)-g=-{𝜕}_x{p}_k+(R-1)g$ for the dispersed phase and $-{𝜕}_x(p/{\rho }_l^0)-g=-(1/R){𝜕}_x{p}_k$ for the liquid phase. Hence, using the kinematic pressure $p_k$, instead of the original pressure p, allows one to consider only one gravitational acceleration in the dispersed phase, i.e., the term $(R-1)g$, which is the buoyancy acceleration.

Reformulating the artificially compressible equations in terms of the kinematic pressure implies that Equation (28) must be redefined as

$${ϵ}_g\left(p\right)={\displaystyle \frac{p^{\prime }}{c_s^2{\rho }_g^0}}={\displaystyle \frac{p_k}{c_s^2}},$$

(111)

without modifying the proposed methodology. As already pointed out, for Equation (19) to be valid also during the dynamics, the following condition must hold: ${𝜕}_t{ϵ}_g=O\left(h^2\right)$. This means that the first derivative in Equation (19) is not mesh-independent. Assuming $h\equiv \epsilon$, it is possible to make explicit such dependence on the mesh spacing by setting ${𝜕}_t{ϵ}_g$ more precisely as ${𝜕}_t{\widehat{ϵ}}_g$ in Equation (19), since ${𝜕}_t{\widehat{ϵ}}_g={\epsilon }^2{𝜕}_t{ϵ}_g$ according to Equation (55). Recalling that ${\widehat{ϵ}}_g={\widehat{p}}_k/c_s^2$ where ${\widehat{p}}_k=c_s^2+{\epsilon }^2{p}_k$, Equation (19), in the one-dimensional case, becomes

$${\displaystyle \frac{{\epsilon }^2}{c_s^2}}{\displaystyle \frac{𝜕p_k}{𝜕t}}+{\displaystyle \frac{𝜕u_g}{𝜕x}}={\displaystyle \frac{𝜕}{𝜕x}}\left[{\alpha }_l(u_g-u_l)\right]=S_g.$$

(112)

Substituting the previous quantities into Equations (23)–(26) in the one-dimensional case yields

$${\displaystyle \frac{𝜕u_g}{𝜕t}}+{\displaystyle \frac{𝜕}{𝜕x}}\left(u_g{u}_g\right)=-{\displaystyle \frac{𝜕p_k}{𝜕x}}+{\displaystyle \frac{𝜕{\sigma }_g}{𝜕x}}+G_g,$$

(113)

where

$$G_g=S_g{u}_g+{\displaystyle \frac{1}{{\alpha }_g}}{\sigma }_g{\displaystyle \frac{𝜕{\alpha }_g}{𝜕x}}+(R-1)g+{\displaystyle \frac{1}{{\alpha }_g{\rho }_g^0}}(F_{gl}+F_g).$$

(114)

Similarly, it holds that

$${\displaystyle \frac{𝜕u_l}{𝜕t}}+{\displaystyle \frac{𝜕}{𝜕x}}\left(u_l{u}_l\right)=-{\displaystyle \frac{1}{R}}{\displaystyle \frac{𝜕p_k}{𝜕x}}+{\displaystyle \frac{𝜕{\sigma }_l}{𝜕x}}+G_l,$$

(115)

where

$$G_l=S_l{u}_l+{\displaystyle \frac{1}{{\alpha }_l}}{\sigma }_l{\displaystyle \frac{𝜕{\alpha }_l}{𝜕x}}+{\displaystyle \frac{1}{{\alpha }_l{\rho }_l^0}}(F_{lg}+F_l).$$

(116)

In the one-dimensional case, the viscous stress tensor per unit volume defined by Equation (7), assuming ${\xi }_{\phi }=-(1/3){\nu }_{\phi }$ (which is a clear indication of the degeneracy of the one-dimensional case because it implies negative kinematic bulk viscosity), becomes

$${\sigma }_{\phi }=\left({\displaystyle \frac{4}{3}}{\nu }_{\phi }+{\xi }_{\phi }\right){\displaystyle \frac{𝜕u_{\phi }}{𝜕x}}={\nu }_{\phi }{\displaystyle \frac{𝜕u_{\phi }}{𝜕x}}.$$

(117)

Concerning the interphase momentum exchange, in the one-dimensional case, Equation (6) becomes

$$F_{gl}={\rho }_g^0{K}_I|u_l-u_g|\left(u_l-u_g\right)=-F_{lg}.$$

(118)

Concerning the momentum exchange with the wall, which cannot be properly modeled in the one-dimensional case because we have no curvature of the velocity field in axes other than ${\mathit{e}}_x$, let us assume $F_g=0$ and

$$F_l={\rho }_g^0{K}_W|-u_l|\left(-u_l\right).$$

(119)

The analogy is clear between Equations (118) and (119), where the latter assumes zero wall velocity. Finally, the dispersed phase volume fraction equation given by Equation (10) in the one-dimensional case becomes

$${\displaystyle \frac{𝜕{\alpha }_g}{𝜕t}}+{\displaystyle \frac{𝜕}{𝜕x}}\left({\alpha }_g{u}_g\right)=0,$$

(120)

The artificially compressible continuity equation given by Equation (112), together with Equations (113), (115) and (120), define a proper system of equations in the one-dimensional case for $p_k$, $u_g$, $u_l$, and ${\alpha }_g$.

Before proceeding to the numerical results, let us search for a special analytical solution indicated by the notation $\overline{·}$. Let us consider a flow regime where all flow quantities have zero gradients at steady state but the gradient of the kinematic pressure is constant, namely,

$$0=-{𝜕}_x{\overline{p}}_k+(R-1)g+{\displaystyle \frac{K_I}{{\overline{\alpha }}_g}}|{\overline{u}}_l-{\overline{u}}_g|\left({\overline{u}}_l-{\overline{u}}_g\right),$$

(121)

$$0=-{\displaystyle \frac{1}{R}}{𝜕}_x{\overline{p}}_k+{\displaystyle \frac{1}{{\overline{\alpha }}_{l}R}}\left[K_I|{\overline{u}}_g-{\overline{u}}_l|\left({\overline{u}}_g-{\overline{u}}_l\right)-K_W\left|{\overline{u}}_l\right|{\overline{u}}_l\right].$$

(122)

Eliminating the kinematic pressure gradient from the previous equations yields

$${\displaystyle \frac{K_I}{{\overline{\alpha }}_g{\overline{\alpha }}_l}}|{\overline{u}}_l-{\overline{u}}_g|\left({\overline{u}}_l-{\overline{u}}_g\right)+{\displaystyle \frac{K_W}{{\overline{\alpha }}_l}}\left|{\overline{u}}_l\right|{\overline{u}}_l+(R-1)g=0,$$

(123)

which can be interpreted as a condition for ${\overline{u}}_l$ as a function of ${\overline{u}}_g$ in this flow regime. In particular, let us search for ${\overline{u}}_g^0$ such that ${\overline{u}}_l^0=0$, namely,

$$(R-1)g={\displaystyle \frac{K_I}{{\overline{\alpha }}_g{\overline{\alpha }}_l}}\left|{\overline{u}}_g^0\right|{\overline{u}}_g^0.$$

(124)

Substituting the previous expression back into the original equation yields

$${\displaystyle \frac{K_W}{{\overline{\alpha }}_l}}|{\overline{u}}_l|{\overline{u}}_l={\displaystyle \frac{K_I}{{\overline{\alpha }}_g{\overline{\alpha }}_l}}|{\overline{u}}_g-{\overline{u}}_l|\left({\overline{u}}_g-{\overline{u}}_l\right)-{\displaystyle \frac{K_I}{{\overline{\alpha }}_g{\overline{\alpha }}_l}}\left|{\overline{u}}_g^0\right|{\overline{u}}_g^0.$$

(125)

Let us assume ${\overline{u}}_l<{\overline{u}}_g$ (which corresponds to the natural circulation loops driven by gas injection), then the previous condition becomes

$$r{\left({\overline{u}}_l\right)}^2={\left({\overline{u}}_g-{\overline{u}}_l\right)}^2-{\left({\overline{u}}_g^0\right)}^2,$$

(126)

where $r=(K_W/K_I){\overline{\alpha }}_g$, which admits the following analytical solution:

$${\overline{u}}_l={\displaystyle \frac{{\overline{u}}_g-\sqrt{{\left({\overline{u}}_g\right)}^2-(1-r)[{\left({\overline{u}}_g\right)}^2-{\left({\overline{u}}_g^0\right)}^2]}}{1-r}}.$$

(127)

It is worth discussing a couple of limiting cases. If $r=0$, then the only possible coupling between the two phases is by the pressure gradient ${𝜕}_x{\overline{p}}_k$: the relation becomes ${\overline{u}}_l={\overline{u}}_g-{\overline{u}}_g^0$. If $r=1$, then the coupling between the phases is ruled by the same proportionality that is found between the liquid and the wall; in this case, the relation becomes ${\overline{u}}_l=({\overline{u}}_g-{\overline{u}}_g^0)(1+{\overline{u}}_g^0/{\overline{u}}_g)/2$.

3.2. Very-Large-Density Ratios

In the limit of very-large-density ratios, namely, $R\gg 1$, some terms proportional to $1/R$ in the momentum equation of the liquid phase become very small and comparable with numerical errors, leading to numerical instabilities. Hence, special numerical ingredients are needed to overcome these instabilities. In this section, we analyze two of such ingredients.

In Reference [16], Ohwada suggested a simple but effective ingredient for the suppression of the spurious acoustic mode in the context of a single-phase artificial compressibility method. The basic idea here is the introduction of a similar dissipation term into the continuity equation for the gas, given by Equation (112), but we also automatically ensure the right asymptotic target equation in the context of the LBM. Using again the usual Boltzmann scaling adopted in the LBM numerical codes, this idea reads

$${\displaystyle \frac{𝜕{\widehat{ϵ}}_g}{𝜕\widehat{t}}}+{\displaystyle \frac{𝜕{\widehat{u}}_g}{𝜕\widehat{x}}}={\widehat{S}}_g-\gamma {\widehat{u}}_g^2\left({\widehat{ϵ}}_g-1\right)\equiv {\widehat{S}}_g^{\prime },$$

(128)

where $\gamma$ is a tunable constant. From a coding point of view, the previous ingredient is equivalent to using the source term ${\widehat{S}}_g^{\prime }$ instead of ${\widehat{S}}_g$. The previous equation can be reformulated as

$$\left({\displaystyle \frac{𝜕}{𝜕\widehat{t}}}+\gamma {\widehat{u}}_g^2\right)\left({\widehat{ϵ}}_g-1\right)+{\displaystyle \frac{𝜕{\widehat{u}}_g}{𝜕\widehat{x}}}={\widehat{S}}_g,$$

(129)

or equivalently

$${\displaystyle \frac{{\epsilon }^2}{c_s^2}}\left({\displaystyle \frac{𝜕p_k}{𝜕t}}+\gamma u_g^2{p}_k\right)+{\displaystyle \frac{𝜕u_g}{𝜕x}}=S_g,$$

(130)

where it is clear that the term multiplied by $\gamma$ acts as a dashpot in a simple mechanical oscillation system. Concerning the continuity equation for the liquid phase, some options are possible, which can be discussed by the following generic expression:

$${\displaystyle \frac{𝜕{\widehat{ϵ}}_l}{𝜕\widehat{t}}}+{\displaystyle \frac{𝜕{\widehat{u}}_l}{𝜕\widehat{x}}}={\widehat{S}}_l-\gamma {\widehat{u}}_l^2{\widehat{\mathsf{\Gamma }}}_l\equiv {\widehat{S}}_l^{\prime },$$

(131)

where ${\widehat{\mathsf{\Gamma }}}_l={ϵ}^2{\mathsf{\Gamma }}_l$ is a function to be specified, or equivalently

$${\epsilon }^2\left({\displaystyle \frac{𝜕{ϵ}_l}{𝜕t}}+\gamma u_l^2{\mathsf{\Gamma }}_l\right)+{\displaystyle \frac{𝜕u_l}{𝜕x}}=S_l.$$

(132)

Different strategies are possible in choosing the function ${\mathsf{\Gamma }}_l={\mathsf{\Gamma }}_l\left(p_k\right)$:

• The strategy most similar to the one adopted for the gas phase implies ${\widehat{\mathsf{\Gamma }}}_l={\widehat{ϵ}}_l-1$ or equivalently ${\mathsf{\Gamma }}_l={ϵ}_l$ because of Equation (58), which would ensure a proper dashpot for the liquid phase as well. The problem is that ${ϵ}_l$ is not simply related to $p_k$ and therefore, for the finite difference engine (considered for comparison), this strategy would require solving an additional equation (precisely for ${ϵ}_l$).
• The second strategy is based on assuming that $p_k$ is finally what really matters for both phases and therefore it assumes ${\widehat{\mathsf{\Gamma }}}_l={\widehat{ϵ}}_g-1$ for the liquid phase as well, which implies ${\mathsf{\Gamma }}_l\left(p_k\right)={ϵ}_g=p_k/c_s^2$ because of Equation (55). This strategy definitively has the advantage of simplicity, but there is the drawback that different quantities are involved in the first two terms of Equation (132).
• The third strategy aims to improve the consistency by using liquid-phase quantities in computing ${\widehat{\mathsf{\Gamma }}}_l$ by including also $\widehat{\varphi }$, namely, ${\widehat{\mathsf{\Gamma }}}_l=\widehat{\varphi }{\widehat{ϵ}}_l-1$, which implies ${\mathsf{\Gamma }}_l\left(p_k\right)={ϵ}_g/R=(p_k/c_s^2)/R$ because of Equation (56). The advantage is that $p_k/R$ is exactly the effective pressure acting on the liquid phase, which makes sense to use in the design of the liquid dashpot as well. On the other hand, the first two terms of Equation (132) are now formulated for ${ϵ}_l$ and $p_k$, respectively, which is different from what happens in canonical modeling of a mechanical dashpot.

As far as the LBM is concerned, these three strategies are substantially equivalent. In this work, for the above reasons, we choose to adopt the third strategy.

The second ingredient for dealing with very-large-density ratios consists in updating the sources of the continuity equations only once in a while to let the fluid equations gradually accommodate the changes. In particular, it consists in updating them only at times ${\widehat{t}}_{\gamma }$ which are multiples of the natural number $n_{\gamma }$, namely,

$${\widehat{S}}_{\phi }^{″}\left(\widehat{x},\widehat{t}\right)={\widehat{S}}_{\phi }^{\prime }\left(\widehat{x},{\widehat{t}}_{\gamma }\right),$$

(133)

where ${\widehat{t}}_{\gamma }$ is the highest multiple of $n_{\gamma }$ but still smaller than $\widehat{t}$, namely, ${\widehat{t}}_{\gamma }=r_{\gamma }{n}_{\gamma }$ where $r_{\gamma }$ is another natural number and $r_{\gamma }{n}_{\gamma }\le \widehat{t}<(r_{\gamma }+1)n_{\gamma }$. Of course $n_{\gamma }$ is a free tunable parameter such that $n_{\gamma }\ll N_t$, where $N_t$ is the total number of time steps. It is worth the effort to estimate the error introduced by the approximation given by Equation (133), which is a means of estimating the difference $|{\widehat{S}}_{\phi }^{\prime }(\widehat{x},\widehat{t})-{\widehat{S}}_{\phi }^{\prime }(\widehat{x},{\widehat{t}}_{\gamma })|$ or equivalently

$$\left|{\widehat{S}}_{\phi }^{\prime }\left(\widehat{x},\widehat{t}\right)-{\widehat{S}}_{\phi }^{\prime \prime }\left(\widehat{x},\widehat{t}\right)\right|\approx (\widehat{t}-{\widehat{t}}_{\gamma })\left|{\displaystyle \frac{𝜕{\widehat{S}}_{\phi }^{\prime }}{𝜕\widehat{t}}}\right|<n_{\gamma }\left|{\displaystyle \frac{𝜕{\widehat{S}}_{\phi }^{\prime }}{𝜕\widehat{t}}}\right|=O\left({ϵ}^4\right).$$

(134)

This proves that the approximation given by Equation (133) does not spoil the order of convergence of the proposed methodology. Even though this ingredient is simple and computationally very cheap, it ensures excellent stability; however, it smooths out the fastest dynamics (which is not compatible anyway with the incompressible limit).

3.3. Realistic Phenomenological Relation for the Drag Force

In order to better analyze the proposed methodology in practical applications, let us consider a more realistic phenomenological relation for the drag force. In particular, let us consider the model by Clift, Grace, and Weber (1978) [22]. In this model, the effective drag coefficient $K_I$ in Equation (118) of the interphase momentum exchange can be expressed as $K_I={\kappa }_I{\alpha }^2{\rho }^0/{\rho }_g^0$, where ${\kappa }_I=\left(3C_d\right)/\left(4d\right)$, $C_d$ is the drag coefficient which depends on the relative Reynolds number, d is the characteristic size of the individual entity of the dispersed phase, $\alpha =\sqrt{{\alpha }_g{\alpha }_l}$, and ${\rho }^0={\alpha }_g{\rho }_g^0+{\alpha }_l{\rho }_l^0$. Combining these definitions yields

$$K_I={\kappa }_I\left({\alpha }_g{\alpha }_l\right)\left({\alpha }_g+{\alpha }_{l}R\right).$$

(135)

The model by Clift, Grace, and Weber (CGW) introduces a further dependence on the volume fraction into the effective drag coefficient. This dependence can be analyzed by setting $K_I={\kappa }_I\mathsf{\Lambda }$, where

$$\mathsf{\Lambda }\left({\alpha }_g\right)\equiv \left({\alpha }_g{\alpha }_l\right)\left({\alpha }_g+{\alpha }_{l}R\right).$$

(136)

The function $\mathsf{\Lambda }\left({\alpha }_g\right)$ goes to zero for both ${\alpha }_g=0$ and ${\alpha }_g=1$, with a positive maximum in between. In the limiting case that the gas is the dispersed phase (namely, that ${\alpha }_g$ is small enough), the function $\mathsf{\Lambda }\left({\alpha }_g\right)$ can be approximated by its tangent at ${\alpha }_g=0$, namely, ${\alpha }^2\approx {\alpha }_g$ and ${\rho }^0\approx {\rho }_l^0$, which imply $\mathsf{\Lambda }\approx {\mathsf{\Lambda }}_0={\alpha }_{g}R$ [11,22]. In the case of large-density ratios, the tangent ${\mathsf{\Lambda }}_0={\alpha }_{g}R$ becomes quite steep and this makes the CGW model stiff because it can significantly change the drag force for moderate changes of the void fraction. For the purpose of containing the numerical instability due to this stiffness, let us update the function $\mathsf{\Lambda }\left({\alpha }_g\right)$ only once in a while to let the equations gradually accommodate the changes

$${\mathsf{\Lambda }}^{\prime }\left(\widehat{x},\widehat{t}\right)=\mathsf{\Lambda }\left(\widehat{x},{\widehat{t}}_{\gamma }\right),$$

(137)

where again ${\widehat{t}}_{\gamma }$ is the highest multiple of $n_{\gamma }$ but still smaller than $\widehat{t}$, namely, ${\widehat{t}}_{\gamma }=r_{\gamma }{n}_{\gamma }$ where $r_{\gamma }$ is a natural number and $r_{\gamma }{n}_{\gamma }\le \widehat{t}<(r_{\gamma }+1)n_{\gamma }$. Again $n_{\gamma }\ll N_t$, where $N_t$ is the total number of time steps. It is possible to prove (see previous section) that this approximation also does not spoil the order of convergence of the proposed methodology.

Another important ingredient for realistic simulations by the LBM is the concept of fluid-dynamic similarity. Because of its kinetic origin, the LBM can not deal directly with macroscopic geometric dimensions. Fortunately, the (kinematic) similarity allows one to apply the LBM to a geometrically similar setup (same shape but different sizes) with the same boundary conditions (e.g., no-slip, inlet velocity) and the same relevant dimensionless numbers. In other words, the velocity at any point in the LBM model flow is proportional by a constant scaling factor to the velocity at the same point in the real flow, while maintaining the same flow streamlines. It is important to identify this scaling factor, i.e., a proper way to convert flow quantities in physical units into lattice quantities coded by the Boltzmann scaling. Let us start with the main driving force, namely, the buoyancy force, driven by the gravitational acceleration g, and its LBM counterpart $\widehat{g}$ in Boltzmann scaling, which must be selected to ensure numerical stability. The ratio between these two quantities defines the first constraint in terms of $c/\tau$, namely,

$$c/\tau ={\displaystyle \frac{g}{\widehat{g}}}.$$

(138)

A second constraint is given by a similar ratio between the drag factor in the CGW model, i.e., ${\kappa }_I$, and its LBM counterpart, i.e., ${\widehat{\kappa }}_I$, which must ensure stable simulations. It is possible to express the last ratio in terms of $c\tau$, namely,

$$c\tau ={\displaystyle \frac{{\widehat{\kappa }}_I}{{\kappa }_I}}.$$

(139)

The previous constraints allow us to compute both c and $\tau$. In particular, the so-called lattice speed, which is the average fictitious particle velocity, can be computed as

$$c=\sqrt{(c/\tau )\left(c\tau \right)}=\sqrt{{\displaystyle \frac{g}{\widehat{g}}}{\displaystyle \frac{{\widehat{\kappa }}_I}{{\kappa }_I}}}.$$

(140)

This poses an upper limit to the maximum magnitude of the velocity field $u_{\phi }(x,t)$ which can be simulated by stable simulations, because the latter relation requires that ${\widehat{u}}_{\phi }=u_{\phi }/c$ is small enough, coherently with the incompressible limit. If these quantities are chosen consistently with regard to realistic setups, this is usually not problematic.

In particular, it is worth comparing the two most important driving forces of the momentum equation for the gas phase given by Equation (113), namely, the interphase momentum exchange force and the buoyancy force. For the purpose of doing so, the relevant fields, e.g., the velocity field $u_{\phi }(x,t)$, can be characterized by a reference value identified by the dagger superscript, e.g., $u_{\phi }^{†}$, which is typically the inlet (known) value. Using these reference values, the ratio between the magnitudes of the exchange force and the buoyancy force for the gas phase can be expressed as $M_{ex}$, and according to the CGW model, it can be computed as

$$M_{ex}={\displaystyle \frac{{\kappa }_I{\mathsf{\Lambda }}^{†}{\left|u_g^{†}-u_l^{†}\right|}^2/{\alpha }_g^{†}}{(R-1)g}}.$$

(141)

where ${\mathsf{\Lambda }}^{†}=\mathsf{\Lambda }\left({\alpha }_g^{†}\right)={\alpha }_g^{†}{\alpha }_l^{†}({\alpha }_g^{†}+{\alpha }_l^{†}R)$. Computing the same dimensionless number by LBM quantities in Boltzmann scaling yields

$${\widehat{M}}_{ex}={\displaystyle \frac{{\widehat{\kappa }}_I{\mathsf{\Lambda }}^{†}{\left|{\widehat{u}}_g^{†}-{\widehat{u}}_l^{†}\right|}^2/{\alpha }_g^{†}}{(R-1)\widehat{g}}}=(c/\tau ){\displaystyle \frac{c\tau }{c^2}}{M}_{ex}=M_{ex},$$

(142)

which clearly proves that ${\widehat{M}}_{ex}=M_{ex}$ and hence the fluid-dynamic similarity ensures the same ratio between the two main driving forces.

3.4. Finite Difference Solver for the Reference Solution

In this section, we develop an algorithm based on the finite difference (FD) method for solving the system of equations given by Equations (112), (113), (115) and (120) in order to obtain numerically a reference solution. The reference solution will be used to validate the LBM results. Hence, in order to simplify the comparisons between the results of the two methods, let us formulate both numerical engines in terms of $(\widehat{x},\widehat{t})$, where $\widehat{x}$ is the space coordinate divided by the distance $\lambda$ between two neighboring lattice nodes (mean free path) and $\widehat{t}$ is the physical time divided by the time $\tau$ between two consecutive lattice collisions (mean collision time). Let us define a computational domain which is a multiple $N_x$ of $\lambda$ and let us search for a solution of the previous system of equations in the nodal points ${\widehat{x}}_i\in \{1,2,\dots ,N_x\}$ where $1\le i\le N_x$. Let us consider the generic quantity $\widehat{u}\left(\widehat{x}\right)$ and let us call the nodal values as $\widehat{u}\left({\widehat{x}}_i\right)={\widehat{u}}_i$. Let us store the nodal values in a vector $\left\{\widehat{u}\right\}=\{{\widehat{u}}_1,{\widehat{u}}_2,\dots ,{\widehat{u}}_{N_x}\}$ with elements $\left\{\widehat{u}\right\}\left(i\right)={\widehat{u}}_i$ for $1\le i\le N_x$. It is possible to include also boundary conditions (BCs) into this nomenclature. From the nodal vector of the generic quantity $\left\{\widehat{u}\right\}$, by wrapping it with proper BCs, let us construct a larger nodal vector $\langle \widehat{u}\rangle =\{{\widehat{u}}_0,{\widehat{u}}_1,{\widehat{u}}_2,\dots ,{\widehat{u}}_{N_x},{\widehat{u}}_{N_x+1}\}$ with elements $\langle \widehat{u}\rangle \left(i\right)={\widehat{u}}_i$ for $0\le i\le (N_x+1)$, where ${\widehat{u}}_0$ and ${\widehat{u}}_{N_x+1}$ are some BCs which must be specified for the generic known (as a function of the other nodal values). Let us introduce also the following combinatorial rule. Given two known vectors $\langle \widehat{u}\rangle$ and $\langle \widehat{v}\rangle$, let us assume that $\left(\langle \widehat{u}\rangle \langle \widehat{v}\rangle \right)\left(i\right)=\langle \widehat{u}\rangle \left(i\right)\langle \widehat{v}\rangle \left(i\right)$. The same combinatorial rule applies also to vectors $\{·\}$, namely, $\left(\left\{\widehat{u}\right\}\left\{\widehat{v}\right\}\right)\left(i\right)=\left\{\widehat{u}\right\}\left(i\right)\left\{\widehat{v}\right\}\left(i\right)$.

Moreover, it is possible to introduce the central difference operator ${\widehat{D}}_x:\langle \widehat{u}\rangle \to \left\{{\widehat{D}}_x\widehat{u}\right\}$ (contraction) defined as

$$\left({\widehat{D}}_x\langle \widehat{u}\rangle \right)\left(i\right)=\left\{{\widehat{D}}_x\widehat{u}\right\}\left(i\right)=\left[\langle \widehat{u}\rangle (i+1)-\langle \widehat{u}\rangle (i-1)\right]/2,$$

(143)

where $1\le i\le N_x$. Analogously, by applying differencing formulas in a recursive manner, it is possible to introduce ${\widehat{D}}_x^2:\langle \widehat{u}\rangle \to \left\{{\widehat{D}}_x^2\widehat{u}\right\}$ (contraction) defined as

$$\left({\widehat{D}}_x^2\langle \widehat{u}\rangle \right)\left(i\right)=\left\{{\widehat{D}}_x^2\widehat{u}\right\}\left(i\right)=\langle \widehat{u}\rangle (i+1)-2\langle \widehat{u}\rangle \left(i\right)+\langle \widehat{u}\rangle (i-1),$$

(144)

where again $1\le i\le N_x$. These are the essential ingredients of the FD engine.

The FD engine searches for a numerical solution of the following vectors: $\left\{{\widehat{p}}_k\right\}$, $\left\{{\widehat{u}}_g\right\}$, $\left\{{\widehat{u}}_l\right\}$, and $\left\{{\widehat{\alpha }}_g\right\}$. Multiplying Equation (112) by ${\epsilon }^2$ and applying the code scaling yields

$${\displaystyle \frac{d\left\{{\widehat{p}}_k\right\}}{d\widehat{t}}}=-c_s^2{\widehat{D}}_x\langle {\widehat{u}}_g\rangle +c_s^2{\widehat{D}}_x\left[\langle {\widehat{\alpha }}_l\rangle \left(\langle {\widehat{u}}_g\rangle -\langle {\widehat{u}}_l\rangle \right)\right].$$

(145)

Multiplying Equations (113) and (115) by ${\epsilon }^3$ and applying the code scaling yields

$$\begin{array}{c}{\displaystyle \frac{d\left\{{\widehat{u}}_g\right\}}{d\widehat{t}}}=-{\widehat{D}}_x\left(\langle {\widehat{u}}_g\rangle \langle {\widehat{u}}_g\rangle \right)-{\widehat{D}}_x\langle {\widehat{p}}_k\rangle +{\nu }_g{\widehat{D}}_x^2\langle {\widehat{u}}_g\rangle +\left\{{\widehat{S}}_g\right\}\left\{{\widehat{u}}_g\right\}+\{{\widehat{\sigma }}_g/{\widehat{\alpha }}_g\}{\widehat{D}}_x\langle {\widehat{\alpha }}_g\rangle \dots \hfill \\ +(R-1)\widehat{g}+\{{\widehat{K}}_I/{\widehat{\alpha }}_g\}|\left\{{\widehat{u}}_l\right\}-\left\{{\widehat{u}}_g\right\}|\left(\left\{{\widehat{u}}_l\right\}-\left\{{\widehat{u}}_g\right\}\right),\hfill \end{array}$$

(146)

and

$$\begin{array}{c}{\displaystyle \frac{d\left\{{\widehat{u}}_l\right\}}{d\widehat{t}}}=-{\widehat{D}}_x\left(\langle {\widehat{u}}_l\rangle \langle {\widehat{u}}_l\rangle \right)-(1/R){\widehat{D}}_x\langle {\widehat{p}}_k\rangle +{\nu }_l{\widehat{D}}_x^2\langle {\widehat{u}}_l\rangle +\left\{{\widehat{S}}_l\right\}\left\{{\widehat{u}}_l\right\}+\{{\widehat{\sigma }}_l/{\widehat{\alpha }}_l\}{\widehat{D}}_x\langle {\widehat{\alpha }}_l\rangle \dots \hfill \\ +(1/R)\{{\widehat{K}}_I/{\widehat{\alpha }}_l\}|\left\{{\widehat{u}}_g\right\}-\left\{{\widehat{u}}_l\right\}|\left(\left\{{\widehat{u}}_g\right\}-\left\{{\widehat{u}}_l\right\}\right)+(1/R)\{{\widehat{K}}_W/{\widehat{\alpha }}_l\}\left|\left\{{\widehat{u}}_l\right\}\right|\left\{{\widehat{u}}_l\right\},\hfill \end{array}$$

(147)

where we assume $\epsilon K_W={\widehat{K}}_W$ in analogy with the scaling ${\widehat{K}}_I=\epsilon K_I$ which was adopted in the asymptotic analysis of the LBM schemes. Finally, multiplying Equation (120) by ${\epsilon }^2$ and applying the code scaling yields

$${\displaystyle \frac{d\left\{{\widehat{\alpha }}_g\right\}}{d\widehat{t}}}=-{\widehat{D}}_x\left(\langle {\widehat{\alpha }}_g\rangle \langle {\widehat{u}}_g\rangle \right).$$

(148)

Equations (145)–(148) define a system of ordinary differential equations (ODEs) for $\left\{{\widehat{p}}_k\right\}$, $\left\{{\widehat{u}}_g\right\}$, $\left\{{\widehat{u}}_l\right\}$, and $\left\{{\widehat{\alpha }}_g\right\}$, as far as proper boundary conditions are specified for computing the larger vector $\langle \widehat{u}\rangle$ from the generic vector $\left\{\widehat{u}\right\}$. For the kinematic pressure, this mapping is realized by the following wrapping:

$$\langle {\widehat{p}}_k\rangle =\{2{\widehat{p}}_k\left(1\right)-{\widehat{p}}_k\left(2\right),{\widehat{p}}_k\left(1\right),\dots ,{\widehat{p}}_k\left(N_x\right),2c_s^2-{\widehat{p}}_k\left(N_x\right)\},$$

(149)

where ${\widehat{p}}_k\left(0\right)=2{\widehat{p}}_k\left(1\right)-{\widehat{p}}_k\left(2\right)$ at the inlet is an extrapolation and ${\widehat{p}}_k(N_x+1)=2c_s^2-{\widehat{p}}_k\left(N_x\right)$ at the outlet is a Dirichlet condition corresponding to ${\widehat{p}}_k(N_x+1/2)=c_s^2$ (halfway). Other flow quantities have the following mappings:

$$\langle {\widehat{u}}_g\rangle =\{2{\widehat{u}}_g^{IN}-{\widehat{u}}_g\left(1\right),{\widehat{u}}_g\left(1\right),\dots ,{\widehat{u}}_g\left(N_x\right),2{\widehat{u}}_g\left(N_x\right)-{\widehat{u}}_g(N_x-1)\},$$

(150)

$$\langle {\widehat{u}}_l\rangle =\{2{\widehat{u}}_l^{IN}-{\widehat{u}}_l\left(1\right),{\widehat{u}}_l\left(1\right),\dots ,{\widehat{u}}_l\left(N_x\right),2{\widehat{u}}_l\left(N_x\right)-{\widehat{u}}_l(N_x-1)\},$$

(151)

$$\langle {\widehat{\alpha }}_g\rangle =\{2{\widehat{\alpha }}_g^{IN}-{\widehat{\alpha }}_g\left(1\right),{\widehat{\alpha }}_g\left(1\right),\dots ,{\widehat{\alpha }}_g\left(N_x\right),2{\widehat{\alpha }}_g\left(N_x\right)-{\widehat{\alpha }}_g(N_x-1)\},$$

(152)

where, for the generic quantity, $\widehat{u}\left(0\right)=2{\widehat{u}}^{IN}-\widehat{u}\left(1\right)$ at the inlet is a Dirichlet condition corresponding to $\widehat{u}(1/2)={\widehat{u}}^{IN}$ (halfway) and $\widehat{u}(N_x+1)=2\widehat{u}\left(N_x\right)-\widehat{u}(N_x-1)$ at the outlet is an extrapolation. In order to be consistent with the incompressible limit, the generic inlet quantity ${\widehat{y}}^{IN}\in \{{\widehat{\alpha }}_g^{IN},{\widehat{u}}_g^{IN},{\widehat{u}}_l^{IN}\}$ involved in the previous formulas is progressively increased by the following function:

$${\widehat{y}}^{IN}\left(\widehat{t}\right)=({\widehat{y}}^{max}-{\widehat{y}}^{min})tanh(\widehat{t}/n_t)+{\widehat{y}}^{min},$$

(153)

where ${\widehat{y}}^{max}$ and ${\widehat{y}}^{min}$ are quantity-specific values which depend on the considered test case. The parameter $n_t<N_t$, where $N_t$ is the total number of time steps.

The above system of ODEs will be solved in Matlab® R2024b by means of ode45 solver, which is a variable step solver (which means that it automatically chooses the value of the time stepping) and is based on an explicit Runge–Kutta (4,5) formula, the Dormand–Prince pair, namely, a combination of fourth- and fifth-order methods. During the iteration procedure, once every few time steps (e.g., 100 iterations), the solution vectors are smoothed in order to avoid the checkerboard instability by means of a Gaussian-weighted moving average filter (with a window containing 12 points). It is remarkable that LBM schemes do not need such additional smoothing because they are more robust against the checkerboard instability. The reason is due to the third term of the left-hand side of Equation (47) in the LBM asymptotic equations [16].

3.5. LBM Solver

Before discussing practical details of the LBM solver, it is worth realizing that the one-dimensional case is actually degenerate, and this may require some modifications in the formulas involving the transport coefficients. For example, recalling Equation (68) in this case yields

$${\sigma }_{\phi }={\nu }_{\phi }^{ef}{\displaystyle \frac{𝜕u_{\phi }}{𝜕x}}+O\left({\epsilon }^2\right),$$

(154)

where

$${\nu }_{\phi }^{ef}=\left({\displaystyle \frac{1}{{\omega }_{\phi }}}-{\displaystyle \frac{1}{2}}\right)-{\displaystyle \frac{c_s^2{\psi }_{\phi }}{{\omega }_{\phi }}}.$$

(155)

Using Equations (65) and (66) leads to an effective viscosity ${\nu }_{\phi }^{ef}={\nu }_{\phi }{d}_{\phi }$ where $d_{\phi }$ is a corrective factor for one-dimensional degeneracy, namely,

$$d_{\phi }={\displaystyle \frac{4}{3}}+{\displaystyle \frac{{\xi }_{\phi }}{{\nu }_{\phi }}}.$$

(156)

Hence, two strategies are possible for recovering the given kinematic viscosity are as follows:

• ${\xi }_{\phi }=-(1/3){\nu }_{\phi }$, as reported in the previous section, and consequently $d_{\phi }=1$ (with ${\psi }_{\phi }=2{\omega }_{\phi }{\nu }_{\phi }/c_s^2$), which ensures the maximum consistency with the multidimensional cases but also some small oscillations during the transient dynamics (up to 10% in the tested cases) without impacting on the steady state solution;
• ${\xi }_{\phi }=(5/3){\nu }_{\phi }$ and consequently $d_{\phi }=3$ (with ${\psi }_{\phi }=0$), which ensures the best performance also during the transient dynamics.

In the following, the second strategy is adopted. This has an impact also on the way one computes the stress in the one-dimensional case. Recalling Equation (61) in this case yields

$${\displaystyle \frac{𝜕u_{\phi }}{𝜕x}}={\omega }_{\phi }({\mathsf{\Pi }}_{\phi }^{eq}-{\mathsf{\Pi }}_{\phi })+{\psi }_{\phi }{c}_s^2{S}_{\phi }+O\left({\epsilon }^2\right),$$

(157)

and substituting it into Equation (154) yields

$${\sigma }_{\phi }={\nu }_{\phi }^{ef}\left[{\omega }_{\phi }({\mathsf{\Pi }}_{\phi }^{eq}-{\mathsf{\Pi }}_{\phi })+{\psi }_{\phi }{c}_s^2{S}_{\phi }\right]+O\left({\epsilon }^2\right),$$

(158)

where the effective viscosity is used.

For solving the one-dimensional test case, let us adopt the standard implementation for the D1Q3 lattice [1], with the equilibrium distributions reported in Appendix A. Aside from the bulk implementation discussed so far, BCs in LBM are quite critical for stability and efficiency. The proposed BCs are those which showed the best compromise between stability and accuracy. They can be formulated by the two steps described below:

• STEP #1. First of all, the generic flow quantity $\widehat{y}\in \{{\widehat{ϵ}}_g,{\widehat{ϵ}}_l,{\widehat{\alpha }}_g,{\widehat{\alpha }}_l,{\widehat{\beta }}_g,{\widehat{\beta }}_l,{\widehat{u}}_g,{\widehat{u}}_l,{\widehat{c}}_g,{\widehat{c}}_l\}$ at the boundary ${\widehat{x}}_B$ (boundary) can be imposed (Dirichlet) or extrapolated. Concerning extrapolation, there are two cases: halfway (hw), where the computed generic quantity is intended at the position ${\widehat{x}}_B$ midway between the last mesh node at ${\widehat{x}}_E$ (edge) and the missing node outside the mesh, namely, $|{\widehat{x}}_B-{\widehat{x}}_E|=1/2$, and full-way (fw), where the computed quantity is intended in the missing node, namely, $|{\widehat{x}}_B-{\widehat{x}}_E|=1$. These two cases can be summarized as

  $$|{\widehat{x}}_B-{\widehat{x}}_E|=\left\{\begin{array}{cc}1/2,\hfill & \mathrm{if}\mathrm{half-way}\left(\mathrm{hw}\right),\hfill \\ 1,\hfill & \mathrm{if}\mathrm{full-way}\left(\mathrm{fw}\right).\hfill \end{array}\right.$$

  (159)
  The choice between these two options depends on the LBM boundary condition (see the following step). At the position ${\widehat{x}}_B$, the generic flow quantity can be imposed or extrapolated

  $${\widehat{y}}^{B\left(in\right)}=\left\{\begin{array}{cc}{\widehat{y}}^{IN},\hfill & \mathrm{if}\mathrm{Dirichlet},\hfill \\ (3/2)\widehat{y}\left(1\right)-(1/2)\widehat{y}\left(2\right),\hfill & \mathrm{if}\mathrm{EX}\left(\mathrm{hw}\right),\hfill \\ 2\widehat{y}\left(1\right)-\widehat{y}\left(2\right),\hfill & \mathrm{if}\mathrm{EX}\left(\mathrm{fw}\right),\hfill \end{array}\right.$$

  (160)

  and

  $${\widehat{y}}^{B\left(out\right)}=\left\{\begin{array}{cc}{\widehat{y}}^{OUT},\hfill & \mathrm{if}\mathrm{Dirichlet},\hfill \\ (3/2)\widehat{y}\left(N_x\right)-(1/2)\widehat{y}(N_x-1),\hfill & \mathrm{if}\mathrm{EX}\left(\mathrm{hw}\right),\hfill \\ 2\widehat{y}\left(N_x\right)-\widehat{y}(N_x-1),\hfill & \mathrm{if}\mathrm{EX}\left(\mathrm{fw}\right).\hfill \end{array}\right.$$

  (161)
  The proposed BCs for the LBM framework are described in

  Table 1. BCs for LBM schemes: INLET ($\widehat{x}=1$). Acronyms stand for bounce back (BB); anti-bounce back (ABB); extrapolation (EX); and equilibrium (EQ). Uppercase letters in parentheses stand for incompressible equilibrium (I) and standard equilibrium (S). Lowercase letters in parentheses stand for halfway (hw) and full-way (fw).

  ${\mathit{f}}_{*\mathit{\phi }}$	INLET ($\widehat{\mathit{x}}=1$): Compute ${\widehat{\mathit{y}}}^{\mathit{B}\left(\mathit{in}\right)}$
  	Type	Generic Density ${\widehat{\mathit{y}}}_{\mathbf{ϵ}}^{\mathit{B}\left(\mathit{in}\right)}$	Generic Velocity ${\widehat{\mathit{y}}}_{\mathit{u}}^{\mathit{B}\left(\mathit{in}\right)}$
  $f_g$	BB(I)	${\widehat{ϵ}}_g$: EX(hw)	${\widehat{u}}_g={\widehat{u}}_g^{IN}$
  $f_l$	BB(I)	${\widehat{ϵ}}_l$: EX(hw)	${\widehat{u}}_l={\widehat{u}}_l^{IN}$
  $f_{\alpha g}$	EQ(S)	${\widehat{\alpha }}_g={\widehat{\alpha }}_g^{IN}$	${\widehat{u}}_g={\widehat{u}}_g^{IN}$
  $f_{\alpha l}$	EQ(S)	${\widehat{\alpha }}_l=1-{\widehat{\alpha }}_g^{IN}$	${\widehat{u}}_l={\widehat{u}}_l^{IN}$
  $f_{\beta g}$	EQ(S)	${\widehat{\beta }}_g$: EX(fw)	${\widehat{c}}_g$: EX(fw)
  $f_{\beta l}$	EQ(S)	${\widehat{\beta }}_l$: EX(fw)	${\widehat{c}}_l$: EX(fw)

  for the inlet at $\widehat{x}=1$ and in

  Table 2. BCs for LBM schemes: OUTLET ($\widehat{x}=N_x$). Acronyms stand for bounce back (BB); anti-bounce back (ABB); extrapolation (EX); and equilibrium (EQ). Uppercase letters in parentheses stand for incompressible equilibrium (I) and standard equilibrium (S). Lowercase letters in parentheses stand for halfway (hw) and full-way (fw).

  ${\mathit{f}}_{*\mathit{\phi }}$	OUTLET ($\widehat{\mathit{x}}={\mathit{N}}_{\mathit{x}}$): Compute ${\widehat{\mathit{y}}}^{\mathit{B}\left(\mathit{out}\right)}$
  	Type	Generic Density ${\widehat{\mathit{y}}}_{\mathit{ϵ}}^{\mathit{B}\left(\mathit{out}\right)}$	Generic Velocity ${\widehat{\mathit{y}}}_{\mathit{u}}^{\mathit{B}\left(\mathit{out}\right)}$
  $f_g$	ABB(I)	${\widehat{ϵ}}_g=1$	${\widehat{u}}_g$: EX(hw)
  $f_l$	ABB(I)	${\widehat{ϵ}}_l=1$	${\widehat{u}}_l$: EX(hw)
  $f_{\alpha g}$	ABB(S)	${\widehat{\alpha }}_g$: EX(hw)	${\widehat{u}}_g$: EX(hw)
  $f_{\alpha l}$	ABB(S)	${\widehat{\alpha }}_l$: EX(hw)	${\widehat{u}}_l$: EX(hw)
  $f_{\beta g}$	EQ(S)	${\widehat{\beta }}_g$: EX(fw)	${\widehat{c}}_g$: EX(fw)
  $f_{\beta l}$	EQ(S)	${\widehat{\beta }}_l$: EX(fw)	${\widehat{c}}_l$: EX(fw)

  for the outlet at $\widehat{x}=N_x$, respectively. For the sake of the following step, the generic flow quantities can be divided in two subgroups: generic densities ${\widehat{y}}_{ϵ}\in \{{\widehat{ϵ}}_g,{\widehat{ϵ}}_l,{\widehat{\alpha }}_g,{\widehat{\alpha }}_l,{\widehat{\beta }}_g,{\widehat{\beta }}_l\}$ and generic velocities ${\widehat{y}}_u\in \{{\widehat{u}}_g,{\widehat{u}}_l,{\widehat{c}}_g,{\widehat{c}}_l\}$. All previous options are summarized in Table 1 for the inlet and in Table 2 for the outlet by using the same acronyms (see columns for generic density and for generic velocity).
• STEP #2. Secondly, once the flow quantities are imposed or extrapolated, the usual LBM techniques can be used to transfer the boundary condition at the position ${\widehat{x}}_B$ to the generic distribution function $f_{*\phi }\in \{f_g,f_l,f_{\alpha g},f_{\alpha l},f_{\beta g},f_{\beta l}\}$ in the mesh node ${\widehat{x}}_E$ during streaming. Let us consider some popular approaches: bounce-back (BB) rule, anti-bounce-back (ABB) rule, and equilibrium (EQ) rule [1]. It is worth noticing also that BB and ABB are formulated in terms of the equilibrium distribution, which must be coherent with the one used in the bulk, namely, incompressible equilibrium (I) $f_I^{eq}(\varphi ,\widehat{ϵ},\widehat{u})$ or standard equilibrium (S) $f_S^{eq}(\widehat{\alpha },\widehat{u})$ (see Appendix A). Let us refer to the generic equilibrium distribution function as $f_Y^{eq}({\widehat{y}}_{ϵ},{\widehat{y}}_u)$, which can coincide with either $f_I^{eq}$ or $f_S^{eq}$ depending on the considered distribution function. The BB, ABB, and EQ rule for computing the incoming distribution function during the streaming can be expressed as

  $$f_{*\phi }({\widehat{x}}_E,\widehat{t}+1,BB\left(q^{*}\right))=\left\{\begin{array}{cc}{f}_{*\phi }^{*}({\widehat{x}}_E,\widehat{t},q^{*})+{\mathsf{\Delta }}_Y^{BB}({\widehat{y}}_{ϵ}^B,{\widehat{y}}_u^B,q^{*}),\hfill & \mathrm{if}\mathrm{BB}\left(\mathrm{Y}\right),\hfill \\ -f_{*\phi }^{*}({\widehat{x}}_E,\widehat{t},q^{*})+{\mathsf{\Delta }}_Y^{ABB}({\widehat{y}}_{ϵ}^B,{\widehat{y}}_u^B,q^{*}),\hfill & \mathrm{if}\mathrm{ABB}\left(\mathrm{Y}\right),\hfill \\ f_Y^{eq}({\widehat{y}}_{ϵ}^B,{\widehat{y}}_u^B,BB\left(q^{*}\right)),\hfill & \mathrm{if}\mathrm{EQ}\left(\mathrm{Y}\right),\hfill \end{array}\right.$$

  (162)

  where ${\widehat{x}}_E$ is the edge node (in the one-dimensional case, it can be either ${\widehat{x}}_E=1$ or ${\widehat{x}}_E=N_x$), $q^{*}$ is the identifier of the velocity $v_{q^{*}}$ leaving the computational domain ($v_{q^{*}}=-1$ for ${\widehat{x}}_E=1$ and $v_{q^{*}}=+1$ for ${\widehat{x}}_E=N_x$), $BB\left(q^{*}\right)$ is the opposite direction (bounce-back), and $f_{*\phi }^{*}$ is the generic post-collision distribution function [1]. The operators ${\mathsf{\Delta }}_Y^{BB}$ and ${\mathsf{\Delta }}_Y^{ABB}$ can be constructed by means of the proper equilibrium for the considered distribution function as

  $${\mathsf{\Delta }}_Y^{BB}=f_Y^{eq}({\widehat{y}}_{ϵ}^B,-{\widehat{y}}_u^B)-f_Y^{eq}({\widehat{y}}_{ϵ}^B,{\widehat{y}}_u^B),$$

  (163)

  $${\mathsf{\Delta }}_Y^{ABB}=f_Y^{eq}({\widehat{y}}_{ϵ}^B,-{\widehat{y}}_u^B)+f_Y^{eq}({\widehat{y}}_{ϵ}^B,{\widehat{y}}_u^B).$$

  (164)
  The rationale behind the reported choices is the following: The BB rule is typically used to transfer a Dirichlet condition for a generic velocity ${\widehat{y}}_u$, the ABB rule to transfer a Dirichlet condition for a generic density ${\widehat{y}}_{ϵ}$ (and hence also for a generic pressure), while the EQ rule to transfer a Dirichlet condition for both a generic velocity and a generic density at the same time. The BB and the ABB rules impose conditions halfway, namely, at position ${\widehat{x}}_B$ where $|{\widehat{x}}_B-{\widehat{x}}_E|=1/2$, while the EQ rule streams the distribution function from a missing node located at the full-way distance, namely, from the position ${\widehat{x}}_B$ where $|{\widehat{x}}_B-{\widehat{x}}_E|=1$. See Equations (159)–(161) from which we started.

3.6. Numerical Results and Discussion

In this section, we report the numerical results for some meaningful test cases of the proposed methodology, which are grouped into a preliminary category and an advanced category. The preliminary category (TESTS #1 and #2) is intended to realize the basic essential features of the methodology, while the advanced category (TESTS #3 and #4) discusses challenging features, i.e., very-high-density ratios and realistic phenomenological relations for the interphase momentum exchange. The proposed test cases are also described through their distinctive minimal set of features in

Table 3. Numerical test cases of the proposed methodology, organized in a “preliminary” and an “advanced” category. The distinctive parameters are the density ratio R and the possible realistic definition of the momentum exchange coefficient through a drag model.

Category	Test	R	Drag Model
Preliminary	#1	2	None
	#2	5	None
Advanced	#3	833.3	None
	#4	833.3	CGW

.

First of all, let us consider first the preliminary category with preliminary numerical results. In particular, let us consider the following test case (corresponding to a natural circulation loop driven by gas injection), called TEST #1: ${\rho }_g^0=1.2$, ${\rho }_l^0=2.4$ ($R=2$), ${\nu }_g=1.1667$, ${\nu }_l=1.1667$, $\widehat{g}={10}^{-6}$, ${\widehat{K}}_I={10}^{-2}$, and ${\widehat{K}}_W={10}^{-2}$. The progressively increased quantities at the inlet (see Equation (153)) for this test case are ${\widehat{\alpha }}_g^{max}=0.8$ and ${\widehat{\alpha }}_g^{min}={10}^{-2}$ for the dispersed phase volume fraction; ${\widehat{u}}_l^{max}={10}^{-3}$ and ${\widehat{u}}_l^{min}=0$ for the liquid phase velocity; while, for the dispersed phase velocity, ${\widehat{u}}_g^{max}={10}^{-2}$ and ${\widehat{u}}_g^{min}$ is given by Equation (124), namely,

$${\widehat{u}}_g^{min}={\displaystyle \frac{1}{\sqrt{{\widehat{K}}_I}}}\sqrt{{\widehat{\alpha }}_g^{min}(1-{\widehat{\alpha }}_g^{min})(R-1)\widehat{g}}.$$

(165)

For this test case, we used $N_x=200$ which is the number of nodal values, $N_t=6\times {10}^6$ which is number of time steps, and $n_t=5\times {10}^5=N_t/12$ which is the characteristic number of time steps which parametrize the transient smooth ramp-up (see Equation (153)). Similarly, for the purpose of testing the capability of the proposed methodology to deal with phases with different average densities, let us consider also another test case, called TEST #2, where ${\rho }_g^0=1.2$, but this time ${\rho }_l^0=6.0$ ($R=5$), $\widehat{g}=2.5\times {10}^{-7}$, in such a way that $(R-1)\widehat{g}$ is equal in the two tests discussed so far, and all remaining parameters are the same as in TEST #1.

Next, let us consider the advanced category with advanced numerical results for testing the proposed methodology in challenging setups, i.e., very-high-density ratios and stiff (but realistic) phenomenological relations for the interphase momentum exchange. Let us consider a test case, called TEST #3, where ${\rho }_g^0=1.2$, but this time we take the very challenging value ${\rho }_l^0=1000.0$ ($R=833.3$), $\widehat{g}=1.2\times {10}^{-9}$, in such a way that $(R-1)\widehat{g}$ is equal in all cases discussed so far. This third test case is intended to explore how the solvers deal with a very-large-density ratio—typically very challenging for the LBM—which could trigger some numerical instabilities. For this reason, this test case requires also the stabilization ingredients discussed in Section 3.2: $\gamma =1$ with the third stabilization strategy (for better consistency) and $n_{\gamma }=200\ll N_t$. All remaining parameters are the same as in other test cases discussed so far.

Moreover, for the purpose of testing also the additional dependency of the drag force on the volume fraction, let us also consider a test case, called TEST #4, where the interphase drag force is modeled by the CGW model. In this case, the simulation parameters must be derived from physical values, which are consistent with a realistic setup (despite the limitations of the one-dimensional configuration). For this aim, let us focus on the experimental setup described in Reference [22] for extracting the most relevant physical quantities: $g=9.81$, ${\kappa }_I=3\times 0.66/(4\times 0.002)=247.5$, $u_g^{max}=0.3$, and ${\alpha }_g^{max}=0.1$, where we assume $U=1m/s$ as the characteristic flow speed and $L=1m$ as the characteristic length scale of the flow field. Assuming $\widehat{g}=1.2\times {10}^{-9}$ and ${\widehat{\kappa }}_I=1.45\times {10}^{-4}$ (${\widehat{\kappa }}_W={\widehat{\kappa }}_I$) for stability reasons, applying Equations (138) and (139) yields $c/\tau =8.18\times {10}^9$ and $c\tau =5.86\times {10}^{-7}$, respectively. Therefore the lattice speed is $c=\sqrt{(c/\tau )\left(c\tau \right)}=69.2$. This means that ${\widehat{u}}_g^{max}=u_g^{max}/c=0.0043$, which ensures a Mach number small enough to be consistent with the incompressible limit. Moreover, let us assume ${\widehat{u}}_l^{max}={\widehat{u}}_g^{max}/4=0.0011$ for having a balanced inlet condition, as we prove below. Adopting $u_g^{†}=u_g^{max}$, $u_l^{†}=u_l^{max}$, and ${\alpha }_g^{†}={\alpha }_g^{max}$ as reference values, it is possible to estimate the ratio between the momentum exchange force and the buoyancy force in the momentum equation of the gas phase by Equation (141), which is equal to $M_{ex}=1.04$. This means that the drag force of this setup is expected to almost balance the buoyancy force at the inlet. Finally, let us assume ${\widehat{u}}_g^{min}={\widehat{u}}_g^{max}/10$, ${\widehat{u}}_l^{min}={\widehat{u}}_l^{max}/10$, and ${\alpha }_g^{min}={10}^{-2}$. All remaining parameters are the same as in other test cases discussed so far.

Numerical results are reported below for all test cases, comparing those obtained by the FD engine and those by the LBM engine. Figure 1 and Figure 2 present the most relevant features and additional computational details for TEST #1. Similarly, Figure 3 and Figure 4 illustrate the corresponding information for TEST #2. Moreover, Figure 5 shows the main features of TEST #3 about a very-large-density ratio, together with additional computational details for the same test case in Figure 6. Even more remarkably, Figure 7 shows the main features of TEST #4 about a very-large-density ratio with a stiff (but realistic) relation for the drag force. More computational details about this very challenging test case can be found in Figure 8.

Concerning these numerical results, let us comment first the preliminary ones below.

• It is important to highlight that the proposed LBM schemes agree with the FD numerical results in an excellent way. This opens a promising venue for simulating multiphase flows in large HPC facilities. In fact, it is worth highlighting that the proposed methodology and all LBM formulas reported in Section 2 can be automatically applied to any dimension, including all boundary conditions.
• The key point, namely, the artificially compressible continuity equation for each phase, works well, and Figure 2a and Figure 4a prove that the individual phase sources can be computed in LBM schemes without FD corrections.
• LBM schemes without FD corrections can be used effectively to compute all terms in multiphase equations, including gradients of the volume fractions and stress tensors, as clearly reported in Figure 2b–f and Figure 4b–f, where the LBM results show an excellent agreement with those obtained by FD operators.
• It is important to highlight that incompressible multiphase flows has divergence-free mixture velocity, as prescribed by Equation (12), but this condition does not hold for individual phase velocity. The one-dimensional test case is enough to show this important difference: indeed, ${\widehat{\alpha }}_g{\widehat{u}}_g+{\widehat{\alpha }}_l{\widehat{u}}_l$ is constant (the only way to ensure the divergence-free condition in one dimension), but ${\widehat{u}}_g$ and ${\widehat{u}}_l$ are not. It is clear that Figure 1c and Figure 3c confirm this expectation. Hence the proposed LBM framework ensures, as it should be, the divergence-free condition for the mixture velocity, but it does not force it also for the individual phase velocities. This is one of the most important features of the proposed method in comparison with what is already available in the literature.
• Another consideration is to investigate the relation between the numerical solution at the outlet and the analytical solution derived in the previous section. For the sake of simplicity, let us consider TEST #1. At the outlet, the LBM framework provides ${\widehat{u}}_g\left(N_x\right)=8.4237\times {10}^{-3}$, ${\widehat{u}}_l\left(N_x\right)=3.9750\times {10}^{-3}$, ${\widehat{\alpha }}_g\left(N_x\right)=0.950$, and ${\widehat{\alpha }}_l\left(N_x\right)=0.050$, which corresponds to the following mixture velocity: ${\widehat{\alpha }}_g\left(N_x\right){\widehat{u}}_g\left(N_x\right)+{\widehat{\alpha }}_l\left(N_x\right){\widehat{u}}_l\left(N_x\right)=8.1999\times {10}^{-3}$. In this test case, $r=0.9496$. Using ${\widehat{\alpha }}_g\left(N_x\right)$ instead of ${\overline{\alpha }}_g$ in Equation (124) leads to ${\overline{u}}_g^0=2.1859\times {10}^{-3}$. Using the latter velocity in Equation (127) and assuming ${\overline{u}}_g={\widehat{u}}_g\left(N_x\right)$ leads to ${\overline{u}}_l=3.9754\times {10}^{-3}$, which is in excellent agreement with ${\widehat{u}}_l\left(N_x\right)$ (mismatch $0.01$ %). Because in this case r is pretty close to 1, it is also possible to use the approximated formula ${\overline{u}}_l\approx ({\overline{u}}_g-{\overline{u}}_g^0)(1+{\overline{u}}_g^0/{\overline{u}}_g)/2=3.9282\times {10}^{-3}$ (mismatch 1 %).
• It is also worth comparing the numerical results between TEST #1 and TEST #2. In Figure 1c and Figure 3c the difference is clear in the slope of the kinematic pressure profiles of the two phases for the TEST #1 ($R=2$) and TEST #2 ($R=5$), respectively. This proves that the proposed methodology can describe properly the effects due to the density ratio between the phases.

Secondly, advanced results are discussed below:

• The previous preliminary results highlight some challenges, mainly about large-density ratios, which are discussed here in the category about advanced results. In the limit of very-large-density ratios, namely, $R\gg 1$, some terms proportional to $1/R$ in the momentum equation of the liquid phase become very small and hence comparable with the numerical errors. For this reason, TEST #3 ($R=833.3$) also requires the stabilization ingredients discussed in Section 3.2: $\gamma =1$ with the third stabilization strategy and $n_{\gamma }=200\ll N_t$. The transient profiles of the LBM results are slightly smoother than those of the FD results, as shown in Figure 5a. The kinematic pressure profiles computed by the two engines in Figure 5d reveal a small discrepancy, but this is acceptable because the pressure gradient is what really matters. The numerical details of the proposed methodology reported in Figure 6 are excellent with the exception of the computed second term of the force $G_l$ (in the one-dimensional case) given by Equation (26) and reported in Figure 6f, which shows some numerical oscillations (but the magnitude of these oscillations is extremely small).
• An important feature to be discussed in the category about the advanced numerical results is the need to include realistic phenomenological relations. In particular, TEST #4 adopts the model by Clift, Grace, and Weber (CGW) [22], which introduces a further dependence on the volume fraction into the effective drag coefficient (stiff coupling). The transient profiles of the LBM results show some discrepancies with regard to those of the FD results, as shown in Figure 7a. In particular, the LBM solution is not necessarily smoother than the reference solution, likely because of the stiffness of the CGW model. At steady state, in spite of the excellent numerical details reported in Figure 8, there is a small mismatch for this mesh in the volume fraction profiles reported in Figure 7b and in the velocity profiles reported in Figure 7c (e.g., looking at the gas phase, there is an 8% discrepancy at the outlet). Moreover, the kinematic pressure profiles computed by the two engines in Figure 7d reveal a negligible discrepancy in absolute terms but which may have an impact on the effective pressure gradient and hence on the momentum equations. It is important to recall that a small discrepancy in ${\alpha }_g$ at small values, but with very-large-density ratios, may lead to a significant impact on $\mathsf{\Lambda }\left({\alpha }_g\right)$ and hence on the drag force acting in the momentum equation.

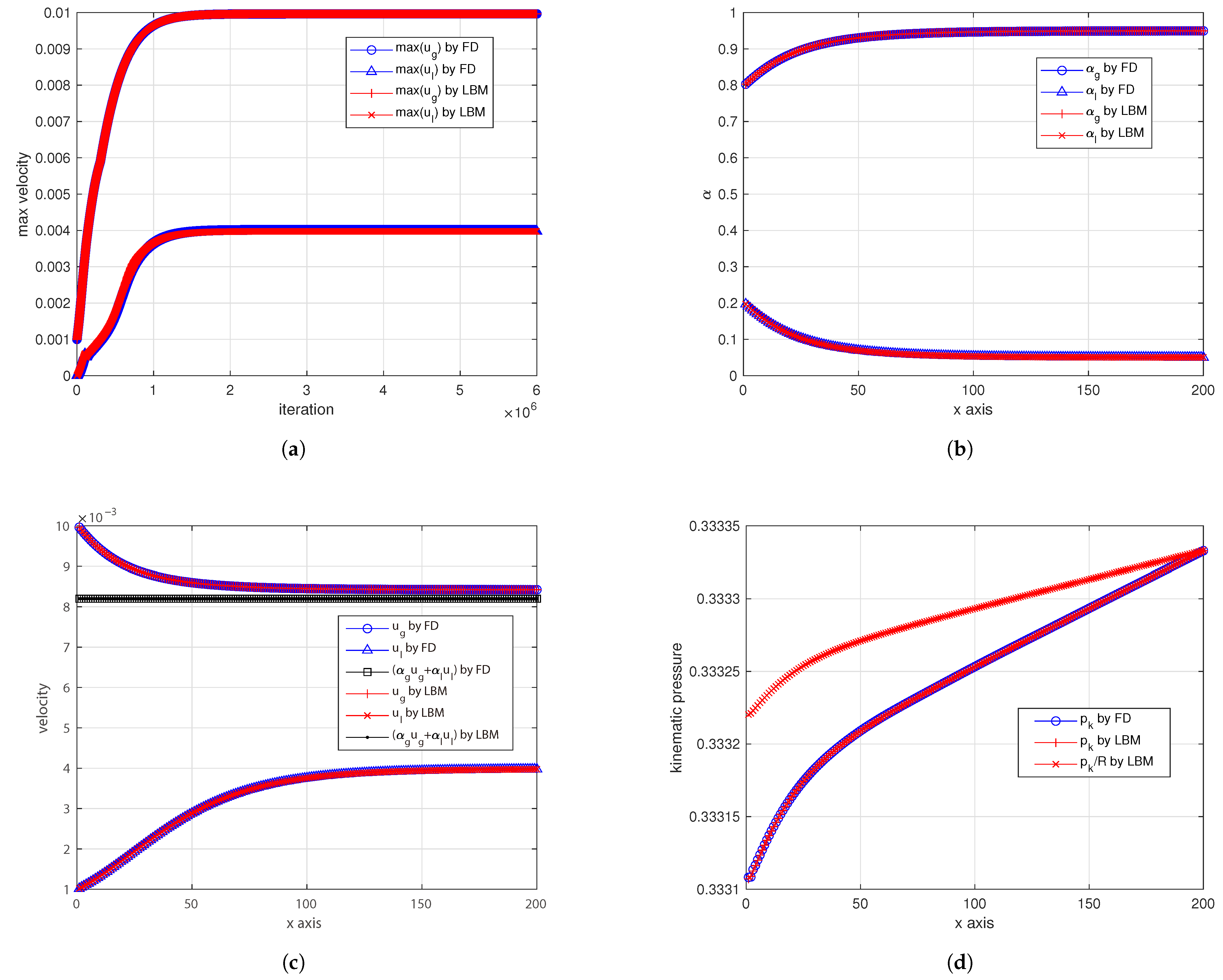
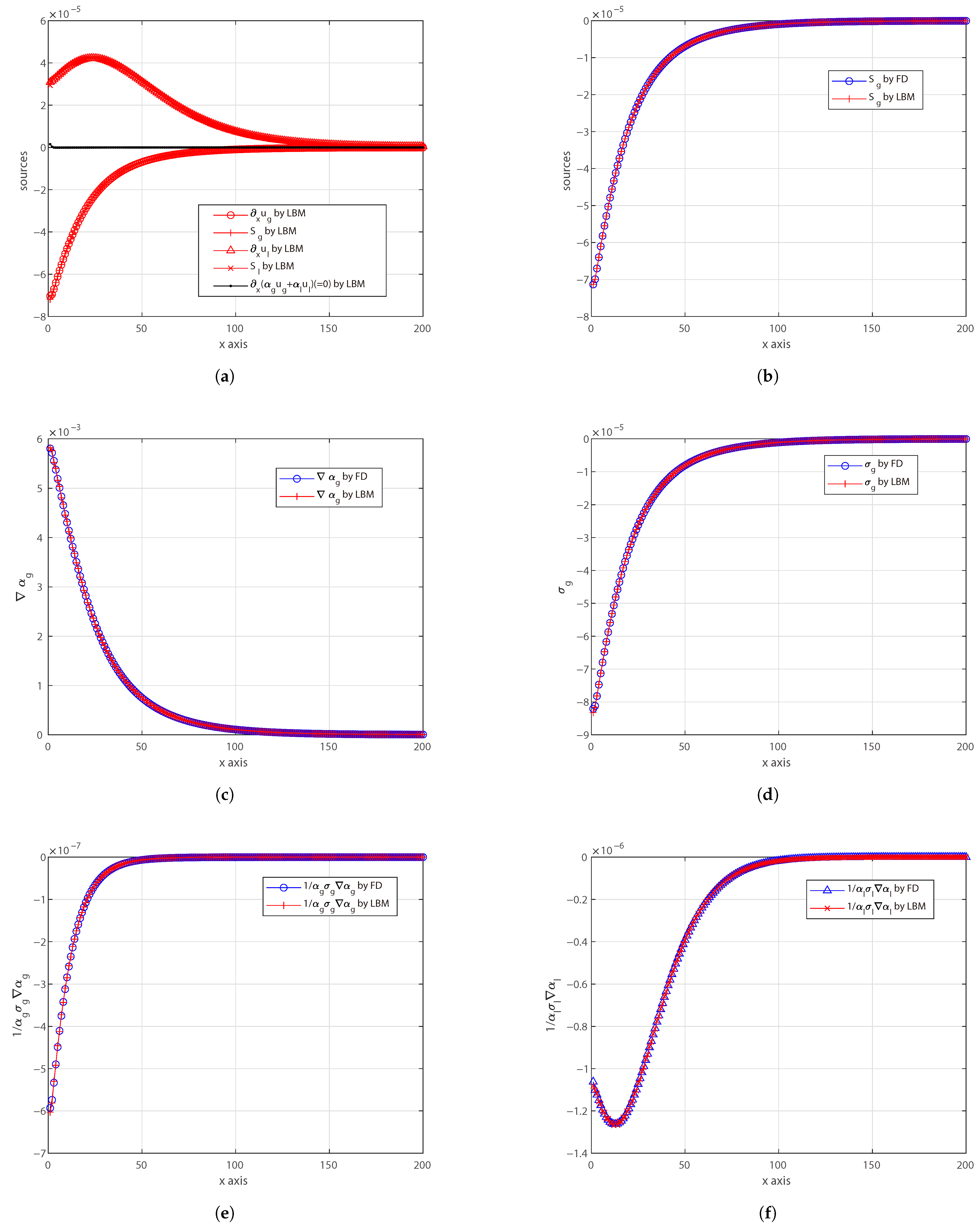
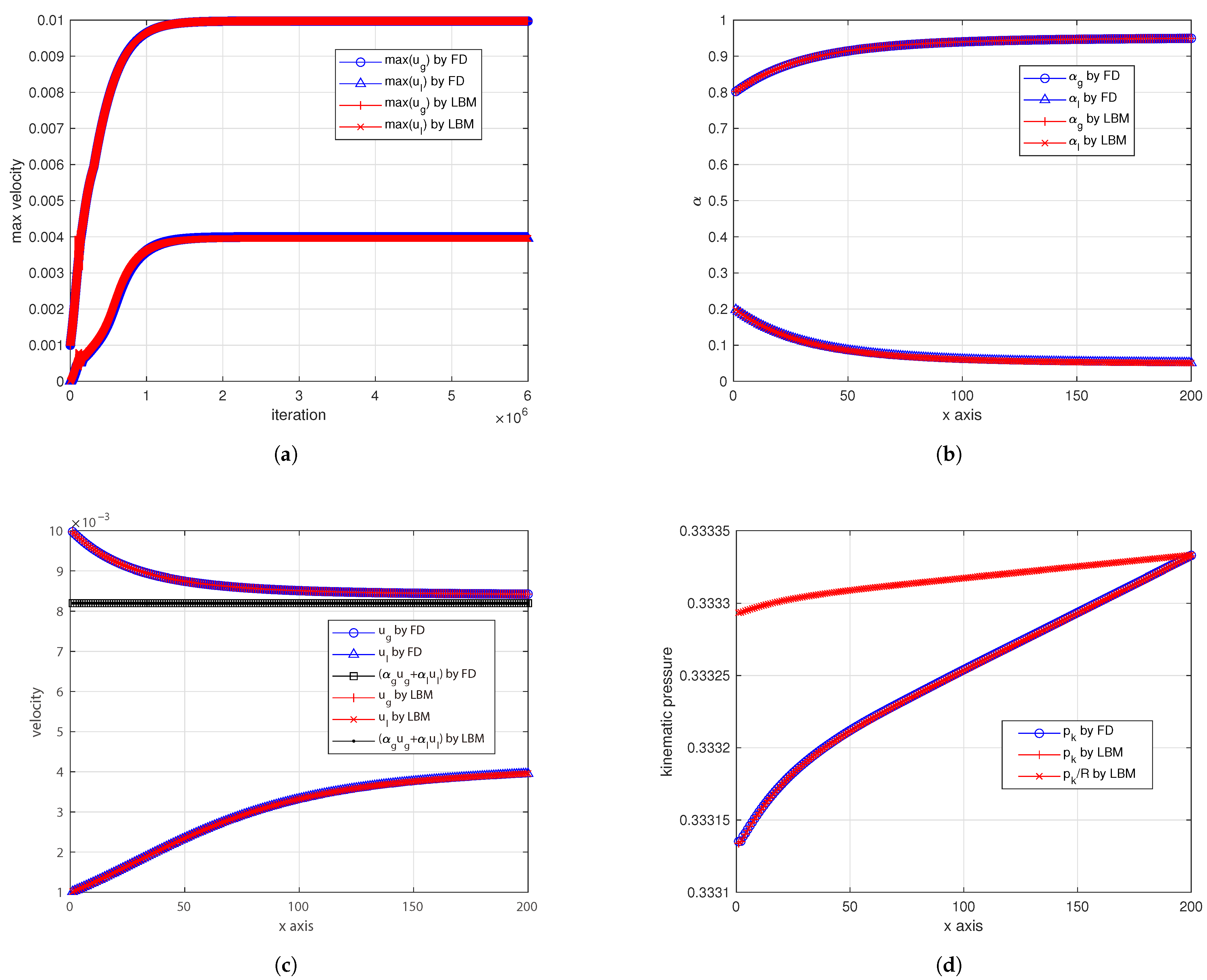
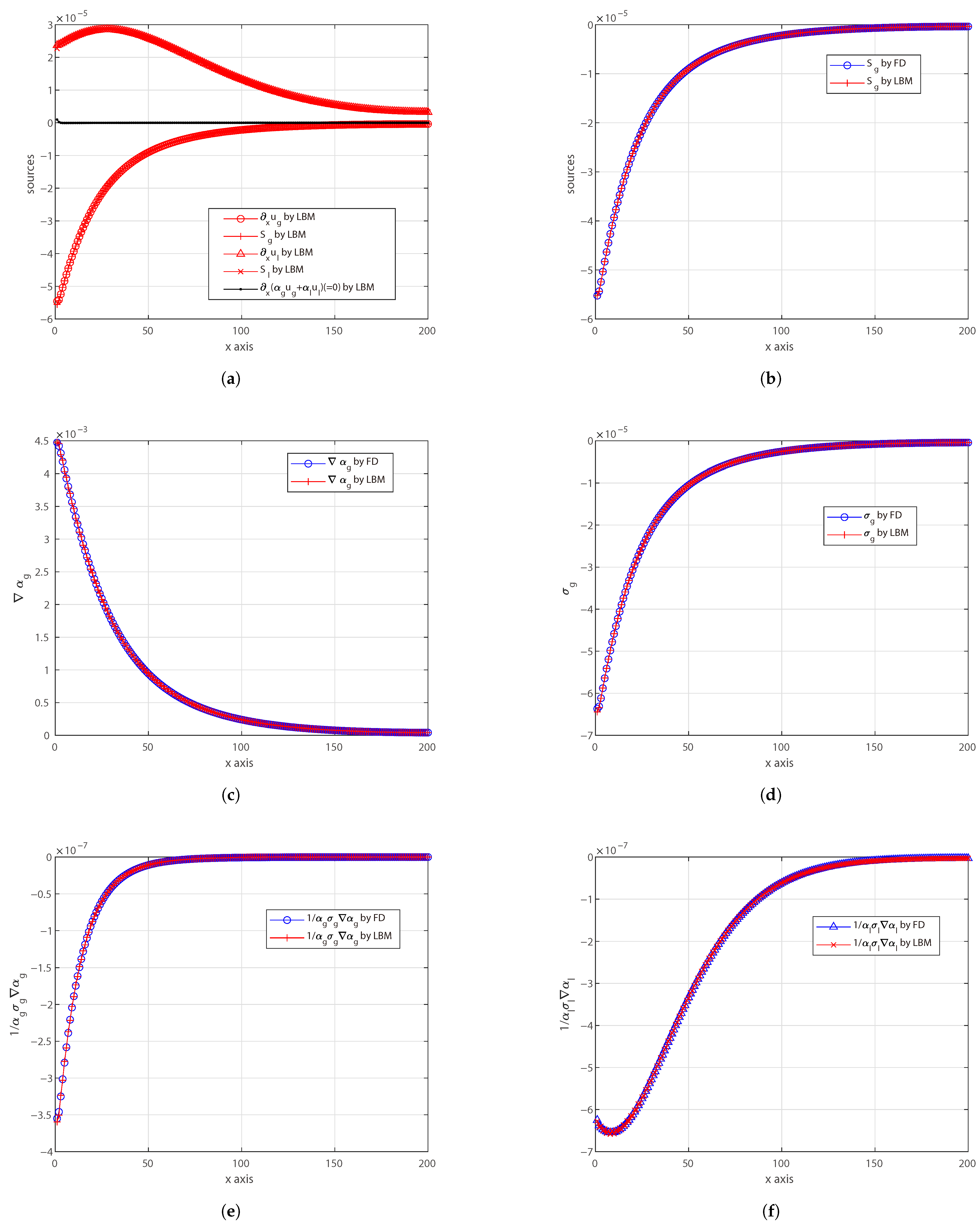
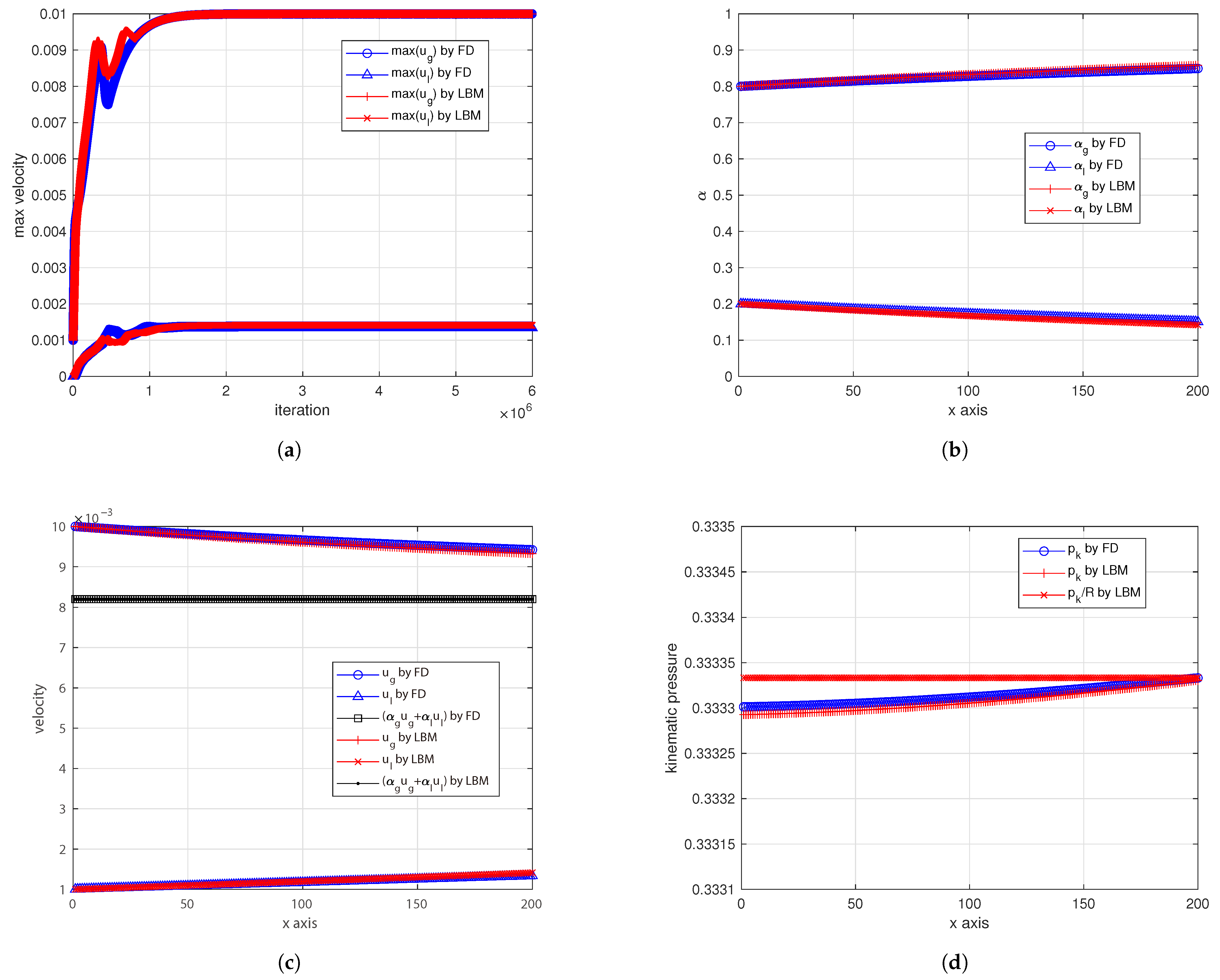
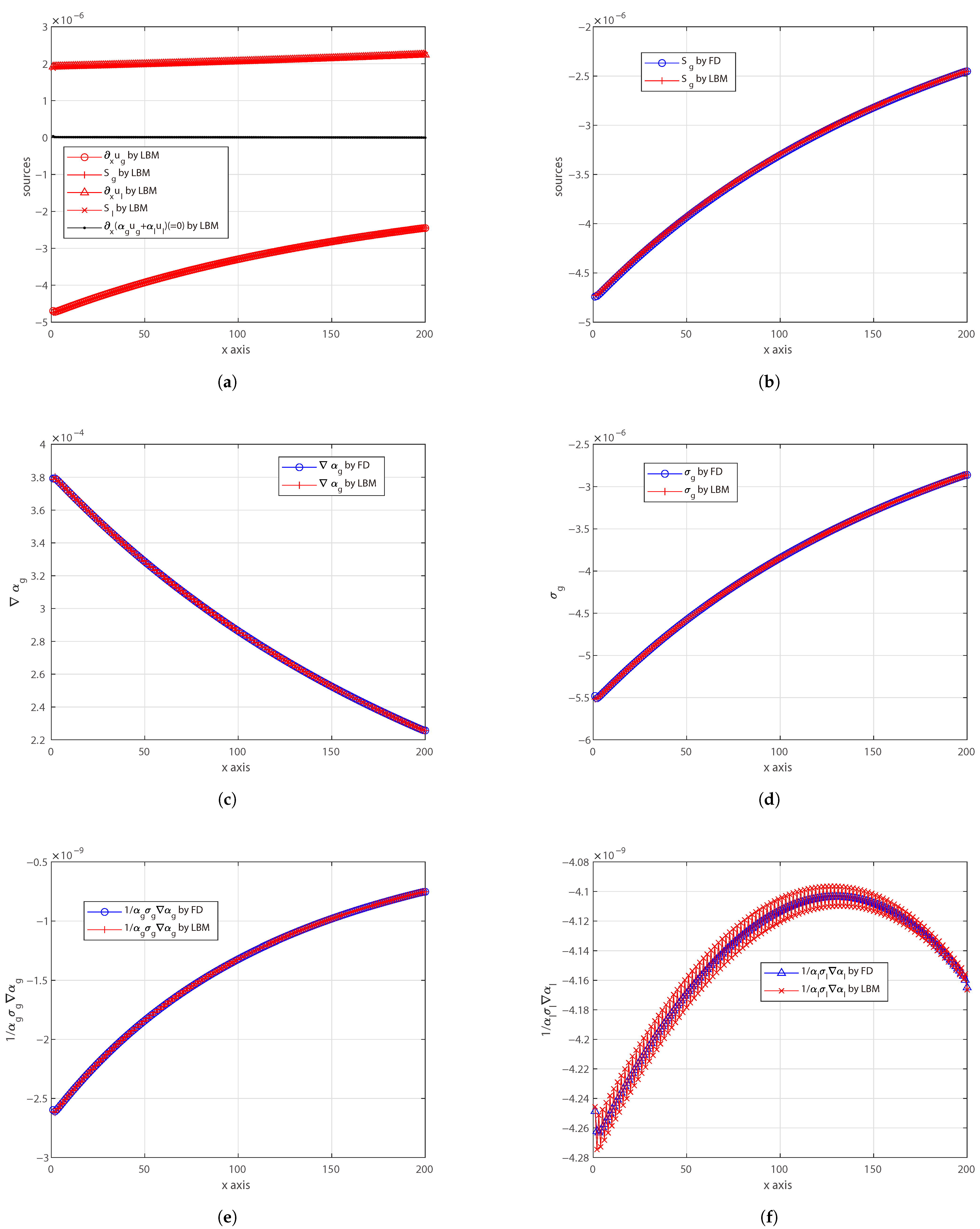
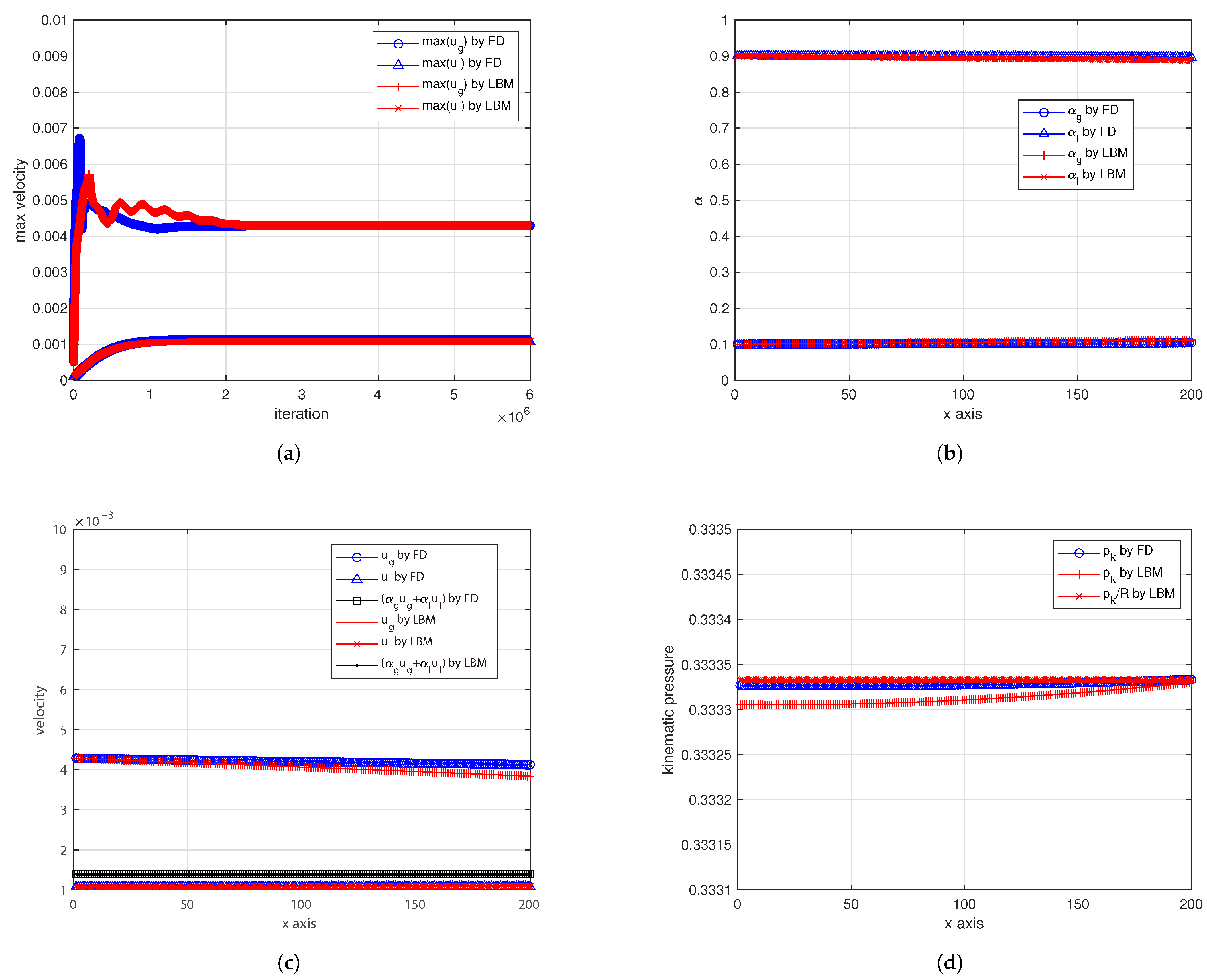
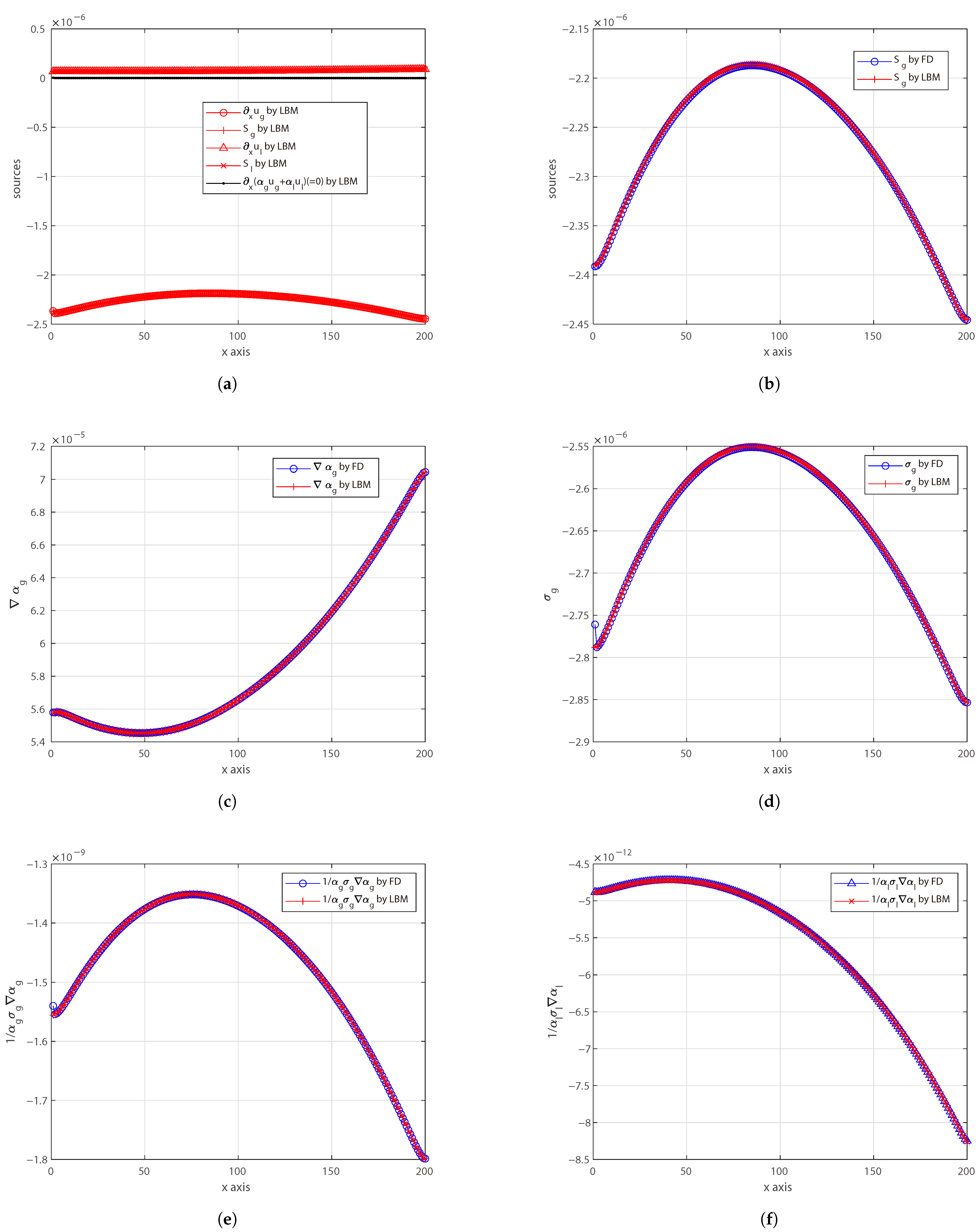
4. Conclusions

In spite of its apparent simplicity, the LBM requires a careful design of the overall framework to be used for solving complex systems of partial differential equations, as needed by multiphase flows. By framework, we mean (at least) the following information: minimum set of distribution functions, the definitions of the relevant target quantities as functions of the distribution functions (which are just auxiliaries), the definitions of the equilibrium distribution functions and how to compute them, including the proper equation of states, the proper additional forces, sources, etc. The framework is essential because the LBM is defined in an auxiliary space of variables and also, more importantly, because only a subset of this auxiliary space ensures stable calculations (e.g., zeroth-order moment of the distribution function usually must not be too small in order to avoid singularities, lattice sound speed cannot be too large, etc.).

For the first time to our knowledge, this work proposes a novel LBM framework to solve Eulerian–Eulerian multiphase flow equations without any finite difference correction, including very-large-density ratios and also a realistic model for the drag coefficient. The proposed methodology and all reported LBM formulas can be applied to any dimension. This opens a promising venue for simulating multiphase flows in large HPC facilities and on novel parallel hardware. This LBM framework consists of six LBM schemes for the two phases, so it naturally comes with a large memory footprint and a certain level of coding complexity. It includes the following: two LBM schemes ($f_g$ and $f_l$) for artificially compressible continuity equations and momentum equations; two LBM schemes ($f_{\alpha g}$ and $f_{\alpha l}$) for phase volume fractions; and two LBM schemes ($f_{\beta g}$ and $f_{\beta l}$) for phase continuity sources. All of these schemes are run on the same lattice and are coupled with each other, ensuring the best synergy for efficient implementation in large codes with minimum effort. Its memory-demanding nature, however, combined with the intrinsic locality of LBM operations, makes it particularly well-suited for HPC applications. Nonetheless, some limitations were observed. In simulations with very-high-density ratios, small mismatches in the volume fraction profiles—especially when the absolute value of ${\alpha }_g$ is small—may lead to a significant impact on the drag force computation, particularly when using realistic drag coefficient models. Furthermore, possible numerical instabilities might emerge when extending the model to multidimensional configurations. These aspects suggest directions for future refinement of the method.