Multiscale Modeling of Mechanical Response of Carbon Nanotube Yarn with Orthotropic Properties Across Hierarchies
Abstract
1. Introduction
2. Hierarchy in the Multiscale Model
2.1. Nanoscale Level
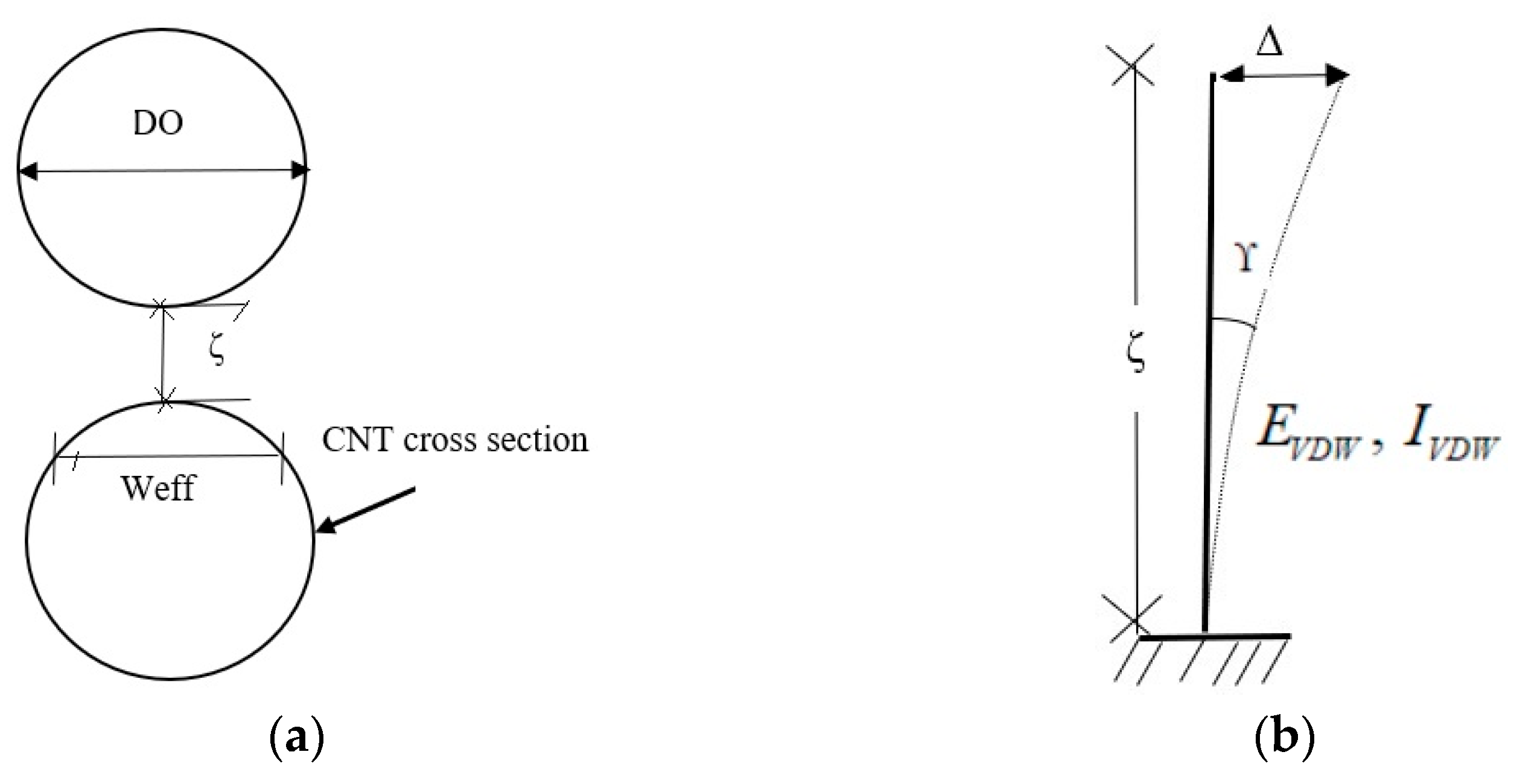
2.1.1. Geometric Definition of the CNT Bundle Structure
2.1.2. Mechanical Characterizations of vdW Force Interacting Between Pairs of Aligned CNTs Under Transverse Loading
2.1.3. Equivalent Shell Representing vdW Forces Between Adjacent CNTs
2.1.4. FE Modeling of CNT Bundle
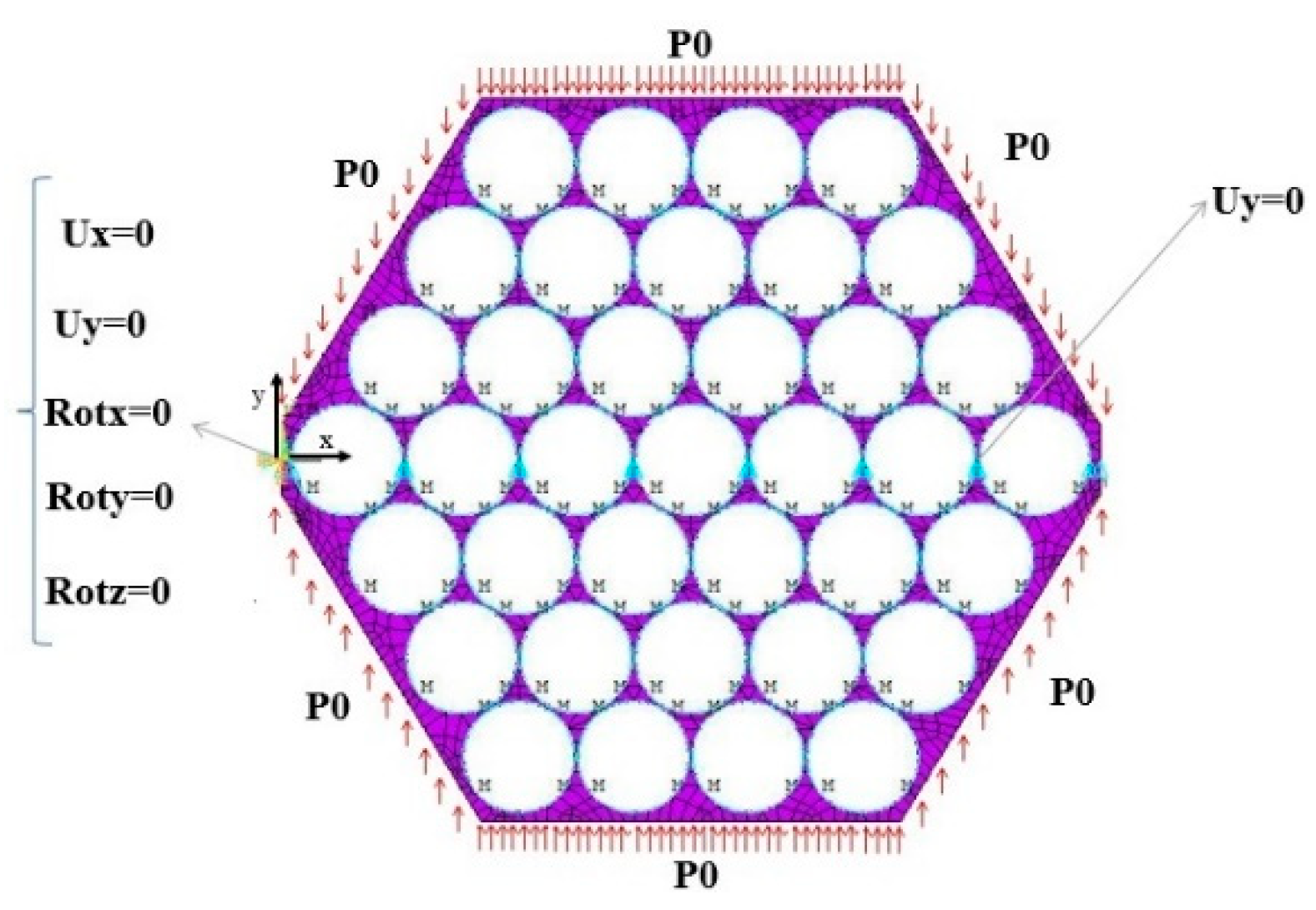
2.1.5. Assigned Boundary/Loading Conditions
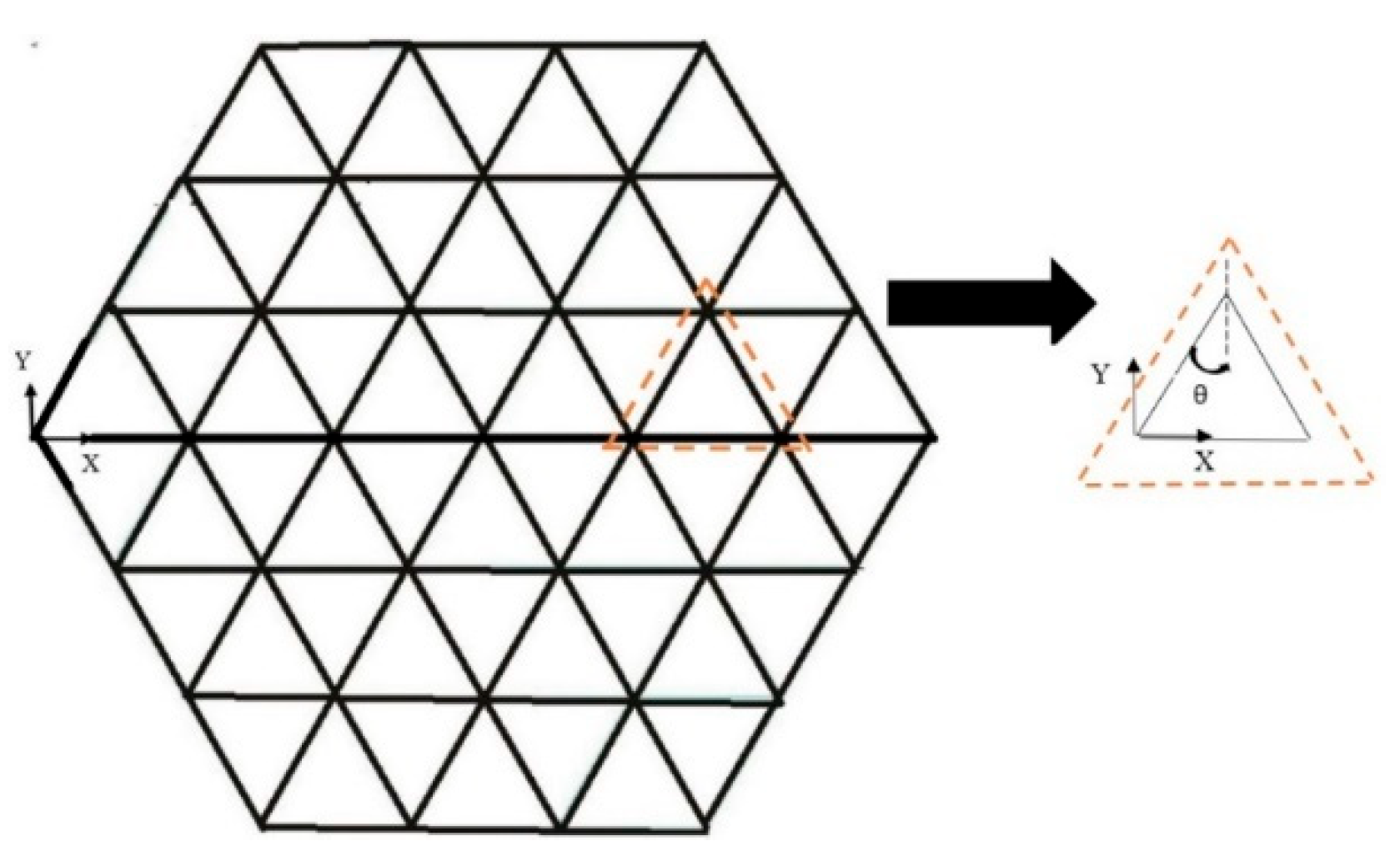
2.2. Mesoscale Level
2.2.1. Mechanical Modeling of CNT Fibrillar
2.2.2. FE Modeling of the CNT Fibrillar
2.3. Microscale Level
2.3.1. General Model to Simulate CNT Yarn
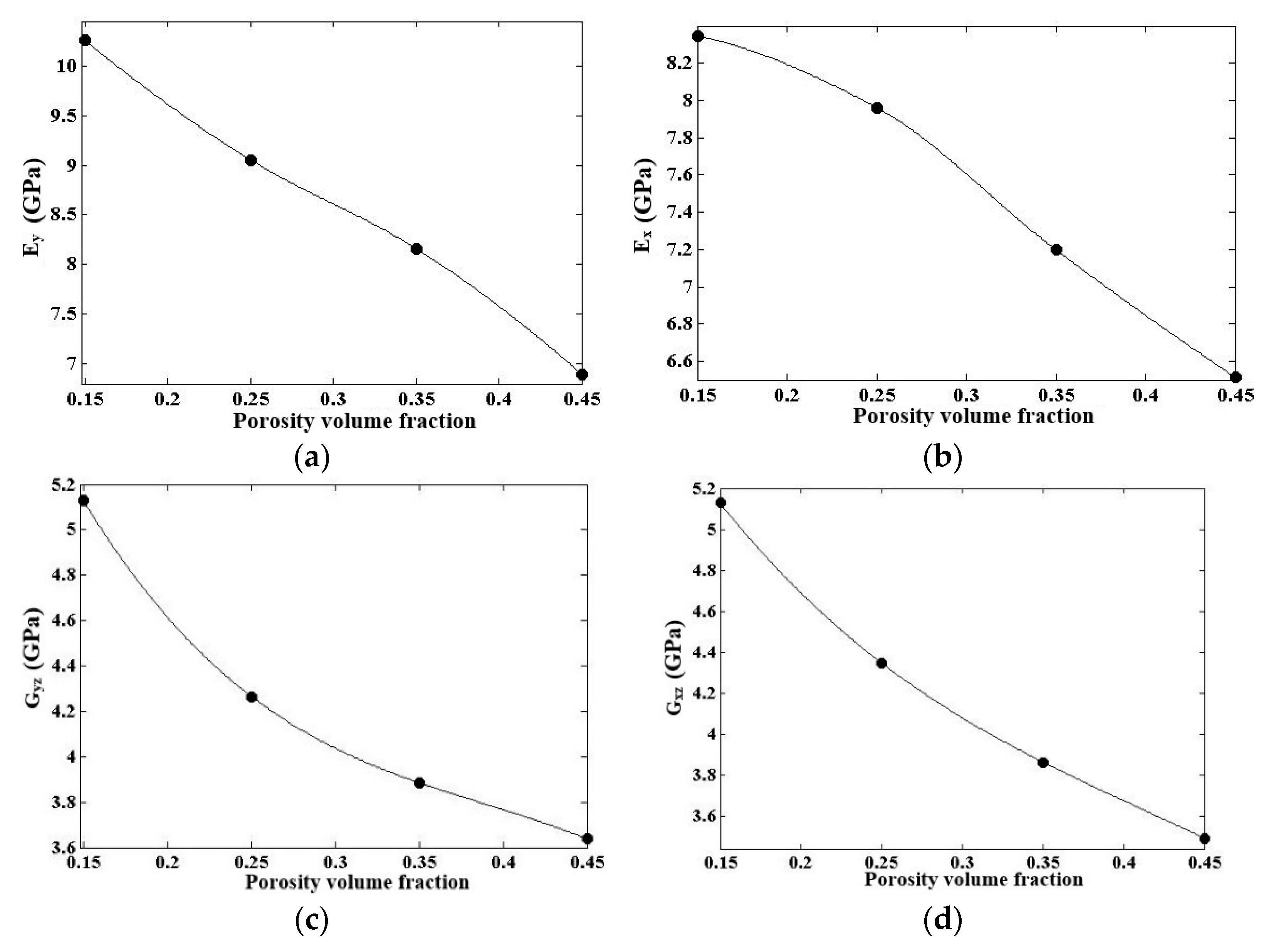
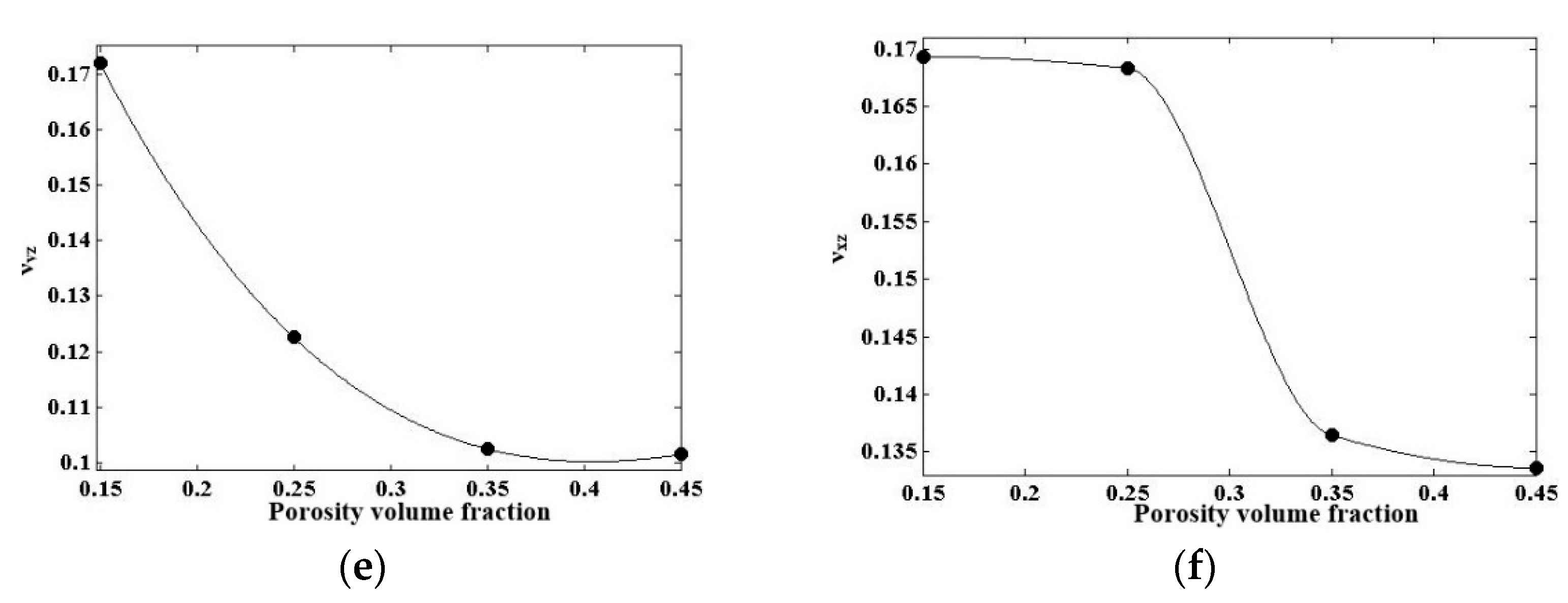
2.3.2. Incorporating Porosities Effects into the CNTY Model
3. Results
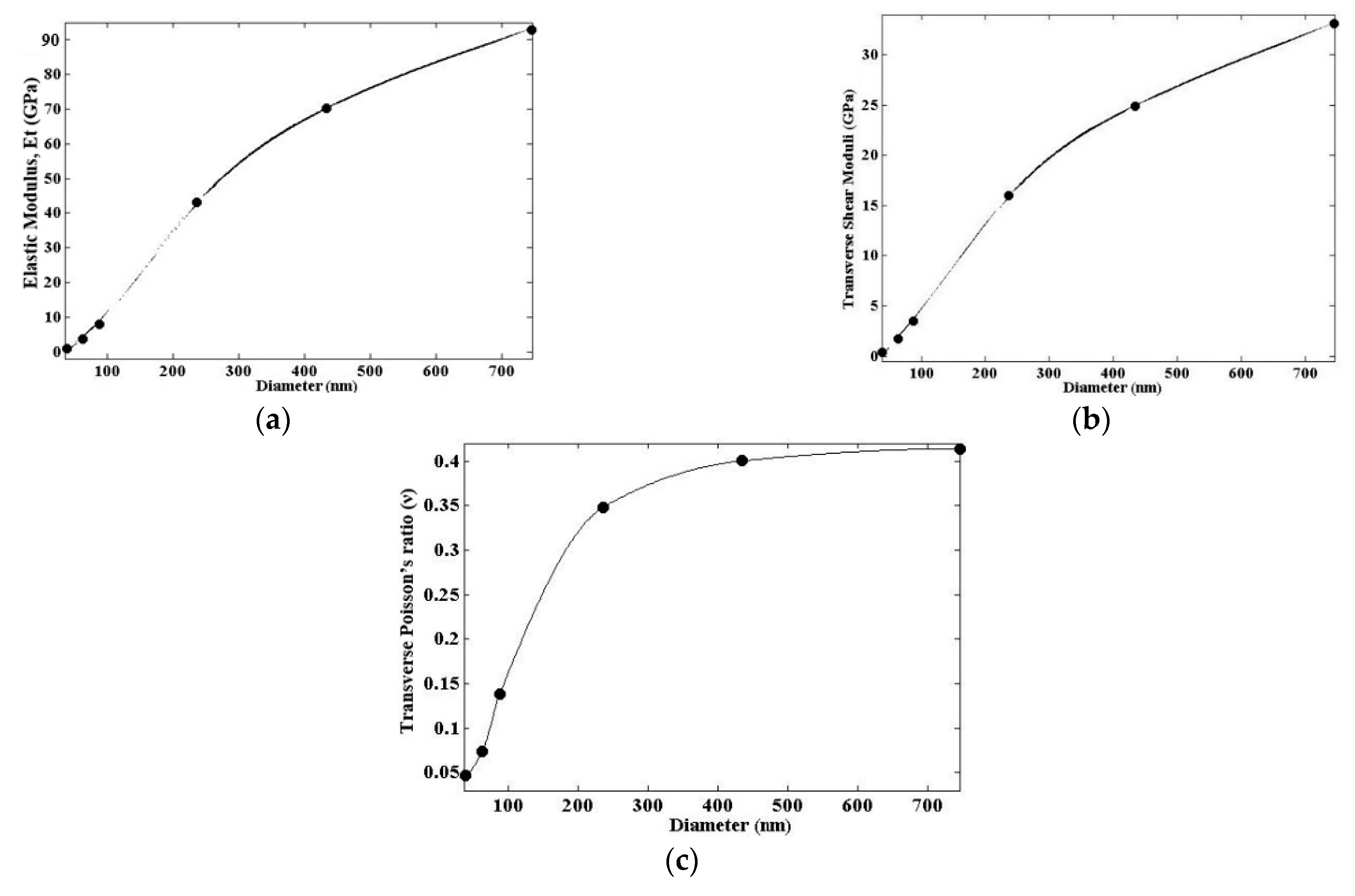
3.1. CNT Bundle
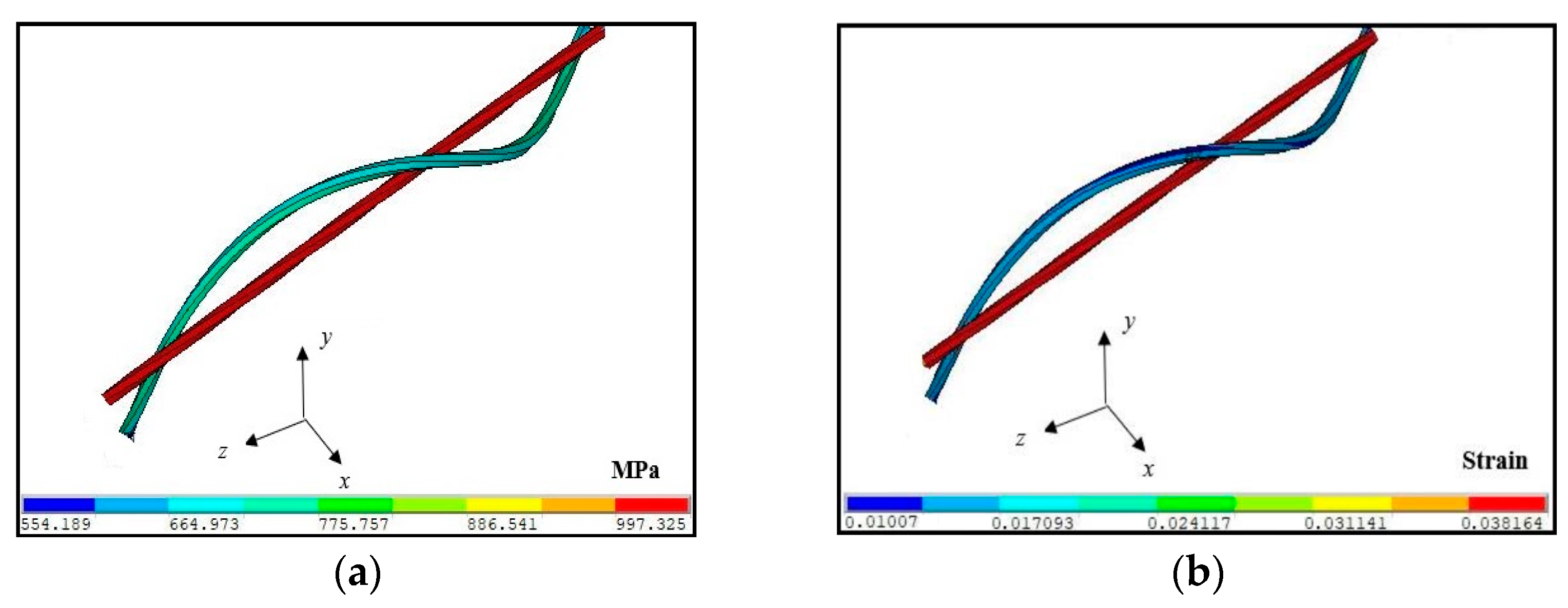
3.2. CNT Fibrillar
3.3. CNTY in Microscale Structure
Comparison with Experimental Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vilatela, J.J.; Windle, A.H. Yarn-like carbon nanotube fibers. Adv. Mater. 2010, 22, 4959–4963. [Google Scholar] [CrossRef] [PubMed]
- Cumings, J.; Zettl, A. Low-friction nanoscale linear bearing realized from multiwall carbon nanotubes. Science 2000, 289, 602–604. [Google Scholar] [CrossRef] [PubMed]
- Paci, J.T.; Furmanchuk, A.O.; Espinosa, H.D.; Schatz, G.C. Shear and friction between carbon nanotubes in bundles and yarns. Nano Lett. 2014, 14, 6138–6147. [Google Scholar] [CrossRef] [PubMed]
- Vilatela, J.J.; Elliott, J.A.; Windle, A.H. A model for the strength of yarn-like carbon nanotube fibers. ACS Nano 2011, 5, 1921–1927. [Google Scholar] [CrossRef]
- Samsonidze, G.G.; Samsonidze, G.G.; Yakobson, B.I. Kinetic theory of symmetry-dependent strength in carbon nanotubes. Phys. Rev. Lett. 2002, 88, 065501. [Google Scholar] [CrossRef]
- Shenderova, O.; Zhirnov, V.; Brenner, D. Carbon nanostructures. Crit. Rev. Solid State Mater. Sci. 2002, 27, 227–356. [Google Scholar] [CrossRef]
- Yu, M.-F. Fundamental mechanical properties of carbon nanotubes: Current understanding and the related experimental studies. J. Eng. Mater. Technol. 2004, 126, 271–278. [Google Scholar] [CrossRef]
- Yu, M.-F.; Lourie, O.; Dyer, M.J.; Moloni, K.; Kelly, T.F.; Ruoff, R.S. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load. Science 2000, 287, 637–640. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.-W. Elastic moduli of multi-walled carbon nanotubes and the effect of van der Waals forces. Compos. Sci. Technol. 2003, 63, 1517–1524. [Google Scholar] [CrossRef]
- Filleter, T.; Yockel, S.; Naraghi, M.; Paci, J.T.; Compton, O.C.; Mayes, M.L.; Nguyen, S.T.; Schatz, G.C.; Espinosa, H.D. Experimental-computational study of shear interactions within double-walled carbon nanotube bundles. Nano Lett. 2012, 12, 732–742. [Google Scholar] [CrossRef]
- Ghavamian, A.; Rahmandoust, M.; Öchsner, A. On the determination of the shear modulus of carbon nanotubes. Compos. Part B Eng. 2013, 44, 52–59. [Google Scholar] [CrossRef]
- Li, D.; Yang, Q.-S.; Liu, X.; Shang, J.-J. Experimental investigation on tensile properties of carbon nanotube wires. Mech. Mater. 2017, 105, 42–48. [Google Scholar] [CrossRef]
- Beese, A.M.; Wei, X.; Sarkar, S.; Ramachandramoorthy, R.; Roenbeck, M.R.; Moravsky, A.; Ford, M.; Yavari, F.; Keane, D.T.; Loutfy, R.O. Key factors limiting carbon nanotube yarn strength: Exploring processing-structure-property relationships. ACS Nano 2014, 8, 11454–11466. [Google Scholar] [CrossRef]
- Galiakhmetova, L.K.; Bachurin, D.; Korznikova, E.; Bayazitov, A.; Kudreyko, A.; Dmitriev, S. Shock loading of carbon nanotube bundle. Mech. Mater. 2022, 174, 104460. [Google Scholar] [CrossRef]
- Naraghi, M.; Bratzel, G.H.; Filleter, T.; An, Z.; Wei, X.; Nguyen, S.T.; Buehler, M.J.; Espinosa, H.D. Atomistic investigation of load transfer between DWNT bundles “crosslinked” by PMMA oligomers. Adv. Funct. Mater. 2013, 23, 1883–1892. [Google Scholar] [CrossRef]
- Miao, M.; McDonnell, J.; Vuckovic, L.; Hawkins, S.C. Poisson’s ratio and porosity of carbon nanotube dry-spun yarns. Carbon 2010, 48, 2802–2811. [Google Scholar] [CrossRef]
- Hu, X.; Zheng, Y.; Sun, G.; Wang, P. Understanding the torsional mechanical behavior of twisting carbon nanotube ribbon with different boundary conditions. Mech. Mater. 2024, 190, 104906. [Google Scholar] [CrossRef]
- Abdullina, D.U.; Korznikova, E.A.; Dubinko, V.I.; Laptev, D.V.; Kudreyko, A.A.; Soboleva, E.G.; Dmitriev, S.V.; Zhou, K. Mechanical response of carbon nanotube bundle to lateral compression. Computation 2020, 8, 27. [Google Scholar] [CrossRef]
- Wei, H.; Ting, H.Z.J.; Gong, Y.; Lü, C.; Glukhova, O.E.; Zhan, H. Torsional Properties of Bundles with Randomly Packed Carbon Nanotubes. Nanomaterials 2022, 12, 760. [Google Scholar] [CrossRef]
- Park, J.; Lee, J.; Lee, D.-M.; Lee, S.-H.; Jeong, H.S.; Lee, K.-H.; Kim, S.M. Mathematical model for the dynamic mechanical behavior of carbon nanotube yarn in analogy with hierarchically structured bio-materials. Carbon 2019, 152, 151–158. [Google Scholar] [CrossRef]
- Kim, J.-G.; Suh, D.; Kang, H. Large variation in Young’s modulus of carbon nanotube yarns with different diameters. Curr. Appl. Phys. 2021, 21, 96–100. [Google Scholar] [CrossRef]
- Zhang, W.; Xi, A.; Siriguleng, B.; Liu, G. An equivalent cylindrical shell model of vibration analysis based on simplified repeating unit cell for ring truss structure. J. Sound Vib. 2019, 459, 114847. [Google Scholar] [CrossRef]
- Johnston, E.R.J.; DeWolf, J.T.; Beer, F.P. Mechanics of Materials; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Lu, J.P. Elastic properties of carbon nanotubes and nanoropes. Phys. Rev. Lett. 1997, 79, 1297. [Google Scholar] [CrossRef]
- Li, H.; Guo, W. Transversely isotropic elastic properties of single-walled carbon nanotubes by a rectangular beam model for the C-C bonds. J. Appl. Phys. 2008, 103, 103501. [Google Scholar] [CrossRef]
- Pirmoz, A.; Abot, J.; Avilés, F. Simulation of mechanical response of carbon nanotube yarns under uniaxial tensile loading. Mech. Mater. 2022, 165, 104144. [Google Scholar] [CrossRef]
- Lekawa-Raus, A.; Koziol, K.K.; Windle, A.H. Piezoresistive effect in carbon nanotube fibers. ACS Nano 2014, 8, 11214–11224. [Google Scholar] [CrossRef]
- Palaci, I.; Fedrigo, S.; Brune, H.; Klinke, C.; Chen, M.; Riedo, E. Radial elasticity of multiwalled carbon nanotubes. Phys. Rev. Lett. 2005, 94, 175502. [Google Scholar] [CrossRef]
- Anike, J.C. Carbon Nanotube Yarns: Tailoring Their Piezoresistive Response Towards Sensing Applications. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 2018. [Google Scholar]






| Membrane Stiffness | |
|---|---|
| where | |
| Elastic Moduli (GPa) | Shear Moduli (GPa) | Poisson’s Ratios | |||
|---|---|---|---|---|---|
| Ey | Ex | Gyx | Gxz | νyz | νxz |
| 6.898 | 6.514 | 3.637 | 3.490 | 0.145 | 0.134 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehditabar, A.; Esfandian, H.; Hasankola, S.S.M. Multiscale Modeling of Mechanical Response of Carbon Nanotube Yarn with Orthotropic Properties Across Hierarchies. Computation 2025, 13, 119. https://doi.org/10.3390/computation13050119
Mehditabar A, Esfandian H, Hasankola SSM. Multiscale Modeling of Mechanical Response of Carbon Nanotube Yarn with Orthotropic Properties Across Hierarchies. Computation. 2025; 13(5):119. https://doi.org/10.3390/computation13050119
Chicago/Turabian StyleMehditabar, Aref, Hossein Esfandian, and Seyed Sadegh Motallebi Hasankola. 2025. "Multiscale Modeling of Mechanical Response of Carbon Nanotube Yarn with Orthotropic Properties Across Hierarchies" Computation 13, no. 5: 119. https://doi.org/10.3390/computation13050119
APA StyleMehditabar, A., Esfandian, H., & Hasankola, S. S. M. (2025). Multiscale Modeling of Mechanical Response of Carbon Nanotube Yarn with Orthotropic Properties Across Hierarchies. Computation, 13(5), 119. https://doi.org/10.3390/computation13050119







