Rigorous Asymptotic Perturbation Bounds for Hermitian Matrix Eigendecompositions
Abstract
1. Introduction
2. Asymptotic Perturbation Bounds
2.1. Asymptotic Bounds for the Perturbation Parameters
2.2. Asymptotic Componentwise Eigenvector Bounds
2.3. Eigenvalue Sensitivity
2.4. Sensitivity of One-Dimensional Invariant Subspaces
3. Probabilistic Asymptotic Bounds
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| , | the set of complex numbers; |
| , | the space of complex matrices; |
| , | a matrix with entries ; |
| , | the jth column of A; |
| , | the ith row of an matrix A; |
| , | the jth column of an matrix A; |
| , | the strictly lower triangular part of A; |
| , | the matrix of absolute values of the elements of A; |
| , | the Hermitian transpose of A; |
| , | the zero matrix; |
| , | the identity matrix; |
| , | the perturbation of A; |
| , | the spectral norm of A; |
| , | the Frobenius norm of A; |
| , | equality by definition; |
| ⪯, | partial order: if , then means ; |
| , | the subspace spanned by the columns of X; |
| , | the orthogonal complement of U, ; |
References
- Kato, T. Perturbation Theory for Linear Operators, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1995; ISBN 978-0-540-58661-6. [Google Scholar]
- Wilkinson, J. The Algebraic Eigenvalue Problem; Clarendon Press: Oxford, UK, 1965; ISBN 978-0-19-853418-1. [Google Scholar]
- Parlett, B.N. The Symmetric Eigenvalue Problem; Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar] [CrossRef]
- Stewart, G.W.; Sun, J.-G. Matrix Perturbation Theory; Academic Press: New York, NY, USA, 1990; ISBN 978-0126702309. [Google Scholar]
- Bhatia, R. Perturbation Bounds for Matrix Eigenvalues; Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; ISBN 978-0-898716-31-3. [Google Scholar] [CrossRef]
- Stewart, G. Matrix Algorithms; Vol. II: Eigensystems; SIAM: Philadelphia, PA, USA, 2001; ISBN 0-89871-503-2. [Google Scholar]
- Chatelin, F. Eigenvalues of Matrices; Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 2012; ISBN 978-1-611972-45-0. [Google Scholar] [CrossRef]
- Sun, J.-G. Stability and Accuracy. Perturbation Analysis of Algebraic Eigenproblems; Technical Report; Department of Computing Science, Umeå University: Umeå, Sweden, 1998; pp. 1–210. [Google Scholar]
- Li, R. Matrix perturbation theory. In Handbook of Linear Algebra, 2nd ed.; Hogben, L., Ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 21-1–21-20. [Google Scholar]
- Barlow, J.; Slapničar, I. Optimal perturbation bounds for the Hermitian eigenvalue problem. Linear Algebra Appl. 2000, 309, 19–43. [Google Scholar] [CrossRef]
- Mathias, R. Quadratic residual bounds for the Hermitian eigenvalue problem. SIAM J. Matrix Anal. Appl. 1998, 19, 541–550. [Google Scholar] [CrossRef]
- Stewart, G.W. Error and perturbation bounds for subspaces associated with certain eigenvalue problems. SIAM Rev. 1973, 15, 727–764. [Google Scholar] [CrossRef]
- Sun, J.-G. Perturbation expansions for invariant subspaces. Linear Algebra Appl. 1991, 153, 85–97. [Google Scholar] [CrossRef]
- Ipsen, I.C.F. An overview of relative sin(Θ) theorems for invariant subspaces of complex matrices. J. Comp. Appl. Math. 2000, 123, 131–153. [Google Scholar] [CrossRef]
- Veselić, K.; Slapničar, I. Floating-point perturbations of Hermitian matrices. Linear Algebra Appl. 1993, 195, 81–116. [Google Scholar] [CrossRef]
- Greenbaum, A.; Li, R.-C.; Overton, M.L. First-order perturbation theory for eigenvalues and eigenvectors. SIAM Rev. 2020, 62, 463–482. [Google Scholar] [CrossRef]
- Barbarino, G.; Serra–Capizzano, S. Non-Hermitian perturbations of Hermitian matrix–sequences and applications to the spectral analysis of the numerical approximation of partial differential equations. Numer. Linear Algebra Appl. 2020, 27, 31. [Google Scholar] [CrossRef]
- Davis, C.; Kahan, W.M. The Rotation of Eigenvectors by a Perturbation. III. SIAM J. Numer. Anal. 1970, 7, 1–46. [Google Scholar] [CrossRef]
- Nakatsukasa, Y. Sharp error bounds for Ritz vectors and approximate singular vectors. Math. Comput. 2018, 89, 1843–1866. [Google Scholar] [CrossRef]
- Wang, W.-G.; Wei, Y. Mixed and componentwise condition numbers for matrix decompositions. Theor. Comput. Sci. 2017, 681, 199–216. [Google Scholar] [CrossRef]
- Carlsson, M. Spectral perturbation theory of Hermitian matrices. In Bridging Eigenvalue Theory and Practice—Applications in Modern Engineering; Carpentieri, B., Ed.; IntechOpen: London, UK, 2025; ISBN 978-1-83634-248-9. [Google Scholar] [CrossRef]
- Li, R.-C.; Nakatsukasa, Y.; Truhar, N.; Wang, W.-G. Perturbation of multiple eigenvalues of Hermitian matrices. Linear Algebra Appl. 2012, 437, 202–213. [Google Scholar] [CrossRef]
- Konstantinov, M.; Petkov, P. Perturbation Methods in Matrix Analysis and Control; NOVA Science Publishers, Inc.: New York, NY, USA, 2020; Available online: https://novapublishers.com/shop/perturbation-methods-in-matrix-analysis-and-control (accessed on 4 October 2025).
- Petkov, P. Componentwise perturbation analysis of the Schur decomposition of a matrix. SIAM J. Matrix Anal. Appl. 2021, 42, 108–133. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 2013; ISBN 978-1-4214-0794-4. [Google Scholar]
- The MathWorks, Inc. MATLAB, Version 9.9.0.1538559 (R2020b); The MathWorks, Inc.: Natick, MA, USA, 2020. Available online: https://www.mathworks.com (accessed on 4 October 2025).
- Björck, A.; Golub, G. Numerical methods for computing angles between linear subspaces. Math. Comp. 1973, 27, 579–594. [Google Scholar] [CrossRef]
- Bai, Z.; Demmel, J.; Mckenney, A. On computing condition numbers for the nonsymmetric eigenproblem. ACM Trans. Math. Softw. 1993, 19, 202–223. [Google Scholar] [CrossRef]
- Petkov, P. Probabilistic perturbation bounds of matrix decompositions. Numer. Linear Algebra Appl. 2024, 31, 1–40. [Google Scholar] [CrossRef]
- Petkov, P. Probabilistic perturbation bounds for invariant, deflating and singular subspaces. Axioms 2024, 13, 597. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables and Stochastic Processes, 3rd ed.; McGraw Hill, Inc.: New York, NY, USA, 1991; ISBN 0-07-048477-5. [Google Scholar]
- Zhang, G.; Li, H.; Wei, Y. Componentwise perturbation analysis for the generalized Schur decomposition. Calcolo 2022, 59, 19. [Google Scholar] [CrossRef]
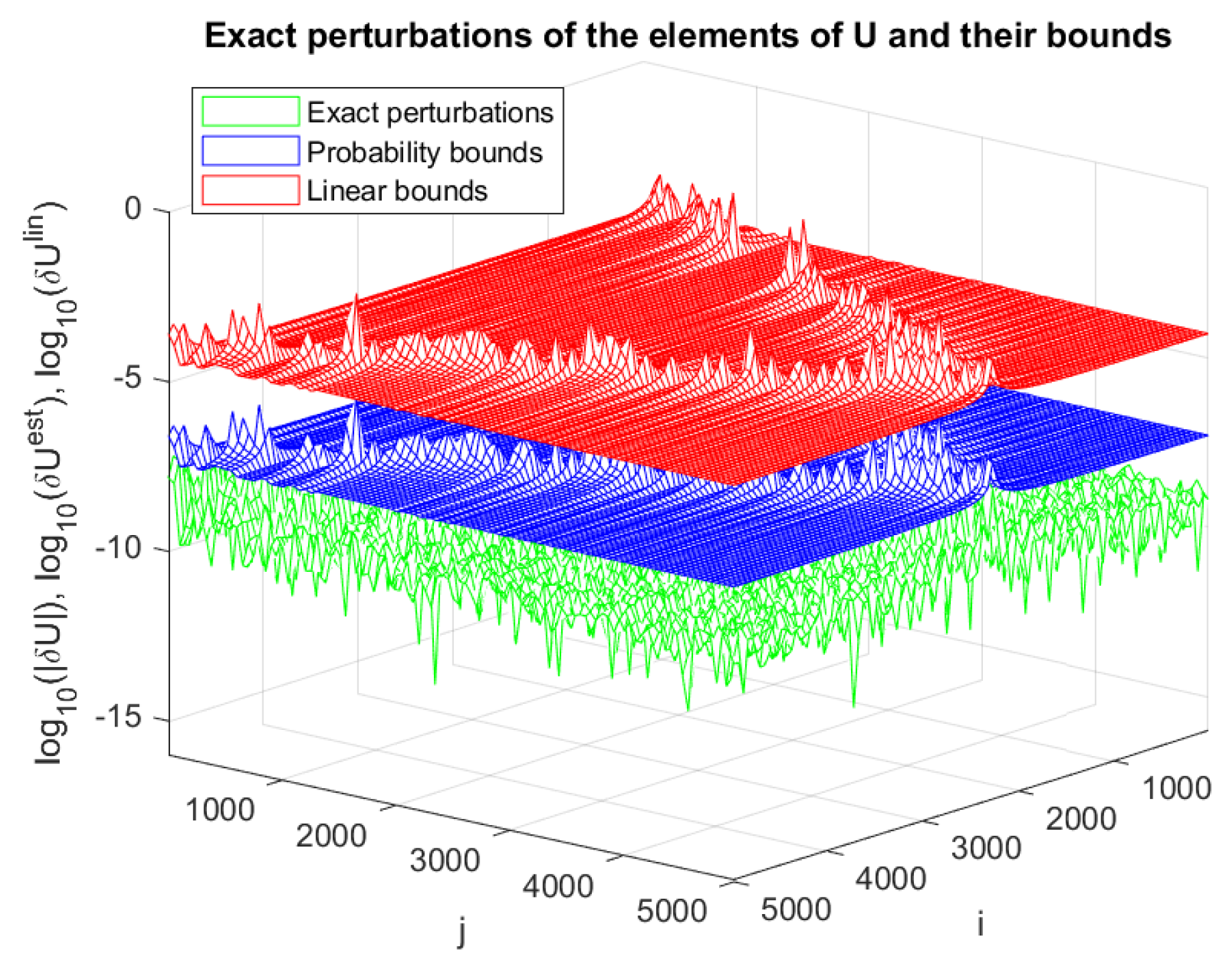




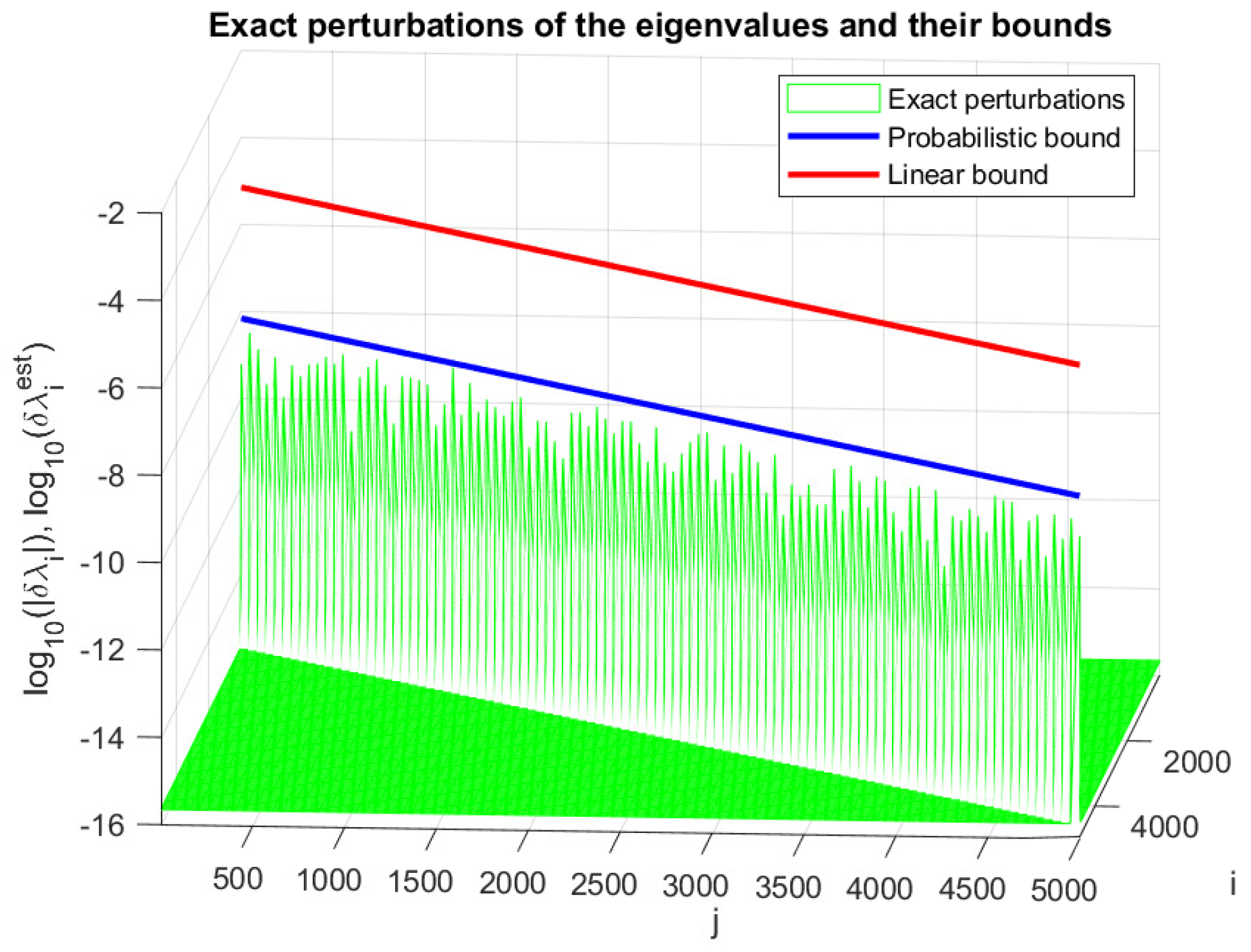
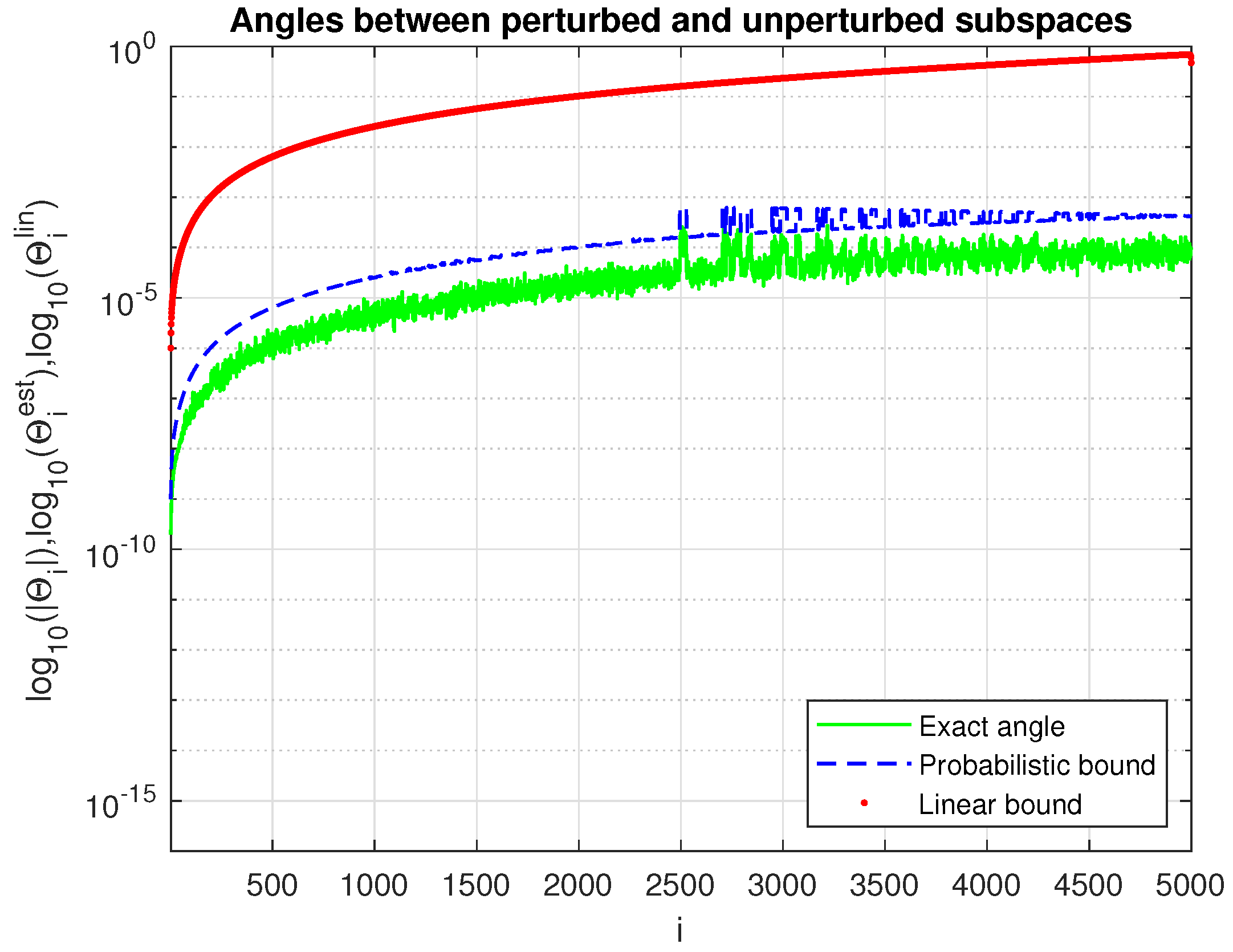
| j | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstantinov, M.; Petkov, P.H. Rigorous Asymptotic Perturbation Bounds for Hermitian Matrix Eigendecompositions. Computation 2025, 13, 237. https://doi.org/10.3390/computation13100237
Konstantinov M, Petkov PH. Rigorous Asymptotic Perturbation Bounds for Hermitian Matrix Eigendecompositions. Computation. 2025; 13(10):237. https://doi.org/10.3390/computation13100237
Chicago/Turabian StyleKonstantinov, Mihail, and Petko Hristov Petkov. 2025. "Rigorous Asymptotic Perturbation Bounds for Hermitian Matrix Eigendecompositions" Computation 13, no. 10: 237. https://doi.org/10.3390/computation13100237
APA StyleKonstantinov, M., & Petkov, P. H. (2025). Rigorous Asymptotic Perturbation Bounds for Hermitian Matrix Eigendecompositions. Computation, 13(10), 237. https://doi.org/10.3390/computation13100237





