Beyond the Gold Standard: Linear Regression and Poisson GLM Yield Identical Mortality Trends and Deaths Counts for COVID-19 in Italy: 2021–2025
Abstract
1. Introduction
2. Materials and Methods
2.1. Sources of COVID-19 Deaths Data
2.2. Linear Regression Fit to COVID-19 Deaths Data
2.3. Statistical Tests for Linear Regression on COVID-19 Mortality Data
2.4. Developing a Poisson GLM for COVID-19 Deaths Data
3. Results
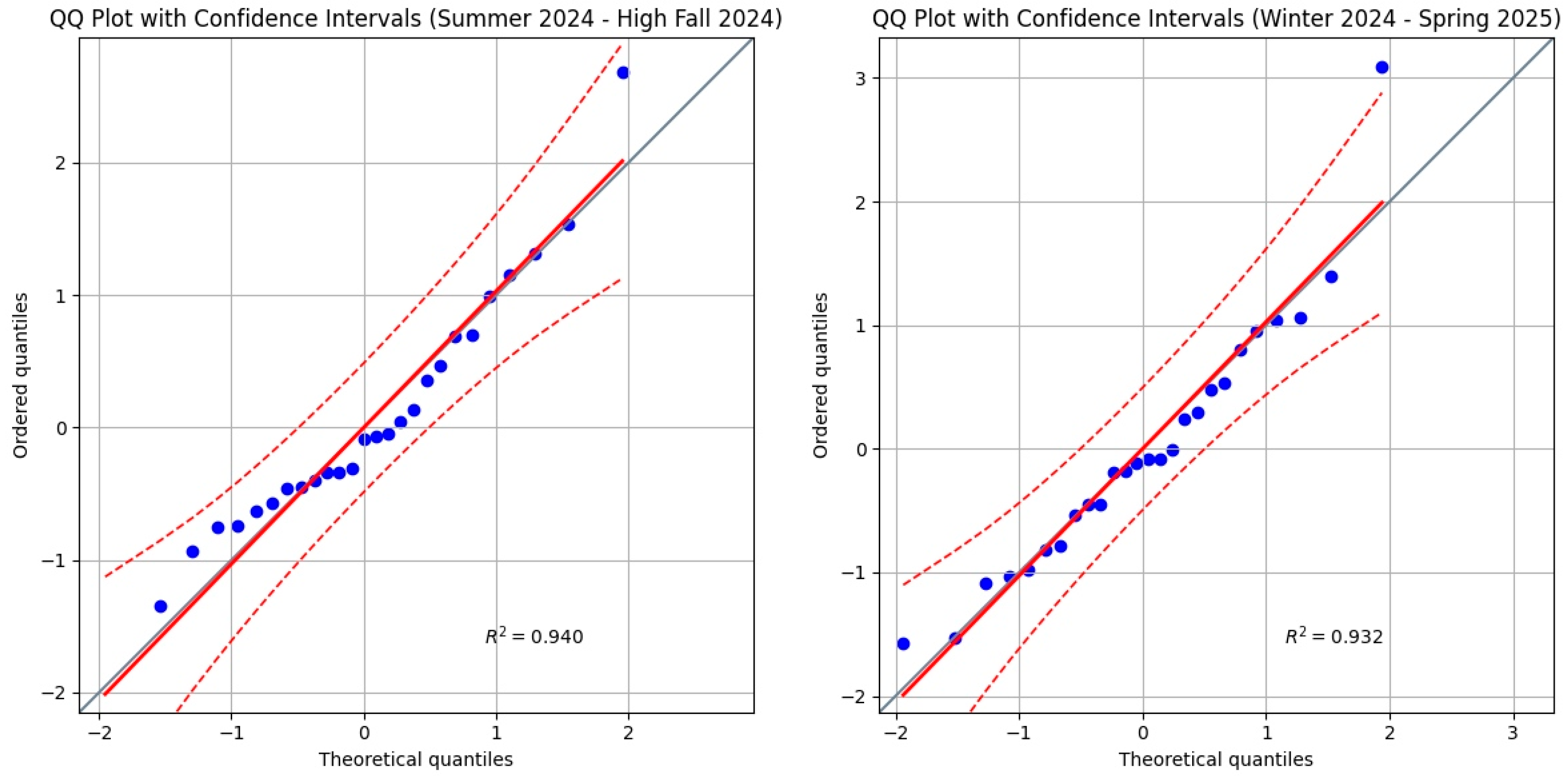
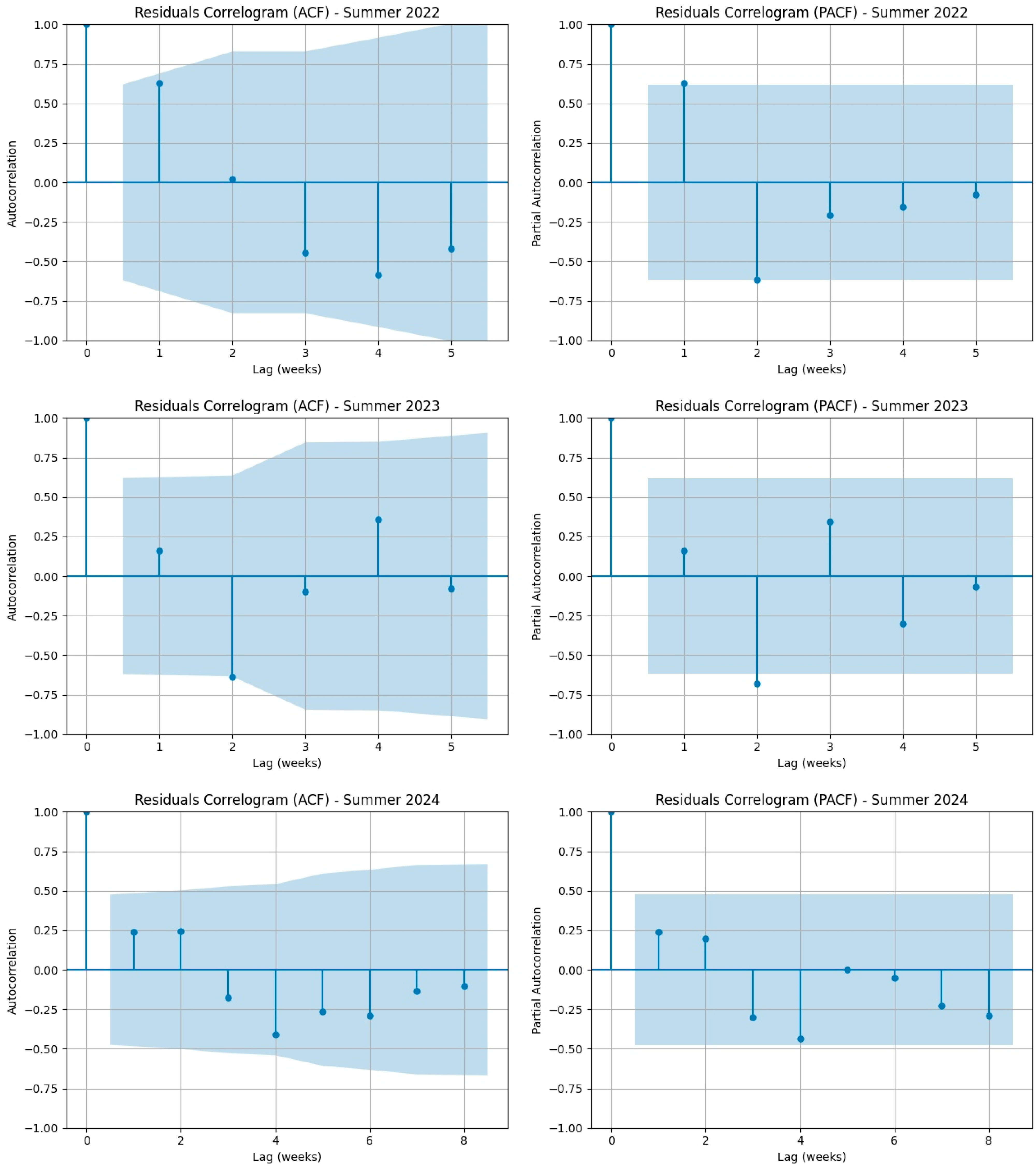
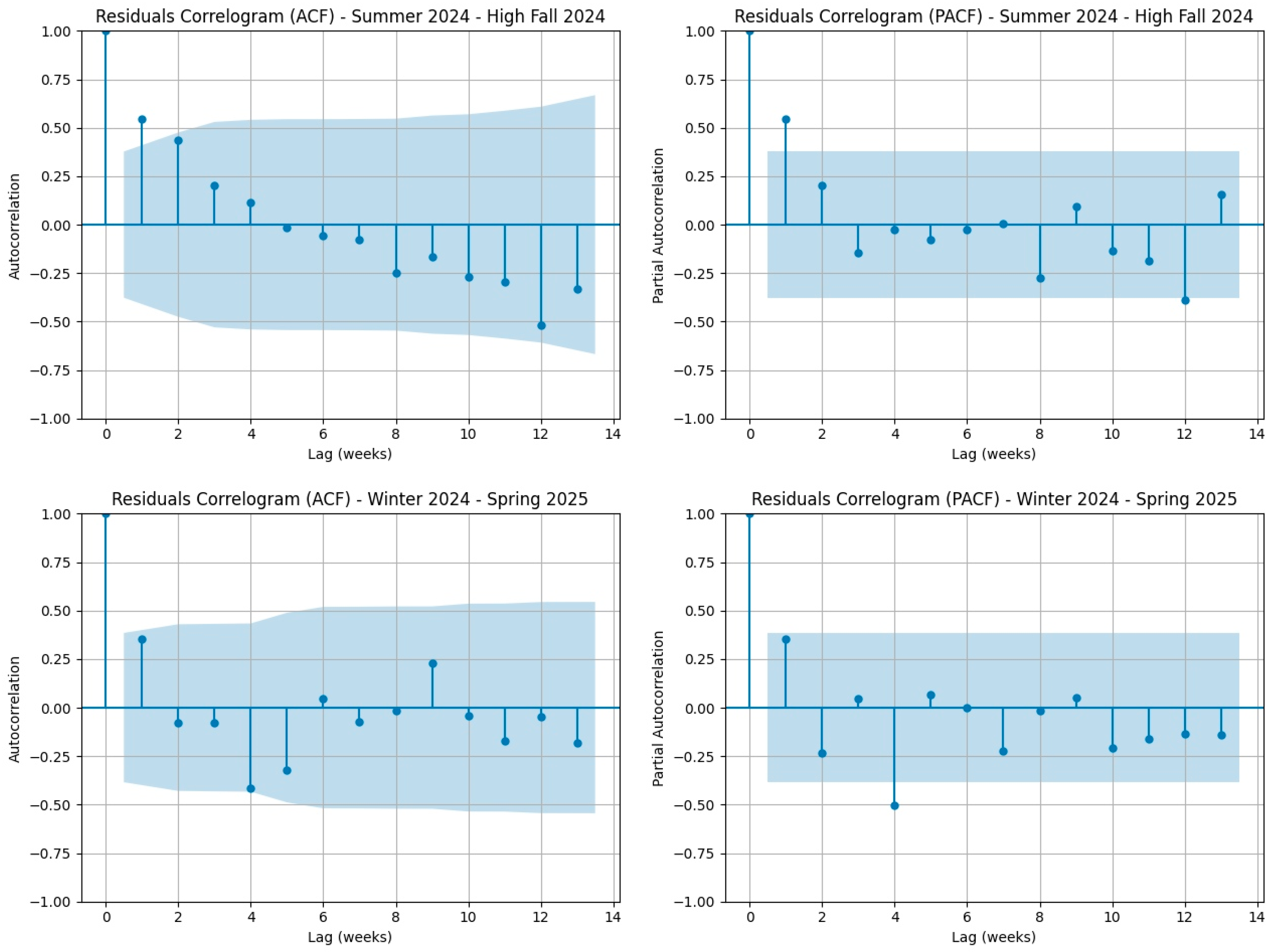
3.1. Results from the Statistical Validation of the Linear Regression Model for COVID-19 Mortality Data in Italy (2021–2025)
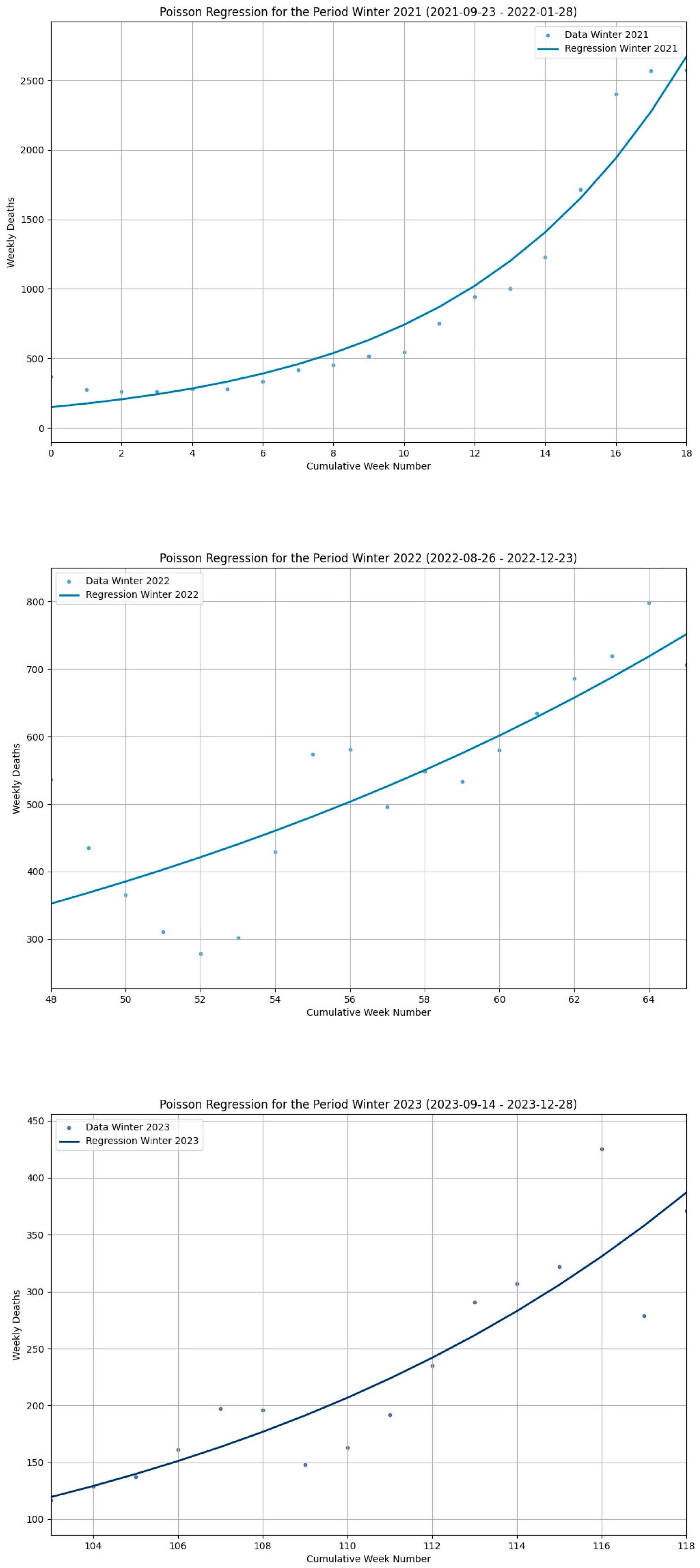
3.2. Results from the Poisson GLM for COVID-19 Mortality Data in Italy (2021–2025)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cameron, A.C.; Trivedi, P.K. Regression Analysis of Count Data; Cambridge University Press: Cambridge, UK, 1998; ISBN 9781139013567. [Google Scholar] [CrossRef]
- Hilbe, J.M. Modeling Count Data; Cambridge University Press: Cambridge, UK, 2014; ISBN 9781139236065. [Google Scholar] [CrossRef]
- Gardner, W.; Mulvey, E.P.; Shaw, E.C. Regression Analyses of Counts and Rates: Poisson, Overdispersed Poisson, and Negative Binomial Models. Psychol. Bull. 1995, 118, 392–404. [Google Scholar] [CrossRef]
- Chan, S.; Chu, J.; Zhang, Y.; Nadarajah, S. Count regression models for COVID-19. Phys. A Stat. Mech. Appl. 2021, 563, 125460. [Google Scholar] [CrossRef] [PubMed]
- Schober, P.; Vetter, T.R. Count Data in Medical Research: Poisson Regression and Negative Binomial Regression. Anesth. Analg. 2021, 132, 1378–1379. [Google Scholar] [CrossRef]
- Luo, R. Hypothesis testing of Poisson rates in COVID-19 offspring distributions. Infect. Dis. Model. 2023, 8, 980–1001. [Google Scholar] [CrossRef]
- Cohn, J.B.; Liu, Z.; Wardlaw, M.I. Count (and count-like) data in finance. J. Financ. Econ. 2022, 146, 529–551. [Google Scholar] [CrossRef]
- Roccetti, M.; De Rosa, E.M. A Segmented Linear Regression Study of Seasonal Profiles of COVID-19 Deaths in Italy: September 2021–September 2024. Computation 2025, 13, 165. [Google Scholar] [CrossRef]
- Roccetti, M. Seasonal Trends of COVID-19 Deaths in Italy: A Confirmatory Linear Regression Study with Time Series Data from 2024/2025. MedRxiv 2025, MedRxiv:25328619. [Google Scholar] [CrossRef]
- Altman, N.; Krzywinski, M. Simple Linear Regression. Nat. Methods 2015, 12, 999–1000. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; ISBN 978-1-119-57872-7. [Google Scholar]
- Breusch, T.S.; Pagan, A.R. A Simple Test for Heteroscedasticity and Random Coefficient Variation. Econometrica 1979, 47, 1287–1294. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2021; ISBN 978-0987507136. [Google Scholar]
- Bhaskaran, K.; Gasparrini, A.; Hajat, S.; Smeeth, L.; Armstrong, B. Time Series Regression Studies in Environmental Epidemiology. Int. J. Epidemiol. 2013, 42, 1187–1195. [Google Scholar] [CrossRef] [PubMed]
- Di Loro, P.A.; Böhning, D.; Sau, S.K. A Bayesian spatio-temporal Poisson auto-regressive model for the disease infection rate: Application to COVID-19 cases in England. J. R. Stat. Soc. Ser. C Appl. Stat. 2025, 74, 551–575. [Google Scholar] [CrossRef]
- Asai, M.; Chu, A.M.Y.; So, M.K.P. Dynamic Network Poisson Autoregression with Application to COVID-19 Count Data. J. Data Sci. 2025, 23, 208–224. [Google Scholar] [CrossRef]
- Tosi, D.; Campi, A. How Data Analytics and Big Data Can Help Scientists in Managing COVID-19 Diffusion: Modeling Study to Predict the COVID-19 Diffusion in Italy and the Lombardy Region. J. Med. Internet Res. 2020, 22, e21081. [Google Scholar] [CrossRef]
- Agosto, A.; Giudici, P. Poisson Autoregressive Model to Understand COVID-19 Contagion Dynamics. Risks 2020, 8, 77. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Vinod, D.; Aghion, E.; Chechkin, A.V.; Metzler, R. Time averaging, ageing and delay analysis of financial time series. New J. Phys. 2017, 19, 063045. [Google Scholar] [CrossRef]
- Vinod, D.; Cherstvy, A.G.; Metzler, R.; Sokolov, I.G. Time-averaging and nonergodicity of reset geometric Brownian motion with drift. Phys. Rev. E 2022, 106, 034137. [Google Scholar] [CrossRef]
- D’Amico, F.; Marmiere, M.; Righetti, B.; Scquizzato, T.; Zangrillo, A.; Puglisi, R.; Landoni, G. COVID-19 seasonality in temperate countries. Environ. Res. 2022, 206, 112614. [Google Scholar] [CrossRef]
- Truong, C.; Oudre, L.; Vayatis, N. Selective review of offline change point detection methods. Signal Process 2020, 167, 107299. [Google Scholar] [CrossRef]
- Venturelli, F.; Mancuso, P.; Vicentini, M.; Ottone, M.; Storchi, C.; Roncaglia, F.; Bisaccia, E.; Ferrarini, C.; Pezzotti, P.; Giorgi Rossi, P. High temperature, COVID-19, and mortality excess in the 2022 summer: A cohort study on data from Italian surveillances. Sci. Total Environ. 2023, 887, 164104. [Google Scholar] [CrossRef] [PubMed]
- Chirumbolo, S.; Pandolfi, S.; Valdenassi, L. Seasonality of COVID-19 deaths. Did social restrictions and vaccination actually impact the official reported dynamic of COVID-19 pandemic in Italy? Environ. Res. 2022, 212, 113229. [Google Scholar] [CrossRef]
- Fontal, A.; Bouma, M.J.; San-José, A.; Lopez, L.; Pascual, M.; Rodo, X. Climatic signatures in the different COVID-19 pandemic waves across both hemispheres. Nat. Comput. Sci. 2021, 1, 655–665. [Google Scholar] [CrossRef] [PubMed]
- Sera, F.; Armstrong, B.; Abbott, S.; Meakin, S.; O’Reilly, K.; von Borries, R.; Schneider, R.; Royé, D.; Hashizume, M.; Pascal, M.; et al. A cross-sectional analysis of meteorological factors and SARS-CoV-2 transmission in 409 cities across 26 countries. Nat. Commun. 2021, 12, 5968. [Google Scholar] [CrossRef] [PubMed]
- Wong, C. Why do covid cases rise in summer? New Sci. 2024, 263, 11. [Google Scholar] [CrossRef]
- De Meijere, G.; Valdano, G.; Castellano, C.; Debin, M.; Kengne-Kuetche, C.; Turbelin, C.; Noël, H.; Weitz, J.S.; Paolotti, D.; Hermans, L.; et al. Attitudes towards booster, testing and isolation, and their impact on COVID-19 response in winter 2022/2023 in France, Belgium, and Italy: A cross-sectional survey and modelling study. Lancet Reg. Health Eur. 2023, 28, 100614. [Google Scholar] [CrossRef]
- Khajanchi, S.; Sarkar, K.; Mondal, J.; Nisar, K.S.; Abdelwahab, S.F. Mathematical modeling of the COVID-19 pandemic with intervention strategies. Results Phys. 2021, 25, 104285. [Google Scholar] [CrossRef]
- Corradini, F.; Gorrieri, R.; Roccetti, M. Performance preorder and competitive equivalence. Acta Inform. 1997, 34, 805–835. [Google Scholar] [CrossRef]
- Palazzi, C.E.; Ferretti, S.; Cacciaguerra, S.; Roccetti, M. On maintaining interactivity in event delivery synchronization for mirrored game architectures. In Proceedings of the Globecom IEEE Global Telecommunications Conference, Dallas, TX, USA, 29 November–3 December 2004; pp. 157–165. [Google Scholar] [CrossRef]
- Morotti, E.; Stacchio, L.; Donatiello, L.; Roccetti, M.; Tarabelli, J.; Marfia, G. Exploiting fashion x-commerce through the empowerment of voice in the fashion virtual reality arena. Virtual Real. 2022, 26, 871–884. [Google Scholar] [CrossRef]
- Yang, H.; Lin, X.; Li, J.; Zhai, Y.; Wu, J. A Review of Mathematical Models of COVID-19 Transmission. Contemp. Math. 2023, 4, 75–98. [Google Scholar] [CrossRef]
- Hao, B.; Liu, C.; Wang, Y.; Zhu, N.; Ding, Y.; Wu, J.; Wang, Y.; Sun, F.; Chen, L. A mathematical-adapted model to analyze the characteristics for the mortality of COVID-19. Sci. Rep. 2022, 12, 5493. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, with Applications in Python; Springer Nature: Berlin/Heidelberg, Germany, 2023; ISBN 9783031387470. [Google Scholar]
- Ozili, P.K. The acceptable R-square in empirical modelling for social science research. Soc. Res. Methodol. Publ. Results 2022, 4128165, 1–9. [Google Scholar] [CrossRef]
- Li, M.; Giurcăneanu, C.D.; Liu, J. Automatic method for identification of cycles in Covid-19 time-series data. Data Sci. Manag. 2025, in press. [Google Scholar] [CrossRef]
- Taljaard, M.; McKenzie, J.E.; Ramsay, C.R.; Grimshaw, J.M. The use of segmented regression in analysing interrupted time series studies: An example in pre-hospital ambulance care. Implement. Sci. 2014, 9, 77. [Google Scholar] [CrossRef] [PubMed]





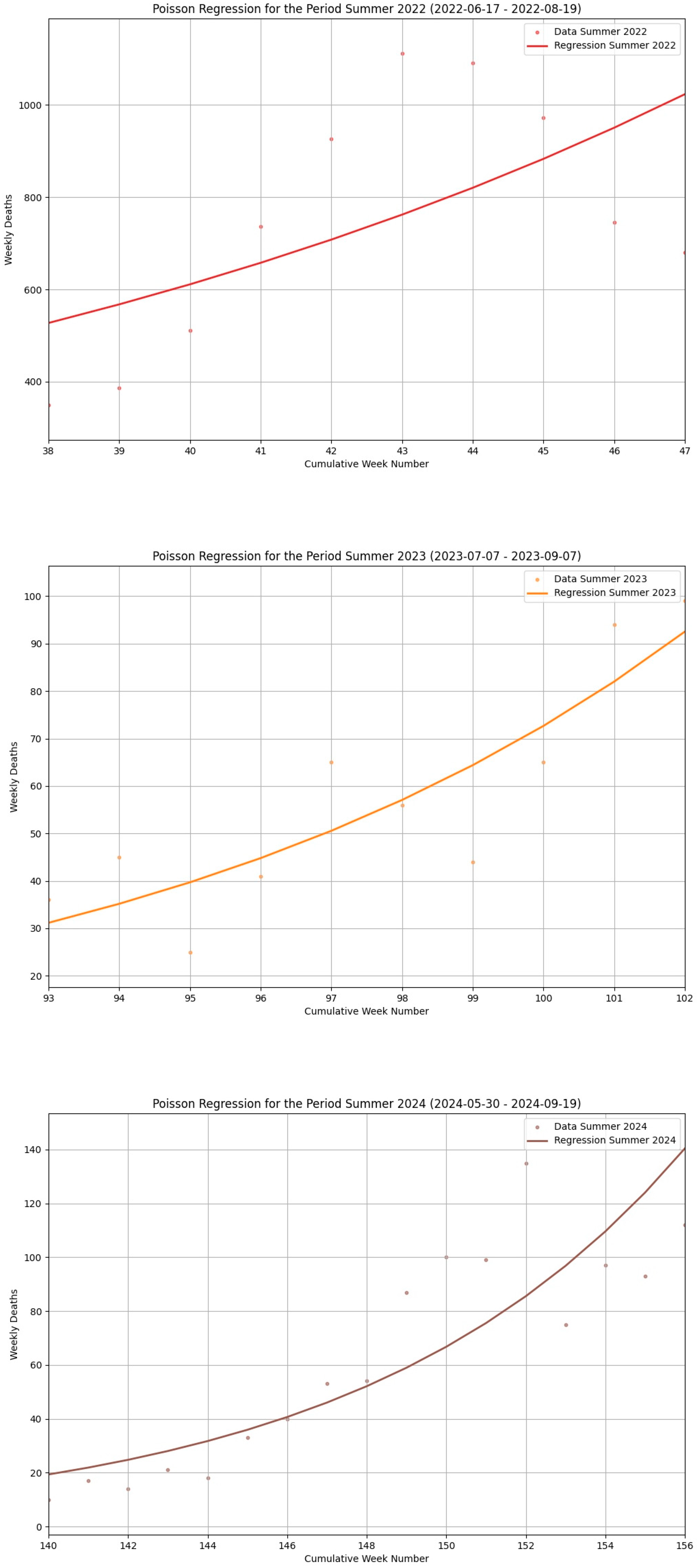

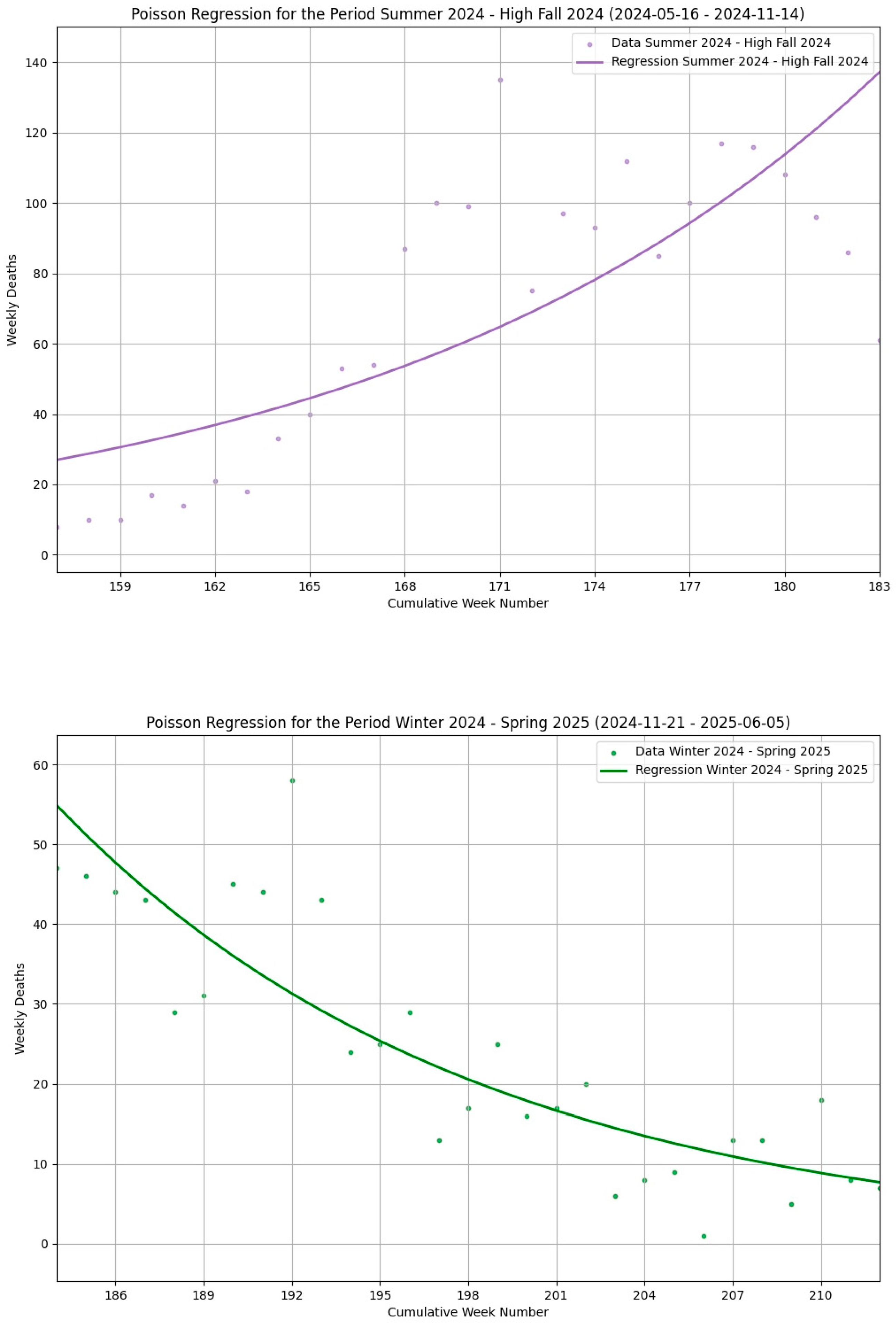
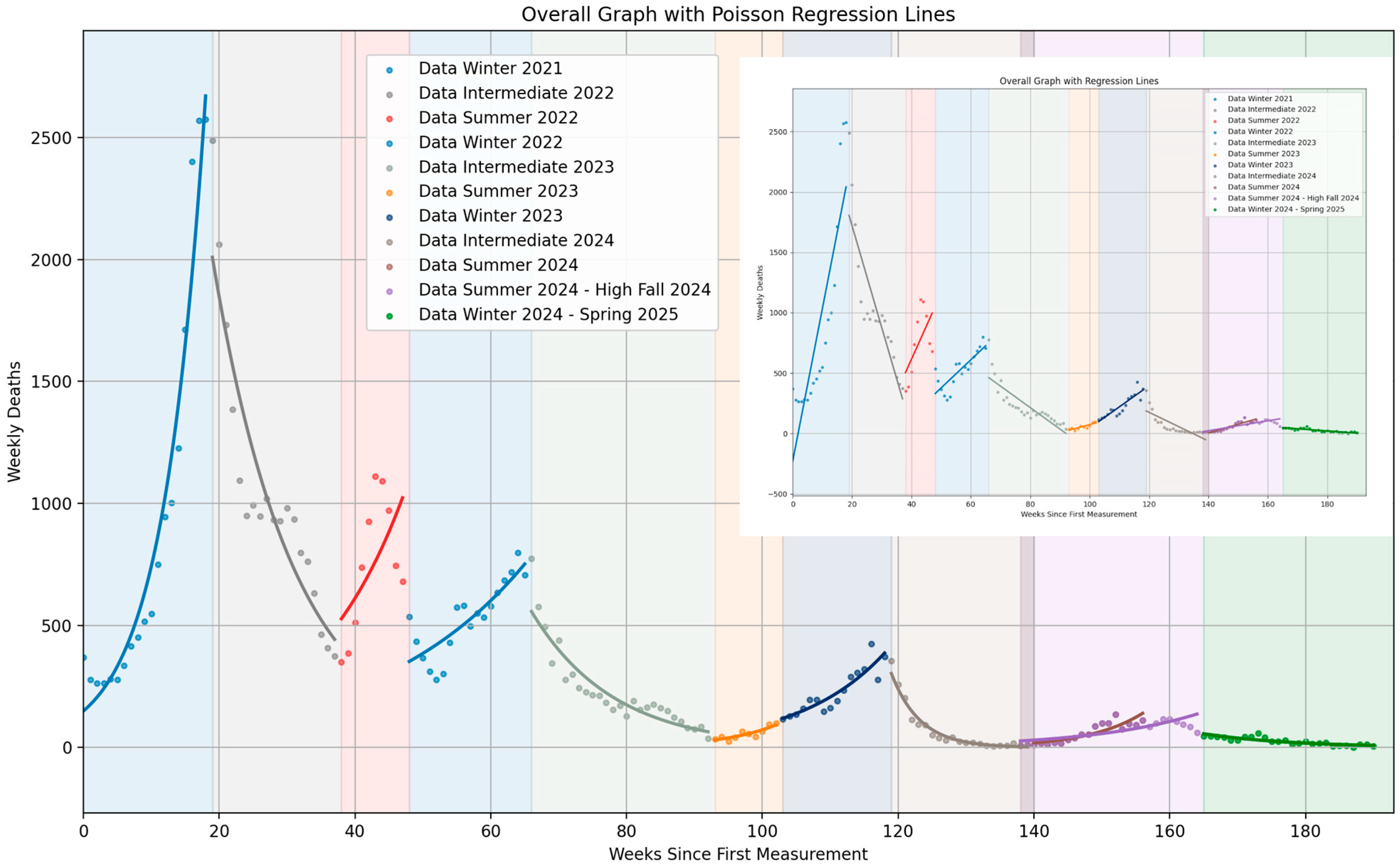
| Seasonal Segment | Season Type | Abbreviation | Number of Weeks | Segment Beginning | Segment End |
|---|---|---|---|---|---|
| Winter 2021 | Fall-Winter | Wint21 | 19 | 9/23/21 | 1/28/22 |
| Intermediate 2022 | Extended Spring | Inter22 | 19 | 2/4/22 | 6/10/22 |
| Summer 2022 | Summer | Summ22 | 10 | 6/17/22 | 8/19/22 |
| Winter 2022 | Fall-Winter | Wint22 | 18 | 8/26/22 | 12/23/22 |
| Intermediate 2023 | Extended Spring | Inter23 | 27 | 12/30/22 | 6/30/23 |
| Summer 2023 | Summer | Summ23 | 10 | 7/7/23 | 9/7/23 |
| Winter 2023 | Fall-Winter | Wint23 | 16 | 9/14/23 | 12/28/23 |
| Intermediate 2024 | Extended Spring | Inter24 | 21 | 1/4/24 | 5/23/24 |
| Summer 2024 | Summer | Summ24 | 17 | 5/30/24 | 11/19/24 |
| Summer–Winter 2024-25 | Summer + Winter | Sum-Wint24-25 | 21 | 5/16/24 | 11/14/24 |
| Extended Spring 2025 | Extended Spring | Extd-Spr25 | 17 | 11/21/24 | 5/21/25 |
| Week/Season | Trend/β1 | Deaths/Predictions/Residuals | Week/ Season | Trend/β1 | Deaths/Predictions/Residuals |
|---|---|---|---|---|---|
| 1/Wint21 | >/126.45 | 370/−233.70/603.70 | 25/Inter22 | </−84.38 | 949/1384−435.00 |
| 2/Wint21 | >126.45 | 277/−107.25/384.25 | 26/Inter22 | </−84.38 | 994/1299.61/−305.61 |
| 3/Wint21 | >126.45 | 263/19.20/243.80 | 27/Inter22 | </−84.38 | 947/1215.23/−268.23 |
| 4/Wint21 | >/126.45 | 263/145.65/117.35 | 28/Inter22 | </−84.38 | 1019/1130.85/−111.85 |
| 5/Wint21 | >/126.45 | 280/272.10/7.90 | 29/Inter22 | </−84.38 | 934/1046.47/−112.47 |
| 6/Wint21 | >/126.45 | 279/398.56/−119.56 | 30/Inter22 | </−84.38 | 928/962.09/−34.09 |
| 7/Wint21 | >/126.45 | 335/525.01/−190.01 | 31/Inter22 | </−84.38 | 980/877.71/102.29 |
| 8/Wint21 | >/126.45 | 416/651.46/−235.46 | 32/Inter22 | </−84.38 | 935/793.33/141.67 |
| 9/Wint21 | >/126.45 | 452/777.91/−325.91 | 33/Inter22 | </−84.38 | 797/708.95/88.05 |
| 10/Wint21 | >/126.45 | 517/904.37/−387.37 | 34/Inter22 | </−84.38 | 762/624.57/137.43 |
| 11/Wint21 | >/126.45 | 548/1030.82/−482.82 | 35/Inter22 | </−84.38 | 633/540.19/92.81 |
| 12/Wint21 | >/126.45 | 750/1157.27/−407.27 | 36/Inter22 | </−84.38 | 464/455.81/8.19 |
| 13/Wint21 | >/126.45 | 944/1283.73/−339.73 | 37/Inter22 | </−84.38 | 407/371.43/35.57 |
| 14/Wint21 | >/126.45 | 1002/1410.18/−408.18 | 38/Inter22 | </−84.38 | 375/287.05/87.95 |
| 15/Wint21 | >/126.45 | 1227/1536.63/−309.63 | 39/Summ22 | >/54.80 | 350/504.40/−154.40 |
| 16/Wint21 | >/126.45 | 1714/1663.08/50.92 | 40/Summ22 | >/54.80 | 386/559.20/−173.20 |
| 17/Wint21 | >/126.45 | 2402/1789.54/612.46 | 41/Summ22 | >/54.80 | 511/614.00/−103.00 |
| 18/Wint21 | >/126.45 | 2569/1915.99/653.01 | 42/Summ22 | >/54.80 | 737/668.80/68.20 |
| 19/Wint21 | >/126.45 | 2575/2042.44/532.56 | 43/Summ22 | >/54.80 | 926/723.60/202.40 |
| 20/Inter22 | </−84.38 | 2487/1805.90/681.10 | 44/Summ22 | >/54.80 | 1111/778.40/332.60 |
| 21/Inter22 | </−84.38 | 2061/1721.52/339.48 | 45/Summ22 | >/54.80 | 1091/833.20/257.80 |
| 22/Inter22 | </−84.38 | 1731/1637.14/93.86 | 46/Summ22 | >/54.80 | 972/888.00/84.00 |
| 23/Inter22 | </−84.38 | 1386/1552.76/−166.76 | 47/Summ22 | >/54.80 | 746/942.80/−196.80 |
| 24/Inter22 | </−84.38 | 1094/1384.00/−374.38 | 48/Summ22 | >/54.80 | 680/997.60/−317.60 |
| Week/Season | Trend/β1 | Deaths/Predictions/Residuals | Week/Season | Trend/β1 | Deaths/Predictions/Residuals |
|---|---|---|---|---|---|
| 49/Wint22 | >/23.28 | 536/330.72/205.28 | 77/Inter23 | </−17.76 | 212/285.29/−73.29 |
| 50/Wint22 | >/23.28 | 435/354.00/81.00 | 78/Inter23 | </−17.76 | 183/267.52/−84.52 |
| 51/Wint22 | >/23.28 | 366/377.29/−11.29 | 79/Inter23 | </−17.76 | 156/249.76/−93.76 |
| 52/Wint22 | >/23.28 | 311/400.57/−89.57 | 80/Inter23 | </−17.76 | 173/232.00/−59.00 |
| 53/Wint22 | >/23.28 | 279/423.85/−144.85 | 81/Inter23 | </−17.76 | 129/214.24/−85.24 |
| 54/Wint22 | >/23.28 | 302/447.13/−145.13 | 82/Inter23 | </−17.76 | 191/196.47/−5.47 |
| 55/Wint22 | >/23.28 | 429/470.41/−41.41 | 83/Inter23 | </−17.76 | 156/178.71/−22.71 |
| 56/Wint22 | >/23.28 | 574/493.69/80.31 | 84/Inter23 | </−17.76 | 166/160.95/5.05 |
| 57/Wint22 | >/23.28 | 581/516.97/64.03 | 85/Inter23 | </−17.76 | 176/143.19/32.81 |
| 58/Wint22 | >/23.28 | 496/540.25/−44.25 | 86/Inter23 | </−17.76 | 162/125.42/36.58 |
| 59/Wint22 | >/23.28 | 549/563.53/−14.53 | 87/Inter23 | </−17.76 | 150/107.66/42.34 |
| 60/Wint22 | >/23.28 | 533/586.81/−53.81 | 88/Inter23 | </−17.76 | 125/89.90/35.10 |
| 61/Wint22 | >/23.28 | 580/610.09/−30.09 | 89/Inter23 | </−17.76 | 108/72.14/35.86 |
| 62/Wint22 | >/23.28 | 635/633.37/1.63 | 90/Inter23 | </−17.76 | 81/54.37/26.63 |
| 63/Wint22 | >/23.28 | 686/656.65/29.35 | 91/Inter23 | </−17.76 | 76/36.61/39.39 |
| 64/Wint22 | >/23.28 | 719/679.94/39.06 | 92/Inter23 | </−17.76 | 86/18.85/67.15 |
| 65/Wint22 | >/23.28 | 798/703.21/94.79 | 93/Inter23 | </−17.76 | 38/1.09/36.91 |
| 66/Wint22 | >/23.28 | 706/725.50/−20.50 | 94/Summ23 | >/6.72 | 36/26.73/9.27 |
| 67/Inter23 | </−17.76 | 775/462.91/312.09 | 95/Summ23 | >/6.72 | 45/33.45/11.55 |
| 68/Inter23 | </−17.76 | /576/445.15130.85 | 96/Summ23 | >/6.72 | 25/40.18/−15.18 |
| 69/Inter23 | </−17.76 | 495/427.39/67.61 | 97/Summ23 | >/6.72 | 41/46.91/−5.91 |
| 70/Inter23 | </−17.76 | 345/409.62/−64.62 | 98/Summ23 | >/6.72 | 65/53.64/11.48 |
| 71/Inter23 | </−17.76 | 439/391.86/47.14 | 99/Summ23 | >/6.72 | 56/60.36/−4.36 |
| 72/Inter23 | </−17.76 | 279/374.10/−95.10 | 100/Summ23 | >/6.72 | 44/67.09/−23.09 |
| 73/Inter23 | </−17.76 | 299/356.34/−57.34 | 101/Summ23 | >/6.72 | 65/73.82/−8.82 |
| 74/Inter23 | </−17.76 | 244/338.57/−94.57 | 102/Summ23 | >/6.72 | 94/80.54/13.46 |
| 75/Inter23 | </−17.76 | 228/320.81/−92.81 | 103/Summ23 | >/6.72 | 99/87.27/11.73 |
| 76/Inter23 | </−17.76 | 216/330.72/−87.805 | / | / | / |
| Week/Season | Trend/β1 | Deaths/Predictions/Residuals | Week/Season | Trend/β1 | Deaths/Predictions/Residuals |
|---|---|---|---|---|---|
| 104/Wint23 | >/17.52 | 117/97.99/19.01 | 131/Inter24 | </−11.89 | 20/56.30/−36.30 |
| 105/Wint23 | >/17.52 | 129/115.51/13.49 | 132/Inter24 | </−11.89 | 21/44.41/−23.41 |
| 106/Wint23 | >/17.52 | 137/133.03/3.97 | 133/Inter24 | </−11.89 | 15/32.52/−17.52 |
| 107/Wint23 | >/17.52 | 161/150.54/10.46 | 134/Inter24 | </−11.89 | 9/20.63/−11.63 |
| 108/Wint23 | >/17.52 | 197/168.06/28.94 | 135/Inter24 | </−11.89 | 7/8.74/−1.74 |
| 109/Wint23 | >/17.52 | 196/185.58/10.42 | 136/Inter24 | </−11.89 | 9/−3.15/12.15 |
| 110/Wint23 | >/17.52 | 148/203.10/−55.10 | 137/Inter24 | </−11.89 | 9/−15.15/26.05 |
| 111/Wint23 | >/17.52 | 163/220.62/−57.62 | 138/Inter24 | </−11.89 | 17/−26.94/43.94 |
| 112/Wint23 | >/17.52 | 192/238.13/−46.13 | 139/Inter24 | </−11.89 | 8/−38.83/46.83 |
| 113/Wint23 | >/17.52 | 235/255.65/−20.65 | 140/Inter24 | </−11.89 | 10/−50.72/60.72 |
| 114/Wint23 | >/17.52 | 291/273.17/17.83 | 141/Summ24 | >/7.20 | 10/4.67/5.33 |
| 115/Wint23 | >/17.52 | 307/290.69/16.31 | 142/Summ24 | >/7.20 | 17/11.86/5.14 |
| 116/Wint23 | >/17.52 | 322/308.20/13.80 | 143/Summ24 | >/7.20 | 14/19.06/−5.06 |
| 117/Wint23 | >/17.52 | 425/325.72/99.28 | 144/Summ24 | >/7.20 | 21/26.25/−5.25 |
| 118/Wint23 | >/17.52 | 279/343.24/−64.24 | 145/Summ24 | >/7.20 | 18/33.45/−15.45 |
| 119/Wint23 | >/17.52 | 371/360.76/10.24 | 146/Summ24 | >/7.20 | 33/40.65/−7.65 |
| 120/Inter24 | </−11.89 | 355/187.10/167.90 | 147/Summ24 | >/7.20 | 40/47.84/−7.84 |
| 121/Inter24 | </−11.89 | 258/175.21/82.79 | 148/Summ24 | >/7.20 | 53/55.04/−2.04 |
| 122/Inter24 | </−11.89 | 203/163.32/39.68 | 149/Summ24 | >/7.20 | 54/62.23/−8.23 |
| 123/Inter24 | </−11.89 | 115/151.43/−36.43 | 150/Summ24 | >/7.20 | 87/69.43/17.57 |
| 124/Inter24 | </−11.89 | 95/139.54/−44.54 | 151/Summ24 | >/7.20 | 100/76.63/23.37 |
| 125/Inter24 | </−11.89 | 92/127.64/−35.64 | 152/Summ24 | >/7.20 | 99/83.82/15.18 |
| 126/Inter24 | </−11.89 | 52/115.75/−63.75 | 153/Summ24 | >/7.20 | 135/91.02/43.98 |
| 127/Inter24 | </−11.89 | 39/103.86/−64.86 | 154/Summ24 | >/7.20 | 75/98.22/−23.22 |
| 128/Inter24 | </−11.89 | 31/91.97/−60.97 | 155/Summ24 | >/7.20 | 97/105.41/−8.41 |
| 129/Inter24 | </−11.89 | 41/80.08/−39.08 | 156/Summ24 | >/7.20 | 93/112.61/−19.61 |
| 130/Inter24 | </−11.89 | 26/68.19/−42.19 | 157/Summ24 | >/7.20 | 112/119.80/7.80 |
| Week/Season | Trend/β1 | Deaths/Predictions/Residuals | Week/Season | Trend/β1 | Deaths/Predictions/Residuals |
|---|---|---|---|---|---|
| 1/Sum-Wint24-25 | >/4.08 | 8/15.25/−7.25 | 28/Extd-Spr25 | </−1.81 | 47/48.49/−1.49 |
| 2/ Sum-Wint24-25 | >/4.08 | 10/19.33/−9.33 | 29/Extd-Spr25 | </−1.81 | 46/46.67/−0.67 |
| 3/Sum-Wint24-25 | >/4.08 | 10/23.41/−13.41 | 30/Exdt-Spr25 | </−1.81 | 44/44.86/−0.86 |
| 4/Sum-Wint24-25 | >/4.08 | 17/27.50/−10. 50 | 31/Extd-Spr25 | </−1.81 | 43/43.04/−0.04 |
| 5/Sum-Wint24-25 | >/4.08 | 14/31.58/−17.58 | 32/Extd-Spr25 | </−1.81 | 29/41.23/−12.23 |
| 6/Sum-Wint24-25 | >/4.08 | 21/35.66/−14.66 | 33/Extd-Spr25 | </−1.81 | 31/39.41/−8.41 |
| 7/Sum-Wint24-25 | >/4.08 | 18/39.75/−21.75 | 34/Extd-Spr25 | </−1.81 | 45/37.60/7.40 |
| 8/Sum-Wint24-25 | >/4.08 | 33/43.83/−10.83 | 35/Extd-Spr25 | </−1.81 | 44/35.79/8.21 |
| 9/Sum-Wint24-25 | >/4.08 | 40/47.91/−7.91 | 36/Extd-Spr25 | </−1.81 | 58/33.97/24.03 |
| 10/Sum-Wint24-25 | >/4.08 | 53/52.00/1.00 | 37/Extd-Spr25 | </−1.81 | 43/32.16/10.84 |
| 11/Sum-Wint24-25 | >/4.08 | 54/56.08/−2.08 | 38/Extd-Spr25 | </−1.81 | 24/30.34/−6.34 |
| 12/Sum-Wint24-25 | >/4.08 | 87/60.17/26.83 | 39/Extd-Spr25 | </−1.81 | 25/28.53/−3.53 |
| 13/Sum-Wint24-25 | >/4.08 | 10064.25//35.75 | 40/Extd-Spr25 | </−1.81 | 29/26.71/2.29 |
| 14/Sum-Wint24-25 | >/4.08 | 99/68.33/30.67 | 41/Extd-Spr25 | </−1.81 | 13/24.90/−11.90 |
| 15/Sum-Wint24-25 | >/4.08 | 135/72.42/62.58 | 42/Extd-Spr25 | </−1.81 | 17/23.09/−6.09 |
| 16/Sum-Wint24-25 | >/4.08 | 75/76.50/−1.50 | 43/Extd-Spr25 | </−1.81 | 25/21.27/3.73 |
| 17/Sum-Wint24-25 | >/4.08 | 97/80.58/16.42 | 44/Extd-Spr25 | </−1.81 | 16/19.46/−3.46 |
| 18/Sum-Wint24-25 | >/4.08 | 93/84.67/8.33 | 45/Extd-Spr25 | </−1.81 | 17/17.64/−0.64 |
| 19/Sum-Wint24-25 | >/4.08 | 112/88.75/23.25 | 46/Extd-Spr25 | </−1.81 | 20/15.83/4.17 |
| 20/Sum-Wint24-25 | >/4.08 | 85/92.83/−7.83 | 47/Extd-Spr25 | </−1.81 | 6/14.01/−8.01 |
| 21/Sum-Wint24-25 | >/4.08 | 100/96.92/3.08 | 48/Extd-Spr25 | </−1.81 | 8/12.20/−4.20 |
| 22/Sum-Wint24-25 | >/4.08 | 117/101.00/16.00 | 49/Extd-Spr25 | </−1.81 | 9/10.39/−1.39 |
| 23/Sum-Wint24-25 | >/4.08 | 116/105.09/10.91 | 50/Extd-Spr25 | </−1.81 | 1/8.57/−7.57 |
| 24/Sum-Wint24-25 | >/4.08 | 108/109.17/−1.17 | 51/Extd-Spr25 | </−1.81 | 13/6.76/6.24 |
| 25/Sum-Wint24-25 | >/4.08 | 96/113.25/−17.25 | 52/Extd-Spr25 | </−1.81 | 13/4.94/8.06 |
| 26/Sum-Wint24-25 | >/4.08 | 86/117.34/−31.34 | 53/Extd-Spr25 | </−1.81 | 5/3.13/1.87 |
| 27/Sum-Wint24-25 | >/4.08 | 61/121.42/−60.42 | / | / | / |
| Seasonal Segment | Statistic W | p-Value | Residuals Normality |
|---|---|---|---|
| Winter 2021 | 0.88622 | 0.00276 | NO (but p-value close to α) |
| Intermediate 2022 | 0.93572 | 0.22053 | YES |
| Summer 2022 | 0.94192 | 0.57459 | YES |
| Winter 2022 | 0.96558 | 0.71180 | YES |
| Intermediate 2023 | 0.83198 | 0.00051 | NO |
| Summer 2023 | 0.86921 | 0.09788 | YES |
| Winter 2023 | 0.87167 | 0.02885 | NO (but p-value close to α) |
| Intermediate 2024 | 0.88452 | 0.01773 | NO (but p-value close to α) |
| Summer 2024 | 0.90292 | 0.07604 | YES |
| Summer–Winter 2024/25 | 0.95906 | 0.35177 | YES |
| Extended Spring 2025 | 0.94154 | 0.14620 | YES |
| Seasonal Segment | Statistics LM | p-Value | Heteroscedasticity |
|---|---|---|---|
| Winter 2021 | 2.9880 | 0.08388 | No |
| Intermediate 2022 | 7.0823 | 0.00778 | Yes |
| Summer 2022 | 2.3209 | 0.12764 | No |
| Winter 2022 | 5.3495 | 0.02020 | No |
| Intermediate 2023 | 5.4031 | 0.02010 | No |
| Summer 2023 | 0.3138 | 0.57535 | No |
| Winter 2023 | 2.45566 | 0.11710 | No |
| Intermediate 2024 | 4.43587 | 0.03519 | Yes (but p-value close to α) |
| Summer 2024 | 2.42003 | 0.11979 | No |
| Summer–Winter 2024/25 | 2.12175 | 0.14522 | No |
| Extended Spring 2025 | 0.52298 | 0.46957 | No |
| Segment | Normality | Homoscedasticity | No Correlation |
|---|---|---|---|
| Winter 2021 | Nearly | Yes | Yes |
| Intermediate 2022 | Yes | No | Yes |
| Summer 2022 | Yes | Yes | Yes |
| Winter 2022 | Yes | Yes | Yes |
| Intermediate 2023 | No | Yes | Yes |
| Summer 2023 | Yes | Yes | Yes |
| Winter 2023 | Nearly | Yes | Yes |
| Intermediate 2024 | Nearly | Nearly | Yes |
| Summer 2024 | Yes | Yes | Yes |
| Summer–Winter 2024/25 | Yes | Yes | Yes |
| Extended Spring 2025 | Yes | Yes | Yes |
| Seasonal Segment | Deaths | MAE (Linear) | MAE (Poisson) | Percentage Error MAE (Linear) | Percentage Error MAE (Poisson) | RMSE (Linear) | RMSE (Poisson) |
|---|---|---|---|---|---|---|---|
| Winter21 | 17,183 | 337.47 | 128.45 | 1.96% | 0.75% | 384.72 | 167.70 |
| Intermediate22 | 19,883 | 190.36 | 157.55 | 0.96% | 0.79% | 252.53 | 201.07 |
| Summer22 | 7510 | 189.00 | 201.25 | 2.52% | 2.68% | 208.28 | 221.52 |
| Winter22 | 9515 | 66.16 | 62.77 | 0.69% | 0.66% | 84.63 | 80.01 |
| Intermediate23 | 6264 | 67.81 | 45.23 | 1.08% | 0.72% | 88.28 | 60.78 |
| Summer23 | 570 | 11.47 | 9.52 | 2.01% | 1.67% | 12.50 | 11.04 |
| Winter23 | 3670 | 30.47 | 28.26 | 0.83% | 0.77% | 39.83 | 38.30 |
| Intermediate24 | 1432 | 45.53 | 11.72 | 3.18% | 0.82% | 56.63 | 17.28 |
| Summer24 | 1058 | 13.01 | 16.84 | 1.23% | 1.59% | 16.47 | 21.45 |
| Winter–Sumer2024-25 | 1845 | 17.40 | 22.11 | 0.94% | 1.20% | 23.35 | 28.77 |
| ExtendedSpring25 | 671 | 5.91 | 6.65 | 0.88% | 0.99% | 7.77 | 8.58 |
| Average per period | 6327 | 88.60 | 62.76 | 1.48% | 1.15% | 106.82 | 84.79 |
| (Standard Deviation) | (6447) | (100.95) | (64.90) | (0.78%) | (0.59%) | (116.94) | (76.81) |
| W | Poisson | W | Poisson | W | Poisson | W | Poisson | W | Poisson |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 149.43 | 43 | 707.91 | 85 | 125.66 | 127 | 58.08 | 169 | 53.69 |
| 2 | 175.39 | 44 | 762.01 | 86 | 115.68 | 128 | 45.87 | 170 | 57.16 |
| 3 | 205.86 | 45 | 820.23 | 87 | 106.50 | 129 | 36.22 | 171 | 60.85 |
| 4 | 241.62 | 46 | 882.91 | 88 | 98.04 | 130 | 28.60 | 172 | 64.78 |
| 5 | 283.59 | 47 | 950.37 | 89 | 90.26 | 131 | 22.59 | 173 | 68.96 |
| 6 | 332.86 | 48 | 1022.99 | 90 | 83.09 | 132 | 17.84 | 174 | 73.41 |
| 7 | 390.69 | 49 | 352.62 | 91 | 76.50 | 133 | 14.08 | 175 | 78.15 |
| 8 | 458.55 | 50 | 368.67 | 92 | 70.42 | 134 | 11.12 | 176 | 83.19 |
| 9 | 538.21 | 51 | 385.45 | 93 | 64.83 | 135 | 8.78 | 177 | 88.56 |
| 10 | 631.71 | 52 | 402.99 | 94 | 31.17 | 136 | 6.94 | 178 | 94.28 |
| 11 | 741.45 | 53 | 421.33 | 95 | 35.17 | 137 | 5.48 | 179 | 100.36 |
| 12 | 870.26 | 54 | 440.51 | 96 | 39.70 | 138 | 4.32 | 180 | 106.84 |
| 13 | 1021.44 | 55 | 460.56 | 97 | 44.80 | 139 | 3.41 | 181 | 113.74 |
| 14 | 1198.88 | 56 | 481.53 | 98 | 50.55 | 140 | 2.70 | 182 | 121.08 |
| 15 | 1407.15 | 57 | 503.44 | 99 | 57.05 | 141 | 19.32 | 183 | 128.90 |
| 16 | 1651.60 | 58 | 526.36 | 100 | 64.38 | 142 | 21.87 | 184 | 137.22 |
| 17 | 1938.51 | 59 | 550.32 | 101 | 72.65 | 143 | 24.76 | 185 | 56.34 |
| 18 | 2275.27 | 60 | 575.37 | 102 | 81.99 | 144 | 28.03 | 186 | 52.29 |
| 19 | 2670.52 | 61 | 601.56 | 103 | 92.53 | 145 | 31.72 | 187 | 48.53 |
| 20 | 2009.31 | 62 | 628.94 | 104 | 119.49 | 146 | 35.91 | 188 | 45.04 |
| 21 | 1847.41 | 63 | 657.57 | 105 | 129.23 | 147 | 40.65 | 189 | 41.80 |
| 22 | 1698.56 | 64 | 687.50 | 106 | 139.77 | 148 | 46.02 | 190 | 38.80 |
| 23 | 1561.70 | 65 | 718.79 | 107 | 151.16 | 149 | 52.09 | 191 | 36.01 |
| 24 | 1435.87 | 66 | 751.51 | 108 | 163.48 | 150 | 58.96 | 192 | 33.42 |
| 25 | 1320.17 | 67 | 557.00 | 109 | 176.81 | 151 | 66.74 | 193 | 31.02 |
| 26 | 1213.80 | 68 | 512.78 | 110 | 191.22 | 152 | 75.55 | 194 | 28.79 |
| 27 | 1116.00 | 69 | 472.07 | 111 | 206.81 | 153 | 85.52 | 195 | 26.72 |
| 28 | 1026.08 | 70 | 434.59 | 112 | 223.66 | 154 | 96.81 | 196 | 24.80 |
| 29 | 943.40 | 71 | 400.09 | 113 | 241.89 | 155 | 109.58 | 197 | 23.01 |
| 30 | 867.39 | 72 | 368.32 | 114 | 261.61 | 156 | 124.04 | 198 | 21.36 |
| 31 | 797.50 | 73 | 339.08 | 115 | 282.93 | 157 | 140.41 | 199 | 19.82 |
| 32 | 733.24 | 74 | 312.16 | 116 | 306.00 | 158 | 26.98 | 200 | 18.40 |
| 33 | 674.16 | 75 | 287.38 | 117 | 330.94 | 159 | 28.73 | 201 | 17.08 |
| 34 | 619.84 | 76 | 264.56 | 118 | 357.91 | 160 | 30.58 | 202 | 15.85 |
| 35 | 569.90 | 77 | 243.56 | 119 | 387.08 | 161 | 32.55 | 203 | 14.71 |
| 36 | 523.98 | 78 | 224.22 | 120 | 303.31 | 162 | 34.66 | 204 | 13.65 |
| 37 | 481.76 | 79 | 206.42 | 121 | 239.52 | 163 | 36.89 | 205 | 12.67 |
| 38 | 442.94 | 80 | 190.03 | 122 | 189.14 | 164 | 39.27 | 206 | 11.76 |
| 39 | 527.31 | 81 | 174.94 | 123 | 149.36 | 165 | 41.81 | 207 | 10.91 |
| 40 | 567.60 | 82 | 161.05 | 124 | 117.95 | 166 | 44.51 | 208 | 10.13 |
| 41 | 610.98 | 83 | 148.27 | 125 | 93.14 | 167 | 47.38 | 209 | 9.40 |
| 42 | 657.66 | 84 | 136.50 | 126 | 73.55 | 168 | 66.74 | 210 | 8.72 |
| Seasonal Segment | Linear: β1 (Slope) CI 95% | Poisson β1 CI 95% | · (exp(β1) − 1)) (Slope) CI 95% |
|---|---|---|---|
| Winter21 | 126.45 [90.51, 162.39] | 0.1602 [0.1568, 0.1635] | 157.3 [153.55, 160.67] |
| Intermediate22 | −84.38 [−107.973, −60.79] | −0.0840 [−0.0867, −0.0813] | −84.23 [−86.91, −81.72] |
| Summer22 | 54.80 [20.24, 142.29] | 0.0736 [0.0656, 0.0816] | 57.38 [50.96, 63.86] |
| Winter22 | 23.28 [14.64, 31.93] | 0.0445 [0.0406, 0.0484] | 23.79 [21.89, 26.24] |
| Intermediate23 | −17.76 [−22.43, −13.09] | −0.0827 [−0.0863, −0.0791] | −18.42 [−19.18, −17.65] |
| Summer23 | 6.72 [3.18, 10.27] | 0.1209 [0.0913, 0.1505] | 7.33 [5.45, 9.26] |
| Winter23 | 17.52 [12.56, 22.47] | 0.0784 [0.0711, 0.0856] | 18.81 [16.89, 20.51] |
| Intermediate24 | −11.89 [−16.38, −7.40] | −0.2361 [−0.2496, −0.2226] | −14.35 [−15.06, −13.60] |
| Summer24 | 7.20 [5.34, 9.04] | 0.1240 [0.1103, 0.1376] | 8.21 [7.26, 9.18] |
| Winter–Summer 2024-25 | 4.08 [2.85, 5.32] | 0.0625 [0.0563, 0.0688] | 4.41 [3.95, 4.87] |
| Extended Spring 2025 | −1.81 [−2.25, −1.38] | −0.0746 [−0.0856, −0.0636] | −1.85 [−2.12, −1.59] |
| Kolmogorov–Smirnov | Null Hypothesis | D Statistic | p Value |
|---|---|---|---|
| Significance level = 0.05 | H0 = there is no statistically significant difference between the two series of slope values | 0.1819 | 0.9971 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roccetti, M.; Cacciapuoti, G. Beyond the Gold Standard: Linear Regression and Poisson GLM Yield Identical Mortality Trends and Deaths Counts for COVID-19 in Italy: 2021–2025. Computation 2025, 13, 233. https://doi.org/10.3390/computation13100233
Roccetti M, Cacciapuoti G. Beyond the Gold Standard: Linear Regression and Poisson GLM Yield Identical Mortality Trends and Deaths Counts for COVID-19 in Italy: 2021–2025. Computation. 2025; 13(10):233. https://doi.org/10.3390/computation13100233
Chicago/Turabian StyleRoccetti, Marco, and Giuseppe Cacciapuoti. 2025. "Beyond the Gold Standard: Linear Regression and Poisson GLM Yield Identical Mortality Trends and Deaths Counts for COVID-19 in Italy: 2021–2025" Computation 13, no. 10: 233. https://doi.org/10.3390/computation13100233
APA StyleRoccetti, M., & Cacciapuoti, G. (2025). Beyond the Gold Standard: Linear Regression and Poisson GLM Yield Identical Mortality Trends and Deaths Counts for COVID-19 in Italy: 2021–2025. Computation, 13(10), 233. https://doi.org/10.3390/computation13100233







