Abstract
In avian biology, the radius of curvature, or R, has hardly ever been used to study the mechanics of birds’ egg shape formation. However, it is essential for introducing important details about the form, function, and performance of an object, which is useful in biomedicine, manufacturing, and precision design. In order to determine a possible biological mechanism and the location of load application that creates the distinctive asymmetric egg shape in nature, the goal of this study was to develop a formula for computing R at any point over an egg contour. We derived a relatively simple means of computing R and identified the location that muscular compression is carried out to give the egg its characteristic form. This location (x/L), the angle (α) of compression and the relative magnitude of the load proportional to R can help identify a specific section of the oviduct and the squeezing muscle involved. Novel equations for computing R, x/L and α were proposed, based on standard geometric parameters. Our findings demonstrate how the theoretical knowledge of physical, mechanical and mathematical processes can contribute to the solution of biological problems and resonates with the fields of egg-inspired engineering.
1. Introduction
Measurement of the radius of curvature (R) is a key aspect of mathematics that provides critical information about an object’s shape, function and performance. It has found utility in fields involving precision design, manufacturing and analysis. These include optics (lenses, mirrors, microscopes, telescopes, cameras, eyeglasses, etc.), alignment of mechanical parts (e.g., aerodynamic/hydrodynamic profiles) and verifying that curved surfaces (e.g., automotive parts including turbine blades) match design specifications. In material stress analysis R is used to detect warping, buckling or deformation under load or heat, as well as in reverse engineering, i.e., replicating or analyzing existing objects such as legacy parts. Commonly used tools that incorporate R include spherometers, profilometers, interferometers, 3D scanning tools and Computer-Aided Design and Computer-Aided Manufacturing (CAD/CAM) software with curvature analysis features [1,2,3,4,5,6,7,8].
In biological, biomedical and veterinary fields, knowledge and application of R is used to design and fit implants (e.g., lenses for eye surgery), prosthetics, dental constructs, orthopedic tools and for measuring the curvature of the spine, bones and corneas [9,10,11,12,13,14]. An area that has received comparatively little attention, however, is that of one of the most well-known curved objects in nature, the avian egg. The potential uses of R in egg biology (“eggology”) [15,16] and egg-inspired engineering [17] include hatching, table egg production, conservation and veterinary medicine. Despite numerous works devoted to the geometric features of a bird’s egg [18,19,20,21,22,23,24,25,26,27], the issue of determining R has, however, eluded the scope of these studies. The only exception to this of which we are aware is Narushin et al. [28] who present a version of computing R derived from Hügelschäffer’s model. It was, however, shown later [26,27,29] that such a calculation is suitable for describing only a limited number of eggs of a certain shape. In addition, some generalizations and assumptions led to the fact that the derived dependence was the same for all possible nuances of Hügelschäffer’s ovoids without accounting for variation in their asymmetry and conicity. Indeed, R has the potential to be in high demand for the analysis of shell strength [30,31,32,33,34,35,36] and to assess the accuracy of the description of shape of any individual egg [37].
A further biological aspect concerning the utility of R of a volumetric body that, so far, has remained outside the attention of scientists involved in egg research is the feasibility of analyzing the muscular actions of the hen to give the egg its unique shape. Over 130 years ago, studies of the principles of egg formation suggested that its unique shape is laid down before the calcification process and because of the contraction of certain muscles of the oviduct (e.g., [38]). Further research in this direction (e.g., [39,40]) confirmed these results, although it did not reveal the mechanism of such an effect. A more thorough study of this process made it possible to link the mechanical action on the elastic mass of the egg contents with the mathematical aspects of its final shape. According to the premises set out by Smart [20,41] and Todd and Smart [42]: ‘The asymmetry of the classic egg-shape must result from differential action of the walls of the isthmus.’ The isthmus muscles first compress the uncalcified egg along its central axis, transforming the sphere into an ellipsoid. After this, the pressure of the isthmus muscles is exerted along a certain tangent, making contact with the egg at some point (possibly a specific contact spot) on its surface, swinging like a lever relative to the vertical axis of the ovoid being formed. As a result, this process became the basis for deriving a mathematical relationship describing the geometry of the egg postulated by Smart [20]. According to Mao et al. [43], in chicken eggs, significant effects are exerted in the magnum–isthmus junction (MIJ) of the oviduct and, after the yolk–albumin mass is covered by the subshell membrane, the egg acquires its final oviform shape. Judging by photographs of eggs extracted at different stages of formation [43], it is the MIJ that has the greatest effect on the shape, squeezing the egg-shaped ovoid from the blunt end, thereby redistributing the contents to give it its characteristic geometric features. Deeming [44] further hypothesized that the egg contents, moving from the magnum to the isthmus, are compressed by the isthmus lumen. As a result, the mass of the egg is forced to protrude outward, which leads to its asymmetrical shape. It can be thus assumed that the unique oviform shape of an egg is given either by direct muscular action at the magnum–isthmus boundary [43] or by mechanical action of this connecting part when squeezing the egg mass along the oviduct [44]. Because in vivo experiments are extremely complex and difficult, both from a laboratory research viewpoint and for ethical reasons, we turned our attention to the physics of the deformation process of elastic bodies, the principles of which have been thoroughly worked out. After analyzing the classical principles of the effect of load on shell structures [45,46,47] and theoretical approaches regarding thin elastic shells of revolution [48,49,50,51] and egg-shaped shells [52,53,54,55,56], including those made of elastic materials [57,58], it has become possible to formulate a number of provisions that would help solve the issue of the conditions needed for the formation of the required asymmetric egg profile. When a concentrated load is applied to a flexible thin elastic shell, the material of such a shell is locally pressed in at the point of force application. If the shell is flexible enough, the material redistributes stresses to minimize the deformation energy. As a result, the shell “smooths out”, forming an almost flat contact surface. In thin shells, the bending resistance is usually much lower than the tensile resistance. To avoid strong stretching (which is more energy-consuming), the shell is locally straightened (becomes flat), since, in a flat area, the curvature is zero, and the bending stresses are minimal. In view of this, the shell section with minimal curvature, i.e., the maximum R value, can be safely considered the place of application of the maximum load. Confirmation of this hypothesis can be found not only among examples of classical elasticity theory or thin-walled engineering structures, but also directly in studies on the strength of bird eggs. Many authors, implementing a force impact on the shell, note its deflection, and, as a consequence, some horizontal alignment at the place of application of the load [59,60,61,62,63,64]. Hence, having a diagram of the distribution of R values along the egg surface, one can judge the nature and magnitude of the muscular efforts of the hen’s oviduct during its formation.
For all the above reasons, R values are relevant when analyzing the strength, properties and function of both individual and collections of birds’ eggs; furthermore, the theoretical principles for calculating the strength, rigidity and stability of engineering structures indicate a direct impact of the R values on all or most of these characteristics [65,66,67]. R also interacts with several other indicators, including the thickness and properties of the shell, the contact point(s), the contact area and the characteristics of anything acting upon the egg. Despite this, the computation of R has not been given due attention in the literature. The lack of published methods for measuring the curvature of the egg profile, as well as formulae for computing it, may be an obstacle to a more in-depth analysis of the relationship between the physiological characteristics of the egg formation process and the geometric features of egg shape. It is the lack of such information that prompted us to focus on the following investigation goals. In particular, the aim of this research was first to derive a formula for calculating R in any bird’s egg, taking into account its unique geometric features. The second aim was to analyze R values along the egg contours to identify the location of potential application of the load that forms its unique asymmetric egg shape.
2. Theory and Methodology
2.1. Radius of Egg Curvature
The formula for the R estimation of any smooth curve, as, for example, presented by Hobson [68], is as follows:
That is, to derive the formula for computing the R value, it is necessary to proceed from the mathematical dependence y = f(x) describing the geometry of the egg profile. Recent studies in this area [26,27] have demonstrated that an egg of any shape can be extremely accurately described mathematically using the following geometric parameters: maximum breadth (B), egg length (L), the distance (w) by which the maximum breadth of the egg is shifted from its center, i.e., from the point x = L/2, and the egg diameter (Dp) at a point located at a distance of L/4 from its pointed end (Figure 1).
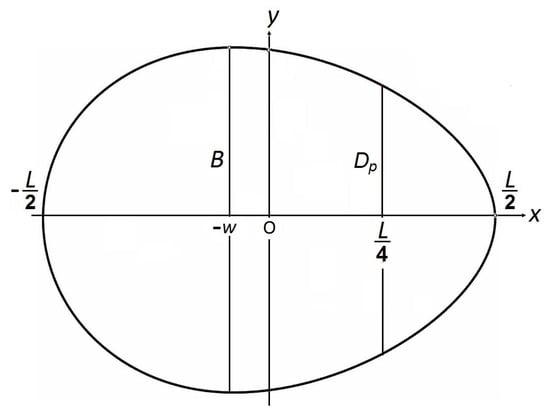
Figure 1.
Schematic representation of an egg with the main measured parameters.
Based on the four-parameter data (Figure 1) and Hügelschäffer’s model for ovoid eggs [28], a general mathematical form of a universal equation was proposed that can describe the contours of any egg [27]:
In Equation (2), yb is the equation describing the blunt part of the egg, i.e., in the interval x = [−L/2 … −w] (Figure 1); yp corresponds to the equation for the pointed part, i.e., in the interval x = [−w … L/2] (Figure 1); yj is a connecting function that allows one to mathematically ensure the smoothness of the geometric transition of the function yb to yp.
For each function in Equation (2), corresponding mathematical dependences were developed [27]:
- For the blunt end (yb):
- For the pointed end (yp):
For Equation (4), the values of Bp and wp do not correspond to the analogous B and w in Equation (3). While the parameters of Equation (3) can be measured relatively easily, i.e., directly on the egg to be studied or on its image, the values of Bp and wp are estimated as follows [27]:
Narushin et al. [27] proposed two equations for the connecting function (yj). One of them is a simpler formula that mathematically connects, or, as phrased in the manuscript, “sews” the two halves of the egg together. The second version of the formula provides a smooth transition from the blunt part yb (Equation (3)) to the pointed one yp (Equation (4)) but has a more complex mathematical form. Since further theoretical work will involve complex mathematical transformations, we decided to take as a basis a simpler version of the connecting function (yj), for which
In the same study, Narushin et al. [27] compiled all three equations (Equations (3), (4) and (7)) into a single mathematical model that represented a universal relationship for describing the contours of any egg:
Thus, the problem of deriving the computation equation for R (Equation (1)) was reduced to finding, respectively, the first and second derivatives of the function defined by Equation (8).
The relevant mathematical calculations and transformations are presented in detail in Supplementary Data SA. Since the analysis of the radii of curvature is much more convenient when using the geometric parameters of eggs in index form [15,69], where B/L is the shape index, w/L the asymmetry index, and Dp/B the conicity index, the radius of curvature function in Equation (1) was expressed as a fraction of the egg length (R/L). As a consequence, Equation (1) was rewritten in its final form:
Let us represent the R/L (Equation (9)) function graphically. In this case, taking into account that the possible variations in the values x = [−L/2 … L/2] (Figure 1), for x/L this interval will be equal to [−1/2 … 1/2]. The permissible variability of other indices: B/L, w/L and Dp/B, as well as their possible interrelations for the overwhelming majority of bird eggs were considered in detail in the work of Narushin et al. [29]. The maximum possible limits of their variability are approximately: for the ratio B/L = [0.55 … 0.90], for w/L = [0 … 0.16] and for Dp/B = [0.60 … 0.86]. However, given specific values of B/L, the maximum possible values of w/L and the maximum permissible values of Dp/B have their limitations, expressed by the following dependences [29]:
By going through possible variants of index changes with an approximate step of 0.05 for each of them, i.e., using a simulation approach, we calculated the R/L value (Equation (9)) for each set of B/L, w/L and Dp/B values corresponding to a certain virtual egg. A total of 136 virtual eggs were analyzed, each of which corresponded to a unique set of indices. Briefly, the virtual egg database was compiled in such a way as to cover all possible variants of the indices when enumerating the boundaries of their variability with a step of 0.05. After that, those variants were rejected whose calculated values of the indices (w/L)max, (Dp/B)min and (Dp/B)max did not correspond to the values obtained as a result of calculation according to Equations (10)–(12). The remaining 136 combinations characterized the entire set of geometric shapes of eggs present in nature. Examples for correspondence/coincidence between theoretical (blue line) and actual contours of eggs of various shapes were shown in Figure 2.

Figure 2.
Examples for correspondence between theoretical (blue line) and actual contours of eggs from the Natural History Collections of the Museum Wiesbaden: (a) lesser kestrel (Falco naumanni; https://commons.wikimedia.org/wiki/File:Falco_naumanni_MWNH_2023.JPG (accessed on 16 June 2025)); (b) graylag goose (Anser anser; https://commons.wikimedia.org/wiki/File:Anser_anser_MWNH_0955.JPG (accessed on 16 June 2025)); (c) Caspian tern (Hydroprogne caspia; https://commons.wikimedia.org/wiki/File:Hydroprogne_caspia_MWNH_0386.JPG (accessed on 16 June 2025)). Credit: Klaus Rassinger and Gerhard Cammerer (2012; CC-BY-SA-3.0). For better visualization, the images of eggs were unified under a single size of their length with full compliance and corresponding recalculation of all other geometric parameters.
An example of possible metamorphoses of egg forms in the created virtual database is presented in Figure 3. For this visualization, we used the value of the shape index B/L = 0.75 to change the values of w/L and Dp/B within the range of their possible variation.
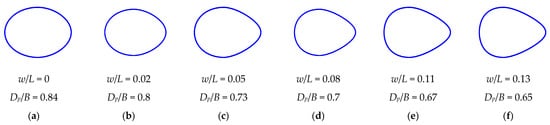
Figure 3.
Example of six generated virtual egg contours in a subset of eggs with shape index B/L = 0.75.
In the example of egg contours (Figure 3), we did not present all the intermediate variants, limiting ourselves to the main ones that demonstrate some stages of shape modification. The images in Figure 3a,f display the boundary variants of egg profiles. That is, say, an even greater increase in the value of w/L and/or a decrease in Dp/B will lead to the creation of virtual eggs that cannot be found in real-world conditions.
As an example, the visualizations of the obtained graphical dependences of R/L for several categories of eggs with the value of B/L = 0.75 and w/L, respectively, equal to 0.03 and 0.11, are presented in Figure 4.
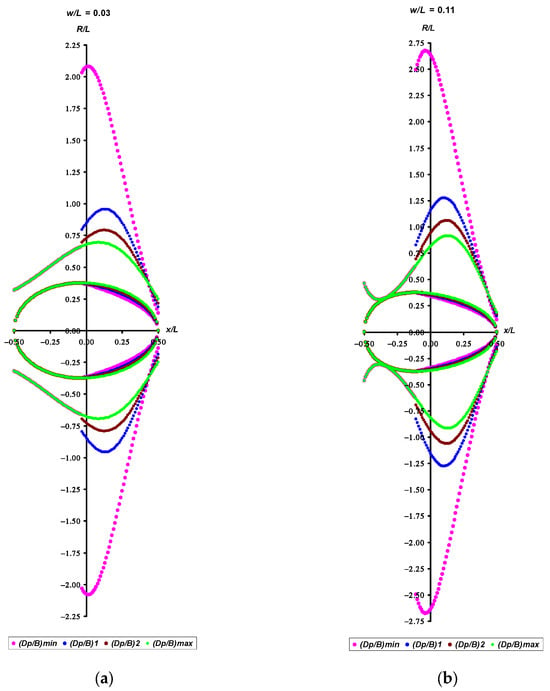
Figure 4.
Visualization of the R/L graphical dependences for egg categories with B/L = 0.75 and w/L = 0.03 (a) and w/L = 0.11 (b). The conicity index symbols correspond to the following values: (Dp/B)min = 0.70, (Dp/B)1 = 0.76, (Dp/B)2 = 0.80, (Dp/B)max = 0.84 (a); and (Dp/B)min = 0.65, (Dp/B)1 = 0.70, (Dp/B)2 = 0.74, (Dp/B)max = 0.77 (b). The values (Dp/B)min and (Dp/B)max conform to the rounded values obtained as a result of calculation using Formulae (11) and (12). The values (Dp/B)1 and (Dp/B)2 are approximately equidistant from (Dp/B)min and (Dp/B)max. For convenience, the color characteristics of the egg profiles and the corresponding R/L functions coincide.
Also shown in Figure 4 are the contours of the corresponding egg, for which its mathematical model (Equation (8)) was rewritten in the following index form:
A pattern similar to that shown in Figure 4 was also observed for other variants of egg contours and, accordingly, the R/L values calculated for them. That is, the radii of curvature for the blunt part of the eggs completely coincided with each other regardless of their degree of conicity. However, the R/L values for the pointed end had obvious differences with a clearly defined peak for each of the variants of the Dp/B values.
Determining the coordinates of the extremum point for each of the peaks of the R/L function for the pointed end of the eggs became the next stage of our theoretical research.
2.2. Radius of Curvature of the Pointed Egg End
For these purposes, we focused on the analysis of the functional dependence yp (Equation (4)), mathematically modeling the pointed end of the egg. By performing the appropriate mathematical transformations of Equation (4), the formula for calculating Rp/L value for the pointed part of the egg took the following form:
A detailed output of Equation (14) is presented in Supplementary Data SB.
2.3. Methods for Evaluation of the Extremum and Tangent
To find the coordinates of the extremum of the function Rp/L (Equation (14)), we need to find its derivative and equate it to zero. However, it is difficult to do this due to complex mathematical transformations and calculations. In this regard, we decided to use approximate methods. For this, it is advisable to approximate the obtained Rp/L dependencies with a suitable polynomial equation, the mathematical analysis of which is more convenient than the cumbersome Equation (14). The derivative of such a polynomial, equated to zero, will give the horizontal coordinate of the extremum point (x/L)ext. Substituting this value into Equation (14) will allow us to determine the coordinate of the extremum point along the vertical axis (Rp/L)ext that, in our case, will correspond to the maximum possible value of the function Rp/L (Equation (14)).
The matter of the inclination angle of the tangent to the point of the egg profile (y/L) corresponding to the extremum of the function Rp/L (Equation (14)) is also important. Following Smart’s hypothesis [20], the muscles of the bird’s oviduct, acting at a certain angle, form a conical shape of the pointed end of its egg. In view of this, it can be assumed, with some degree of hypothetical caution, that this angle can characterize the conditions of the impact of the bird’s muscular efforts during egg formation. According to Honnens and Hibbard [70], the tangent of the inclination angle will be equal to the derivative of the function y/L at the point of our interest. We determined the derivative of the pointed end when deducing Equations (9) and (14) (Supplementary Data SB):
Then, to determine the tangent of the inclination angle (α), it is sufficient to substitute the values x/L = (x/L)ext into Equation (15):
The minus sign in Equation (16) indicates that the contact point of the tangent is to the right of it on the horizontal axis.
To perform the corresponding mathematical operations described in Section 2.3, we used the same database of 136 virtual eggs with the same set of B/L, w/L and Dp/B indices as in the analysis of R of the whole egg (Section 2.1).
3. Results
3.1. Graphical Dependencies of Rp/L
According to the methodological approaches described in Section 2.3, each of the obtained Rp/L (Equation (14)) dependences was approximated by a 3rd degree polynomial, the accuracy of which fully satisfied the required conditions, and the determination coefficient was at a level of no less than r2 = 0.997. The value of another approximation accuracy indicator, root-mean-square error (RMSE), was in the range of 0 … 0.018. An example of the calculated Rp/L (Equation (14)) values and approximated by a cubic polynomial is shown in Figure 5 for the same index values as those shown above in Figure 4. In this case, taking into account the symmetry of the egg profile relative to the horizontal axis, we limited ourselves to only its upper half.
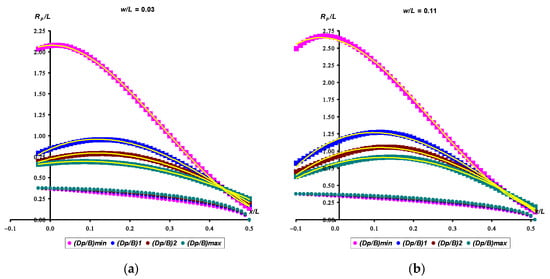
Figure 5.
Visualization of the graphical dependencies of Rp/L for egg categories with B/L = 0.75 and w/L = 0.03 (a) and w/L = 0.11 (b). The symbols for the conicity index correspond to the following values: (Dp/B)min = 0.70, (Dp/B)1 = 0.76, (Dp/B)2 = 0.80, (Dp/B)max = 0.84 (a); and (Dp/B)min = 0.65, (Dp/B)1 = 0.70, (Dp/B)2 = 0.74, (Dp/B)max = 0.77 (b). The values (Dp/B)min and (Dp/B)max conform to the rounded values obtained as a result of calculation using Formulae (11) and (12). The values (Dp/B)1 and (Dp/B)2 are approximately equidistant from (Dp/B)min and (Dp/B)max. For convenience, the color characteristics of the egg profiles and the corresponding Rp/L functions coincide. The trend lines approximated by cubic polynomials are shown in yellow.
3.2. Extremum Points of the Rp/L Function and Correlation Between (x/L)ext, (Rp/L)ext, α and Corresponding Indices
The calculated values of the extremum points of the Rp/L function were within the following limits: (x/L)ext = −0.05 … 0.16; (Rp/L)ext = 0.56 … 2.99. The inclination angle, converted from Equation (16) to degrees, was within the limits α = [ –1.1° … –23.7°].
The maximum absolute value of the angle α (23.7°) seems to be large enough that the egg contours that demonstrated such high values were subjected to a more detailed analysis. As a result, it was noted that high values of α are inherent in almost spherical eggs with a clearly defined conical pointed end (Figure 6a,b). For example, the index values of the generated virtual egg contours were: B/L = 0.9, w/L = 0.06, Dp/B = 0.76 (Figure 6a, blue contour), and B/L = 0.88, w/L = 0.09, Dp/B = 0.73 (Figure 6b, blue contour). For both contours, the absolute value of α was 23.7°.

Figure 6.
Comparison of artificially generated contours of virtual eggs (blue lines) with those for actual eggs: (a) a virtual egg with dimensions B/L = 0.9, w/L = 0.06 and Dp/B = 0.76 (blue line) and a Eurasian bullfinch (Pyrrhula pyrrhula) egg (https://commons.wikimedia.org/wiki/File:Pyrrhula_pyrrhula_MWNH_2359.JPG (accessed on 16 June 2025), by Klaus Rassinger and Gerhard Cammerer, 2012; Natural History Collections of the Museum Wiesbaden, CC-BY-SA-3.0); (b) a virtual egg with dimensions B/L = 0.88, w/L = 0.09 and Dp/B = 0.73 (blue line) and a Northern bobwhite (Colinus virginianus) egg (https://commons.wikimedia.org/wiki/File:Colinus_virginianus_MWNH_1121.JPG (accessed on 16 June 2025), by Klaus Rassinger and Gerhard Cammerer, 2012; Natural History Collections of the Museum Wiesbaden, CC-BY-SA-3.0); (c) a virtual egg with dimensions B/L = 0.742, w/L = 0.016 and Dp/B = 0.824 (blue line) and a chicken (Gallus gallus) egg; (d) a virtual egg with dimensions B/L = 0.751, w/L = 0.085 and Dp/B = 0.722 (blue line) and a chukar partridge (Alectoris chukar) egg (https://commons.wikimedia.org/wiki/File:Alectoris_chukar_MWNH_1084.JPG (accessed on 16 June 2025), by Klaus Rassinger and Gerhard Cammerer, 2012; Natural History Collections of the Museum Wiesbaden, CC-BY-SA-3.0). For better visualization, the images of eggs were unified under a single size of their length with full compliance and corresponding recalculation of all other geometric parameters.
We were unable to find absolutely identical profiles of actual eggs; however, of the closest ones, the contour of the Eurasian bullfinch (Pyrrhula pyrrhula) egg (Figure 6a, image of an egg inside a blue contour) with geometric parameters B/L = 0.81, w/L = 0.06 and Dp/B = 0.76, although not identical, clearly resembles the virtual blue contour. The contour of the Northern bobwhite (Colinus virginianus) egg (Figure 6b, image of an egg inside a blue contour) with geometric parameters B/L = 0.79, w/L = 0.09, Dp/B = 0.73 closely resembled the virtual blue contour. Recalculation of the inclination angle value resulted in α = 20.3° for the Eurasian bullfinch egg (Figure 6a) and α = 19.9° for the Northern bobwhite egg (Figure 6b). Geometric discrepancies between the theoretical contours and the images of actual eggs are clearly visible. Despite the discrepancy, this fact can be considered evidence that a sufficiently large variety of egg profiles was generated for the analysis, even exceeding the actually encountered geometric parameters with some reservation. The given example only demonstrates a fairly wide range of shapes of the employed virtual database of bird eggs. This does not mean that there are no eggs in nature with a profile identical to the blue contour of its virtual counterpart (Figure 6a,b). Perhaps they are so rare that it is quite difficult to find them in existing museum collections. In order not to make a false impression of some inaccuracies between the generated and actual egg profiles and possible inaccuracies in determining the values of α, Figure 6c,d show additional examples of determining and corresponding theoretical calculation of the inclination angle. For these purposes, a common chicken (Gallus gallus) egg that was purchased from Woodlands Farm, Canterbury and Staveleys Eggs Ltd., Coppull, UK (Figure 6c) was used, the shape of which can be conditionally attributed to typical egg-shaped ovals. An image of the chukar partridge (Alectoris chukar) egg characterized by a rather unusual, so-called pear-shaped form (Figure 6d) was also used. In this case, there is a complete geometric conformation of the virtual contours (blue lines) to the images of actual eggs (Figure 6c,d). The measured parameters allowed us to compute the corresponding indices and the value of the inclination angle as follows: B/L = 0.742, w/L = 0.016, Dp/B = 0.824 and α ≈ 12° (in its absolute value) for the chicken egg (Figure 6c) and B/L = 0.751, w/L = 0.085, Dp/B = 0.722 and α ≈ 19° for chukar partridge egg (Figure 6d). Geometrical constructions performed on the images of these eggs (Figure 6c,d) fully confirmed the computation data for α, according to Equation (16).
We also analyzed the correlation relationships between the values of (x/L)ext, (Rp/L)ext, α and the corresponding indices B/L, w/L and Dp/B, the visualization of which is presented in Figure 6. For greater clarity, the values of α are taken in absolute values.
Since the evaluated data are quantitative (not ranked) and rather monotonous, without any sudden outliers, the relationship between the parameters (Figure 7) was assessed using the Pearson correlation coefficient (r). The significance of r was set at p < 0.05. Briefly, the obtained dependences (Figure 7) can be characterized as follows. The (x/L)ext value is significantly influenced, to a greater extent, by the Dp/B (r = 0.455) (Figure 7a’) and B/L (r = 0.489) (Figure 7a’’) indices. The influence of the w/L value (Figure 7a) is practically absent (r = −0.030) and is statistically insignificant. A similar correlation dependence is observed with other response functions. The w/L value demonstrated the smallest, although significant, relationship, both with (Rp/L)ext (r = 0.299) (Figure 7b), and the insignificant one with the α values (r = 0.173) (Figure 7c). The largest and most reliable dependencies were noted between Dp/B and (Rp/L)ext (r = −0.860) (Figure 7b’), as well as B/L and α (r = 0.605) (Figure 7c’’). The relationships of B/L with (Rp/L)ext (r = −0.423) (Figure 7b’’), as well as Dp/B with α (r = −0.434) (Figure 7c’), were significant and had intermediate values. Obviously, such a distribution of the influence degree of the indices is associated with a much greater impact of w/L on the formation of the blunt end of the egg. At the same time, the conicity (Dp/B) and shape (B/L) indices form the sharp end, which undergoes the main process of geometric metamorphosis. A more thorough analysis is given below in the subsequent subsections.
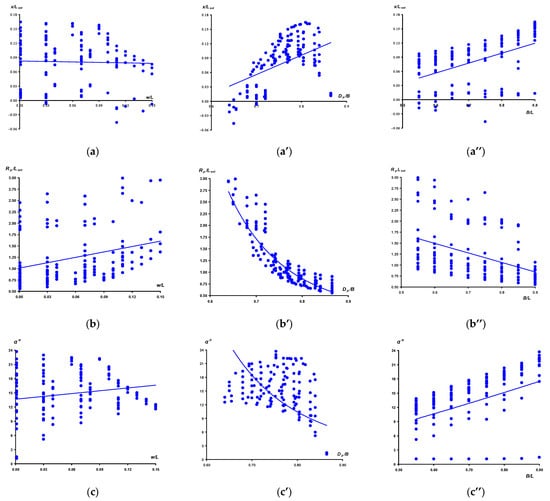
Figure 7.
Visualization of correlation links between, respectively, (x/L)ext (a,a’,a’’), (Rp/L)ext (b,b’,b’’) and α (c,c’,c’’) and the corresponding egg indices w/L (a,b,c), Dp/B (a’,b’,c’) and B/L (a’’,b’’,c’’).
3.3. Location of the Load Application That Forms an Egg
By analyzing R values along the egg contours, we then set out to identify the location of potential application of the load that forms its unique asymmetric egg shape. Analysis of the graphical dependencies in Figure 4 and Figure 5 showing the distribution of the R values along the egg contour clearly demonstrates the place of application of the muscular load. High values of R indicate small values of curvature of a given section of the surface, which is a consequence of the application of a greater load. The peak is characteristic of eggs of all shapes, and its value increases both with an increase in the degree of conicity (Figure 7b’), i.e., with a narrowing of the pointed end (a decrease in of Dp/B value), and with a shift in the maximum breadth towards the blunt part, i.e., an increase in the w/L value (Figure 7b). Without a doubt, any biological system is much more perfect, more functional and unique in its internal and external interrelations than any mechanical analogue. In this regard, the basic postulates of the theory of elasticity should be transferred with some caution to biological laws. Nevertheless, based on the above-mentioned principles of the dynamics of elastic bodies, demonstrating the most even section of the surface at the point of application of the maximum load, we hypothetically assume that this situation may suggest an increase in the impact of the muscular efforts of the bird in order to give the egg the required shape. The least efforts, or a complete absence of such, are demonstrated by eggs whose shape is close to ellipsoidal, or, as a variety of it, spherical. For example, Figure 8a shows a visualization of the distribution of R/L values for an egg with the following index values: B/L = 0.9, w/L = 0.001 and Dp/B ranging from 0.753 to 0.865. In other words, the peak in Figure 8a showed us the greatest value of R, and its reciprocal, the lowest curvature, which means the flattest area across the egg profile.
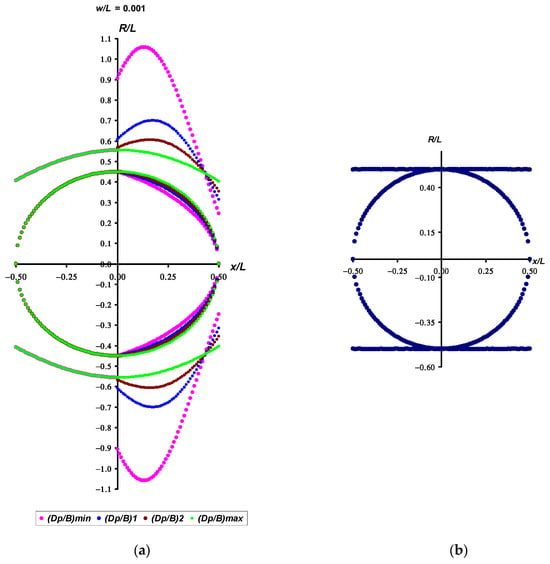
Figure 8.
Visualization of the R/L graphical dependences for egg categories with B/L = 0.9 and w/L = 0.001 (a). The conicity index symbols correspond to the following values: (Dp/B)min = 0.753, (Dp/B)1 = 0.809, (Dp/B)2 = 0.837, (Dp/B)max = 0.865. The values (Dp/B)min and (Dp/B)max conform to the rounded values obtained as a result of calculation using Formulae (11) and (12). The values (Dp/B)1 and (Dp/B)2 are approximately equidistant from (Dp/B)min and (Dp/B)max. For convenience, the color characteristics of the egg profiles and the corresponding R/L functions are the same. (b) The R/L curvature radii for a circle.
The more the egg shape tends towards an ellipsoid (green lines in Figure 8a), the more uniformly distributed are the R/L values, with a relatively small peak lying on the vertical axis. As an illustration, the absence of any stress on spherical eggs (Figure 8b), for which the R/L value is constant for any point on the surface. Such constancy is consistent with the hypothesis of Deeming [44] that spherical eggs are not stressed at the magnum–isthmus boundary. The greater the deviation of the egg from a sphere, the correspondingly higher are the R/L values, which is a consequence of the increasing efforts to impart ovoidness to the egg (Figure 7b’’).
Based on the fact that the main shape-forming section of the oviduct is the MIJ area [43], there is a high probability that this place corresponds to the values of (x/L)ext, i.e., the coordinate on the horizontal axis demonstrating the peak load on the egg, i.e., (Rp/L)ext. Analysis of the correlation links between (x/L)ext and egg indices demonstrates almost complete absence of any dependence of this value on the asymmetry index, i.e., w/L (Figure 7a). If we again hypothetically suggest that the flat areas in the graphical dependence of the distribution of radii of curvature along the surface, according to the theory of elastic bodies, are caused by more significant loads, we can assume that the desire of the mother bird to form a more elongated and narrow egg forces her to apply squeezing forces closer to the blunt end (Figure 7a’,a’’). It is possible that the root cause lies in the structural features of the MIJ section, which forces the egg mass to be squeezed precisely in this place. This occurs not only in a certain place, but also at a certain angle that also introduces its own characteristics into the formation of the egg with certain nuances of shape (Figure 7c,c’,c’’).
3.4. Simplification of the Formulae Through the Use of 2nd Order Polynomials
The theoretical formulae used in the work, although based on the measurement data of four geometric parameters of the egg (Figure 1), are extremely complex and cumbersome. In order to facilitate their use, both for practical purposes and, possibly, for further analysis and research of the process of giving the egg its unique shape, we decided to approximate the obtained data of the virtual eggs involved in this work with simpler mathematical dependences for calculating such indicators as (x/L)ext, (Rp/L)ext and α°. The accuracy of the approximation was assessed by the value of the coefficient of determination (r2) and the root-mean-square error (RMSE). The obtained formulae are based on the use of 2nd order polynomials, which have shown sufficient accuracy of calculation in comparison with theoretical results. For convenience, the values of the inclination angle α° are taken in their absolute values:
with r2 = 0.932 and RMSE = 0.013;
with r2 = 0.990 and RMSE = 0.061;
with r2 = 0.923 and RMSE = 1.440.
Figure 9 shows graphical dependences (scatter plots, fitted line plots, and residual plots) characterizing the accuracy of computing (x/L)ext, (Rp/L)ext and α° using the derived approximation models (Equations (17)–(19)).
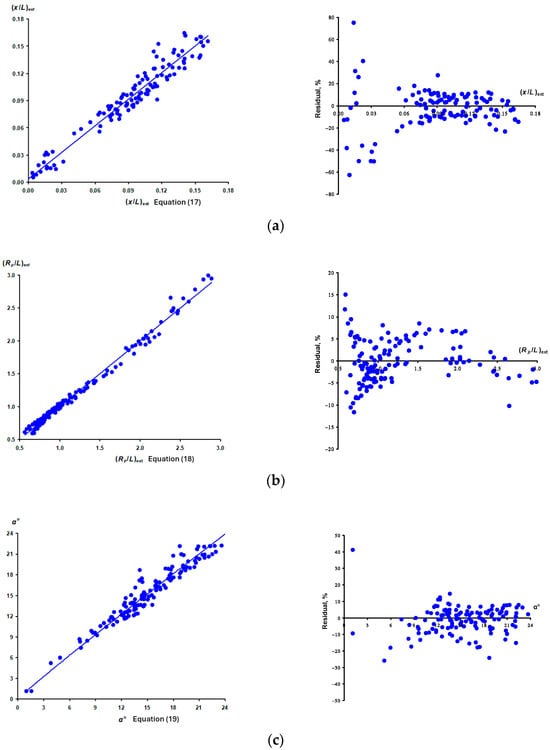
Figure 9.
Visualization of statistical characteristics of computation accuracy (scatter plots plus fitted line plots and residual plots) for (x/L)ext (a), (Rp/L)ext (b) and α° (c) using the derived approximation models (Equations (17)–(19), respectively).
The largest error range is observed when computing (x/L)ext according to Equation (17) (Figure 9a). Apparently, this is due to the small values of this response function. Hereby, the maximum deviations are observed for eggs in which the extremum of the Rp/L function is located closer to the vertical axis, that is, to the geometric center of the egg. A similar relationship is noted for other assessed indicators, (Rp/L)ext (Equation (18), Figure 9b) and α° (Equation (19), Figure 9c). In this regard, when calculating the indicators (x/L)ext, (Rp/L)ext and α° for eggs with a pronounced location of the point of minimum curvature of the shell closer to the central axis of the egg, it is recommended to use more accurate Formulae (14) and (16), as well as the methodical approach to determining (x/L)ext as described in Section 3.2.
4. Discussion
To the best of our knowledge, this study is unique in that it is the first to describe a means of determining R at any point along its contours. It supersedes our previous work [28] in which, although R was computed from Hügelschäffer’s model, we subsequently demonstrated [26,27,29] the limitations of this calculation. While deriving a formula for computing R is not such an achievement in and of itself (i.e., it is just a routine mathematical work), it is nonetheless, to the best of our knowledge, the first time that it has been achieved universally for any egg shape. Of course, the greatest differences in R/L values are observed on the side of the pointed end (Figure 4). However, with an increase in w/L, the radii of curvature also begin to increase when approaching the blunt end of the egg (Figure 4b). This situation can be explained as follows: The relationship between the indices of conicity (Dp/B) and asymmetry (w/L) was demonstrated by ourselves previously [29,69]. That is, by giving the egg a conical shape, the corresponding pressure on a certain surface area leads to a shift in the contents (previously uniformly distributed throughout the volume) closer to the blunt part. With an increase in asymmetry, i.e., an increase in the w/L values, the yolk–white mass rests against the muscular obstacle of the magnum, which does not allow it to stretch more than a certain permissible length. This emphasis results in forces being exerted on the blunt end, making it flatter and, accordingly, the radii of curvature in this area increase.
Measurement of R is usually carried out to calculate the strength characteristics of an object. Since it is the value of R that is included in the strength calculation formula. In this study, by analyzing R values along the egg contours, we were successful in identifying the location of the potential application of the load that forms its unique asymmetric egg shape. In other words, by considering the nature of the change in the value of R along the surface of the egg, it became possible to understand how it is formed. Significantly here, however, the nature of the changes in the values of R unexpectedly suggested to us an unexpected finding in the bird’s oviduct, i.e., the location and the means by which it affects the shell-less egg to give it the characteristic oviform shape. Some eggs may not conform to the derived mathematical model. However, this will most likely not apply to eggs with an atypical shape, e.g., spherical and/or elongated. The used database of virtual eggs provides for such geometric variability with a reservation. Such restrictions may be applicable for eggs of asymmetrical shape with possible growths, bulges and other anomalies. It is recommended to separate such eggs from the main sample before performing further computations of the geometric indicators of their curvature. As far as we are aware, this is one of the first occasions in which the laws of mathematics, physics and mechanics have allowed us to look, virtually, inside the bird’s oviduct. Previous studies addressed this question by dissecting hens, photographing eggs at different stages of their formation and observing their passage through the oviduct [43,71,72,73]. Such work led to various hypotheses about where and how the bird squeezes or pushes the egg, ultimately resulting in its iconic shape [20,41,44,74,75]. Here, however, we examined this issue only by analyzing the radii of curvature of the egg profile, applying our logic and theoretical foundations of the deformation of solids. The hypothesis put forward here may be useful in subsequent studies aimed at both a greater understanding of the mechanisms of egg shape formation and the study of various processes of the developmental biology of birds in terms of evolutionary morphology and the evolutionary links between behavior, ecology, and adaptation to the environment. Knowledge of the degree of involvement and coordination of the oviduct muscles in the formation process can help develop breeding programs in the poultry industry [76,77,78,79] aimed at obtaining eggs of a given shape, as well as for deep learning for subsequent automatic sorting of eggs depending on various quality parameters [80]. Understanding the fine-tuning of muscle efforts can inspire bioengineers to optimize technological solutions in creating appropriate designs and products of an egg shape, combining the strength and lightness characteristics of bird eggs.
The theoretical basis proposed here is based on a mathematical model of the geometry of bird eggs that undoubtedly has its advantages, the main ones being the possibility of deriving clear, mathematically verified and logically justified computation formulae, unification of the entire variety of shapes and sizes by three indices involved in the calculations, and the prospects for using this methodological approach to study other similar systems. However, in fairness, it should be noted that the present study is purely theoretical in nature and can only be considered as a hypothesis.
5. Conclusions
Collectively, this research was a demonstration of how the theoretical knowledge of physical, mechanical and mathematical processes can be helpful in the solution of biological problems. The distribution pattern of the R values along the surface of an already laid, full-fledged egg allowed us to conclude that there is a certain surface point on the egg profile at which the R values exceed, and in some eggs, quite significantly, at other points. In the aligned, geometrically smooth and rounded egg contour, an abnormally flat section appears. In accordance with the theory of asymmetrically loaded elastic bodies, it is very likely that at this point (or section), a concentrated muscular load is carried out, in most cases, directed at some acute angle to the longitudinal axis of the egg, in order to give it a unique egg-shaped form. Since these investigations were purely theoretical, i.e., without appropriate biomechanical and/or anatomical confirmation, this assumption is only hypothetical. Theoretical computations aimed at identifying the location of application of this load, angle and muscle effort, indirectly dependent on the maximum R value, made it possible to link these parameters with the three egg indices: shape (B/L), asymmetry (w/L), and conicity (Dp/B). The resultant computation equations will help, in further research, to judge the location and, as a consequence, the possible identification of the form-generating muscle of the bird’s oviduct.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/computation13100232/s1, Supplementary Data SA and SB.
Author Contributions
Conceptualization, V.G.N.; methodology, V.G.N.; software, V.G.N.; validation, V.G.N., M.N.R. and D.K.G.; formal analysis, V.G.N.; investigation, V.G.N.; data curation, V.G.N.; writing—original draft preparation, V.G.N.; writing—review and editing, V.G.N., M.N.R. and D.K.G.; visualization, V.G.N.; supervision, D.K.G.; project administration, M.N.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.
Acknowledgments
We are most grateful to the anonymous reviewers for their very useful advice, recommendations and correction suggestions, owing to which the manuscript acquired its scientific significance and essential improvement.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CAD/CAM | Computer-Aided Design and Computer-Aided Manufacturing |
| MIJ | magnum–isthmus junction |
| Nomenclature | |
| B | Egg maximum breadth |
| Bp | An auxiliary parameter characterizing the conditional maximum breadth of an egg in a mathematical model for the shape of its pointed part and calculated according to Equation (5) |
| Dp | Egg diameter at a point located at a distance of L/4 from the pointed end |
| L | Egg length |
| R | Radius of egg curvature |
| RMSE | Root-mean-square error |
| r | Correlation coefficient |
| w | Distance by which the maximum breadth of the egg is shifted from its center, i.e., from the point x = L/2 |
| wp | An auxiliary parameter characterizing the conditional distance of the shift in the middle axis of the egg in the mathematical model for the shape of its pointed part and calculated according to Equation (6) |
| x | Horizontal coordinate |
| y | Vertical coordinate |
| p, b, j, ext | The corresponding indices denote the pointed part of the egg, its blunt part, the connecting function and the extreme point |
| α | Angle of inclination of the tangent to a point on the egg contour |
References
- Hsu, F.H.; Liu, C.S.; Li, Y.C. Design of a measurement system for the radius of curvature, thickness, and refractive index of spherical transparent materials. Appl. Phys. B 2025, 131, 112. [Google Scholar] [CrossRef]
- Zhong, T.; Guo, G.; Chow, Y.; Yang, Y.; Zhang, T.; Yang, J.; Lu, M.; Wang, Y.; Zhu, Y.; Jia, T.; et al. Measurement method of refractive index for optical lenses based on curvature radius fitting of small-sized aspheric surfaces. Optics 2025, 6, 4. [Google Scholar] [CrossRef]
- Wu, Y.; Hou, X.; Zhang, S.; Zhao, Y.; Hu, X. High-precision interferometric measurement method for the radius of curvature with a computer-aided adjustment model. Opt. Express 2025, 33, 18791–18809. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, B.; Yang, Y.; Liu, Z.; Pan, H. Influence mechanism of cathode curvature radius on corona discharge at microscale. Energies 2024, 17, 3411. [Google Scholar] [CrossRef]
- Więcek, T.; Warsza, Z.L.; Puchalski, J.; Bubela, T. Theoretical basis of the laser reflection method of measuring the radius of curvature of circular-symmetrical lenses. Phys. Economy 2024, 6, 47–59. [Google Scholar] [CrossRef]
- Santos, A.V.; Canavarro, D.; Horta, P.; Collares-Pereira, M. Assessment of the optimal curvature radius of linear Fresnel primary mirrors. Sol. Energy 2024, 270, 112376. [Google Scholar] [CrossRef]
- Ali, A.; Amer, M.; Nada, N. Error analysis of laser interferometric system for measuring radius of curvature. J. Opt. 2024, 53, 1360–1373. [Google Scholar] [CrossRef]
- Singer, W.; Totzeck, M.; Gross, H. Handbook of Optical Systems: Vol. 2. Physical Image Formation; Gross, H., Ed.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2006; Available online: https://d-nb.info/971960925/04 (accessed on 16 June 2025).
- Wang, J.; Zhou, J. Relationship between the axial length/corneal radius of curvature ratio and hyperopia reserve in preschool children aged 3–6 years. BMC Ophthalmol. 2025, 25, 198. [Google Scholar] [CrossRef]
- Jerban, S.; Tabbaa, S.M.; Caldwell, P.E., III; Jones, K.J.; Bugbee, W.; Crawford, D.C.; Chang, E.Y. Evaluation of the femoral condyle radius of curvature at the chondral surface shows significant correlation with the anterior-posterior length. Cartilage 2025, 19476035251314109. [Google Scholar] [CrossRef]
- Wu, S.; Liu, S.; Huang, M.; Liu, Z.; Shi, J.; Ling, M. Different radius of curvature at the talus trochlea from northern Chinese population measured using 3D model. J. Orthop. Surg. Res. 2024, 19, 266. [Google Scholar] [CrossRef]
- Park, S.; Park, K.; Yang, S.; Byon, I.S.; Lee, J.E.; Park, S.W. Diagnosis of posterior staphyloma using the radius of steepest curvature among retinal pigment epithelium segmentation line measured by optic coherent tomography. BMC Ophthalmol. 2024, 24, 58. [Google Scholar] [CrossRef]
- Chan, C.; Sueyoshi, T.; Maruyama, M.; Nissen, C.; Shea, K. Poster 174: Is articular width or epicondylar width superior to age to optimize radius of curvature matching in capitellar osteochondral allografts? Orthop. J. Sports Med. 2024, 12 (Suppl. S2), 2325967124S00143. [Google Scholar] [CrossRef]
- Griswold, B.G.; Steflik, M.J.; Adams, B.G.; Hebert-Davies, J.; Tokish, J.M.; Parada, S.A.; Galvin, J.W. Radius of curvature of the radial head matches the capitellum: A magnetic resonance imaging analysis. JSES Int. 2023, 7, 668–672. [Google Scholar] [CrossRef] [PubMed]
- Narushin, V.G.; Volkova, N.A.; Dzhagaev, A.Y.; Griffin, D.K.; Romanov, M.N.; Zinovieva, N.A. Coupling artificial intelligence with proper mathematical algorithms to gain deeper insight into the biology of birds’ eggs. Animals 2025, 15, 292. [Google Scholar] [CrossRef] [PubMed]
- Narushin, V.G.; Volkova, N.A.; Vetokh, A.N.; Sotnikov, D.A.; Volkova, L.A.; Griffin, D.K.; Romanov, M.N.; Zinovieva, N.A. ‘Eggology’ and mathematics of a quail egg: An innovative non-destructive technology for evaluating egg parameters in Japanese quail. Food Bioprod. Process. 2024, 146, 49–57. [Google Scholar] [CrossRef]
- Narushin, V.G.; Romanov, M.N.; Griffin, D.K. Egg-inspired engineering in the design of thin-walled shelled vessels: A theoretical approach for shell strength. Front. Bioeng. Biotechnol. 2022, 10, 995817. [Google Scholar] [CrossRef]
- Preston, F.W. The shapes of birds’ eggs. Auk 1953, 70, 160–182. [Google Scholar] [CrossRef]
- Carter, T.C. The hen’s egg: A mathematical model with three parameters. Br. Poult. Sci. 1968, 9, 165–171. [Google Scholar] [CrossRef]
- Smart, I.H.M. The method of transformed co-ordinates applied to the deformations produced by the walls of a tubular viscus on a contained body: The avian egg as a model system. J. Anat. 1969, 104, 507–518. Available online: https://pmc.ncbi.nlm.nih.gov/articles/PMC1231951/ (accessed on 16 June 2025).
- Baker, D.E. A geometric method for determining shape of bird eggs. Auk 2002, 119, 1179–1186. [Google Scholar] [CrossRef]
- Troscianko, J. A simple tool for calculating egg shape, volume and surface area from digital images. Ibis 2014, 156, 874–878. [Google Scholar] [CrossRef]
- Biggins, J.D.; Thompson, J.E.; Birkhead, T.R. Accurately quantifying the shape of birds’ eggs. Ecol. Evol. 2018, 8, 9728–9738. [Google Scholar] [CrossRef]
- Biggins, J.D.; Montgomerie, R.; Thompson, J.E.; Birkhead, T.R. Preston’s universal formula for avian egg shape. Ornithology 2022, 139, ukac028. [Google Scholar] [CrossRef]
- Shi, P.; Gielis, J.; Niklas, K.J. Comparison of a universal (but complex) model for avian egg shape with a simpler model. Ann. N. Y. Acad. Sci. 2022, 1514, 34–42. [Google Scholar] [CrossRef]
- Narushin, V.G.; Romanov, M.N.; Griffin, D.K. Egg and math: Introducing a universal formula for egg shape. Ann. N. Y. Acad. Sci. 2021, 1505, 169–177. [Google Scholar] [CrossRef]
- Narushin, V.G.; Orszulik, S.T.; Romanov, M.N.; Griffin, D.K. A novel approach to egg and math: Improved geometrical standardization of any avian egg profile. Ann. N. Y. Acad. Sci. 2023, 1529, 61–71. [Google Scholar] [CrossRef]
- Narushin, V.G.; Romanov, M.N.; Lu, G.; Cugley, J.; Griffin, D.K. Digital imaging assisted geometry of chicken eggs using Hügelschäffer’s model. Biosyst. Eng. 2020, 197, 45–55. [Google Scholar] [CrossRef]
- Narushin, V.G.; Romanov, M.N.; Salamon, A.; Kent, J.P.; Griffin, D.K. Creating a simulated collection of avian egg shapes for industrial grading and application. In Egg Sensing Technologies; Khaliduzzaman, A., Ed.; CRC Press: Boca Raton, FL, USA, 2025. (in print) [Google Scholar]
- Carter, T.C. The hen’s egg: Some factors affecting deformation in statically loaded shells. Br. Poult. Sci. 1970, 11, 15–38. [Google Scholar] [CrossRef]
- Khairy, M.F.A.E.F.; Mosallam, M. Shell radii of curvature and thickness effects on egg puncture. In Role and Horizons of Agricultural Engineering in the Contemporary World, Proceedings of the 13th Annual Conference of the Misr Society of Agricultural Engineering, Cairo, Egypt, 14–15 December 2005; Misr Society of Agricultural Engineering: Cairo, Egypt, 2005; pp. 68–80. Available online: https://www.researchgate.net/publication/344289967 (accessed on 16 June 2025).
- Macleod, N.; Bain, M.M.; Hancock, J.W. The mechanics and mechanisms of failure of hens’ eggs. Int. J. Fract. 2006, 142, 29–41. [Google Scholar] [CrossRef]
- Nedomová, Š.; Severa, L.; Buchar, J. Influence of hen egg shape on eggshell compressive strength. Int. Agrophys. 2009, 23, 249–256. [Google Scholar]
- Trnka, J.; Buchar, J.; Severa, L.; Nedomová, S.; Stoklasová, P. Effect of loading rate on hen’s eggshell mechanics. J. Food Res. 2012, 1, 96–105. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, W.; Tang, W.; Wang, M. Experimental study on the geometrical and mechanical properties of goose eggshells. Braz. J. Poult. Sci. 2017, 19, 455–464. [Google Scholar] [CrossRef]
- Hahn, E.N.; Sherman, V.R.; Pissarenko, A.; Rohrbach, S.D.; Fernandes, D.J.; Meyers, M.A. Nature’s technical ceramic: The avian eggshell. J. R. Soc. Interface 2017, 14, 20160804. [Google Scholar] [CrossRef]
- Lian, M.; He, K.; Ratkowsky, D.A.; Chen, L.; Wang, J.; Wang, L.; Yao, W.; Shi, P. Comparison of egg-shape equations using relative curvature measures of nonlinearity. Poult. Sci. 2024, 103, 104069. [Google Scholar] [CrossRef] [PubMed]
- Ryder, J.A. The mechanical genesis of the form of the fowl’s egg. Proc. Am. Philos. Soc. 1893, 31, 203–209. Available online: https://www.jstor.org/stable/982830 (accessed on 16 June 2025).
- Romanoff, A.L.; Romanoff, A.J. The Avian Egg; John Wiley & Sons Inc.: New York, NY, USA, 1949. [Google Scholar]
- Aitken, R.N.C.; Johnston, H.S. Observations on the fine structure of the infundibulum of the avian oviduct. J. Anat. 1963, 97 Pt 1, 87–99. Available online: https://pmc.ncbi.nlm.nih.gov/articles/PMC1244259/ (accessed on 16 June 2025). [PubMed]
- Smart, I.H.M. Egg-shape in birds. In Egg Incubation: Its Effects on Embryonic Development in Birds and Reptiles; Deeming, D.C., Ferguson, M.W.J., Eds.; Cambridge University Press: Cambridge, UK, 1991; pp. 101–116. [Google Scholar] [CrossRef]
- Todd, P.H.; Smart, I.M. The shape of birds’ eggs. J. Theor. Biol. 1984, 106, 239–243. [Google Scholar] [CrossRef]
- Mao, K.M.; Sultana, F.; Howlider, M.A.R.; Iwasawa, A.; Yoshizaki, N. The magnum-isthmus junction of the fowl oviduct participates in the formation of the avian-type shell membrane. Zool. Sci. 2006, 23, 41–47. [Google Scholar] [CrossRef]
- Deeming, D.C. Factors determining persistent asymmetry and egg shape in birds: A hypothesis. Ibis 2024, 166, 551–559. [Google Scholar] [CrossRef]
- Pogorelov, A.V. Bendings of Surfaces and Stability of Shells; American Mathematical Society: Providence, RI, USA, 1988. [Google Scholar]
- Calladine, C.R. Theory of Shell Structures; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar] [CrossRef]
- Goriely, A. The Mathematics and Mechanics of Biological Growth; Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Reissner, E. On finite axi-symmetrical deformations of thin elastic shells of revolution. Comput. Mech. 1989, 4, 387–400. [Google Scholar] [CrossRef]
- Tovstik, P.Y. Axially symmetric deformation of thin shells of revolution made of a non-linearly elastic material. J. Appl. Math. Mech. 1997, 61, 639–651. [Google Scholar] [CrossRef]
- Knoche, S.; Kierfeldy, J. Buckling of spherical capsules. Phys. Rev. E 2011, 84, 046608. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, J.W. Buckling of spherical shells revisited. Proc. R. Soc. A 2016, 472, 20160577. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, B.; Wang, F.; Tang, W.; Wang, W.; Zhang, M. Buckling of prolate egg-shaped domes under hydrostatic external pressure. Thin-Walled Struct. 2017, 119, 296–303. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Wang, W.; Tang, W.; Zhu, Y. Investigation on egg-shaped pressure hulls. Mar. Struct. 2017, 52, 50–66. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, J.; Tang, W.; Zhao, X.; Zhu, Y. Experimental and numerical collapse properties of externally pressurized egg-shaped shells under local geometrical imperfections. Int. J. Press. Vessels Pip. 2019, 175, 103893. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, M.; Wang, F.; Tang, W.; Zhao, X. Buckling performance of egg-shaped shells fabricated through free hydroforming. Int. J. Press. Vessels Pip. 2021, 193, 104435. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, P.; Wang, F.; Tang, W.; Zhao, X. Hydroforming and buckling of an egg-shaped shell based on a petal-shaped perform. Ocean Eng. 2022, 250, 111057. [Google Scholar] [CrossRef]
- Vella, D.; Ajdari, A.; Vaziri, A.; Boudaoud, A. Indentation of ellipsoidal and cylindrical elastic shells. Phys. Rev. Lett. 2012, 109, 144302. [Google Scholar] [CrossRef]
- Lazarus, A.; Florijn, H.C.B.; Reis, P.M. Geometry-induced rigidity in nonspherical pressurized elastic shells. Phys. Rev. Lett. 2012, 109, 144301. [Google Scholar] [CrossRef]
- Juang, J.Y.; Chen, P.Y.; Yang, D.C.; Wu, S.-P.; Yen, A.; Hsieh, H.-I. The avian egg exhibits general allometric invariances in mechanical design. Sci. Rep. 2017, 7, 14205. [Google Scholar] [CrossRef]
- Carter, T.C. The hen’s EGG: Shell forces at impact and quasi-static compression. Br. Poult. Sci. 1976, 17, 199–214. [Google Scholar] [CrossRef]
- Nedomová, Š.; Trnka, J.; Dvořáková, P.; Buchar, J.; Severa, L. Hen’s eggshell strength under impact loading. J. Food Eng. 2009, 94, 350–357. [Google Scholar] [CrossRef]
- Nedomová, Š.; Buchar, J.; Strnková, J. Goose’s eggshell strength at compressive loading. Potravinárstvo Slovak J. Food Sci. 2014, 8, 54–61. [Google Scholar] [CrossRef]
- Nedomová, Š.; Kumbár, V.; Trnka, J.; Buchar, J. Effect of the loading rate on compressive properties of goose eggs. J. Biol. Phys. 2016, 42, 223–233. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Narushin, V.G.; Chausov, M.G.; Shevchenko, L.V.; Pylypenko, A.P.; Davydovych, V.A.; Romanov, M.N.; Griffin, D.K. Shell, a naturally engineered egg packaging: Estimated for strength by non-destructive testing for elastic deformation. Biosyst. Eng. 2021, 210, 235–246. [Google Scholar] [CrossRef]
- Gordon, J.E. Structures, or Why Things Don’t Fall Down, 2nd ed.; Penguin Books Limited: Harmondsworth, UK, 2003. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; Dover Publications, Inc.: Mineola, NY, USA, 2009. [Google Scholar]
- Zingoni, A. Shell Structures in Civil and Mechanical Engineering: Theory and Analysis, 2nd ed.; ICE Publishing: Ashton-Under-Lyne, UK, 2017. [Google Scholar] [CrossRef]
- Hobson, A.J. “Just the Maths”. Unit Number 11.4. Differentiation Applications 4. Circle, Radius & Center of Curvature. University of East Anglia, Norwich, UK, 2002. Available online: https://archive.uea.ac.uk/jtm/11/dg11p4.pdf (accessed on 16 June 2025).
- Narushin, V.G.; Romanov, M.N.; Griffin, D.K. Pear-shaped eggs evolved to maximize the surface area-to-volume ratio, increase metabolism, and shorten incubation time in birds. Integr. Zool. 2025. [Google Scholar] [CrossRef]
- Honnens, J.; Hibbard, D. Chapter 20. Applications of differentiation of polynomials. In Essential Mathematical Methods 1 & 2 CAS; Evans, M., Lipson, K., Wallace, D., Eds.; Cambridge University Press: Cambridge, UK, 2008; Available online: https://www.cambridge.edu.au/downloads/education/extra/209/PageProofs/MM1and2%20CAS%20on-line/MM1and2%20CAS%202nd%20pp/Chapter%2020.pdf (accessed on 16 June 2025).
- Harper, J.A.; Marble, D.R. Egg shape. II. Muscular and other oviducal influences. Poult. Sci. 1945, 24, 61–65. [Google Scholar] [CrossRef]
- Du, J.; Hincke, M.T.; Rose-Martel, M.; Hennequet-Antier, C.; Brionne, A.; Cogburn, L.A.; Nys, Y.; Gautron, J. Identifying specific proteins involved in eggshell membrane formation using gene expression analysis and bioinformatics. BMC Genom. 2015, 16, 792. [Google Scholar] [CrossRef]
- Mishra, B.; Sah, N.; Wasti, S. Genetic and hormonal regulation of egg formation in the oviduct of laying hens. In Poultry—An Advanced Learning; Kamboh, A.A., Ed.; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Birkhead, T.R.; Thompson, J.E.; Biggins, J.D.; Montgomerie, R. The evolution of egg shape in birds: Selection during the incubation period. Ibis 2019, 161, 605–618. [Google Scholar] [CrossRef]
- Deeming, D.C. Effect of composition on shape of bird eggs. J. Avian Biol. 2018, 49, jav-01528. [Google Scholar] [CrossRef]
- Bondarenko, Y.V.; Khvostik, V.P. Pokrashhennya produktyvnosti m’yaso-yayechnyh kurej vitchyznyanoyi selekciyi [Improving the productivity of meat and egg chickens of domestic selection]. Vìsn. Sumsʹkogo Nac. Agrar. Unìv. Ser. Tvarynnytstvo [Bull. Sumy Natl. Agrar. Univ. Ser. Livest.] 2020, 2, 29–32. [Google Scholar] [CrossRef]
- Romanov, M.N. Qualitative and Quantitative Egg Characteristics in Laying Hens of Different Genotype. In Egg and Egg Products Quality, Proceedings of the 6th European Symposium on Quality of Eggs and Eggs Products, Zaragoza, Spain, 25–29 September 1995; World’s Poultry Science Association, Spanish Branch: Madrid, Spain, 1995; pp. 203–206. Available online: https://scholar.google.com/citations?view_op=view_citation&citation_for_view=1fz40BYAAAAJ:KYgttONoxcsC (accessed on 16 June 2025).
- Baydevlyatova, O.N.; Ogurtsova, N.S.; Shomina, N.V.; Tereshchenko, A.V. Morfologicheskiye pokazateli kachestva yaits novoy subpopulyatsii kur myaso-yaichnogo napravleniya produktivnosti [Morphological indicators of egg quality in a new chicken subpopulation of the meat-egg type of productivity]. Ptakhivnytstvo [Poult. Farm.] 2009, 64, 109–115. Available online: http://avianua.com/archiv/ptahivnictvo/64/15.pdf (accessed on 16 June 2025).
- Moiseeva, I.G. Vliyaniye inbridinga na kachestvo kurinykh yaits [The effect of inbreeding on the quality of fowl eggs]. Genetika 1970, 6, 99–107. Available online: https://www.cabidigitallibrary.org/doi/full/10.5555/19700104311 (accessed on 16 June 2025).
- Wu, Z.; Zhang, H.; Fang, C. Research on machine vision online monitoring system for egg production and quality in cage environment. Poult. Sci. 2025, 104, 104552. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).