Abstract
The fractional regularized long wave equation and the fractional nonlinear shallow-water wave equation are the noteworthy models in the domains of fluid dynamics, ocean engineering, plasma physics, and microtubules in living cells. In this study, a reliable and efficient improved F-expansion technique, along with the fractional beta derivative, has been utilized to explore novel soliton solutions to the stated wave equations. Consequently, the study establishes a variety of reliable and novel soliton solutions involving trigonometric, hyperbolic, rational, and algebraic functions. By setting appropriate values for the parameters, we obtained peakons, anti-peakon, kink, bell, anti-bell, singular periodic, and flat kink solitons. The physical behavior of these solitons is demonstrated in detail through three-dimensional, two-dimensional, and contour representations. The impact of the fractional-order derivative on the wave profile is notable and is illustrated through two-dimensional graphs. It can be stated that the newly established solutions might be further useful for the aforementioned domains.
1. Introduction
In recent years, mathematical modeling, coupled with fractional calculus, has garnered significant attention from researchers across diverse applied sciences, such as fluid dynamics, plasma physics, optical fiber, and signal processing [1,2,3,4]. The applications of fractional models are broad and impactful, including the characterization of viscoelastic behavior with fewer parameters [5], insights into the behavior, stability, and unpredictability of chaotic systems [6], accurate predictions of contaminant transport at large scales in anomalous surfaces [7], and the description of damping in mechanical systems with materials exhibiting non-integer-order viscoelasticity [8], among various other contexts, providing a comprehensive framework for addressing complex phenomena. Several definitions of fractional order differentiation have been proposed by prominent academics. For example, the Grunwald–Letnikov definition, the Caputo definition, the modified Riemann–Liouville (R-L) definition, the Caputo–Fabrizio definition, the Atangana–Baleanu definition, the conformable definition, the beta definition, etc. [9,10,11,12]. Various fractional derivative definitions, such as the R-L, Caputo, and conformable, have been utilized in research articles to seek solutions for different models. However, these definitions exhibit shortcomings in adhering to fundamental principles of derivatives; for instance, for a constant function, the R-L definition is unable to yield zero; for the only-zero domain, the conformable derivative produces zero; and the Caputo definition is restricted to highly smooth functions. In contrast, the beta fractional derivative, presented in 2016 by Atangana et al. [12], addresses these issues and is widely employed for fractional modeling.
Beta derivative: Let be a function, then the beta derivative of can be denoted by and defined as follows [12]:
where is the order of beta derivative.
The nonlinear mathematical models along with fractional calculus of science and engineering are frequently termed fractional nonlinear evolution equations (FNLEEs). Examining a phenomenon through mathematical models is insufficient. It is imperative to obtain analytical solutions for these models to extract valuable insights and effectively address inherent limitations associated with the studied phenomena. Solitary wave solitons, a special type of analytical solution for the FNLEEs, can be obtained through the homogeneous balance principle. Solitary wave solutions exhibit significant features such as the ability to travel long distances without deviation, and after colliding, they preserve their shapes and velocities. The discovery of soliton solutions for these models has prompted numerous researchers to employ various approaches. Through dedicated efforts, they have introduced multiple analytical and numerical methods to uncover soliton solutions and conducted extensive research to illustrate the intricate behaviors exhibited by these solitons. For example, the modified auxiliary equation scheme [13], the extended tanh function method [14], the improved Bernoulli sub-equation function method [15], the extended Kudryashov method [16], the two-variable -expansion strategy [17], the Jacobi elliptic method, the sine-Gordon function procedure [18], the hyperbolic function approach [19], the F-expansion approach [20], the improved F-expansion technique [21], the enhanced modified simple equation method [22], the higher-order Haar wavelet method [23], etc.
The regularized long wave (RLW) equation, introduced by Benjamin et al. in 1972, serves as an approximation for describing the unidirectional propagation of long waves within specific nonlinear dispersive systems [24]. This mathematical model stands as an alternative to the KdV (Korteweg–de Vries) equation, which is widely employed to model various physical phenomena such as shallow-water dynamics, ion-acoustic plasma waves, nonlinear wave diffusion, phonon packets in nonlinear crystals, and similitude dissipations arising from processes such as heat conduction, chemical reactions, thermal radiation, and others [25]. In [26], the author represents the space-time fractional regularized long wave (FRLW) equation in the following form after introducing a spatial evolution parameter:
In Equation (2), signifies the vertical displacement of the water surface and in the study of plasma physics, it represents negative electrostatic potential. The nonzero arbitrary constants , and control the nonlinear, dispersive, and propagation effects, respectively. Since the RLW equation is of significant importance in fluid mechanics and plasma physics, several studies have employed diverse approaches to seek the soliton solutions of the RLW equation. For example, Akbar et al. [25], Abdel-Salam et al. [26], Kumar et al. [27], Maarouf et al. [28], and others in [29,30,31,32] examined the FRLW equation.
Another fractional nonlinear model that describes wave propagation in a weakly nonlinear and dispersive media is known as the weakly nonlinear shallow-water wave (SWW) equation. The time-fractional weakly nonlinear SWW equation is [33]:
where signifies the displacement of the wave particles, the parameter represents the height of the wave, and is the gravitational force. This equation is derived under the assumptions of a non-rotating, incompressible, and inviscid flow with the -axis and -axis oriented positively upward from the free surface in the gravitational field. The fractional nonlinear SWW equation and its soliton solutions are of significant importance in the study of nonlinear phenomena in ocean engineering and applied science. Inspired by this significance, numerous academics have applied various methodologies, such as the new extended direct algebraic scheme [33], the modified Riccati-expansion approach [34], analytical and semi-analytical techniques [35], generalized rational and Kudryashov methods [36], the Jacobi elliptic function approach [37], the extended Jacobian elliptic function expansion scheme [38], etc., in both the integer- and fractional-order weakly nonlinear shallow-water wave equations. However, despite previous studies demonstrating the effectiveness of the improved F-expansion scheme and its systematic approach, soliton solutions of the FRLW and fractional nonlinear SWW equations using this approach have not been explored in the academic literature. Consequently, the goal of this article is to establish soliton solutions for the aforementioned nonlinear fractional models exploiting the F-expansion approach. Unlike earlier studies, this research introduces several novel soliton solutions for the FRLW and SWW equations. Specifically, rational solutions involving hyperbolic and trigonometric functions are ascertained for both equations. Additionally, solutions for the FRLW equation have been derived that incorporate both trigonometric and hyperbolic functions. In addition, the results of this study reveal a rich variety of robust soliton solutions, including the bell-shaped soliton, anti-bell-shaped soliton, singular periodic soliton, flat kink soliton, and other types.
The rest of this article is structured as follows: Section 2 elucidates the fundamental steps of the suggested scheme. In Section 3, soliton solutions for the aforementioned fractional nonlinear evolution equations are derived. Section 4 compares our outcomes with prior studies. Section 5 presents 3D, 2D, and contour plots of some attained solutions and describes the influence of fractional derivatives. Finally, Section 6 concludes the article.
2. Methodology
In this section, we represent the key procedure of the F-expansion method to extract the soliton solutions of the FNLEEs. Let us assume an FNLEE in the form of a polynomial including the function and its fractional partial derivatives, where is the spatial coordinates, and is the temporal coordinate:
Here , represents the order of the fractional derivative. To implement the recommended approach for finding the soliton solutions of FNLEE (4), the solution needs to adhere to the ensuing suggested steps.
Step 1: The referred FNLLE (4) has to be transformed into a nonlinear differential equation of a single variable. To achieve this, we employ the traveling wave transformation:
Using the transformation (5) leads to the reform of Equation (4) into a nonlinear equation in terms of :
where is the polynomial of and its derivatives with respect to .
Step 2: Unlike in the F-expansion method, the solutions of Equation (6) can be expressed as the finite power series in the form:
where , , and are arbitrary parameters, and must be a positive integer that can be computed from the homogeneous balance between the nonlinear and highest-order derivative term in Equation (7). and cannot be zero simultaneously, but they can each be zero individually. is the general solution to the well-known Riccati differential equation:
The solutions to Equation (8) depend on the value of the parameter . These solutions are written as follows:
Step 3: By assigning the values of and its corresponding derivative into Equation (6), we arrive at a new equation that incorporates and its associated derivatives. Upon replacing the derivatives with those from Equation (7) within the derived equation, we completely eliminate the presence of derivatives in the equation. Then, an algebraic system of equations has been attained by equating the coefficient of to zero.
Step 4: After solving the algebraic system of equations for the coefficients of the solution, the expected soliton solutions of Equation (6) have been determined. The solutions for the given FNLEE (4) are generated by substituting these solutions into the traveling wave transformation described in (5).
3. Mathematical Analysis
This section contains some mathematical calculations and the soliton solutions of the FRLW and fractional nonlinear NSW equation attained by utilizing the improved F-expansion approach.
3.1. The Space-Time Fractional Regularized Wave (FRLW) Equation
According to Step 1, consider the following traveling wave transformation to modify Equation (2) into an ordinary differential equation
where is the amplitude of the wave, and the constants and denote the wave number and velocity, respectively.
Thus, the converted differential equation of independent variable is
In this article, we are searching for solitary wave solutions, which are naturally localized and diminish as . Accordingly, we have applied the boundary conditions , , and as which results in a zero integration constant.
Integrating Equation (10) with a zero integration constant, we attain
The homogeneous balance between the nonlinear term and highest-order derivative provide the positive integer value of the solution (7). Thus, the solution of Equation (11) becomes
Applying Step 4, the following sets of the values of the parameters are obtained.
Set 1: , , , , , , .
Set 2: , , , , , , .
Set 3: , , , , , .
Set 4: , , , , , .
Set 5: , , , , , .
Set 6: , , , , , .
Set 7: , , , , , , .
Set 8: , , , , , .
This set of coefficients leads to a variety of soliton solutions to Equation (2) depending on the values of . Below are the solutions for different cases of :
Family 1: For ,
where in the solutions and we assume, .
Family 2: For ,
where, in the solutions and we assume .
Family 1: For ,
3.2. The Time Fractional Weakly Nonlinear Shallow-Water Wave Equation
To obtain a single-variable differential equation from Equation (3), we apply the following traveling wave transformation:
Applying the transformation (13) to Equation (3), we obtain the following differential equation
Solitary wave solutions, which are inherently localized and decay as , are under study. To appropriately characterize these solutions, boundary conditions of the form , , … as have been applied, which results in a zero integration constant.
Subsequently, after integrating with a zero integration constant, we arrive at the following form:
Balancing the terms with in Equation (15) yields . Consequently, the solution to Equation (15) can be represented in the form:
here, , , , and are arbitrary constants yet to be determined. After substituting into Equation (16) and equating the coefficients of to zero, a system of equations is derived. Solving this system yields the following set of values for the coefficients: , , , and .
Set-1: , , , , .
Set-2:, , , , .
Set-3: , , , , .
The determined sets of coefficients yield many soliton solutions, which are categorized into three distinct families based on the value of .
Family 1: For ,
Family 2: For ,
Family 3: For ,
4. Comparison
In this segment, we analyze the comparison between the solutions proposed in previous articles and the results obtained in our study. The comparisons are outlined in Table 1 and Table 2.

Table 1.
Comparison between solutions.

Table 2.
Comparison between solutions.
The tables presented above indicate that some of the solution structures derived in this article are novel, while others bear similarities with solutions found in earlier studies. Notably, a large number of the solutions derived in this article do not align with any previously documented results across various parameter combinations. Specifically, rational solutions involving hyperbolic and trigonometric functions have been obtained for both equations, and solutions incorporating both trigonometric and hyperbolic functions have been derived for the FRLW equation. This observation leads to the conclusion that our study has successfully revealed several novel soliton solutions for the given equation that have not been documented in prior research.
5. Results and Discussion
This section displays the derived solutions through two- and three-dimensional as well as contour graphs, utilizing Mathematica. These graphs are presented for appropriate values of the arbitrary constants inherent in the solutions. The 3D and contour graphs are sketched within the range , while the 2D graph is plotted within the range .
The subsequent description outlines the physical characteristics of the solitons obtained in this investigation: Figure 1, Figure 2, Figure 3 and Figure 4 illustrate the graphical representations of solutions for the FRLW equation, while Figure 5, Figure 6 and Figure 7 depict the graphical representations of solutions for the fractional nonlinear SWW equation. Figure 1 illustrates a bell-shaped soliton in the solution with specific parameter values: , , , , , and . The corresponding 2D graphs are plotted for various fractional parameter values at , confirming that with variations in the fractional parameter, the soliton’s amplitude remains constant while its shape diminishes. Notably, when the nonlinear parameter switches to a negative value, this bell-shaped soliton transforms into an anti-bell-shaped soliton. It can be observed that both solitons exhibit robust stability, maintaining a constant value as . Bell-shaped solitons in ocean engineering can be used for efficient wave energy conversion, given their stable waveforms, which makes them suitable for reliable energy harvesting. A peakon soliton is derived from the solution , as visualized in Figure 2, by selecting parameter values: , , , , , , and . When the parameter takes a positive value, the compacton soliton transforms into an anti-compacton soliton, as depicted in Figure 3 with . The 2D graphs in Figure 2 and Figure 3 both illustrate the impact of the fractional parameter at . This impact is similar to the observed behavior of the bell-shaped soliton. Figure 4 depicts the plotted solution of for specific parameter values , , , , , , and , revealing a singular periodic soliton. The accompanying 2D graph highlights the effect of the fractional parameter for and at time . Additionally, the contour plot provides insights into the density distribution of this soliton. The solution of the SWW equation exhibits a kink-type soliton in Figure 5 for the choice of , , , , , , and . The 2D graph (b) is drawn for different values of the fractional parameter at time , and we observe that the amplitudes of this soliton remain unaltered with the variation of the fractional parameter. Kink solitons, also known as topological solitons, exhibit distinctive characteristics; they are localized structures with particle-like properties and possess stability in their structure. When , , , , , , and the solution generates a flat-kink-shaped soliton as visualized in Figure 6. The 2D graph for , and at time confirms that there is no change in the amplitude of the soliton with the fractional parameter . Moreover, it can be seen that this flat kink soliton maintains a constant value as . The physical behavior of the solution is depicted in Figure 7 for the given values , , , , , and . This solution offers a singular periodic shape soliton. The accompanying 2D graph represents this soliton for different values of the fractional parameter , and at time .
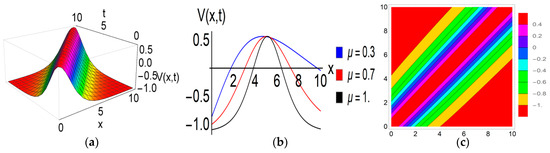
Figure 1.
Graphical exhibition of the bell-shaped soliton of the solution . (a) 3D figure. (b) 2D figure. (c) Contour plot.
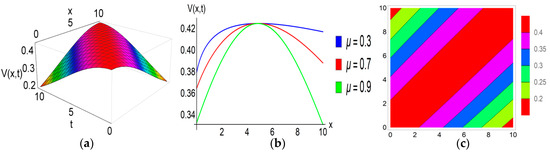
Figure 2.
Graphical exhibition of the compacton soliton of the solution . (a) 3D figure. (b) 2D figure. (c) Contour plot.
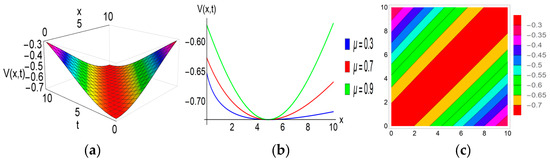
Figure 3.
Graphical exhibition of the anti-compacton soliton of the solution . (a) 3D figure. (b) 2D figure. (c) Contour plot.
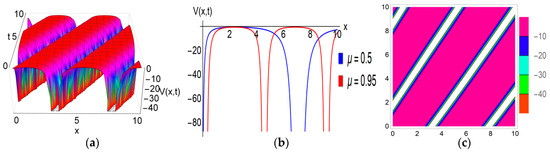
Figure 4.
Graphical exhibition of the singular periodic soliton of the solution . (a) 3D figure. (b) 2D figure. (c) Contour plot.
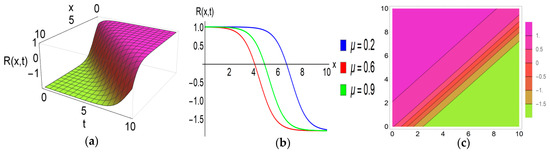
Figure 5.
Graphical exhibition of the kink soliton of the solution . (a) 3D figure. (b) 2D figure. (c) Contour plot.
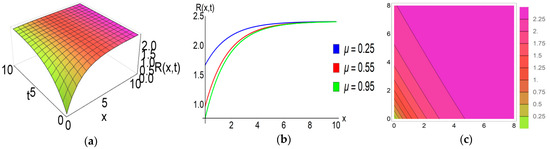
Figure 6.
Graphical exhibition of the general soliton of the solution . (a) 3D figure. (b) 2D figure. (c) Contour plot.
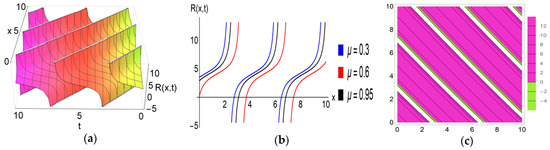
Figure 7.
Graphical exhibition of the singular periodic soliton of the solution . (a) 3D figure. (b) 2D figure. (c) Contour plot.
6. Conclusions
In this study, we investigate the fractional-order regularized long wave equation and the fractional nonlinear shallow-water wave equation, prominent models in surface water waves. Through the improved F-expansion technique with the fractional beta derivative, the study presents novel soliton solutions in terms of trigonometric, hyperbolic, rational, and algebraic functions. The derived solutions include compacton, anti-compacton, kink, bell-shaped, anti-bell-shaped, singular periodic, and flat kink solitons, offering a diverse range of reliable outcomes. The physical attitude of the established solitons is efficiently analyzed through three-dimensional, two-dimensional, and contour representations. The impact of the fractional-order derivative on the wave profile is particularly illustrated in the two-dimensional graphs. These newly established solutions hold potential efficacy in fluid dynamics, ocean engineering, plasma physics, and related domains, indicating the significance of the findings in advancing our understanding and applications in these fields. Therefore, the soliton solution of other wave equations can be investigated using the improved F-expansion method, which is the focus of our next study.
Author Contributions
S.D.: Methodology, Formal analysis, Investigation, Visualization, Validation, Writing—review editing. M.M.H.: Data Curation, Software, Funding acquisition, Writing—original draft. M.A.A.: Conceptualization, Resources, Project administration, Supervision, Writing—original draft. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-289).
Institutional Review Board Statement
This article does not involve any human or animal studies. The authors affirm that they have read and adhered to the statement of ethical standards for manuscript submission to this journal. Furthermore, the manuscript has not been copyrighted, published, or submitted elsewhere.
Data Availability Statement
The research described in the article did not involve the use of any data.
Conflicts of Interest
The authors assert that they do not have any known competing financial interests or personal relationships that could have been perceived as influencing the work presented in this paper.
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Akbar, M.A.; Wazwaz, A.M.; Mahmud, F.; Baleanu, D.; Roy, R.; Barman, H.K.; Mahmoud, W.; Al Sharif, M.A.; Osman, M.S. Dynamical behavior of solitons of the perturbed nonlinear Schrödinger equation and microtubules through the generalized Kudryashov scheme. Results Phys. 2022, 43, 106079. [Google Scholar] [CrossRef]
- Devnath, S.; Akbar, M.A.; Gómez-Aguilar, J.F. Diverse optical soliton solutions of two space-time fractional nonlinear evolution equations by the extended Kudryashov method. Phys. Scr. 2023, 98, 115235. [Google Scholar] [CrossRef]
- Islam, M.T.; Akter, M.A.; Gomez-Aguilar, J.F.; Akbar, M.A.; Pérez-Careta, E. Innovative and diverse soliton solutions of the dual core optical fiber nonlinear models via two competent techniques. J. Nonlinear Opt. Phys. Mater. 2023, 32, 2350037. [Google Scholar] [CrossRef]
- Su, X.; Chen, W.; Xu, W. Characterizing the rheological behaviors of non-Newtonian fluid via a viscoelastic component: Fractal dashpot. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Ryehan, S. Numerically Unveiling Hidden Chaotic Dynamics in Nonlinear Differential Equations with Riemann-Liouville, Caputo-Fabrizio, and Atangana-Baleanu Fractional Derivatives. arXiv 2023, arXiv:2307.03251. [Google Scholar]
- Suzuki, J.L.; Gulian, M.; Zayernouri, M.; D’Elia, M. Fractional modeling in action: A survey of nonlocal models for subsurface transport, turbulent flows, and anomalous materials. J. Peridyn. Nonlocal Model. 2023, 5, 392–459. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, D.L. Fractional derivatives in the description of damping materials and phenomena. In The Role of Damping in Vibration and Noise Control; ASME: New York, NY, USA, 1987; pp. 125–135. [Google Scholar]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Al-Shawba, A.A.; Abdullah, F.A.; Azmi, A.; Akbar, M.A.; Nisar, K.S. Compatible extension of the (G′/G)-expansion approach for equations with conformable derivative. Heliyon 2023, 9, e15717. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Akram, G.; Sadaf, M.; Khan, M.A. Soliton solutions of the resonant nonlinear Schrödinger equation using modified auxiliary equation method with three different nonlinearities. Math. Comput. Simul. 2023, 206, 1–20. [Google Scholar] [CrossRef]
- El-shamy, O.; El-barkoki, R.; Ahmed, H.M.; Abbas, W.; Samir, I. Exploration of new solitons in optical medium with higher-order dispersive and nonlinear effects via improved modified extended tanh function method. Alex. Eng. J. 2023, 68, 611–618. [Google Scholar] [CrossRef]
- Yao, S.W.; Islam, M.E.; Akbar, M.A.; Inc, M.; Adel, M.; Osman, M.S. Analysis of parametric effects in the wave profile of the variant Boussinesq equation through two analytical approaches. Open Phys. 2022, 20, 778–794. [Google Scholar] [CrossRef]
- Devnath, S.; Khan, K.; Akbar, M.A. Numerous analytical wave solutions to the time-fractional unstable nonlinear Schrödinger equation with beta derivative. Partial Differ. Equ. Appl. Math. 2023, 8, 100537. [Google Scholar] [CrossRef]
- Devnath, S.; Khatun, M.M.; Akbar, M.A. Analytical solutions and soliton behaviors in the space fractional Heisenberg ferromagnetic spin chain equation. Partial Differ. Equ. Appl. Math. 2024, 11, 100783. [Google Scholar] [CrossRef]
- Ma, Y.L.; Li, B.Q.; Fu, Y.Y. A series of the solutions for the Heisenberg ferromagnetic spin chain equation. Math. Methods Appl. Sci. 2018, 41, 3316–3322. [Google Scholar] [CrossRef]
- Malik, S.; Almusawa, H.; Kumar, S.; Wazwaz, A.M.; Osman, M.S. A (2+1)-dimensional Kadomtsev–Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions. Results Phys. 2021, 23, 104043. [Google Scholar] [CrossRef]
- Bashir, M.A.; Alhakim, L.A. New F expansion method and its applications to modified KdV equation. J. Math. Res. 2013, 5, 83. [Google Scholar] [CrossRef]
- Islam, M.S.; Khan, K.; Akbar, M.A. Application of the improved F-expansion method with Riccati equation to find the exact solution of the nonlinear evolution equations. J. Egypt. Math. Soc. 2017, 25, 13–18. [Google Scholar] [CrossRef]
- Devnath, S.; Khan, S.; Akbar, M.A. Exploring solitary wave solutions to the simplified modified camassa-holm equation through a couple sophisticated analytical approaches. Results Phys. 2024, 59, 107580. [Google Scholar] [CrossRef]
- Ratas, M.; Salupere, A.; Majak, J. Solving nonlinear PDEs using the higher order Haar wavelet method on nonuniform and adaptive grids. Math. Model Anal. 2021, 26, 147–169. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1972, 272, 47–78. [Google Scholar]
- Akbar, M.A.; Abdullah, F.A.; Khatun, M.M. Comprehensive geometric-shaped soliton solutions of the fractional regularized long wave equation in ocean engineering. Alex. Eng. J. 2023, 72, 593–604. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.; Yousif, E.A. Solution of nonlinear space-time fractional differential equations using the fractional Riccati expansion method. Math. Probl. Eng. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Physica A 2018, 492, 155–167. [Google Scholar] [CrossRef]
- Maarouf, N.; Maadan, H.; Hilal, K. Lie symmetry analysis and explicit solutions for the time-fractional regularized long-wave equation. Int. J. Differ. Equ. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Aminikhah, H.; Refahi Sheikhani, A.H.; Rezazadeh, H. Sub-equation method for the fractional regularized long-wave equations with conformable fractional derivatives. Sci. Iran 2016, 23, 1048–1054. [Google Scholar] [CrossRef]
- Jhangeer, A.; Muddassar, M.; Kousar, M.; Infal, B. Multistability and dynamics of fractional regularized long wave equation with conformable fractional derivatives. Ain Shams Eng. J. 2021, 12, 2153–2169. [Google Scholar] [CrossRef]
- Islam, S.R.; Khan, K.; Akbar, M.A. Exact solutions of unsteady Korteweg-de Vries and time regularized long wave equations. SpringerPlus 2015, 4, 124. [Google Scholar] [CrossRef]
- Korkmaz, A.; Hepson, O.E.; Hosseini, K.; Rezazadeh, H.; Eslami, M. Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class. J. King Saud Univ. Sci. 2020, 32, 567–574. [Google Scholar] [CrossRef]
- Jhangeer, A.; Faridi, W.A.; Asjad, M.I.; Inc, M. A comparative study about the propagation of water waves with fractional operators. J. Ocean Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.; Attia, R.A.; Eleuch, H. Exact traveling and nano-solitons wave solitons of the ionic waves propagating along microtubules in living cells. Mathematics 2020, 8, 697. [Google Scholar] [CrossRef]
- Alotaibi, M.F.; Omri, M.; Khalil, E.M.; Abdel-Khalek, S.; Bouslimi, J.; Khater, M.M. Abundant solitary and semi-analytical wave solutions of nonlinear shallow water wave regime model. J. Ocean Eng. Sci. 2022; in press. [Google Scholar]
- Khater, M.M. Abundant accurate solitonic water and ionic liquid wave structures of the nanoparticle hybrid system. Comput. Appl. Math. 2022, 41, 177. [Google Scholar] [CrossRef]
- Ashraf, F.; Javeed, T.; Ashraf, R.; Rana, R.; Akgül, A.; Rezapour, S.; Hafeez, M.B. Some new soliton solutions to the higher dimensional Burger-Huxley and Shallow water waves equation with couple of integration architectonic. Results Phys. 2022, 43, 106048. [Google Scholar] [CrossRef]
- Zahran, E.H.M. Exact traveling wave solutions for Nano-solitons of Ionic waves propagation along Microtubules in living cells and Nano-Ionic currents of MTs. World J. Nano Sci. Eng. 2015, 5, 78–87. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
