Abstract
In this paper, we introduce a new algorithm for calculating the radial and axial magnetic forces between two non-coaxial circular loops with parallel axes. These formulas are derived from a modified version of Grover’s formula for mutual inductance between the coils in question. Utilizing these formulas, we compute the radial and axial magnetic forces between two non-coaxial thick coils of rectangular cross-sections with parallel axes. In these calculations, we apply the filament method and conduct investigations to determine the optimal number of subdivisions for the coils in terms of computational time and accuracy. The method presented in this paper is also applicable to all conventional non-coaxial coils, such as disks, solenoids, and non-conventional coils like Bitter coils, all with parallel axes. This paper emphasizes the accuracy and computational efficiency of the calculations. Furthermore, the new method is validated according to several previously established methods.
1. Introduction
The calculation of mutual inductance and magnetic force between coils of various shapes and positions has been the subject of numerous studies [1,2,3,4]. Most of these calculations are presented in analytical form for coils with simple configurations.
Analytical and semi-analytical methods for calculating self and mutual inductances of conducting elements in electrical circuits, as well as magnetic force interactions between these elements, have emerged as powerful mathematical tools [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. These methods have been instrumental in advancing power transfer, wireless communication, sensing, and actuation technologies and have found applications across a wide range of scientific disciplines, including electrical and electronic engineering, medicine, physics, nuclear magnetic resonance, mechatronics, and robotics, among others.
While several efficient numerical methods are available in commercially developed software, analytical and semi-analytical methods offer the advantage of providing calculation results in the form of a final formula with a finite number of input parameters. This feature can significantly reduce computational effort when applicable. In this paper, we present new formulas for calculating the radial and axial magnetic forces between two non-coaxial circular loops with parallel axes. Using these formulas and the filament method, we calculate the forces between two non-coaxial coils of rectangular cross-sections with parallel axes. We emphasize the importance of accuracy and computational efficiency by selecting different numbers of subdivisions for the coils. Our analysis demonstrates that using the same number of subdivisions is not preferable due to significant computational time. Therefore, we choose varying numbers of subdivisions that considerably reduce computational time without compromising accuracy, which is crucial from an engineering perspective.
The results are compared with those obtained and presented in terms of line integrals [14]. These semi-analytical expressions [14] may not be familiar to most engineers, who may require simpler expressions for practical use. In this paper, we provide straightforward formulas that also utilize single integrals for Maxwell coils, as employed in the filament method. This approach is highly accessible and suitable for professionals, including engineers and physicists, working in this field.
We also employ another method [5], where the single integral is replaced by the summation of its kernel function over very small segments within the integration interval [0, π]. This method achieves considerably reduced computational time with satisfactory accuracy. All methods are validated according to the methods given in [13,14].
2. Basic Expressions
In this paper, we use the modified formula for calculating the mutual inductance between two circular loops with parallel axes to calculate the radial and the axial magnetic force between them (see Figure 1) [5],
wherein
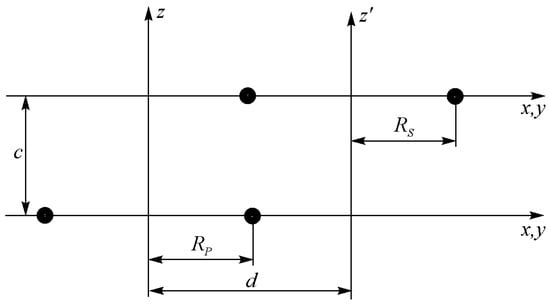
Figure 1.
Filamentary circular loops with parallel axes.
- —are the radii of the primary and secondary loops in (m), respectively.
- —is the perpendicular displacement between parallel axes of coils in (m).
- —is the axial displacement between the centers of coils in (m).
- K(k) and E(k) are the complete elliptical integrals of the first and the second kind [28,29].
- is the permeability of the vacuum.
The radial and the axial magnetic force can be obtained by [1],
IP and IS—are the currents in the primary and secondary loops in (A), respectively.
According to [1], the force between two filaments is one of the attractions if the currents in them are in the same direction around the common axis. If the currents in the two filaments are in opposite directions around the common axis, the force between them is one of repulsion.
Using (1)–(3) we have,
wherin
3. Filament Method for Calculating the Magnetic Force Fr and Fa between Two Non-Coaxial Coils of Rectangular Cross-Section with Parallel Axes
- Let us treat two non-coaxial coils of rectangular cross-section with parallel axes (see Figure 2).
- Using the filament method [8,10,12], the formulas for the mutual inductance M, as well as for the magnetic forces and are as follows,
And
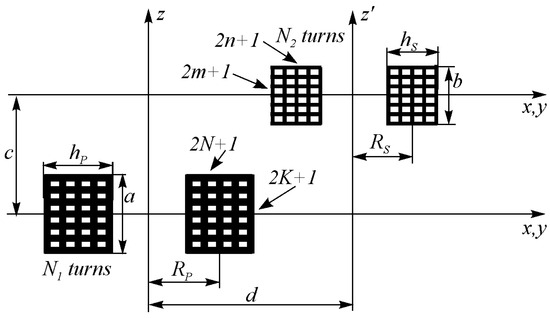

Figure 2.
Configuration of mesh matrix: Two non-coaxial coils of rectangular cross-section with parallel axes.
- IP—current in the primary coil.
- IS—current in the secondary coil.
- N1—number of turns in the primary coil.
- N2—number of turns in the secondary coil.
- R1—inner radius of the primary coil of the rectangular cross-section.
- R2—outer radius of the primary coil of the rectangular cross-section.
- R3—inner radius of the secondary coil of the rectangular cross-section.
- R4—outer radius of the secondary coil of the rectangular cross-section.
- a and b—heights of the primary and the secondary coil, respectively.
- d—perpendicular displacement between axes of coils.
- c—displacement between the plans of centers of coils.
- RP(h)—average radius of the primary coil positioned in the plane (x, y) whose axis is ‘z’ axis.
- RS(l)—average radius of the inclined secondary coil.
- K, N, n, and m—the number of the subdivisions of thick coils.
In this paper, we used the Gaussian numerical integration for the single integrals [28].
4. The Optimal Choice of the Number of the Subdivisions
Here, we discussed and presented the relationship between the radial and axial divisions as a function of the number of subdivisions of the coils.
Let us define the following radial distances LN and Ln, which correspond to radial subdivisions N and n, respectively,
As well as the following axial distances La and Lb, which correspond to radial subdivisions K and m, respectively,
From (10)–(13), we obtain the following system of equations where N, K, m and are given in the function of dimensions
for the first coil, and
or the second coil.
Thus,
LN/Ln = N/n = (R2 − R1)/(R4 − R3)
La/Ln = K/n =a/(R4 − R3)
Lb/Ln =m/n = b/(R4 − R3)
La/Lb = K/m
Now, let us conduct the following analysis concerning the coil dimensions and the number of subdivisions. We propose the optimization method to minimize the three subdivisions (variables) in the function of one subdivision (variable) for the given coils’ dimensions. The relations between the two subdivisions are linear. It means that we have the problems of four linear homogenic equations where one depends on the other three. We use the following reasoning to find the minimal number of subdivisions (variables) to reduce the computational time and keep good accuracy. Choosing the smallest dimension between the radial and axial coils dimensions (LN = R2 − R1, Ln = R4 − R3, La = z2 − z1 = a, Lb = z4 − z3 = b), we arbitrarily choose the corresponding subdivision. The other three subdivisions will depend on this arbitrarily chosen subdivision. The procedures are as follows:
- (A)
- Find
- (B)
- For obtained , we choose the corresponding variable (subdivision), for example,
- (C)
- Now we have,
Choosing the number of subdivisions, we make the pre-calculation for the different values of n controlling the computational time and the accuracy.
4.1. Definitions and Initial Values
Let K0= [l1] n0, N0 = [l2] n0, m0 = [l3] n0 and n0 = n be the initial variables that correspond to larger coil’s dimensions, where [l1] = [], [l2] = [], and [l3] = [] are the nearest ones to whole numbers.
Let n0 be the initial variable corresponding to the smaller coil’s dimension.
Let us calculate the mutual inductance for this number of subdivisions and denote the Mutual inductance as M0, as well as record the computational time.
If we are satisfied with these results, we will choose the two largest and two smallest subdivisions. Let us say that K0 and m0 are the two largest subdivisions, and N0 and n0 are the two smallest subdivisions.
4.2. Operations Description
The first step:
Decrease K0 and m0 by 1 so that K1 = K0 − 1, and m0 = m0 − 1.
Increase N0 and n0 by 1 so that N1 = N0 + 1, and n0 = n0 + 1.
Let us calculate the mutual inductance for these new subdivisions and denote the mutual inductance as M1, as well as record the computational time.
After the second calculation, we find
where is the small positive given number.
If the condition (13) is not satisfied, we proceed to the next step.
We are describing a convergence criterion for an iterative method. The procedure continues iterating until the relative difference between consecutive iterations is less than a small positive number ε, indicating that the sequence has converged.
In the general form, the convergence criterion can be written as
where:
- Mn and M(n+1) are the results of the n-th and (n + 1)-th iterations, respectively.
- ε is a small positive number that determines the desired accuracy of the solution.
If this condition is satisfied, the iterative procedure is stopped because the solution has converged to within the desired tolerance. If not, the procedure continues until the condition is met.
5. Examples
5.1. Example 1
In this example, we calculate the mutual inductance, the radial, and the axial magnetic force as a function of the displacement of two non-coaxial loops with the parallel axes where we have RP = 42.5 mm, RS = 20 mm. The perpendicular displacement between coils axes is d = 3 mm [10]. All currents in the coils are 1 A.
In this example, we compare the results for the mutual inductance obtained by [1] and Equation (1).
The absolute relative error is zero in each case. Here, we present another numerical approach to solve Equation (2) [5], which is particularly interesting from an engineering perspective. Equation (1) is solved in Table 1, using the summation of small segments of the interval over the range [0, π], thereby avoiding numerical integration. This approach allows for a considerable reduction in computational time with very high accuracy. In Table 2, we provide a comparative calculation of Equation (1) using both integration and summation methods.

Table 1.
Mutual inductance as a function of the axial displacement c of two non-coaxial loops with the parallel axes, using single integration.

Table 2.
Mutual inductance as a function of the axial displacement c of two non-coaxial loops with the parallel axes, using single integration and summation.
Here, we use another numerical approach to solve Equations (4) and (5) [5], which is particularly interesting from an engineering perspective. Equations (4) and (5) are solved using the summation of small intervals over the range [0, π], thereby avoiding numerical integration. From Table 2, we can see a very good agreement between the two numerical approaches with the absolute relative error 0.0097%. ARE is the absolute relative error.
In Table 3 and Table 4, the radial and axial force calculations given for (4) and (5) are compared with the results obtained in [10]. The single integration is used in (4) and (5). Clearly, we obtained identical results from the two approaches.

Table 3.
Radial force as a function of the axial displacement c of two non-coaxial loops with the parallel axes, using single integration.

Table 4.
Axial force as a function of the axial displacement c of two non-coaxial loops with the parallel axes, using single integration.
In Table 5 and Table 6, we provide a comparative calculation of Equations (4) and (5) using both integration and summation methods.

Table 5.
Radial force as a function of the axial displacement c of two non-coaxial loops with the parallel axes, using single integration and summation.

Table 6.
Axial force as a function of the axial displacement c of two non-coaxial loops with the parallel axes, using single integration and summation.
The results of the radial and axial forces are given in Table 5 and Table 6. All results are in very good agreement either by the numerical integration or the numerical summation. The absolute relative error is about 0.0075%. Thus, the validity of formulas (1), (4), and (5) is confirmed by the previous calculations.
In this example, all calculations were performed using a Dell laptop equipped with an Intel Core i5-12500H processor (Intel, Mountain View, CA, USA) running at 2.5 GHz, either for the single integration by the Gaussian numerical integration or the summation method.
5.2. Example 2
Parameters for two non-coaxial cylindrical coils with parallel axes given in [13] are as follows, Table 7.

Table 7.
Description of coils [13].
The axial displacement between coils is c = 0.
Here, we will calculate the mutual inductance by the presented method using the filament method using the same and different numbers of the subdivisions. Our goal is to find the best accuracy and the smallest computational time, if possible.
Let us begin with the same number of subdivisions K = N = m = n = 20.
Table 8 presents the comparative results for the mutual inductance, obtained using both [13] and Equation (6) from this work.

Table 8.
Mutual inductance as a function of the perpendicular displacement d [13], K = N = m = n = 20.
It is obvious from Table 8 that results obtained by two different approaches are in very good agreement with the absolute relative error of about 0.055%, but the computational time for the filament method is considerably enormous and is not preferable from the engineering point of consideration. Thus, the same number of subdivisions is not the smart choice in the mutual inductance calculation using the filament method. We can have very good precision of obtained results but with considerably big computational time. This is why one must find a good compromise between the accuracy and the computational time in the choice of the number of subdivisions of coils. The computational time of the calculation in [13] is not given.
This passage suggests that in Table 8, the computational time varies despite having the same number of subdivisions. This inconsistency is likely due to the different numerical methods used. The method mentioned here uses a fixed number of segments, meaning the computation time is dependent on the number of segments rather than on specific parameter values. In contrast, more advanced numerical methods employ adaptive procedures. These adaptive methods adjust the computation dynamically based on the specific parameter values, which can lead to variations in computational time even if the number of segments remains constant.
Now, let’s conduct the following analysis concerning the coil dimensions and the number of subdivisions respecting the procedures given in Section 4, by (9)–(14).
In this example, we have,
- R2 − R1 = 4.15485 cm; R4 − R3 = 1.397 cm; a = 2.413 cm; b = 14.2748 cm. The smallest dimension is R4 − R3 = 1.397 cm, which corresponds to the radial subdivision n of the second coil. Let us express all subdivisions in the function of n.
N/n = [(R2 − R1)/(R4 − R3)] = [2.9727] = 3 or N = 3n
K/n = [a/(R4 − R3)] = [1.72727] = 2 or K = 2n
m/n = [b/(R4 − R3)] = [10.218218] = 10 or m = 10n
In Table 8, Table 9 and Table 10, we give the calculations of the mutual inductance by the filament method where the values of n subdivisions are different. All other subdivisions K, N and m are in the function of n as previously discussed.

Table 9.
Mutual inductance as a function of the perpendicular displacement d [13], n = 3, K = 6, N = 9, m = 30.

Table 10.
Mutual inductance as a function of the perpendicular displacement d [13], K = 8, n = 4, N = 12. m = 40.
From Table 8, Table 9 and Table 10, we can see very good agreement between the two approaches. In all calculations, we have very high accuracy between two different approaches where the absolute relative error is about 0.0069% (Table 9), 0.0043% (Table 10), and 0.0029% (Table 11). Also, for both methods, we have the same four significant figures for each calculation. Moreover, the calculation for the different numbers of subdivisions considerably reduced the computational time (Table 7 and Table 9) regarding the calculation for the same number of subdivisions (Table 8).

Table 11.
Mutual inductance as a function of the perpendicular displacement d [13], n = 5, K = 10, N = 15, m = 50.
Even though there is no considerable difference between the calculations regarding the accuracy given in Table 7 and Table 9, it is recommended to choose K = 6, N = 9, m = 30 and n = 3. Also, without any reserve, one can take K = 8, N = 12, m = 40, and n = 4 because of a very good accuracy and the relatively small computational time.
Figure 3 illustrates the required computation time as the subdivision numbers increase for the Example 2 parameters when c (m) = 0. In this figure, the proposed subdivision selection method is compared with the conventional, even subdivision selection. The convergence to the exact solution [13], which is depicted in the red line, is illustrated. Similar to Figure 3, the evenly distributed subdivisions demand a high amount of computation time as n increases, yielding only marginal accuracy improvements. In contrast, the proposed subdivision selection method exhibits rapid convergence to the exact solution with 0.002 ARE in a short time. Remarkably, it outperforms the conventional method within the same computational time frame. The proposed method achieves instant convergence when n = 1 in under 0.1 s, making it highly effective for scenarios with varying computational resources.
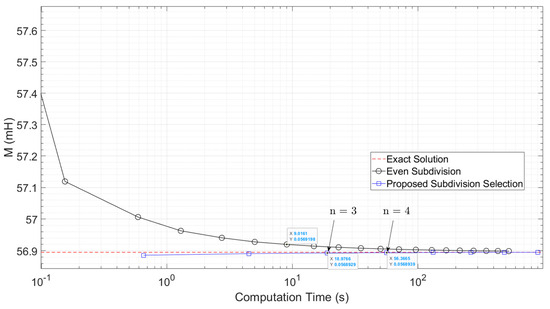
Figure 3.
Computation time for mutual inductance using the conventional even subdivisions method (black lines) and the proposed subdivision selection method (blue line) for Example 2 when c (m) = 0. The exact solution [13] is taken as a reference point for comparisons.

Table 12.
Mutual inductance as a function of the perpendicular displacement d [13], using the summation [5], n = 5, K = 10, N = 15, m = 50.
Also, we give the mutual inductance calculation obtained by the summation [5] in Table 12. These results are expected regarding the accuracy and the computational time because we used the summation [5] instead of the integration [1]. The number of the subdivisions is K = N = m = n = 20. These results are in good agreement with those obtained by two previous methods,
In the calculations of the radial and the axial forces, we will use the same reasoning when choosing the number of subdivisions.
In this example, all calculations were performed using different hardware setups. The single integration (Gaussian numerical integration) and the summation method were carried out on a Dell laptop with an Intel Core i5-12500H processor running at 2.5 GHz.
For the calculations using the Finite Element Method (FEM), a PC with an Intel Core i7-7700K CPU @ 4.20 GHz and 16.0 GB of RAM was used.
5.3. Example 3
From Example 2, let’s calculate the radial and axial magnetic forces between the coils in question. All currents in the coils are units.
Here, we utilize the number of subdivisions, K = 8, N = 12, m = 40, and n = 4, as determined in the previous example. This selection ensures both good accuracy and minimal computational time for the integral approach. In contrast, for the summation approach, the number of subdivisions is set to K = N = m = n = 20.
The comparison will involve using the Formula (8) for the radial magnetic force and (9) for the axial magnetic force, obtained through integration (as presented in this work), alongside the method that employs summation instead of integration, as outlined in reference [5].
From Table 13, we have a good agreement between the results obtained from two methods in which the numerical integration [1] and the numerical summation [5] are used on the interval of the consideration . Obviously, the results for the radial magnetic force Fr, (8) obtained by the numerical integration are more precise, but the method [5] is usable as a comparative benchmark. The absolute relative error is between 0.1% and 1.06%.

Table 13.
The radial magnetic force as a function of the perpendicular displacement d using the numerical integration [1] and the summation [5].
From Table 14, the axial magnetic force Fa is zero for all points of the calculation, which is practically confirmed by the presented method, Equation (8). The second method [5] doesn’t give exactly zero for the axial force Fa because of the positive and negative variations during the summation on the interval of the consideration. The third method [15] gives exactly zero due to the axial factor involved in the force Expression (15):
where h1 = a/2 and h2 = b/2, and κ are the eigenvalues due to the introduction of artificial boundary, and it can be concluded that Fa = 0 from f2(κ, 0) = 0.

Table 14.
The axial magnetic force as a function of the perpendicular displacement d using the numerical integration [1,5,15].
In this example, all calculations were performed using a Dell laptop equipped with an Intel Core i5-12500H processor running at 2.5 GHz.
In this example, all calculations were performed using different hardware setups. The single integration (Gaussian numerical integration) and the summation method were carried out on a Dell laptop with an Intel Core i5-12500H processor running at 2.5 GHz.
For the calculations using the Finite Element Method (FEM), a PC with an Intel Core i7-7700K CPU @ 4.20 GHz and 16.0 GB of RAM was used.
5.4. Example 4
Here, we give this example that can be used as the benchmark problem for testing the different methods that treat the coils in question. All currents in the coils are units.
Parameters for two non-coaxial cylindrical coils with parallel axes given in [6] and used in [14] are in the following Table 15.

Table 15.
Description of coils [6,14].
Let us find the following values:
LN = R2 − R1= 0.01397 m, Ln = R4 − R3 = 0.041529 m,
La = z2 − z1 = a = 0.142748 m, Lb = z4 − z3 = b = 0.02413 m.
Now, let’s conduct the following analysis concerning the coil dimensions and the number of subdivisions respecting the procedures given in Section 4, by (9)–(14).
The smallest dimension is R2 − R1 = 0.01397 m, which corresponds to the radial subdivision N of the first coil. Let us express all subdivisions in the function of N.
K= [a/(R2 − R1)] N = [10.218181] = 10 or K = 10N
m/N = [b/(R2 − R1)] = [1.72727] = 2 or m = 2N
n/N = [(R4 − R3)/(R2 − R1)] = [2.9727] = 3 or n= 3N
The next step is to find the best choice of subdivisions for the arbitrarily chosen smallest variable.
In Table 16, for one calculation of the mutual inductance given in [14], with d = 0.006 m, c = 0.059309 m, and M = 44.7454180199 mH, we test different values of .

Table 16.
The test for the accuracy and the computational time for the different number of subdivisions.
Obviously, it is not logical to increase the number of subdivision N beyond 4 because the accuracy doesn’t change significantly while the computational time increases enormously. Moreover, it is not practical from the engineering point of view. Thus, the best choice is to take N = 3 or even N = 4.
We can further improve the accuracy and computational time of calculations by adjusting the number of subdivisions based on (13) and (14).
These two subdivisions may be increased by 1, 2, or 3, while the other two are decreased by 1, 2, or 3. This approach can significantly improve both accuracy and computational time.
After, we increase the two smallest variables by 1 and decrease the two largest variables by 1 1, Table 17. This process can be continued using the same logic, successively incrementing and decrementing the variables by 1. This means K2 = 29, N2 = 4, m2 = 7, N2 = 8 and so on.

Table 17.
The best choice of the different number of subdivisions.
From Table 17, one can see that the previous statement is effective, as the accuracy does not change significantly, and neither does the computational time.
Practically, we proposed a new approach to choosing the optimal numbers for the variables (subdivisions) that archives very high accuracy and the shortest possible time of calculation.
Let us choose N = 3, that gives
K = 30; N = 3; m = 6; n = 9
Now, we calculate the mutual inductance given [14] by the presented method and test the computational time and accuracy. All comparative results are given in Table 18.

Table 18.
Mutual inductance M (mH) as a function of the perpendicular displacement d [14], K = 30; N = 3; m = 6; n = 9.
For the previously chosen number of subdivisions, K = 30; N = 3; m = 6; n = 9, we calculate the radial and the axial magnetic force between the coils in question. The method given in [15,16] is used as the comparative method. The calculation of Fr and Fa can be used as the benchmark problem for tasting other methods for calculating these two magnetic forces for coils in question regarding the accuracy and the computational time.
From Table 17 and Table 18, one can see very good agreements of results obtained by two different methods, even though there are some differences for some points of the calculations. It can be explained by the following facts.
- (1)
- The presented method treats two coils of the rectangular cross-section with the parallel axes in the unbounded space libre, which are divided into circular filamentary coils. To account for the finite dimensions of the coils, massive solenoids are subdivided into meshes of filamentary coils, as shown in Figure 2. The cross-sectional areas of two coils are divided into (2K + 1) by (2N + 1) cells for the first coil and (2m + 1) by (2n + 1) cells for the second coil, where K, N, m, and n are the numbers of the subdivisions of coils [8,10,12]. Even though we use the analytical Maxwell’s formulas for the mutual inductance or the magnetic force between two circular loops, we cannot say that the presented filament method for the massive coils is purely analytical because its precision and the computational time depend on the number of subdivisions. This statement was studied in the previous examples. As shown, the number of subdivisions has an influence on accuracy.
- (2)
- The compared method is a boundary value problem of circular coils with parallel axes shielded by a cuboid of high permeability. This means the coils are bounded by a medium of high permeability regarding the free space, in which there are coils, where the mixed boundary conditions are satisfied on six surfaces of the artificial cuboid. Thus, this approach is approximate, but it proves to be accurate and efficient enough for practical applications. This means that this method can bring some differences in accuracy.
In Table 19 and Table 20, the computation of the radial and axial forces is presented, comparing the results of this work, Equations (7) and (8), with those given in [15,16].

Table 19.
Radial magnetic force Fr (mN) as a function of the perpendicular displacement d [14], K = 30; N = 3; m = 6; n = 9.

Table 20.
Axial magnetic force Fa (mN) as a function of the perpendicular displacement d [14], K = 30; N = 3; m = 6; n = 9.
Even though we compare the results obtained by two different methods, one for open space and the other for artificial boundaries in bounded space, both give very satisfactory results for calculating the magnetic force between two coils of rectangular cross-sections with parallel axes.
With (1) and (2), we explain the possible differences in accuracy for some cases of calculation.
In this example, all calculations were performed using different hardware setups. The single integration, including the Gaussian numerical integration, was carried out on a Dell laptop (Dell, Inc., Round Rock, TX, USA) with an Intel Core i5-12500H processor running at 2.5 GHz. For the calculations using the Finite Element Method (FEM), a PC with an Intel Core i7-7700K CPU @ 4.20 GHz and 16.0 GB of RAM was used.
5.5. Example 5
Finally, we give the rare examples that can be found in the literature to calculate the mutual inductance between two non-coaxial coils of the rectangular cross-section with the parallel axes [1]. All currents in the coils are units.
For this combination, the dimensions and the number of turns is as follows:
R1 = 4 cm, R2 = 6 cm, z2 − z1 = a = 10 cm, N1 = 150
R3 = 2.5 cm, R4 = 3.5 cm, z4 − z3 = b = 5 cm, N1 = 50
The perpendicular displacement of two coil axes is d = 10 cm, and the axial displacement of the centers of the two coils is c = 10.5 cm.
In [1] the mutual inductance is,
M = 3.144 µH
According to the optimal minimizing method given by the presented approach concerning the high accuracy and the short computational time, after some tests, we choose the number of the subdivisions K = 30; N = 6; m = 15 for arbitrarily chosen n = 9.
Using the approach presented in this paper, the mutual inductance is
M = 3.13606092090 µH
The elapsed time is 17.133452 s, Intel Core i5-12500H @ 2.5 GHz.
The method of [15,16] gives
M = 3.136970 μH
The elapsed time is 5.2 s on an Intel Core i7-8700 @ 3.2 GHz.
The absolute relative error regarding the accuracy between the presented method and the one given in [15,16] is around 0.029%.
In [1], the mutual inductance is calculated using the general formula of Dwight and Purssell, ref. [19] arranged as series involving zonal harmonics, Equations (190) and (191) [1]. The convergence of this series is sufficient for most purposes as long as all distances are greater than (A + a), where dm, ρ is the perpendicular displacement of two coil axes and the axial displacement of the centers of the two coils, respectively. A and a are the mean radii of two coils of rectangular cross-section, respectively, refs. [1,30]. Since the general term of the series is known, it should be possible to use over the full range. However, the calculation of higher power terms becomes very tedious and time-consuming [1]. This is why Grover took only four terms of this series and obtained M = 3.144 µH. It was problematic to take more terms because of the mentioned issues [1] as well as very slow convergence.
We did many tests of (190) and (191), ref. [1] from which we found very slow convergence. For two terms more, we obtain
The absolute relative error discrepancy is 0.27%. Taking still more terms whose signs change alternatively will oscillate without significantly improving the accuracy because of the slow convergence.
However, these formulas are not working correctly for the different coil dimensions, as mentioned in [1]. This is why we consider the approach presented here as general for any coil’s dimensions.
Now, let us calculate the radial and the axial magnetic force between the coils in question, respecting all parameters in the previously calculated mutual inductance.
Fr = −136.725877825 µN
Fa = 39.3340997099 µN
As a comparison, the method of [15,16] gives
Fr = −136.753948 µN
Fa = 39.344618 µN
Obviously, all results are in very good agreement.
The calculation provided by the presented method could also serve as a benchmark for other methods addressing this problem. Additionally, this method could be automatically applied to calculate the mutual inductance and the magnetic force between other coil configurations (solenoids, disks) with parallel axes.
6. Conclusions
In this paper, we provide a new algorithm for calculating the radial and axial magnetic forces between two non-coaxial coils of rectangular cross-sections with parallel axes. These formulas are derived from modified Grover’s formula for the mutual inductance between two non-coaxial loops with parallel axes. The validity of the presented approach is validated with an already established method. Presented formulas are used for calculating the radial and the axial force between two non-coaxial coils of rectangular cross-sections with parallel axes using the filament method. Also, we presented the method to minimize the variables (subdivisions) in the filament method to find the compromise between satisfactory accuracy and the corresponding small time of the calculation. We mention this method is applicable between non-coaxial conventional coils with parallel axes (massive-loop; massive-disk; massive-solenoid; two disks; disk-loop; disk-solenoid; two solenoids and solenoid-loop). This method can be useful for engineers who are working in this domain because of its simplicity. The proposed method is comprehensible, fast, and very precise.
Author Contributions
S.B.: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, writing original draft preparation, writing review and editing, visualization. E.G.: Validation, Formal analysis, Investigation, Software, visualization. K.-H.S.: Validation, Software, visualization. Y.L.: Validation, Software, visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
If readers have further questions or need more detailed information, they are encouraged to contact the corresponding author, who is responsible for managing these inquiries.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grover, F.W. Inductance Calculations: Working Formulas and Tables; Dover Publications, Inc.: New York, NY, USA, 1946. [Google Scholar]
- Dwight, H.B. Electrical Coils and Inductors: Their Electrical Characteristics and Theory; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1945. [Google Scholar]
- Butterworth, S. On the coefficients of mutual induction of eccentric coils. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1916, 31, 443–454. [Google Scholar] [CrossRef]
- Snow, C. Formulas for Computing Capacitance and Inductance. In National Bureau of Standards Circular 544; US Government Printing Office: Washington, DC, USA, 1954. [Google Scholar]
- Song, K.-H.; Feng, J.; Zhao, R.; Wu, X.-L. A General Mutual Inductance Formula for Parallel Non-coaxial Circular Coils. ACES J. 2019, 34, 1385–1390. [Google Scholar]
- Conway, J.T. Inductance calculations for non-coaxial coils using Bessel functions. IEEE Trans. Magn. 2007, 43, 1023–1034. [Google Scholar] [CrossRef]
- Conway, J.T. Noncoaxial inductance calculations without the vector for axisymmetric coils and planar coils. IEEE Trans. Magn. 2008, 44, 453–462. [Google Scholar] [CrossRef]
- Akyel, C.; Babic, S.I.; Mahmoudi, M.M. Mutual inductance calculation for non-coaxial circular air coils with parallel axes. Prog. Electromagn. Res. 2009, 91, 287–301. [Google Scholar] [CrossRef]
- Kim, K.B.; Levi, E.; Zabar, Z.; Birenbaum, L. Mutual inductance of noncoaxial circular coils with constant current density. IEEE Trans. Magn. 1997, 33, 4303–4309. [Google Scholar]
- Babic, S.; Akyel, C. Magnetic Force Between Inclined Circular Filaments Placed in Any Desired Position. IEEE Trans. Magn. 2012, 48, 69–80. [Google Scholar] [CrossRef]
- Babic, S.I.; Sirois, F.; Akyel, C. Validity check of mutual inductance formulas for circular filaments with lateral and angular misalignments. Prog. Electromagn. Res. M 2009, 8, 15–26. [Google Scholar] [CrossRef]
- Babic, S.I.; Akyel, C.; Ren, Y.; Chen, W. Magnetic Force Calculation between Circular Coils of Rectangular Cross Section with Parallel Axes for Superconducting Magnets. Prog. Electromagn. Res. B 2012, 37, 275–288. [Google Scholar] [CrossRef]
- Conway, J.T. Mutual inductance of thick coils for arbitrary relative orientation and position. In Proceedings of the Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017. [Google Scholar]
- Conway, J.T. Inductance Calculations for Circular Coils of Rectangular Cross Section and Parallel Axes Using Bessel and Struve Functions. IEEE Trans. Magn. 2010, 46, 75–81. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, Y.; Yu, Y.; Zhang, L. Inductance and force calculations of circular coils with parallel axes shielded by a cuboid of high permeability. IET Electr. Power Appl. 2018, 12, 717–727. [Google Scholar] [CrossRef]
- Yang, X.; Luo, Y.; Kyrgiazoglou, A.; Zhou, X.; Theodoulidis, T.; Tytko, G. Impedance variation of a reflection probe near the edge of a magnetic metal plate. IEEE Sens. J. 2023, 23, 15479–15488. [Google Scholar] [CrossRef]
- Yu, D.; Chen, B.; Luo, Y.; Zhou, X.; Yu, Y.; Yang, X.; Xiang, Y. Mutual inductance calculation for rectangular and circular coils with parallel axes. IET Electr. Power Appl. 2023, 7, 379–388. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, B.; Luo, Y.; Kyrgiazoglou, A. Integral and series solutions for inductance of rectangular coils with parallel end faces. IET Electr. Power Appl. 2019, 13, 1032–1041. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, B.; Luo, Y.; Zhu‚, R. Inductance calculations for coils with an iron core of arbitrary axial position. Electromagnetics 2019, 39, 99–119. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, B.; Luo, Y.; Zhu, R. Analytical Calculation of Mutual Inductance of Finite-Length Coaxial Helical Filaments and Tape Coils. Energies 2019, 12, 566. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, Y. Inductance calculations for non-coaxial Bitter coils with rectangular cross-section using inverse Mellin transform. IET Electr. Power Appl. 2019, 13, 119–125. [Google Scholar] [CrossRef]
- Palka, R. Fast Analytic–Numerical Algorithms for Calculating Mutual and Self-Inductances of Air Coils. Energies 2024, 17, 325. [Google Scholar] [CrossRef]
- Syrimi, P.; Tsiatas, G.; Tsopelas, P. Magnetic restoring forces on rocking blocks. Earthq. Eng. Struct Dyn. 2023, 53, 3381–3404. [Google Scholar] [CrossRef]
- Maisnam, N.; Saxena, V.K.; Kumar, K.; Kant, S. Effect of misalignment issues for different coil structures in dynamic wireless charging system. In Electric Vehicle Propulsion Drives and Charging Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Kong, L.; Chen, Z.; Hu, C.; Zhang, C.; Wang, J.; Zhou, X.; Jia, L.; Li, Z. Mutual Inductance Calculation Method of Rectangular Coils with Bilateral Bounded Single-Hole Type Magnetic Medium in Wireless Power Transfer Systems. Prog. Electromagn. Res. C 2024, 143, 75–86. [Google Scholar] [CrossRef]
- Hussain, I.; Woo, D.K. Calculation of mutual inductance between arbitrarily positioned planar spiral coils for wireless power applications. Int. J. Appl. Electromagn. Mech. 2024, 74, 234–249. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, M. Mutual inductance calculation of circular coils arbitrary positioned with magnetic tiles for wireless power transfer system. IET Power Electron. 2020, 13, 3522–3527. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, Ser. 55; National Bureau of Standards Applied Mathematics: Washington, DC, USA, 1972; p. 595. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press: New York, NY, USA; London, UK, 1965. [Google Scholar]
- Dwight and Purssell, General Electric Review; Forgotten Books: London, UK, 1930; Volume 33, p. 401.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).