Modeling of Mean-Value-at-Risk Investment Portfolio Optimization Considering Liabilities and Risk-Free Assets

Abstract

This paper aims to design a quadratic optimization model of an investment portfolio based on value-at-risk (VaR) by entering risk-free assets and company liabilities. The designed model develops Markowitz’s investment portfolio optimization model with risk aversion. Model development was carried out using vector and matrix equations. The entry of risk-free assets and liabilities is essential. Risk-free assets reduce the loss risk, while liabilities accommodate a fundamental analysis of the company’s condition. The model can be applied in various sectors of capital markets worldwide. This study applied the model to Indonesia’s mining and energy sector. The application results show that risk aversion negatively correlates with the mean and VaR of the return of investment portfolios. Assuming that risk aversion is in the 5.1% to 8.2% interval, the maximum mean and VaR obtained for the next month are 0.0103316 and 0.0138270, respectively, while the minimum mean and VaR are 0.0102964 and 0.0137975, respectively. The finding of this study is that the vector equation for investment portfolio weights is obtained, which can facilitate calculating investment portfolio weight optimization. This study is expected to help investors control the quality of appropriate investment, especially in some stocks in Indonesia’s mining and energy sector.

1. Introduction

The investing technique of buying several assets with different rates of loss, rates of return, and performance in a portfolio can make fluctuations in returns and losses mutually compensated between assets. It causes the fluctuations to be more controlled overall [1,2,3,4]. It is then called portfolio diversification. In portfolio diversification, allocating investment funds for each asset is critical. The allocation of each asset must be calculated so that the portfolio generates maximum returns and minimum losses [5,6,7]. The problem is determining the allocation weight for each asset.

The problem of determining the weight of asset allocation in a general investment portfolio is solved using the Markowitz asset allocation optimization model [8,9]. For ease of mention, after this, the model is referred to as the Markowitz model. The Markowitz model is based on two simple objective objectives in portfolio preparation: maximizing the mean and minimizing the variance of portfolio returns in a single period. Then, the two objectives are integrated into one as an optimization model for maximizing the subtraction between the mean and variance of portfolio returns in a single period. Because of this, the Markowitz model is often referred to as the mean-variance model.

Previous studies have simulated the Markowitz model. Ivanova and Dospatliev [10] applied the Markowitz model to determine the allocation of asset weights to investment portfolios on stock data in Bulgaria from 2013 to 2016. Kulali [11] and Zavera [12] also applied the same model to stock data in Turkey and Romania in 2015, respectively.

Over time, researchers began to develop the Markowitz model. Kashirina et al. [13] developed a long-term Markowitz model. The long period is divided into several short periods that are mutually exclusive. In more detail, the return earned at the end of each short-term period is not withdrawn but is reinvested in the next period. Another development of the model of Kashirina et al. [13] is that the variance of the portfolio returns in the model is calculated based on the geometric mean. Steinbach [14] also developed the Markowitz model to be multi-period by providing a quantitative treatment of the tradeoff between returns and losses.

The previous developments of the Markowitz model still use the variance of the portfolio return as a minimized objective [15]. The variance measure can be substituted for the maximum possible loss. This measure is referred to as value-at-risk (VaR). The use of the VaR measure has advantages over the use of the variance measure. Using VaR measures can make the size of the maximum loss of an investment portfolio experienced by investors more diverse. In other words, investors can set the maximum loss they may experience [16]. This portfolio asset-allocation optimization model based on VaR is called the mean-VaR model.

Banihashimi et al. [15] applied the mean-VaR model to stock data in Iran. The performance of the weight allocation results obtained is then evaluated for non-parametric efficiency using data envelopment analysis (DEA). Then, Sukono et al. [17] formulated the mean-VaR model using vector and matrix forms. The formulation of the model was based on stock data in Indonesia. They used an additional assumption, where the return of each asset was assumed to have non-constant volatility. This non-constant volatility was accommodated through the generalized autoregressive conditional heteroscedastic (GARCH) model. Sukono et al. [17] used the Lagrangian multiplier method and the Kuhn–Tucker theorem to obtain a solution from the model. Then, Pandiangan et al. [18] developed the Sukono et al. [17] model by adding risk aversion and risk-free assets to its investment portfolio. The analysis showed that the greater the risk aversion, the smaller the mean and VaR of the investment portfolio return.

This paragraph briefly discusses the gaps in previous studies. The existing mean-variance and mean-VaR models do not involve risk-free assets. Including risk-free assets in investment portfolios reduces volatility and enhances stability. Financial reports show that portfolios with risk-free assets, such as government bonds, have higher Sharpe ratios, indicating better returns relative to the risk taken compared to risky assets. Examples are Kashirina et al. [13], Steinbach [14], Banihashemi et al. [15], Miyangaskari et al. [16], and Sukono et al. [17]. Only Pandiangan et al. [18] involved such risk-free assets. Then, the existing mean-variance and mean-VaR models have not considered the assets-owning companies’ liabilities. A liability analysis is crucial in investment portfolio preparation, as it reveals credit risks and potential bankruptcy, which can impact investment performance. Moody’s report indicates that companies with high debt-to-equity ratios are more likely to default, which can negatively affect an investor’s portfolio value if not calculated carefully. Examples of these researchers are Kashirina et al. [13], Steinbach [14], Banihashemi et al. [15], Miyangaskari et al. [16], Sukono et al. [17], and Pandiangan et al. [18].

Based on the explanation of the brief gap, this study aims to formulate a value-at-risk (VaR)-based investment portfolio optimization model involving risk-free assets and company liabilities. The advantage of the model is that the maximum loss of the portfolio can be reduced due to the involvement of risk-free assets, and the maximum loss can be adjusted based on the size of the tolerable quantile. The optimization model designed has a quadratic programming form to accommodate the quadratic form of the VaR measure. In more detail, the solution of the model is calculated using the Lagrange multiplier method and the Khun–Tucker theorem, as calculated by Sukono et al. [17]. Formulating the portfolio optimization model is performed using vector and matrix equations to simplify the form of the equation further. Finally, a numerical illustration is conducted on this model using stock data from the mining and energy sectors as risky assets and bank deposits as risk-free assets. This study is expected to help quality control in forming investment portfolios, especially in the mining and energy sector stocks, for investors both organizationally and individually.

2. Literature Review

This section discusses references in portfolio model development. It includes a brief explanation of the general optimization model of the investment portfolio, the quadratic optimization model of the mean-VaR investment portfolio, and the asset-liability model.

2.1. The Explanation of Mathematical Notations

The essential mathematical notations used in this study are as follows:

(a)

$t_0=0$ represents the time an investor starts investing.

(b)

$t_1=1$ represents the time an investor ends investing.

(c)

There is one number of risk-free assets in the portfolio.

(d)

$N\ge 1$ with $N\in \mathbb{Z}$ represents many risky assets.

(e)

$V_{t_0}$ represents the total initial investment assets.

(f)

$E\left(V_{t_1}\right)$ represents the expected total initial investment assets at time $t_1$.

(g)

$h_0$ represents the amount of capital allocated to risk-free assets. We assume that the value of $h_0$ is determined in advance.

(h)

$h_k$ with $k=1,2,\dots ,N$ represents the amount of capital allocated to the $k$-th risky asset.

(i)

${\gamma }_k$ with $k=1,2,\dots ,N$ represents the company’s liability to the $k$-th risky asset.

(j)

${\sigma }_{k_1,k_2}$ with $k_1=1,2,\dots ,N$ and $k_2=1,2,\dots ,N$ represents the covariance between the $k_1$-th and $k_2$-th risky assets.

(k)

$w_0$ represents the weight of capital allocation on risk-free assets. It can be formulated mathematically as $w_0=\frac{h_0}{V_{t_0}}$. Since $h_0$ is assumed to be determined in advance, the value of $w_0$ is also known.

(l)

$w_k,k=1,2,\dots ,N$ represents the weight of the capital allocation on the $k$-th risky asset. It can be formulated mathematically as $w_k=\frac{h_k}{V_{t_0}}$.

(m)

${\mu }_0$ represents the return from the risk-free asset at time $t_1$. We assume the value has been determined in advance.

(n)

$r_k$ represents the return from the $k$-th risky asset at $t_1$, assumed to be distributed normal random variables with a mean of $E\left(r_k\right)={\mu }_k$ and a variance of $Var\left(r_k\right)={\sigma }_k^2$.

(o)

$R$ represents the total return of the investment portfolio at time $t_1$.

(p)

$\mathcal{R}$ represents the total return of the investment portfolio without the return of a risk-free asset at time $t_1$.

(q)

$B_{t_i},i=0,2$ represents the price of the risk-free asset at time $t_i$.

(r)

$S_{t_0}^k,k=1,2,\dots ,N$ represents the initial spot price of the $k$-th risk asset. The spot price is the asset price when the buyer and seller carry out the transaction [19].

(s)

$E\left(S_{t_1}^k\right),k=1,2,\dots ,N$ represents the expected spot price of the $k$-th asset at time $t_1$.

(t)

${\sigma }_{k,L}$ represents the covariance between the $k$-th risky asset and liability.

2.2. The General Optimization Model of the Investment Portfolio

The total assets at time $t_0$ at time $t_1$ from the portfolios are, respectively, as follows [20,21,22]:

$$V_{t_0}=\sum _{j=0}^N{h}_j.$$

(1)

Suppose that $V_{t_0}=1$. Equation (1) can be formulated in the form of weights by substituting $h_j=w_j{V}_{t_0}$, $j=0,1,2,\dots ,N$. This substitution results in the following equations:

$$\sum _{j=0}^N{w}_j=1.$$

(2)

Equation (2) shows that the total weight of the assets in the portfolio is 1. In this study, $w_0$ has been determined first so that we are left with determining $w_k$ with $k=1,2,\dots ,N$. Therefore, the total amount of asset weights and returns from a portfolio without risk-free assets is as follows:

$$\sum _{k=1}^N{w}_k=1-w_0.$$

(3)

The mean return of the portfolio without risk-free assets is formulated as follows:

$$E\left(\mathcal{R}\right)=\sum _{k=1}^N{w}_{k}E\left(r_k\right)=\sum _{k=1}^N{w}_k{\mu }_k.$$

(4)

Meanwhile, the variance return of the portfolio without risk-free assets can be briefly stated as follows [23,24]:

$$V\left(\mathcal{R}\right)={\sum }_{k_1=1}^N{\sum }_{k_2=1}^N{w}_{k_1}{w}_{k_2}Cov(r_{k_1},r_{k_2})={\sum }_{k_1=1}^N{\sum }_{k_2=1}^N{w}_{k_1}{w}_{k_2}{\sigma }_{k_1,k_2}.$$

(5)

The forms of Equations (3)–(5) can, respectively, be expressed in the form of the vector and matrix multiplication as follows:

$${\mathbf{w}}^{\mathrm{T}}\mathit{e}=1-w_0,E\left(\mathcal{R}\right)={\mathbf{w}}^{\mathrm{T}}\mathsf{\mu },\mathrm{a}\mathrm{n}\mathrm{d}V\left(\mathcal{R}\right)={\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w},$$

(6)

where ${\mathbf{e}}^{\mathrm{T}}=\left(\begin{array}{cccc}1& 1& \cdots & 1\end{array}\right)$, ${\mathbf{w}}^{\mathrm{T}}=\left(\begin{array}{cccc}{w}_1& w_2& \cdots & w_N\end{array}\right)$, ${\mathsf{\mu }}^{\mathrm{T}}=\left(\begin{array}{cccc}{\mu }_1& {\mu }_2& \cdots & {\mu }_N\end{array}\right)$, and $\mathsf{\Sigma }=\left[{\sigma }_{k_1,k_2};k_1,k_2=1,2,\dots ,N\right]$, which is a negative semi-definite matrix [25].

In the face of loss from the investment portfolio, investors have different risk aversion. Risk aversion is investors’ tendency to establish certainty in investments. In other words, the smaller the investor’s risk aversion, the more courageous the investor is to face uncertainty and vice versa. Mathematically, risk aversion is expressed as a comparison between the relative constant and twice the initial capital $V_{t_0}=1$ as follows [4]:

$$\rho =\frac{c}{2V_{t_0}}=\frac{c}{2},$$

where $\rho$ represents the risk aversion and $c$ represents the relative constant [26].

The mean-variance model for asset allocation in the investment portfolio is mathematically expressed as follows:

$$\begin{array}{c}\mathrm{m}\mathrm{a}\mathrm{x}.E\left(\mathcal{R}\right)-\rho V\left(\mathcal{R}\right)={\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }-\frac{c}{2}{\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w},\\ \mathrm{s}.\mathrm{t}.{\mathbf{w}}^{\mathrm{T}}\mathbf{e}=1-w_0.\end{array}$$

(7)

The Lagrange multiplier method can determine the solution of the model in Equation (7). This method results in the Lagrange function for Equation (7) expressed as follows [18]:

$$L\left(\mathbf{w},{\lambda }_1\right)={\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }-\frac{c}{2}{\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}+{\lambda }_1\left({\mathbf{w}}^{\mathrm{T}}\mathbf{e}-1+w_0\right),$$

(8)

where ${\lambda }_1$ represents the Lagrange multiplier. The solution $\mathbf{w}$ in Equation (7) is the one that maximizes (8). Briefly, the solution is as follows [6]:

$${\mathbf{w}}^{\mathbf{*}}=\frac{2}{c}{\mathsf{\Sigma }}^{-1}\left(\mathsf{\mu }+{\lambda }_1\mathbf{e}\right),$$

(9)

where

$${\lambda }_1^{\mathrm{*}}=\frac{\frac{c}{2}\left(1-w_0\right)-{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\mathsf{\mu }}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\mathbf{e}}.$$

The Hessian matrix of Equation (8) must satisfy Equation (10) as follows to guarantee the solution ${\mathbf{w}}^{\mathbf{*}}$ in Equation (9) as a local maximum solution [27]:

$$\forall \mathbf{x}\in {\mathbb{R}}^{N+1}-\left\{0\right\},{\mathbf{x}}^{\mathrm{T}}\mathbf{H}\left({\mathbf{w}}^{\mathbf{*}},{\lambda }_1^{*}\right)\mathbf{x}<0$$

(10)

where

$$\mathbf{H}\left(\mathbf{w},{\lambda }_1\right)=\left[\begin{array}{cc}\frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_1\right)}{\partial {\mathbf{w}}^2}& \frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_1\right)}{\partial \mathbf{w}\partial {\lambda }_1}\\ \frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_1\right)}{\partial {\lambda }_1\partial \mathbf{w}}& \frac{\partial L\left(\mathbf{w},{\lambda }_1\right)}{\partial {\lambda }_1^2}\end{array}\right].$$

2.3. Quadratic Optimization Model of the Mean-VaR Investment Portfolio

This section briefly describes the quadratic optimization model of the mean-VaR investment portfolio. Value-at-risk (VaR) measures the maximum potential loss that may occur from a portfolio at a certain level of confidence under normal market conditions [28]. Sukono et al. [29] stated that the VaR of the portfolio without risk-free assets is expressed as follows:

$$Va{R}_{\alpha }\left(\mathcal{R}\right)={\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }+z_{\alpha }{\left({\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}},$$

(11)

where $z_{\alpha }$ represents the ($1-\alpha$)-th percentile of the standard normal distribution. The value of $\alpha$ can be adjusted according to the investor’s expectation. The greater the value of $\alpha$, the smaller the maximum loss from the investment portfolio desired by the investor and vice versa.

The quadratic optimization model of the mean-VaR investment portfolio formulates the objective function as a maximization problem of subtraction returns and multiplying risk aversion with VaR. Mathematically, this is written as follows [22]:

$$\begin{array}{c}\mathrm{m}\mathrm{a}\mathrm{x}.E\left(\mathcal{R}\right)-\rho Va{R}_{\alpha }\left(\mathcal{R}\right)={\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }-\frac{c}{2}\left[{\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }+z_{\alpha }{\left({\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}\right],\\ =\left(1-\frac{c}{2}\right){\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }-\frac{c}{2}{z}_{\alpha }{\left({\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}},\\ \mathrm{s}.\mathrm{t}.{\mathbf{w}}^{\mathrm{T}}\mathbf{e}=1-w_0.\end{array}$$

(12)

The Lagrange multiplier method can determine the solution of the model in Equation (12). This method results in the Lagrange function for Equation (12) expressed as follows [22]:

$$L\left(\mathbf{w},{\lambda }_2\right)=\left(1-\frac{c}{2}\right){\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }-\frac{c}{2}{z}_{\alpha }{\left({\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}+{\lambda }_2({\mathbf{w}}^{\mathrm{T}}\mathbf{e}-1+w_0),$$

(13)

where ${\lambda }_2$ represents the Lagrange multiplier. The solution $\mathbf{w}$ of Equation (12) is the one that maximizes (13). Briefly, the solution is as follows [22]:

$${\mathbf{w}}^{\mathbf{*}}=\frac{\left(1-w_0\right){\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{c}{2}\right)\mathsf{\mu }+{\lambda }_2\mathbf{e}\right]}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{c}{2}\right)\mathsf{\mu }+{\lambda }_2\mathbf{e}\right]}.$$

(14)

In detail,

$${\lambda }_2^{\mathrm{*}}=\frac{-b\pm \sqrt{b^2-4ac}}{2a},$$

where $a={\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\mathbf{e}$, $b=2\left(1-\frac{c}{2}\right){\mathsf{\mu }}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\mathbf{e}$, and $c={\left(1-\frac{c}{2}\right)}^2{\mathsf{\mu }}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\mathsf{\mu }-{\left(\frac{c{z}_{\alpha }}{2}\right)}^2$. The Hessian matrix of Equation (13) must satisfy Equation (15) as follows to guarantee the solution ${\mathbf{w}}^{\mathbf{*}}$ in Equation (14) as a local maximum solution [22]:

$$\forall \mathbf{x}\in {\mathbb{R}}^{N+1}-\left\{0\right\},{\mathbf{x}}^{\mathrm{T}}\mathbf{H}\left({\mathbf{w}}^{\mathbf{*}},{\lambda }_2^{*}\right)\mathbf{x}<0$$

(15)

where

$$\mathbf{H}\left(\mathbf{w},{\lambda }_2\right)=\left[\begin{array}{cc}\frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_2\right)}{\partial {\mathbf{w}}^2}& \frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_2\right)}{\partial \mathbf{w}\partial {\lambda }_2}\\ \frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_2\right)}{\partial {\lambda }_2\partial \mathbf{w}}& \frac{\partial L\left(\mathbf{w},{\lambda }_2\right)}{\partial {\lambda }_2^2}\end{array}\right].$$

2.4. Asset Liability Model

Suppose that $s_{t_i}^k$, $i=0,1,$ represents the surplus of the $k$-th asset at time $t_i$. It can be mathematically expressed as follows:

$$s_{t_i}^k=S_{t_i}^k-L_{t_i}^k=S_{t_{i-1}}^k\left(1+{\mu }_k\right)-L_{t_{i-1}}^k\left(1+{\mu }_L^k\right),$$

(16)

where $L_{t_i}$ represents the $k$-th liabilities and assets at time $t_i$ and ${\mu }_L^k$ represents the return of the $k$-th liabilities. The return of the surplus from the $k$-th asset can be expressed in the following equation [30,31,32]:

$${\mu }_S^k=\frac{s_{t_i}^k-s_{t_{i-1}}^k}{S_{t_{i-1}}^k}=\frac{S_{t_{i-1}}^k{\mu }_k-L_{t_{i-1}}^k{\mu }_L^k}{S_{t_{i-1}}^k}={\mu }_k-\frac{L_{t_{i-1}}^k}{S_{t_{i-1}}^k}{\mu }_L^k={\mu }_k-f_{t_{i-1}}{\mu }_L^k,$$

(17)

where $f_{t_i}$ is the ratio between liabilities and capital assets at time $t_i$. Meanwhile, the variance of return surplus is stated as follows:

$${{\sigma }_S^k}^2={\sigma }_k^2-\frac{2}{f_0}{\sigma }_{k,L}+\frac{1}{f_0^2}{{\sigma }_L^k}^2,$$

(18)

where ${\sigma }_{k,L}$ represents the covariance between the $k$-th return assets and the liability return and ${{\sigma }_L^k}^2$ represents the variance of the liability return of $k$-th asset [33].

3. Materials and Methods

This section briefly describes the materials and methods, which contain the materials and steps in this study.

3.1. Materials

This study had two activities: model development and numerical illustration. The model development was carried out using the model of Pandiangan et al. [18], which formulated an investment portfolio optimization model in the form of mean-VaR involving risk-free assets. This development was in the form of adding the liability variable from the asset owner company. In addition, the model development was carried out using vector and matrix forms, as performed by Sukono et al. [17]. Then, the material for numerical illustration was stock data in the mining and energy sectors, which are traded on the Indonesian capital market through the Indonesia Stock Exchange (IDX). Note that the model can not only be applied to IDX’s stock data but also to other capital markets worldwide. The data are historical monthly return data from 11 stocks obtained through the website http://finance.yahoo.com (accessed on 1 March 2024). The period considered was 1 January 2017 to 1 December 2020. Of the mining and energy stocks, 11 selected stocks had the best performance. In addition to data on 11 stocks, we sued data on risk-free assets in deposits determined by the Central Bank of Indonesia. In this study, the company’s liability data were also used. However, because the company’s liability data are not open, the liability data used were simulation data [18,22].

3.2. Methods

The steps for developing numerical models and illustrations are described in this section. The stages of model development were carried out by examining them in depth, especially in the research of Pandiangan et al. [18]. This study was conducted to develop a mean-VaR quadratic investment portfolio optimization model based on investor risk aversion considering the risk-free assets and liabilities of the company. The formulation of the portfolio weight model here was carried out using a vector and matrix equation approach.

The stages of numerical illustration were carried out to show the application of the model. The data used were the return of 11 stock assets in the mining and energy sectors, returns on company liabilities, and risk-free assets, as described in Section 3.1. The stages of data analysis were broadly carried out in the following way:

(1)

The descriptive analysis was carried out first on the 11 stock return data. The descriptive statistics analyzed were stock code, mean value, variance, covariance, and standard deviation. The mean of each asset was then used to form the vector of return mean $\mathsf{\mu }$. Then, the variance and covariance values formed the $\mathsf{\Sigma }$ covariance matrix.

(2)

Next was to generate monthly liability return data from the company via simulation. The covariance between stock asset returns and liability returns was determined first. The covariance value was then used to form the covariance vector of asset and liability returns.

(3)

Next was the stage of determining the optimum asset weight in the investment portfolio based on the mean vector, covariance matrix, and covariance vector between assets and liabilities obtained. In this stage, investors’ risk aversion values were determined via simulation.

(4)

Based on the results of the optimization of asset weights in the investment portfolio, the formation of an efficient portfolio surface graph was carried out. This graph illustrated the feasible points for a rational investor to invest accordingly.

4. Results and Discussions

4.1. Quadratic Optimization Modeling for Mean-VaR Investment Portfolio with Risk-Free Assets and Liabilities

In this section, the development of a quadratic optimization model of the mean-VaR investment portfolio, which includes risk-free assets and liabilities, is designed. The model is inclusive for a single period, e.g., daily, monthly, quarterly, or yearly. Suppose that the covariance vector between asset and liability returns is expressed as ${\mathsf{\gamma }}^T=({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_N)$ with ${\gamma }_k=\frac{1}{f_0}{\sigma }_{k,L}$. The quadratic optimization model for the mean-VaR investment portfolio without the risk-free asset, involving risk-free assets and liabilities, is expressed as follows:

$$\begin{array}{c}\mathrm{m}\mathrm{a}\mathrm{x}.{\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }+{\mathbf{w}}^{\mathrm{T}}\mathsf{\gamma }-\frac{c}{2}\left[{\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }+z_{\alpha }{\left({\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}\right],\\ =\left(1-\frac{c}{2}\right){\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }+{\mathbf{w}}^{\mathrm{T}}\mathsf{\gamma }-\frac{c}{2}{z}_{\alpha }{\left({\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}},\\ \mathrm{s}.\mathrm{t}.{\mathbf{w}}^{\mathrm{T}}\mathbf{e}=1-w_0.\end{array}$$

(19)

The determination of the solution to the problem in Equation (19) is carried out using the Lagrange multiplier method. The Lagrange function of the problem in Equation (19) is expressed as follows:

$$L\left(\mathbf{w},{\lambda }_3\right)=\left(1-\frac{c}{2}\right){\mathbf{w}}^{\mathrm{T}}\mathsf{\mu }+{\mathbf{w}}^{\mathrm{T}}\mathsf{\gamma }-\frac{c}{2}{z}_{\alpha }{\left({\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}+{\lambda }_3\left({\mathbf{w}}^{\mathrm{T}}\mathbf{e}-1+w_0\right),$$

(20)

where ${\lambda }_3$ represents the Lagrange multiplier. Based on the Khun–Tucker theorem, the solution of Equation (20) is carried out based on necessary and sufficient conditions [18,33]. The necessary conditions for the solution to Equation (20) fulfill the following equation:

$$\frac{\partial L\left(\mathbf{w},{\lambda }_3\right)}{\partial \mathbf{w}}=\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }-\frac{c}{2}{z}_{\alpha }\frac{\mathsf{\Sigma }\mathbf{w}}{{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}}+{\lambda }_3\mathbf{e}=0,$$

$$\frac{\partial L\left(\mathbf{w},{\lambda }_3\right)}{\partial {\lambda }_3}={\mathbf{w}}^{\mathrm{T}}\mathbf{e}-1+w_0=0.$$

First, determine the vector $\mathbf{w}$ as follows:

$$\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }-\frac{c}{2}{z}_{\alpha }\frac{\mathsf{\Sigma }\mathbf{w}}{{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}}+{\lambda }_3\mathbf{e}=0,$$

$$\frac{c}{2}{z}_{\alpha }\frac{\mathsf{\Sigma }\mathbf{w}}{{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}}=\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}.$$

(21)

Multiply both sides of Equation (21) by $\frac{2}{c{z}_{\alpha }}{\mathsf{\Sigma }}^{-1}$ so that this results in the following equation:

$$\frac{\mathbf{w}}{{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}}=\frac{2}{c{z}_{\alpha }}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right],$$

(22)

Then, multiply both sides of Equation (22) by ${\mathbf{e}}^{\mathrm{T}}$ so that this results in the following equation:

$$\frac{1-w_0}{{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}}=\frac{2}{c{z}_{\alpha }}{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right],$$

$${\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}=\frac{c{z}_{\alpha }}{2}\frac{1-w_0}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}.$$

(23)

Substitute Equation (23) into Equation (22) so that this results in the following equation:

$$\frac{\mathbf{w}}{{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}}=\frac{2}{c{z}_{\alpha }}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right],$$

$$\mathbf{w}={\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}\frac{2}{c{z}_{\alpha }}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right],$$

$$\mathbf{w}=\frac{c{z}_{\alpha }}{2}\frac{1-w_0}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}\frac{2}{c{z}_{\alpha }}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right],$$

$${\mathbf{w}}^{\mathbf{*}}=\frac{(1-w_0){\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{c}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{c}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}.$$

(24)

Next is the determination of the solution ${\lambda }_3$. Multiply both sides of Equation (24) by ${\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }$ so that this results in the following equation:

$${\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}=\frac{(1-w_0){\mathbf{w}}^{\mathrm{T}}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]},$$

or

$${\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}=\frac{(1-w_0)\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}+{\lambda }_3{\mathbf{e}}^{\mathrm{T}}\right]\mathbf{w}}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}.$$

(25)

From Equation (23), obtain the following equation:

$$\frac{1-w_0}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}={\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}\frac{2}{c{z}_{\alpha }}.$$

(26)

Substitute Equation (26) into (25) to obtain the following equation:

$${\mathbf{w}}^{\mathrm{T}}\mathsf{\Sigma }\mathbf{w}={\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}\frac{2}{c{z}_{\alpha }}\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}+{\lambda }_3{\mathbf{e}}^{\mathrm{T}}\right]\mathbf{w},$$

$$\frac{c{z}_{\alpha }}{2}{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}=\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}+{\lambda }_3{\mathbf{e}}^{\mathrm{T}}\right]\mathbf{w}.$$

(27)

Substitute Equations (23) and (24) into Equation (27) so that this results in the following equation:

$$\frac{c{z}_{\alpha }}{2}\left\{\frac{c{z}_{\alpha }}{2}\frac{1-w_0}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}\right\}=\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}+{\lambda }_3{\mathbf{e}}^{\mathrm{T}}\right]\frac{\left(1-w_0\right){\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]}{{\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right]},$$

$${\left(\frac{c{z}_{\alpha }}{2}\right)}^2=\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}+{\lambda }_3{\mathbf{e}}^{\mathrm{T}}\right]{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }+{\lambda }_3\mathbf{e}\right],$$

$${\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\mathbf{e}{\lambda }_3^2+2\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}\right]{\mathsf{\Sigma }}^{-1}\mathbf{e}{\lambda }_3+\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}\right]{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }\right]-{\left(\frac{c{z}_{\alpha }}{2}\right)}^2=0.$$

(28)

Equation (28) is a quadratic equation, so the possible values of ${\lambda }_3>0$ are as follows:

$${\lambda }_3=\frac{-q\pm \sqrt{q^2-4pr}}{2p},$$

where $p={\mathbf{e}}^{\mathrm{T}}{\mathsf{\Sigma }}^{-1}\mathbf{e}$, $q=2\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}\right]{\mathsf{\Sigma }}^{-1}\mathbf{e}$, and $r=\left[\left(1-\frac{\mathrm{c}}{2}\right){\mathsf{\mu }}^{\mathrm{T}}+{\mathsf{\gamma }}^{\mathrm{T}}\right]{\mathsf{\Sigma }}^{-1}\left[\left(1-\frac{\mathrm{c}}{2}\right)\mathsf{\mu }+\mathsf{\gamma }\right]-{\left(\frac{c{z}_{\alpha }}{2}\right)}^2$.

After the weight allocation of funds from each asset is obtained, the next step is to examine the terms of sufficient solutions as the maximum solution. It is calculated by examining the Hessian matrix of the Lagrange function in Equation (20). Equation (19) is converted into a minimization problem via the dual method. Then, the solution ${\mathbf{w}}^{\mathbf{*}}$ to Equation (24) is called the global maximum solution of Equation (20) if the Hessian matrix is positive definite. The Hessian matrix of Equation (20) is expressed as follows:

$$\mathbf{H}\left(\mathbf{w},{\lambda }_3\right)=\left[\begin{array}{cc}\frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_3\right)}{\partial {\mathbf{w}}^2}& \frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_3\right)}{\partial \mathbf{w}\partial {\lambda }_3}\\ \frac{{\partial }^{2}L\left(\mathbf{w},{\lambda }_3\right)}{\partial {\lambda }_3\partial \mathbf{w}}& \frac{\partial L\left(\mathbf{w},{\lambda }_3\right)}{\partial {\lambda }_3^2}\end{array}\right]=\left[\begin{array}{cc}\frac{-c{z}_{\alpha }}{{2\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}^{\frac{1}{2}}}\left[\mathsf{\Sigma }-\frac{\left(\mathsf{\Sigma }\mathbf{w}\right)\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\right)}{\left({\mathbf{w}}^{\mathbf{T}}\mathsf{\Sigma }\mathbf{w}\right)}\right]& \mathbf{e}\\ {\mathbf{e}}^{\mathrm{T}}& 0\end{array}\right].$$

The $\mathbf{H}(\mathbf{w},{\lambda }_3)$ matrix is called positive definite if $\forall \mathbf{x}\in {\mathbb{R}}^{N+1}-\left\{0\right\},{\mathbf{x}}^{\mathrm{T}}\mathbf{H}(\mathbf{w},{\lambda }_3)\mathbf{x}>0$. Since the values of $c$ and $z_{\alpha }$ are positive, it is evident that the problem in Equation (20) is convex [34,35,36].

4.2. Numerical Illustration Results

4.2.1. Descriptive Statistics of Stock Data

This section analyzes descriptive statistics of the stock data used in the numerical illustration.

Table 1. Descriptive Statistics of Stock Data.

Stock Code	Mean	Variance	Standard Deviation
BSSR	0.0199	0.0185	0.1362
BYAN	0.0314	0.0242	0.1556
CITA	0.0374	0.0288	0.1698
HRUM	0.0214	0.0283	0.1683
MBAP	0.0272	0.0199	0.1412
MDKA	0.0469	0.0141	0.1187
MEDC	0.0354	0.0487	0.2207
PSAB	0.0135	0.0270	0.1642
PTBA	0.0855	0.3504	0.5919
PTRO	0.0340	0.0239	0.1546
RUIS	0.0135	0.0184	0.1357

gives the stock code, mean, variance, and standard deviation of the 11 stock data.

Table 1 shows that of the 11 stocks, the most significant mean is in PTBA, while the most minor mean is obtained from RUIS. The values from Table 1 are then used for the mean vector, vector one, and the covariance matrix. The vector of the mean return of 11 stocks is expressed as follows:

$$\mathsf{\mu }=\left[\begin{array}{c}0.0199\\ 0.0314\\ 0.0374\\ 0.0214\\ 0.0272\\ 0.0469\\ 0.0354\\ 0.0135\\ 0.0855\\ 0.0340\\ 0.0135\end{array}\right]$$

Furthermore, the covariance between 11 stock asset returns must first be determined to form a covariance matrix. We formed it with the help of Microsoft Excel software, and the results are given in

Table A1. Covariance matrix of 11 Stocks.

	BSSR	BYAN	CITA	HRUM	MBAP	MDKA	MEDC	PSAB	PTBA	PTRO	RUIS
BSSR	0.0186	0.0028	−0.0003	0.0068	0.0031	−0.0003	0.0114	−0.0055	0.0037	0.0030	0.0011
BYAN	0.0028	0.0242	0.0056	0.0034	0.0130	0.0001	0.0018	−0.0005	0.0032	0.0032	−0.0017
CITA	−0.0003	0.0056	0.0288	−0.0069	0.0000	0.0101	−0.0075	0.0002	0.0016	−0.0061	−0.0035
HRUM	0.0068	0.0034	−0.0069	0.0283	0.0066	−0.0013	0.0146	0.0053	−0.0022	0.0098	0.0055
MBAP	0.0031	0.0130	0.0000	0.0066	0.0199	0.0002	0.0046	−0.0015	−0.0077	0.0060	0.0022
MDKA	−0.0003	0.0001	0.0101	−0.0013	0.0002	0.0141	0.0044	0.0053	−0.0003	0.0032	−0.0012
MEDC	0.0114	0.0018	−0.0075	0.0146	0.0046	0.0044	0.0487	0.0032	0.0251	0.0162	0.0053
PSAB	−0.0055	−0.0005	0.0002	0.0053	−0.0015	0.0053	0.0032	0.0270	−0.0035	0.0105	−0.0007
PTBA	0.0037	0.0032	0.0016	−0.0022	−0.0077	−0.0003	0.0251	−0.0035	0.3504	0.0341	−0.0004
PTRO	0.0030	0.0032	−0.0061	0.0098	0.0060	0.0032	0.0162	0.0105	0.0341	0.0239	0.0003
RUIS	0.0011	−0.0017	−0.0035	0.0055	0.0022	−0.0012	0.0053	−0.0007	−0.0004	0.0003	0.0184

(See Appendix A). The next step is determining the covariance vector between stock asset returns and company liability returns. Monthly liability data are calculated with a simulation. To generate monthly liability data, we assume that it is normally distributed based on the parameters of each stock asset liability return. Furthermore, the covariance value between stock asset returns and liability returns is determined, and the results are given as follows:

$$\mathsf{\gamma }=\left[\begin{array}{c}0.0016\\ -0.1449\\ -0.0009\\ 0.0020\\ -0.0268\\ -0.1198\\ 0.6424\\ -0.0024\\ -0.5944\\ 0.0127\\ 0.0025\end{array}\right]$$

In this study, risk-free assets are deposits with a monthly interest rate set by the Central Bank of Indonesia, namely ${\mu }_0=0.07$ per year $\approx \frac{0.07}{12}$ per month. Then, the weight allocation for risk-free assets $w_0$ is assumed to be 0.5.

4.2.2. Determination of Optimum Weight Allocation

In this section, the determination of the optimum weight allocation for the investment portfolio uses Equation (24). Risk aversion is determined with a simulation [37,38] whose value is $5.1<c\le 8.2$ with an increase of $\mathsf{\Delta }c=0.05$. In other words, $c$ is in the set of $\left\{5.1,5.15,\dots ,8.15,8.2\right\}$. This interval is chosen because the weight allocation of each stock obtained is positive. Calculations are carried out using the Matlab version 2007a and the Microsoft Excel version 2403. The optimum weighting results for each of these shares are given in

Table A2. Optimization Process with Risk-Free Assets $\left(w_0=0.5\right)$ and Liabilities.

$\mathit{c}$	${\mathit{w}}_1$	${\mathit{w}}_2$	${\mathit{w}}_3$	${\mathit{w}}_4$	${\mathit{w}}_5$	${\mathit{w}}_6$	${\mathit{w}}_7$	${\mathit{w}}_8$	${\mathit{w}}_9$	${\mathit{w}}_{10}$	${\mathit{w}}_{11}$	${\mathbf{w}}^{\mathbf{T}}\mathbf{e}$	$\mathit{E}\left(\mathcal{R}\right)$	$\mathit{V}\mathit{a}{\mathit{R}}_{0.05}\left(\mathcal{R}\right)$	$\mathbf{Ratio}$
5.10	0.0060	0.0006	0.0552	0.1620	0.0049	0.0028	0.0002	0.0108	0.0000	0.0369	0.2206	0.5	0.0103	0.0138	0.7486
5.15	0.0060	0.0006	0.0552	0.1621	0.0048	0.0027	0.0002	0.0108	0.0000	0.0370	0.2206	0.5	0.0103	0.0138	0.7485
5.20	0.0060	0.0006	0.0551	0.1621	0.0048	0.0027	0.0002	0.0108	0.0000	0.0370	0.2206	0.5	0.0103	0.0138	0.7484
5.25	0.0061	0.0006	0.0550	0.1622	0.0047	0.0027	0.0002	0.0108	0.0000	0.0371	0.2206	0.5	0.0103	0.0138	0.7483
5.30	0.0061	0.0006	0.0550	0.1622	0.0047	0.0027	0.0002	0.0108	0.0000	0.0371	0.2206	0.5	0.0103	0.0138	0.7483
5.35	0.0061	0.0006	0.0549	0.1623	0.0047	0.0027	0.0002	0.0108	0.0000	0.0371	0.2206	0.5	0.0103	0.0138	0.7481
5.40	0.0061	0.0006	0.0548	0.1623	0.0046	0.0027	0.0002	0.0108	0.0000	0.0372	0.2206	0.5	0.0103	0.0138	0.7481
5.45	0.0061	0.0006	0.0548	0.1624	0.0046	0.0027	0.0002	0.0108	0.0000	0.0372	0.2207	0.5	0.0103	0.0138	0.7480
5.50	0.0061	0.0006	0.0547	0.1624	0.0046	0.0027	0.0002	0.0108	0.0000	0.0372	0.2207	0.5	0.0103	0.0138	0.7479
5.55	0.0061	0.0006	0.0546	0.1625	0.0045	0.0027	0.0002	0.0108	0.0000	0.0372	0.2207	0.5	0.0103	0.0138	0.7477
5.60	0.0061	0.0006	0.0546	0.1625	0.0045	0.0027	0.0002	0.0108	0.0000	0.0373	0.2207	0.5	0.0103	0.0138	0.7477
5.65	0.0062	0.0006	0.0545	0.1626	0.0045	0.0027	0.0002	0.0108	0.0000	0.0373	0.2207	0.5	0.0103	0.0138	0.7476
5.70	0.0062	0.0006	0.0545	0.1626	0.0044	0.0027	0.0002	0.0108	0.0000	0.0373	0.2207	0.5	0.0103	0.0138	0.7476
5.75	0.0062	0.0006	0.0544	0.1627	0.0044	0.0027	0.0002	0.0108	0.0000	0.0374	0.2207	0.5	0.0103	0.0138	0.7475
5.80	0.0062	0.0006	0.0544	0.1627	0.0044	0.0027	0.0002	0.0108	0.0000	0.0374	0.2207	0.5	0.0103	0.0138	0.7475
5.85	0.0062	0.0006	0.0543	0.1628	0.0043	0.0027	0.0002	0.0107	0.0000	0.0374	0.2208	0.5	0.0103	0.0138	0.7473
5.90	0.0062	0.0005	0.0543	0.1628	0.0043	0.0027	0.0002	0.0107	0.0000	0.0374	0.2208	0.5	0.0103	0.0138	0.7472
5.95	0.0062	0.0005	0.0542	0.1628	0.0043	0.0027	0.0002	0.0107	0.0000	0.0375	0.2208	0.5	0.0103	0.0138	0.7472
6.00	0.0062	0.0005	0.0542	0.1629	0.0043	0.0027	0.0002	0.0107	0.0000	0.0375	0.2208	0.5	0.0103	0.0138	0.7471
6.05	0.0062	0.0005	0.0541	0.1629	0.0042	0.0027	0.0002	0.0107	0.0001	0.0375	0.2208	0.5	0.0103	0.0138	0.7470
6.10	0.0062	0.0005	0.0541	0.1630	0.0042	0.0027	0.0002	0.0107	0.0001	0.0375	0.2208	0.5	0.0103	0.0138	0.7469
6.15	0.0063	0.0005	0.0540	0.1630	0.0042	0.0027	0.0002	0.0107	0.0001	0.0376	0.2208	0.5	0.0103	0.0138	0.7469
6.20	0.0063	0.0005	0.0540	0.1630	0.0041	0.0027	0.0002	0.0107	0.0001	0.0376	0.2208	0.5	0.0103	0.0138	0.7469
6.25	0.0063	0.0005	0.0539	0.1631	0.0041	0.0027	0.0002	0.0107	0.0001	0.0376	0.2208	0.5	0.0103	0.0138	0.7467
6.30	0.0063	0.0005	0.0539	0.1631	0.0041	0.0027	0.0002	0.0107	0.0001	0.0376	0.2209	0.5	0.0103	0.0138	0.7467
6.35	0.0063	0.0005	0.0538	0.1631	0.0041	0.0027	0.0002	0.0107	0.0001	0.0377	0.2209	0.5	0.0103	0.0138	0.7466
6.40	0.0063	0.0005	0.0538	0.1632	0.0040	0.0027	0.0002	0.0107	0.0001	0.0377	0.2209	0.5	0.0103	0.0138	0.7465
6.45	0.0063	0.0005	0.0537	0.1632	0.0040	0.0027	0.0002	0.0107	0.0001	0.0377	0.2209	0.5	0.0103	0.0138	0.7465
6.50	0.0063	0.0005	0.0537	0.1633	0.0040	0.0027	0.0002	0.0107	0.0001	0.0377	0.2209	0.5	0.0103	0.0138	0.7464
6.55	0.0063	0.0005	0.0537	0.1633	0.0040	0.0027	0.0002	0.0107	0.0001	0.0377	0.2209	0.5	0.0103	0.0138	0.7464
6.60	0.0063	0.0005	0.0536	0.1633	0.0040	0.0027	0.0002	0.0107	0.0001	0.0378	0.2209	0.5	0.0103	0.0138	0.7464
6.65	0.0063	0.0005	0.0536	0.1634	0.0039	0.0026	0.0002	0.0107	0.0001	0.0378	0.2209	0.5	0.0103	0.0138	0.7462
6.70	0.0063	0.0005	0.0535	0.1634	0.0039	0.0026	0.0002	0.0107	0.0001	0.0378	0.2209	0.5	0.0103	0.0138	0.7461
6.75	0.0064	0.0005	0.0535	0.1634	0.0039	0.0026	0.0002	0.0107	0.0001	0.0378	0.2209	0.5	0.0103	0.0138	0.7461
6.80	0.0064	0.0005	0.0535	0.1635	0.0039	0.0026	0.0002	0.0107	0.0001	0.0378	0.2209	0.5	0.0103	0.0138	0.7461
6.85	0.0064	0.0005	0.0534	0.1635	0.0038	0.0026	0.0002	0.0107	0.0001	0.0379	0.2210	0.5	0.0103	0.0138	0.7459
6.90	0.0064	0.0005	0.0534	0.1635	0.0038	0.0026	0.0002	0.0106	0.0001	0.0379	0.2210	0.5	0.0103	0.0138	0.7459
6.95	0.0064	0.0005	0.0534	0.1635	0.0038	0.0026	0.0002	0.0106	0.0001	0.0379	0.2210	0.5	0.0103	0.0138	0.7459
7.00	0.0064	0.0005	0.0533	0.1636	0.0038	0.0026	0.0002	0.0106	0.0001	0.0379	0.2210	0.5	0.0103	0.0138	0.7458
7.05	0.0064	0.0005	0.0533	0.1636	0.0038	0.0026	0.0002	0.0106	0.0001	0.0379	0.2210	0.5	0.0103	0.0138	0.7458
7.10	0.0064	0.0005	0.0532	0.1636	0.0037	0.0026	0.0002	0.0106	0.0001	0.0380	0.2210	0.5	0.0103	0.0138	0.7457
7.15	0.0064	0.0005	0.0532	0.1637	0.0037	0.0026	0.0002	0.0106	0.0001	0.0380	0.2210	0.5	0.0103	0.0138	0.7457
7.20	0.0064	0.0005	0.0532	0.1637	0.0037	0.0026	0.0002	0.0106	0.0001	0.0380	0.2210	0.5	0.0103	0.0138	0.7457
7.25	0.0064	0.0005	0.0531	0.1637	0.0037	0.0026	0.0002	0.0106	0.0001	0.0380	0.2210	0.5	0.0103	0.0138	0.7456
7.30	0.0064	0.0005	0.0531	0.1637	0.0037	0.0026	0.0002	0.0106	0.0001	0.0380	0.2210	0.5	0.0103	0.0138	0.7456
7.35	0.0064	0.0005	0.0531	0.1638	0.0037	0.0026	0.0002	0.0106	0.0001	0.0380	0.2210	0.5	0.0103	0.0138	0.7455
7.40	0.0064	0.0005	0.0530	0.1638	0.0036	0.0026	0.0002	0.0106	0.0001	0.0381	0.2210	0.5	0.0103	0.0138	0.7454
7.45	0.0064	0.0005	0.0530	0.1638	0.0036	0.0026	0.0002	0.0106	0.0001	0.0381	0.2210	0.5	0.0103	0.0138	0.7454
7.50	0.0065	0.0005	0.0530	0.1638	0.0036	0.0026	0.0002	0.0106	0.0001	0.0381	0.2211	0.5	0.0103	0.0138	0.7454
7.55	0.0065	0.0005	0.0530	0.1639	0.0036	0.0026	0.0002	0.0106	0.0001	0.0381	0.2211	0.5	0.0103	0.0138	0.7453
7.60	0.0065	0.0005	0.0529	0.1639	0.0036	0.0026	0.0002	0.0106	0.0001	0.0381	0.2211	0.5	0.0103	0.0138	0.7453
7.65	0.0065	0.0005	0.0529	0.1639	0.0036	0.0026	0.0002	0.0106	0.0001	0.0381	0.2211	0.5	0.0103	0.0138	0.7453
7.70	0.0065	0.0005	0.0529	0.1639	0.0035	0.0026	0.0002	0.0106	0.0001	0.0382	0.2211	0.5	0.0103	0.0138	0.7453
7.75	0.0065	0.0005	0.0528	0.1640	0.0035	0.0026	0.0002	0.0106	0.0001	0.0382	0.2211	0.5	0.0103	0.0138	0.7451
7.80	0.0065	0.0005	0.0528	0.1640	0.0035	0.0026	0.0002	0.0106	0.0001	0.0382	0.2211	0.5	0.0103	0.0138	0.7451
7.85	0.0065	0.0005	0.0528	0.1640	0.0035	0.0026	0.0002	0.0106	0.0001	0.0382	0.2211	0.5	0.0103	0.0138	0.7451
7.90	0.0065	0.0005	0.0528	0.1640	0.0035	0.0026	0.0001	0.0106	0.0001	0.0382	0.2211	0.5	0.0103	0.0138	0.7451
7.95	0.0065	0.0005	0.0527	0.1641	0.0035	0.0026	0.0001	0.0106	0.0001	0.0382	0.2211	0.5	0.0103	0.0138	0.7450
8.00	0.0065	0.0005	0.0527	0.1641	0.0034	0.0026	0.0001	0.0106	0.0001	0.0382	0.2211	0.5	0.0103	0.0138	0.7450
8.05	0.0065	0.0005	0.0527	0.1641	0.0034	0.0026	0.0001	0.0106	0.0001	0.0383	0.2211	0.5	0.0103	0.0138	0.7450
8.10	0.0065	0.0005	0.0526	0.1641	0.0034	0.0026	0.0001	0.0106	0.0001	0.0383	0.2211	0.5	0.0103	0.0138	0.7449
8.15	0.0065	0.0005	0.0526	0.1641	0.0034	0.0026	0.0001	0.0106	0.0001	0.0383	0.2211	0.5	0.0103	0.0138	0.7449
8.20	0.0065	0.0005	0.0526	0.1642	0.0034	0.0026	0.0001	0.0106	0.0001	0.0383	0.2211	0.5	0.0103	0.0138	0.7448

(See Appendix B).

Table A2 shows that with the value of $c=5.1$, there is a weight of $w_9=-0.0000004$. It shows the existence of short sales. This analysis assumes that the capital market authority does not permit short sales, so this is not analyzed further. Table A2 shows that the greater the value of risk aversion, the smaller the mean and VaR of the portfolio return. Using the mean and VaR of the portfolio returns in Table A2, the efficient surface graph given in Figure 1 is presented.

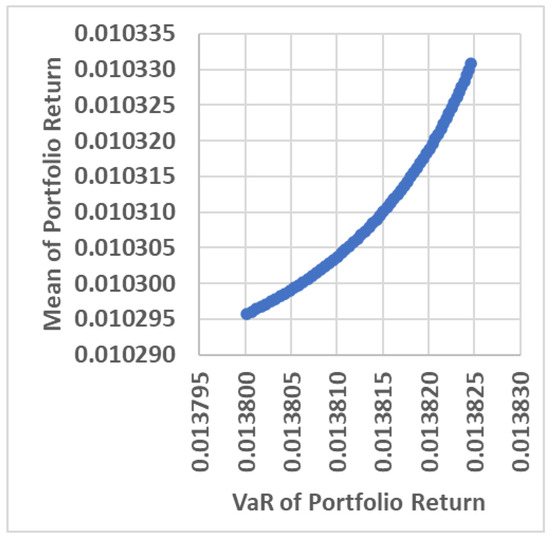
Figure 1 informs investors that investments in 11 stocks worth making are at points along the efficient surface line. In this study, an efficient portfolio surface graph is formed for the constant level of investor risk aversion in the interval $5.1<c\le 8.2$. In that interval, the minimum values of VaR and mean of the portfolio returns are 0.013797 and 0.0102941, respectively. The VaR and the mean return are obtained when the risk aversion investor is $c=8.2$. Meanwhile, the maximum values of VaR and the mean of the portfolio return are 0.013827 and 0.0103316, respectively. The VaR and mean values are obtained when the risk aversion investor is $c=5.2$.

4.3. Discussion

4.3.1. Relationship Analyses

The relationship between risk aversion and mean of the portfolio return is the first thing to be analyzed in this section. Using the values of risk aversion and mean of the portfolio return in Table A2 (see Appendix B), the relationship between the two can be visualized in a Cartesian diagram. The visualization of the relationship between risk aversion and mean of the portfolio return is presented in Figure 2.

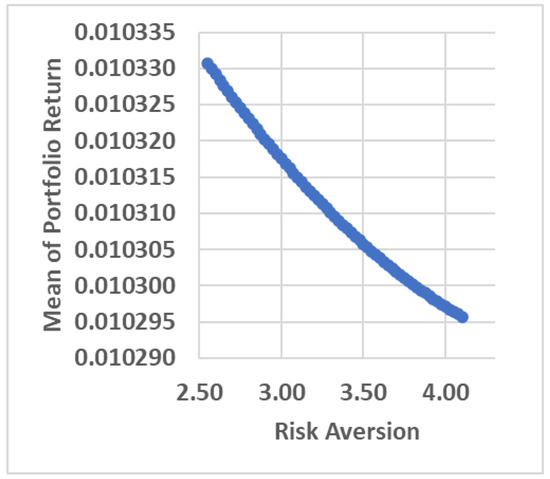
Figure 2 shows that risk aversion and mean of the portfolio return have a negative relationship. It means that the greater the risk aversion of the investor, the smaller the mean of the portfolio return becomes and vice versa. It is logical because if investors avoid uncertainty (this means they have high-risk aversion), the mean of the portfolio return that may be obtained is also very small [39,40].

Next, the relationship between risk aversion and the VaR of the portfolio is analyzed. Using the values of risk aversion and VaR portfolio in Table A2 (see Appendix B), the relationship between the two can be visualized in a Cartesian diagram. The visualization of the relationship between risk aversion and portfolio VaR is presented in Figure 3.

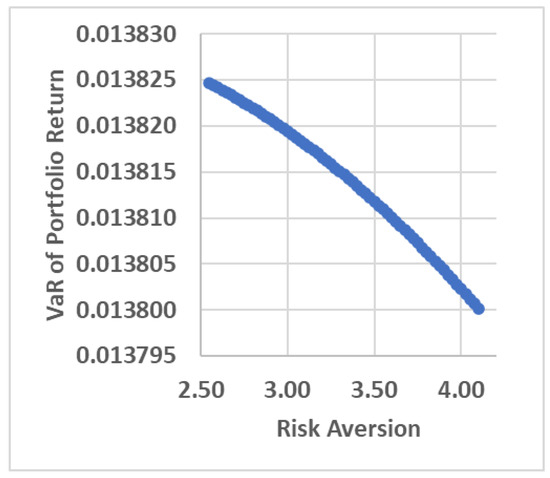
Figure 3 also shows that risk aversion has a relationship that is not in line with the VaR of the portfolio. In other words, this is similar to the relationship between risk aversion and mean of the portfolio return, where the greater the risk aversion of the investor, the smaller the VaR of the portfolio return and vice versa. Practically speaking, if investors are highly uncertainty averse (this means the risk aversion is large), their VaR of portfolio returns will also be small.

Next is a discussion on choosing the optimum portfolio. Optimum portfolio selection can be reviewed by comparing the largest comparison of return and VaR. After this, the comparison is referred to as the ratio. The smallest ratio value indicates that the portfolio has the lowest efficiency level, while the largest ratio value indicates that the portfolio has a high efficiency level (most optimum). To further illustrate this point, we present a visualization of the relationship between portfolio VaR and its ratio in Figure 4.

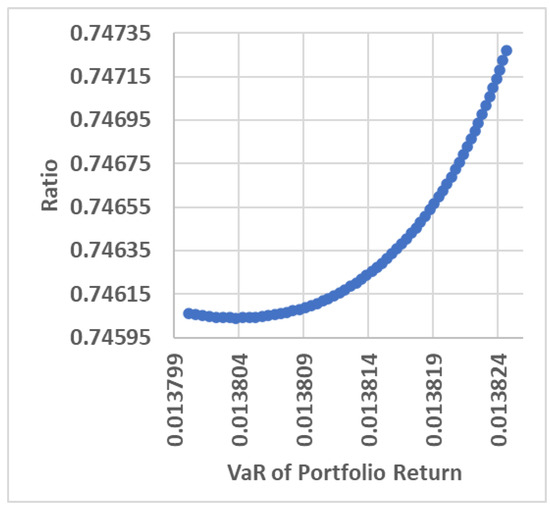
Figure 4 shows that the smallest ratio value is 0.7448. This ratio is obtained from the mean and VaR of portfolio returns 0.0102964 and 0.0137975, respectively. The portfolio is then said to be the portfolio with the lowest efficiency level. Then, the largest ratio value is 0.7486182. This ratio is obtained from the mean and VaR of the portfolio returns 0.0103316 and 0.0138270, respectively. This portfolio is then said to be the optimum portfolio. Coincidentally, this optimum portfolio occurs at the maximum portfolio for the value of investors’ risk aversion in the interval $5.1<c\le 8.2$.

Based on the discussion in the previous sections, a summary of the risk aversion intervals, minimum portfolio, maximum portfolio, optimum portfolio, and composition of weights on the optimum portfolio are given in

Table 2. Summary of Stock Weight Optimization Results on Investment Portfolios.

Variable	Value(s)
Risk Aversion	$5.1<c\le 8.2;∆c=0.05$
Minimum Portfolio	$E\left(\mathcal{R}\right)=0.0102964;Va{R}_{0.05}\left(\mathcal{R}\right)=0.0137975$
Maximum Portfolio	$E\left(\mathcal{R}\right)=0.0103316;Va{R}_{0.05}\left(\mathcal{R}\right)=0.0138270$
Optimum Portfolio	$E\left(\mathcal{R}\right)=0.0103316;Va{R}_{0.05}\left(\mathcal{R}\right)=0.0138270$
Optimum Capital Weight Allocation of Each Stocks	$w_1=0.0497$ $w_2=0.0545$ $w_3=0.0510$ $w_4=0.0333$ $w_5=0.0239$ $w_6=0.1275$ $w_7=0.0027$ $w_8=0.0248$ $w_9=0.0085$ $w_{10}=0.0294$ $w_{11}=0.0947$

.

The summary in Table 2 is expected to be a reference for investors, individuals, and organizations in making investment decisions, especially in the 11 mining and energy sector stocks, including risk-free assets and company liabilities in forming investment portfolios.

4.3.2. Comparation with Other Models

This subsection compares the accuracy of the mean of the optimum portfolio returns of the introduced model (we call it model I) and previous models. The previous models were explained in Section 2.2 (we call it model II) and 2.3 (we call it model III). To measure this accuracy, we first conducted repeated calculations of the mean of the portfolio return from each model for different observation periods. The initial observation period is 1 January 2017 to 1 December 2020, and the subsequent observation period was an additional one month from the previous one. The number of observation periods is thirteen. Then, we determine the optimum portfolio for each observation period. Each mean of the return from the optimum portfolio is used as a forecast of the mean of the portfolio return from the portfolio one month ahead. After that, we compare each forecast with the actual return from each model. We then measure the accuracy of the forecast using the absolute error. The accuracy measurement results show that model I tends to have a smaller absolute error than models II and III in each observation period. It is also shown by the mean absolute error (MAE) of thirteen predictions from the three models, where the MAE from model I is smaller than models II and III. Although this is not analytical evidence, it can show that the model introduced in this study is reliable practically. In summary, the results of the accuracy comparison can be seen in

Table 3. Accuracy comparison between the mean of the optimum portfolio returns from models I, II, and III.

Observation Period	Forecasting Date	Absolute Error of Portfolio Return Mean
		Model I	Model II	Model III
1 January 2017 to 1 December 2020	1 January 2021	0.0756	0.0134	0.0535
1 January 2017 to 1 January 2021	1 February 2021	0.0301	0.0281	0.0277
1 January 2017 to 1 February 2021	1 March 2021	0.0382	0.1150	0.0653
1 January 2017 to 1 March 2021	1 April 2021	0.0051	0.0799	0.0161
1 January 2017 to 1 April 2021	1 May 2021	0.0030	0.0390	0.0141
1 January 2017 to 1 May 2021	1 June 2021	0.0190	0.0149	0.0105
1 January 2017 to 1 June 2021	1 July 2021	0.0038	0.0128	0.0114
1 January 2017 to 1 July 2021	1 August 2021	0.0204	0.0207	0.0218
1 January 2017 to 1 August 2021	1 September 2021	0.0560	0.1102	0.0750
1 January 2017 to 1 September 2021	1 October 2021	0.0063	0.0394	0.0275
1 January 2017 to 1 October 2021	1 November 2021	0.0140	0.0715	0.0389
1 January 2017 to 1 November 2021	1 December 2021	0.0177	0.0089	0.0147
1 January 2017 to 1 December 2021	1 January 2022	0.0507	0.0270	0.0407
Mean Absolute Error (MAE)		0.0261	0.0447	0.0321

The smallest absolute error for each forecasting date and the smallest MAE are boldface.

.

5. Conclusions

This study designs the development of a quadratic optimization model for the mean-VaR investment portfolio, which involves risk-free assets and liabilities. The model can determine the combination of capital allocation weights on each stock asset in forming an investment portfolio. The optimum portfolio weight determination model is expressed using vector and matrix equations, which can simplify and speed up computing with specific software, i.e., the Matlab version 2007a and the Microsoft Excel version 2403.

The numerical illustration is completed to illustrate the use of the model. Note that the model can be illustrated in various capital markets worldwide. In this study, the illustration is based on data on 11 stock assets of Indonesia’s mining and energy sectors. Then, risk-free assets are time deposits whose interest rates are adjusted to Bank Indonesia’s policy. Then, the company’s liabilities are used as simulation data. The numerical illustration shows that risk aversion and the mean of the portfolio return have a negative relationship. Therefore, it means that the greater the risk aversion of the investor, the smaller the mean of the portfolio return becomes and vice versa. This relationship is similar to the relationship between risk aversion and the VaR of the portfolio return. It is logical because if investors avoid uncertainty (this means that their risk aversion is significant), their mean and VaR of portfolio returns will be small and vice versa. We also compare the accuracy of the mean of the optimum portfolio returns of the introduced model and previous models. This comparation shows that the mean of the return from the model introduced in this study has the best accuracy based on its MAPE. Therefore, the model introduced in this study is reliable practically.

This study has its shortcomings. The weaknesses include the fact that the model development is carried out for only a single period, so it cannot accommodate the wishes of investors who invest for multiple periods. Therefore, future research needs further development for models with multi-period time indices. In addition, weaknesses occur in the analysis of numerical illustrations, where the monthly liability data used are the result of a simulation.