Abstract
This study presents a machine learning-based approach to predict blockage in multiphase flow with cohesive particles. The aim is to predict blockage based on parameters like Reynolds and capillary numbers using a random forest classifier trained on experimental and simulation data. Experimental observations come from a lab-scale flow loop with ice slurry in the decane. The plugging simulation is based on coupled Computational Fluid Dynamics with Discrete Element Method (CFD-DEM). The resulting classifier demonstrated high accuracy, validated by precision, recall, and F1-score metrics, providing precise blockage prediction under specific flow conditions. Additionally, sensitivity analyses highlighted the model’s adaptability to cohesion variations. Equipped with the trained classifier, we generated a detailed machine-learning-based flow map and compared it with earlier literature, simulations, and experimental data results. This graphical representation clarifies the blockage boundaries under given conditions. The methodology’s success demonstrates the potential for advanced predictive modelling in diverse flow systems, contributing to improved blockage prediction and prevention.
1. Introduction
The issue of pipeline blockage is relevant in multiple industries, resulting in environmental concerns and financial losses. Applying machine learning methods is becoming a promising solution in flow assurance [1]. This methodology is a potentially powerful tool for analyzing, classifying, and predicting flow regimes, including critical aspects such as pipeline blockage. Numerous studies exist where machine learning methods consider challenges associated with multiphase flows and pipeline blockages.
Manikonda et al. [2] applied machine learning methods to identify vertical gas-liquid two-phase flow regimes. The study aimed to determine the current flow regime using data collected from over thirty articles and two experimental flow loops. They utilized supervised and unsupervised ML classification models, including a Multi-class Support Vector Machine, K-nearest neighbour Classifier, K-means clustering, and hierarchical clustering to separate different flow regions. The study found that the K-Nearest Neighbor Classifier achieved a 98% classification accuracy and matched the flow regime maps from Hasan et al. [3].
Similarly, Alhashem [4] employed a machine learning model using a Stanford Multiphase Flow Data dataset to classify multiphase flow regimes in a horizontal pipe. Fluid flow and pipe configuration descriptions were used as input variables, while the output corresponded to the flow regime type. The authors used the F-1 accuracy score as the performance metric to compare five machine learning methods. After evaluating five methods, including decision tree, random forest, logistic regression, support vector machine, and neural network (multi-layer perceptron), the authors observed that the Decision Tree and Random Forest achieved the highest accuracy rates with 86% and 89%, respectively, with minimal training times less than 0.005 s.
While these studies have primarily focused on horizontal flows, Chaari et al. [5] introduces an Artificial Neural Network (ANN) model for steady-state liquid holdup estimation in two-phase gas-liquid flow, designed to be unifying and applicable across all pipe inclinations and flow patterns. Utilizing the ANN model, this study incorporates 16 dimensionless groups to effectively account for the inertial, viscous, and gravitational effects experienced by both the liquid and gas phases, based on a Stanford Multiphase Flow Database dataset. The proposed model outperformed two established models, showing improved coefficients of determination and significantly lower average absolute relative errors, with improvements of up to 57% in inclination ranges and 66% in various flow patterns.
In addition to the aforementioned non-particle-based studies, certain works show that machine learning methods have great potential for the future of hydrate management and studies of plugging in multiphase flows. It is relevant to evaluate these ML-models using three main criteria defining their industrial applicability: accuracy, size of the datasets, and scalability of the model parameters. Qin et al. [6] considered two machine learning methods: the support vector classifier (SVC) and the regression neural network (NN). The models were trained using 4500 experimental cases, which was the largest dataset of those used in plugging studies. The authors applied the ML-methods to analyze hydrate risks and construct field risk maps using an experimental flow loop and field databases. The accuracy of the SVC was about 0.99, while the NN method was ∼ 96%. Their study demonstrates that a coupled regression and classification learning model can simultaneously predict hydrate volume fraction and plugging risk using process variables. These variables include water cut, gas-oil ratio, liquid velocity, operating time within the hydrate domain, oil properties, and the inter-particle cohesive force of hydrates. However, these variables were not made dimensionless using the standard -theorem analysis [7] so that the ML-models could be hardly scaled for applications other than hydrates.
Furthermore, Wang et al. [8] applied ML to assess the risk of hydrate formation and blockage in a pure water system. The multi-layer perceptron (MLP) model and the logistic regression (LR) model were used in this work. Although the models achieved 99% accuracy, the training dataset’s size was dramatically limited as six cases were fed into the model. The researchers used data from experiments conducted in a high-pressure, entirely visual flow loop for the training. The input variables for these models included time, temperature, pressure drop, gas consumption, remaining water, and the water-cut ratio at each data point. The output of the models aimed to determine the risk of blockage and was based on defining three regions and two critical transition points in the hydrate formation process, namely the “action point” and the “blockage point”. The input data was non-dimensionalized using the statistical parameters with StandardScaler [9]. However, the nondimensionalization did not follow the principles of -theorem [7].
In recent years, scientists have started using machine learning techniques to predict and reduce wax deposits in petroleum pipelines, offering fresh approaches to address this common issue in the oil sector.
For instance, Kim et al. [10] integrated Artificial Intelligence (AI) through the Stacked Auto-Encoder (SAE) model, using an OLGA simulator to generate learning data and employing the RRR (Ryg, Rydahl, and Ronningen) model to describe the molecular diffusion and shear dispersion aspects of wax deposition. It demonstrates impressive accuracy in predicting the location and maximum volume of wax accumulation with over 90% accuracy. However, there may be discrepancies between the predicted wax thickness and actual data, possibly due to the limited initial dataset. Despite this, the model performs effectively at the early detection of wax deposition and accurately predicts the location and amount of wax buildup, showing potential in maintaining a continuous flow of petroleum pipelines.
Additionally, Amar et al. [11] proposed a multilayer perceptron model (MLP) for predicting the weight percent of deposited wax under different production conditions using experimental measurements. After utilizing the Levenberg-Marquardt algorithm (MLP-LMA) and Bayesian Regularization algorithm (MLP-BR) during the MLP’s learning phase, it became evident that MLP-LMA outperformed MLP-BR with an overall root mean square error of 0.2198. Furthermore, its potential for digital implementation makes it more useful in controlling wax deposition in oil and gas pipelines.
Ahmadi [12] proposed a novel approach: combining fuzzy logic and genetic algorithm (GA) to create an efficient method for predicting wax deposition. The model considers important input variables such as oil composition, temperature, pressure, and oil-specific gravity. Parameters like mean square error and relative deviation are quantitative benchmarks, highlighting the model’s accuracy and reliability. The developed model demonstrates high performance and reliability compared to other methods in determining wax deposition values, with the key advantage of rapid calculations and cost-effectiveness. However, like other modelling methods, the proposed machine learning models have limitations related to the range of input and output values. They can only be applied to oil samples and conditions similar to the available data.
After reviewing the aforementioned research, it becomes evident that the application of machine learning methods represents a potent tool for flow assurance issues, particularly for predicting multiphase flow regimes. Collectively, these studies contribute to the ongoing efforts to improve predictive methods for flow patterns, providing valuable insights into potential challenges such as pipeline blockages.
In previous studies, our group focused on understanding how particles can clog up flowing systems. In the work by Struchalin et al. [13], we expanded upon the experimental approach of Hirochi et al. [14] by conducting flow loop experiments employing a decane-oil slurry. These experiments involved controlling particle concentration and size and carefully regulating temperature to affect particle cohesion. Our work led to an improved understanding of the plugging process with the given experimental conditions. These findings act as a reference point for validating numerical models of plugging. In the second study by Saparbayeva and Balakin [15], we applied a CFD-DEM to better understand plug formation in a multiphase system with a cohesive dispersed phase. The process parameters were dimensionless according to the -theorem principles [13]. Many models from the literature lacked validation against actual plugging experiments. To address these limitations, we introduced a CFD-DEM model validated against the well-defined experimental benchmark for plugging. Notably, our prior work by Saparbayeva et al. [16] laid the foundation for this model by investigating ice-ice cohesive collisions, offering valuable insights into successful application in understanding the entire flow process.
The novelty of this paper is highlighted by its ability to predict blockage without the need for model execution or experimental trials. This is achieved by integrating a machine learning model that utilizes experimental and CFD-DEM model datasets as inputs. In contrast to the previously discussed studies in machine learning application, our research introduces the application of a machine learning classification model to predict blockages in multiphase systems with unique characteristics, specifically the presence of ice particles in a decane-oil slurry. The presence of ice particles introduces an extra layer of complexity. In our case, this involves utilizing a more precise CFD-DEM model.
2. Methodology
The dataset used for the classifier’s training consists of two parts: the plugging data collected in the flow loop experiments and the database of CFD-DEM simulations expanding the experimental dataset.
2.1. Experiments
The flow experiments were carried out using a lab-scale multiphase flow loop. A cohesive slurry of ice in decane circulated in the loop. These materials were chosen due to the known cohesive surface energy for different temperatures below the ice formation point [17]. The ice particles were produced outside the flow loop by crushing ice blocks. The size of the particles was in the interval 200–400 µm. The particle size distribution was log-normal. The maximum volume fraction of particles used in experiments was 15%. The maximum Reynolds number Re = ∼25,000, where , are the density and the viscosity of decane, v is the mean flow velocity, and d is the diameter of the pipe. The flow loop consisted of a centrifugal pump, a temperature-controlled stirred tank, and a steel test section (ID = 22 mm). Negative temperatures of −3 … −1 °C were set in the loop by connecting tank coils to a chiller and thermally insulating the flow loop. Plugging occurred in the test section, where a 9.5-mm orifice was installed. The local resistance of the orifice and secondary wake flow in the corners of the orifice promoted the deposition and sticking of cohesive particles.
The flow loop and its hydraulic scheme are presented in Figure 1. The experiments were carried out by loading a controlled amount of ice in a highly agitated and pre-cooled flow, reducing the flow rate to a set point, increasing the temperature to a given value, and monitoring the flow using the mass flow meter. In addition, the measurement system of the loop included a differential manometer controlling the test section and thermocouples for temperature control. A successful plugging event was defined as a sensor-confirmed zero flow condition following the set point without further action from the loop operator. More details about the experiments are found in [13].
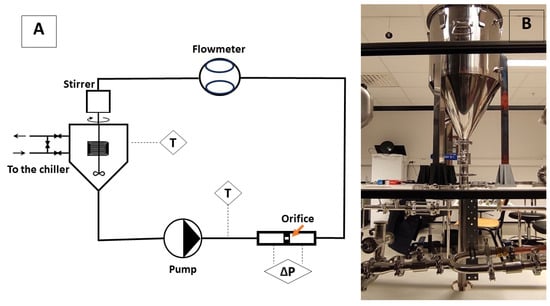
Figure 1.
Hydraulic diagram of the experimental flow loop (A) with the orifice indicated by an orange arrow and photo of the central part of the flow loop (B).
2.2. CFD-DEM Model
To complement relatively few flow loop experiments, we generated additional data points from the CFD-DEM model developed for this study. In particular, the CFD model allowed us to study cohesion parameters more closely. In the experiments, the cohesion was altered by changing the temperature of the coils in the tank. However, due to the large thermal inertia of the flow loop, the cohesion was defined with significant uncertainties. Therefore, a multiphase CFD-DEM model of the test section was built to highlight the influence of cohesive forces and to consider the physics of the plugging process in greater detail. The model was based on the Eulerian-Lagrangian approach, where Navier-Stokes equations described the flow of decane, while the particles were treated as Lagrangian objects following Newtonian mechanics. The phases were coupled via drag, lift, and pressure gradient forces calculated in each computational cell of the model. The contact interactions between the particles were resolved using the so-termed “soft-sphere” technique, accounting for their deformations upon collisions. The Hertz-Mindlin approach was used for this purpose, considering cohesive forces acting during the collision. While the inter-particle cohesive energy was known from the third-party experiments, the particle-wall cohesion was not known in the experiments. Therefore, a ratio of the cohesive energy of the walls to the cohesive energy of the ice = was used as a fitting parameter to validate the model. As the model treated every particle separately, and many particles were present in the experiments, this was required to limit the computational costs. Therefore, as shown in Figure 2 (left), the geometry of the experiment was simplified to a thin slice of the test section bounded by periodic boundaries. A constant pressure drop resulting in the experimental flow rate was set at the ends of the model. The model is described in greater detail in Saparbayeva and Balakin [15].
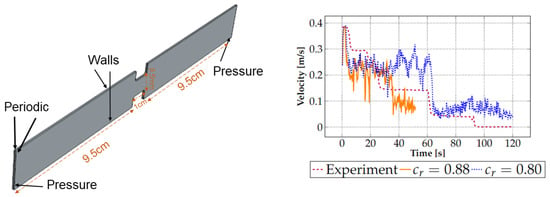
Figure 2.
Geometry and boundary conditions of the model (left) and comparison between experimental data and CFD-DEM model: average flow velocity over time with different cohesion-to-adhesion ratios = / in comparison to the findings of Struchalin et al. [13] at Reynolds number Re = 4996 and particle volume fraction = 6.8% (right).
2.3. Machine Learning
We employ the random forest classifier as our machine-learning tool to analyze blockage in the considered multiphase flow. This choice is driven by the classifier’s adaptability and robustness when dealing with multidimensional datasets, making the classifier a well-suited approach for our case with multiple parameters and features [18,19]. The random forest classifier offers the advantage of feature importance analysis, enabling the identification of the critical factors of the process [20]. Additionally, this classifier type can handle non-linear data and overfits at a lower rate than similar ML techniques.
We implemented this method using the scikit-learn library, a standard Python tool for machine learning tasks [21]. Scikit-learn offers a user-friendly interface for methods like the random forest and supports various models and data processing techniques. Adjusting model parameters and evaluating performance allows for a comprehensive analysis of the classifier’s usage.
The flowchart of the constructed ML technique is presented in Figure 3. We used input data from two primary sources to train our model: experimental flow loop data and CFD-DEM simulations. Each entry in the input file contains four key parameters: Reynolds number, concentration, capillary number, and the fourth parameter, a binary classifier indicating whether blockages are present or absent in the system. The Reynolds number is a dimensionless parameter used to evaluate the significance of inertial forces compared to viscous forces in a fluid motion, while the capillary number indicates the balance between viscous forces and surface tension forces in a system. To evaluate the model’s performance and ensure its stability, we employed a cross-validation method with a parameter k = 5. This means the treated multidimensional datasets were divided into five folds (subsets) for training and testing. Each model was trained on four folds. 80% of data and tested on the remaining 20% of the data. The cross-validation procedure was repeated five times with different fold combinations. The outcome is the model performance verification. In total, 150 cases were used for the training.
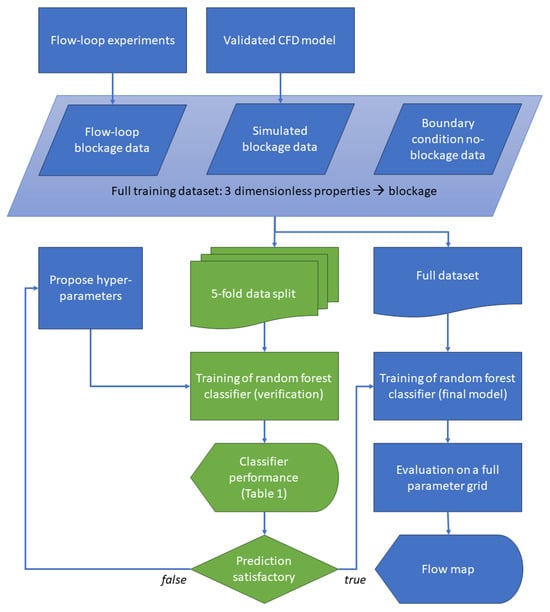
Figure 3.
Schematic description of the developed ML model.
In the machine learning model, we adjusted several key parameters to optimize the model’s performance. We selected a fixed random seed value of 42 and set the random forest classifier with 100 estimators while limiting the maximum depth of each decision tree to 10. These parameters were selected to establish a well-balanced model combining accuracy and adaptability across various parameter conditions. Other parameters are configured with their default values. After selecting the best hyperparameters, we train a final Random Forest classifier on 100% of data to produce the most accurate flow map.
3. Results
3.1. Machine Learning
Dataset
Using the classifier, we predicted the presence of blockages across a range of parameter conditions. In this figure, we present an array of process conditions at which the classifier forecasts plugging events. The contrast between the plugging and non-plugging conditions defines boundaries where blockages occur, as depicted in Figure 4. At lower concentrations, up to about 15%, the boundary appears around a Reynolds number of 10,000. Later, as concentrations increase, this boundary reduces. Figure 4 shows that the model predicted blockades at high Re and low particle concentrations. This happens because the imported dataset contains several specific experimental data points with high Reynolds numbers that indicate the cases when the pump of the flow loop experienced blockage.
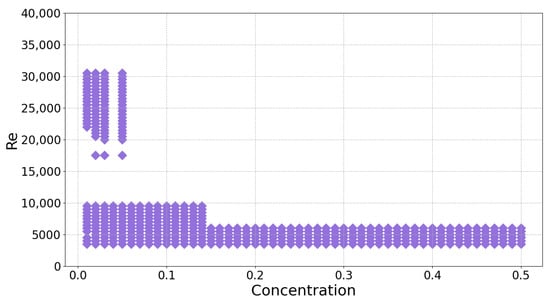
Figure 4.
ML-predicted process conditions resulted with plugging. Intermediate result produced from the original dataset.
3.2. Experiments and CFD-DEM Model
An example of the experimental log is presented in Figure 2 (right) in terms of the history of flow velocity. The plot shows that the velocity gradually reduced until the plugging condition. There were several significant steps of the velocity reduction. This is related to the propagation of particulate slugs, which were formed due to the accumulation of particles in quiescent zones of the flow loop. Depending on the set point, the duration of the plugging process in different experiments was in the interval 50 …1000 s. The experimental results for various flow conditions are summarized in Figure 5, where the flow map of plugging is presented in terms of flow Reynolds number and the concentration of particles. A referent flow map from similar experiments of Hirochi et al. [14] is shown in the figure. As follows from the map, plugging happened when the concentration of particles was above 14%, and the Reynolds number below 10,000. These values differ from Hirochi et al. [14] as ice particles in decane are more cohesive than ice particles in an aqueous media, as considered in the referent study. There were also untypical cases where the plugging was registered at low concentrations and high Re. These plugging events, labelled separately in the figure, are attributed to the blockage of clearances in the pump.
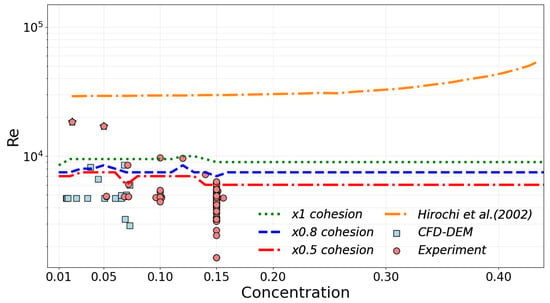
Figure 5.
Flow map from the random forest classifier with three different cohesion values. The datapoints in the plot represent experimental [13] and the CFD-DEM cases where the blockage was detected. Experimental points excluded from training are labeled with star-like markers. Flow map from Hirochi et al. [14] shown for comparison. The lines present the boundaries of the plugging regime predicted by the ML-model and shown in Hirochi et al. [14].
The CFD-DEM model was validated against the experimental logs; an example of the validation plot is shown in Figure 2 (right) for different values of . As shown by Saparbayeva and Balakin [15], and presented in the figure, the best match of the experiment is found for = 0.88. The model does not entirely reproduce the stepwise drops of the flow velocity as it does not replicate the entire flow loop with places where the particle slugs are formed. After the validation, the CFD-DEM model produced new points for the flow map (Figure 5). The model data correspond to the experimental dataset. Additional simulations were carried out to test how the process is sensitive to variation of . This was done by altering the dimensionless granular capillary number , where v is the mean flow velocity, is the viscosity of the continuous phase, and is the cohesive surface energy of the ice particles. In the simulations, the capillary number was in the range from 0.001 to 0.003.
3.2.1. Validation
Our accuracy evaluation analyzed key performance measures, including precision, recall, and F1-score. The results are presented in Table 1, with accuracy scores ranging from 0, indicating the worst, to 1, indicating the best accuracy. Precision represents the proportion of true positive predictions among all positive predictions made by the classifier. Recall measures the proportion of true positive predictions among all actual positive cases. The F1-score is the harmonic mean of precision and recall, providing a balanced assessment of the classifier’s performance. As demonstrated in Table 1, all of these measures show notably high values for both cases, whether with or without blockage. The case without blockage exhibited a minimum recall value of 0.80 and a maximum precision value of 1, while the blockage case achieved a maximum recall value of 1. The F1-score for both cases is high, indicating that the classification model performs well. These metrics collectively demonstrate the effectiveness of the chosen method.

Table 1.
Summary of random forest classifier performance.
3.2.2. Results
Figure 5 represents a flow map by Hirochi et al. [14] in comparison with a representation of the three blockage boundaries predicted by the classifier, as well as experimental [13] and simulation data points. The boundaries of the ML-predicted plugging regimes are presented as in Figure 4. We have excluded an unphysical boundary showing blockage at high Reynolds numbers for the flow map construction. Four data points from the imported dataset discussed earlier in Figure 4 were excluded for the training of the final version of the ML model. Furthermore, we presented three different results for machine learning lines corresponding to changes in cohesion. As depicted in the figure, the scaling of the cohesive surface energy by factors 0.5 and 0.8, and the respective increase of the granular capillary number, lower the boundary predicted by the machine learning model. An interesting observation is that the upper limit set by the machine learning classifier closely aligns with the line when the Reynolds number is around . This alignment is particularly in line with the upper boundaries observed in CFD-DEM simulations and experimental results. We also point out that the isolines of cohesion set horizontal at the concentrations above 15% which might not be entirely realistic as more particles might enhance plugging and thus lift the boundary as in Hirochi et al. [14]. This artifact is related to the fact that the training dataset was limited by 15% due to the experimental limitations and enhanced computational costs in the CFD-DEM model.
It has to be noted that the time spent for every CFD-DEM case was about 3.0 h when running on 30 cores AMD Ryzen Treadripper RO 3975WX (3.8 GHz), and a typical plugging experiment was run for 2.5–4.0 h. The ML code was significantly faster, returning the entire flow map within 10 s of physical time using an ordinary laptop (Intel Core i5-1235U).
4. Conclusions
In this study, we applied the machine-learning tool, a random forest classifier, to predict the occurrence of blockage caused by cohesive particles in the multiphase flow loop. Our methodology combined experimental data from flow loop experiments and CFD-DEM simulations to train a predictive model. Evaluating the model’s performance using precision, recall, and F1-score metrics showed its high accuracy in blockage prediction in given conditions, demonstrating a maximum precision score of 1 for the blockage case and 0.96 for the case without.
As the important contribution of the study, we presented the flow map detailing comparisons between the machine-learning predictions, CFD-DEM simulations, and experimental data. Our multi-parameter ML model allowed us to extend traditional flow maps to assess the blockage boundary’s sensitivity to changes in cohesion. The secondary contributions include the developed ML methodology, the code, and the databases (available upon request).
The methodology’s success highlights the potential for further advancements in predictive modelling. Exploring advanced machine learning techniques, refining datasets, and incorporating real-time data can lead to models capable of predicting and preventing blockages in diverse and dynamic flow systems.
Author Contributions
Conceptualisation, data curation, formal analysis, investigation, methodology, and writing—original draft, N.S.; Investigation, methodology, experiments, editing, P.G.S.; Supervision, conceptualisation, data curation, formal analysis, investigation, methodology, software and writing—original draft, B.V.B.; Supervision, resources, conceptualisation, data curation, formal analysis, investigation, methodology, writing—review and editing, S.A.; Supervision and editing, T.R. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by the Research Council of Norway (project 300286).
Data Availability Statement
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lal, B.; Bavoh, C.B.; Sayani, J.K.S. Machine Learning and Flow Assurance in Oil and Gas Production; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Manikonda, K.; Hasan, A.R.; Obi, C.E.; Islam, R.; Sleiti, A.K.; Abdelrazeq, M.W.; Rahman, M.A. Application of Machine Learning Classification Algorithms for Two-Phase Gas-Liquid Flow Regime Identification. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 2–5 October 2021; p. D041S121R004. [Google Scholar]
- Hasan, A.R.; Kabir, C.S.; Sarica, C. Fluid Flow and Heat Transfer in Wellbores; Society of Petroleum Engineers: Richardson, TX, USA, 2018. [Google Scholar]
- Alhashem, M. Machine learning classification model for multiphase flow regimes in horizontal pipes. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 28 March 2020; p. D023S042R001. [Google Scholar]
- Chaari, M.; Seibi, A.C.; Hmida, J.B.; Fekih, A. An optimized artificial neural network unifying model for steady-state liquid holdup estimation in two-phase gas–liquid flow. J. Fluids Eng. 2018, 140, 101301. [Google Scholar] [CrossRef]
- Qin, H.; Srivastava, V.; Wang, H.; Zerpa, L.E.; Koh, C.A. Machine learning models to predict gas hydrate plugging risks using flowloop and field data. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 16–19 August 2019; p. D011S010R003. [Google Scholar]
- Evans, J.H. Dimensional analysis and the Buckingham Pi theorem. Am. J. Phys. 1972, 40, 1815–1822. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Q.; Meng, Y.; Yao, H.; Zhang, L.; Jiang, B.; Liu, Z.; Zhao, J.; Song, Y. Flow characteristic and blockage mechanism with hydrate formation in multiphase transmission pipelines: In-situ observation and machine learning predictions. Fuel 2022, 330, 125669. [Google Scholar] [CrossRef]
- Muller, A.C.; Guido, S. Introduction to Machine Learning with Python; O’Reilly: Farnham, UK, 2017. [Google Scholar]
- Kim, J.; Han, S.; Seo, Y.; Moon, B.; Lee, Y. The development of an AI-based model to predict the location and amount of wax in oil pipelines. J. Pet. Sci. Eng. 2022, 209, 109813. [Google Scholar] [CrossRef]
- Amar, M.N.; Ghahfarokhi, A.J.; Ng, C.S.W. Predicting wax deposition using robust machine learning techniques. Petroleum 2022, 8, 167–173. [Google Scholar] [CrossRef]
- Ahmadi, M. Data-driven approaches for predicting wax deposition. Energy 2023, 265, 126296. [Google Scholar] [CrossRef]
- Struchalin, P.G.; Øye, V.H.; Kosinski, P.; Hoffmann, A.C.; Balakin, B.V. Flow loop study of a cold and cohesive slurry. Pressure drop and formation of plugs. Fuel 2023, 332, 126061. [Google Scholar] [CrossRef]
- Hirochi, T.; Yamada, S.; Shintate, T.; Shirakashi, M. Ice/water slurry blocking phenomenon at a tube orifice. Ann. N. Y. Acad. Sci. 2002, 972, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Saparbayeva, N.; Balakin, B.V. CFD-DEM model of plugging in flow with cohesive particles. Sci. Rep. 2023, 13, 17188. [Google Scholar] [CrossRef] [PubMed]
- Saparbayeva, N.; Chang, Y.F.; Kosinski, P.; Hoffmann, A.C.; Balakin, B.V.; Struchalin, P.G. Cohesive collisions of particles in liquid media studied by CFD-DEM, video tracking, and Positron Emission Particle Tracking. Powder Technol. 2023, 426, 118660. [Google Scholar] [CrossRef]
- Yang, S.O.; Kleehammer, D.M.; Huo, Z.; Sloan, E.; Miller, K.T. Temperature dependence of particle–particle adherence forces in ice and clathrate hydrates. J. Colloid Interface Sci. 2004, 277, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Saeys, Y.; Abeel, T.; Van de Peer, Y. Robust feature selection using ensemble feature selection techniques. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2008, Antwerp, Belgium, 15–19 September 2008; Proceedings, Part II 19. Springer: Berlin/Heidelberg, Germany, 2008; pp. 313–325. [Google Scholar]
- Qi, Y. Random forest for bioinformatics. Ensemble Machine Learning: Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; pp. 307–323. [Google Scholar]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).