Multivariate Peristalsis in a Straight Rectangular Duct for Carreau Fluids
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Formulation
2.2. Governing Equations and Boundary Conditions
2.3. Computational Method
3. Results and Discussion
3.1. Transport Efficiency
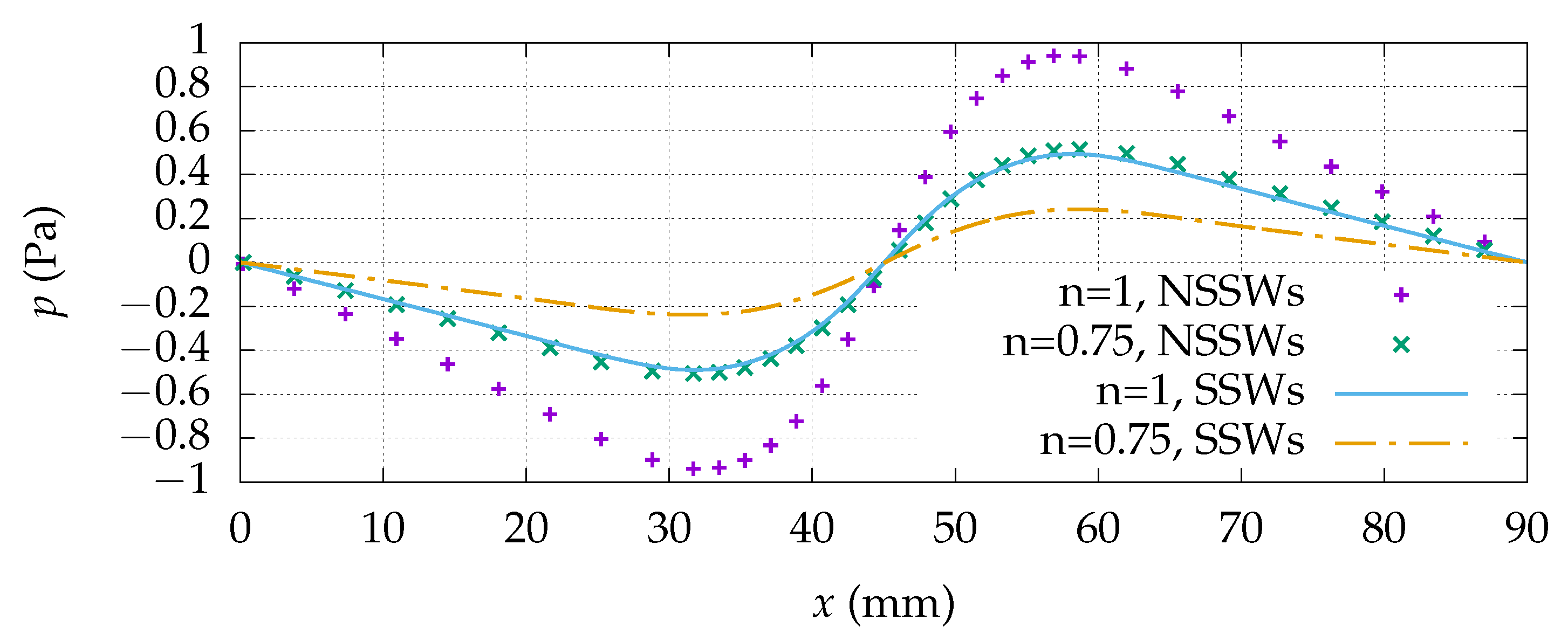
3.2. Peristaltic Characteristic Curves
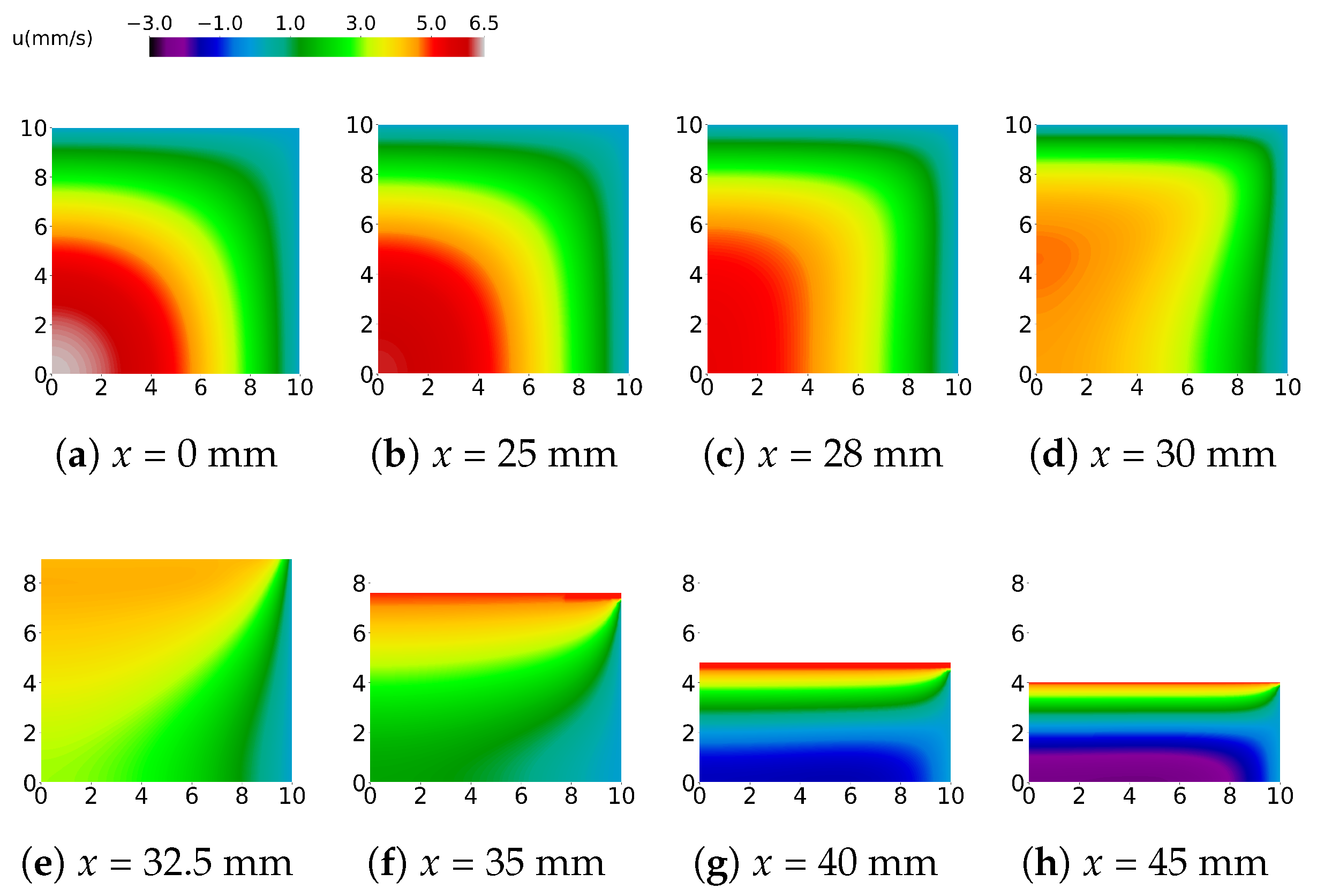
3.3. Effect of Finite Width
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalayeh, K.; Xie, H.; Fowlkes, B.; Sack, B.; Schultz, W. Longitudinal wall motion during peristalsis and its effect on reflux. J. Fluid Mech. 2023, 964, A30. [Google Scholar] [CrossRef]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Hosseini, G.; Ji, C.; Xu, D.; Rezaienia, M.A.; Avital, E.; Munjiza, A.; Williams, J.J.R.; Green, J.S.A. A computational model of ureteral peristalsis and an investigation into ureteral reflux. Biomed. Eng. Lett. 2018, 8, 117–125. [Google Scholar]
- Takaddus, A.T.; Chandy, A.J. A three-dimensional (3D) two-way coupled fluid–structure interaction (FSI) study of peristaltic flow in obstructed ureters. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3122. [Google Scholar] [CrossRef]
- Waldrop, L.D.; He, Y.; Battista, N.A.; Peterman, T.N.; Miller, L.A. Uncertainty quantification reveals the physical constraints on pumping by peristaltic hearts. J. R. Soc. Interface 2020, 17, 20200232. [Google Scholar]
- Sharp, M.K. Pulsatile cerebral paraarterial flow by peristalsis, pressure and directional resistance. Fluids Barriers CNS 2023, 20, 41. [Google Scholar]
- Javed, T.; Ahmed, B.; Hamid, A.H.; Sajid, M. Numerical analysis of peristaltic transport of Casson fluid for non-zero Reynolds number in presence of the magnetic field. Nonlinear Eng. 2018, 7, 183–193. [Google Scholar] [CrossRef]
- Abd-Alla, A.M.; Abo-Dahab, S.M.; Thabet, E.N.; Abdelhafez, M.A. Heat and mass transfer for MHD peristaltic flow in a micropolar nanofluid: Mathematical model with thermophysical features. Sci. Rep. 2022, 12, 21540. [Google Scholar] [CrossRef] [PubMed]
- Prakash, J.; Yadav, A.; Tripathi, D.; Kumar Tiwari, A. Computer modelling of peristalsis-driven intrauterine fluid flow in the presence of electromagnetohydrodynamics. Eur. Phys. J. Plus 2019, 134, 81. [Google Scholar] [CrossRef]
- Akram, S.; Athar, M.; Saeed, K.; Razia, A. Influence of an induced magnetic field on double diffusion convection for peristaltic flow of thermally radiative Prandtl nanofluid in non-uniform channel. Tribol. Int. 2023, 187, 108719. [Google Scholar]
- Alharbi, K.A.M.; Adnan, A.; Eldin, S.M.; Akgul, A. Investigation of Williamson nanofluid in a convectively heated peristaltic channel and magnetic field via method of moments. AIP Adv. 2023, 13, 065313. [Google Scholar] [CrossRef]
- Rafiq, M.; Shaheen, A.; Trabelsi, Y.; Eldin, S.M.; Khan, M.I.; Suker, D.K. Impact of activation energy and variable properties on peristaltic flow through porous wall channel. Sci. Rep. 2023, 13, 3219. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar]
- Tanveer, A.; Hina, S.; Hayat, T.; Mustafa, M.; Ahmad, B. Effects of the Cattaneo–Christov heat flux model on peristalsis. Eng. Appl. Comput. Fluid Mech. 2016, 10, 373–383. [Google Scholar] [CrossRef][Green Version]
- Tanner, F.X.; Al-Habahbeh, A.A.; Feigl, K.A.; Nahar, S.; Jeelani, S.A.K.; Case, W.R.; Windhab, E.J. Numerical and experimental investigation of a non-Newtonian flow in a collapsed elastic tube. Appl. Rheol. 2012, 22, 63910. [Google Scholar]
- Nahar, S.; Jeelani, S.A.K.; Windhab, E.J. Peristaltic flow characterization of a shear thinning fluid through an elastic tube by UVP. Appl. Rheol. 2012, 22, 43941. [Google Scholar]
- Nahar, S.; Dubey, B.N.; Windhab, E.J. Influence of flowing fluid property through an elastic tube on various deformations along the tube length. Phys. Fluids 2019, 31, 101905. [Google Scholar]
- Al-Habahbeh, A.A. Simulations of Newtonian and Non–Newtonian Flows in Deformable Tubes. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2013. [Google Scholar]
- Alokaily, S.; Feigl, K.; Tanner, F.X.; Windhab, E.J. Numerical simulations of the transport of Newtonian and non-Newtonian fluids via peristaltic motion. Appl. Rheol. 2018, 28, 32832. [Google Scholar]
- Alokaily, S.; Feigl, K.; Tanner, F.X. Characterization of peristaltic flow during the mixing process in a model human stomach. Phys. Fluids 2019, 31, 103105. [Google Scholar]
- Dufour, D.; Tanner, F.X.; Feigl, K.A.; Windhab, E.J. Investigation of the dispersing characteristics of antral contraction wave flow in a simplified model of the distal stomach. Phys. Fluids 2021, 33, 083101. [Google Scholar]
- Feigl, K.; Tanner, F.X. Computational investigation of drop behavior and breakup in peristaltic flow. Phys. Fluids 2022, 34, 012111. [Google Scholar]
- Ellahi, R.; Riaz, A.; Nadeem, S. Three dimensional peristaltic flow of Williamson fluid in a rectangular duct. Indian J. Phys. 2013, 87, 1275–1281. [Google Scholar] [CrossRef]
- Ali Abbas, A.; Bai, Y.Q.; Bhatti, M.M.; Rashidi, M.M. Three dimensional peristaltic flow of hyperbolic tangent fluid in non-uniform channel having flexible walls. Alex. Eng. J. 2016, 55, 653–662. [Google Scholar]
- Ellahi, R.; Hussain, F.; Ishtiaq, F.; Hussain, A. Peristaltic transport of Jeffrey fluid in a rectangular duct through a porous medium under the effect of partial slip: An application to upgrade industrial sieves/filters. Pramana J. Phys. 2019, 93, 34. [Google Scholar]
- Ali, N.; Javid, K.; Sajid, M.; Anwar Bég, O. Numerical simulation of peristaltic flow of a biorheological fluid with shear-dependent viscosity in a curved channel. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 614–627. [Google Scholar]
- Narla, V.K.; Prasad, K.M.; Ramana Murthy, J.V. Time-dependent peristaltic analysis in a curved conduit: Application to chyme movement through intestine. Math. Biosci. 2017, 293, 21–28. [Google Scholar]
- Liao, F.; Yang, X.; Wang, S.; He, G. Grid-dependence study for simulating propeller crashback using large-eddy simulation with immersed boundary method. Ocean. Eng. 2020, 218, 108211. [Google Scholar]
- Khosronejad, A.; Kang, S.; Flora, K. Fully coupled free-surface flow and sediment transport modelling of flash floods in a desert stream in the Mojave Desert, California. Hydrol. Process. 2019, 33, 2772–2791. [Google Scholar]
- Moulinos, I.; Manopoulos, C.; Tsangaris, S. Computational analysis of active and passive flow control for backward facing step. Computation 2022, 10, 12. [Google Scholar]
- Moulinos, I.; Manopoulos, C.; Tsangaris, S. Modification of Poiseuille flow to a pulsating flow using a periodically expanding-contracting balloon. Fluids 2023, 8, 129. [Google Scholar]
- Santoni, C.; Khosronejad, A.; Seiler, P.; Sotiropoulos, F. Toward control co-design of utility-scale wind turbines: Collective vs. individual blade pitch control. Energy Rep. 2023, 9, 793–806. [Google Scholar]
- Asgharzadeh, H.; Borazjani, I. A Newton–Krylov method with an approximate analytical Jacobian for implicit solution of Navier–Stokes equations on staggered overset-curvilinear grids with immersed boundaries. J. Comput. Phys. 2017, 331, 227–256. [Google Scholar]
- Liao, F.; Yang, X. On the capability of the curvilinear immersed boundary method in predicting near-wall turbulence of turbulent channel flows. Theor. Appl. Mech. Lett. 2021, 11, 100279. [Google Scholar] [CrossRef]
- Moulinos, I.; Manopoulos, C.; Tsangaris, S. A computational analysis for active flow and pressure control using moving roller peristalsis. Computation 2021, 9, 144. [Google Scholar]
- Ge, L.; Sotiropoulos, F. A numerical method for solving the 3D unsteady incompressible Navier—Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 2007, 225, 1782–1809. [Google Scholar] [PubMed]
- Nahar, S. Steady and Unsteady Flow Characteristics of Non–Newtonian Fluids in Deformed Elastic Tubes. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2012. [Google Scholar]
- Alokaily, S. Modeling and Simulation of the Peristaltic Flow of Newtonian and Non–Newtonian Fluids with Application to the Human Body. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2017. [Google Scholar]
- Latham, T.W. Fluid Motion in a Peristaltic Pump. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Esmaily, M.; Villafane, L.; Banko, A.J.; Iaccarino, G.; Eaton, J.K.; Mani, A. A benchmark for particle-laden turbulent duct flow: A joint computational and experimental study. Int. J. Multiph. Flow 2020, 132, 103410. [Google Scholar]
- Yasuda, K.; Armstrong, R.C. and Cohen, R.E. Shear flow properties of concentrated solutions of linear and star branched polystyrenes. Rheol. Acta 1981, 20, 163–178. [Google Scholar]
- Eckmann, D.M.; Bowers, S.; Stecker, M.; Cheung, A.T. Hematocrit, volume expander, temperature, and shear rate effects on blood viscosity. Anesth. Analg. 2000, 91, 539–545. [Google Scholar] [PubMed]
- Walker, A.M.; Xiao, Y.; Johnston, C.R.; Rival, D.E. The viscous characterization of hydroxyethyl starch (HES) plasma volume expanders in a non-Newtonian blood analog. Biorheology 2013, 50, 177–190. [Google Scholar] [CrossRef]
- Kilbride, P.; Rull, M.V.; Townsend, A.; Wilson, H.; Morris, J. Shear-thickening fluids in biologically relevant agents. Biorheology 2019, 56, 39–50. [Google Scholar]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Yang, X.; Angelidis, D.; Khosronejad, A.; Le, T.; Kang, S.; Gilmanov, A.; Ge, L.; Borazjani, I.; Calderer, A. Virtual Flow Simulator v1.0. Computer Software; USDOE Office of Energy Efficiency and Renewable Energy (EERE): Washington, DC, USA, 2015. Available online: https://github.com/SAFL-CFD-Lab/VFS-Wind (accessed on 10 January 2021).
- Manopoulos, C.; Savva, G.; Tsoukalis, A.; Vasileiou, G.; Rogkas, N.; Spitas, V.; Tsangaris, S. Optimal design in roller pump system applications for linear infusion. Computation 2020, 8, 35. [Google Scholar] [CrossRef]
- Capata, R. Peristaltic roller pump: Parametric optimization for hemolysis control. In Proceedings of the ASME 2020 International Mechanical Engineering Congress and Exposition (IMECE2020), Portland, OR, USA, 15–18 November 2020; 21681. [Google Scholar]
- Hadjesfandiari, N.; Serrano, K.; Levin, E.; Johal., P.; Feenstra, S.; Shih, A.W.; Devine, D.V. Effect of modern infusion pumps on RBC quality. Transfusion 2022, 62, 797–808. [Google Scholar] [CrossRef] [PubMed]
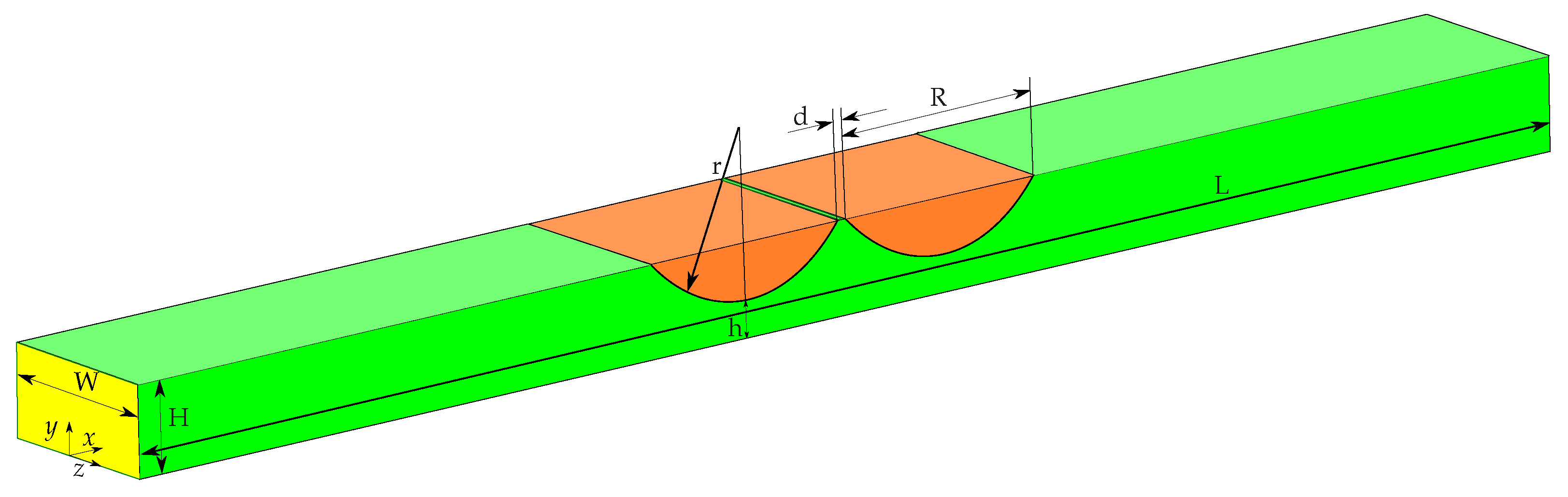










| Quantity | Symbol | Value | Unit |
|---|---|---|---|
| Half height | H | 10 | mm |
| Width | W | 20 | mm |
| Length | L | 90 or 180 | mm |
| Radius of cylindrical segment | r | 15 | mm |
| Inter cylindrical segment distance | d | 1 | mm |
| Fluid density | 1000 | ||
| Dynamic viscosity | 0.1452 |
| c (mm/s) | TE IW (%) | TE FW (%) |
|---|---|---|
| 2.5 | 78.8 | 61.3 |
| 5 | 78.4 | 61.3 |
| 10 | 78.8 | 61.3 |
| RO | TE IW (%) | TE FW (%) |
|---|---|---|
| 0.2 | 28.4 | 16.5 |
| 0.4 | - | 34.9 |
| 0.6 | 78.4 | 61.3 |
| 0.8 | 95.6 | 89.4 |
| Power-Law Index | TE IW (%) | TE FW (%) |
|---|---|---|
| 1 | 78.4 | 61.3 |
| 0.75 | 77.5 | 50.3 |
| Pulse Modality | TE IW (%) | TE FW (%) |
|---|---|---|
| 1 | 60 | 42.8 |
| 2 | 78 | 60.7 |
| 3 | 87 | 70.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moulinos, I.C.; Manopoulos, C.; Tsangaris, S. Multivariate Peristalsis in a Straight Rectangular Duct for Carreau Fluids. Computation 2024, 12, 62. https://doi.org/10.3390/computation12030062
Moulinos IC, Manopoulos C, Tsangaris S. Multivariate Peristalsis in a Straight Rectangular Duct for Carreau Fluids. Computation. 2024; 12(3):62. https://doi.org/10.3390/computation12030062
Chicago/Turabian StyleMoulinos, Iosif C., Christos Manopoulos, and Sokrates Tsangaris. 2024. "Multivariate Peristalsis in a Straight Rectangular Duct for Carreau Fluids" Computation 12, no. 3: 62. https://doi.org/10.3390/computation12030062
APA StyleMoulinos, I. C., Manopoulos, C., & Tsangaris, S. (2024). Multivariate Peristalsis in a Straight Rectangular Duct for Carreau Fluids. Computation, 12(3), 62. https://doi.org/10.3390/computation12030062






