Creation of a Simulated Sequence of Dynamic Susceptibility Contrast—Magnetic Resonance Imaging Brain Scans as a Tool to Verify the Quality of Methods for Diagnosing Diseases Affecting Brain Tissue Perfusion
Abstract
1. Introduction
2. Materials
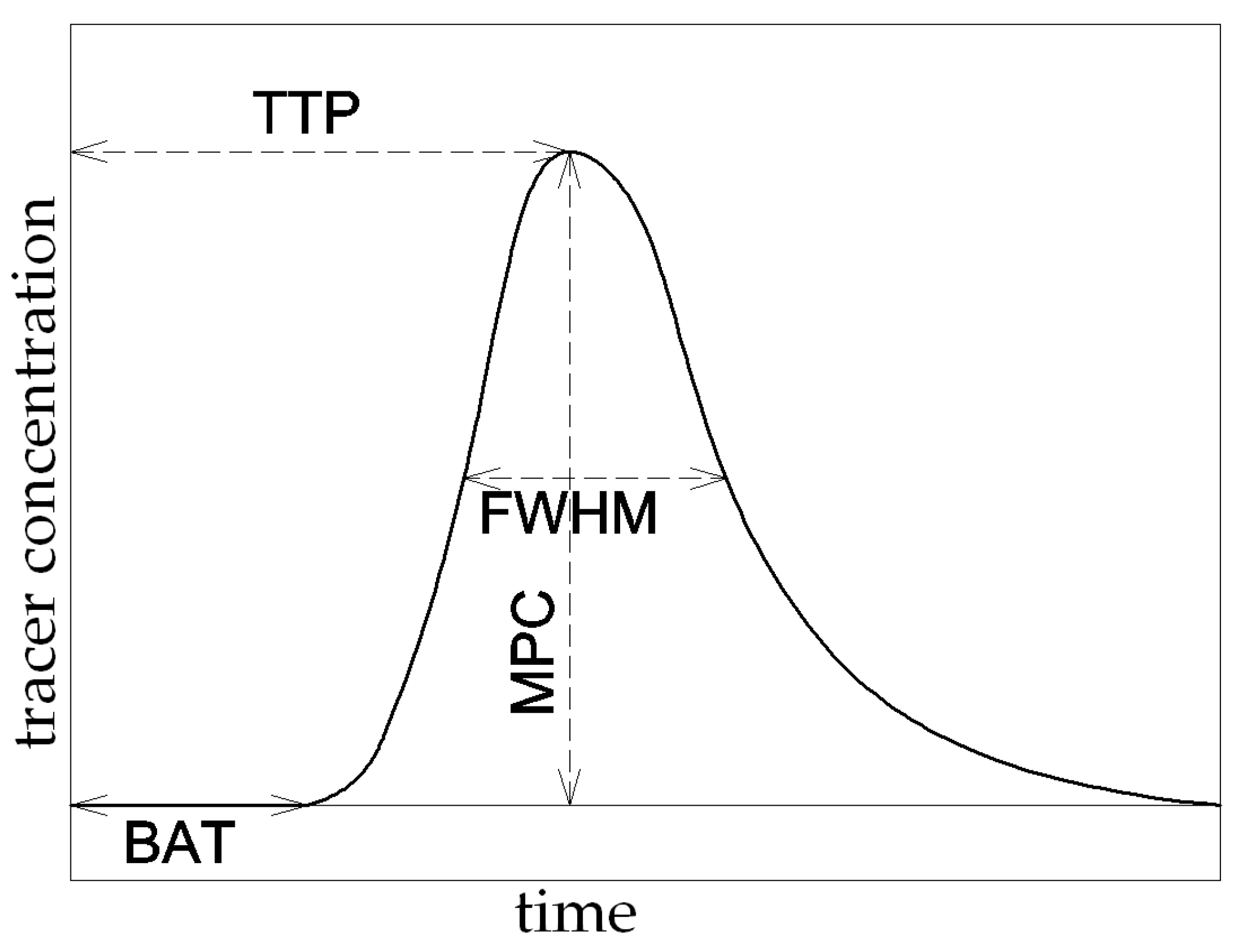
3. Basic Perfusion Descriptors
- The time of appearance of the tracer in the ROI—BAT (Bolus Arrival Time);
- The maximum amplitude of the tracer concentration in the ROI—MPC (Maximum Peak Concentration);
- The time taken to reach the maximum amplitude by the curve—TTP (Time to Peak);
- The width of the tracer concentration curve at the height of half the maximum of the curve—FWHM (Full Width at Half Maximum).
- ;
- ;
- .
4. Method of Calculating Selected Perfusion Descriptors
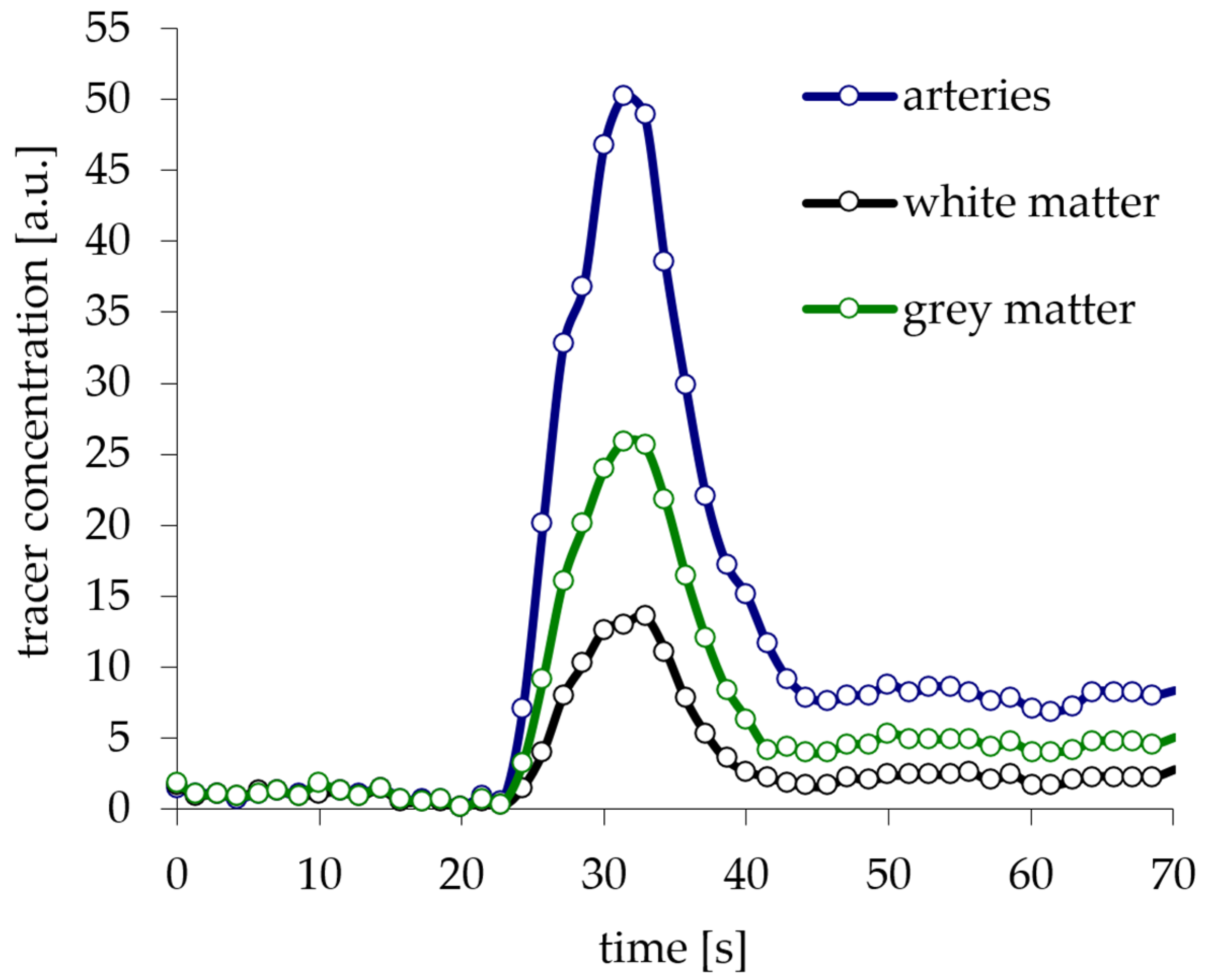
5. Creation and Verification of Model Curves
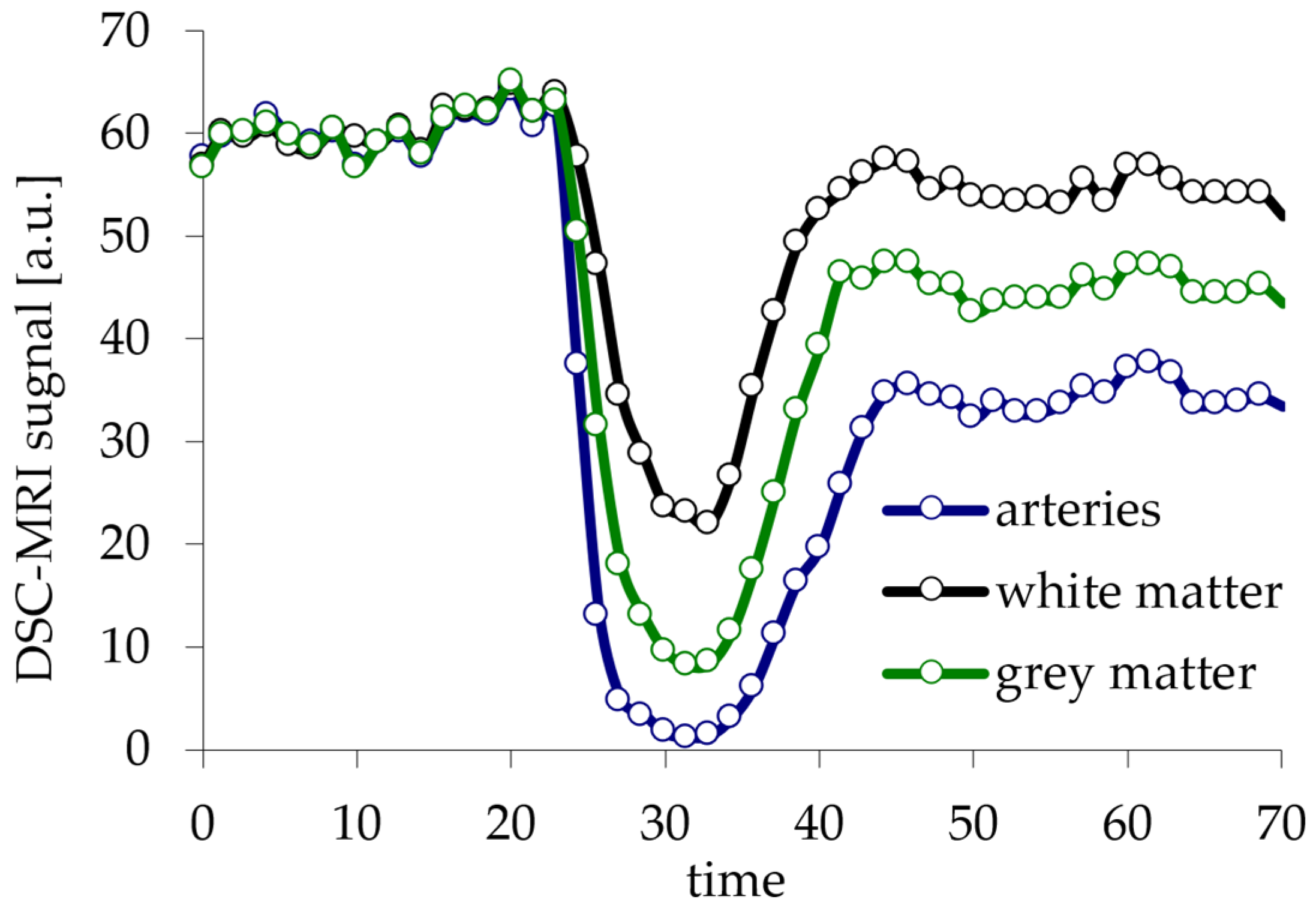
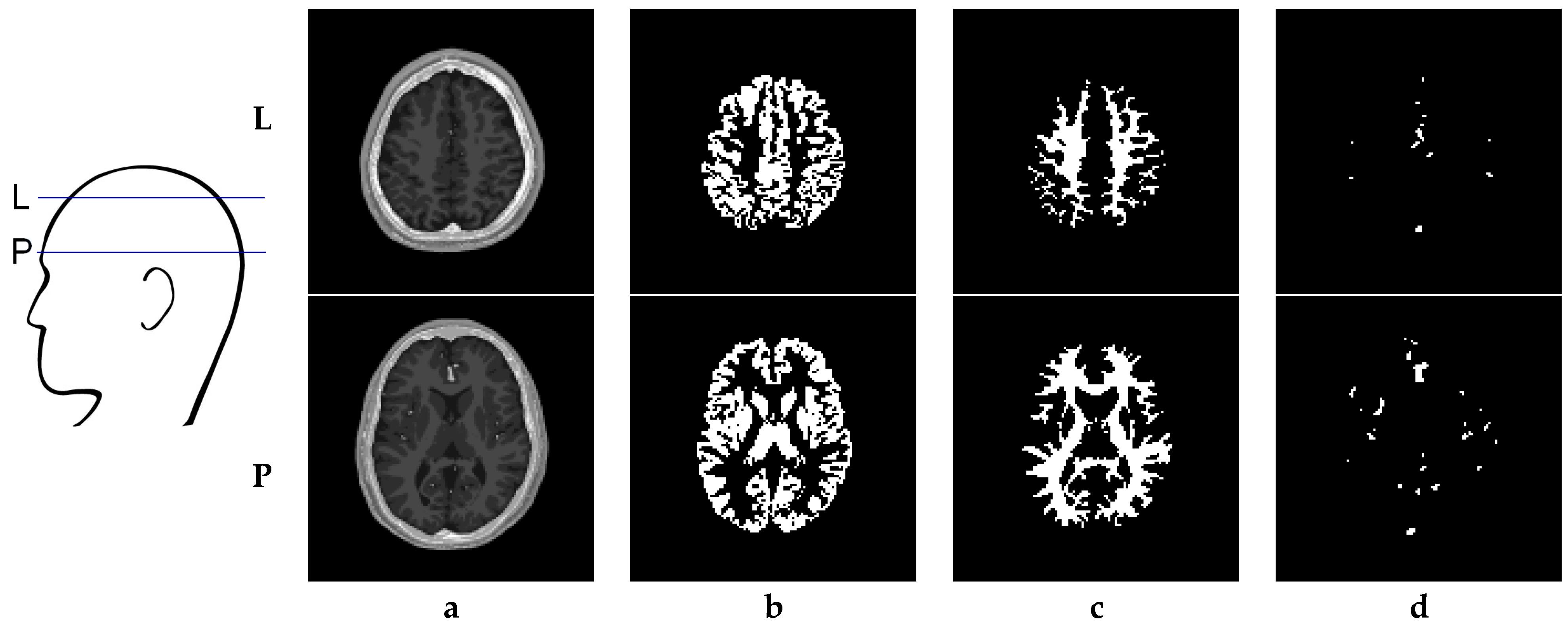
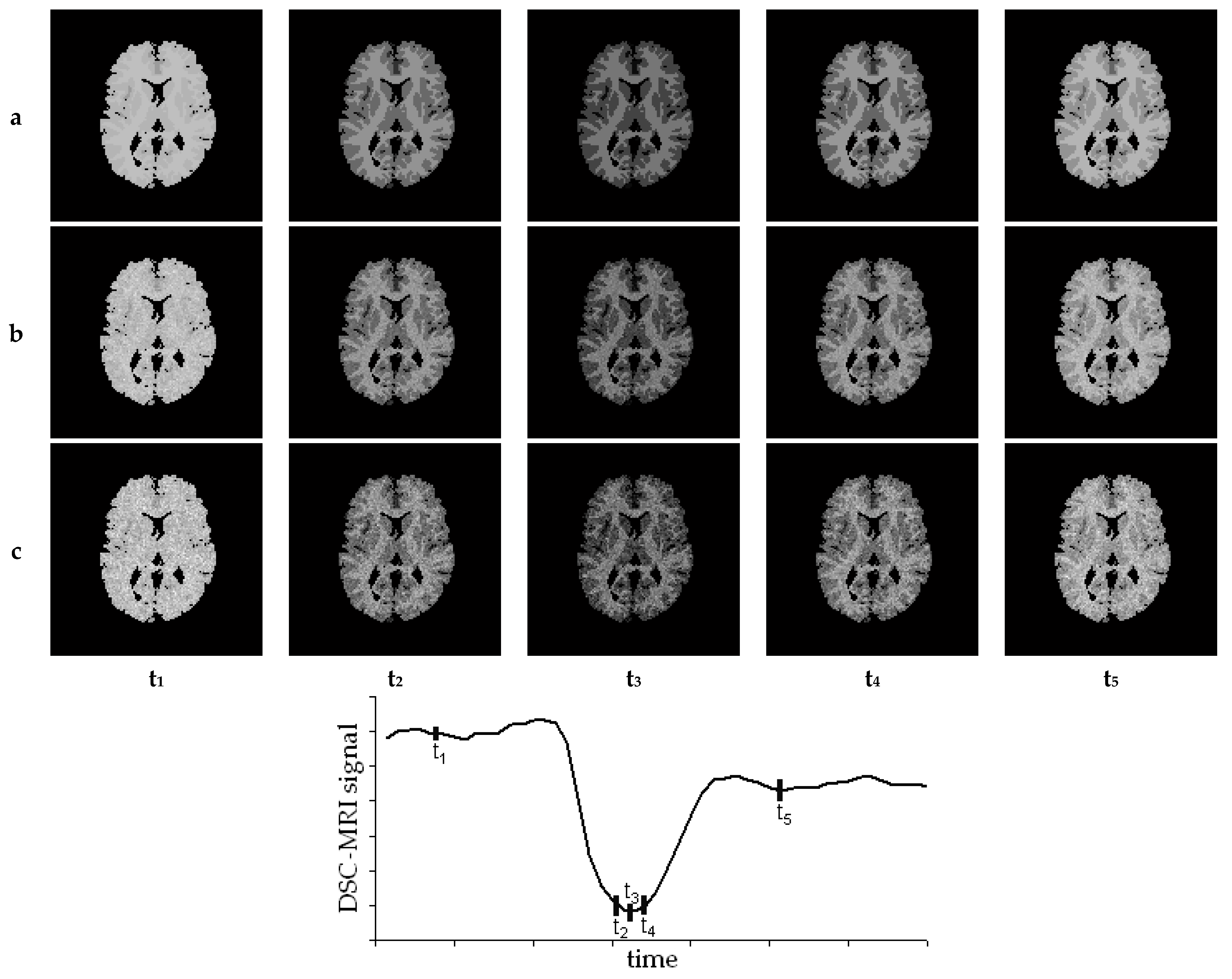
6. Creation of DSC-MRI Measurement Curves and a Brain Anatomy Model
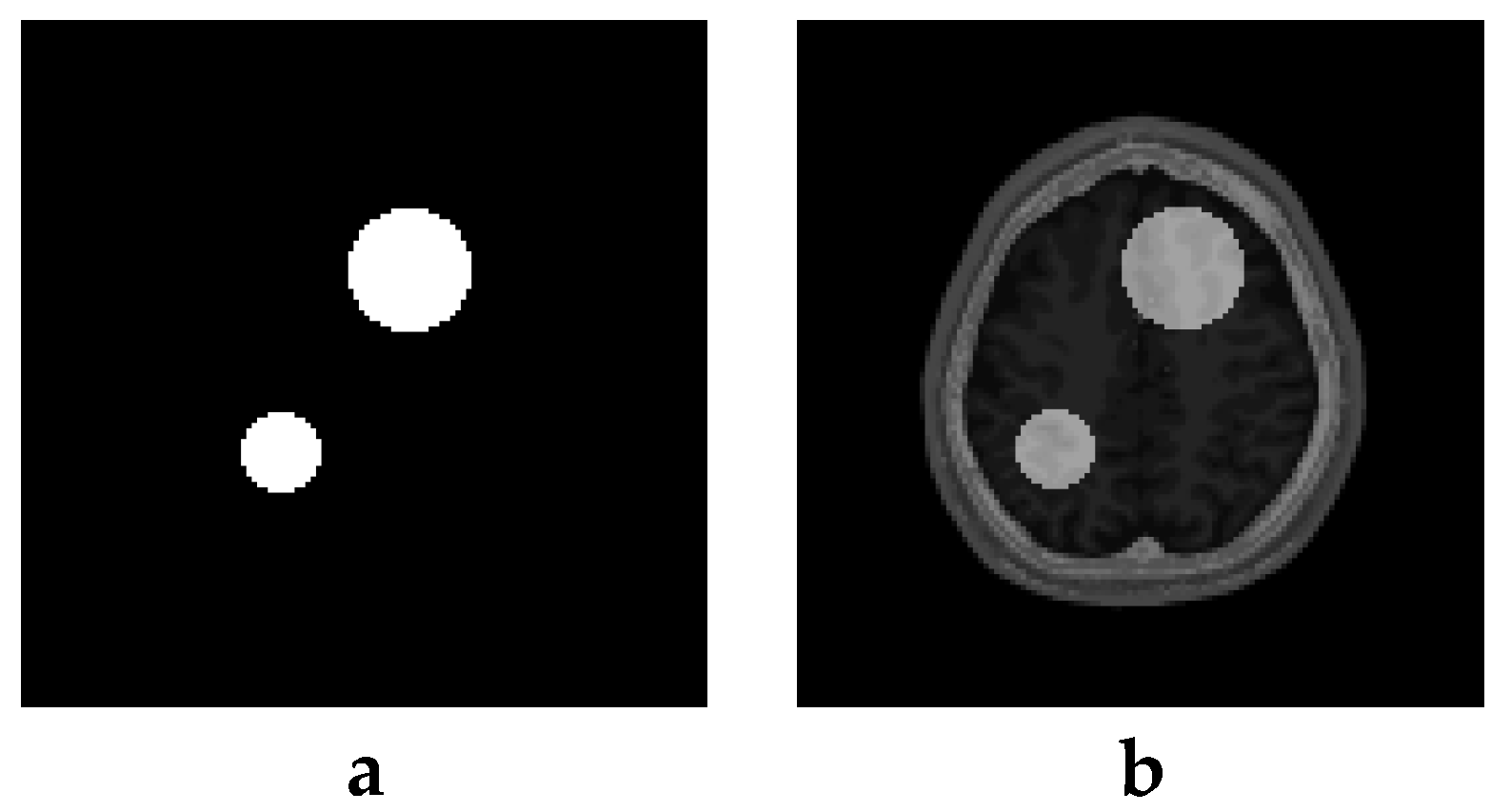
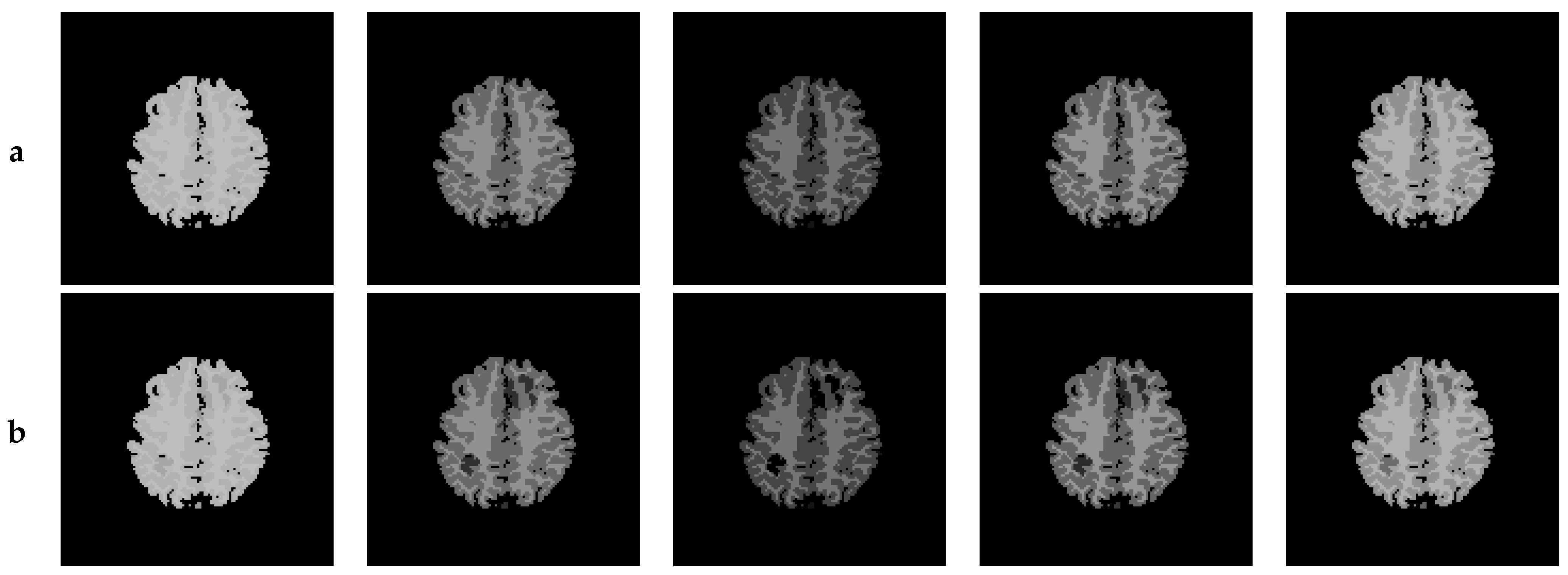
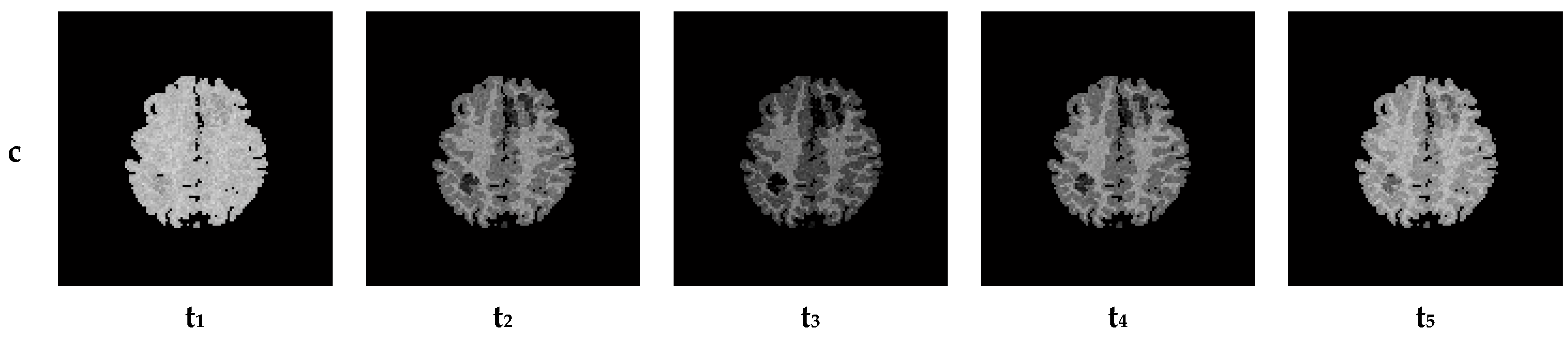
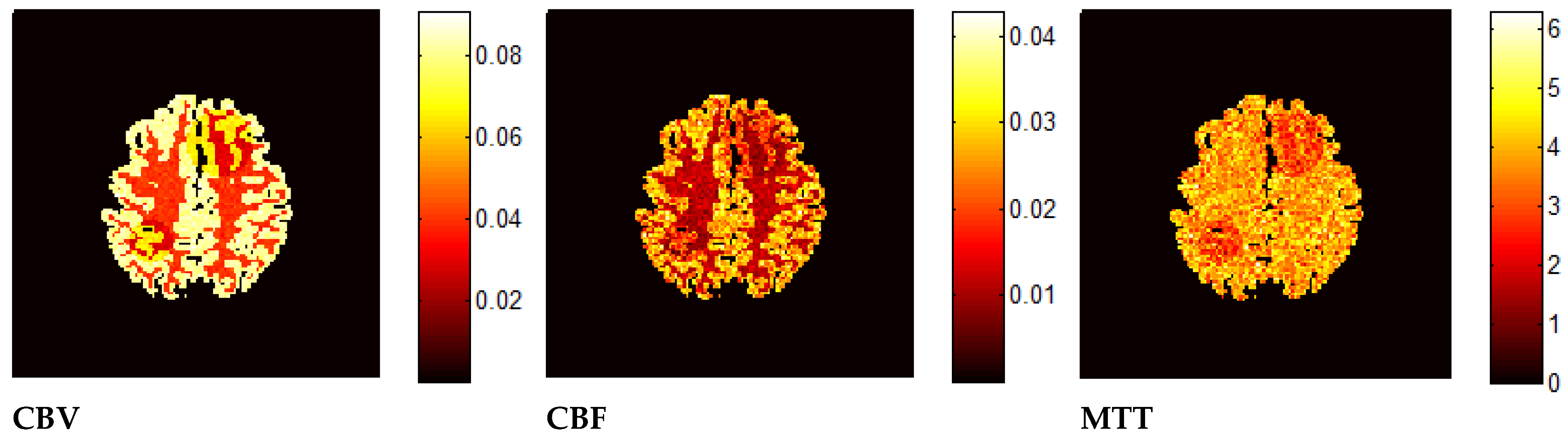
7. Results—Exemplary DSC-MRI Study Models
8. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Forsting, M.; Weber, J. MR perfusion imaging: A tool for more than a stroke. Eur. Radiol. Suppl. 2004, 14 (Suppl. 5), M2–M7. [Google Scholar]
- Lanzman, B.; Heit, J. Advanced MRI measures of cerebral perfusion and their clinical applications. Top. Magn. Reson. Imaging 2017, 26, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Fu, J.F.; Gaudet, K.; Bryant, A.G.; Price, J.C.; Bennett, R.E.; Johnson, K.A.; Hyman, B.T.; Hedden, T.; Salat, D.H.; et al. Aberrant vascular architecture in the hippocampus correlates with tau burden in mild cognitive impairment and Alzheimer’s disease. J. Cereb. Blood Flow Metab. 2023, 0271678X231216144. [Google Scholar] [CrossRef]
- Petrella, J.R.; Provenzale, J.M. MR Perfusion Imaging of the Brain: Techniques and Applications. Am. J. Roentgenol. 2000, 175, 207–219. [Google Scholar] [CrossRef] [PubMed]
- Zuloaga, K.L.; Zhang, W.; Yeiser, L.A.; Stewart, B.; Kukino, A.; Nie, X.; Roese, N.E.; Grafe, M.R.; Pike, M.M.; Raber, J.; et al. Neurobehavioral and imaging correlates of hippocampal atrophy in a mouse model of vascular cognitive impairment. Transl. Stroke Res. 2015, 6, 390–398. [Google Scholar] [CrossRef] [PubMed]
- Bakhtiari, A.; Vestergaard, M.B.; Benedek, K.; Fagerlund, B.; Mortensen, E.L.; Osler, M.; Lauritzen, M.; Larsson, H.B.W.; Lindberg, U. Changes in hippocampal volume during a preceding 10-year period do not correlate with cognitive performance and hippocampal blood–brain barrier permeability in cognitively normal late-middle-aged men. GeroScience 2023, 45, 1161–1175. [Google Scholar] [CrossRef]
- Choi, J.D.; Moon, Y.; Kim, H.J.; Yim, Y.; Lee, S.; Moon, W.J. Choroid plexus volume and permeability at brain MRI within the Alzheimer disease clinical spectrum. Radiology 2022, 304, 635–645. [Google Scholar] [CrossRef]
- Gordon, Y.; Partovi, S.; Müller-Eschner, M.; Amarteifio, E.; Bäuerle, T.; Weber, M.A.; Kauczor, H.-U.; Rengier, F. Dynamic contrast-enhanced magnetic resonance imaging: Fundamentals and application to the evaluation of the peripheral perfusion. Cardiovasc. Diagn. Ther. 2014, 4, 147. [Google Scholar]
- Koh, T.S.; Bisdas, S.; Koh, D.M.; Thng, C.H. Fundamentals of tracer kinetics for dynamic contrast-enhanced MRI. J. Magn. Reson. Imaging 2011, 34, 1262–1276. [Google Scholar] [CrossRef]
- Kalicka, R.; Lipiński, S. A fast method of separation of the noisy background from the head-cross section in the sequence of MRI scans. Biocybern. Biomed. Eng. 2010, 30, 15–27. [Google Scholar]
- Calamante, F.; Thomas, D.L.; Pell, G.S.; Wiersma, J.; Turner, R. Measuring Cerebral Blood Flow Using Magnetic Resonance Imaging Techniques. J. Cereb. Blood Flow. Metab. 1999, 19, 701–735. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D. Analysis of dynamic contrast enhanced MRI. Br. J. Radiol. 2004, 77, S154–S166. [Google Scholar] [CrossRef] [PubMed]
- van Osch, T. Evaluation of Cerebral Hemodynamics by Quantitative Perfusion MRI; PrintPartners Ipskamp: Enschede, The Netherlands, 2002. [Google Scholar]
- Sorensen, A.G.; Reimer, P. Cerebral MR Perfusion Imaging. Principles and Current Applications; Georg Thieme Verlag: Stuttgart, Germany, 2000. [Google Scholar]
- Kane, I.; Carpenter, T.; Chappell, F.; Rivers, C.; Armitage, P.; Sandercock, P.; Wardlaw, J. Comparison of 10 Different Magnetic Resonance Perfusion Imaging Processing Methods in Acute Ischemic Stroke. Stroke 2007, 38, 3158–3164. [Google Scholar] [CrossRef]
- Perthen, J.E.; Calamante, F.; Gadian, D.G.; Connelly, A. Is Quantification of Bolus Tracking MRI Reliable Without Deconvolution? Magn. Reson. Med. 2002, 47, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Kalicka, R.; Pietrenko-Dąbrowska, A. Parametric Modeling of DSC-MRI Data with Stochastic Filtration and Optimal Input Design Versus Non-Parametric Modeling. Ann. Biomed. Eng. 2007, 35, 453–464. [Google Scholar] [CrossRef] [PubMed]
- Lipiński, S.; Kalicka, R. Automatic selection of arterial input function in DSC-MRI measurements for calculation of brain perfusion parameters using parametric modelling. Math. Model. Nat. Phenom. 2018, 13, 58. [Google Scholar] [CrossRef]
- Salluzzi, M.; Frayne, R.; Smith, M.R. Is correction necessary when clinically determining quantitative cerebral perfusion parameters from multi-slice dynamic susceptibility contrast MR studies? Phys. Med. Biol. 2006, 51, 407–424. [Google Scholar] [CrossRef]
- Smith, M.R.; Lu, H.; Frayne, R. Signal-to-Noise Ratio Effects in Quantitative Cerebral perfusion Using Dynamic Susceptibility Contrast Agents. Magn. Reson. Med. 2003, 49, 122–128. [Google Scholar] [CrossRef]
- Knutsson, L.; Stahlberg, F.; Wirestam, R. Aspects on the accuracy of cerebral perfusion parameters obtained by dynamic susceptibility contrast MRI: A simulation study. Magn. Reson. Imaging 2004, 22, 789–798. [Google Scholar] [CrossRef]
- Calamante, F.; Ganesan, V.; Kirkham, F.J.; Chir, B.; Jan, W.; Chong, W.K.; Gadian, D.G.; Connelly, A. MR Perfusion Imaging in Moyamoya Syndrome. Stroke 2001, 32, 2810–2816. [Google Scholar] [CrossRef]
- Grandin, C.B.; Duprez, T.P.; Smith, A.M.; Oppenheim, C.; Peeters, A.; Robert, A.R.; Cosnard, G. Which MR-derived perfusion parameters are the best predictors of infarct growth in hyperacute stroke? Comparative study between relative and quantitative measurements. Radiology 2002, 223, 361–370. [Google Scholar] [CrossRef] [PubMed]
- Akella, N.S.; Twieg, D.B.; Mikkelsen, T.; Hochberg, F.H.; Grossman, S.; Cloud, G.A.; Nabors, L.B. Assessment of Brain Tumor Angiogenesis Inhibitors Using Perfusion Magnetic Resonance Imaging: Quality and Analysis Results of a Phase I Trial. J. Magn. Reson. Imaging 2004, 20, 913–922. [Google Scholar] [CrossRef]
- Wintermark, M.; Sesay, M.; Barbier, E.; Borbély, K.; Dillon, W.P.; Eastwood, J.D.; Glenn, T.C.; Grandin, C.B.; Pedraza, S.; Soustiel, J.-F.; et al. Comparative Overview of Brain Perfusion Imaging Techniques. Stroke 2005, 36, e83–e99. [Google Scholar] [CrossRef]
- Bitar, R.; Leung, G.; Perng, R.; Tadros, S.; Moody, A.R.; Sarrazin, J.; McGregor, C.; Christakis, M.; Symons, S.; Nelson, A.; et al. MR pulse sequences: What every radiologist wants to know but is afraid to ask. Radiographics 2006, 26, 513–537. [Google Scholar] [CrossRef]
- Mouridsen, K.; Christensen, S.; Gyldensted, L.; Ostergaard, L. Automatic Selection of Arterial Input Function Using Cluster Analysis. Magn. Reson. Med. 2006, 55, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Koshimoto, Y.; Yamada, H.; Kimura, H.; Maeda, M.; Tsuchida, C.; Kawamura, Y.; Ishii, Y. Quantitative Analysis of Cerebral Microvascular Hemodynamics with T2-Weighted Dynamic MR Imaging. J. Magn. Reson. Imaging 1999, 9, 462–467. [Google Scholar] [CrossRef]
- Artzi, M.; Aizenstein, O.; Hendler, T.; Bashat, D.B. Unsupervised multiparametric classification of dynamic susceptibility contrast imaging: Study of a healthy brain. Neuroimage 2011, 56, 858–864. [Google Scholar] [CrossRef] [PubMed]
- Kao, Y.-H.; Guo, W.-Y.; Wu, Y.-T.; Liu, K.-C.; Chai, W.-Y.; Lin, C.-Y.; Hwang, Y.-S.; Liou, A.J.-K.; Wu, H.-M.; Cheng, H.-C.; et al. Hemodynamic Segmentation of MR Brain Perfusion Images Using Independent Component Analysis, Thresholding, and Bayesian Estimation. Magn. Reson. Med. 2003, 49, 885–894. [Google Scholar] [CrossRef]
- Bjornerud, A.; Emblem, K.E. A fully automated method for quantitative cerebral hemodynamic analysis using DSC-MRI. J. Cereb. Blood Flow. Metab. 2010, 30, 1066–1078. [Google Scholar] [CrossRef]
- Kalicka, R.; Lipiński, S. Valuation of usefulness of Kalman filtration to improve noise properties of DSC-MRI brain research data. Meas. Automat. Monit. 2008, 54, 118–121. [Google Scholar]
- Theodoridis, S.; Pikrakis, A.; Kotroumbas, K.; Cavouras, D. An Introduction to Pattern Recognition: A MATLAB Approach; Elsevier Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical Pattern Recognition: A review. IEEE Trans. Pattern Anal. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Calamante, F.; Gadian, D.G.; Connelly, A. Quantification of Perfusion Using Bolus Tracking Magnetic Resonance Imaging in Stroke: Assumptions, Limitations, and Potential Implications for Clinical Use. Stroke 2002, 33, 1146–1151. [Google Scholar] [CrossRef]
- Ibaraki, M.; Ito, H.; Shimosegawa, E.; Toyoshima, H.; Ishigame, K.; Takahashi, K.; Kanno, I.; Miura, S. Cerebral vascular mean transit time in healthy humans: A comparative study with PET and dynamic susceptibility contrast-enhanced MRI. J. Cereb. Blood Flow. Metab. 2007, 27, 404–413. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, W.G.; Guckel, F.; Stritzke, P.; Schmiedek, P.; Schwartz, A.; Brix, G. Cerebral Blood Flow and Cerebrovascular Reserve Capacity: Estimation by Dynamic Magnetic Resonance Imaging. J. Cereb. Blood Flow. Metab. 1998, 18, 1143–1156. [Google Scholar] [CrossRef]
- Wenz, F.; Rempp, K.; Brix, G.; Knopp, M.V.; Gückel, F.; Hess, T.; van Kaick, G. Age dependency of the regional cerebral blood volume (rCBV) measured with dynamic susceptibility contrast MR imaging (DSC). Magn. Reson. Imaging 1996, 14, 157–162. [Google Scholar] [CrossRef]
- Fuss, M.; Wenz, F.; Scholdei, R.; Essig, M.; Debus, J.; Knopp, M.V.; Wannenmacher, M. Radiation-induced regional cerebral blood volume (rCBV) changes in normal brain and low-grade astrocytomas: Quantification and time and dose-dependent occurrence. Int. J. Radiat. Oncol. Biol. Phys. 2000, 48, 53–58. [Google Scholar] [CrossRef]
- Ostergaard, L.; Weisskoff, R.M.; Chesler, D.A.; Gyldensted, C.; Rosen, B.R. High resolution Measurement of Cerebral Blood Flow using Intravascular Tracer Bolus Passages. Part I: Mathematical Approach and Statistical Analysis. Magn. Reson. Med. 1996, 36, 715–725. [Google Scholar] [CrossRef] [PubMed]
- Cocosco, C.A.; Kollokian, V.; Kwan, R.K.-S.; Evans, A.C. BrainWeb: Online Interface to a 3D MRI Simulated Brain Database. NeuroImage 1997, 5, 1996. [Google Scholar]
- Kwan, R.K.-S.; Evans, A.C.; Pike, G.B. An Extensible MRI Simulator for Post-Processing Evaluation. Lect. Notes Comput. Sci. 1996, 1131, 135–140. [Google Scholar]
- Aubert-Broche, B.; Griffin, M.; Pike, G.B.; Evans, A.C.; Collins, D.L. Twenty new digital brain phantoms for creation of validation image data bases. IEEE Trans. Med. Imaging 2006, 25, 1410–1416. [Google Scholar] [CrossRef]
- Aubert-Broche, B.; Evans, A.C.; Collins, D.L. A new improved version of the realistic digital brain phantom. NeuroImage 2006, 32, 138–145. [Google Scholar] [CrossRef]
- Fujita, S.; Mori, S.; Onda, K.; Hanaoka, S.; Nomura, Y.; Nakao, T.; Yoshikawa, T.; Takao, H.; Hayashi, N.; Abe, O. Characterization of brain volume changes in aging individuals with normal cognition using serial magnetic resonance imaging. JAMA Netw. Open 2023, 6, e2318153. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Ramírez, J.; Fernández-Blázquez, M.A.; González-Rosa, J.J. A causal analysis of the effect of age and sex differences on brain atrophy in the elderly brain. Life 2022, 12, 1586. [Google Scholar] [CrossRef] [PubMed]
- Usui, K.; Yoshimura, T.; Tang, M.; Sugimori, H. Age Estimation from Brain Magnetic Resonance Images Using Deep Learning Techniques in Extensive Age Range. Appl. Sci. 2023, 13, 1753. [Google Scholar] [CrossRef]
- Tofts, P. (Ed.) Quantitative MRI of the Brain. Measuring Changes Caused by Disease; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bambach, S.; Smith, M.; Morris, P.P.; Campeau, N.G.; Ho, M.L. Arterial spin labeling applications in pediatric and adult neurologic disorders. J. Magn. Reson. Imaging 2022, 55, 698–719. [Google Scholar] [CrossRef] [PubMed]
- Iutaka, T.; de Freitas, M.B.; Omar, S.S.; Scortegagna, F.A.; Nael, K.; Nunes, R.H.; Pacheco, F.T.; Maia Júnior, A.C.M.; do Amaral, L.L.F.; da Rocha, A.J. Arterial spin labeling: Techniques, clinical applications, and interpretation. Radiographics 2022, 43, e220088. [Google Scholar] [CrossRef] [PubMed]
- Qin, Q.; Alsop, D.C.; Bolar, D.S.; Hernandez-Garcia, L.; Meakin, J.; Liu, D.; Nayak, K.S.; Schmid, S.; van Osch, M.J.P.; Wong, E.C.; et al. Velocity-selective arterial spin labeling perfusion MRI: A review of the state of the art and recommendations for clinical implementation. Magn. Reson. Med. 2022, 88, 1528–1547. [Google Scholar] [CrossRef]
| CBVA/CBVGM | CBVGM/CBVWM | |
|---|---|---|
| Based on the Model Curves Presented in This Work | 1.97 | 2.19 |
| Artzi et al. [29] | 1.60–2.10 | 2–2.4 |
| Bjornerud and Emblem [31] | (not investigated) | 1.60–1.98 or 1.74–2.18 (depending on the calculation method) |
| Ibaraki et al. [36] | (not investigated) | 1.60–2.40 or 2.30–2.50 (depending on the ROI) |
| Schreiber et al. [37] | (not investigated) | 1.90–2.30 |
| Wenz et al. [38] | (not investigated) | 1.60–2.60 |
| Fuss et al. [39] | (not investigated) | 1.50–2.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipiński, S. Creation of a Simulated Sequence of Dynamic Susceptibility Contrast—Magnetic Resonance Imaging Brain Scans as a Tool to Verify the Quality of Methods for Diagnosing Diseases Affecting Brain Tissue Perfusion. Computation 2024, 12, 54. https://doi.org/10.3390/computation12030054
Lipiński S. Creation of a Simulated Sequence of Dynamic Susceptibility Contrast—Magnetic Resonance Imaging Brain Scans as a Tool to Verify the Quality of Methods for Diagnosing Diseases Affecting Brain Tissue Perfusion. Computation. 2024; 12(3):54. https://doi.org/10.3390/computation12030054
Chicago/Turabian StyleLipiński, Seweryn. 2024. "Creation of a Simulated Sequence of Dynamic Susceptibility Contrast—Magnetic Resonance Imaging Brain Scans as a Tool to Verify the Quality of Methods for Diagnosing Diseases Affecting Brain Tissue Perfusion" Computation 12, no. 3: 54. https://doi.org/10.3390/computation12030054
APA StyleLipiński, S. (2024). Creation of a Simulated Sequence of Dynamic Susceptibility Contrast—Magnetic Resonance Imaging Brain Scans as a Tool to Verify the Quality of Methods for Diagnosing Diseases Affecting Brain Tissue Perfusion. Computation, 12(3), 54. https://doi.org/10.3390/computation12030054






