The Mechanism of Resonant Amplification of One-Dimensional Detonation Propagating in a Non-Uniform Mixture

Abstract

The propagation of detonation waves (i.e., supersonic combustion waves) in non-uniform gaseous mixtures has become a matter of interest over the past several years due to the development of rotating detonation engines. It was shown in a number of recent theoretical studies of one-dimensional pulsating detonation that perturbation of the parameters in front of the detonation wave can lead to a resonant amplification of intrinsic pulsations for a certain range of perturbation wavelengths. This work is dedicated to the clarification of the mechanism of this effect. One-dimensional reactive Euler equations with single-step Arrhenius kinetics were solved. Detonation propagation in a gas with sine waves in density was simulated in a shock-attached frame of reference. We carried out a series of simulations, varying the wavelength of the disturbances. We obtained a non-linear dependence of the amplitude of these pulsations on the wavelength of disturbances with resonant amplification for a certain range of wavelengths. The gain in velocity was about 25% of the Chapman–Jouguet velocity of the stable detonation wave. The effect is explained using the characteristic analysis in the x-t diagram. For the resonant case, we correlated the pulsation period with the time it takes for the C₊ and C₋ characteristics to travel through the effective reaction zone. A similar pulsation mechanism is realized when a detonation wave propagates in a homogeneous medium.

1. Introduction

Depending on the initiating conditions, the geometry of the problem, and other factors, the combustion of a gas mixture can occur in different modes. Subsonic, or deflagration, is the most prevalent combustion mode in applications. In this case, the flame propagation mechanism is determined mainly by the viscosity, diffusion, and heat transfer in the gas. The opposite is the supersonic or detonation combustion mode, which occurs if energy is released in a reacting gas mixture that exceeds a certain threshold value. In this case, the propagation of the combustion wave is associated with the adiabatic compression of the reacting mixture in the leading shock wave. Detonation waves have been studied for many decades. Both the mechanism of detonation propagation and the practical aspects of the initiation or suppression of detonation waves are of interest. It is hard to find a single monograph covering the entire range of issues related to the mechanics of the detonation phenomenon. We can mention one monograph [1] as one of the most famous books with a modern view on the mechanics of detonation, and another monograph [2] as the most recent example.

Most numerical simulations of flows of compressible media with detonation waves, including, for example, those in [1,2], are carried out in a quiescent, uniform environment. However, for many practical applications, the gas mixture in front of a detonation wave is non-uniform.

The dynamics of the propagation of a one-dimensional pulsating detonation wave in a non-uniform medium were revealed in the following numerical studies [3,4,5]. Despite some differences in mathematical models and numerical methods, the results obtained by the authors are largely similar. At the same time, there is a lack of mechanical explanation of the mechanisms of the observed effects from a detonation gas dynamics point of view. This fact motivated our current study.

In [3], one-dimensional, unsteady gaseous detonation propagation in a non-homogeneous medium was investigated using the reactive, compressible Navier–Stokes equations with detailed chemistry. The effect of concentration inhomogeneity on the pulsating mode was modeled by a sinusoidal distribution of the H₂ mole fraction in the H₂–O₂ mixture. The main finding in [3] is that small perturbations of parameters can lead not only to a chaotization of pulsations (although this is the most likely scenario) but also, on the contrary, to a regularization of pulsations. This effect can be important for a number of practical applications, in particular in the development of rotating detonation engines.

In [4], similar studies were performed for the case of a mixture with variable density. Unlike [3], simulations were based on the solution of one-dimensional Euler equations with an overall one-stage kinetic scheme [6]. In [4], the range of dimensionless activation energies E from 28.5 to 30.0 was studied. Such activation energies qualitatively correspond to mixtures with irregular detonations. It is shown in [4] that a small-amplitude sinusoidal perturbation of the density of the medium can lead to different modes of pulsations, depending on the wavelength of the perturbation λ. In particular, as in [3], it was shown that the regularization of initially chaotic pulsations of parameters behind the detonation wave was possible. Thus, due to the small-amplitude pulsations of the parameters, it is possible to achieve more stable and therefore predictable dynamics of detonation propagation.

The study in [5] largely summarizes the results obtained in [3,4]. For the purpose of numerically solving the governing equations, they were transformed into a shock-attached frame of reference. The shock-fitting algorithm from [7] generalized to the non-uniform media case was used. In order to bring the formulation closer to the real mixing processes in a rotating detonation engine, both the temperature of the mixture and the mass fraction of the reagent changed simultaneously. Studies were conducted for E = 25 (stable detonation) and E = 26 (weakly unstable detonation). For each of the values of E, a wide range of wave numbers of disturbance was studied. The authors highlighted two main results. First, the detonation instability responds resonantly to the upstream perturbations by significantly increasing the amplitude of its velocity pulsations for certain ranges of perturbation wavelength. On the other hand, as in [3,4], it was found that the regularization of pulsations was possible for some upstream perturbations of the medium. Although the conclusions in [5] were made on the basis of a much larger number of simulations compared with [3,4], the considered activation energies were lower and qualitatively worse and corresponded to the realistic fuel–air mixtures common in practice.

This work continues our research [8,9,10,11]. The goal is to clarify the mechanism of the resonant amplification of intrinsic pulsations behind the front of a one-dimensional detonation wave.

2. Mathematical Model and Statement of the Problem

The mathematical model is based on the one-dimensional Euler equations written in the shock-attached frame of references (x, t) with single-step Arrhenius kinetics:

$$\frac{\partial u}{\partial t}+\frac{\partial }{\partial x}\left(f-Du\right)=s, x=\xi -{\displaystyle \underset{0}{\overset{t}{\int }}D\left(\tau \right)d\tau },$$

(1)

$$u=\left[\begin{array}{c}\rho \\ \rho v\\ e\\ \rho Z\end{array}\right],f=\left[\begin{array}{c}\rho v\\ \rho v^2+p\\ \left(p+e\right)v\\ \rho vZ\end{array}\right], s=\left[\begin{array}{c}0\\ 0\\ -\rho Q\omega \\ \rho \omega \end{array}\right],$$

(2)

$$e=\rho \epsilon +\frac{1}{2}\rho v^2, \epsilon =\frac{p}{\rho \left(\gamma -1\right)}, \omega =-AZ\exp \left(\frac{-E\rho }{p}\right).$$

(3)

Here, ρ is the density, v is the velocity in the laboratory frame (ξ, t), D is the leading shock wave velocity, p is the pressure, Q is the heat release of the chemical reactions, Z is the mass fraction of the reactive component of the mixture, ω is the rate of chemical reactions, e is the total energy per unit of volume, ε is the specific internal energy of the gas, A is the pre-exponential factor, and E is the activation energy. The gas was considered to be ideal with the specific heat ratio γ. The defining equations were rescaled following the traditional convention [6] using a half-reaction zone length l_1/2 and parameters in front of the detonation wave as characteristic scales.

The leading shock speed is obtained by integrating the governing equations along the C₊ characteristic near the shock [12], taking into account the varying gas density:

$$\left\{\begin{array}{l}\frac{dp}{dt}+\rho c\frac{dv}{dt}-\left(\gamma -1\right)Q\rho \omega =0,\\ \frac{dx}{dt}=v+c-D,\\ {\rho }_{\mathrm{init}}={\rho }_{\mathrm{init}}\left(x_{\mathrm{init}}+{\displaystyle \underset{0}{\overset{t}{\int }}D(\tau )d\tau }\right), p_{\mathrm{init}}=\mathrm{const}, v_{\mathrm{init}}=0.\end{array}\right.$$

(4)

Here, d/dt in the first equation is the material derivative along the C₊ characteristic, and c is the speed of sound. The index «init» is used for the parameters in front of the leading shock wave. These parameters are considered to be known functions in space in the laboratory frame. The initial coordinate of the detonation wave is denoted as x_init.

The defining system of equations was solved on a fixed interval [−H;0]. The right boundary corresponded to the leading shock wave front. The Rankine–Hugoniot jump conditions for the current velocity D, obtained from the system of Equation (4), were set as boundary conditions. Zero-order extrapolation conditions were used for the left boundary. The length of the computational domain H was chosen to be large enough so that the left boundary did not affect the solution. The Zel’dovich–von Neumann–Döring solution was used as the initial condition.

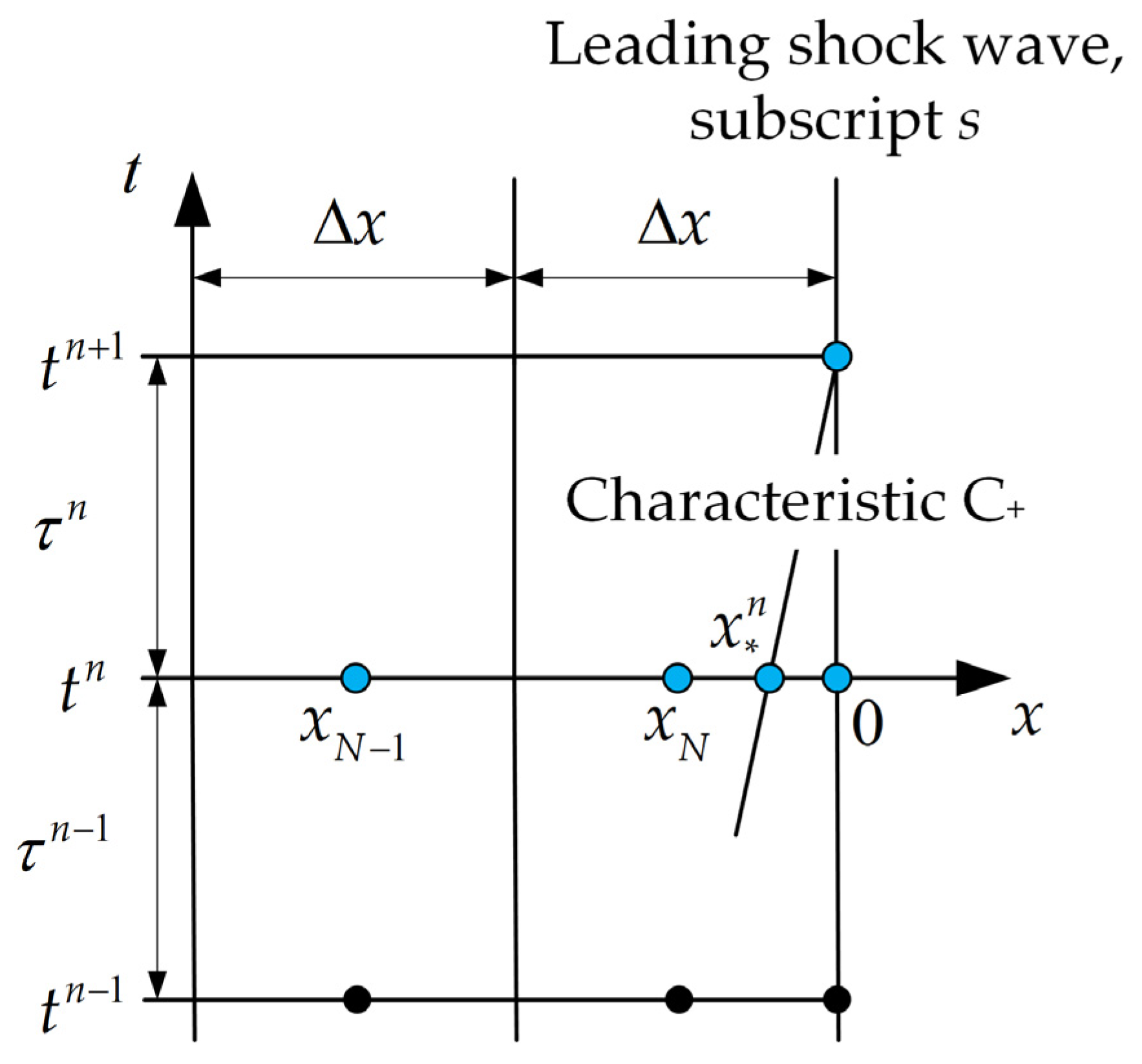
3. Numerical Algorithm

The computational domain was covered with a uniform grid with N cells. The computational algorithm was based on the Strang splitting principle. At the gas dynamics stage of the algorithm, spatial discretization was carried out using the finite-volume method. Time integration was carried out using an explicit Euler method. The numerical flux was calculated using the Courant–Isaacson–Rees upwind scheme extended for the case of a two-component mixture written in the shock-attached frame of reference. For the accuracy increase, the minmod reconstruction of the grid functions was applied. In the second stage of the algorithm, the system of ordinary differential equations of chemical kinetics for Z and p/ρ in each computational cell of the grid was solved. The details can be found elsewhere [8,9].

The numerical method in use differs from most CFD algorithms; see, for example, [13,14,15], which imply that the defining system of equations is solved in a fixed laboratory frame of reference. When building a computational algorithm, the main difficulty was in integrating the system of Equation (4) due to the non-uniform distribution of density. The system was discretized in the following way:

$$\left\{\begin{array}{l}\left[p_s^{n+1}-p_{*}^n\right]+\frac{1}{2}\left[{\left(\rho c\right)}_{*}^n+{\left(\rho c\right)}_s^{n+1}\right]\cdot \left[v_s^{n+1}-v_{*}^n\right]=\left(\gamma -1\right)Q{\rho }_s^{n+1}{\omega }_s^{n+1}{\tau }^n,\\ -x_{*}^n=\left(v_{*}^n+c_{*}^n-D^n\right)\cdot {\tau }^n,\\ {\rho }_{\mathrm{init}}^{n+1}={\rho }_{\mathrm{init}}\left(x_{\mathrm{init}}+L^n+\sqrt{\gamma \frac{p_{\mathrm{init}}}{{\rho }_{\mathrm{init}}^{n+1}}}{M}^{n+1}{\tau }^n\right).\end{array}\right.$$

(5)

The subscript s denotes parameters behind the leading shock at x_s = 0 (see Figure 1); L_n is the distance traveled by the leading shock at ${\tau }^n$. The star subscript denotes the point of intersection of the C₊ characteristic with the x-axis. Parameters at this point were computed using the linear interpolation between the known parameters at x_N = −Δx/2 and x_s; see [10] for details.

The coordinate $x_{*}^n$ was found from the second equation of the system of Equation (5):

$$x_{*}^n=-\frac{\left(c_s^n+v_s^n-D^n\right)\cdot {\tau }^n}{1+2\cdot \left(c_s^n-c_N^n+v_s^n-v_N^n\right)\cdot {\tau }^n/\Delta x}.$$

(6)

Parameters at point x_s at the time instant t = tⁿ⁺¹ were determined using the Rankine–Hugoniot jump conditions:

$$p_s^{n+1}=p_{\mathrm{init}}\cdot \left(1+\frac{2\gamma \left[{\left(M^{n+1}\right)}^2-1\right]}{\gamma +1}\right), {\rho }_s^{n+1}={\rho }_{\mathrm{init}}^{n+1}\cdot \frac{\left(\gamma +1\right){\left(M^{n+1}\right)}^2}{\left(\gamma -1\right){\left(M^{n+1}\right)}^2+2},$$

(7)

$$v_s^{n+1}=2c_s^{n+1}\cdot \frac{{\left(M^{n+1}\right)}^2-1}{\left(\gamma +1\right)M^{n+1}}, c_s^{n+1}=\sqrt{\gamma \frac{p_s^{n+1}}{{\rho }_s^{n+1}}}.$$

(8)

Substituting these equations into the first and third equations of the system of Equation (5) leads to a system of two non-linear algebraic equations with respect to the unknowns Mⁿ⁺¹ and ${\rho }_{\mathrm{init}}^{n+1}$, which is solved numerically using Newton’s method.

It was shown in [11] that the computational algorithm has a first order of accuracy. The on-practice estimation was conducted for the mild test case without internal shocklets. Minmod reconstruction of the grid functions in computational cells was also applied. The test case corresponded to the so-called surfing mode of detonation propagation in a non-uniform medium [5]. The issue of the accuracy of the algorithm was also discussed earlier in [8]. The overall accuracy of the algorithm is limited by the accuracy of the leading shock wave velocity calculation (5)–(8). As was shown in [8] for the case of a homogeneous mixture, if, instead of a linear approximation of the characteristic in the vicinity of the leading shock wave (see Figure 1), a quadratic approximation is used, then the accuracy of the entire algorithm increases to a value approaching two in practice. For future work, the increase in the accuracy order of the numerical algorithm should be carried out in the case of an inhomogeneous mixture.

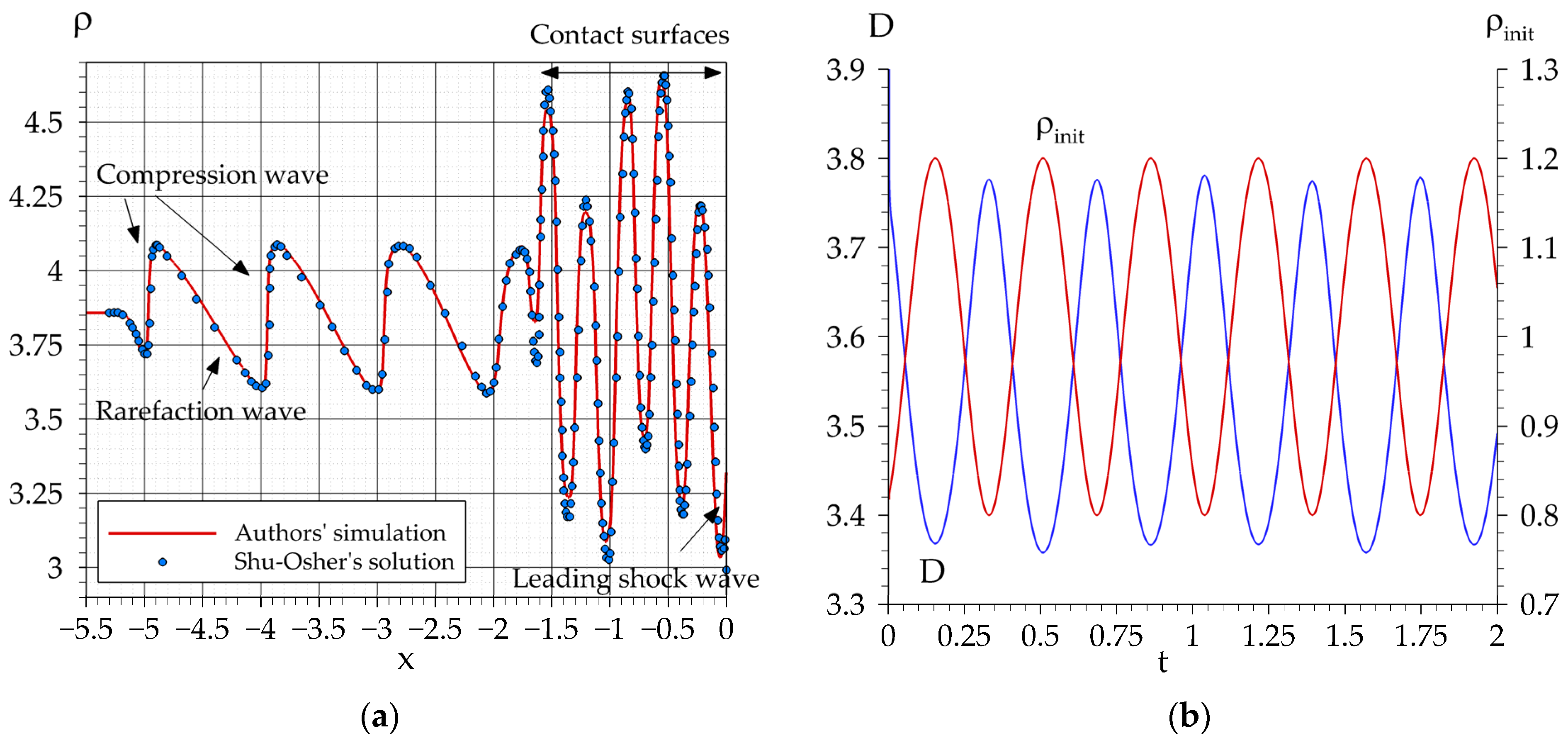
4. Verification

The computational algorithm for the inert case (s = 0 in (1)) was verified in [10] for the linear gradient of density in front of the leading shock. The obtained results were compared with the analytical Chisnell–Whitham theory [16]. Good agreement was obtained for the decreasing density, and a discrepancy was obtained for the increasing density. The analytics did not take into account the effect of re-reflected waves on the leading shock, and this effect was stronger in the case of increasing density.

We also considered the challenging problem of an inert, moving, strong shock wave interacting with sine waves in density. We call it the Shu–Osher problem [17]. At the initial time moment, the whole computational domain is filled with air with the parameters behind the shock wave with a Mach number of 3.0 for the background parameters p₀ = 1.0, v₀ = 0.0, and ρ₀ = 1.0. The length of the domain H is equal to 20, and the cell number N is equal to 4000. The density changes according to the following law:

$${\rho }_{\mathrm{init}}=1+0.2\cdot \sin \left(-20+5\cdot {\displaystyle \underset{0}{\overset{t}{\int }}D\left(\tau \right)d\tau }\right).$$

(9)

The interaction of the leading shock wave with sine waves leads to the oscillating solution (see Figure 2a). Due to fluctuations in the density of the gas, compression and rarefaction waves in series propagate in the direction back from the leading wave in the shock-attached frame of reference. At the same time, fluctuations in the velocity of the leading wave and the density of the gas in front of the wave are in antiphase (see Figure 2b). Eventually, each compression wave front becomes steeper, and a shock train is formed behind the leading shock wave front. However, for earlier moments, the solution behind the shock remains smooth. We can imagine a step function that approximates the smooth sinusoid. Then, the oscillating part of the curve in Figure 2 is associated with a series of contact discontinuities at density jumps, which are constantly generated as the leading wave moves. It can be seen from Figure 2a that the density profiles calculated by the authors and profiles from [17] coincide except for several peak amplitudes in the region of contact surfaces.

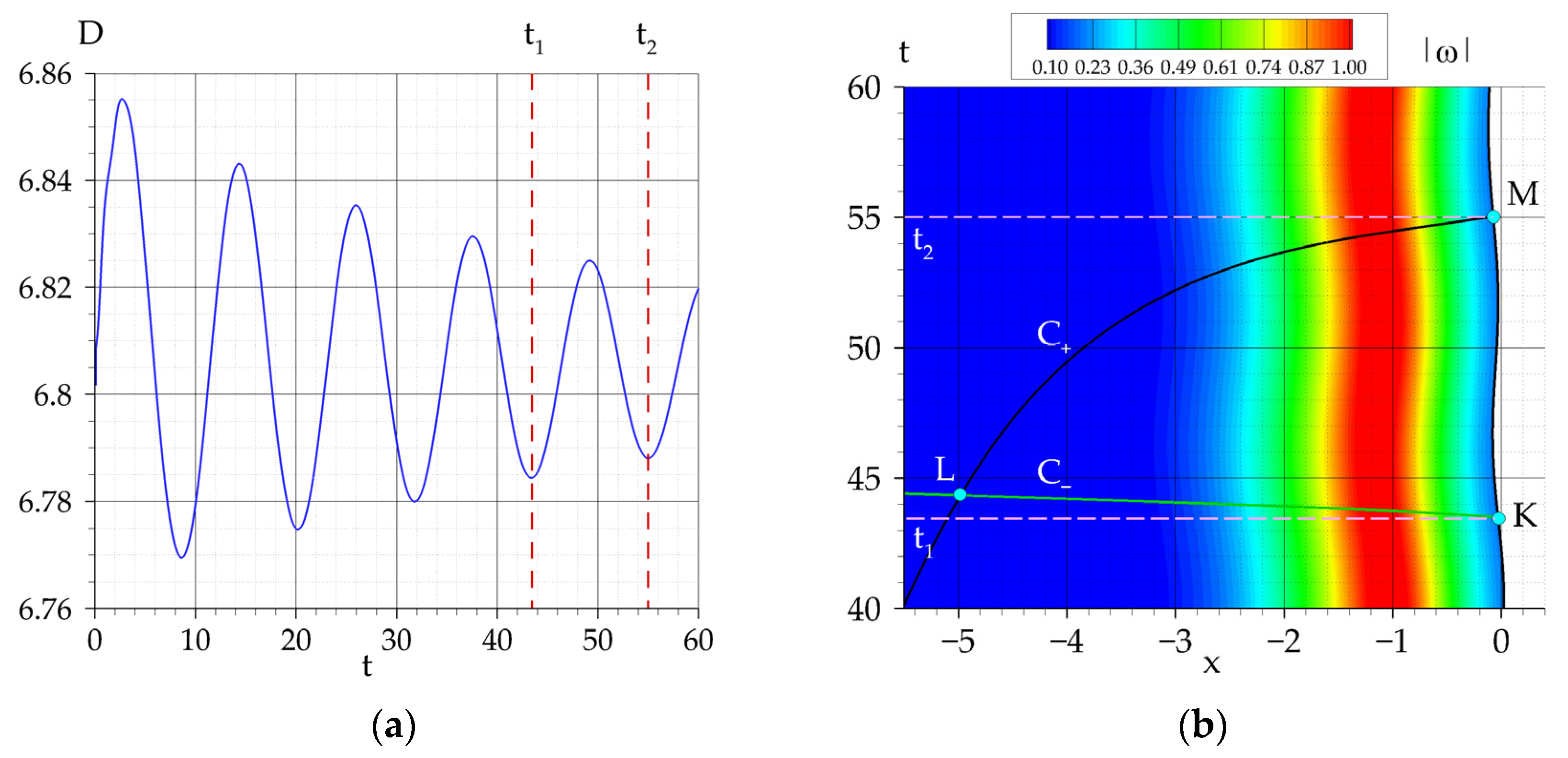
5. Results and Discussion

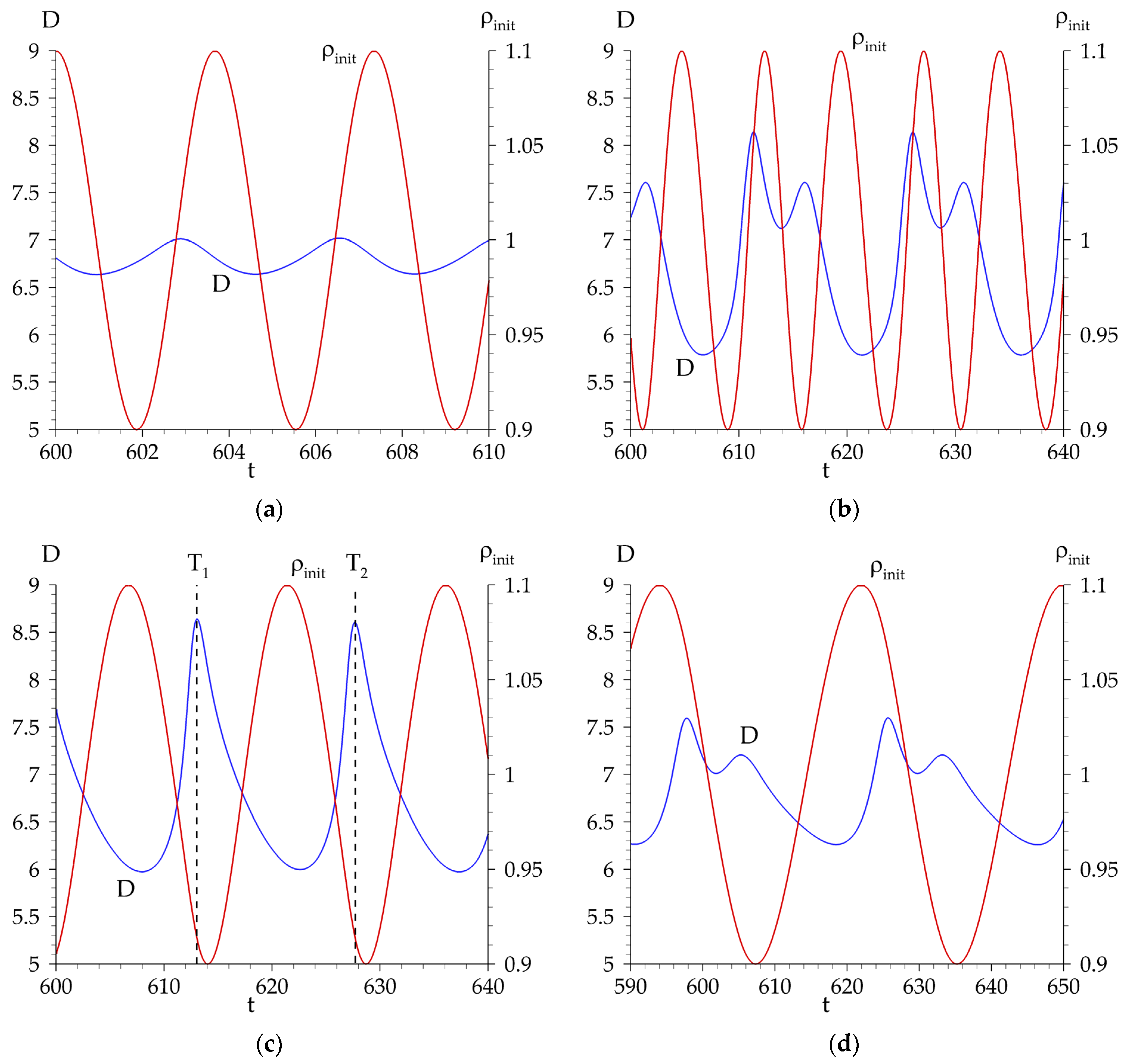
5.1. Variation in the Disturbance’s Wavelength

The following parameters of the mixture were considered:

$$\gamma =1.2, Q=50, E=25.$$

(10)

The linear theory predicts that the Zel’dovich–von Neumann–Döring solution is stable for this set of parameters [6]. In this case, detonation propagates at a constant Chapman–Jouguet speed:

$$D_{CJ}=\sqrt{\gamma +\frac{1}{2}\left({\gamma }^2-1\right)Q}+\sqrt{\frac{1}{2}\left({\gamma }^2-1\right)Q}\approx 6.8095.$$

(11)

The parameters (10) are canonical and were used in the study of the mechanisms of detonation propagation in [5,7,8,12,18] and many other works.

Up to the time instant t₁ = 500, a detonation wave propagated in the uniform mixture to obtain a fully developed, self-sustaining regime. Then, the density of the mixture varied according to the sine law:

$${\rho }_{\mathrm{init}}=1.0+k\cdot \sin \left(\frac{2\pi }{\lambda }\cdot {\displaystyle {\int }_{t_1}^{t}D\left(\tau \right)d\tau }\right), k=0.1.$$

(12)

The relatively small amplitude of the disturbances k was chosen based on the results from [3,4,5]. Next, we carried out a series of simulations varying the wavelength of the disturbances λ from several tens to several hundred units.

The length of the computational domain was equal to H = 20. For the case λ = 100, which is discussed below, simulations were also carried out for the domain lengths H = 60 and H = 100, as was performed in [9]. The simulation results for the lengths of domains 20, 60, and 100 are very similar, so all simulations were conducted for the domain length H = 20. The total cell number was equal to 2000. So, the grid resolution was 100 cells per half-reaction zone length l_1/2. The grid convergence study was carried out in our previous paper [11] for the case λ = 25, along with the estimation of the accuracy order of the numerical method.

Several different modes of pulsations of the detonation wave speed were obtained depending on λ (see Figure 3). As in [5], we obtained a non-linear dependence of the amplitude of these pulsations on λ with resonant amplification of pulsations for a certain range of λ. For example, the amplitude of leading shock velocity oscillations for λ = 100 is obviously greater than for λ = 25, 50, and 190. At λ = 25, we obtained a regime that corresponded to the “surfing” mode from [5]. It means that the detonation wave follows the ambient state oscillations; see Figure 3a. We studied this regime in our previous paper [11]. It was shown that the phase shift between the oscillations of the velocity of the detonation wave and the density of the gas before the wave can be estimated as the maximum time of passage of the characteristic C₊ through the “induction zone”.

A detonation wave has a complex structure consisting of an induction zone with almost no heat release due to active radicals that absorb energy to form and a reaction zone with heat release due to recombination of the radicals to form the final products of combustion. The significant drawback of the use of single-stage Arrhenius kinetics is that the induction and reaction zones are not well defined. Heat release, although at a small but finite rate, starts immediately behind the leading shock wave front and stops at infinity. Nevertheless, we preferred the single-step Arrhenius kinetics model since a number of reliable results about the stability of one-dimensional pulsating detonations have already been obtained for this model, including those for the non-uniform medium. At each instant, the induction zone length can be estimated as a distance behind the leading shock at which |ω|, where ω is defined by (3), reaches the maximal value. This distance also correlates well with the half-reaction zone length l_1/2.

The obtained mechanism of detonation propagation for λ = 25 was very similar to that described in [19] for the so-called high-frequency mode. The numerical study in [19] was conducted within the framework of the two-stage kinetics of chemical reactions. The basic element was also a characteristic triangle formed by the characteristics C₀ and C₊. The high-frequency mode in [19] was characterized by a period of oscillations of the detonation parameters exceeding but comparable with the induction time. Now, we would like to analyze the detonation propagation mechanism for the resonant amplification case λ = 100; see Figure 3c.

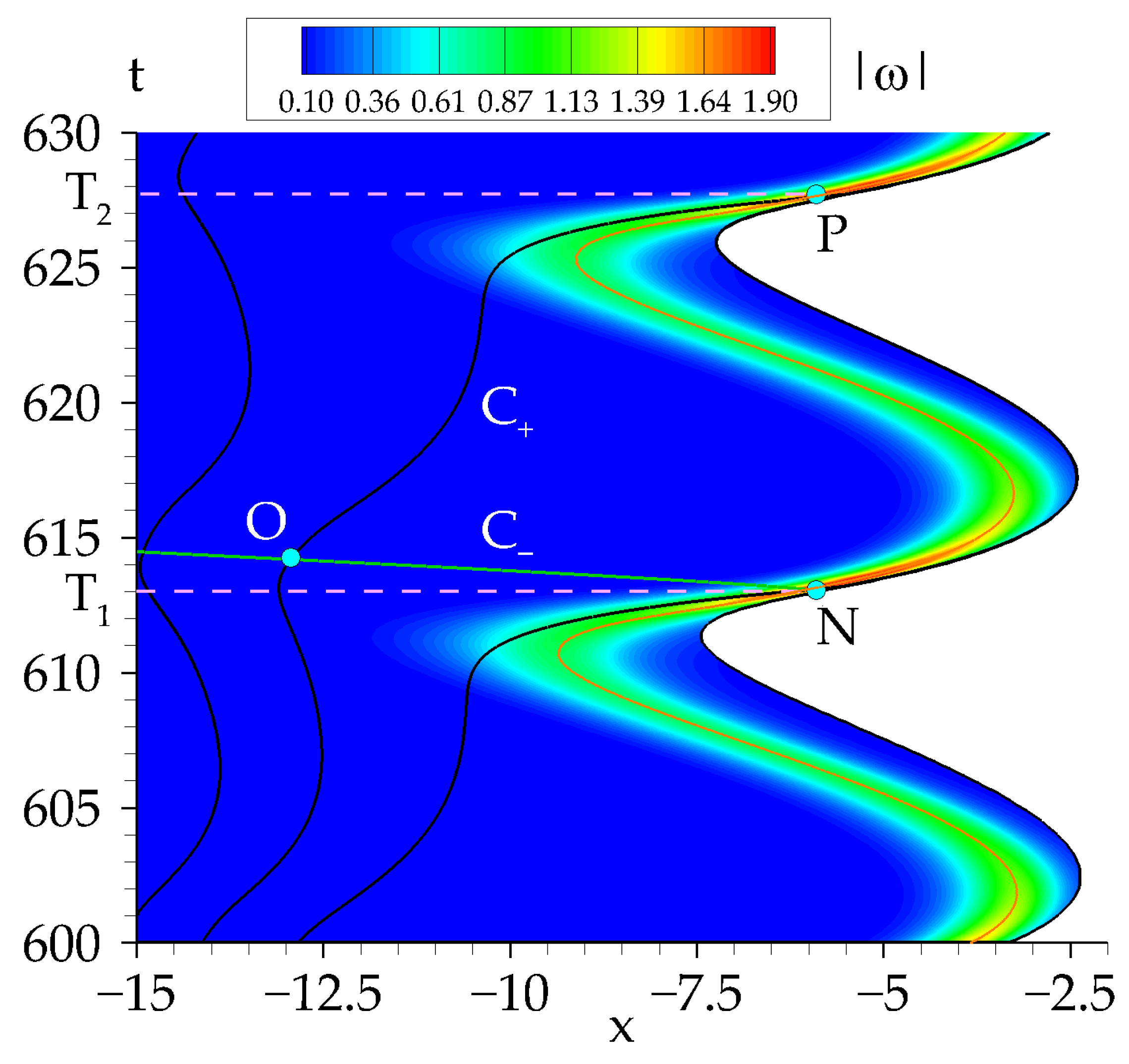
5.2. The Resonant Amplification Case

First of all, note that λ = 100 is not an exact extremum that provides the strongest amplification of the detonation wave. The value was chosen as a typical representative that clearly shows the amplification effect. This value is consistent with the order of magnitude with the value of 80l_1/2 reported in [5] as an optimal wavelength for disturbances. The detonation velocity oscillation period in Figure 3c is ΔT = T₂ − T₁ ≈ 14.7 and coincides with the period of density perturbations. The situation is the same as in Figure 3a, but the mechanics of the processes totally differ. Figure 3c qualitatively looks like Figure 2b for the inert Shu–Osher test. There are no additional secondary peaks, like in Figure 3b,d. So, in the resonant mode, the detonation wave propagates over sine waves in density like a strong inert shock wave with a constant piston support.

Figure 4 demonstrates wave dynamics in the x-t diagram. Details of the process of building the characteristics can be found elsewhere [10]. We analyzed one period of pulsations between time instants T₁ and T₂; see Figure 3c. The leading shock dynamics is determined by the disturbances propagating along the C₊ characteristic; see the black lines in Figure 4. The limiting C₊ characteristics for the considered circle end at points N and P. The green line in Figure 4 is the C₋ characteristic. Point O at the intersection of the C₋ and C₊ characteristics conditionally corresponds to the end of the effective “reaction zone”. The noticeable change in the C₊ characteristic’s inclination takes place in the vicinity of point O. For earlier time instants, it propagated parallel to the left C₊ characteristic, which propagates almost parallel to the leading shock wave and thus does not affect it at the considered times. However, after time instant t ≈ 614, the C₊ characteristic OP starts moving in the direction of the leading shock. The oscillation period ΔT is mainly determined by the time of passage of the C₊ characteristic through the reaction zone, while the time interval t_O − t_N is much smaller than ΔT.

To understand the resonant amplification mechanism, let us also consider the case of detonation propagation in a homogeneous medium, i.e., k = 0 in (12). As we mentioned above, from a theoretical point of view, for the parameters (10), the detonation should propagate with the velocity (11) without oscillations. So, we cannot indicate a natural frequency of the internal pulsation of the detonation wave for the parameters (10). However, in all simulations, see, for example [5,7,12,18], the numerical solution demonstrates decaying low-frequency and low-amplitude oscillations of parameters behind the leading front; see Figure 5a. Usually, this effect is attributed to the fact that the exact theoretical steady-state solution (used as an initial condition) is not the exact solution of the numerical discretization [5]. For this reason, the amplitude and some features of this pulsation evolution can differ from paper to paper depending on the method or resolution in use. However, in all studies, oscillations have the same period Δt within the accuracy of their measurements, for example, 11.68 in [7] (averaged over several oscillations), 11.61 in [18], and 11.66 in Figure 5a. So, in simulations, the period of oscillations of even a theoretically stable detonation wave is determined by some intrinsic factors of the model.

As in the resonant case, the characteristic analysis in the x-t diagram was carried out. Figure 5b illustrates the wave dynamics within one oscillation period between time moments t₁ = 43.43 and t₂ = 55.0. So, we plotted the limiting C₊ characteristic that comes to the point M, which corresponds to the time instant t₂, and traced it back. For the estimation of the backward signal that propagates back from the leading shock, we plotted the limiting C₋ characteristic starting from point K. Point L of the intersection of these characteristics provides the spatial scale of the effective “reaction zone” of about 5l_1/2 responsible for the pulsations of the detonation wave front. The real reaction zone for the single-stage Arrhenius kinetics in use is infinitely long, and all C₊ characteristics sooner or later will affect the leading front. We can suggest that the period of pulsations is mainly determined by the time it takes for a C₊ characteristic to travel between points L and M. The same observation was made in [19] for the low-frequency mode. The conclusion is also consistent with the mechanism for the resonant amplification case. The time of wave propagation along the C₋ characteristic between points K and L is much smaller.

So, the detonation velocity oscillation period ΔT for λ = 100 is close to Δt = 11.7 for the non-disturbance case, which is in fact the necessary condition for the occurrence of amplification.

6. Conclusions

The current work is largely motivated by research in the field of rotating detonation engines, which is currently being intensively conducted around the world. Issues of detonation propagation in non-uniform media and, most importantly, of the control of the stability of this process are of great interest today.

We conducted simulations of one-dimensional pulsating detonations in a non-uniform medium with sine waves in density. For that, we solved Euler equations with single-step Arrhenius kinetics in the shock-attached frame. The numerical algorithm for such simulations has been developed over the past few years in our previous work. In [8], we proposed the quadratic approximation of the C₊ characteristic near the leading shock to obtain the second accuracy order of the algorithm. In [9], we proposed the shock-attached frame approach for a two-stage model of kinetics. In [10], we developed the algorithm for the simulation of inert shock wave propagation in a medium with a non-uniform distribution of density. Recently, the numerical algorithm has been further developed for the case of a non-uniform distribution of the parameters of the medium [11].

Shock-attached frame simulations work well for stability studies and characteristics analyses of pulsating detonation waves. The computational burden in shock-attached frame simulations is significantly less than that for simulations in the laboratory frame of reference. In shock-attached frame simulations, the computational domain is always only a small area behind the detonation wave front. In addition, they provide exact (i.e., without numerical smearing) parameters behind the leading shock wave. The quantitative effect when simulating different detonation modes (stable, weakly unstable, irregular, and strongly unstable) in a homogeneous medium in the shock-attached frame of reference and in the laboratory frame was described in [8].

Different wavelengths of density perturbation were considered. We obtained a non-linear dependence of the amplitude of pulsations on the wavelength of disturbances λ with resonant amplification of pulsations for a certain range of wavelengths. For λ = 100, the mechanism of the amplification was studied using the x-t diagram. This value of λ is consistent with the paper [5], in which the problem was studied using the methods of non-linear dynamics. It was figured out that the mechanism of pulsations in this case is very close to that in the simulation of stable detonation wave propagation without perturbations of the medium’s parameters. The period of oscillation is roughly correlated with the time it takes for the C₊ characteristic to travel across the effective “reaction zone”. At the same time, the time scale for a C₋ characteristic to traverse the “reaction zone” is, by comparison, very small. The same tendencies were observed in [19] for the low-frequency regime of pulsations of chain-branching detonations.

The main novelty of the paper that makes it different from [3,4,5] is the usage of characteristic analysis for revealing the underlying mechanisms of the process. In [4], the authors investigated the spectra of pressure pulsations behind the detonation wave. For E = 28.5, a bifurcation diagram was plotted. It demonstrated the presence of two wavelength ranges of density perturbation, at which a mode with detonation stabilization was realized. In [5], Fourier spectral analysis was applied to the resulting time series to extract dominating frequencies. The power spectra for all wavenumbers in consideration were combined together in a color map with pulsation frequencies plotted on the horizontal axis and perturbation wavenumbers plotted on the vertical axis. In other words, in [4,5], the problem was studied using the methods of dynamical systems. Such an approach alone is not sufficient to gain insight into the gas dynamics of the process. In contrast to [4,5], the authors in [3] used the analysis of spatial distributions of pressure, temperature, and mass fraction of the reagent. However, no clear explanation of the mechanisms of the observed effects was given. The main results were established using the analysis of curves of maximal pressure in the computational domain over time.

The use of a single-step Arrhenius kinetics model in the current research makes it difficult to analyze the wave dynamics in the x-t diagram. We are planning to address this issue by using kinetic models with a finite reaction zone [12] or with an induction zone and a reaction zone clearly separated from each other [9,19].