Abstract
This paper presents modern methods of mathematical modeling, which are widely used in the development of new inhalation and intranasal drugs, including those necessary for the treatment of socially significant diseases, which include: tuberculosis, bronchial asthma, and mental and behavioral disorders. Based on the conducted studies, it was revealed that the methods of mathematical modeling used in the development of drugs are fragmented, and there is no single approach that would combine the existing methods. The results presented in the work should contribute to the development of a unified multiscale model as a new approach in mathematical modeling that contributes to the accelerated development and introduction to the market of new drugs with high bioavailability and the required therapeutic efficacy.
1. Introduction
Socially significant diseases are those whose occurrence and spread are, to some extent, dependent on the socio-economic conditions of the population’s lives. They also cause significant socio-economic damage due to a loss of productivity, treatment costs, disability, and population mortality.
According to the World Health Organization, noncommunicable, socially significant diseases (NCDs) include cardiovascular diseases (heart attacks and stroke), which are the cause of the majority of deaths from NCDs, and account for 17.9 million people per year, followed by cancer, with 9.3 million deaths per year, and chronic respiratory diseases (chronic obstructive pulmonary disease and asthma), with 4.1 million deaths per year [1]. The NCDs also include major mental and behavioral disorders. In addition to NCDs, infectious lung diseases such as tuberculosis, bronchitis and multidrug-resistant tuberculosis are included in the group of socially significant diseases. According to the statistics for 2021, about 10.6 million people fell ill with tuberculosis, of which 1.6 million people died [2]. Worldwide, tuberculosis is the thirteenth leading cause of death and the second leading cause of death after COVID-19 [2,3]; however, tuberculosis is curable and preventable. At the same time, multidrug-resistant tuberculosis poses a much more serious public health threat. In 2021, one in three people with drug-resistant tuberculosis sought medical care [2].
Thus, the development and introduction to the market of promising drugs based on modern delivery systems and new forms for the treatment of socially significant diseases is an urgent task today. The most promising technologies for drug delivery in the treatment of socially significant diseases are intranasal and inhalation technologies. Intranasal and inhalation delivery methods offer several advantages, including direct access of a drug to the systemic circulation, the potential for direct drug delivery to the brain through the olfactory nerves, convenience, and a rapid attainment of therapeutic drug levels in the bloodstream [4]. In addition, the use of nasal and inhaled forms of drugs avoids first-pass metabolism, allowing a drug to be delivered directly to the nasal cavity or lungs, thereby reducing the likelihood of adverse reactions from the gastrointestinal tract, and it removes the influence of pH and the fact of food intake on the rate of drug entry into the bloodstream [5]. The development of new pharmaceutical drugs, however, remains relatively slow due to several factors, including a low bioavailability, limited therapeutic efficacy, and a range of adverse reactions in the body, such as resistance, that may occur with high doses or repeated drug administration, as observed during clinical trials.
Mathematical modeling is recognized as an effective approach to expedite the development and improve the bioavailability of new pharmaceutical drugs. This approach involves the application of computational fluid dynamics methods, which enable the accurate prediction of the trajectory and deposition place of drug particles within the nasal cavity or lungs [6]. Furthermore, the development of cellular automaton models provides valuable insights into the release kinetics of drug substances from dosage forms [7]. Additionally, there are existing models [8] that comprehensively describe the pharmacokinetics and pharmacodynamics of these pharmaceutical drugs.
However, in the currently available scientific articles and literature reviews, there is no approach that combines the aforementioned methods of mathematical modeling. According to the authors, the development of a multiscale model that encompasses a unified set of mathematical modeling methods and incorporates sequential stages for predicting the trajectory and deposition sites of drug particles, as well as calculating the release kinetics of drugs from the dosage form and determining a drug’s distribution throughout the body via blood flow, is a pressing task in the development of new drugs for the treatment of socially significant diseases.
The utilization of multiscale modeling as a novel approach in drug development offers a significant cost reduction in experimental studies. It enables the creation of a digital replica of a drug and facilitates the modeling of its structure and dissolution process in various environments, including the nasal cavity or lungs. Additionally, modern visualization methods for medical data, such as computed tomography (CT)—Figure 1 [9,10], allow for the precise digital representation of anatomical models of the nasal cavity or lungs. This, in turn, enables the accurate prediction of the flight path and deposition sites of drug particles during the developmental stage. Consequently, it provides the opportunity to optimize the composition of a medication to achieve the desired therapeutic effect, even prior to the commencement of clinical trials.
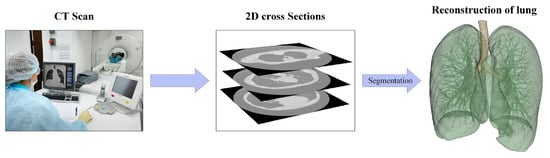
Figure 1.
Stages of reconstruction of the geometry of the human respiratory system by CT.
The literature review conducted by the authors discusses the existing mathematical modeling methods extensively employed in the realm of drug development. The integration of these methods into a unified framework enables the development of a multiscale model capable of accelerating the process and market entry of novel drugs aimed at addressing socially significant diseases.
2. Analysis of Scientific and Technical Literature in the Field of Mathematical Modeling as a Decision Support Tool in Pharmaceutical Development
2.1. Mathematical Modeling of the Movement and Deposition of Drops/Particles during Inhalation and Intranasal Administration of a Medicinal Substance
Inhalation and intranasal routes of drug administration hold promise for the treatment of various diseases; however, achieving the desired therapeutic effect relies on the deposition of the drug substance in specific areas of the respiratory system [6,11]. Therefore, studying and predicting the deposition zones of medicinal substances administered via the intranasal or inhalation route is a crucial scientific and technical task to maximize the effectiveness of disease therapy.
Currently, in vivo studies provide reliable and accurate results regarding the movement and deposition of drugs in the respiratory system through different routes of administration. Modern methods of medical data visualization, such as scintigraphy or single photon emission computed tomography [9], are employed to investigate drug deposition zones. Radio-labeled particles enable the tracking of drug movement and determination of precise deposition sites; however, this approach is constrained by the high cost of imaging tools, complexities in particle labeling, and the potential risks associated with radioactive markers. Furthermore, in vivo studies are limited by patient-specific anatomical variations and the complexities of drug administration, making it challenging to analyze the acquired data and comprehend the mechanisms of drug transport and deposition in the respiratory tract [12].
An alternative to in vivo studies is in vitro diagnostics, which allows the study of drug deposition zones using simplified devices or physical replicas of the respiratory system [13]. This approach is cheaper and is not regulated by medical ethics; however, the in vitro approach is limited by the complexity of recreating an exact copy of the human respiratory system, taking into account the anatomical features [14].
With the increasing computational power in studying drug behavior in the respiratory system, in silico studies become viable, overcoming the limitations of in vivo and in vitro investigations. Mathematical models based on computational fluid dynamics equations have been employed to design inhalation and intranasal delivery devices [15,16] and to predict the movement and deposition of drug particles or droplets for various administration routes [17,18].
Computational fluid dynamics presents a promising approach in developing innovative inhalation and intranasal drug delivery systems; however, when utilizing this approach to study drug behavior, it is crucial to consider the numerous factors that influence the movement and deposition of particles or droplets in the respiratory system.
2.1.1. The Structure of the Respiratory System
The human respiratory system is a complex anatomical structure. It consists of the respiratory tract (i.e., the extrathoracic and tracheobronchial region) and lungs (i.e., the alveolar region) [19]. The airways, in turn, are divided into the upper and lower airways—Figure 2.
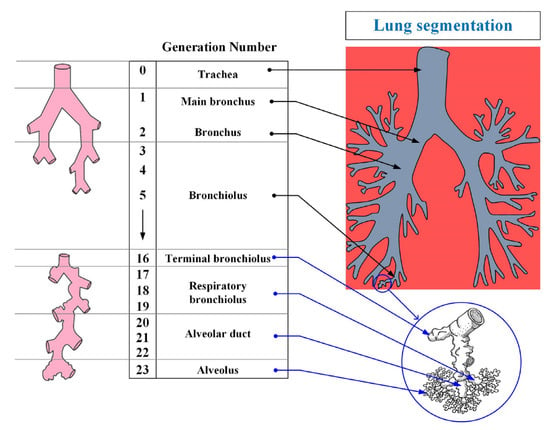
Figure 2.
The structure of the organs of the human respiratory system.
The respiratory system is divided into 23 segments (orders) from the trachea to the alveoli as shown in Figure 2. The upper respiratory tract includes the nasal cavity, the oral and nasal parts of the pharynx, and the larynx; the lower tract includes the trachea and bronchi (bronchial tree). Separately, it is worth highlighting the epiglottis, the function of which is to close the lumen of the larynx when swallowing.
The lower respiratory tract (tracheobronchial region) is the region of the respiratory tract from the trachea to the terminal bronchioles (16th order bronchi). The main function of the respiratory tract is to conduct air into the lungs, and to warm it and cleanse it of foreign particles and pathogens. The trachea is divided into two main bronchi, which, in turn, are divided into lobar (with two in the left and three in the right lung), and they are segmental up to the terminal bronchioles (i.e., a dichotomous type of branching). A feature of the structure of the trachea and large bronchi is the presence in their wall of cartilaginous semirings and rings, respectively. According to some studies [20], this feature leads to a greater deposition of particles in these parts of the respiratory tract.
The alveolar region (lungs) begins with the so-called respiratory bronchioles (bronchi of the 17th order) and connects through them with the final sections of the lower respiratory tract (terminal bronchioles). The respiratory bronchioles pass into the alveolar ducts, into which the alveoli open. The alveolar region consists of bronchi from 17 to 23 orders (Figure 2). The main function of the alveolar region is gas exchange.
Modern methods of medical data visualization make it possible to build anatomically-similar models of the respiratory system and use them for in silico studies to predict the movement and deposition of particles or drops of drugs using computational fluid dynamics methods; however, at the moment there is a limited number of publications on the study of the movement of drugs in all areas of the respiratory system simultaneously due to the complexity of describing the nature of the air flow. It is noted in [10,21,22] that the reconstruction of a complete 3D model of the entire lung is currently not feasible due to the difficulty of segmenting the small airways using CT images; however, if the entire lung were fully segmented, it would be computationally-impossible to accurately model a complete tree of lungs, since this would require billions of mesh elements. Therefore, modeling of the particle flow through the lungs is carried out separately for the upper and for the lower respiratory tracts, as shown in Figure 3 (Stages 1 and 2).
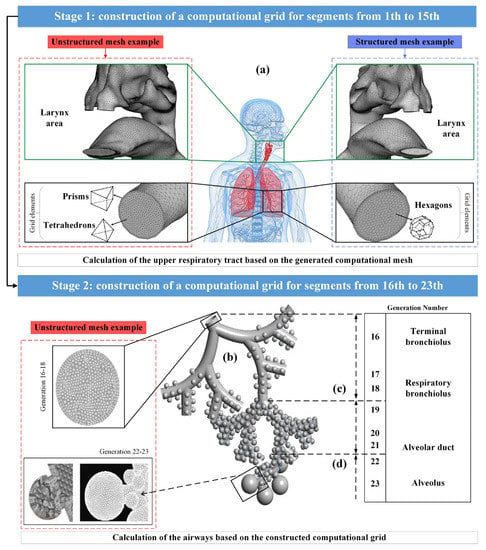
Figure 3.
Multifaceted mesh image for the upper airways (a), and full alveolar model for the lower airways (b); image of the terminal conductive airways ending in the acinar region (c); image of a fully alveolar airway (d).
The pulmonary trunk, that was presented in [10,21], ending before the beginning of the bronchi of the 16th order, had from 2 106 to 4 106 cells of the computational grid (Figure 3a). However, in the developed complex acinar model in [22], spherical alveoli were attached to triple bifurcation units to represent generations of alveolar airways from 16 to 18 and 19 to 21 orders (Figure 3c,d), where the alveoli were separated by a minimum distance to allow for expansion by presenting septa that separate the alveoli. The final computational grid for single-generation, single-cell and multi-cell alveolar models contained 100,000 and 280,000 grid elements, respectively, while there were 2×106 grid elements in triple bifurcation units. Thus, the fragmentation of the lungs into the upper and lower airways, when calculating the flight and deposition of drug particles, is beneficial in terms of saving computational power and time.
2.1.2. Computational Fluid Dynamics Method for Describing the Movement of Air in the Respiratory System
The use of computational fluid dynamics makes it possible to predict the properties of a liquid or gas flow by solving the differential equations of the basic conservation laws, presented in the form of the Navier–Stokes equations [23]. The model equations that represent the movement of drug particles flowing through the nasal cavity or lungs include a system of equations for a continuous medium, and an equation for a dispersed phase, which describes the movement of particles and includes the sum of all forces that affect their movement.
The system of equations for a continuous medium (1) includes the continuity equation, the momentum conservation equation, and the energy conservation equation [24]:
where α and αp are the proportion of the continuous medium and the dispersed phase; ρ is the density of the continuous medium, kg/m3; is the velocity vector of the continuous medium, m/s; is the particle velocity vector, m/s; p is the static pressure, Pa; is the viscous stress tensor; ρg⃗ is the gravity force, kg/m2·s2; is the force that characterizes the effect of the dispersed phase on the continuous medium, kg/m2·s2; is the force characterizing the resistance of the particle, N; Vp is the particle volume, m3; Ksl is the momentum exchange between phases, kg/(m3·s); μ is the dynamic viscosity, Pa·s; CP is the specific heat capacity of the mixture, J/kg·K; T is the temperature of the mixture, K; λ is the thermal conductivity of the mixture, W/m·K; is the unit tensor; and i is the particle index.
To describe the motion of the dispersed phase, Equation (2) [25] is used:
In this case, the interaction between a particle and a continuous medium is described by the following equations:
where mp is the particle mass, kg; g⃗ is the free fall acceleration, m/s2; is the force of interaction between a continuous medium and a particle, N; is the force of interaction between particles, N; is the force of interaction between the particle and the wall, N; is the pressure gradient force acting on a particle, N; ∇p is the pressure gradient, Pa; is the viscous force, N; Num is the number of particles, i; and j is the particle indices.
For ∀i from 1 to Num (i ≠ j),
In addition to the equations described above, in a number of works [24,25], interactions between colliding particles are taken into account; for this, the stiffness coefficient is calculated, on the basis of which the forces of interaction between particles are calculated.
Depending on the region of the respiratory system under consideration, a change in the nature of the movement of the air flow is observed. In [23], the authors demonstrated the presence of turbulent and transient flows in the extrathoracic region. The presence of turbulent air flow in the nasal and oral cavities can have a significant impact on the nature of the movement and the deposition zone of drug particles; however, a number of works [26,27,28] have shown that there is no turbulent flow in the tracheobronchial and alveolar regions.
The described features of the air flow in various areas of the respiratory system necessitate the correct choice of the method for calculating turbulent flows in the study of motion and drug deposition zones in silico using computational fluid dynamics.
At the moment, there are a large number of methods for calculating turbulent flows based on the representation of a turbulent flow as a spectrum of eddies of various scales: the method of direct numerical simulation (DNS), the method of large eddies (LES) and the method of averaging the Navier–Stokes equations according to Reynolds (RANS). One of the priority areas for calculating turbulent flows is numerical simulation based on the construction of difference calculation methods.
A significant place in modern research is occupied by the DNS calculation method, which allows for solving the complete non-stationary, three-dimensional Navier–Stokes equations without using special turbulence models, i.e., models k-ε, and k-ω. The complexity of the DNS method is primarily due to the fact that unsteady turbulent flows are characterized by a wide range of spatial and temporal scales. Turbulence scales are distributed over a range of linear dimensions—from the largest eddies interacting with an average flow, the time scale of which is comparable to the scale of large eddies, to the smallest eddies, called the Kolmogorov scale, dissipating under the action of viscous forces. To perform calculations using the DNS method, the computational grid must be fine enough to resolve the smallest eddies, the dimensions of which are of the order of the Kolmogorov length scale:
where ηk is the Kolmogorov scale, m/s; ν is the kinematic viscosity, m2/s; and ε is the energy dissipation, m2/s3.
The DNS method is applicable only for limited Reynolds numbers (Re), because the number of NDNS grid nodes required for calculations is proportional to the following ratio:
Using relation (8), one can estimate the number of NDNS grid nodes. At Reynolds numbers of the order of 104, the number of nodes of the computational grid will be 1.4 × 107, and with the Reynolds number equal to 105, the number of nodes of the computational grid will be 2.49 109. Therefore, calculations by the DNS method require high-performance computing equipment and an efficient numerical method that makes it possible to obtain reliable numerical results. Such requirements limit the widespread use of the DNS method in describing the movement of drug particles in the respiratory system. In [29], the emergence of a turbulent vortex in the oral cavity was studied; the DNS method was used to calculate turbulent flows. The data obtained indicate the presence of high turbulence in the oral cavity and larynx.
The presence of turbulent vortices in the oral cavity and larynx was proved in [30,31] using the RANS method based on the replacement of changing flow characteristics (i.e., velocity, pressure, and density) by sums of averaged and pulsation components, using semi-empirical turbulence models. The approaches proposed in the papers have demonstrated a significant reduction in computing power by reducing the requirements for the discretization of the computational domain and the time step. In addition, the LES method [32,33] can also be used to calculate turbulent eddies.
The RANS (Reynolds-Averaged Navier–Stokes) calculation method is commonly used to study the airflow dynamics in the respiratory system due to its adequate accuracy and low computational requirements; however, in order to solve the system of Reynolds-averaged Navier–Stokes equations, additional empirical relationships are needed, specifically, rheological models of states. These relationships are based on hypotheses related to the turbulent viscosity, mixing paths, and turbulent flows.
It is worth noting that when modeling the movement and deposition of particles or droplets of drugs, it is essential to consider not only the methods for calculating turbulent flows but also models that describe the motion and interaction of particles with each other, the continuous phase, and the walls of the respiratory system or nasal cavity.
2.1.3. Methods for Describing the Movement of Particles or Droplets of Drugs in the Respiratory System
The Euler and Lagrange models can be used to describe the movement of particles or droplets of drugs in the inhalation and intranasal routes of administration; however, when implementing the Euler model, drug particles or drops are considered as one continuous phase. In turn, the behavior of the flow is predicted based on the resolution of the laws of conservation of mass and momentum.
The Lagrange model allows us to consider drug particles or drops as a separate dispersed phase in a continuous gaseous medium. Particle motion is predicted by integrating Newton’s second law with respect to time. The Lagrange model makes it possible to study the dynamics of the movement of particles or drops and the zone of their deposition.
Depending on the consideration of the interaction of particles of the dispersed phase with each other, this approach can be divided into the discrete particle method (DPM), which does not consider the particle–particle, or the particle–wall interaction, and the discrete element method (DEM), which takes into account these interactions.
When using the discrete particle method (DPM), it is assumed that the volume fraction of the dispersed phase in a continuous medium is insignificant; therefore, it does not affect the nature of the air flow, and particle–particle interactions are not taken into account [34]. In addition, it is assumed that the precipitation of particles or droplets of a drug occurs upon contact with the walls of the organs of the respiratory system. In most studies, in order to carry out mathematical modeling and achieve the required accuracy of calculations, the method of discrete particles has been used when considering the forces of resistance and gravity [35,36,37]. The authors of [38] evaluated the effect of gravitational forces on the zones of deposition of drug particles. It was established that in the absence of gravity, the total deposition of particles in the tracheobronchial region of the respiratory system was reduced by 10%. This was due to an increase in the proportion of precipitated drug particles in the area of administration (i.e., the oral cavity).
In turn, at a high concentration of particles in the dispersed phase, about 104 or 5·103 particles/mL of gas for aerosols and 1.2·109 particles per dose for inhalation powders [39,40], it is necessary to take into account the interaction between particles, between particles and the flow continuous medium, and between particles and the walls of the respiratory system organs. The presented interactions can be taken into account when using computational fluid dynamics in conjunction with the discrete element method [41]. In this case, particle–particle, particle–wall, and particle–continuous medium interactions are taken into account. This approach is widely used in the development and evaluation of the effectiveness of new inhalation and intranasal drug delivery systems; however, there are limitations to using this approach for the mathematical modeling of particle movement and deposition zones.
The authors of [42] carried out mathematical modeling of particle motion using the method of computational fluid dynamics in combination with the method of discrete elements in the Weibel light model. The data obtained indicated that the initial parameters of the introduction of particles have a significant impact on their movement in the respiratory system. In [43], the authors compared two approaches to modeling particle motion (i.e., the discrete particle method and the discrete element method) in the extrathoracic region of the respiratory system. When using the discrete element method, a complex trajectory of particles in the upper part of the trachea was revealed, due to the strong interaction between the particles.
Therefore, when employing the discrete element method to simulate particle movement, a notable deposition of particles in the extrathoracic region is observed. These findings are consistent with the studies presented in [44].
2.1.4. Influence of Flow Characteristics on the Deposition Zones and Movement of Medicinal Substances
Airflow characteristics play a crucial role in determining flow patterns and drug deposition zones. Currently, substantial advancements have been made in the research focused on investigating the impact of airflow parameters on particle deposition zones [45,46,47].
- Effect of flow rate.
Increasing the velocity results in turbulence and the inertial settling of drug particles, which causes deposition in the extrathoracic region of the respiratory system. In [48], the authors studied the transition from a laminar to turbulent flow in the respiratory system. It was found that an increase in the flow velocity leads to the formation of turbulent vortices in the oral cavity. In turn, fluctuations in the flow velocity have a significant effect on the movement of particles and their deposition. The authors of [49] analyzed the effect of the inhalation velocity of drug particles, equal to 30 and 60 L/min (3.6 and 7.2 m/s, respectively, with the cross-sectional area of the inlet opening equal to 0.00014 m2), corresponding to pharmacopeia data, on their deposition zones using computational fluid dynamics and a lung model built on the basis of computed tomography. It was found in the work that with an increase in the flow rate, a significant settling of particles in the oral cavity was observed. However, the authors of [50] found that the flow velocity does not affect the deposition zones below the extrathoracic region.
In turn, the authors of [51] carried out CFD modeling of the flow with an inlet velocity of 28.3 and 60 L/min in a cascade Andersen impactor divided into 7 stages, each of which had a characteristic hole diameter used to study the aerodynamic distribution of fine particles. Based on the simulation results, it was found that at the impactor stages 0 and 1 (i.e., a hole diameter of 2.55–1.89 mm), the flow was divided in directions due to the central hole, the formation of small eddy currents around the impactor outlet holes was observed, which were most noticeable at stages 2 and 3 (i.e., a hole diameter of 0.91–0.71 mm) and they become less pronounced in steps 4 to 7 (i.e., a hole diameter of 0.53–0.25 mm). Table 1 shows the characteristic particle diameters deposited on the respective impactor stages at different flow rates.

Table 1.
The characteristic particle diameters predicted by the CFD method are deposited on the corresponding stages of the impactor at different flow rates [51].
The authors of [51] showed that at a higher inlet flow rate of 60 L/min, the characteristic particle size deposited in the first three stages of the impactor is less than at a rate of 28.3 L/min.
To study the effect of flow velocity on particle deposition zones, the authors of [52] used casts of the human upper respiratory tract with a subsequent digitization of the periphery of the airway contour (Figure 4a). The authors of [52] measured the cross-sectional area and perimeter of the oral cavity, pharynx, and larynx by cutting the cast into 0.3 cm sections (Figure 4b).
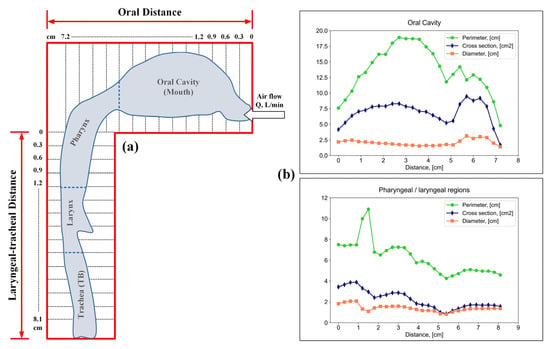
Figure 4.
Appearance of the periphery of the airway contour (a); perimeter, cross-sectional area and cross-sectional diameter of the oral cavity, pharynx and larynx (b).
Using an airway model, the authors of [53] studied the effect of various flow rates, namely, 15, 30 and 60 L/min, on the deposition efficiency of particles of various sizes in the respiratory system. The results of the studies of the authors of [53] are presented in Figure 5a,b.
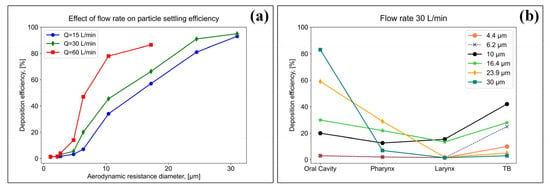
Figure 5.
Study of the influence of flow rates on the efficiency of particle settling (a), and study of the efficiency of settling particles of various sizes in the respiratory system at a flow rate of 30 L/min (b).
The results showed that the particle settling increased with an increasing flow rate. At the highest flow rate (60 L/min), more than 90% of the particles, with a characteristic size >20 µm, were deposited in the oral cavity (Figure 5a). At a flow rate of 30 L/min for particles <10 µm, a more uniform settling pattern was observed in three regions of the respiratory system: the oral cavity, pharyngeal and laryngeal regions, and tracheobronchial (TB), while the settling efficiency did not exceed 10%; however, for particles >10 µm, the deposition efficiency in the oral cavity was higher (Figure 5b).
At the same time, the authors of work [54] note that in order to perform correct calculations, the number of cells of the computational grid should be at least 480,000 for flow rates of 15 and 30 L/min, and 640,000 for a flow rate of 60 L/min.
- 2.
- Influence of unsteady flow.
To study the particle settling zone, different respiratory modes are compared, which affect the flow rate. The authors of works [55,56,57,58] carried out mathematical modeling using computational fluid dynamics to study the influence of a non-stationary and stationary inspiratory velocity flow for a simplified model of the oral cavity and larynx (Figure 6).
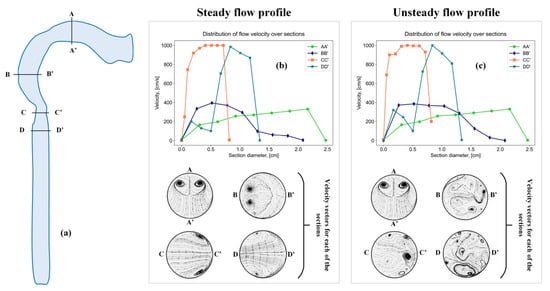
Figure 6.
Sections in a simplified model of the oral cavity and larynx (a), sections with a steady flow profile (b), and sections with an unsteady flow profile (c).
The results presented in the work indicate the presence of vortex flows in the oral cavity, larynx and trachea region both in a stationary and non-stationary air flow; however, with an unsteady flow, the vortex motion takes on a more complex character.
In addition, a study conducted by researchers in [57] demonstrated that the presence of an unsteady flow, characterized by time-dependent velocity and pressure fields, leads to the increased deposition of medicinal substances. Moreover, when the airflow exhibits a cyclic nature corresponding to the inhalation and exhalation cycles, it was observed that turbulent flow develops during the acceleration phase of inspiration, followed by a transition to a laminar flow as the flow decelerates [58].
- 3.
- Influence of the physiological model of breathing.
In [59] it was demonstrated that the nature of breathing, especially during inhalation, has a significant effect on the movement and deposition of medicinal substances. The effect of the respiration cycle on the deposition and movement of medicinal substances was also studied by the authors of [60]. It was concluded that with each breathing cycle, the concentration of drugs deposited in the organs of the respiratory system increases, and subsequent breathing cycles lead to the further movement of particles to the lower parts of the respiratory system. When considering the delivery of drugs based on nanoparticles, it was found that, towards the end of inhalation, the efficiency of particle deposition increases with a decreasing flow rate due to an increase in the residence time of the particles [61].
For some dosing devices, it is necessary to hold the breath in order to precipitate suspended particles of the medicinal substance in the organs of the respiratory system. The authors of [62], using computational fluid dynamics, studied the movement and deposition of drug particles in the respiratory tract from the oral cavity to the bronchi of the 7th order.
The data obtained indicate the presence of turbulence during breath holding. It was found in the work that for particles with an average size of 5 μm, holding the breath makes it possible to reduce the probability of deposition of particles in the oral cavity with an increase in deposition in the bronchi. Thus, for a number of drug delivery systems, the deposition of which is necessary in the lower respiratory tract (Figure 2), it is necessary to hold the breath.
2.1.5. Computational Fluid Dynamics for Studying the Motion and Deposition of Medicinal Substances
Studying the movement and deposition of drug particles using computational fluid dynamics and in vivo experimental studies is an important tool in the development of new innovative inhalation and intranasal drug delivery systems. For the first time, the use of computational fluid dynamics for the development of an inhalation delivery system was presented by the authors of [63]. Various dosing device designs and continuum compositions were investigated to achieve the required area of drug particle deposition in the respiratory system.
The data obtained indicate that the reduction in the metering device valve outlets and the presence of a spacer allow the delivery of drugs to the bronchi without deposition in the oral cavity.
In [64], the possibility of a targeted delivery of inhaled drugs using magnetic targeting was studied. The authors conducted a computational experiment using computational fluid dynamics with the method of calculating turbulent flows with averaging the Navier–Stokes equations according to Reynolds (Figure 7).
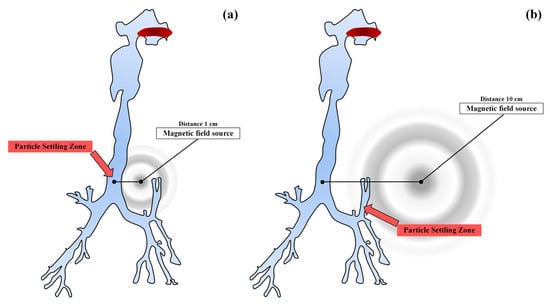
Figure 7.
Scheme of a magnetic source for two zones remote from the wall of the trachea by 1 cm (a), and by 10 cm (b).
The authors of [64] showed that the local and overall efficiency of particle deposition can be significantly increased by activating the strength of the magnetic field. The data obtained indicate the possible further development of the targeted delivery of drugs through magnetic targeting for the treatment of diseases of the respiratory system.
Based on the considered approaches to modeling the movement and deposition of drug particles in various lung segments, the main conclusions can be drawn. First, depending on the region of the respiratory system under consideration, a change in the nature of the movement of the air flow is observed; therefore, to calculate the movement and deposition of drug particles, it is necessary to take into account the occurrence of turbulent flow—the most appropriate and widely used calculation method, in the opinion of the authors, is RANS, since the hypotheses of turbulent viscosity, mixing paths and turbulent flows, and the computing power requirements are lower than for the DNS method. Secondly, it was shown that at a high concentration of particles or drops in the dispersed phase, it is necessary to consider not only methods for calculating the turbulent flows, but also models of the movement and interaction of particles or drops with each other, the continuous phase and the walls of the respiratory system. Thirdly, the considered influence of the air flow parameters on the particle deposition zones made it possible to determine that an increase in the inlet flow rate contributes to the deposition of a significant amount of particles in the oral cavity; however, by choosing the right dosing device it is possible to achieve the deposition of drug particles directly in the bronchi without deposition in the oral cavity. In addition, the presence of breathing cycles (i.e., inhalation and exhalation) also affects the efficiency of the delivery of drug particles to the lungs. A decrease in the flow rate is observed towards the end of inspiration, which leads to an increase in the residence time of the particles; therefore, the efficiency of their deposition increases. The authors of this paper believe that the considered approaches to mathematical modeling of the trajectory of movement and deposition of particles or drops of a drug will contribute to the accelerated development of new inhaled drugs needed to treat common lung diseases.
2.1.6. Computational Fluid Dynamics for Studying the Movement and Deposition of Medicinal Substances in the Nasal Cavity
Currently, the development of intranasal drug delivery systems for the treatment of various neurological disorders is relevant and promising [65]. The onset of the desired therapeutic effect is possible when it is reached (Figure 8).
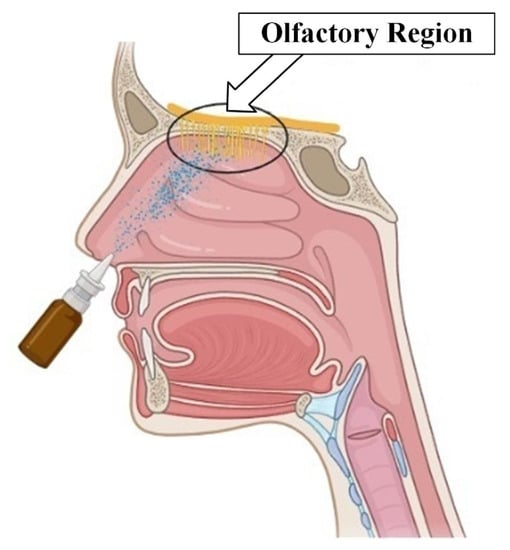
Figure 8.
Olfactory region of the nasal cavity.
Existing approaches, however, do not allow for achieving a high concentration of particles in the required area. This is due to both the complex structure of the nasal cavity, in which inhaled particles are filtered long before reaching the olfactory region, and the complexity of controlling the trajectory of drug particles. Various approaches to intranasal drug administration have been studied to improve delivery efficiency to the olfactory region.
In [66], using computational fluid dynamics, a numerical simulation of the flow trajectory was carried out when a drug was injected into a certain area of the nasal cavity. The obtained results indicate that the introduction of drugs into the region of the anterior wall of the nasal cavity increases the deposition coefficient of particles in the olfactory region compared to the traditional method of administration.
The authors of [67], using the method of computational fluid dynamics in an anatomically-accurate model of the nose, studied the efficiency of delivering a group of charged aerosols to the osteomeatal complex (OMC) when exposed to an electric field. The work considered both monodisperse and polydisperse aerosol profiles. Figure 9 schematically shows the effect of the electric field on the deposition zones of drug particles during the intranasal route of administration [67].
Figure 9.
The influence of the electric field on the areas of deposition of particles of drugs in the intranasal route of administration: the areas of deposition of particles with electric impact and without electric impact.
Mathematical modeling made it possible to determine that the synthesis of electrical guidance and the point release of the drug allows for achieving a focused deposition of aerosol droplets with a significantly increased dosage in the OMC. Table 2 shows the mass fractions of deposited monodisperse particles in the OMC region.

Table 2.
Monodisperse particle deposition fraction [67].
Meanwhile, Table 3 shows the mass fractions of deposited polydisperse particles in the OMC region.

Table 3.
Polydisperse particle deposition fraction [67].
The results of the performed mathematical modeling (Table 2 and Table 3) showed the delivery efficiency in the OMC to be 51.6% for monodisperse aerosols and 34.4% for polydisperse aerosols. These differences indicate that the aerosol profile has a significant impact on intranasal drug administration.
The considered approaches to mathematical modeling using computational fluid dynamics can be useful in the development of new intranasal drug delivery systems needed to treat a wide range of diseases from rhinosinusitis to neurological and mental disorders. In the authors’ opinions, however, mathematical modeling of intranasal drug delivery using new approaches (e.g., exposure to electric and electromagnetic fields), which increase the delivery efficiency and drug concentration in the target area of the nasal cavity, should be carefully tested by conducting a series of in vitro experiments.
In the development of innovative systems for inhalation and intranasal drug delivery, studies aimed at multiscale modeling are becoming increasingly important. In order to evaluate the effectiveness of the developed delivery systems, computational fluid dynamics is used to study the areas of deposition of particles or drops of drugs in the respiratory system, using various dissolution models, namely, the kinetics of dissolution, and the release of drugs in a specific area of the respiratory system are predicted, while the results obtained are used to build pharmacokinetic models to describe the distribution of an active pharmaceutical ingredient throughout the body depending on the area of deposition [68].
2.2. Description of the Kinetics of the Release of the Active Substance from the Dosage Form
After the precipitation of particles or droplets of drugs in the respiratory system, the active substance is released from the dosage form. The release is a complex process that sequentially includes the following stages: the interaction of the active substance with the environment in which the precipitation of the drug particles occurred; dissolution of the active substance; and the movement of the dissolved active substance within the dosage form and, then, in the human body.
Thus, the task of modeling the drug release process includes the following steps:
- Prediction of drug particle deposition zones in the respiratory system.
- Modeling the internal heterogeneous structure of a dosage form with an embedded active substance.
- Modeling the process of dissolution of the active substance.
- Simulation of the active substance’s transportation within the dosage form, considering the medium’s heterogeneity, and subsequent transportation outside the dosage form.
Mathematical models for the dissolution process are based on the solution of differential equations. Their fundamental principle is to examine the entire system and track the changes in the concentration of the dissolved active substance over time.
Currently, numerous models have been developed to describe the release of active substances from dosage forms. The most widely used models include the zero-order, first-order, Hickson–Crowell, and Higuchi models, which are extensively discussed in [69,70,71,72,73,74,75].
However, a significant drawback of these models is their inaccurate description of the dissolution process for multicomponent solids and bodies with complex internal structures. This limitation stems from various factors and the stochastic nature of the multicomponent dosage form’s structure. Therefore, the development of models that consider the complex and heterogeneous internal structure of the dosage form remains an urgent task in the pursuit of a comprehensive multiscale model.
2.2.1. Modeling the Internal Structure of a Dosage form with an Embedded Active Substance and Release from It
Modeling the structure of a dosage form can be considered at several hierarchical levels: the molecular level, micro level and macro level, each of which has its own methods and approaches, as well as limitations.
As part of the development of a single multiscale model, the most promising are approaches that consider the system at the micro level, since they are still sufficiently detailed to take into account the geometry of the structure of the dosage form, in contrast to the macro level, but they do not require such large computing power as approaches related to the molecular level.
At the micro level, the main modeling methods are the method of dissipative particle dynamics, the method of lattice Boltzmann equations, the method of Brownian dynamics, and the method of a self-consistent field. The system in this case is represented by describing the field or conditional microscopic particles.
In the case of heterogeneous nanoporous structures, such as aerogel dosage forms, it is often necessary to apply special modeling approaches. This is due to the fact that the shape of such structures is stochastic in nature and cannot be described by geometric objects [76]. One of the promising approaches for describing nanoporous systems at the microlevel is the cellular automaton (CA) approach.
The essence of the CA approach is to divide the system into identical local areas (cells), while each cell at any given time can only be in one of a finite, predetermined set of states. In this case, time is also divided into equal discrete steps, and the change in the state of the cell at each time step is determined in accordance with the specified transition rules. This approach allows us to move away from a complex system of equations, in which many factors must be taken into account, to local rules of cell behavior that do not depend on each other. This makes it possible to significantly simplify the mathematical apparatus in the calculation of complex systems while maintaining the required accuracy. This makes the CA approach a suitable tool for describing complex heterogeneous systems such as nanoporous dosage forms [77], various kinds of coated or uncoated polymer particles, and polymer particles embedded in an active pharmaceutical ingredient (API). Figure 10 shows examples of modeling various structures of drug particles based on the cellular automaton approach.

Figure 10.
Various structures of drug particles reproduced using a cellular automaton approach.
It should be noted that the CA approach can also be used in modeling the dissolution of an active substance and is a promising alternative to the traditional approach, which consists in developing and solving differential equations. In particular, the CA approach has been successfully used in modeling the dissolution of the active substance from solid dosage forms. In [77], a model for the dissolution of three-dimensional solids was proposed based on the cellular automaton approach.
In addition, one of the advantages of the CA approach is the ability to combine different CA models. In [7], a CA model was implemented that described the release of melatonin in a model nasal cavity during the deposition of aerogel particles based on chitosan. Thus, it was possible to develop a unified CA model of the structure of the dosage form and the process of dissolution and transportation of the active substance in it.
2.2.2. Existing Approaches for Modeling the Movement of the Active Substance after Its Release
Simulation of the transport of an active substance in solution is the problem of modeling the hydrodynamics of a multiphase multicomponent system.
Currently, the most common methods for modeling hydrodynamics rely on solving the system of Navier–Stokes differential equations; however, these methods have limited applicability when dealing with multi-phase and multi-component systems, and they are also computationally demanding.
The most suitable method for developing a multiscale model, which allows for simplified mathematical modeling and reduced computational costs, is the lattice Boltzmann method based on lattice Boltzmann equations [78].
The main idea behind the lattice Boltzmann method is to divide the system into identical cells. Each cell represents a volume of the simulated medium containing fictitious fluid particles. Fluid particles can only move between adjacent cells in each time step. The direction of particle movement in the next time step is strictly defined. The calculation of each time step occurs in two phases: the flow propagation phase and the collision phase.
In [7], the movement of fluid particles to neighboring cells was considered in detail in accordance with their direction (Figure 11).
Figure 11.
Movement of liquid particles to neighboring cells in accordance with their direction.
During the first phase, particles move from one cell to another in accordance with their directions. The number of possible directions of particle motion depends on the number of dimensions of the system (i.e., a two-dimensional or three-dimensional lattice), the required accuracy, and the computational power [79].
The flow propagation phase is followed by the collision phase. At this step, the collision of particles with each other inside the cell is calculated, thereby changing the distribution of particles along the directions of movement. How a collision is handled is determined by the collision operator; therefore, the distribution after collisions will be different.
The method of lattice Boltzmann equations has shown itself well in modeling multicomponent systems with complex geometry [80]. In addition, it is also used in medical research, in particular in [81], where a variant of the model is proposed, which is suitable for modeling the blood flow in vessels.
This conducted literature review has enabled the identification of the most pressing tasks and directions in the field of mathematical modeling of the respiratory system. The combination of computational fluid dynamics approaches to calculate the trajectory of particle movement and deposition in the respiratory system, along with the cellular automaton (CA) approach to model the kinetics of drug dissolution and release from the dosage form, followed by the calculation of drug redistribution throughout the body via blood flow based on the deposition area [82,83,84,85,86,87,88,89], will facilitate the development of a unified multiscale model.
Based on the collected scientific and technical information presented in this review, at the moment it is possible to propose the following type of a single multi-scale model, as a new approach for the accelerated development of inhaled and intranasal drugs necessary for the treatment of socially significant diseases—Figure 12.
Figure 12.
View of a single multi−scale model for accelerated development of inhaled and intranasal drugs.
The data collected from the literature analysis will be utilized by the authors of this study in the development of a multiscale model. The objective of this model is to expedite the development and introduction of new inhaled and intranasal drugs required for the treatment of socially significant diseases into the market.
3. Conclusions
A review of the scientific and technical literature in the field of mathematical modeling showed that, at the moment, there is considerable experience in using models of different levels to describe certain classes of forecasting problems: flow hydrodynamics during spraying and the further movement of particles or drops, as well as the area of their deposition; the kinetics of dissolution and release of the drug substance; and the adsorption, redistribution and excretion of a medicinal substance in the organs and tissues of the body. The research results presented in this article give a broad idea of the problems that arise in the mathematical modeling of anatomically-similar organs of the respiratory system, and they draw attention to various factors that affect the relationship between the quality of the computational grid and the computation time. The presented studies in the field of CFD modeling allow for choosing the most optimal calculation methods suitable for the organs of the respiratory system. In addition, the results of the studies draw attention to promising methods for the targeted delivery of drugs to the organs of the human respiratory system. With the help of mathematical modeling tools, it is shown how a particular method affects the efficiency of drug delivery in specific zones/segments of the respiratory system. The presented results in the field of cellular automaton models show that this mathematical modeling tool is promising in the field of drug development, due to simplified mathematical modeling and a reduced computational time. Combining models of different levels also gives researchers a comprehensive tool for preliminary reverse engineering in development. Nevertheless, despite significant advances in the field of mathematical modeling, the parametrization of models and verification of their adequacy remain a current problem, since complex models require a significant amount of experimental data at the stages of parameterization and verification. Modern medicine today does not have a non-invasive, commercially available and accurate tool for obtaining complete information about the transformation of the delivery system and drug substances inside the body. The developers of mathematical models have to work with disparate blocks of data coming from different sources, both at the stage of preclinical trials and from the stages of clinical trials. A significant part of the parameters of complex models is currently determined by optimization methods, and they do not guarantee a single correct solution, and not from experimental procedures. The problem of the lack of complete information hinders the widespread use of mathematical models as one of the main reverse engineering tools in the pharmaceutical development process. The collected literature review should be the first step towards the development of a single multiscale model aimed at the development of new drugs needed for the treatment of socially significant diseases.
Author Contributions
Conceptualization, N.M.; Methodology, A.A. and E.M.; Formal analysis, N.M. and A.A.; Investigation, E.M.; A.A. and N.M.; Writing original draft—review and editing, E.M., A.A. and N.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research was carried out with the financial support of the Ministry of Science and Higher Education of the Russian Federation within the framework of scientific topics FSSM-2022-0004.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Health Organization. Noncommunicable Diseases Country Profiles 2018; WHO Press: Geneva, Switzerland, 2018; Available online: https://apps.who.int/iris/handle/10665/274512 (accessed on 22 April 2023).
- World Health Organization. Global Tuberculosis Report 2021; WHO Press: Geneva, Switzerland, 2021; Available online: https://www.who.int/publications/i/item/9789240037021 (accessed on 22 April 2023).
- World Health Organization. Global Tuberculosis Report 2022; WHO Press: Geneva, Switzerland, 2022; Available online: https://www.who.int/publications/i/item/9789240061729 (accessed on 22 April 2023).
- Djupesland, P.G. Nasal drug delivery devices: Characteristics and performance in a clinical perspective-a review. Drug Deliv. Transl. Res. 2013, 3, 42–62. [Google Scholar] [CrossRef]
- Irngartinger, M.; Camuglia, V.; Damm, M.; Goede, J.; Frijlink, H.W. Pulmonary delivery of therapeutic peptides via dry powder inhalation: Effects of micronisation and manufacturing. Eur. J. Pharm. Biopharm. 2004, 58, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xiong, G.; Tsang, W.C.; Schätzlein, A.G.; Uchegbu, I.F. Nose-to-Brain Delivery. J. Pharmacol. Exp. Ther. 2019, 370, 593–601. [Google Scholar] [CrossRef]
- Lebedev, I.; Uvarova, A.; Mochalova, M.; Menshutina, N. Active Pharmaceutical Ingredients Transportation and Release from Aerogel Particles Processes Modelling. Computation 2022, 10, 139–157. [Google Scholar] [CrossRef]
- Kolli, A.R.; Kuczaj, A.K.; Martin, F.; Hayes, A.W.; Peitsch, M.C.; Hoeng, J. Bridging inhaled aerosol dosimetry to physiologically based pharmacokinetic modeling for toxicological assessment: Nicotine delivery systems and beyond. Crit. Rev. Toxicol. 2019, 49, 725–741. [Google Scholar] [CrossRef]
- Jaafar-Maalej, C.; Andrieu, V.; Elaissari, A.; Fessi, H. Assessment methods of inhaled aerosols: Technical aspects and applications. Expert. Opin. Drug Deliv. 2009, 6, 941–959. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Zhao, J.; Hayati, H.; Sperry, T.; Yi, H. Tutorial: Understanding the transport, deposition, and translocation of particles in human respiratory systems using Computational Fluid-Particle Dynamics and Physiologically Based Toxicokinetic models. J. Aerosol Sci. 2021, 151, 105672. [Google Scholar] [CrossRef]
- Borghardt, J.M.; Kloft, C.; Sharma, A. Inhaled Therapy in Respiratory Disease: The Complex Interplay of Pulmonary Kinetic Processes. Can. Respir. J. 2018, 2018, 2732017. [Google Scholar] [CrossRef]
- Carrigy, N.; Martin, A.; Finlay, W. Use of Extrathoracic Deposition Models for Patient-Specific Dose Estimation during Inhaler Design. Curr. Pharm. Des. 2015, 21, 3984–3992. [Google Scholar] [CrossRef]
- Agu, R.U.; Ugwoke, M.I. In vitro and in vivo testing methods for respiratory drug delivery. Expert. Opin. Drug Deliv. 2011, 8, 57–69. [Google Scholar] [CrossRef]
- Byron, P.R. Prediction of drug residence times in regions of the human respiratory tract following aerosol inhalation. J. Pharm. Sci. 1986, 75, 433–438. [Google Scholar] [CrossRef] [PubMed]
- Ruzycki, C.A.; Javaheri, E.; Finlay, W.H. The use of computational fluid dynamics in inhaler design. Expert. Opin. Drug Deliv. 2013, 10, 307–323. [Google Scholar] [CrossRef]
- Park, H.; Han, C.S.; Park, C.W.; Kim, K. Change in spray behavior of pharmaceutical particles by creating bypass hole in dry powder inhaler. Powder Technol. 2022, 397, 117034. [Google Scholar] [CrossRef]
- Sundström, E.; Talat, R.; Sedaghat, A.R.; Khosla, S.; Oren, L. Computational Modeling of Nasal Drug Delivery Using Different Intranasal Corticosteroid Sprays for the Treatment of Eustachian Tube Dysfunction. J. Eng. Sci. Med. Diagn. Ther. 2022, 5, 031103. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Zhang, Z.; Lessmann, R. Computer Simulation of the Flow Field and Particle Deposition by Diffusion in a 3-D Human Airway Bifurcation. Aerosol Sci. Technol. 1996, 25, 338–352. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z.; Donohue, J.F. Targeted drug-aerosol delivery in the human respiratory system. Annu. Rev. Biomed. Eng. 2008, 10, 195–220. [Google Scholar] [CrossRef]
- Kannan, R.R.; Przekwas, A.J.; Singh, N.; Delvadia, R.; Tian, G.; Walenga, R. Pharmaceutical aerosols deposition patterns from a Dry Powder Inhaler: Euler Lagrangian prediction and validation. Med. Eng. Phys. 2017, 42, 35–47. [Google Scholar] [CrossRef]
- Pandal-Blanco, A.; Barrio-Perotti, R.; Agujetas-Ortiz, R.; Fernández-Tena, A. Implementation of a specific boundary condition for a simplified symmetric single-path CFD lung model with OpenFOAM. Biomech. Model. Mechanobiol. 2019, 18, 1759–1771. [Google Scholar] [CrossRef]
- Kolanjiyil, A.V.; Kleinstreuer, C. Modeling Airflow and Particle Deposition in a Human Acinar Region. Comput. Math. Methods Med. 2019, 2019, 5952941. [Google Scholar] [CrossRef]
- Longest, P.W.; Vinchurkar, S. Validating CFD predictions of respiratory aerosol deposition: Effects of upstream transition and turbulence. J. Biomech. 2007, 40, 305–316. [Google Scholar] [CrossRef]
- Jiaa, L.; Zhang, L.; Yu, S. Deposition of non-spherical microparticles in the human upper respiratory tract. Particuology 2018, 36, 185–189. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z.; Li, Z. Modeling airflow and particle transport/deposition in pulmonary airways. Respir. Physiol. Neurobiol. 2008, 163, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Vinchurkar, S.; Longest, P.W. Evaluation of hexahedral, prismatic and hybrid mesh styles for simulating respiratory aerosol dynamics. Comput. Fluids 2008, 37, 317–331. [Google Scholar] [CrossRef]
- Longest, P.W.; Oldham, M.J. Numerical and experimental deposition of fine respiratory aerosols: Development of a two-phase drift flux model with near-wall velocity corrections. J. Aerosol Sci. 2008, 39, 48–70. [Google Scholar] [CrossRef]
- Longest, P.W.; Vinchurkar, S. Effects of mesh style and grid convergence on particle deposition in bifurcating airway models with comparisons to experimental data. Med. Eng. Phys. 2007, 29, 350–366. [Google Scholar] [CrossRef]
- Lin, C.L.; Tawhai, M.H.; McLennan, G.; Hoffman, E.A. Characteristics of the turbulent laryngeal jet and its effect on airflow in the human intra-thoracic airways. Respir. Physiol. Neurobiol. 2007, 157, 295–309. [Google Scholar] [CrossRef]
- Koullapis, P.; Kassinos, S.C.; Muela, J.; Perez-Segarra, C.; Rigola, J.; Lehmkuhl, O.; Cui, Y.; Sommerfeld, M.; Elcner, J.; Jicha, M.; et al. Regional aerosol deposition in the human airways: The SimInhale benchmark case and a critical assessment of in silico methods. Eur. J. Pharm. Sci. 2018, 113, 77–94. [Google Scholar] [CrossRef]
- Ghahramani, E.; Abouali, O.; Emdad, H.; Ahmadi, G. Numerical analysis of stochastic dispersion of micro-particles in turbulent flows in a realistic model of human nasal/upper airway. J. Aerosol Sci. 2014, 67, 188–206. [Google Scholar] [CrossRef]
- Dolovich, M.B.; Kuttler, A.; Dimke, T.J.; Usmani, O.S. Biophysical model to predict lung delivery from a dual bronchodilator dry-powder inhaler. Int. J. Pharm. X 2019, 1, 100018. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C. Laminar-to-turbulent fluid-nanoparticle dynamics simulations: Model comparisons and nanoparticle-deposition applications. Int. J. Numer. Method. Biomed. Eng. 2011, 27, 1930–1950. [Google Scholar] [CrossRef]
- Dehbi, A. A CFD model for particle dispersion in turbulent boundary layer flows. Nucl. Eng. Des. 2008, 238, 707–715. [Google Scholar] [CrossRef]
- Kolanjiyil, A.V.; Kleinstreuer, C. Computationally efficient analysis of particle transport and deposition in a human whole-lung-airway model. Part I: Theory and model validation. Comput. Biol. Med. 2016, 79, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Koullapis, P.G.; Hofemeier, P.; Sznitman, J.; Kassinos, S.C. An efficient computational fluid-particle dynamics method to predict deposition in a simplified approximation of the deep lung. Eur. J. Pharm. Sci. 2018, 113, 132–144. [Google Scholar] [CrossRef] [PubMed]
- Li, Z. Particle Deposition in Oral-tracheal Airway Models with Very Low Inhalation Profiles. J. Bionic Eng. 2012, 9, 252–261. [Google Scholar] [CrossRef]
- Ma, B.; Lutchen, K.R. CFD simulation of aerosol deposition in an anatomically based human large-medium airway model. Ann. Biomed. Eng. 2009, 37, 271–285. [Google Scholar] [CrossRef] [PubMed]
- Darquenne, C.; Prisk, G.K. Aerosol Deposition in the Human Respiratory Tract Breathing Air and 80:20 Heliox. J. Aerosol Med. 2004, 17, 278–285. [Google Scholar] [CrossRef] [PubMed]
- Cilfone, N.A.; Pienaar, E.; Thurber, G.M.; Kirschner, D.E.; Linderman, J.J. Systems Pharmacology Approach Toward the Design of Inhaled Formulations of Rifampicin and Isoniazid for Treatment of Tuberculosis. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 193–203. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Chen, X.; Zhong, W.; Zhou, X.; Jin, B.; Sun, B. CFD–DEM simulation of particle transport and deposition in pulmonary airway. Powder Technol. 2012, 228, 309–318. [Google Scholar] [CrossRef]
- Islam, M.S.; Paul, G.; Ong, H.X.; Young, P.M.; Gu, Y.T.; Saha, S.C. A Review of Respiratory Anatomical Development, Air Flow Characterization and Particle Deposition. Int. J. Environ. Res. Public Health 2020, 17, 380. [Google Scholar] [CrossRef]
- Feng, Y.; Kleinstreuer, C. Micron-particle transport, interactions and deposition in triple lung-airway bifurcations using a novel modeling approach. J. Aerosol Sci. 2014, 71, 1–15. [Google Scholar] [CrossRef]
- Longest, P.W.; Tian, G.; Walenga, R.L.; Hindle, M. Comparing MDI and DPI aerosol deposition using in vitro experiments and a new stochastic individual path (SIP) model of the conducting airways. Pharm. Res. 2012, 29, 1670–1688. [Google Scholar] [CrossRef] [PubMed]
- Tian, G.; Longest, P.W.; Su, G.; Hindle, M. Characterization of respiratory drug delivery with enhanced condensational growth using an individual path model of the entire tracheobronchial airways. Ann. Biomed. Eng. 2011, 39, 1136–1153. [Google Scholar] [CrossRef]
- Koullapis, P.G.; Kassinos, S.C.; Bivolarova, M.P.; Melikov, A.K. Particle deposition in a realistic geometry of the human conducting airways: Effects of inlet velocity profile, inhalation flowrate and electrostatic charge. J. Biomech. 2016, 49, 2201–2212. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z. Laminar-to-turbulent fluid-particle flows in a human airway model. Int. J. Multiph. Flow 2003, 29, 271–289. [Google Scholar] [CrossRef]
- Jayaraju, S.T.; Brouns, M.; Verbanck, S.; Lacor, C. Fluid flow and particle deposition analysis in a realistic extrathoracic airway model using unstructured grids. J. Aerosol Sci. 2007, 38, 494–508. [Google Scholar] [CrossRef]
- Koullapis, P.G.; Nicolaou, L.; Kassinos, S.C. In silico assessment of mouth-throat effects on regional deposition in the upper tracheobronchial airways. J. Aerosol Sci. 2018, 117, 164–188. [Google Scholar] [CrossRef]
- Flynn, S.J.; Tong, Z.B.; Yang, R.Y.; Kamiya, H.; Yu, A.B.; Chan, H.K. Computational fluid dynamics (CFD) investigation of the gas–solid flow and performance of Andersen cascade impactor. Powder Technol. 2015, 285, 128–137. [Google Scholar] [CrossRef]
- Cheng, K.H.; Cheng, Y.S.; Yeh, H.C.; Swift, D.L. Measurements of Airway Dimensions and Calculation of Mass Transfer Characteristics of the Human Oral Passage. J. Biomech. Eng. 1997, 119, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.S.; Zhou, Y.; Chen, B.T. Particle Deposition in a Cast of Human Oral Airways. Aerosol Sci. Technol. 1999, 31, 286–300. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C.; Kim, C.S. Micro-particle transport and deposition in a human oral airway model. Aerosol Sci. 2002, 33, 1635–1652. [Google Scholar] [CrossRef]
- Cui, X.G.; Gutheil, E. Large eddy simulation of the unsteady flow-field in an idealized human mouth-throat configuration. J. Biomech. 2011, 44, 2768–2774. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Wu, W.; Gutheil, E. Numerical study of the airflow structures in an idealized mouth-throat under light and heavy breathing intensities using large eddy simulation. Respir. Physiol. Neurobiol. 2018, 248, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Gutheil, E. Three-dimensional unsteady large eddy simulation of the vortex structures and the mono-disperse particle dispersion in the idealized human upper respiratory system. J. Aerosol Sci. 2017, 114, 195–208. [Google Scholar] [CrossRef]
- Cui, X.; Gutheil, E. Large eddy simulation of the flow pattern in an idealized mouth-throat under unsteady inspiration flow conditions. Respir. Physiol. Neurobiol. 2018, 252–253, 38–46. [Google Scholar] [CrossRef]
- Rissler, J.; Gudmundsson, A.; Nicklasson, H.; Swietlicki, E.; Wollmer, P.; Löndahl, J. Deposition efficiency of inhaled particles (15–5000 nm) related to breathing pattern and lung function: An experimental study in healthy children and adults. Part. Fibre Toxicol. 2017, 14, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Park, S.S.; Wexler, A.S. Particle deposition in the pulmonary region of the human lung: Multiple breath aerosol transport and deposition. J. Aerosol Sci. 2007, 38, 509–519. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C. Airflow structures and nano-particle deposition in a human upper airway model. J. Comput. Phys. 2004, 198, 178–210. [Google Scholar] [CrossRef]
- Kadota, K.; Imanaka, A.; Shimazaki, M.; Takemiya, T.; Kubo, K.; Uchiyama, H.; Tozuka, Y. Effects of inhalation procedure on particle behavior and deposition in the airways analyzed by numerical simulation. J. Taiwan Inst. Chem. Eng. 2018, 90, 44–50. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Shi, H.; Zhe, Z. Computational Analyses of a Pressurized Metered Dose Inhaler and a New Drug–Aerosol Targeting Methodology. J. Aerosol Med. 2007, 20, 294–309. [Google Scholar] [CrossRef]
- Kenjereš, S.; Tjin, J.L. Numerical simulations of targeted delivery of magnetic drug aerosols in the human upper and central respiratory system: A validation study. R. Soc. Open Sci. 2017, 4, 170873. [Google Scholar] [CrossRef]
- Shrestha, K.; Walenga, R.; Xi, J.; Shang, Y.; Salati, H.; Bartley, J.; White, D. Clinical and Biomedical Engineering in the Human Nose: CFD Applications for Drug Delivery. Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Si, X.A.; Xi, J.; Kim, J.W.; Zhou, Y.; Zhong, H. Modeling of release position and ventilation effects on olfactory aerosol drug delivery. Respir. Physiol. Neurobiol. 2013, 186, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Yuan, J.E.; Si, X.A. Simulation study of electric-guided delivery of0.4 mm monodisperse and polydisperse aerosols to the ostiomeatal complex. Comput. Biol. Med. 2016, 72, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Rygg, A.; Hindle, M.; Longest, P.W. Absorption and Clearance of Pharmaceutical Aerosols in the Human Nose: Effects of Nasal Spray Suspension Particle Size and Properties. Pharm. Res. 2016, 33, 909–921. [Google Scholar] [CrossRef] [PubMed]
- Balcerzak, J.; Mucha, M. Analyais of model drug release kinetics from complex matrices of polylactide-chitosan. Prog. Chem. Appl. Chitin Deriv. 2010, 15, 117–126. [Google Scholar]
- Hattori, Y.; Haruna, Y.; Otsuka, M. Dissolution process analysis using model-free Noyes-Whitney integral equation. Colloids Surf. B Biointerfaces 2013, 102, 227–231. [Google Scholar] [CrossRef]
- Kose-Ozkan, C.; Savaser, A.; Tas, C.; Ozkan, Y. The Development and In Vitro Evaluation of Sustained Release Tablet Formulations of Benzydamine Hydrochloride and its Determination. Comb. Chem. High Throughput Screen. 2010, 13, 683–689. [Google Scholar] [CrossRef]
- Wu, X.; Liu, F.; Li, J.; Chen, X.; Chen, S. Modeling and simulation of neodymium oxide dissolution in molten fluorides. Trans. Nonferrous Met. Soc. China 2022, 32, 2414–2427. [Google Scholar] [CrossRef]
- Siepmann, J.; Peppas, N.A. Higuchi equation: Derivation, applications, use and misuse. Int. J. Pharm. 2011, 418, 6–12. [Google Scholar] [CrossRef]
- Higuchi, T.; York, N. Mechanism of sustained-action medication. Theoretical analysis of rate of release of solid drugs dispersed in solid matrices. J. Pharm. Sci. 1963, 52, 1145–1149. [Google Scholar] [CrossRef]
- Ramteke, K.H. Mathematical Models of Drug Dissolution: A Review. Sch. Acad. J. Pharm. 2014, 3, 388–396. [Google Scholar]
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Menshutina, N.V.; Kolnoochenko, A.V.; Lebedev, E.A. Cellular automata in chemistry and chemical engineering. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 87–108. [Google Scholar] [CrossRef] [PubMed]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Liu, W.; Wu, C.Y. Modelling Complex Particle–Fluid Flow with a Discrete Element Method Coupled with Lattice Boltzmann Methods (DEM-LBM). ChemEngineering 2020, 4, 55. [Google Scholar] [CrossRef]
- Fu, S.C.; Leung, W.W.F.; So, R.M.C. A Lattice Boltzmann and Immersed Boundary Scheme for Model Blood Flow in Constricted Pipes: Part 1—Steady Flow. Commun. Comput. Phys. 2013, 14, 126–152. [Google Scholar] [CrossRef]
- Ouared, R.; Chopard, B. Lattice Boltzmann Simulations of Blood Flow: Non-Newtonian Rheology and Clotting Processes. J. Stat. Phys. 2005, 121, 209–221. [Google Scholar] [CrossRef]
- Roberts, D.J.; Hall, R.I. Drug absorption, distribution, metabolism and excretion considerations in critically ill adults. Expert. Opin. Drug Metab. Toxicol. 2013, 9, 1067–1084. [Google Scholar] [CrossRef]
- Gopinath, A.; Wilson, M. Factors affecting drug absorption and distribution. Anaesth. Intensive Care Med. 2020, 21, 223–228. [Google Scholar] [CrossRef]
- Sarangapani, R.; Teeguarden, J.G.; Clewell, H.J.; Andersen, M.E. Physiologically based pharmacokinetic modeling of Styrene and Styrene Oxide Respiratory-Tract dosimetry in rodents and humans. Inhal. Toxicol. 2002, 14, 789–834. [Google Scholar] [CrossRef]
- Byers, J.P.; Sarver, J.G. Pharmacokinetic Modeling; Elsevier Inc.: Amsterdam, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Soulele, K.; Macheras, P.; Karalis, V. On the pharmacokinetics of two inhaled budesonide/formoterol combinations in asthma patients using modeling approaches. Pulm. Pharmacol. Ther. 2018, 48, 168–178. [Google Scholar] [CrossRef]
- Bäckman, P.; Cabal, A.; Clark, A.; Ehrhardt, C.; Forbes, B.; Hastedt, J.; Hickey, A.; Hochhaus, G.; Jiang, W.; Kassinos, S.; et al. iBCS: 2. Mechanistic Modeling of Pulmonary Availability of Inhaled Drugs versus Critical Product Attributes. Mol. Pharm. 2022, 19, 2040–2047. [Google Scholar] [CrossRef]
- Muria, M.D.; Lamberti, G.; Titomanlio, G. Physiologically based pharmacokinetics: A simple, all purpose model. Ind. Eng. Chem. Res. 2010, 49, 2969–2978. [Google Scholar] [CrossRef]
- Bäckman, P.; Arora, S.; Couet, W.; Forbes, B.; Kruijf, W.; Paudel, A. Advances in experimental and mechanistic computational models to understand pulmonary exposure to inhaled drugs. Eur. J. Pharm. Sci. 2018, 113, 41–52. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).