A Flexible and General-Purpose Platform for Heterogeneous Computing

Abstract

In the big data era, processing large amounts of data imposes several challenges, mainly in terms of performance. Complex operations in data science, such as deep learning, large-scale simulations, and visualization applications, can consume a significant amount of computing time. Heterogeneous computing is an attractive alternative for algorithm acceleration, using not one but several different kinds of computing devices (CPUs, GPUs, or FPGAs) simultaneously. Accelerating an algorithm for a specific device under a specific framework, i.e., CUDA/GPU, provides a solution with the highest possible performance at the cost of a loss in generality and requires an experienced programmer. On the contrary, heterogeneous computing allows one to hide the details pertaining to the simultaneous use of different technologies in order to accelerate computation. However, effective heterogeneous computing implementation still requires mastering the underlying design flow. Aiming to fill this gap, in this paper we present a heterogeneous computing platform (HCP). Regarding its main features, this platform allows non-experts in heterogeneous computing to deploy, run, and evaluate high-computational-demand algorithms following a semi-automatic design flow. Given the implementation of an algorithm in C with minimal format requirements, the platform automatically generates the parallel code using a code analyzer, which is adapted to target a set of available computing devices. Thus, while an experienced heterogeneous computing programmer is not required, the process can run over the available computing devices on the platform as it is not an ad hoc solution for a specific computing device. The proposed HCP relies on the OpenCL specification for interoperability and generality. The platform was validated and evaluated in terms of generality and efficiency through a set of experiments using the algorithms of the Polybench/C suite (version 3.2) as the input. Different configurations for the platform were used, considering CPUs only, GPUs only, and a combination of both. The results revealed that the proposed HCP was able to achieve accelerations of up to 270× for specific classes of algorithms, i.e., parallel-friendly algorithms, while its use required almost no expertise in either OpenCL or heterogeneous computing from the programmer/end-user.

1. Introduction

The amount of data generated in the world has increased exponentially in recent decades [1], leading to the big data era [2]. This has also increased the need to process such data and obtain useful information in a timely manner, which has created a higher demand for computational power and associated tools. The training of deep learning models [3] or large-scale simulations such as flood simulations for real-time disaster prevention and mitigation responses [4] are examples of practical use cases for high-performance computing. However, the existing physical barriers have limited the enhancement of transistors in processors and, hence, computing power. Because of this, since the beginning of the 2000s, alternative techniques and methods have been used to improve performance in the execution of algorithms [5].

Most parallel computing approaches optimize implementation for a single device using a specific implementation framework: for example, Python/HLS for FPGAs [6], Python/CUDA for GPUs [7], or C/HLS for ASICs/FPGAs [8,9]. Ad hoc solutions do not allow changes to the originally defined computing architecture to support algorithms other than those for which they were created. The adaptation of an existing solution to execute other algorithms requires internal changes in the coding or drastic changes that even require modifications to the programming logic. Thus, highly optimized solutions present the following disadvantages: the parallel solution cannot be reused, and they demand a programmer who is experienced in the underlying implementation frameworks.

Heterogeneous computing is an approach to high-performance computing and an attractive alternative for executing computationally demanding algorithms. The acceleration capacity arises because, in heterogeneous computing, the tasks in the algorithms are distributed in parallel over multiple devices, such as central processing units (CPUs), graphics processing units (GPUs), and field-programmable gate arrays (FPGAs), taking advantage of their different computing capabilities. All of these devices are used simultaneously. This could result in a more flexible computation approach than developing a solution for a specific device using a custom design flow, as presented in [6,7,8,9]; the main advantage of heterogeneous computing lies in its flexibility and generality, possibly at the cost of performance.

However, in heterogeneous computing, there are several problems associated with the implementation and parallel deployment of algorithms using various computational devices simultaneously: for example, the proper partitioning of processing tasks in the algorithm, the coordination of all the computing devices being used, and the manual management of communication between them [10]. Likewise, another challenge is to correctly assign the parallel tasks for the different types of devices used, which have different hardware and software components [11]. Furthermore, the programmer/end-user must demonstrate knowledge and a degree of mastery regarding programming tools for heterogeneous computing, the most popular being the OpenCL framework.

From the point of view of the programmer, who aims to implement an algorithm in parallel, taking advantage of a heterogeneous platform that makes effective use of different available computing resources (CPUs, GPUs, and FPGAs), the abovementioned issues could slow down the adoption of truly heterogeneous computing.

In this paper, a computing platform is presented with the aim of minimizing the complexity of implementing algorithms under the heterogeneous computing model. The proposed platform is general in regards to the types of algorithms that it can execute as well as the types and numbers of computing devices that can be used. It is also flexible, enabling new computing devices to be added or changed quickly and easily without requiring any algorithmic alterations by the end-user. The flexibility and generality of the proposed platform are the key features that allow solutions to be scaled. These properties also allow non-specialists to implement computationally demanding algorithms faster. We believe that such a platform could promote the use of and increase interest in heterogeneous computing as a potential alternative to parallel computing.

The platform for heterogeneous computing presented in this paper is based on the OpenCL framework, which is the most popular framework for heterogeneous computing development. The use of OpenCL makes our proposal general-purpose without compromising on performance. We would like to stress that OpenCL is a framework that allows one to execute code across heterogeneous platforms (CPUs, GPUs, DSPs, FPGAs, processors, and hardware accelerators). The proposed platform was validated and evaluated using the Polybench/C suite (version 3.2), a benchmark suite of 30 numerical computations representative of various application domains, such as linear algebra, image processing, physics simulations, dynamic programming, and statistics. This benchmark is generally used in parallel computing applications, and it was used in this work to show the generality of the proposed platform. The experiments and obtained results showed that our platform is viable for practical applications, demonstrating accelerations of up to 270× in most cases. The resources associated with the heterogeneous computing platform proposed herein are publicly available [12], particularly the user manual and source code.

Our solution could allow the faster development of high-performance solutions and still serve as a proof of concept for computationally demanding algorithms in order to identify further optimizations that could be translated into ad hoc implementations for custom devices and specialized frameworks if required by the end application.

The rest of this paper is organized as follows. Section 2 presents the work related to this project. Section 3 describes the platform, its structure, and how it addressed certain issues to achieve flexibility and generality. Section 4 describes the experiments carried out to validate the correct functioning of the platform and the results obtained. Finally, Section 5 concludes this work.

2. Related Work

Several issues are associated with the development of platforms for heterogeneous computing. On the one hand, mapping an algorithm to a custom hardware platform or, conversely, modifying an existing platform to meet the requirements of a given algorithm is highly complex. This situation has contributed to a paucity of interest in heterogeneous computing, despite its advantages. The literature provides solutions addressing these problems, though only partially.

With libWater, the authors of [13] aimed at simplifying the complexity of algorithm implementation for heterogeneous computing. This library abstracts the coding process in heterogeneous computing using high-level functions for tasks such as the management of the various devices being applied in a simpler manner than if using the OpenCL or CUDA frameworks. The approach of PACXX [14], Hydra [15], and LogFit [16] is also to simplify the implementation process using custom high-level functions, but these solutions also include mechanisms to automate the task distribution among the underlying computing devices. Thus, the coding complexity for the programmer is considerably reduced. However, these solutions still assume that the user has a deep understanding of parallel computing, because tasks such as the identification of parallel parts in the source code, the  coordination of execution among all the involved devices, and memory management are manually implemented by the programmer. Flexibility is also not achieved by the abovementioned solutions, as only certain devices are supported (CPU + GPU).

The tools H${}^2$TA [17] and FlexTensor [18] were recently proposed to simplify the complexity of both the algorithm design and the management of devices. H${}^2$TA uses OpenCL as the basis to support a wider variety of computing devices and applies high-level functions to address the most complex tasks in the implementation process. However, this solution is focused on a cluster platform, so many aspects of its implementation are closely related to that infrastructure. FlexTensor uses Python as the underlying programming language and employs a mechanism to automatically distribute tasks among the computing devices. However, this solution is oriented towards tensor computing and is not general-purpose.

There is, in the literature, a lot of work about hand-crafted models for heterogeneous computing. Although hand-crafted solutions may perform better, that approach is not portable across architectures. It has been suggested that low-level programming models and expertly optimized libraries should be implemented without being exposed to programmers [19].

3. Proposed Platform Architecture

The flexible and general-purpose heterogeneous computing platform presented in this paper is a tool developed with the objective of addressing the two main problems that limit the use of heterogeneous computing: the lack of generality and flexibility and the reduction in the high complexity associated with the process of coding and executing algorithms that exists in this environment.

To address these issues, this paper presents a platform that fully automates the process of coding and executing algorithms in heterogeneous computing, regardless of the type of algorithm or the number and type of computing devices employed. This frees the user from these tasks and allows the generation of heterogeneous solutions in a fast and semi-automatic manner. The platform allows the execution of algorithms in the context of heterogeneous computing with a level of transparency for the user, who only provides the sequential version of the algorithm and selects the computing devices that will be used by the platform to execute the algorithm. The platform automatically generates the parallel versions of the algorithms as long as they comprise sections that can be executed in parallel.

With the automated generation of parallel codes, the platform allows the exploration and rapid analysis of the possible acceleration of the entered algorithms, offering flexibility in the direct selection of devices that enables one to observe the performance of all cases without requiring any internal change to the input source code.

3.1. Platform Architecture

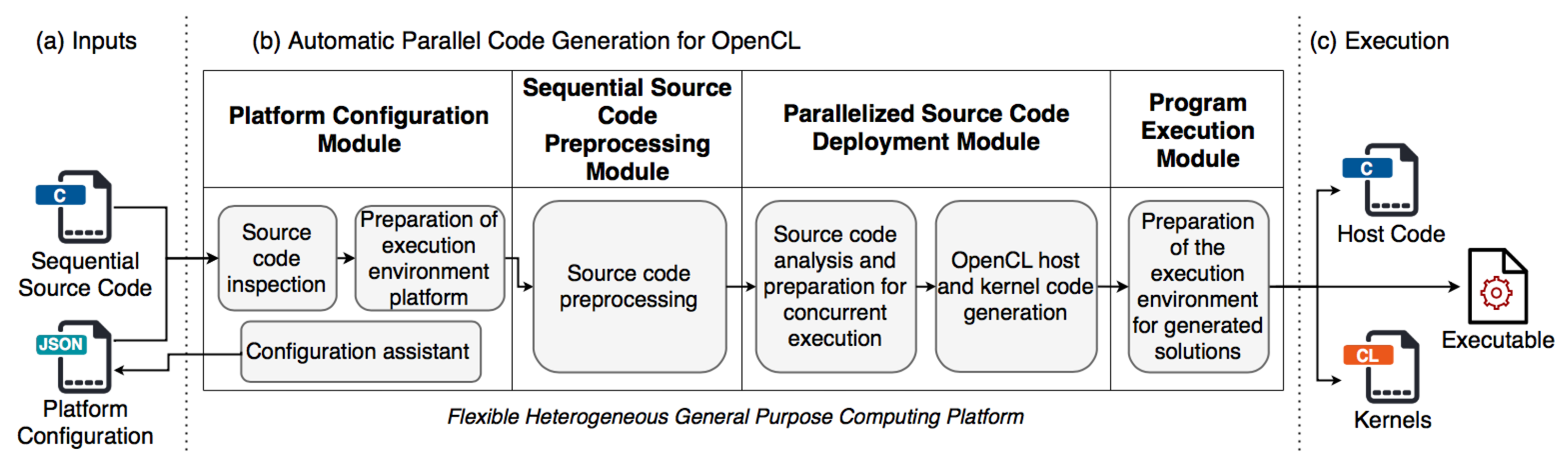
The automatic parallelization process performed internally by the proposed platform is divided into multiple modules. Figure 1 provides an overview of the modules that make up the platform and general descriptions of the tasks they perform internally.

As can be seen, the platform architecture comprises three stages of execution: (a) the reception and preprocessing of the files that will be analyzed by the platform; (b) the transformation and adaptation process of the input source code; and (c) the execution of the resulting codes, i.e., the OpenCL host and kernel codes, by the computer equipment. The following section details the automatic parallelization process performed by the platform in each of its modules.

3.2. Platform Configuration Module

This is the module in charge of preparing the platform execution environment. This module verifies the sequential source code provided by the user, checking that it is correct code written in the C programming language that can be compiled and executed correctly for its subsequent analysis on the platform.

3.2.1. Preprocessing Module

This is the module in charge of preparing the sequential source code for its subsequent analysis in the algorithm deployment module. Figure 2 presents the preprocessing module. This module delimits the sequential code sections with parallel characteristics and inspects if the sections are suitable for parallel execution with OpenCL. This process involves searching section codes for instructions or functions that cause problems in a parallel environment with OpenCL. The inspection is performed by searching for functions in the analyzed code section and checking that they are supported by the OpenCL specification (e.g., mathematical functions). User-defined functions can only be used if they do not cause problems in a heterogeneous environment. In cases where the instructions of a possibly parallel code section compromise the parallel execution of the algorithm, they are marked as non-parallelizable and are not taken into account in further analyses.

The correct delimitation of the parallel sections prevents the generated solutions from presenting compilation and/or execution errors, which may cause erroneous execution results.

3.2.2. Algorithm Deployment Module

Figure 3 shows an overview of the algorithm deployment module. This module is in charge of transforming the sequential code entered into a parallel version. The transformation process is performed in multiple stages: first, an internal analysis is performed to validate if the algorithm can be executed simultaneously without causing problems in the execution of the algorithm in parallel; next, its parallel transformation is performed.

Polyhedral Parallel Code Generation (PPCG)

PPCG [20] is a source-to-source compiler that enables parallel execution of sequential codes written in the C programming language for architectures composed of multicore CPUs and GPUs. This tool allows the acceleration of algorithms based on the analysis of loops using the polyhedral method for the automatic generation of Kernel, which can be from CUDA or OpenCL. PPCG implements a multilevel tiling strategy fitted to the levels of parallelism of accelerators; the approach decouples multilevel parallelization from locality optimization, allowing to select the block and thread count independently from the array blocks allocated to on-chip shared memory and registers. Also, the imperfect loop nests may be broken down into multiple GPU kernels. Affine partitioning heuristics and code generation algorithms for locality enhancement specific to the registers and shared memory are used to improve the performance.

Modifications to the PPCG Compiler on the Platform

On our platform, the PPCG compiler is used internally for the transformation of the processed sequential code to its parallel version with OpenCL. For the integration of PPCG into the platform, it was necessary to make multiple internal changes to the compiler since PPCG only generates parallel codes for a single computing device, either a CPU or GPU, which cannot be determined by the user but is decided by the tool itself based on availability. Since the platform seeks flexibility in the use of algorithms, an internal modification was made to PPCG so that the compiler generated host codes to be executed on a variable set of computing devices.

Support for the simultaneous execution of the parallel sections on multiple computing devices was added to the host codes. To enable this feature, an analysis is automatically performed to determine whether or not a parallel section of the source code can be executed on multiple computing devices. Two rules must be met to confirm that a parallel section is safe to be executed simultaneously. First, the operations must not modify values outside the range of the array that corresponds to them in the execution stage. Second, they must not alter other variables that other devices may require. If the necessary rules are not met, the execution continues normally in parallel on each computing device, with each having to wait for the completion of its predecessor’s work to proceed.

Because of these features, a set of modifications were made to the PPCG compiler. First, we modified how the compiler configured and prepared the OpenCL environment. Second, we modified how the device configuration instructions were ordered in OpenCL for the host code. Third, the memory transfer process and device coordination were changed. In the memory transfer process, each device is allocated a portion of an array, and only that device can make changes to the values within that range. The range is determined to be equal for all computing devices. All these modifications were necessary to enable the more effective multi-device execution of a given algorithm.

Due to the problems introduced by the simultaneous execution, an internal platform analyzer was included in the kernel writing process. This tool analyzes the code sections involving loops that are suitable for simultaneous execution. This is achieved using PET [21], a library that provides a representation of the iterations on the form of a polyhedral model, revealing the relationships of the analyzed for cycles. This representation is used for task distribution, since it allows one to observe the operations performed within the for cycles that will be parallelized.

3.2.3. Algorithm Execution Module

This module is in charge of executing the resulting host and kernel codes in the computer equipment. The module allows execution monitoring, revealing in real time the performance of the computing devices. The data obtained from monitoring can be displayed on the console or stored in the secondary memory. Figure 4 shows the tasks performed by the Algorithm Execution Module.

The compilation of the resulting codes is carried out using the GCC compiler [22], which includes the files of the host code, the kernels, and the functions defined in its execution. These files make it possible to generate an executable file compatible with the configuration of computing devices defined in the platform and the operating system it is running.

Once the executable is generated, the execution of the program begins. Various execution options are offered, such as execution monitoring, which allows real-time observation of the computing devices’ performance.

3.3. Software Features of the Platform

The platform is written in the C programming language and receives as input sequential source codes written in C. A JSON configuration file is used to describe the computing devices employed. The platform supports all OpenCL-compliant computing devices (version 1.0 and later), and the resulting host and kernel codes can be executed on these computing devices.

4. Experimentation

To validate the capabilities of the platform in the automatic parallelization of sequential algorithms, multiple experiments were performed. These experiments allowed us to validate the generality, flexibility, and feasibility of the platform for heterogeneous computing. The following section describes the experimental methodology used, the specifications of each experiment, and the results obtained.

4.1. Hardware and Software Specifications

The evaluation was carried out using Intel i9-9920X computing equipment, 3.50 GHz, 32 GB DDR4, which is referred to in the following as CPU1. We also used Nvidia Quadro P5000 16 GB and Nvidia GeForce GT 710 2 GB graphics cards, which are referred to as GPU1 and GPU2, respectively. CPU1 used the Ubuntu Linux version 20.04.2.0 LTS with 390.87 server drivers for Linux and the OpenCL 2020.1.395 SDK for Intel CPUs.

In the OpenCL execution environment, two entities were defined, the host processor and the computation devices. In all the experiments performed, the host device was CPU1. Using this device, we executed the platform as well as the generated OpenCL host code; in cases where the CPU was also used as an accelerator, the generated parallel code was also executed on this device.

4.2. Specifications of the Parallelized Algorithms

In all the experiments, the 30 algorithms of the Polybench/C suite (version 3.2) [23] were used for implementation on the proposed platform. This suite comprises a set of algorithms written in the C language that are used to evaluate automatic parallelization capabilities in a heterogeneous environment. It contains the sequential form of each algorithm in a single source code file ready to be parallelized, explicitly delimiting the parallelizable parts. Because one of the main functions of the platform proposed in this work is the automatic identification of the parallelizable sections of a sequential source code, each of the Polybench/C suite algorithms was adapted to have a formatting style similar to a sequential code provided by a user, that is, the explicit definition of the parallelizable sections in the input algorithms as provided in the benchmark was removed.

4.3. Experimental Results

This section describes and analyzes the execution results obtained from the parallel codes automatically generated by the platform during three experiments. In the first experiment, the generality and correct execution of the algorithms was validated by observing the values resulting from their parallel execution. The second experiment validated the ability of the platform to simultaneously execute algorithms in several computing devices, and the third experiment evaluated the performance of the solutions generated by the platform.

4.3.1. Experiment 1: Validation of the Sequential Code Parallelization Capacity

The main objectives of this experiment were to verify the generality property of the platform by evaluating its ability to automatically generate parallel code suitable for OpenCL translation and to assess its flexibility in using different computing devices as defined by the user. We verified that the generated solutions produced the correct execution results.

The experiment comprised several tests that were performed for each algorithm of the Polybench/C suite. Each test involved executing the algorithm in the heterogeneous platform with the standard input sizes defined in the suite. To test the capacity of the platform to use different devices and a combination of these, the execution process considered the following combinations of computing devices for the heterogeneous platform: CPU1, CPU1 + GPU1, and CPU1 + GPU1 + GPU2. The output was stored in a text file. This file was compared to the results obtained from the execution of the sequential version of the algorithm under test. The content similarity percentage was computed using a text parser. The test was evaluated as valid when the results matched completely.

In this experiment, all tests were performed successfully. We observed that the platform generated valid source codes in OpenCL for all Polybench/C algorithms and that these were correctly executed under several combinations of computing devices, producing correct results in all cases. However, in the execution of the algorithms 2 mm, 3 mm, adi, atax, covariance, fdtd-2d, gemver, symm, trmm, and floydwarshall, there was minimal variation in the resulting values after the decimal point, since these were of the floating type. This was due to the difference in the representation of floating numbers between the C language and OpenCL. It should be noted that these variations did not occur in all algorithms that used floating numbers, but were found only in certain cases. Because of this characteristic, and the fact that no algorithm presented significantly modified final values, the tests were considered valid.

From the results obtained in this experiment, we verified that the platform successfully ran all Polybench/C algorithms under different combinations of computing devices and produced correct results.

4.3.2. Experiment 2: Validation of the Simultaneous Use of Computing Devices

The purpose of this experiment was to validate the platform’s ability to generate parallel code in OpenCL that was executed simultaneously on multiple computing devices. This was an important feature of the platform, allowing it to support several devices of different types, as expected in heterogeneous computing. Simultaneous execution is possible only if one ensures that no inconsistencies in the results are generated due to synchronization, memory transfer, or computation problems in the devices. This experiment validated the ability of the platform to find codes in the input suitable for simultaneous execution.

Again, all the algorithms of the Polybench/C suite were parallelized on the platform using the maximum input sizes allowed by the computing devices employed. Two combinations of devices, CPU1 and GPU2, were used in all tests. The algorithms were executed using the platform’s verbose option to display the information of the analyses performed internally by the platform. Using this option, the platform indicated if any section of the code presented a problem that would affect its simultaneous execution. We also used the platform monitor to check the simultaneous use of the devices. For the test to be valid, the algorithm had to be executed on more than one device simultaneously, on at least one part of the algorithm.

The tests performed showed that all the algorithms in the Polybench/C suite were parallelized to make use of multiple computing devices simultaneously for the execution of at least one part of the algorithm. The algorithms that were fully executed simultaneously on the defined computing devices were: 2 mm, 3 mm, doitgen, tdtd-2d, gemm, gemver, gesummv, mvt, syr2k, and syrk. These algorithms had the necessary characteristics to avoid problems during simultaneous execution. The other algorithms contained sections that did not comply with these rules; nevertheless, in their sections that did comply, they achieved simultaneous execution.

The results obtained in the second experiment revealed that the platform made adequate use of the parallelization feature and that all the algorithms in the Polybench/C suite contained at least one section that could be divided between multiple computing devices for simultaneous execution.

4.3.3. Experiment 3: Acceleration Achieved

The purpose of this experiment was to determine the speedup levels achieved when using the platform for execution of an algorithm in a heterogeneous environment. We used the largest possible input sizes for the algorithms according to the limitations of the hardware employed in the tests. The speed up obtained for each case is shown in

Table 1. Acceleration for the algorithms in the Polybench/C suite, for the different configurations of the heterogeneous computing platform (first run).

#	Algorithm	Speedup
		CPU	CPU + GPU1	GPU1
1	2 mm	86.552	54.097	14.926
2	3 mm	76.292	45.774	16.954
3	adi	6.369	7.593	1.103
4	atax	0.428	0.321	0.183
5	bicg	0.649	0.520	0.260
6	cholesky	7.961	1.753	0.914
7	correlation	157.205	94.324	58.961
8	covariance	42.142	25.282	12.645
9	doitgen	0.070	0.035	0.023
10	durbin	0.047	0.047	0.039
11	dynprog	0.992	0.992	0.996
12	fdtd-2d	0.002	0.001	0.001
13	fdtd-apml	0.511	0.511	0.213
14	gemm	116.612	58.322	33.322
15	gemver	0.812	0.558	0.357
16	gesummv	0.485	0.485	0.277
17	gramschidt	12.841	13.517	4.428
18	jacobi-1d	2.814	5.170	2.443
19	jacobi-2d	3.855	4.961	0.985
20	lu	5.942	5.671	2.655
21	ludcmp	26.988	7.871	47.211
22	mvt	1.002	0.858	0.546
23	reg-detect	23.051	4.610	1.720
24	seidel	5.050	3.570	1.726
25	symm	17.717	3.743	0.526
26	syr2k	41.112	32.886	6.091
27	syrk	29.104	21.823	7.275
28	trisolv	0.129	0.159	0.138
29	trmm	0.001	0.002	0.003
30	floydwarshall	0.001	0.002	0.002

.

Figure 5 shows a comparison of all the speedup levels in Table 1 achieved by the algorithms parallelized on the platform if compared to the implementation of the sequential versions (baseline). The runs on CPU1, CPU1 + GPU1, and CPU1 + GPU1 + GPU2 were compared. These combinations allowed us to observe and confirm that speedup is achieved in most of the cases, using any of the three heterogeneous computing platform configuration, and some configurations are more suitable for achieving a better acceleration.

The algorithm with the best speedup was correlation, which obtained an acceleration of 157.20× when running on CPU1 only, 94.32× when using CPU1 + GPU1, and 58.96× when running on a combination of all devices (CPU1 + GPU1 + GPU2). These results indicated that the more available devices, the lower the speedup, since this phenomenon was observed in many algorithms, with CPU1 achieving the shortest execution time. However, we determined that this was not the case, as in the algorithm ludcmp, an acceleration of 47.21× was achieved, which was the highest of all the tests executed using all three computing devices. The speedup increased because this algorithm performed better when run on a GPU; hence, the execution was faster when using both GPUs compared to CPU1 alone. Therefore, the speedup was not completely dependent on the number of available devices, as it was also affected by the devices’ capabilities.

The algorithms dynprog and mvt did not achieve any speedup for two of the three configurations of the heterogeneous computing platform, presenting practically the same execution times. On the other hand, an increase in execution time was observed in the algorithms adi, atax, doitgen, durbin, fdtd-2d, fdtd-ampl, gemver, gesummv, trisolv, trmm, and floydwarshall, whose sequential versions ran faster than the parallel versions. However, this problem arose because of the use of small input sizes due to the memory limitations of GPU2, which meant that the input size could occupy no more than 2 GB of memory. For this reason, a second series of tests was performed wherein GPU2 was excluded and a comparison with GPU1 was added, increasing the input sizes.

A second round of experiments was run, now increasing the input sizes and also using computing devices with more available memory (CPU1 and GPU1). The results obtained are presented in

Table 2. Acceleration for the algorithms in the Polybench/C suite, for the different configurations of the heterogeneous computing platform (second run).

#	Algorithm	Speedup
		CPU	CPU + GPU1	GPU1
1	2 mm	86.552	54.097	144.281
2	3 mm	76.292	45.774	152.575
3	adi	6.369	7.593	10.391
4	atax	0.980	0.952	1.851
5	bicg	0.672	0.597	1.194
6	cholesky	7.961	1.753	9.552
7	correlation	209.248	139.467	278.953
8	covariance	42.142	25.282	42.141
9	doitgen	1.848	1.422	1.848
10	durbin	0.311	0.212	0.350
11	dynprog	0.992	0.992	2.304
12	fdtd-2d	0.002	0.001	0.004
13	fdtd-apml	0.900	0.777	1.425
14	gemm	116.612	58.322	233.223
15	gemver	1.543	1.350	3.324
16	gesummv	0.651	0.732	1.172
17	gramschidt	12.841	13.517	42.790
18	jacobi-1d	2.814	5.170	24.697
19	jacobi-2d	3.855	4.961	8.683
20	lu	5.942	5.671	12.478
21	ludcmp	27.452	7.877	50.977
22	mvt	1.539	1.539	3.498
23	reg-detect	23.051	4.610	2.590
24	seidel	5.116	3.574	17.422
25	symm	17.717	3.743	88.568
26	syr2k	41.112	32.886	54.795
27	syrk	29.104	21.823	43.634
28	trisolv	0.212	0.224	1.009
29	trmm	0.001	0.002	0.024
30	floydwarshall	0.001	0.002	0.065

and graphically shown in Figure 6. In this second test, we observed that most of the parallelized algorithms achieved a high speedup, with more favorable results than in the previous test. The correlation algorithm again presented the highest speedup of 278.95× when using only GPU1. The other algorithms that were previously not accelerated or accelerated only slightly achieved improved speedups in this run. For example, symm presented a speedup of 88.56× when using only GPU1 but was previously slowed down when using all computational devices.

We also observed that the number of decelerated algorithms was significantly reduced, with only durbin, fdtd-2d, trmm, and floydwarshall presenting no acceleration. This was due to the internal structures of these algorithms.

The algorithms atax, bicg, dynprog, fdtd-apml, gesummv, and trisolv were not accelerated when executed on CPU1 and CPU1 + GPU1, but were accelerated when executed only on GPU1. This was due to the execution capabilities of the devices employed; for example, GPU1 had more computational power for the execution of this type of algorithm in parallel than CPU1.

This experiment showed that the platform generated solutions with high speedups for most of the algorithms of the Polybench/C suite; speedups of 50× were achieved in most cases, with 278.95× being the highest result. The speedup was limited by the capabilities of the slowest device employed by the platform; the greater the input size, the greater the speedup achieved. Another factor that influenced the speedup was the structure of the algorithms themselves, some of which did not favor parallelism.

4.4. Comparison with Previous Works

To the best of our knowledge, this is the first platform aiming at achieving generality and flexibility in high-performance heterogeneous computing for non-experts in either specific programming languages or implementation frameworks (CUDA, HLS, VHDL, and Verilog). Thus, we could not conduct a fair quantitative comparison with other works that have used custom devices and implementation frameworks, sacrificing generality for performance. Regardless, a qualitative comparison between our platform and several related works in the literature is shown in

Table 3. Qualitative comparison with previous works.

Ref.	Programming Language (End-User)	Implementation Framework	Devices Used	Algorithms/Application Domain
[6]	Python	HLS C	FPGA	Benchmark (general-purpose)
[7]	Python	Cuda	GPUs	Matrix multiplication
[8]	C/C++	HLS	ASIC, FPGA	Embedded applications benchmark
[9]	C, C++	Multilevel intermediate representation (MLIR)	ASIC, FPGA	ML accelerators
This study	C ANSI	OpenCL	CPU, GPUs	Benchmark (general-purpose)

. This comparison was carried out in terms of the most relevant characteristics that define the implementation of a platform. The programming language used by the programmer is relevant as it provides flexibility and simplicity. The implementation framework is relevant as it allows generality or specificity. The devices supported are crucial to achieving truly heterogeneous computing, taking advantage of available computing resources and allowing the implementer to change (add/remove) the devices as convenient. Finally, the underlying algorithms executed over the devices are relevant as they show the generality and reusability of the computing platform. As indicated by the data in Table 3, our proposal relies on OpenCL to guarantee interoperability and generality and on ANSI C to achieve flexibility and the easy of programming for non-experts. Also, it was tested with representative programs (the Polybench suite) in more than one domain (algebra, statistics, matrix multiplication, etc.).

An implementation using the platform proposed in this work may not achieve more favorable results than one optimized by hand. However, our solution could allow faster development times and still achieve considerable acceleration compared to a sequential solution. Our system also serves as a proof of concept for computationally demanding algorithms in order to identify further optimizations that could be translated to ad hoc implementations using specific devices and frameworks by an experienced implementer, if desired.

4.5. Limitations

Computing power is closer to programmers and users than before. Computing capabilities are now available in several forms, from tiny devices to high-performance computers. However, from the programmer’s point of view or from the user’s perspective, parallel computing could suppose an advantage but also a challenge for mastering a design flow for specific frameworks, such as CUDA, VHDL, and High-Level Synthesis, among others. This is where our proposed platform may help programmers or users to explore speedups in their implementations using the computing devices available as computing engines. However, seeking simplicity and generality in favor of programmers or users, a cost is paid in terms of performance compared to a custom parallel design for specific devices with specific frameworks and design flows. Now, the performance obtained by the proposed heterogeneous platform so far described depends strongly on the algorithm nature and the efficiency of the model for parallel task mapping. But, despite this, the platform provides the user with a framework to test different configurations based on the available computing devices in a simple manner. This capability enables programmers and users to explore speedup opportunities, make possible proof of concept implementations, and invest more effort in obtaining custom designs if needed.

Another limitation of the current platform is that it uses only one model for mapping the parallel tasks, based on the polyhedral method for the automatic generation of Kernel, which can be from CUDA or OpenCL. This critical part deserves a deeper study, and other parallel models that can serve as the engine that generates executable code for effective parallelism could also be explored and incorporated into the platform.

Finally, the platform does not infer its best configuration for achieving the best speedup for a given input algorithm. This is a complex and challenging task that can be further explored. Of course, there is room for improvement in reducing the gap in achieving two main goals: on the one hand, having a significant speedup, and on the other, configuring, at run time, the platform that allows achieving that speedup.

5. Conclusions

This paper presented a flexible, general-purpose, heterogeneous computing platform that addressed existing development complexity issues in heterogeneous computing by fully automating the process of coding and executing algorithms in a heterogeneous environment with OpenCL. The automation capabilities of the platform as well as its non-functional characteristics, such as its generality and flexibility, were validated with three experiments, wherein Polybench/C 3.2 suite algorithms were used as input data on a heterogeneous platform comprising a multicore CPU (Intel i9-9920X) and two GPUs (Nvidia Quadro P5000 and Nvidia GeForce GT 710).

We verified the values resulting from the execution of each algorithm in the experiments and observed that the platform generated solutions that provided correct values in all cases, regardless of the number and/or type of devices used. Therefore, the platform demonstrated flexibility, allowing one to select any available computing device for execution of an algorithm.

The capacity for simultaneous execution across multiple devices is an important characteristic of the platform that was tested using all Polybench/C algorithms. We observed that for all algorithms, the simultaneous execution of at least one section of the algorithm across multiple computing devices was achieved, resulting in considerable accelerations. However, we also found that the acceleration was limited by the slowest device used for the execution.

In general, we observed that the accelerations achieved were high, with an average of 50× and a maximum of 270×. We also observed that the acceleration was dependent on the amount of work performed internally by the algorithms. As some Polybench/C algorithms performed little work with small input sizes, no speedups were achieved when these were implemented in parallel, since their sequential execution was terminated earlier than their parallel versions. However, we observed that after considerably increasing the data input size, the parallel versions outperformed the sequential ones.

We proved that the platform allows the effective exploitation of the advantages of heterogeneous computing, is flexible in terms of the devices used, and has sufficient generality to receive any algorithm for execution. For sequential implementation, the platform generates the executable code and takes advantage of the parallel parts for deployment on the available heterogeneous devices. The platform also offers a high level of usability for the end-user, which allows the quick configuration of devices and the generation of any algorithm in its parallel version. Immediate future work will include an evaluation of the proposed platform in cases where high-computational-complexity algorithms are used, such as homomorphic encryption, deep learning, and large-scale simulations, and in cases that involve more computing devices, such as FPGAs or ASICs.