1. Introduction
Rotated quadratic cone programming (RQCP) problems are convex conic optimization problems [
1,
2,
3,
4,
5,
6] in which we minimize a linear objective function over the intersection of an affine linear manifold with the Cartesian product of rotated quadratic cones, where the
nth-dimensional rotated quadratic cone is defined as
where,
is the set of positive real numbers and
is the Euclidean norm.
Many optimization problems are formulated as RQCPs (see Section 2.3 in [
7] and
Section 4 in [
8], for example, but not limited to the problem of minimizing the harmonic mean of positive affine functions, the problem of maximizing the geometric mean of non-negative affine functions, the logarithmic Tchebychev approximation problem, problems involving fractional quadratic functions, problems with inequalities involving rational powers, problems with inequalities involving
p-norms, and problems involving pairs of quadratic forms (also called minimum-volume covering ellipsoid problems).
It is known that the rotated quadratic cone is converted into the second-order cone under a linear transformation. In fact, the restricted hyperbolic constraint is equivalent to the set of linear and second-order cone constraints: , and . Based on this observation, all earlier work on RQCP problems has converted them to second-order cone programming problems, but while doing this can be easier than developing special-purpose algorithms for solving RQCPs, this approach may not always be the cheapest one in terms of computational cost.
Mathematical optimization together with evolutionary algorithms are today a state-of-the-art methodology in solving hard problems in machine learning and artificial intelligence, see for example [
9,
10,
11]. Going back years in time, the introduction of the interior-point methods (IPMs) during in the 1980s perhaps was one of the most notable developments in the field of mathematical programming since its origination in the 1940s. Karmarker [
12] was the first to propose them for linear programming, where their work generated a stir due to the superiority of their polynomial complexity results over that of the simplex method. It then seemed natural to expand these methods created for linear programming to solve nonlinear programs.
Nesterov and Nemirovskii [
3] laid the groundwork for IPMs to solve convex programming problems, where primal (and dual) IPMs based on the so-called self-concordant barrier functions were taken into consideration. Nesterov and Todd [
4] later presented symmetric primal–dual IPMs for problems over a specific class of cones termed as self-scaled cones, allowing for a symmetric approach to the primal and dual problems.
We point out that Nesterov and Todd’s work [
4] did not take a Jordan algebraic approach, but rather Güler’s work [
13] is credited with being the first to link Jordan algebras and optimization. Güler [
13] noted that the family of self-scaled cones are the same as the family of the so-called symmetric cones for which a thorough classification theory is available [
14]. The characteristics of these algebras act as a key toolkit for the analysis of IPMs for optimization over symmetric cones. Due to their diverse applications, the most important classes of symmetric cone optimization problems are linear programming, second-order cone programming [
7], and semi-definite programming [
15] (see also Part IV in [
16] which gives a thorough presentation of these three classes of optimization problems). Several IPMs have been developed for these classes of conic optimization problems; for example, [
2,
7,
15,
17,
18,
19,
20,
21,
22,
23,
24].
There are two classes of IPMs for solving linear and non-linear convex optimization problems. The first class solely uses dual or primal methods (see, for example, [
25,
26,
27]). The second class is based on primal–dual methods, which were developed by [
23] and [
24] and are more useful and efficient than the first. These methods involve applying Newton’s method to the Karush–Kuhn–Tucker (KKT) system up until a convergence condition is satisfied.
In [
28], the authors have set up the Euclidean Jordan algebra (EJA) associated with the rotated quadratic cone and presented several spectral and algebraic characteristics of this EJA, where the authors have found that the rotated quadratic cone is the cone of squares of some EJAs (confirming that it is a symmetric cone). To our knowledge, no specialized algorithms for RQCPs that make use of the EJA of the underlying rotated quadratic cones. This paper is an attempt to introduce RQCPs as another self-contained paradigm of symmetric cone optimization, where we introduce RQCP as a “self-made” class of optimization problems and develop special purpose primal–dual interior-point algorithms (second class of IPMs) for solving RQCP problems based on the EJA in [
28], which offers a useful set of tools for the analysis of IPMs related to RQCPs.
The so-called commutative class of primal–dual IPMs was designed by Monteiro and Zhang [
29] for semi-definite programming, and by Alizadeh and Goldfarb [
7] for second-order cone programming, and then extended by Schmieta and Alizadeh [
30] for symmetric cone programming. This paper uses the machinery of EJA built in [
28] to carry out an extension of this commutative class to RQCP. We prove polynomial complexities for versions of the short-, semi-long-, and long-step path-following IPMs using NT, HRVW/KSH/M, or dual HRVW/KSH/M directions (equivalent to NT,
, or
directions in semi-definite programming).
This paper is organized as follows: In
Section 2, we calculate the derivatives of the logarithmic barrier function associated with the rotated quadratic cone and prove the corresponding self-concordance property. The formulation of the RQCP problems with the optimality conditions are provided in
Section 3.
Section 4 applies Newton’s method and discusses the commutative direction. The proposed path-following algorithm for RQCP and its complexity are given in
Section 5.
Section 6 shows the efficiency of the proposed algorithm by providing some numerical results. We close this paper with
Section 7, which contains some concluding remarks.
2. The Algebra and the Logarithmic Barrier of the Rotated Quadratic Cone
In
Table 1, we summarize the Jordan algebraic notions associated with the cone
.
In this section, we compute the derivatives of the logarithmic barrier associated with our cone and use them to prove the self-concordance of this barrier. To obtain these results, we do not use concepts outside of the EJA established in [
28] and summarized in
Table 1.
Associated with the cone
, the logarithmic barrier function
is defined as
We provide a proof the following lemma, which is a useful tool in order to prove some fundamental properties of our barrier. The inner product •, inverse
, norm
, and matrices
and
used in Lemma 1 are defined in
Table 1.
Lemma 1. Let having and be a non-zero vector. Then,
- (i)
The gradient . Therefore, .
- (ii)
The Hessian . Therefore, .
- (iii)
The third derivative .
Proof of Lemma 1. For item (i), we have
Item (ii) follows by using item (i) and noting that the Jacobean of
is
and that
For item (iii), note that
It follows that
where we used the fact that
to obtain the last equality. The proof is complete. □
The notion of self-concordance introduced by Nesterov and Nemirovskii [
3] is essential to the existence of polynomial-time interior-point algorithms for convex conic programming problems. We have the following definition.
Definition 1 (Definition 2.1.1 in [
3])
. Let V be a finite-dimensional real vector space, G be an open non-empty convex subset of V, and let f be a , convex mapping from G to . Then, f is called α-self-concordant on G with the parameter if for every and , the following inequality holdsAn α-self-concordant function f on G is called strongly α-self-concordant if f tends to infinity for any sequence approaching a boundary point of G. In the proof of the next theorem, we use the inequalities that
for any
and
residing a Jordan algebra. These two inequalities can be seen by noting that
and
We are now ready to provide a proof for the following theorem.
Theorem 1. The logarithmic barrier function is a 1-strongly self-concordant barrier on .
Proof of Theorem 1. Note that for any sequence approaching the
boundary point,
goes to infinity. Using items (ii) and (iii) in Lemma 1, we have
Thus, the inequality in (
3) holds. Hence, the logarithmic barrier
on
is 1-strongly self-concordant. □
3. Rotated Quadratic Cone Programming
Problem and Duality
In this section, we introduce and define the RQCP problem along with a discussion of the duality theory and the optimality conditions for these problems.
Let
be a real matrix whose
m rows reside in the Euclidean Jordan algebra
, and let
be its transpose. Associated with
A, we define the matrix–vector product “
” as
where
,
is the
ith-row of
A for
, and
H is defined in
Table 1. The operator
is the half-identity matrix defined to map
into
, while the transpose
is defined to map
into
. If
and
, one can easily show that
An RQCP problem in the primal form is the problem
where
is the primal variable,
is the dual variable, and
is the dual slack variable.
Let
and
denote the feasible and strictly feasible primal-dual sets for the pair (P, D), respectively, where
Problem (P) (respectively, Problem (D)) is said to be strictly feasible if (respectively, ). Now, we make two assumptions about the pair (P, D): First, we assume that the matrix A has a full row rank. This assumption is standard and is added for convenience. Second, we assume that the strictly feasible set is non-empty. This assumption guarantees that the strong duality holds for the RQCP problem and suggests that both Problems (P) and (D) have a unique solution.
We give with a proof the following weak duality result.
Lemma 2 (Weak duality). If and , then the duality gap is .
Proof of Theorem 2. Let
and
, then
, and
. Then, using (
5), it follows that
Because
, we have that
Applying the arithmetic inequality to
and
, we obtain
Combining (
6) and (
7), we have
. Taking the square root of both sides and applying the Cauchy–Schwartz inequality, we obtain
The proof is complete. □
It is known that the strong duality property can fail in general conic programming problems, but a slightly weaker property can be shown for them [
3]. Using the Karush–Kuhn–Tucker (KKT) conditions, we provide a proof of the following semi-strong duality result, which provides conditions for such a slightly weaker property to hold in RQCP.
Lemma 3 (Semi-strong duality). Let Problems (P) and (D) be strictly feasible. If Problem (P) is solvable, then so is its dual (D) and their optimal values are equal.
Proof of Theorem 3. Since (P) is strictly feasible and solvable, then there is a solution
to which the KKT conditions can be applied. According to this, there must be Lagrange multiplier vectors
and
such that
satisfies the conditions
It follows that (D) can be solved using
. Let us suppose that
is any feasible solution to the dual problem (D); then,
where the inequality was obtained using weak duality (Lemma 2) and the last equality was obtained using the last equation in (
8). Since
was chosen arbitrarily, the optimal solution to Problem (D) is
and
. The proof is complete. □
The strong duality result in the following lemma can be obtained by applying the duality relations to our problem formulation.
Theorem 2 (Strong duality). Let Problems (P) and (D) be strictly feasible; then, they must also have optimal solutions, say and , respectively, and
As one of the optimality conditions of RQCP, we describe the complementarity condition in the following lemma.
Lemma 4 (Complementarity condition). Let have . Then if and only if .
Proof of Theorem 4. Let
have
. First, we prove the direction from left to right. Assume that
. To show that
, we must show that (see the definition of the Jordan product “∘” used in
Table 1)
If
or
, then
in the first case and
in the second one, indicating that (i), (ii), and (iii) trivially hold. As a result, we need to consider
and
. Then, by taking the square root of both sides in (
7), using the fact that
, and applying the Cauchy–Schwartz inequality, we obtain
Therefore,
if and only if
. This is true if and only if the inequalities in (
9) are satisfied as equalities. This simply holds true if and only if either
or
, in which (i), (ii), and (iii) are trivially held, or
where
.
Note that the first equation in (
10), or equivalently
, implies that
. Using (
10), this can be written as
From (
10), we have that
. Then,
as desired in (i) and (ii). For (iii), using (
10) again, we have
This implies that
, or as desired in (iii).
Now, we prove the direction from right to left. Let us assume that . From (i) and (ii), we have that , or as desired. The proof is complete. □
From the above results, the following corollary is now immediate.
Corollary 1 (Optimality conditions)
. Let us assume that both Problems (P) and (D) are strictly feasible. Then, is an optimal solution to the pair (P, D) if and only if 4. The Newton System and Commutative Directions
In this section, we present the logarithmic barrier problems for the pair (P, D) and the Newton system corresponding to them, as well as a subclass of the MZ family of search directions known as the commutative directions.
The logarithmic barrier problems associated with the pair (P, D) are the problems
where
is a small positive scalar and is typically referred to as the barrier parameter.
The solutions of the pair
can be characterized by the following perturbed KKT optimality conditions.
where
is the identity vector of
as defined in
Table 1, and
is a centering parameter that reduces the barrier term
. For any
, System (
11) has a unique solution, indicated by
, where
is called the
-center for (P) and the pair
is called the
-center for (D). The set of all
-centers that solve the perturbed KKT system (
11) is called the central path of the pair (P, D), and is defined as
Due the assumption that , the central path is well defined. As gets closer to zero, the -central point converges toward an -approximate solution of (P, D).
Now, we reformulate the complementary condition
in (
11), which is a direct consequence of Lemma 28 in [
30].
Lemma 5. Let be such that , and is invertible (i.e., ). Then if and only if .
In order to solve System (
11), we apply Newton’s method to this system and obtain
where
is called the Newton search direction.
In the theory of Jordan algebra, two elements of a Jordan algebra operator commute if they share the same set of eigenvectors. In particular, two vectors
operator commute if
for
, i.e.,
and
. The vectors
and
in System (
12) may not operator commute. We need now to scale the underlying system so that the scaled vectors operator commute. In practice, this scaling is needed to guarantee that we iterate in the interior of the quadratic rotated cone.
Let
be the set of nonsingular elements so that the scaled vectors operator commute, i.e.,
We call the set of directions
arising by choosing
from
the commutative class of directions for RQCP, and call a direction in this class a commutative direction.
As mentioned earlier, the commutative class of primal-dual IPMs was designed by Monteiro and Zhang [
29] for semidefinite programming, and by Alizadeh and Goldfarb [
7] for second-order cone programming, and then extended by Schmieta and Alizadeh [
30] for symmetric cone programming. We concentrate on three prominent choices of
, and each choice leads to a different direction in the commutative class of search directions: First, the choice
is referred to as the HRVW/KSH/M direction, and is equivalent to the XS direction in semidefinite programming (introduced by Helmberg, Rendl, Vanderbei, and Wolkowicz [
31], and Kojima, Shindoh, and Hara [
32] independently, and then rediscovered by Monteiro [
29]). Second, the choice
is referred to as the dual HRVW/KSH/M direction, and is equivalent to the SX direction in semidefinite programming. Third, the choice
is equivalent to the NT direction in semidefinite programming (introduced by Nesterov and Todd [
4]).
Now, associated with
, we make the following change of variables:
Because
(see [
28], Theorem 4.3), System (
12) is equivalent to
where
, and
are given by
Applying block Gaussian elimination to (
13), we obtained the Newton search directions
:
To obtain the search directions
and
for (
12), we apply inverse scaling to
and
as follows:
Finally, we take a step size
so that the new point
is generated in the neighborhood of the central path; see
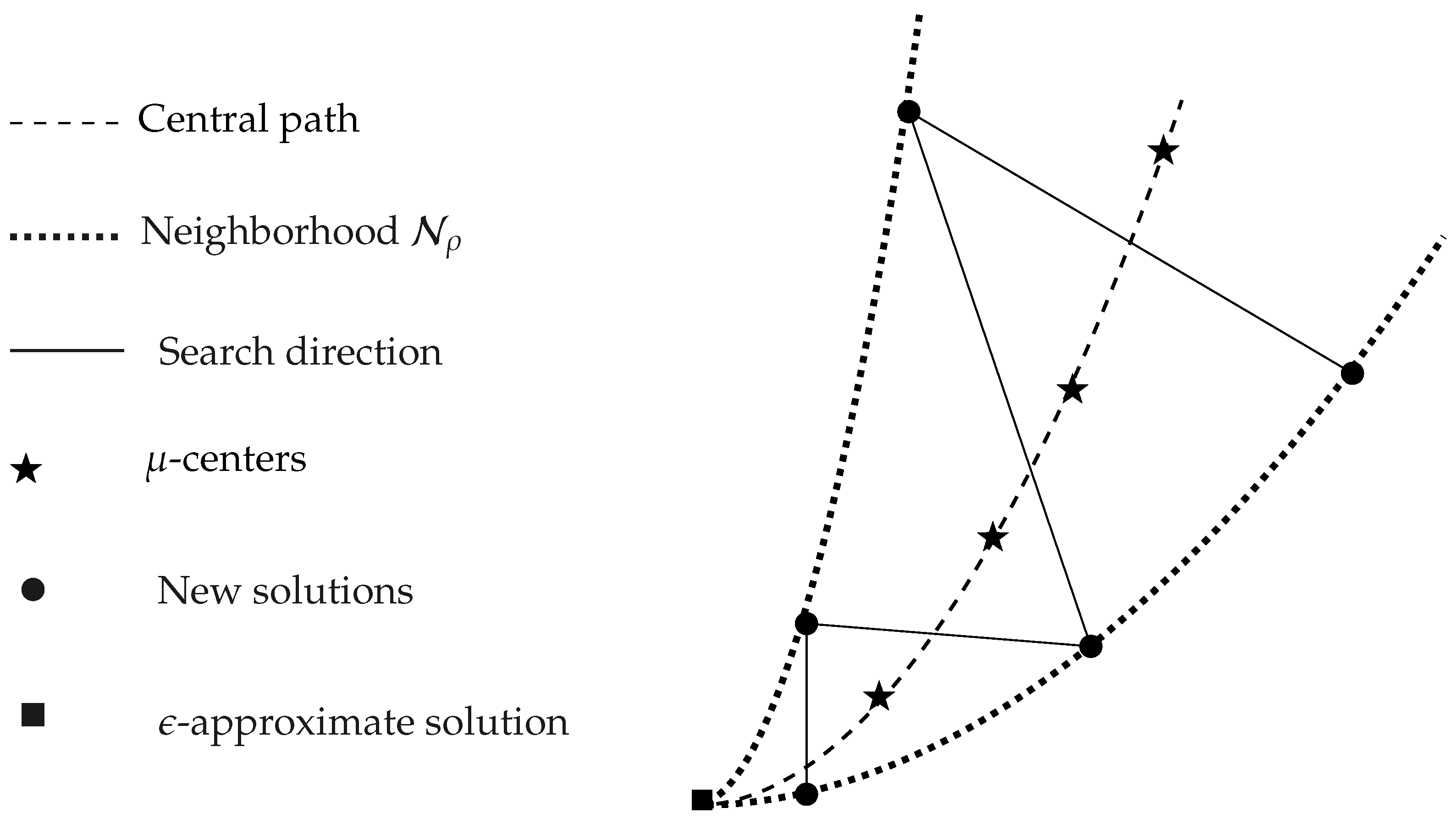
Figure 1.
5. Path-Following Interior-Point Algorithms
Primal–dual path-following IPMs for solving the pair (P, D) are introduced in this section in three different lengths: short, semi-long, and long-step.
The generation of each iteration in the neighborhood of the central path is one of the main issues in the path-following IPMs, and we use proximity measure functions to handle this. With our adherence to the central path, the duality gap sequence will converge, and a bound on the number of iterations needed to obtain the optimal solution of the pair problem (P, D) will be polynomial.
The standard way to classify the proximity measures is to measure the distance to a specific point on the central path
. More specifically, the proximity measures for
are given as
The three different distances in (
14) lead to the following three neighborhoods along the central path:
where
is a constant known as the neighborhood parameter.
By Proposition 21 in [
30], both
and
have the same eigenvalues, and since all neighborhoods
may be described in terms of the eigenvalue of
, one can see that the neighborhoods defined in (
15) are scaling-invariant, i.e.,
where
can be selected as
, or
.
Furthermore, given the eigenvalue characterization of , we can find that , and hence
The performance of the path-following IPMs for RQCP problems greatly depends on the neighborhood of the central path and the centering parameter that we select. These options allow us to divide the path-following IPMs for our problem into three categories: Short, semi-long, and long-step. More specifically:
Selecting as the neighborhood yields the short-step algorithm;
Selecting as the neighborhood yields the semi-long-step algorithm;
Selecting as the neighborhood yields the long-step algorithm.
We indicate that the long-step version of the algorithm seems to outperform the short-step version of the algorithm in practical performance. In
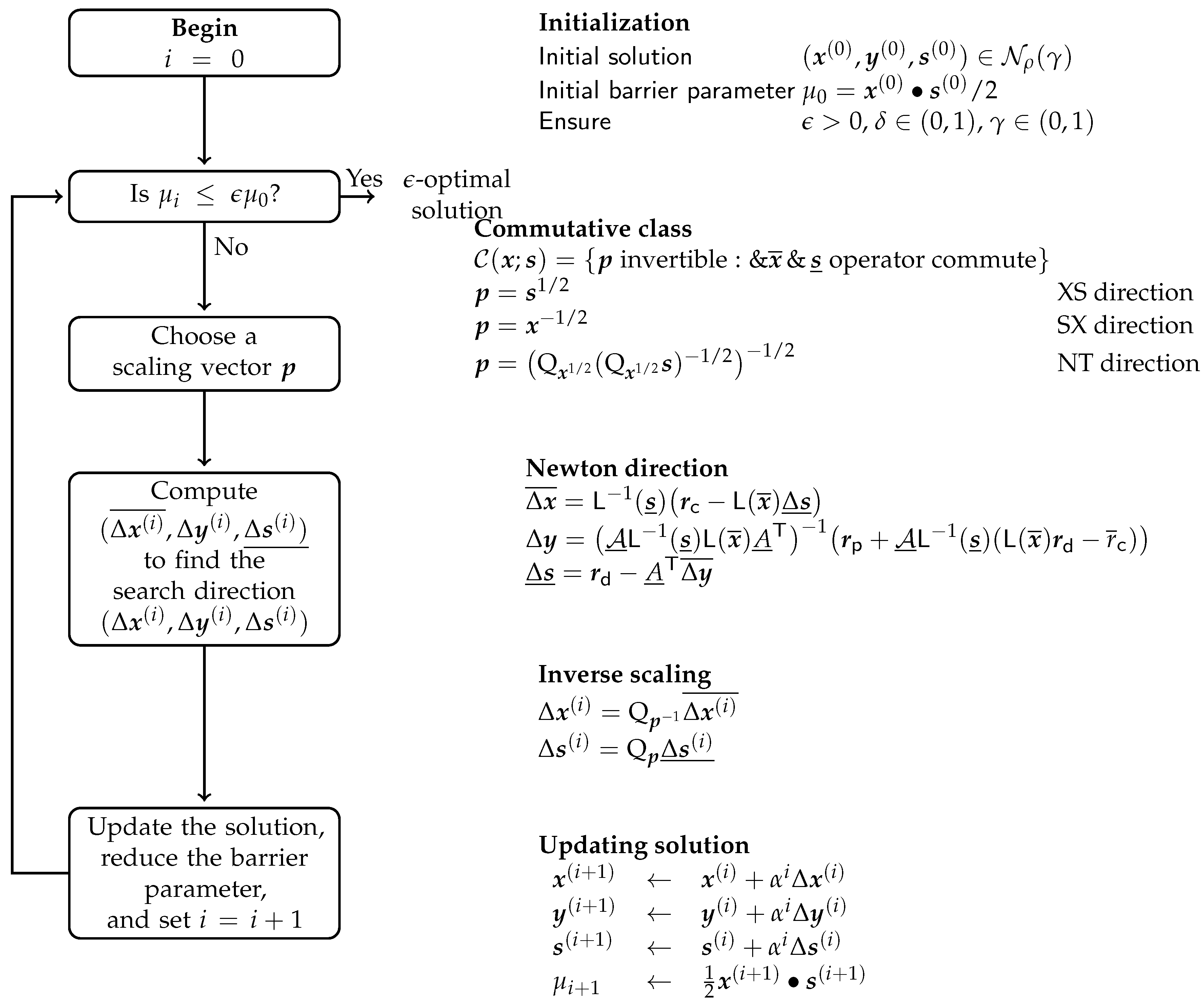
Table 2, we compare some of the categorized versions of this algorithm. The proposed path-following interior-point algorithm for solving the pair of problems (P, D) is described in Algorithm 1 and
Figure 2.
| Algorithm 1: A path-following interior algorithm for solving RQCP problem. |
![Computation 11 00050 i001 Computation 11 00050 i001]() |
The convergence and time complexity for Algorithm 1 is given in the following theorem. This theorem is a consequence of Theorem 1 that we verified in
Section 2 and Theorem 37 in [
30] after taking the rotated quadratic cone
as our underlying symmetric cone.
Theorem 3. If each iteration in Algorithm 1 follows the NT direction, then the short-step algorithm terminates in iterations, and the semi-long and long-step algorithms terminate in iterations. If each iteration in Algorithm 1 follows the HRVW/KSH/M direction or dual HRVW/KSH/M direction, then the short-step algorithm terminates in iterations, the semi-long-step algorithm terminates in iterations, and the long-step algorithm terminates in iterations.
Before closing this section and moving forward to our numerical results below, we indicate that the above analysis can be carried out and extended word-by-word if Problem (P, D) is given in multiple block-setting by using the notations introduced in
Table 1.
6. Numerical Results
In this section, we will assess how well the proposed method performs when implemented to some RQCP problems: The problem of minimizing the harmonic mean of positive affine function, and some randomly generating problems. We also contrast the numerical results of the proposed algorithm for the randomly generated problems with those of the two symmetric cone programming software package systems: CVX [
33] and MOSEK [
34].
We produced our numerical results using MATLAB version R2021a on a PC with an Intel (R) Core (TM) i3-1005G1 processor operating at 1.20 GHz and 4 GB of physical memory. In the first numerical example, we consider a problem in multiple block setting. The dimensions of our test problems are denoted by the letters m and n, and the number of block splittings is denoted by r. “Iter” stands for the typical number of iterations needed to obtain -optimal solutions, while “CPU” stands for the typical CPU time needed to reach an -optimal solution to the underlying problem.
In all of our tests, we use the long-step path-following version of Algorithm 1, and choose the dual HRVW/KSH/M direction (i.e., our scaling vector is
). Furthermore, when the condition of convergence is not satisfied at an iteration step, it will generate a new solution that must be in the neighborhood of the central path. We choose the step size of
that was proposed in [
30].
Example 1 (Minimizing the harmonic mean of affine functions)
. We consider the problem of minimizing the harmonic mean of (positive) affine functions of [7]:We implement this problem for sizes , , and the number of blocks . We generate the coefficients and randomly from a list of numbers uniformly distributed between −1 and 1 for all and . We take the parameters , , and . The initial solutions of are also chosen randomly from a list of uniformly distributed numbers between −1 and 1, while is chosen as the zero vector, and , are all set to take values between 0 and 1. We display the numerical results obtained for this example in Table 3, and visualize them graphically in Figure 3. Example 2 (Randomly generated problems)
. In this example, the coefficients A and b are generated at random from a list of uniformly distributed numbers between −1 and 1. We set and , and choose the parameters , and . The size of the problem is given so that , where m is ranging from 5 to 1000. The initial solutions are chosen as follows: , and . We display our numerical results in Table 4, and visualize them graphically in Figure 4. The results from the CVX and MOSEK solvers are also presented in Table 4 and Figure 4 for comparison purposes. We can see overall that the computational results show that Algorithm 1 performs well in practice. We can see from the numerical results shown in
Table 3 and
Table 4 and represented in
Figure 3 and
Figure 4 that the number of iterations and CPU time required by Algorithm 1 increase as the dimension of the underlying problem increases, indicating that the dimension of the problem and the dimension of rotated quadratic cones have an impact on the number of iterations and the amount of time required by the proposed algorithm. Furthermore, when the randomly generated problems are solved using the CVX and Mosek solvers, we can see that most of the solutions exhibited a slight bias toward Algorithm 1 in terms of both the number of iterations and CPU time. This is most likely because these solvers begin at infeasible points or because the stopping condition of the algorithm used in these solvers differs from that of Algorithm 1.
7. Concluding Remarks
All earlier work on optimization problems over the rotated quadratic cones has formulated these problems as second-order cone programming problems, and while doing this can be easier than developing special-purpose algorithms for solving this class of optimization problems, this approach may not always be the cheapest one in terms of computational cost. In this paper, we have introduced the rotated quadratic cone programming problems as a “self-made” class of optimization problems. We have proved that the barrier function associated with our cone is strongly self-concordant. We have discussed the duality theory associated with these problems, along with the development of the commutative class of search directions, and have developed a primal–dual interior-point algorithm rotated quadratic cone optimization problems based on our own Euclidean Jordan algebra. The efficiency of the proposed algorithm is shown by providing some numerical examples and comparing some of them with results from MOSEK and CVX solvers.
The proposed algorithm is attractive from an algebraic point of view. Most of this attractiveness comes from exploiting the algebraic structure of the quadratic rotated cone which allowed us to explicitly give expressions for the inverse operator, the linear representation, and the quadratic operator, and use these operators to compute the derivatives of the barrier function explicitly. In spite of its attractiveness, the algorithm has several limitations such as producing a good starting point, developing a practical step length selection procedure in the primal space, and reducing the barrier parameter with a practical strategy in our setting. These limitations, however, could be addressed in a future research paper developing practical implementations. Future work can be performed on developing algorithms for solving mixed-integer rotated quadratic cone optimization problems.