Benders Decomposition Method on Adjustable Robust Counterpart Optimization Model for Internet Shopping Online Problem

Abstract

In this paper, the implementation of the Benders decomposition method to solve the Adjustable Robust Counterpart for Internet Shopping Online Problem (ARC-ISOP) is discussed. Since the ARC-ISOP is a mixed-integer linear programming (MILP) model, the discussion begins by identifying the linear variables in the form of continuous variables and nonlinear variables in the form of integer variables. In terms of Benders decomposition, the ARC-ISOP model can be solved by partitioning them into smaller subproblems (the master problem and inner problem), which makes it easier for computational calculations. Pseudo-codes in Python programming language are presented in this paper. An example case is presented for the ARC-ISOP to determine the optimal total cost (including product price and shipping cost) and delivery time. Numerical simulations were carried out using Python programming language with case studies in the form of five products purchased from six shops.

1. Introduction

The Internet is an electronic communication network that connects computer networks and facilities. Internet use in business has changed Internet function from information exchange to strategic business tool use, such as marketing, sales, and customer service. Because of the Internet, marketing companies, products, and services have become an interactive process nowadays; consumers can even do shopping using the Internet. The Internet is used to access smart gadgets, and users may perform surveillance using sensors, cameras, smart cities and employ decision support systems [1,2,3], known as online shopping.

Online shopping is defined as buying products or services from a seller in an interactive way and in real-time through the Internet. Online shopping is a new communication activity that does not need to be conducted face-to-face but separately through communication media connected to Internet services. The advantages of online shopping include customers enjoying online shopping 24 h per day, buying various products and services anytime and anywhere, comparing product prices from multiple shops, and so on. Furthermore, the biggest benefit of online purchasing is the abundance of possibilities [4].

However, the disadvantages of online shopping are the following: The products cannot be touched and felt, delivery time can be late, total costs increase because of additional shipping costs, and so on [4]. In some cases of products purchase, there are difficulties in optimizing the total cost by considering product prices, shipping costs, and delivery times from various online shops. Customers usually take time to choose which shop gives the best price and shipping cost.

Refers to [5], this problem is known as the Internet Shopping Optimization Problem (ISOP), which can be solved to minimize the total costs. Optimization is an action to obtain the best results in a certain situation [6]. The process of determining conditions that yield a function’s maximum or least value is known as optimization, and an optimization model can be created from optimization problems [7]. More than one method is used in solving optimization problems [8]. In any case of construction, design, and maintenance, decision-makers must be able to make many technological decisions. The ultimate goal of all these decisions is to minimize the effort required or maximize the desired benefits.

Chung [9] introduces an ISOP optimization model that involves delivery constraints in the form of cost and delivery time using a multi-objective optimization model. Chaerani et al. [10] consider that Chung’s model can be viewed as a maximum flow problem with circular demand (MFP-CD) because it has multiple sources in the form of several products and multiple sinks in the form of several shops. Chung’s model includes a decision variable of delivery. Chaerani et al. [10] made the decision variable of delivery time into an adjustable variable using the adjustable robust counterpart (ARC) method with the maximum uncertainty set of delivery time.

It can be seen that previous research discussed the Internet Shopping Online Problem (ISOP) using various methods, but none of them used the Benders decomposition method. It can be seen in [11] that there are only 6 articles on ARC Optimization Model using the Benders Decomposition but none of them discuss about ISOP. This research describes the solution of the Adjustable Robust Counterpart for the Internet Shopping Online Problem (ARC-ISOP) model using the Benders decomposition method [12]. Based on [12], the mixed-integer linear programming (MILP) model can be separated based on integer variables that are difficult to solve and continuous variables that are easy to solve, as well as the ARC-ISOP. Therefore, the Benders decomposition method makes it easier to solve the computational calculation of the MILP model because the model is partitioned into smaller subproblems. Then, a numerical simulation is carried out using secondary data from Tokopedia and Python programming language to help calculate the numerical simulation.

2. Literature Review

A literature review was conducted to determine the potential of research on optimization models for Internet shopping online problems that were solved using the Benders decomposition method. Topic-related journals comprised this literature review [13]. The literature review was carried out using the Google Scholar databases and helped by Publish or Perish (PoP) software. The keyword searches of “internet shopping online”, “robust optimization”, and “benders decomposition” produced 992 articles published from 2010 to 2022. Then, preferred reporting items for systematic review and meta-analyses (PRISMA) [14] were used to analyze all the articles obtained. Several related articles were selected based on the four PRISMA steps shown in Figure 1.

The first step is to choose the keywords associated with the intended study topic based on Figure 1. For the article results to be as precise as possible, keyword classification is required. It is possible to organize keywords into categories ranging from general to particular topics before entering them into at least one preferred database to determine the total number of articles found.

Furthermore, article limits are enforced as necessary when entering keywords into the database. The screening phase makes up the second stage. At this point, the first task is to check for duplicate articles. Using multiple article databases may result in duplicate content, i.e., articles with the same author and title. Until the total of the most recent articles is gathered, duplication checks can be carried out either manually or with the aid of the Jabref or Mendeley software. The articles that have been successfully chosen for the duplicate screening stage are filtered in the following stage of the screening process based on the title and abstract.

Additionally, each of the articles chosen at the screening stage is properly checked and read before moving on to the eligibility stage, where non-conforming articles are sent back. Checking is performed by looking at the research’s goals, methods, and results. The outcomes of the article selection at the eligibility stage are articles that proceed to the last stage, which includes state-of-the-art preparation, bibliometric map mapping, and article usage as material for literature reviews.

From the literature review that was conducted with the three keywords already mentioned, 992 articles were identified. Then, several articles were selected at the screening stage. At the screening stage, 718 articles were eliminated because they were not English articles, peer-reviewed articles, or articles published by journals. At the eligibility stage, 20 articles from 714 articles were selected, and 254 other articles were eliminated because the titles and abstracts did not match the qualification. Furthermore, 4 articles were selected, and 16 other articles were eliminated because the manuscript’s content did not match the qualification. In the included stage, four articles were selected as the final result. A summary of the selected articles can be seen in

Table 1. State of the art for ISOP.

Research	Optimization Methods	Benders Decomposition Method
Blazewicz et al. [5], 2010	Minimizing costs	No
Lopez-Loces et al. [15], 2016	Integer linear programming	No
Chung [9], 2017	Multi-objective optimization, Pareto set	No
Chaerani et al. [4], 2021	Adjustable robust counterpart optimization	No

.

In this literature review, we discuss the potential of research on optimization models for Internet shopping online problems that were solved using the Benders decomposition method. Our review complements existing reviews on this topic (Table 1). Table 1 summarizes the differences between our article and the previous review articles. One difference is that we focus on the use of the Benders decomposition method. Based on Table 1, none of the four articles used this method. Therefore, based on this statement, the review provides a gap to be addressed in future research to improve efficiency and accuracy, which is explained in the next section.

3. Materials

3.1. Internet Shopping Optimization Problem with Delivery Constraint (DISOP)

Referring to [9], the formulation for Delivery Constrained Internet Shopping Online Problem (DISOP) is shown in (1)–(5).

$$\min {\displaystyle \sum }_i{\displaystyle \sum }_j{p}_{ij}{x}_{ij}+{\displaystyle \sum }_j{f}_j{y}_j$$

(1)

$$\min \underset{i,j}{\max }\left(d_{ij},x_{ij}\right)$$

(2)

$$s.t{\displaystyle \sum }_j{x}_{ij}=1,\forall i=1,\dots ,n$$

(3)

$${\displaystyle \sum }_i{x}_{ij}\le n{y}_j,j=1,\dots ,m$$

(4)

$$x_{ij},y_j\in \left\{0,1\right\}$$

(5)

where $m$ is the number of shops with index $j$ and $n$ is the number of products with index $i$. Meanwhile, the price of product $i$ at shop $j$ is denoted by $p_{ij}$, and the delivery costs at shop $j$ is denoted by $f_j$. Note that $f_j$is a fixed value regardless of the number of products to buy. In addition, $x_{ij}$ is a binary decision variable that has a value of one if product $i$ is selected from shop $j$, while $y_j$ is a binary decision variable regardless of whether there incurs a delivery cost at shop $j$. The delivery time of the selected product until it reaches the customer is denoted by $d_{ij}$.

The objective Function (1) means that we try to minimize the purchasing cost, including the price of products and delivery cost. The objective Function (2) means that we want to minimize the delivery time of all products. Constraint (3) means that all products to buy must be selected from available shops, and Constraint (4) means that fixed delivery cost incurs whenever there is any product selection from the shop. Constraint (5) requires binary decision variables. Equations (1)–(5) can be reformulated as (6)–(10) by replacing the objective Function (2) with a new Constraint (9). The variable $d\_max$ is an upper limit of the delivery time in the objective Function (2).

$$\min {\displaystyle \sum }_i{\displaystyle \sum }_j{p}_{ij}{x}_{ij}+{\displaystyle \sum }_j{f}_j{y}_j$$

(6)

$$s.t{\displaystyle \sum }_j{x}_{ij}=1,\forall i=1,\dots ,n$$

(7)

$${\displaystyle \sum }_i{x}_{ij}\le n{y}_j,j=1,\dots ,m$$

(8)

$${\displaystyle \sum }_i{d}_{ij}{x}_{ij}\le d_{max},i=1,\dots ,n$$

(9)

$$x_{ij},y_j\in \left\{0,1\right\}$$

(10)

3.2. Adjustable Robust Counterpart for Internet Shopping Online Problem (ARC-ISOP)

The ISOP model introduced by Chung [9] is extended as a maximum flow problem with circular demand (MFP-CD), as discussed by Chaerani et al. [4]. In [4], the ISOP model fulfills the MFP-CD assumption, which involves multiple sources in the form of several products and multiple sinks in the form of several shops. The MFP-CD can be formulated by adding a source node ($s^{*}$) connected to s nodes and sink nodes ($t^{*}$) connected to $t$ nodes [16]. This problem can be solved using the adjustable robust counterpart because it has an uncertain delivery time.

The $d\_max$ in [9] is a decision variable of delivery time that needs to be adjusted so that it can be stated as an uncertain maximum flow problem with circular demand (UMFP-CD) [10]. The formulation of UMFP-CD can be seen as follows:

$$\begin{gathered} \max d_{max} \\ s.t{\displaystyle \sum }_{i,j}{a}_{ij}{z}_{ij}=0 \\ 0\le z_{ij}\le d_{ij},\forall i,j \\ {d}_{ij}\in \mathcal{U} \end{gathered}$$

(11)

The optimal $z_{ij}^{*}$ must be determined where $d\_max$ donates the total maximum delivery time of each product $i$ which is delivered from shop $j$. Matrix $A$ is the incidence matrix for the ISOP network, as illustrated in Figure 2. The delivery time of product $i$ from shop $j$ is denoted as $d_{ij}$, which is in the polyhedral uncertainty set. This is based on the result of the robust counterpart, which yields linear optimization with a close-convex feasible set [4].

The complete formulation in [4] for Adjustable Robust Counterpart for Internet Shopping Online Problem (ARC-ISOP) with polyhedral uncertainty set is the following:

$$\mathrm{Min}{\displaystyle \sum }_i{\displaystyle \sum }_j{p}_{ij}{x}_{ij}+{\displaystyle \sum }_j{f}_j{y}_j,$$

(12)

$$s.t{\displaystyle \sum }_j{x}_{ij}=1,\forall i=1,\dots ,n$$

(13)

$${\displaystyle \sum }{x}_{ij}\le n{y}_j,j=1,\dots ,m$$

(14)

$$d_{ij}{x}_{ij}\le t,i=1,\dots ,n$$

(15)

$${\overline{d}}_{max}+d_x^T{y}_x-t\ge 0$$

(16)

$$Az=0$$

(17)

$$z_{ij}-{\overline{d}}_{ij}{\omega }_{ij}-p_k^T{y}_k\le 0,\forall i,j,k$$

(18)

$$D_k^T{y}_k=P_k^T{\omega }_{ij};$$

(19)

$$D_x^T{y}_x=Q$$

(20)

$${\omega }_{ij}=1;$$

(21)

$$y_x,y_k,z_{ij},t\ge 0,\forall i,j$$

(22)

$$x_{ij},y_j\in \left\{0,1\right\}$$

(23)

The values of the variables $P,D_x,D_k,d_x,$ and $d_k$ are random numbers obtained through Python using the Random Library. Referring to [4], problems (12)–(23) involve the integer variables $x_{ij}$and $y_j$ so that the ARC-ISOP can be solved as a two-stage robust optimization problem. Refer to [17], one of the alternative procedures in solving the mixed-integer linear programming (MILP) is the Benders decomposition method.

4. Methods

4.1. Duality Theory

In linear programming, there are primal and dual problems. These two problems are exciting and closely related. If the optimal solution for one is known, the other optimal solution can be easily obtained [8]. The linear programming calculation depends more on the number of constraint functions than the number of variables. The dual problem is expected to have fewer constraint functions than the primal problem; thus, it is more efficient to use the dual problem to obtain a solution to the primal problem. According to [8], the rules for constructing dual problems are stated in

Table 2. Rules for constructing dual problem.

	Primal Problem	Dual Problem
Objective function	$\min c^{T}x$	$\max b^{T}y$
Variable	$x_i\ge 0$	$i$th constraint$:A_i^{T}y\le c_i$
Variable	$x_i$ free	$i$th constraint$:A_i^{T}y=c_i$
Constraint	$A_{i}x=b_j$	$j$th variable free
Constraint	$A_{i}x\ge b_j$	$j$th variable$:y_j\ge 0$
Technology coefficient	$A$	$A^T$
Right side	$b$	$c$
Cost coefficient	$c$	$b$

.

4.2. Benders Decomposition Method

Jacques F. Benders first discovered Benders decomposition in 1962. As defined in [12], Benders decomposition is the basis of a mathematical model that is required to partition or divide into linear parts that are easy to solve and nonlinear parts that are difficult to solve. According to [12], the Benders decomposition method is an optimization method for solving problems with feasible subproblems. Consider the formulation of the minimization problem called the initial problem P(x,y) as follows. Then, apply the Benders decomposition algorithm (Figure 3) to the partitioned mathematical model.

$$\begin{gathered} \min c^{T}x+f\left(y\right) \\ s.tAx+F\left(y\right)=b \\ x\ge 0,y\in Y \end{gathered}$$

(24)

where $A\in R^{m\times n},x,c\in R^n,b\in R^m,y\in Y\subset R^p$, in cases $f\left(y\right)$ and $F\left(y\right)$, can be nonlinear and Y can be discrete or a continuous range. The main concept in the Benders decomposition algorithm is to partition the variable into two sets, i.e., $x,$ and $y,$ then solve the problem on the difficult variable $Y$.

The Benders decomposition method algorithm can be seen in Figure 3 based on [12] and discussed by Chaerani et al. [18], the steps for working on the Benders decomposition method are as follows:

(1)

First, observe that the fixed value of $y\in Y$ becomes a linear programming problem in terms of $x$. In addition, $P(x|y)$ is the notation of a feasible subproblem. Next, assume that $P\left(x|y\right)$ has a finite optimal solution $x\forall y\in Y$ so that Equation (24) can be reformulated into a constraint equivalent to $P_1\left(x,y\right)$:

$$\underset{y}{\min }\left\{f\left(y\right)+\underset{x}{\min }\left\{c^{T}x:Ax=b-F\left(y\right),x\ge 0\right\}\right\}$$

(25)

where

$$\underset{x}{\min }\left\{c^{T}x:Ax=b-F\left(y\right),x\ge 0\right\}$$

(26)

is an inner optimization problem assumed to have an optimal solution $x$ for every $y\in Y$.

(2)

Second, find a dual problem formulation for the inner optimization problem. Equation (24) can be rewritten as

$$\underset{y}{\min }\left\{f\left(y\right)+\underset{u}{\max }\left\{{\left(b-F\left(y\right)\right)}^{T}u:A^{T}u\le c\right\}\right\}$$

(27)

The constraint function in the inner optimization problem is independent of the $y$ variable. The optimal solution of the inner optimization problem is finite because it assumes that (26) has an optimal solution $x$ for every $y\in Y$ and the optimal solution is at the extreme point $u\in \mathcal{U}$. Equation (27) can be rewritten as follows:

$$\underset{y}{\min }\left\{f\left(y\right)+\underset{u}{\max }{\left(b-F\left(y\right)\right)}^{T}u\right\}$$

(28)

(3)

Third, determine the full master problem by rewriting (28), which is formulated into a simple minimization problem as follows:

$$\begin{array}{cc}\min f\left(y\right)+m\hfill & \\ s.t{\left(b-F\left(y\right)\right)}^{T}u\le m,u\in U\hfill & \\ & \hfill y\in Y\end{array}$$

(29)

From Equation (29), the relaxed master problem $M\left(y,m\right)$ is defined:

$$\begin{array}{cc}\min f\left(y\right)+m\hfill & \\ s.t{\left(b-F\left(y\right)\right)}^{T}u\le m,u\in B\hfill & \\ & \hfill y\in Y\end{array}$$

(30)

where $B$ is an empty set and $m$ is initialized as $0$. The Benders subproblem solves an extreme point $u$ with a fixed value $y\in Y$ so that it can be considered a maximization problem.

$$S\left(u|y\right)=\max \left\{{\left(b-F\left(y\right)\right)}^{T}u:A^{T}u\le c\right\}$$

(31)

where $u\in R$ and $S(u|y)$ has a finite optimal solution. The subproblem $S(u|y)$ is solved to obtain $u$ given the value determined from solving the master problem $M\left(x,y\right)$. Then, a simple test is performed to determine whether a constraint that includes $u$ should be added to the master problem. If so, the next problem is solving the master problem to generate a new value of $y$. Then, input the new value of $y$ to the subproblem, which is solved again. This iteration continues until the optimization is reached.

5. Result and Discussion

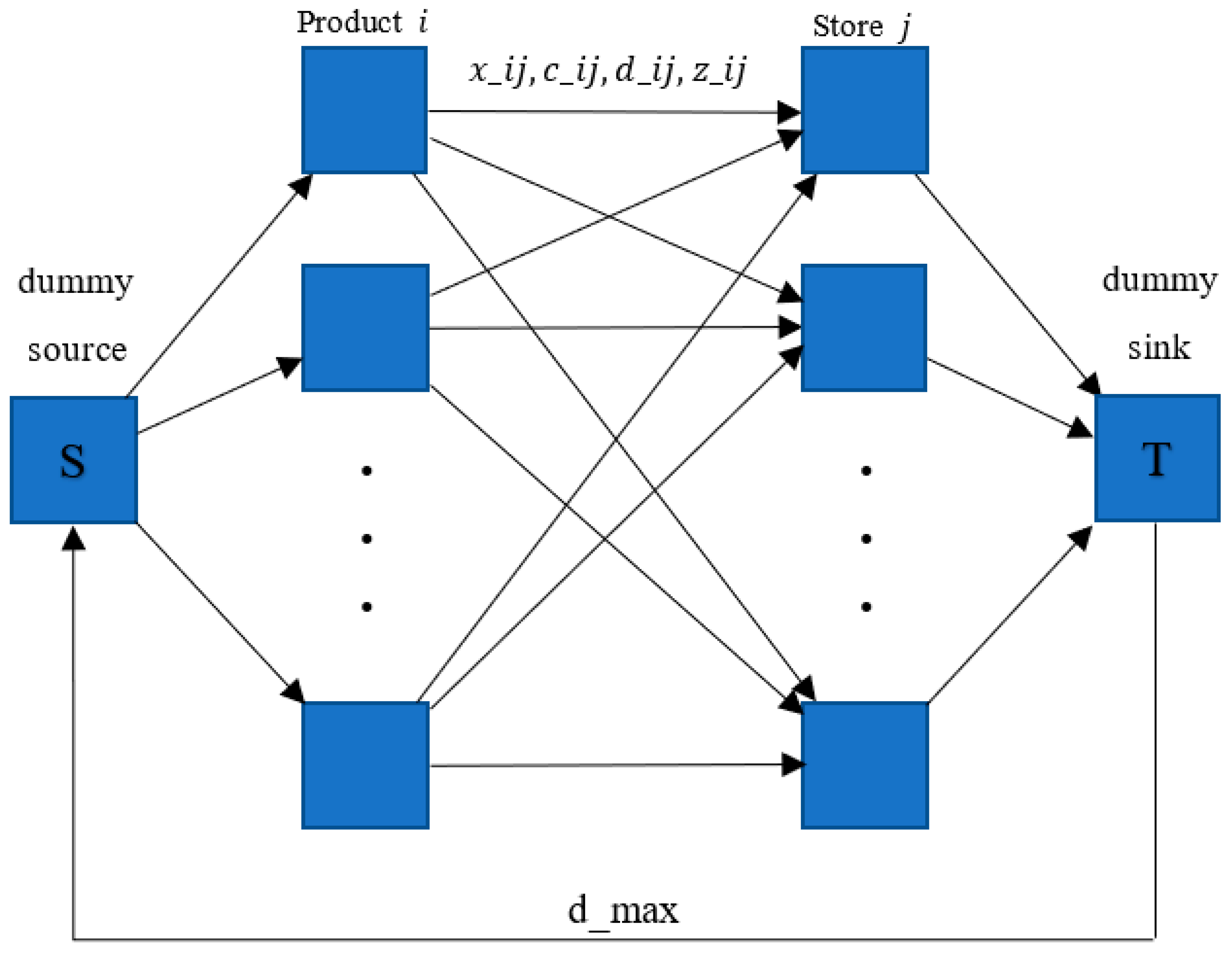
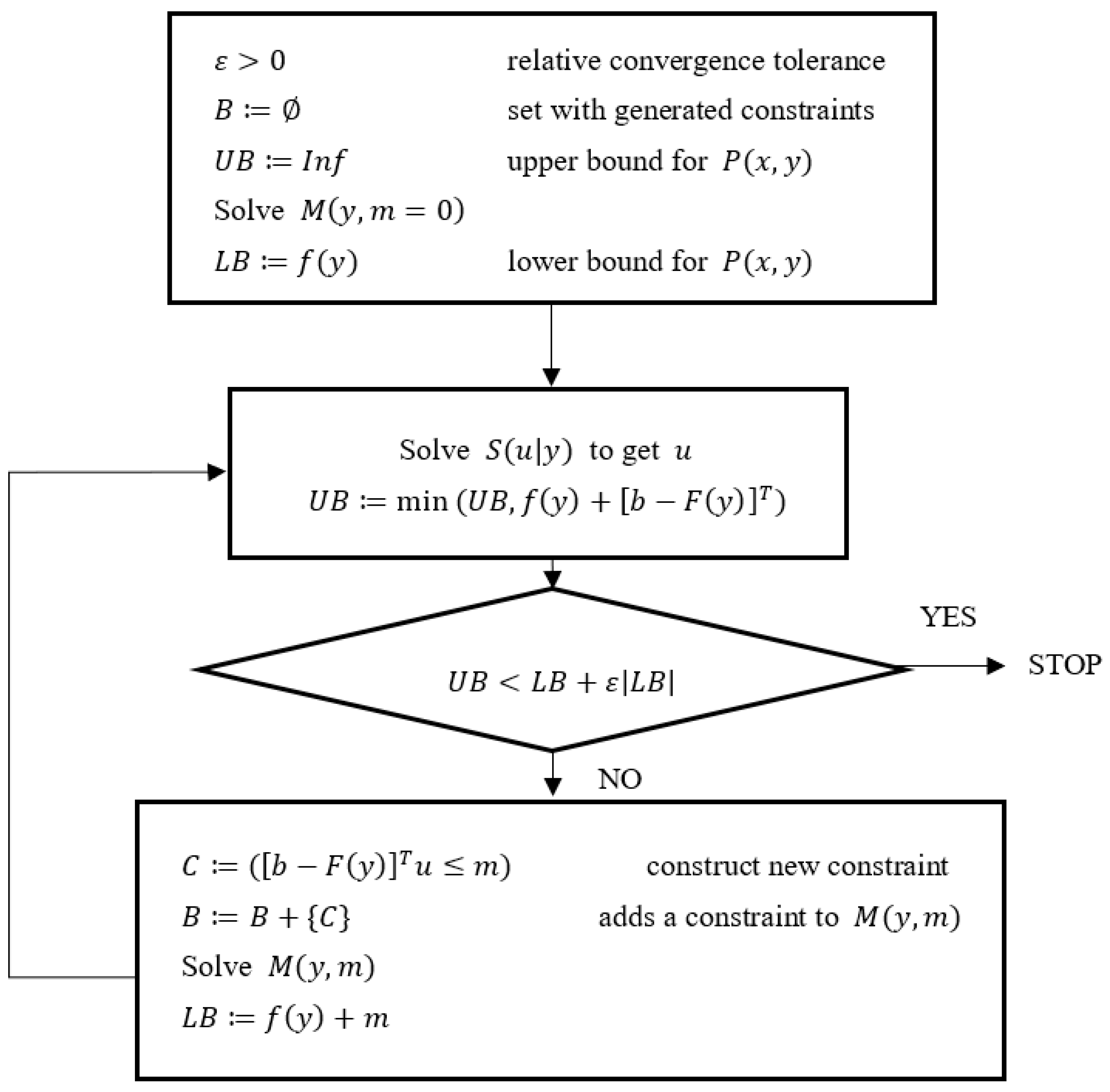
5.1. Application of the Benders Decomposition Method in Completing the ARC-ISOP Optimization Model

Using the theory of decomposition and duality, an Internet Shopping Online Problem (ISOP) can be divided into a master problem and a dual subproblem. To perform the Benders decomposition method, the variables and constraints need to be divided into two groups, linear variables and nonlinear variables, in the ARC-ISOP model (Formulations (12)–(23)). To simplify the work, some variables are denoted as follows:

(1)

The continuous variables $z_{ij},y_x,y_k$, and $t$ are denoted as $v$, with Constraints (16)–(20) and (22) representing the linear parts that will be formulated into dual form.

(2)

The integer variables $x_{ij}$ and $y_j$are denoted as $w$, with Constraints (13)–(15) and (23) representing the set $Y$.

(3)

As detailed below, $\alpha ,\beta ,\gamma ,\sigma$, and $\pi$ are dual variables denoted as $u$, introduced for Constraints (16)–(20).

Based on the denotations mentioned, the model indicators in the Benders decomposition algorithm are equivalent to $P\left(v,w\right)$ as the initial problem $M\left(w,r\right)$ as the master problem and $S(u|w)$ as the subproblem. After identifying the linear and nonlinear variables, the next step is to use the Benders decomposition algorithm.

(1)

First Stage

The first stage is carried out to find the optimal solution of the variables considered difficult to solve; in this case, the integer variables ($x$ and $y$) are denoted as $w$.

• Step 1

Solve the initial master problem $M\left(w,r=0\right)$ as an initial step, obtained from the ARC-ISOP model, which only contains integer variables. Note that $B$ is the empty set, and the limit of the model is $\infty$. Since $B$ is an empty set and $r=0$, then $M\left(w,r=0\right)$ can be written as follows:

$$\begin{gathered} \min {\displaystyle \sum }_i{\displaystyle \sum }_j{p}_{ij}{x}_{ij}+{\displaystyle \sum }_j{f}_j{y}_j \\ s.t{\displaystyle \sum }_j{x}_{ij}=1,\forall i=1,\dots ,n \\ {\displaystyle \sum }{x}_{ij}\le n{y}_j,j=1,\dots ,m \\ {d}_{ij}{x}_{ij}\le t,i=1,\dots ,n \\ x,y\in \left\{0,1\right\} \end{gathered}$$

(32)

Note that Benders cut is not added to this problem (since $r=0$).

2.

Step 2

Determine the inner optimization model $P\left(v,w\right),$ which contains an objective function and a constraint that only has continuous variables $\left(z,y_x,y_k,t\right)$. The term $P\left(v,w\right)$ can be written as follows:

$$\min 0$$

(33)

$$s.t{\overline{d}}_{max}+d_x^T{y}_x-t\ge 0$$

(34)

$$Az=0$$

(35)

$$z_{ij}-{\overline{d}}_{ij}{\omega }_{ij}-p_k^T{y}_k\le 0,\forall i,j$$

(36)

$$D_k^T{y}_k=P_k^T{\omega }_{ij};{\omega }_{ij}=1$$

(37)

$$D_x^T{y}_x=Q$$

(38)

$$z_{ij},y_x,y_k,t\ge 0,\forall i,j$$

(39)

Because the objective function in the minimization optimization model in Equations (33)–(39) is zero, it is necessary to carry out a duality process to avoid a zero value using the duality theory. The zero value in the minimization objective function results in the solution being zero. By introducing the five dual variables $\alpha ,\beta ,\gamma ,\sigma$, and $\pi$ corresponding to five Constraints (34)–(38), respectively, the following is a dual formulation known as subproblem $S(u|w)$ of the inner optimization problem (see Equation (27)):

$$\begin{gathered} \mathsf{M}\mathsf{a}\mathsf{x}\alpha {\overline{d}}_{max}+{\displaystyle \sum }{\beta }_{ij}\left(0\right)+{\displaystyle \sum }{\gamma }_{ij}\overline{d_{ij}}{\omega }_{ij} \\ +{\displaystyle \sum }{\sigma }_{ij}{P}^T{w}_{ij}+\pi Q \\ s.tA\beta +\gamma \le 0 \\ {d}_x^T\alpha +D_x^T\pi \le 0 \\ -d_k^T\gamma +D_k^T\sigma \le 0 \\ \alpha \ge 0 \\ \gamma \le 0 \\ \beta ,\sigma ,\pi \mathrm{free} \end{gathered}$$

(40)

Equation (40) can be solved by substituting the value of $w$ obtained from Step 1 to obtain the value of the dual variables.

3.

Step 3

Test whether the $upperbound<lowerbound+\epsilon \left|lowerbound\right|$, where $\epsilon >0$.

• $Upperbound<lowerbound+\epsilon \left|lowerbound\right|$, where $\epsilon >0$, then stop the iteration and proceed to the second stage.
• $Upperbound>lowerbound+\epsilon \left|lowerbound\right|$, where $\epsilon >0$, then the iteration continues to the next step.

4.

Step 4

Each iteration will add a Benders cut, which is derived from the objective function in Subproblem $S(u|w).$ Here is Benders cut as a new constraint:

$$C=\left(\begin{array}{c}\alpha {\overline{d}}_{max}+{\displaystyle \sum }{\beta }_{ij}\left(0\right)+{\displaystyle \sum }{\gamma }_{ij}\overline{d}{\omega }_{ij}\\ +{\displaystyle \sum }{\sigma }_{ij}{P}_k^T{\omega }_{ij}+\pi Q\le r\end{array}\right)$$

(41)

where $\alpha ,\beta ,\gamma ,\sigma ,\pi$ are parameters and $r$ is unknown. By adding a new constraint to the initial master problem $M\left(w,r=0\right)$ in (32), the regular master problem $M\left(w,r\right)$ can be obtained after introducing the set $B$ of Benders cut generated so far. Note that the dual optimal variables have been assigned an additional index b for each Benders cut. The regular master problem $M\left(w,r\right)$ is stated as follows:

$$\begin{gathered} \min {\displaystyle \sum }_i{\displaystyle \sum }_j{p}_{ij}{x}_{ij}+{\displaystyle \sum }_j{f}_j{y}_j+r \\ s.t{\displaystyle \sum }_j{x}_{ij}=1,\forall i=1,\dots ,n \\ {\displaystyle \sum }{x}_{ij}\le n{y}_j,j=1,\dots ,m \\ {d}_{ij}{x}_{ij}\le t,i=1,\dots ,n \\ \alpha {\overline{d}}_{max}+{\displaystyle \sum }{\beta }_{ij}\left(0\right)+{\displaystyle \sum }{\gamma }_{ij}\overline{d}{\omega }_{ij} \\ +{\displaystyle \sum }{\sigma }_{ij}{P}_k^T{\omega }_{ij}+\pi Q\le r \\ x,y\in \left\{0,1\right\} \\ \alpha ,\beta ,\gamma ,\sigma ,\pi \le B \end{gathered}$$

(42)

Solve (42), then return to Step 3. The calculation continues until the limit test in Step 3 stops.

(2)

Second Stage

The second stage is carried out to find the optimal solution of the inner optimization model $P\left(v,w\right)$ (see Equations (33)–(39)), which only contains continuous variables by completing the initial model that has been substituted with the value of $w$ from the first stage.

The solution obtained from the second stage, added to the optimal solution from the first stage, becomes the total optimal solution from the Benders decomposition method.

5.2. Numerical Simulation

5.2.1. Python Algorithm

The Python algorithm to solve the ARC-ISOP optimization model with the Benders decomposition method is as follows:

Before starting the algorithm, open https://colab.research.google.com/ (accessed on 27 July 2022) or open a programming application that supports Python.

Algorithm 1: Solving the initial master problem.

Begin

Step 1: Define the problem using the syntax “LpMinimize” and the variables using the syntax “LpVariable”.

Step 2: Use the Pulp module to initiate initial_master_model.

Step 3: Read intial_master_model using the syntax “print()”.

Step 4: Use the Pulp module to solve initial_master_model using the syntax “solve()”.

Step 5: Print the results using the following syntax:

For all $j\in m$ do

Print $y_j$

For all $i\in n$ do

Print $x_{ij}$.

End for

End for

End

Algorithm 2: Solving the subproblem model.

Begin

Step 1: Define the problem using the syntax “LpMaximize” and the variables using the syntax “LpVariable”.

Step 2: Use the Pulp module to initiate subproblem_model.

Step 3: Read subproblem_model using the syntax “print()”.

Step 4: Use the Pulp module to solve subproblem_model using the syntax “solve()”.

Step 5: Print the results using the following syntax:

For all $i\in V$ do

For all $j\in V$ do

Print ${\beta }_{ij}$.

Print ${\gamma }_{ij}$.

Print ${\sigma }_{ij}$.

End for

End for

Step 6: Print $\alpha$ and $\pi$.

End

Algorithm 3: Solving inner optimization model.

Begin

Step 1: Define the problem using the syntax “LpMinimize” and the variables using the syntax “LpVariable”.

Step 2: Use the Pulp module to initiate inner_model.

Step 3: Read inner_model using the syntax “print()”.

Step 4: Use the Pulp module to solve inner_model using the syntax “solve()”.

Step 5: Print the results using the following syntax:

For all $i\in V$ do

For all $j\in V$ do

Print $z_{ij}$.

Print $y_k$.

End for

End for

Step 6: Print $y_x$ and $t$.

End

Algorithm 4: Library installation and data upload.

Begin

Step 1: Install the pulp library with the following syntax: “pip install pulp”.

Step 2: Import the required libraries using the following syntax: “import pulp as lp”, “import pandas as pd”, “import numpy as np”, and “import random as rd”.

Step 3: Upload the research data using the following syntax:

“from google.colab import files”

“upload=files.upload()”

Step 4: Import the sheet in Excel files that has been uploaded using the following syntax:

“import io”

“name = pd.read_excel(io.BytesIO(upload[‘file name.xlsx’]),sheet_name=’name’)”

Algorithm 5: Solving the maximum flow problem model.

Begin

Step 1: Define the set of points in the form of an array.

Step 2: Define the problem using the syntax “LpProblem” then “LpMaximize” and the variables using the syntax “LpVariable”.

Step 3: Define the objective function and the constraint function.

For all $i\in V$ do

Define the entry point.

End for

For all $i\in V$ do

Define the exit point.

End for

Step 4: Use the Pulp module to initiate mfp_model.

Step 5: Use the Pulp module to solve mfp_model using the syntax “solve()”.

Step 6: Print the results using the following syntax:

For all $i\in V$ do

For all $j\in V$ do

Print $z_{ij}$.

End for

End for

End

The Benders decomposition method is divided into two stages. The first stage is to find the optimal value of the nonlinear variable using Algorithm 1 and Algorithm 2, while the second stage is to find the optimal value of the linear variable using Algorithm 3. Meanwhile, Algorithm 4 and Algorithm 5 are used before starting the Benders Decomposition Method.

5.2.2. Case Study 1

The data used in this numerical simulation are the secondary data obtained from Tokopedia, accessed on 15 June 2022, using the skincare product category [19]. Data that have previously been collected from primary sources and made easily accessible for academics to use for their own research are known as secondary data. This is the category of information that has previously been collected [20,21]. The data collected include the selling prices of five products from six different online shops in Bandung, including shipping costs and delivery times from each online shop. The data can be seen in

Table 3. Rules for constructing dual problems.

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Product 1	42	43.5	40	40.7	43.2	46.5
Product 2	15.5	14	14.5	12.7	13.9	16.5
Product 3	20.9	21	18	17.8	19.3	22.5
Product 4	21.5	21.5	19.5	20.3	20.7	24.5
Product 5	32	31	27.5	27.6	29.7	35
Shipping cost ($f_j$)	10	13	13	11	10	8
Delivery time ($d_{ij}$)	2 days	1 day	1 day	2 days	2 days	3 days

.

To find the optimal solution on the data in Table 3, the Benders decomposition algorithm consists of two stages.

(1)

First Stage

The first stage is to find the optimal solution for the nonlinear or integer variables.

• Step 1

Solve initial master problem $M(w,r=0$) as an initial step. Note that B is an empty set, and the limit of the model is $\infty$. Substitute data from Table 3 into (32), then use Algorithm 1 in Python to get the optimal solution.

Based on

Table 4. Numerical solution results of the initial master (products).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Product 1	0	0	0	1	0	0
Product 2	0	0	0	1	0	0
Product 3	0	0	0	1	0	0
Product 4	0	0	0	1	0	0
Product 5	0	0	0	1	0	0

and

Table 5. Numerical solution results of the initial master (shops).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Shipping cost indicator	0	0	0	1	0	0
Delivery time	2	1	1	2	2	3

, the following is obtained:

$x_{14}=x_{24}=x_{34}=x_{44}=x_{54}=1$ and $y_4=1$ with a minimum total cost of $Rp130.100$ (lower bound).

2.

Step 2

Solve the subproblem (see Equation (40)) to obtain the values of dual variables. However, in this case, (40) does not contain $x$ and $y$ variables, so the subproblem can be solved immediately using Algorithm 2 in Python.

$\alpha =\beta =\gamma =\sigma =\pi =0$ with a maximum value of $Z=$0.

$\min \left(\infty ,\left(130.100+0=130.100\right)\right)=130.100$ (upper bound).

3.

Step 3

Bound test: $130.100\langle 130.100+\epsilon |130.100|$, where $\epsilon >0$.

Since $upperbound<lowerbound+\epsilon \left|lowerbound\right|,$ where $\epsilon >0$, the first stage is discontinued. The case in this research did not pass Step 4, namely the addition of the Benders cut. Then, the calculation continues to the second stage. From the first stage, the optimal solution is $x_{14}=x_{24}=x_{34}=x_{44}=x_{54}=1and{y}_4=1$ with a minimum total cost of $Rp130.100$.

(2)

Second Stage

The solutions in

Table 6. The result of numerical solution (products).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Product 1	0	0	0	1	0	0
Product 2	0	0	0	1	0	0
Product 3	0	0	0	1	0	0
Product 4	0	0	0	1	0	0
Product 5	0	0	0	1	0	0

and

Table 7. The result of numerical solution (shops).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Shipping cost indicator	0	0	0	1	0	0
Delivery time	2	1	1	2	2	3

are the optimal solutions that minimize the total cost of purchasing skincare products at six online shops. The total cost is optimal if products 1, 2, 3, 4, and 5 are purchased from the fourth shop, with a total cost of Rp130.100, and the delivery time is about two days.

5.2.3. Case Study 2

The data used in this numerical simulation are the secondary data obtained from Tokopedia, accessed on 22 June 2022, using the skincare product category [20]. The data collected include the selling prices of five products from six different online shops in various cities across Java, including shipping costs and delivery times from each online shop. The data can be seen in

Table 8. Skincare sales data on Tokopedia.

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Product 1	38	42.1	35.3	37.6	37.2	39.5
Product 2	12.4	15.2	16.5	12.3	12.9	13.5
Product 3	18.2	19.9	19.2	18.4	18.5	19.9
Product 4	17.5	20.3	23	17.2	17.4	18.5
Product 5	25.5	28.9	27.6	27.6	24	28.5
Shipping cost ($f_j$)	9	10	10	15	9	15
Delivery time ($d_{ij}$)	2 days	3 days	3 days	4 days	3 days	4 days

.

To find the optimal solution based on the data in Table 8, the Benders decomposition algorithm consists of two stages.

(1)

First Stage

The first stage is to find the optimal solution for the nonlinear or integer variables.

• Step 1

Solve initial master problem $M\left(w,r=0\right)$ as an initial step. Note that $B$ is an empty set, and the limit of the model is $\infty$. Substitute data from Table 8 into (32), then use Algorithm 1 in Python to obtain the optimal solution.

Based on

Table 9. Numerical solution results of the initial master (products).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Product 1	0	0	0	0	1	0
Product 2	0	0	0	0	1	0
Product 3	0	0	0	0	1	0
Product 4	0	0	0	0	1	0
Product 5	0	0	0	0	1	0

and

Table 10. Numerical solution results of the initial master (shops).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Shipping cost indicator	0	0	0	0	1	0
Delivery time	2	1	1	2	2	3

, the following is obtained:

$x_{15}=x_{25}=x_{35}=x_{45}=x_{55}=1$ and $y_5=1$ with a minimum cost of Rp 119.000 (lower bound).

2.

Step 2

Solve the subproblem (see Equation (40)) to obtain values of dual variables. However, in this case, (40) does not contain x and y variables so the subproblem can be solved immediately using Algorithm 2 in Python.

$\alpha =\beta =\gamma =\sigma =\pi =0$ with a maximum value of$Z=0$.

$\min \left(\infty ,\left(119.000+0=119.000\right)\right)=119.000$ (upper bound).

3.

Step 3

Bound test: $119.000\langle 119.000+\epsilon |119.000|$, where $\epsilon >0$.

Since $upperbound<lowerbound+\epsilon \left|lowerbound\right|$, where $\epsilon >0$, the first stage is discontinued.

The case in this research did not pass Step 4, namely the addition of the Benders cut. Then, the calculation continues to the second stage. From the first stage, the optimal solution is $x_{15}=x_{25}=x_{35}=x_{45}=x_{55}=1$ and $y_5=1$, with a minimum total cost of Rp 119.000.

(2)

Second Stage

The solutions in

Table 11. The result of numerical solution (products).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Product 1	0	0	0	0	1	0
Product 2	0	0	0	0	1	0
Product 3	0	0	0	0	1	0
Product 4	0	0	0	0	1	0
Product 5	0	0	0	0	1	0

and

Table 12. The result of numerical solution (shops).

	Shop 1	Shop 2	Shop 3	Shop 4	Shop 5	Shop 6
Shipping cost indicator	0	0	0	0	1	0
Delivery time	2	1	1	2	2	3

are the optimal solutions that minimize the total cost of purchasing skincare products at six different online shops. The total cost is optimal if products 1, 2, 3, 4, and 5 are purchased from the fifth shop, with a total cost of Rp. 119.000 and delivery time is about three days. With the emergence of an optimal solution that satisfies the objective function and all constraints on the model, it can be concluded that the Benders decomposition method can be used to complete a robust optimization model in the case of internet shopping online.

6. Conclusions

The Adjustable Robust Counterpart for the Internet Shopping Online Problem (ARC-ISOP) is a mixed-integer linear programming (MILP) model, so the ARC-ISOP model can be solved using the Benders decomposition method. Benders decomposition is a method for solving cases that have feasible subproblems. This is a feasible subproblem that is determined based on the initial MILP model, which is partitioned into linear/continuous parts (considered easy variables) and nonlinear/integer parts (considered hard variables). In this research, an example case is given, namely the optimization of internet shopping online on the ARC-ISOP model to minimize the total cost (including product prices and delivery cost) and delivery time so that the optimal robust solution is obtained. The result indicates that the Benders decomposition method can solve problems by partitioning them into smaller subproblems, which makes it easier for computational calculations and provides computationally tractable solutions. With the emergence of an optimal solution that satisfies the objective function and all constraints on the model, it can be concluded that the Benders decomposition method can be used to complete a robust optimization model in the case of internet shopping online.