Abstract
To reduce traffic congestion and pollution, urban rail transit in China has been in a stage of rapid development in recent years. As a result, rail transit service interruption events are becoming more common, seriously affecting the resilience of the transportation system and user satisfaction. Therefore, determining the changing mechanism of the passenger waiting tolerance, which helps establish a scientific and effective emergency plan, is urgent. First, the variables and levels of the urban rail service interruption scenarios were screened and determined, and the stated preference questionnaire was designed using the orthogonal design method. Further, the data of the waiting tolerance of passengers during service interruptions were obtained through questionnaires. Second, combined with the questionnaire data, an accelerated failure time model that obeys the exponential distribution was constructed. The results indicate that factors such as the service interruption duration, travel distance, bus bridging, information accuracy, attention to operation information, travel frequency and interruption experience affect the waiting tolerance of passengers during service interruptions. Finally, combined with the sensitivity analysis of the key influencing factors, the policy analysis and suggestions are summarized to provide theoretical support for the urban rail operation and management department to capture the passenger waiting tolerance accurately during service interruptions and formulate an efficient, high-quality emergency organization plan.
1. Introduction
As of December 2021, the urban rail transit (URT) has been opened in 50 cities in mainland China, with 283 operating lines, a total length of 9206.8 kilometers and an average daily passenger traffic of 67.113 million passengers. With the increase in the scale of the URT network and passenger flow, the pressure on rail transit operation continues to rise, and service interruptions caused by facility and equipment failures occur frequently. In the top three Chinese cities of Beijing, Guangzhou and Shanghai, the recorded service interruptions in 2015 were 189, 348 and 143, respectively [1]. After a service interruption occurs, a passenger’s travel is blocked, and their travel behavior changes abnormally. They either continue to wait for the service to resume or adopt an alternative travel plan.
For operation managers of the URT, the formulation of emergency management measures for service interruptions needs to be based on a clear understanding of the behavior (especially the waiting tolerance) of the blocked passengers. Formulating an emergency plan that meets the travel needs of the blocked passengers will be impossible if the changes in the waiting tolerance of the different passenger groups after encountering service interruptions during various travel scenarios are not clearly understood. This will result in a backlog of blocked passengers at the station or even cause congestion. Therefore, analyzing the waiting tolerance of the blocked passengers during URT service interruptions is urgent, which can build a theoretical foundation for the formulation of high-quality, efficient emergency plans. However, the research on the passenger waiting tolerance during service interruptions, especially the URT in China, is limited. To fill the gap, in this study, we conducted a waiting tolerance analysis during service interruptions. Meanwhile, the sensitivity analysis of the key factors affecting the waiting tolerance were processed to offer theoretical support for the URT operation and management department to capture the passenger waiting tolerance accurately and formulate an efficient emergency organization plan.
The remainder of this paper is organized as follows. Section 2 presents an overview of the state-of-the-art studies on travel behavior during service interruptions. Section 3 describes the questionnaire survey designed for this study and the data collection process conducted at Chongqing. Section 4 introduces an accelerated failure time model to identify the factors that influence the passenger waiting tolerance during service interruptions. Section 5 presents the estimation results of the accelerated failure time model as well as the discussion and implications. Finally, the conclusions and future works are summarized in Section 6.
2. Literature Review
Some scholars have carried out relevant research on passenger travel behavior during service interruptions. Regarding the focus of the current paper, a review of the studies on traveler response, impact analysis, mode shift/choice and waiting tolerance during service interruptions is presented in Table 1.

Table 1.
Literature on the various aspects of URT service interruptions.
To analyze traveler response to service interruptions, Nazem et al., 2018 [4] used a statistical analysis method to examine the travel pattern changes. The results showed that a medium-term interruption could have a long-term impact on the travel patterns of frequent users. Using data from more than one million bicycle trips, Saberi et al., 2018 [3] measured and characterized the impacts of a public transportation disruption on bicycle sharing mobility patterns in London. The study found that the observed changes were heterogeneously distributed over the space, suggesting that the impact of the interruption was not uniform across the network. Regarding the mode choice, Lin, 2017 [2] developed an MNL model to investigate the transit user commuting mode choice in response to rapid transit service interruptions in the City of Toronto. The result of the MNL model showed that the travel time, cost, frequency of the subway trip, trip purpose, subway delay, shuttle bus delay, weather, age and income were significant at a 95% confidence. In addition, the relevant research of other scholars is also shown in Table 1, according to the study focus and method.
Table 1 shows that most of the existing studies focus on the mode shift/choice and impact analysis during service interruptions, but there are few studies, e.g., Rahimi et al., 2019 [8], on the waiting tolerance of the blocked passengers after service interruptions. Using collected data from transit users in the Chicago metropolitan area, Rahimi et al., 2019 [8] identified that factors such as the experience of using ridesharing services, the density of pedestrian-oriented links and the transit service frequency influence the waiting tolerance. Inappropriately, there is little knowledge from a research perspective regarding the effect of travel characteristics and bus bridging on the passenger waiting tolerance during service interruptions. Concurrently, the sensitivity analysis of the key factors that affect the waiting tolerance has not been studied thoroughly. Thus, there is a need to model and analyze the passenger waiting tolerance during service interruptions considering travel characteristics and bus bridging, which have not been conducted to our best knowledge.
3. Behavioral Investigation and Analysis
The travel behavior survey can be divided into the RP (revealed preference) survey and the SP survey. The RP survey, also known as the behavioral survey, is a search of the selective behaviors that have occurred or have been done. The interviewees were required to complete questionnaires or questionnaires based on their actual travel behaviors to obtain the possibility of their actual use or acceptance, and then build relevant probability models or other models. The SP survey, also known as the intention survey, is a survey of the respondent’s choice intention and how to conduct it under the assumed conditions. The goal was to analyze the need for non-existing service systems by investigating the changes in people’s thinking, consciousness and actions. The questionnaire in this paper adopts the SP questionnaire for the following reasons: (1) service interruption is unpredictable, so respondents cannot be determined in advance; (2) the respondents recall the service interruption from before and forget or have a memory disorder due to the time elapsed; (3) when service interruption occurs, the passengers are often anxious to find alternative travel plans and have no time to answer the questionnaire. The SP survey will be elaborated from the following aspects: the questionnaire design, survey process and statistical analysis of the data.
3.1. Questionnaire Design
This SP questionnaire consists of three parts: the personal attribute survey, travel behavior survey and questionnaire scene survey. The details are as follows.
(1) Questionnaire scene design
The design of the questionnaire scenario directly affects the quality of the SP survey. Therefore, this survey first determines seven influencing factors of the passenger waiting tolerance during service interruptions based on the existing research and pre-survey, and then sets distinct levels of these seven influencing factors based on the actual situation, as shown in Table 2.

Table 2.
Scene variation of the SP questionnaire.
As shown in Table 2, seven variables with multiple levels were used to build the scenarios in the SP survey. If we designed the scene directly, there would have been 3 × 2 × 2 × 2 × 2 × 2 × 3 = 288 scenarios, which would have made it impossible to carry out the questionnaire due to the large number of scenarios. Therefore, using SPSS software, we adopted an orthogonal design, which is an efficient and widely used questionnaire design method, to reduce the number of generated scenarios in this study. Finally, 16 questionnaire scenarios were obtained, as shown in Table 3.

Table 3.
Orthogonal design of the SP questionnaire.
At the same time, existing studies have shown that excessively long questionnaire survey times or excessive questionnaire content will lead to the deterioration of the questionnaire quality and a difficulty in obtaining data from the questionnaire survey [11]. Therefore, we provide three scenarios randomly selected from all the scenarios in each questionnaire to ensure the questionnaire quality (see Appendix A).
(2) Personal attribute survey
Existing relevant studies [16,17,18,19,20] have shown that personal attributes (age, gender, race, education level, occupation, etc.) affect traveler travel preferences. Therefore, the questionnaire survey in this paper included a personal attributes survey, as shown in Table 4.

Table 4.
Questionnaire design of personal attributes.
(3) Travel characteristics survey
Considering that the travel characteristics of travelers may affect their travel preference in the event of service interruptions, the questionnaire in this paper also designed a travel characteristics survey, which included operation information attention, rail transit travel frequency, service interruption experience, etc., as shown in Table 5.

Table 5.
Questionnaire design of travel behavior.
3.2. Investigation Process
This questionnaire was conducted by combining online and offline methods. In May 2022, the questionnaires were distributed online for a week through Wenjuanxing (a professional survey company that has conducted more than 50 million online surveys in China) and face-to-face questionnaires were conducted in Chongqing rail transit stations. In the end, a total of 107 valid questionnaires were collected.
3.3. Statistical Analysis
A total of 428 sample data were obtained from the questionnaire survey. To preliminarily judge the rationality of the questionnaire survey and screen the influencing factors of the passenger waiting tolerance, the statistical analysis of the sample data was conducted below.
As observed in Table 6, the male-to-female ratio and income distribution of the sample are consistent with the survey results published by the Chongqing Bureau of Statistics, which indicates that the sampling in this survey is more reasonable.

Table 6.
Descriptive statistics of socio-demographic attributes.
Further, the waiting time distribution for different personal attributes and travel characteristic attributes were statistically compared, as shown in Figure 1, to preliminarily screen the variables affecting the traveler waiting tolerance.
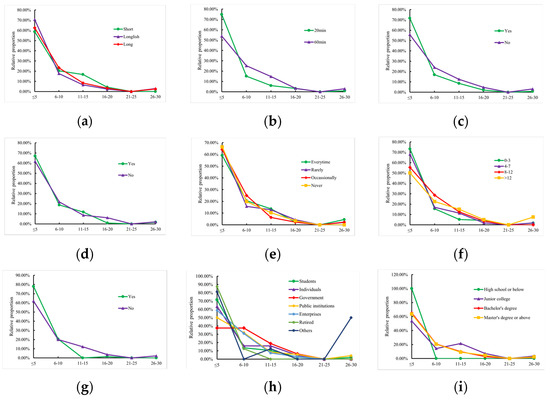
Figure 1.
Line chart of the waiting time distribution for the different attributes ((a). service interruption (SI) duration; (b). travel distance; (c). bus bridging; (d). information accuracy; (e). information usage; (f). travel frequency; (g). SI experience; (h). occupation; (i). education level).
4. Modeling of the Passenger Waiting Tolerance during URT Interruptions
4.1. Symbol Description
For a random time t, its cumulative distribution function can be expressed as
where F(t) represents the probability that the duration t is less than T and is the survival function, which represents the probability of the random variable T being higher than a specific value of interest t. If F(t) is differentiable in the domain, then the probability density function f(t) can be defined as
The above equation represents the probability that passengers would continue to wait after the service interruption occurs when the time is in the differential period []. According to the established requirements of the risk function, it can be obtained as follows.
Therefore, it can be proved that
Finally, the description of the symbols used above is shown in Table 7.

Table 7.
Symbol description.
4.2. Model Construction
The AFT model’s key assumption is that the influence of the explanatory variables is proportional to the time to live. The main reasons for choosing the AFT model are: (1) the structure contains explanatory variables that directly influence the survival time; (2) the goal of this study is to construct a model to predict the duration itself, rather than probability over time.
In the AFT model, the relationship between the logarithm of survival time and the vector of the explanatory variables is linear [21]
where X’ is the vector of the explanatory variable, β is the vector of the coefficient to be estimated and ε is the error term of the known distribution. The survival function of T under the condition of X’ is
It is necessary to transform the probability density estimation problem into a parameter estimation problem using the parameter estimation method. The maximum likelihood estimation provides a way to evaluate the parameters of a model given observational data.
The construct likelihood function of the right deleted data is
The total likelihood function of the right deleted data is
where indicates that time i has occurred, that is, whether it is detected or not.
Then,
The logarithm of the above equation would be
4.3. Model Estimation
It is assumed that a person’s survival time is equal to the population baseline survival time multiplied by the person’s acceleration factor in the AFT model. The assumption of the AFT model can be expressed as [22]
where is the survival function at the time t and the is the baseline survival function at the time t. The factor is known as the acceleration factor, which is the key measure of association obtained in the AFT model. It is a ratio of the survival times corresponding to any fixed value of the survival time. Then, the estimation of the AFT model is essentially the estimation of these factors.
5. Results and Discussion
5.1. Basic Data
The Chi-square test, which was widely used in the hypothesis test for the counting data, was conducted to verify the effect of 15 factors. This method is a nonparametric test for the correlation analysis of two or more sample rates and two categorical variables. The basic idea is to compare the consistency or goodness of fit between the theoretical frequency and the actual frequency. The value of represents the degree of deviation between the observed value and the theoretical value. Its formula is
where is the observation frequency of i level, is the expected frequency of i level, n is the total frequency and is the desired frequency of i level.
The Chi-square test was conducted in SPSS and the Chi-square values of 15 factors were obtained, as shown in Table 8. If the Chi-square value was greater than 0.05, it indicated that this factor had no significant impact on the passenger waiting time. If it was less than 0.05, it indicated that this factor had a significant impact on the passenger waiting time. It can be seen from the table that the Chi-square value of the three factors of travel time, weather and station arrival was greater than 0.05, indicating that these three factors would not significantly affect the waiting time of passengers. The Chi-square values of the remaining factors were all less than 0.05, indicating that they would have a significant impact on the passenger waiting time. The Chi-square test provided a reference and basis for the AFT model construction.

Table 8.
Chi-square test of the data.
Further, considering that there were several types of the above influencing variables, it was coded for the smooth calibration of the AFT model. The specific coding rules are shown in Table 9.

Table 9.
Coding description of the influencing factor variables.
5.2. Model Result
Figure 2 shows the initial Kaplan–Meier survival curve. Without considering these variables, the survival rate decreased gradually, that is, the longer the waiting time, the fewer passengers chose to continue to wait. The backward selection method was used for variable filtering. Considering the possible collinearity between the variables resulting in the significant interaction effects between the variables, we did not delete insignificant variables at one time. Instead, we used the method of deleting and recalibrating the model one by one and then eliminating them again. The final model results are shown in Table 10.
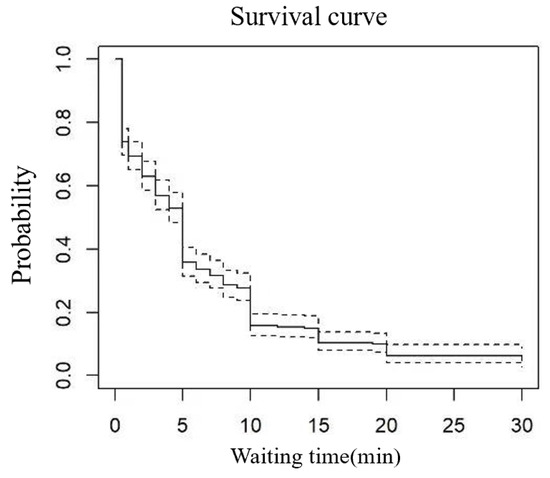
Figure 2.
Survival curve of the passenger waiting tolerance during URT service interruptions.

Table 10.
AFT result of the passenger waiting tolerance during URT service interruptions.
5.3. Discussion
Table 10 shows that variables such as the service interruption duration, travel distance, bus bridging service, information accuracy, information usage, travel frequency, service interruption experience, occupation and education level had significant influences on the passenger waiting tolerance during URT service interruptions. Some personal attributes, such as gender, similar to the findings of Rahimi et al., 2019 [8], failed to be estimated, which suggests that gender does not have a significant impact on the passenger waiting tolerance during URT service interruptions.
Furthermore, the results from Table 10 also reveal that travel characteristic attributes, such as the travel frequency, information service usage and information service accuracy, had significant influences on the passenger waiting tolerance. To our best knowledge, these travel characteristic attributes that provide a basis for the transportation department to formulate efficient emergency plans have not been studied thoroughly in the previous research in the field [2,8]. Specifically, the details about the findings will be explained though the sensitivity analysis of the model parameters in the next section.
5.4. Policy Analysis
One of the main purposes of the establishing AFT model was to improve our understanding of the system, and the sensitivity analysis of the model parameters was to analyze the dynamic change process of the mathematical model parameters, which can provide useful policy suggestion for URT managers.
Therefore, this study set six passengers of various property, listed in Table 11, as the object of the sensitivity analysis, conducted a sensitivity analysis on the service interruption duration (passenger #1 vs. #2), travel distance (passenger #3 vs. #4) and bus bridging service (passenger #5 vs. #6), and obtained the corresponding survival curve, as shown in Figure 3.

Table 11.
Property description of the objects used in the sensitivity analysis.
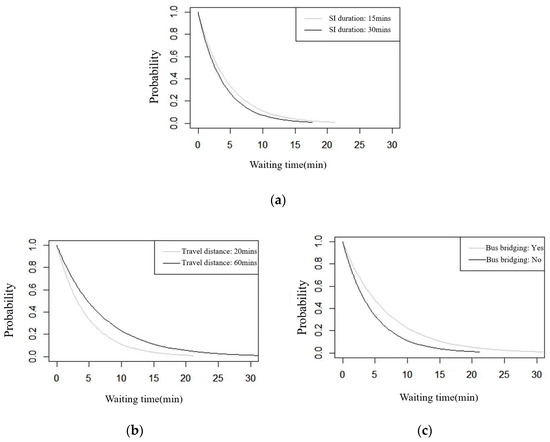
Figure 3.
Survival curves of different passengers. (a) passenger #1 vs. #2. (b) passenger #3 vs. #4. (c) passenger #5 vs. #6.
As seen in Figure 3a, the survival curve of passenger #1 was always above the survival curve of passenger #2, indicating that the passenger waiting tolerance would reduce when the service interruption duration became longer. Similarly, it can also be observed in Figure 3b,c that the survival curve of passenger #4 (#5) was always above the survival curve of passenger #3 (#6). The perspective can be given that the longer the travel distance, the higher the waiting tolerance of passengers. The passengers tended to wait longer with a higher waiting tolerance when bus bridging services were implemented.
Therefore, when formulating emergency plans, URT managers should first consider the expected duration of the service interruption and formulate an evacuation plan for the blocked passengers according to the duration, especially for longer interruptions that require a more timely and effective evacuation plan. At the same time, the results also suggest that URT managers can consider bus bridging services when formulating emergency plans, which can increase the waiting tolerance of the passengers to a certain extent and is helpful for the organization and management of passenger flow.
Moreover, in the light of the sensitivity analyzing results that passenger waiting tolerance would increase with an increase in their travel distance, managers should also pay attention to the travel destinations of the blocked passengers when formulating emergency plans. For the blocked passengers traveling short distances, the key is to timely organize a corresponding evacuation plan to make it possible for them to complete the trip. For long-distance travel passengers, managers can use some optimization models, such as these study forms [23,24,25,26], to obtain the optimal bus bridging plan to save operating costs.
6. Conclusions
In this study, we developed an AFT model for analyzing the passenger waiting tolerance during URT service interruptions based on the stated preference data collected in Chongqing. The major contribution of this study was the identification of the factors affecting the passenger waiting tolerance and the policy advice based on the sensitivity analysis, which could be used to better understand the reaction of the blocked passengers during URT service interruptions.
The estimation results of the proposed model verified that variables such as the service interruption duration, travel distance, bus bridging service, information accuracy, information usage, travel frequency, service interruption experience, occupation and education level had significant influences on the passenger waiting tolerance during URT service interruptions. The sensitivity analysis presented that the passenger waiting tolerance reduced when the service interruption duration (travel distance) became longer (shorter) or when bus bridging services were not implemented. Hence, URT managers formulate an evacuation plan for the blocked passengers according to the service interruption duration, especially for longer interruptions that require a more timely and effective evacuation plan. Meanwhile, managers should also pay attention to the travel destinations of the blocked passengers. Managers can consider bus bridging services when formulating emergency plans, which can increase the waiting tolerance of the passengers to a certain extent and is helpful for the organization and management of passenger flow.
The application of the proposed model was limited in this study, and more investigations into the sensitivity analysis and passenger demand forecasting based on the proposed AFT model will be conducted in the future. Meanwhile, we acknowledge that the results from the SP data may be different from the behavior of the blocked passengers in reality, so we would improve the model by adopting more advanced survey methods, such as interactive virtual reality experiments, to collect more behavioral data in the future study.
Author Contributions
Conceptualization, B.L. and J.L.; methodology, B.L., C.W. and J.L.; formal analysis, S.S.; investigation, B.L., Z.Y. and C.W; writing—original draft preparation, C.W.; writing—review and editing, B.L., Z.Y. and J.L.; supervision, J.L. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is unavailable due to privacy or ethical restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Questionnaire on the Passenger Waiting Tolerance during Urban Rail Transit Service Interruptions
Thank you very much for your help! The frequent occurrence of urban rail service interruptions has brought some troubles to passengers. The purpose of this survey is to analyze and study the waiting tolerance of passengers through questionnaire data collection to ensure passenger travel safety and improve the service level of rail transit. The questionnaire is an anonymous survey. The data obtained from the questionnaire will only be used for academic research. It will take about 5–10 min of your precious time. I hope you can fill in the questionnaire as truthfully and accurately as possible. Thank you for your cooperation and support!
Part I:
1. If you take the urban rail in the evening peak (the journey takes about 20 min), the weather is heavy and the service is interrupted when you are ready to enter the station by swiping your card. The announcement is that passengers who need to continue to take the rail transit should wait in place. It is expected that the interruption time will be short, and emergency shuttle buses are being prepared.
You can wait up to __________ min in this scenario.
2. If you take the urban rail in the morning peak (the journey takes about 20 min), the weather is fine and the service is interrupted when you are ready to enter the station by swiping your card. The announcement is that passengers who need to continue to take the rail transit should wait in place. The interruption time is expected to be 15 min, and emergency shuttle buses are being prepared.
You can wait up to __________ min in this scenario.
3. If you take the urban rail in the evening peak (the journey takes about 60 min), the weather is heavy and the service is interrupted when you are ready to enter the station by swiping your card. The announcement is that passengers who need to continue to take the rail transit should wait in place, and the expected interruption time is 60 min.
You can wait up to __________ min in this scenario.
Part II:
1. Do you usually pay attention to the real-time operation information of Chongqing rail transit during your trip? Such as the line full load rate, current limiting measures, emergencies, etc.
○ Every time
○ Rarely
○ Occasionally
○ Never
2. The number of times you have taken rail transit in the last week (each trip counts as one time):
○ 0–3 times
○ 3–7 times
○ 8–12 times
○ More than 12 times
3. Have you ever encountered a service interruption in the process of taking rail transit:
○ Yes
○ No
4. Your last experience of an urban rail service disruption:
Line ○ Line 1 ○ Line 2 ○ Line 3 ○ Line 5 ○ Line 6 ○ Loop Line
Interruption time ○ 0–10 min ○ 10–20 min ○ 20–30 min ○ more than 30 min
Waiting time ○ 0–5 min ○ 5–10 min ○ 10–20 min ○ 20–30 min ○ over 30 min
Change of travel mode ○ Yes ○ No
Part III:
1. Your gender:
○ Male
○ Female
2. Your age:
○ Under 18 years old
○ 18~30
○ 31~40
○ 41~50
○ 51~60
○ Over 60 years old
3. Your current occupation:
○ Student
○ Individual
○ Government
○ Public institution
○ Enterprise
○ Retired
○ Other
4. Your education level
○ High school and below
○ Junior college
○ Undergraduate
○ Master and above
5. What is your monthly pre-tax income?
○ Below 3000
○ 3000–5000
○ 5000–8000
○ 8000–12,000
○ Over 12,000
References
- Li, B.; Yao, E.; Yamamoto, T.; Tang, Y.; Liu, S. Exploring Behavioral Heterogeneities of Metro Passenger’s Travel Plan Choice under Unplanned Service Disruption with Uncertainty. Transp. Res. Part A Policy Pract. 2020, 141, 294–306. [Google Scholar] [CrossRef]
- Lin, T.Y.-T. Transit User Mode Choice Behaviour in Response to TTC Rapid Transit Service Disruption; University of Toronto: Toronto, ON, Canada, 2017. [Google Scholar]
- Saberi, M.; Ghamami, M.; Gu, Y.; Shojaei, M.H.; Fishman, E. Understanding the Impacts of a Public Transit Disruption on Bicycle Sharing Mobility Patterns: A Case of Tube Strike in London. J. Transp. Geogr. 2018, 66, 154–166. [Google Scholar] [CrossRef]
- Nazem, M.; Lomone, A.; Chu, A.; Spurr, T. Analysis of Travel Pattern Changes Due to a Medium-Term Disruption on Public Transit Networks Using Smart Card Data. Transp. Res. Procedia 2018, 32, 585–596. [Google Scholar] [CrossRef]
- Nguyen-Phuoc, D.Q.; Currie, G.; De Gruyter, C.; Young, W. Transit User Reactions to Major Service Withdrawal—A Behavioural Study. Transp. Policy 2018, 64, 29–37. [Google Scholar] [CrossRef]
- Nguyen-Phuoc, D.Q.; Currie, G.; De Gruyter, C.; Young, W. How Do Public Transport Users Adjust Their Travel Behaviour If Public Transport Ceases? A Qualitative Study. Transp. Res. Part F Traffic Psychol. Behav. 2018, 54, 1–14. [Google Scholar] [CrossRef]
- Adelé, S.; Tréfond-Alexandre, S.; Dionisio, C.; Hoyau, P.-A. Exploring the Behavior of Suburban Train Users in the Event of Disruptions. Transp. Res. Part F Traffic Psychol. Behav. 2019, 65, 344–362. [Google Scholar] [CrossRef]
- Rahimi, E.; Shamshiripour, A.; Shabanpour, R.; Mohammadian, A.; Auld, J. Analysis of Transit Users’ Waiting Tolerance in Response to Unplanned Service Disruptions. Transp. Res. Part D Transp. Environ. 2019, 77, 639–653. [Google Scholar] [CrossRef]
- Rahimi, E.; Shamshiripour, A.; Shabanpour, R.; Mohammadian, A.; Auld, J. Analysis of Transit Users’ Response Behavior in Case of Unplanned Service Disruptions. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 258–271. [Google Scholar] [CrossRef]
- Li, J.; Wang, X. Multimodal Evacuation after Subway Breakdown: A Modeling Framework and Mode Choice Behavior. Transp. Res. Interdiscip. Perspect. 2020, 6, 100177. [Google Scholar] [CrossRef]
- Li, B.; Yao, E.; Yamamoto, T.; Huan, N.; Liu, S. Passenger Travel Behavior Analysis under Unplanned Metro Service Disruption: Using Stated Preference Data in Guangzhou, China. J. Transp. Eng. Part A Syst. 2020, 146, 04019069. [Google Scholar] [CrossRef]
- Liu, T.; Ma, Z.; Koutsopoulos, H.N. Unplanned Disruption Analysis in Urban Railway Systems Using Smart Card Data. Urban Rail Transit 2021, 7, 177–190. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Yu, R. Modeling Disruption Durations of Subway Service via Random Survival Forests: The Case of Shanghai. J. Transp. Saf. Secur. 2023, 15, 215–237. [Google Scholar] [CrossRef]
- Cong, C.; Li, X.; Yang, S.; Zhang, Q.; Lu, L.; Shi, Y. Impact Estimation of Unplanned Urban Rail Disruptions on Public Transport Passengers: A Multi-Agent Based Simulation Approach. Int. J. Environ. Res. Public Health 2022, 19, 9052. [Google Scholar] [CrossRef]
- Valsalan, N.; Haritha, P.C.; Anjaneyulu, M.V.L.R. Travelers’ Response to Network Disruptions in Ernakulam City. In Recent Advances in Transportation Systems Engineering and Management: Select Proceedings of CTSEM 2021; Springer: Singapore, 2023; pp. 885–899. [Google Scholar]
- Pender, B.; Currie, G.; Delbosc, A.; Shiwakoti, N. Addressing Passenger Needs during Unexpected Rail Disruptions—An Internationa Survey. In Proceedings of the WCTR, Rio de Janeiro, Brazil, 15–18 July 2013; pp. 1–20. [Google Scholar]
- Dell’Olio, L.; Ibeas, A.; Barreda, R.; Sañudo, R. Passenger Behavior in Trains during Emergency Situations. J. Saf. Res. 2013, 46, 157–166. [Google Scholar] [CrossRef]
- Murray-Tuite, P.; Wernstedt, K.; Yin, W. Behavioral Shifts after a Fatal Rapid Transit Accident: A Multinomial Logit Model. Transp. Res. Part F Traffic Psychol. Behav. 2014, 24, 218–230. [Google Scholar] [CrossRef]
- Pnevmatikou, A.M.; Karlaftis, M.G.; Kepaptsoglou, K. Metro Service Disruptions: How Do People Choose to Travel? Transportation 2015, 42, 933–949. [Google Scholar] [CrossRef]
- Golshani, N.; Shabanpour, R.; Mohammadian, A.; Auld, J.; Ley, H. Evacuation Decision Behavior for No-Notice Emergency Events. Transp. Res. Part D Transp. Environ. 2019, 77, 364–377. [Google Scholar] [CrossRef]
- Sun, J. The Statistical Analysis of Interval-Censored Failure Time Data; Springer: New York, NY, USA, 2006. [Google Scholar]
- Saikia, R.; Pratim, M. A Review on Accelerated Failure Time Models. Int. J. Stat. Syst. 2017, 12, 311–322. [Google Scholar]
- Pender, B.; Currie, G.; Shiwakoti, N.; Delbosc, A. Economic Viability of Bus Bridging Reserves for Fast Response to Unplanned Passenger Rail Disruption. Transp. Res. Rec. J. Transp. Res. Board 2019, 2537, 13–22. [Google Scholar] [CrossRef]
- Gu, W.; Liu, Y.; Ji, Y.; Zhang, H.M.; Zheng, Y. Optimizing Bus Bridging Strategies during Metro Disruptions Considering Bridging Time and Passenger Delays. In CICTP 2017: Transportation Reform and Change—Equity, Inclusiveness, Sharing, and Innovation, Proceedings of the 17th COTA International Conference of Transportation Professionals, Shanghai, China, 7–9 July 2017; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 1694–1705. [Google Scholar]
- Zheng, Y.J.; Gu, W.; Ji, Y.X.; Zhang, H.J. Optimizing a Bus Bridging Strategy Considering Efficiency and Equity. Jiaotong Yunshu Xitong Gongcheng Yu Xinxi/J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 94–101. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, J.; Currie, G.; Ceder, A.; Dong, W.; Pender, B. Bus Bridging Disruption in Rail Services With Frustrated and Impatient Passengers. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2014–2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).