Abstract
This study examines the mechanism of nonlinear supratransmission (NST), which involves the transfer of disturbance to discrete media at frequencies not supported by the structure. We considered a model crystal with A3B stoichiometry. The investigation was carried out using atomistic modeling through molecular dynamics. The interatomic interaction was determined by a potential obtained through the embedded atom method, which approximates the properties of the Pt3Al crystal. The effect of NST is an important property of many discrete structures. Its existence requires the discreteness and nonlinearity of the medium, as well as the presence of a forbidden zone in its spectrum. This work focuses on the differences in the NST effect due to the anisotropy of crystallographic directions. Three planes along which the disturbance caused by NST propagated were considered: (100), (110), and (111). It was found that the intensity of the disturbance along the (100) plane is an order of magnitude lower than for more densely packed directions. Differences in the shape of solitary waves depending on the propagation direction were shown. Moreover, all waves can be described by a single equation, being a solution of the discrete variational equations of macroscopic and microscopic displacements, with different parameters, emphasizing the unified nature of the waves and the contribution of crystal anisotropy to their properties. Studying the NST phenomenon is essential due to numerous applications of the latter, such as implications in information transmission and signal processing. Understanding how disturbances propagate in discrete media could lead to advancements in communication technologies, data storage, and signal amplification where the earlier mentioned ability to describe it with analytical equations is of particular importance.
1. Introduction
Non-linear discrete structures can produce a range of effects, which are defined by the nature of particle interactions within the system and its geometry. As a result, a synergistic component arises in various processes, such as energy transport and localization. This research focuses on one such process that involves both localization and energy transport-non-linear supratransmission (NST). This phenomenon was first reported in the works of F. Geniet and J. Leon in 2002 [1], building on the foundations laid in the previous year [2]. The core of this effect is the transfer of energy at frequencies that are not supported by the analyzed systems. The initial authors established the conditions for the manifestation of Nonlinear Energy Transfer (NET) in a discrete chain, which facilitates energy transfer at frequencies beyond the system’s spectrum. It is a matter of fact that energy enters the system once the amplitude of the external harmonic excitation surpasses the maximum amplitude of the static discrete breather at the same frequency. However, it is worth noting that more recently, in the work [3], it was shown for graphene that such a threshold is not necessary. However, in this case, we can also talk about infratransmission. The effect of NST comes from the nonlinear nature of interatomic bonding and cannot be related to the simulation artefact since they were observed in various nonlinear periodic systems including mechanical ones [4] and computational models with extremely different nonlinearity types and initial conditions excluding the possibility of the appearance of the common artefact. One can recall Nonlinear Supratransmission in Quartic Hamiltonian Lattices with globally interacting particles and On-Site Potentials [5], Gap soliton formation by nonlinear supratransmission in Bragg media [4], and energy transfer by NST mechanism in finite granular chains [6].
For a more profound comprehension of the energy transmission mechanism in this context, it is crucial to contemplate the notion of a discrete breather (DB). In essence, a DB denotes localized, strictly periodic oscillatory modes with high amplitudes in nonlinear discrete systems [7]. The discovery of DBs as time-periodic solutions localized in discrete space was initially rigorously proven in [8] for infinite chains of locally diffusively coupled nonlinear oscillators.
Numerous studies have been dedicated to this phenomenon, exploring theoretical, applied, and experimental aspects [9,10,11]. The diversity of systems supporting DBs has led to discussions about their contribution to various properties of discrete structures, including macroscopic ones [12]. For example, one recent study demonstrated the contribution of breathers to the heat capacity of crystals [13].
In the context of the discussed issue, it is imperative to discuss discrete breathers in complex systems, whether they are actual or model systems, with precision. The issue is that a precisely periodic entity over time can be solely obtained via numerical modelling or through natural experiments, given the optimum adjustment of the initial conditions of the Cauchy problem to a lower-dimensional manifold in the multidimensional space of all probable initial values of both particles’ coordinates and velocities [14,15]. Achieving such exact adjustment is challenging, even in computational experiments. Moreover, it is exceedingly difficult to achieve this when conducting any physical experiments, particularly in situations where breather-like objects emerge spontaneously [14,15,16,17]. The cause for this phenomenon can be attributed to energy dissipation [17]. In general, the potential presence of discrete breathers can act as an indicator of the nonlinearity of the crystal lattice, which in turn may be a cause for various phenomena such as spontaneous localization, effective mass, and energy transport, as discussed in references [18,19,20,21,22].
Thus, the significance of nonlinear excitations in the manifestation of discrete breathers is fundamental for the accomplishment of the supratransmission effect. F. Geniet and J. Leon highlight the importance of localized excitations in the dissemination of energy throughout the system from the periodic action source. Expanding on this subject in further writings [23,24,25], the authors assert that the noted impact is all-encompassing and applicable to any distinct systems with a restricted range of frequencies from different sources. Supratransmission is irrespective of the integrability of the system, resilient to attenuation, and distinct categories of perimeter conditions. Furthermore, provided that certain general conditions imposed on the structure of nonlinearity are met, the nonlinear discrete medium is capable of causing instability of a decaying profile which has been brought about by external periodic forcing. This instability is a generative process that underlies nonlinear supratransmission, and can occur when the system supports nonlinear modes of various natures.
The main studies of this effect are focused in the field of mathematical physics and address questions related to the search for exact solutions of differential equations, including the Schrödinger equation. This leads to a step-by-step complexity of models of physical systems. On one hand, subjective evaluations are excluded in order to make it impossible to find an analytical solution that would allow for the prediction and study of the NST effect via mathematical modeling in such systems. On the other hand, more complex systems incorporate a wider range of forms and characteristics of nonlinear effects. The works [26,27] address the Schrödinger equation and demonstrate the effectiveness of the proposed asymptotic method for investigation of the supratransmission and solitonic properties. This work presents a method for determining the NST threshold in non-integrable N-component systems by obtaining an asymptotic solution based on the linear decaying profile of a soliton with N parameters. The authors also propose a method for generating and studying the dynamics of spatial optical solitons in a birefringent medium with quadratic nonlinearity, which is developed in [28]. Technical terms are explained upon first usage and objective language is consistently used throughout the passage. In [29], it was demonstrated for the first time that the supratransmission threshold can be identified for the discrete nonlinear Schrödinger equation, which models arrays of optical waveguides with Kerr nonlinearity, through the use of a two-dimensional map method. Current research into systems based on the discrete Schrödinger equation is dedicated to examining the development of dark solitons [30], with a focus on the potential for creating devices for generating discrete gap solitons.
In addition to theoretical studies, numerous works exist addressing the practical application of the NST effect. An interesting and promising application of the NST effect could be the development of a heat pump. The idea was proposed in [31]. The peculiarity of practical application is that the thermal resonance effect does not depend on the size of the considered systems. Therefore, further developments could be expected regarding thermal resonance and energy pumping in various physical systems, for example, in granulated systems. One of the recent works [32] is dedicated to such objects. In it, the NST effect was discovered, as well as four other energy transfer modes. It is emphasized that the obtained results can be useful in the construction of mechanical or other types of flow control. Research on physically more complicated models of systems, such as linked pairs of pendulum chains, is also ongoing [33,34]. Both experimental methodology and numerical experiments were used by the authors. An even more complex configuration is considered in [35], with a comprehensive approach to studying various modes of the mechanical system, including the construction of a nonlinear Schrödinger equation using the perturbation method. The equation is used to search for modulated pulses and dark solitons as approximate solutions of the network equation.
In the discourse on nonlinear supratransmission support systems, emphasis is placed on metastable modular metastructures. Researchers carry out numerical and analytical studies of these structures in the works [36,37,38,39]. The studies reveal that the energy transmission coefficient can greatly increase during bifurcation instability, provided the input signal amplitude surpasses a specific threshold. By incorporating supratransmission properties within a nonlinear periodically asymmetric chain, the metastable structure provides non-reciprocal wave propagation along the chain through the utilization of nonlinear supratransmission. In this study, the authors introduce an effective methodology with considerable potential for designing systems with adaptable characteristics of non-reciprocal wave energy propagation using the concept of reconfigurable metastable modular metastructure.
It should be noted that an article [40] was published in 2020 that presented a summary of the findings from numerous works for one-dimensional cases. When first introduced, technical term abbreviations should be explained. The author advocates for additional local and global stability analysis of simple periodic oscillations in order to identify areas of energy and parameters that are linked to globally stable motion, as well as various strong and weak chaos regimes. The addressed research goes in line with other studies of suptratransmission in lattices of reduced dimensionality [41,42].
Summarizing the provided brief literature review, it can be concluded that interest in this effect is increasing, and there are more practical applications for its implementation. Discrete structures are extremely extensive, with crystalline materials, particularly metals and alloys, being one of the broadest classes. This study focuses on a crystal of stoichiometry A3B, supporting discrete breathers and the effect of nonlinear supratransmission [43,44,45,46,47]. The manifestation of this effect has been examined in our previous works [44,45,46]. Here, a more detailed analysis of the role of crystal anisotropy on the characteristics of solitary waves excited as a result of the NST effect will be conducted.
2. Materials and Methods
Molecular dynamics appears to be a perfect tool for reaching the earlier addressed goal of the research. It has proven to be a reliable and well-established approach for solving problems associated with energy localization issues. Its application allows the detailed analysis of numerous nonlinear effects in realistic structures, such as crystalline lattices of metals and alloys [48,49,50,51]. The study of a two-dimensional model of the Pt3Al alloy can be considered as one of initial works in this direction [47]. The interaction of atoms was described by the Morse pair potential: , where D is the energy parameter corresponding to the depth of the potential well, α—parameter that determines the rigidity of interatomic bonds, —interatomic distance. The verification of the potential is accomplished by comparing it with known experimental data on material parameters. Pair potentials, while having a clear and simple methodology for construction, may not fully describe the properties of materials, such as those with covalent bonds. Also, such potentials are unsuitable for describing the free surface of metals and alloys. In turn, in this work, we use the potential, devoid of these shortcomings, obtained by the embedded atom method [52]. The total energy of the crystal for given potentials can be expressed as
where represents the pair energy between atoms i and j separated from each other by a distance , Fi is the nesting energy associated with embedded atom i at a local position with electron density . The electron density can be calculated using the formula , where —electron density in the area of atom i located at a distance from atom j. The ability of EAM potentials to describe properties of simulated systems that were not included in the fitting dataset is a key advantage of EAM potentials.
We applied an EAM potential for Pt3Al has been obtained using the methodology proposed by Zhou [52]. Atoms in a Pt3Al intermetallic compound are located on the sites of a FCC lattice and belong to Space Group Pm3m, point group 221. Let us consider in more detail the features of constructing potentials according to the methodology suggested in [53]. The EAM potential for a pure element consists of three functions: pair energy φ, electron density ρ, and embedding energy F. For an alloy, the EAM potential contains not only the three functions φ, ρ, and F, for each of the constituent elements but also the pair energy between different elements a and b (a ≠ b). As a result, the φ, ρ, and F functions adapted for elemental metals cannot be directly applied to alloys or multilayer systems. However, by normalizing the EAM potentials and introducing an alloy model, Zhou proposed a procedure for generalizing EAM potentials and their cutoff distances. This procedure enables the construction of EAM potentials for alloys from EAM potentials for individual elements. In this model of the EAM potential for an alloy, the generalized element pair potentials are described as follows:
where re is the equilibrium distance between neighboring atoms, A, B, α, β—are four adjustable parameters, and k and λ is two additional options. The electron density function has the form
In our work [54], tests were conducted on this potential along with others. The preliminary results are in satisfactory agreement with an earlier first-principles study [55].
The experimental setup was similar to the one described in [44,55]. Here, we will discuss the details the experimental procedure for investigating the effect of nonlinear supertransmission as a function of crystal lattice orientation. The crystal models consisted of elongated parallelepipeds, each containing approximately 106 particles, with different orientations along the axes. The linear dimensions along the x and y axes were up to 100 Å, while along the z axis, it was up to 3.5 × 103 Å. For crystal orientations along the x and y axes, periodic boundary conditions were applied, while along the z axis, rigid boundary conditions were used (Figure 1).
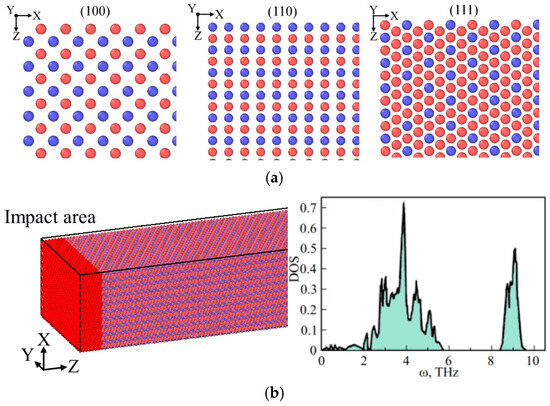
Figure 1.
Fragments of model cells and experimental setup: (a) crystal planes along which the propagation of nonlinear supratransmission waves was initiated, (b) schematic diagram of the experiment and the phonon density of states of the Pt3Al crystal [54].
The modeling process consisted of a conditional partitioning of the computational cell into regions. The first region consisted of 5–10 atomic layers that underwent harmonic oscillations according to specified frequency ranges and amplitudes of atomic vibrations (Figure 1b). The remaining part of the crystal was used to analyze the propagation of energy along the model. On the opposite edge of the affected region, several rows of atoms were rigidly fixed, ensuring that the entire model remained motionless as a whole, which could lead to unjustified conclusions regarding energy absorption. Frequencies corresponding to the forbidden region in the spectrum were considered: from 5.9 to 8.5 THz. The magnitude of the applied amplitude ranged from 0.03 to 0.3 angstroms. The calculations were performed using the LAMMPS software package version 6.1.
After specifying the necessary interaction parameters of the computational system, the next stage involved the minimization and relaxation of the model. This was carried out to reduce the initial stresses in the system. Built-in LAMMPS functions based on the conjugate gradient energy minimization algorithm were used for minimization. Subsequently, simulations were performed with a sweep of frequencies and amplitudes for different directions at an initial temperature of 0 K and pressure of 0 bar using the NVE ensemble. The integration time step was set to 0.3 fs, ensuring an optimal balance between computation time and accuracy of calculations.
3. Results and Discussion
The initialization of nonlinear supratransmission (NST) during normal harmonic excitation of the crystal surface is associated with the excitation of nonlinear high-amplitude modes near the region of the applied excitation. This fact is addressed in the early works [1,2] dedicated to nonlinear supratransmission, as well as in our own works on the studied crystal [41,46]. It is evident that the anisotropy of the crystalline structure influences the parameters of such excitation modes. As we have determined, for a crystal of the stoichiometry A3B, the most favorable directions for the existence of discrete breathers are the {100} set of crystallographic orientations. However, in the presence of external excitation, such oscillations can be sustained and exist for a extended period of time, sufficient for the initialization of NST.
It has been found that the nonlinear modes are most actively excited for all three crystal orientation options at frequencies close to the optical branch. This corresponds to the eigenfrequencies of the breathers in this crystal, which vary in the range of 7.84–8.31 THz [46]. To demonstrate the generated waves, let us consider the wave propagation along the (111) plane (Figure 1a). The characteristic energy profile is shown in Figure 2a. In general, this fact goes in line with results addressing energy transfer by NST mechanism discussed in [56,57,58,59].
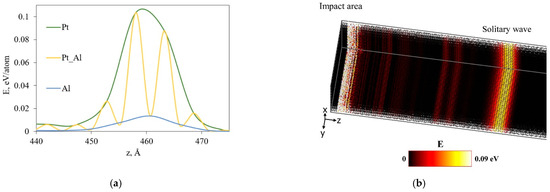
Figure 2.
Energy profile of the excited solitary wave along the (111) plane: (a) distribution of kinetic energy per atom in the solitary wave, (b) visualization of kinetic energy distribution in the computational cell at 10 picoseconds of the experiment, axes oriented along the following crystallographic directions X − [], Y − [111], Z − []. External excitation parameters: frequency 8.25 THz, amplitude 0.18 Å.
In Figure 2a, we can see the energy profile of the solitary wave in the NST. Due to biatomic nature of the crystal, we have an uneven distribution of energy between sublattices. This is caused by the different masses of the alloy components. It is worth noting that the wave profiles in the sublattices are different. The wave in the Al sublattice slightly precedes the wave in the Pt sublattice. The reason for this distribution is the excitation of such waves by discrete breathers near the impact zone. The carriers of the DB are light atoms, i.e., Al, thus when energy is localized on atoms involved in the DB, it is transferred to the Al sublattice and then a transfer to Pt atoms takes place. For a series containing Pt and Al atoms, the energy profile has a complex shape (yellow line on the graph). However, when considering each component separately, we observe the same profile as for the monoatomic series. This effect is typical for all crystallographic directions investigated.
Let us take a closer look at the difference during propagation along the considered planes (Figure 3). To accomplish this, we will choose a moment of observation at the same time interval from the beginning of the numerical experiment and for the same external excitation parameters. It is noteworthy that there is a significantly smaller energy reserve on the more “loose” (100) plane under the same external harmonic excitation parameters.
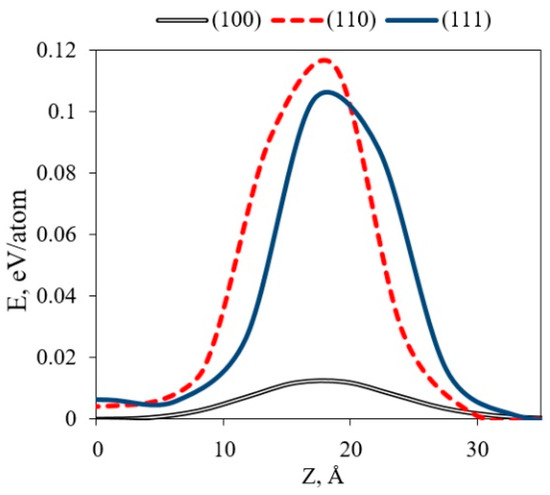
Figure 3.
Distribution of kinetic energy per atom in the solitary wave (Pt rows). The relative coordinates of atoms in angstroms are plotted along the x-axis, and the energy per atom is plotted along the y-axis. For all cases, the conditions for examining the wave profile corresponded to 10 picoseconds from the beginning of the experiment, with external excitation parameters: frequency 8.25 THz, amplitude 0.18 Å.
The reason for such differences may be due to the fact that along this direction, the excitation of nonlinear high-amplitude modes (discrete breathers) is most natural from an energetic point of view. They are more stable and transfer energy to neighboring aluminum atoms with a lower energy threshold. In turn, for the (110) and (111) planes, there is a significant increase in energy per atom in the wave, more than 10 times. This process occurs due to the alternation of Pt and Al atoms along the directions of propagation of isolated waves. Thus, despite the decrease in distance between neighboring atomic rows for the transmission of excitation similar to the type of atoms, a greater energy barrier needs to be overcome in the excitation process of NST waves. This emphasizes the role of crystal anisotropy in the formation of isolated excitations in the nonlinear supratransmission effect.
Let us consider the role of frequencies and amplitudes for each wave propagation plane in NST. Figure 4 shows graphs illustrating the dependence of perturbation energy along the plane on the frequency and amplitude of the impact. Here, three frequencies are presented: 6.48, 7.05, and 8.28 THz. They correspond to the gap regions in the crystal’s phonon spectrum closer to the acoustic branch, in the middle of the forbidden zone, and closer to the optical branch of the spectrum. For all wave propagation planes, the intensity of perturbation penetration into the crystal is two orders of magnitude lower for frequencies close to the acoustic branch. As we mentioned earlier, the reason for this is that these frequencies are far from the DI frequencies and are not multiples of them. Thus, there is no accumulation of energy near the impact zone with subsequent transmission in the form of isolated waves in the crystal. Speaking of the NST threshold in terms of amplitude, it was about 20 Å for the (100) plane and 14 Å for the (110) and (111) planes. In other words, at such an amplitude of harmonic impact, there is a proportional increase in the intensity of the perturbation propagating in the crystal.
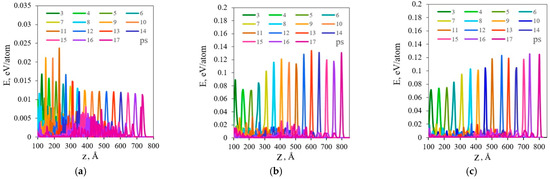
Figure 4.
Evolution of the profile of solitary supratransmission waves from 3 to 17 picoseconds. Propagation plane (100) (a), (110) (b), (111) (c). Atom coordinates in angstroms are plotted along the x-axis, and energy per atom is plotted along the y-axis. Excitation parameters for waves in the model crystal for (a) and (b) are ϖ = 8.28 THz, A = 0.18 Å, and for (c) are ϖ = 8.28 THz, A = 0.24 Å.
The process of evolution of isolated NST waves is shown in Figure 4. Here, the difference in wave shape for the considered directions is also evident. In the case of the (100) plane, there is a slight decrease in amplitude and broadening of the wave, which includes up to 14 atoms of the heavy sublattice. For propagation directions with higher density within the (110) and (111) planes, the opposite effect is observed. Ultimately, it makes sense to talk about eight atoms involved in the NST wave. The periodically changing amplitude of the isolated waves for the (110) and (111) planes is caused by perturbations induced by the impact before the generation of the isolated wave. However, for the (100) plane, this did not occur due to the complete absorption of all external influences.
In conclusion, we will discuss the analytical description of solitary waves excited within the framework of nonlinear supratransmission. In [58], a solution to the discrete variational equations of macroscopic and microscopic displacements in the form of solitary waves for solids was obtained.
The equations considered in [58] are a nonlinear generalization of the linear equations of acoustic and optical modes derived by M. Born and H. Kun [59]. We have modified the arguments (4) to the following form:
where q is the generalized coordinate, —coordination factor, —multiplier having the dimension of speed, α—amplitude multiplier, t—time parameter. This allowed us to switch to generalized coordinates and reconcile theoretical values with data obtained from models. Within the framework of solving the stated problem, coefficients λ, V, and α were selected for each of the propagation planes of solitary supratransmission waves. Thus, Equation (4) is a dimensionless quantity that allows for describing the disturbance profile in the considered discrete medium. Figure 5 shows the corresponding wave parameters and coefficients.
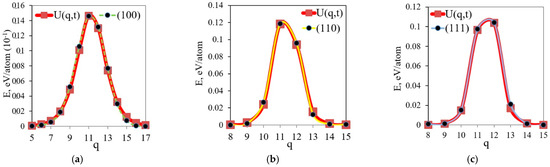
Figure 5.
Profiles of solitary waves of Function (4) and waves of nonlinear supratransmission. Generalized atom coordinates in angstroms are plotted along the x-axis, and energy per atom is plotted along the y-axis. Parts (a–c) of the figures correspond to the propagation planes of waves in the model experiment (100), (110), and (111). Excitation parameters for waves in the model crystal are the same for all planes: ϖ = 8.28 THz, A = 0.18 Å, observation time is 15 ps after the start of the experiment. Parameters for Function (4) in cases (a) are λ = 0.83, V = 0.199, α = 66.01; (b) λ = 1.91, V = 0.378, α = 6.15; (c) λ = 2.195, V = 0.2085, α = 6.38.
The main result is that regardless of the direction of propagation of supratransmission waves in the crystal, each wave is described by the same Equation (4) for discrete structures. This result suggests a unified nature of wave generation-high-amplitude excitations near the region of impact on the crystal. The shape of the wave, however, is determined by the characteristics of the crystallographic direction, i.e., the relative arrangement of lattice atoms.
An important aspect is the propagation velocity of solitary waves. All considered perturbations are supersonic. Their velocity is higher than the speed of sound waves by 5–10%. For the propagation planes (110) and (111), the velocity was approximately 4.75 × 103 m/s. For the (100) propagation plane, the velocity was 4.45 × 103 m/s. The velocity of such waves does not depend on the amplitude or frequency of excitation, as they are generated by discrete breathers near the impact zone. The wave generation process is in this case initiated after reaching the required energy threshold level.
4. Conclusions
Crystallographic directions with the highest packing density are revealed to be the most effective for energy transport by NST mechanism waves. In this case, we are talking about crystallographic rows in which two types of atoms are located and surrounded by rows of atoms of the same type. In this case, such a plane was found to be (110). A slightly lower intensity of NST waves is observed for the (111) plane, which is caused by the mutual displacement of atoms in the light sublattice relative to each other in adjacent planes. In turn, the less dense direction along the (100) plane provided waves with an order of magnitude lower intensity. However, the number of atoms involved in such an oscillation is twice as high.
The profile of the isolated NST waves varies with the direction of propagation (Figure 5). All considered planes of wave motion are described by a single Equation (4), which is a solution to the discrete variational equations of macroscopic and microscopic displacements of atoms in crystalline structures. To demonstrate this, the equation parameters have been chosen to give a satisfactory fit between the profile of the analytical function and the data obtained from the computer model. This emphasizes the unified nature of the waves and the contribution of crystal anisotropy to their properties.
The results obtained in this study are in good agreement with our previous data for the Pt3Al crystal. In particular, the perturbation propagation velocities caused by NST are supersonic isolated waves for all considered propagation planes.
Understanding the dependence of the energy transfer dynamics by the NST mechanism for different crystallographic directions of the crystal and its analytical fitting performed in this work can serve as part of the scientific background required to promote new technologies in communications, data storage and signal amplification.
Author Contributions
Conceptualization, P.V.Z. and E.A.K.; methodology, P.V.Z.; software and investigation, A.S.K.; resources and data curation, A.A.I. All authors have read and agreed to the published version of the manuscript.
Funding
The research is funded by the Ministry of Science and Higher Education of the Russian Federation as part of the World-class Research Center program: Advanced Digital Technologies (contract No. 075-15-2022-311 dated 20 April 2022).
Data Availability Statement
Research data are available from the corresponding author upon reasonable request.
Acknowledgments
The authors wish to acknowledge Peter the Great Saint-Petersburg Polytechnic University Supercomputer Center “Polytechnic” for the computational resources.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Geniet, F.; Leon, J. Energy transmission in the forbidden band gap of a nonlinear chain. Phys. Rev. Lett. 2002, 89, 134102. [Google Scholar] [CrossRef] [PubMed]
- Caputo, J.-G.; Leon, J.S. Nonlinear energy transmission in the gap. Phys. Lett. A 2001, 283, 129–135. [Google Scholar] [CrossRef]
- Evazzade, I.; Lobzenko, I.P.; Korznikova, E.A.; Ovid’ko, I.A.; Roknabadi, M.R.; Dmitriev, S.V. Energy transfer in strained graphene assisted by discrete breathers excited by external ac driving. Phys. Rev. B 2017, 95, 035423. [Google Scholar] [CrossRef]
- Frazier, M.J.; Kochmann, D.M. Band gap transmission in periodic bistable mechanical systems. J. Sound Vib. 2017, 388, 315–326. [Google Scholar] [CrossRef]
- Macías-Díaz, J.; Bountis, T. Nonlinear Supratransmission in Quartic Hamiltonian Lattices with Globally Interacting Particles and On-Site Potentials. J. Comput. Nonlinear Dyn. 2021, 16, 021001. [Google Scholar] [CrossRef]
- Leon, J.; Spire, A. Gap soliton formation by nonlinear supratransmission in Bragg media. Phys. Lett. A 2004, 327, 474–480. [Google Scholar] [CrossRef]
- Flach, S.; Willis, C.R. Discrete Breathers. Phys. Rep. 1998, 295, 181–264. [Google Scholar] [CrossRef]
- MacKay, R.S.; Aubry, S. Proof of existence of breathers for time-reversible or Hamiltonian networks of weakly coupled oscillators. Nonlinearity 1994, 7, 1623–1643. [Google Scholar] [CrossRef]
- Flach, S.; Gorbach, A.V. Discrete breathers—Advances in theory and applications. Phys. Rep. 2008, 467, 1–116. [Google Scholar] [CrossRef]
- Manley, M.E. Impact of intrinsic localized modes of atomic motion on materials properties. Acta Mater. 2010, 58, 2926–2935. [Google Scholar] [CrossRef]
- Cuevas-Maraver, J.; Chacon, R.; Palmero, F. Impulse-induced generation of stationary and moving discrete breathers in nonlinear oscillator networks. Phys. Rev. E 2016, 94, 062206. [Google Scholar] [CrossRef]
- Upadhyaya, A.; Semenova, M.N.; Kudreyko, A.A.; Dmitriev, S.V. Chaotic discrete breathers and their effect on macroscopic properties of triangular lattice. Commun. Nonlinear Sci. Numer. Simul. 2022, 112, 106541. [Google Scholar] [CrossRef]
- Singh, M.; Morkina, A.Y.; Korznikova, E.A.; Dubinko, V.I.; Terentiev, D.A.; Xiong, D.; Naimark, O.B.; Gani, V.A.; Dmitriev, S.V. Effect of Discrete Breathers on the Specific Heat of a Nonlinear Chain. J. Nonlinear Sci. 2021, 31, 12. [Google Scholar] [CrossRef]
- Chechin, G.M.; Dzhelauhova, G.S.; Mehonoshina, E.A. Quasibreathers as a generalization of the concept of discrete breathers. Phys. Rev. E 2006, 74, 036608. [Google Scholar] [CrossRef] [PubMed]
- Ryabov, D.S.; Chechin, G.M.; Upadhyaya, A.; Korznikova, E.A.; Dubinko, V.I.; Dmitriev, S.V. Delocalized nonlinear vibrational modes of triangular lattices. Nonlinear Dyn. 2020, 102, 2793–2810. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Chetverikov, A.P.; Dmitriev, S.V.; Korznikova, E.A. Shock waves in graphene and boron nitride. Comput. Mater. Sci. 2020, 177, 109549. [Google Scholar] [CrossRef]
- Sato, M.; Hubbard, B.E.; Sievers, A.T. Nonlinear energy localization and its manipulation in micromechanical oscillator arrays. Rev. Mod. Phys. 2006, 78, 13. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Evazzade, I.; Korznikova, E.A.; Shepelev, I.A.; Zhou, K.; Dmitriev, S.V. Low-energy channel for mass transfer in Pt crystal initiated by molecule impact. Comput. Mater. Sci. 2019, 163, 248–255. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Dmitriev, S.V.; Kudreyko, A.A.; Velarde, M.G.; Korznikova, E.A. Supersonic voidions in 2D Morse lattice. Chaos Solitons Fractals 2020, 140, 110217. [Google Scholar] [CrossRef]
- Krylova, K.A.; Baimova, J.A.; Murzaev, R.T.; Mulyukov, R.R. Energy exchange between discrete breathers in graphane in thermal equilibrium. Phys. Lett. A 2019, 383, 1583–1588. [Google Scholar] [CrossRef]
- Kikot, I.K.; Rayzan, N.B.; Kovaleva, M.; Starosvetsky, Y. Discrete breathers and discrete oscillating kink solution in the mass-in-mass chain in the state of acoustic vacuum. Commun. Nonlinear Sci. Numer. Simul. 2020, 107, 106020. [Google Scholar] [CrossRef]
- Korznikova, E.A.; Shcherbinin, S.A.; Ryabov, D.S.; Chechin, G.M.; Ekomasov, E.G.; Barani, E.; Zhou, K.; Dmitriev, S.V. Delocalized Nonlinear Vibrational Modes in Graphene: Second Harmonic Generation and Negative Pressure. Phys. Status Solidi B Basic Res. 2019, 256, 1800061. [Google Scholar] [CrossRef]
- Geniet, F.; Leon, J. Nonlinear supratransmission. J. Condens. Matter Phys. 2003, 15, 2933–2949. [Google Scholar] [CrossRef]
- Leon, J. Nonlinear supratransmission as a fundamental instability. Phys. Lett. A 2003, 319, 130–136. [Google Scholar] [CrossRef]
- Leon, J. Slow-light solitons in two-level media generated by evanescent fields. Phys. Rev. A 2007, 75, 063811. [Google Scholar] [CrossRef]
- Anghel-Vasilescu, P.; Dorignac, J.; Geniet, F.; Leon, J.; Taki, M. Nonlinear supratransmission in multicomponent systems. Phys. Rev. Lett. 2010, 105, 074101. [Google Scholar] [CrossRef]
- Anghel-Vasilescu, P.; Dorignac, J.; Geniet, F.; Leon, J.; Taki, A. Generation and dynamics of quadratic birefringent spatial gap solitons. Phys. Rev. A 2011, 834, 043836. [Google Scholar] [CrossRef]
- Yu, G.; Wang, X.; Tao, Z. Resonant emission of solitons from impurity-induced localized waves in nonlinear lattices. Phys. Rev. E 2011, 83, 026605. [Google Scholar] [CrossRef]
- Togueu Motcheyo, A.B.; Tchinang Tchameu, J.D.; Siewe, S.M.; Tchawoua, C. Homoclinic nonlinear band gap transmission threshold in discrete optical waveguide arrays. Commun. Nonlinear Sci. Numer. Simul. 2017, 50, 29–34. [Google Scholar] [CrossRef]
- Togueu Motcheyo, A.B.; Kimura, M.; Doi, Y.; Tchawoua, C. Supratransmission in discrete one-dimensional lattices with the cubic–quintic nonlinearity. Nonlinear Dyn. 2019, 95, 2461–2468. [Google Scholar] [CrossRef]
- Ai, B.Q.; He, D.; Hu, B. Heat conduction in driven Frenkel-Kontorova lattices: Thermal pumping and resonance. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 81, 031124. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.G.; Yang, T.; Niu, M.-Q.; Chen, L.-Q. Interaction effects of driving amplitudes and frequencies on transitivity in a granular chain. J. Sound Vib. 2022, 529, 116966. [Google Scholar] [CrossRef]
- Kamdoum Kuitche, A.; Togueu Motcheyo, A.B.; Kanaa, T.; Tchawoua, C. Modulational instability in transversely connected nonlinear pendulum pairs. Eur. Phys. J. Plus 2023, 138, 142. [Google Scholar] [CrossRef]
- Adile, A.D.; Kenmogne, F.; Tewa, A.K.S.; Simo, H.; Tahir, A.M.; Kumar, S. Dynamics of a mechanical network consisting of discontinuous coupled system oscillators with strong irrational nonlinearities: Resonant states and bursting waves. Int. J. Non-Linear Mech. 2021, 137, 103812. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, K.W. On the wave propagation analysis and supratransmission prediction of a metastable modular metastructure for non-reciprocal energy transmission. J. Sound Vib. 2019, 458, 389–406. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, K.W. Supratransmission in a metastable modular metastructure for tunable non-reciprocal wave transmission. Proc. SPIE—Int. Soc. Opt. Eng. 2018, 10595, 1059514. [Google Scholar] [CrossRef]
- Zhang, Q.; Fang, H.; Xu, J. Programmable stopbands and supratransmission effects in a stacked Miura-origami metastructure. Phys. Rev. E 2020, 101, 042206. [Google Scholar] [CrossRef]
- Liu, X.; Cai, G.; Wang, K.W. Nonreciprocal wave transmission in metastable modular metastructures utilizing asymmetric dual-threshold snap-through. In Proceedings of the Conference on Smart Materials, Adaptive Structures and Intelligent Systems: SMASIS 2019, Louisville, KY, USA, 9–11 September 2019; p. V001T03A007. [Google Scholar] [CrossRef]
- Bountis, A. Complex dynamics and statistics of 1-d hamiltonian lattices: Long range interactions and supratransmission. Nonlinear Phenom. Complex Syst. 2020, 23, 133–148. [Google Scholar] [CrossRef]
- Zakharov, P.V. The effect of nonlinear supratransmission in discrete structures: A review. Comput. Res. Model. 2023, 15, 599–617. [Google Scholar] [CrossRef]
- Bountis, T.; Macías-Díaz, J.-E. The Effect of On-Site Potentials on Supratransmission in One-Dimensional Hamiltonian Lattices. Entropy 2023, 25, 423. [Google Scholar] [CrossRef]
- Pechac, J.E.; Frazier, M.J. Non-Reciprocal Supratransmission in Mechanical Lattices with Non-Local Feedback Control Interactions. Crystals 2021, 11, 94. [Google Scholar] [CrossRef]
- Zakharov, P.V.; Starostenkov, M.D.; Lucenko, I.S.; Kochkin, A.S. Interaction of a soliton wave with nanopores in stoichiometry crystals A3B. J. Phys. Conf. Ser. 2020, 1697, 012076. [Google Scholar] [CrossRef]
- Zakharov, P.V.; Dmitriev, S.V.; Korznikova, E.A. Molecular dynamic analysis of energy transport in a Pt3Al crystal under the impact in the spectrum gap frequency. Lett. Mater. 2021, 11, 338–344. [Google Scholar] [CrossRef]
- Daw, M.S.; Foiles, S.M.; Baskes, M.I. The embedded-atom method: A review of theory and applications. Mater. Sci. Rep. 1993, 9, 251–310. [Google Scholar] [CrossRef]
- Cherednichenko, A.I.; Zakharov, P.V. Modulation of oscillations of nonlinear modes on the cylindrical surface of A3B crystal. Mater. Technol. Des. 2022, 4, 60–65. [Google Scholar] [CrossRef]
- Kolesnikov, I.D.; Shepelev, I.A. Excitation and Propagation of I-crowdion in BCC Niobium lattice. Mater. Technol. Des. 2022, 4, 5–10. [Google Scholar] [CrossRef]
- Xiaoxia, L. Investigation on the Mechanical Properties of Polycrystalline Mg Using Molecular Dynamics Simulation. Comput. Model. Eng. Sci. 2022, 131, 919–927. [Google Scholar] [CrossRef]
- Matsumoto, R.; Nakagaki, M.; Nakatani, A.; Kitagawa, H. Molecular-dynamics Study on Crack Growth Behavior Relevant to Crystal Nucleation in Amorphous Metal. Comput. Model. Eng. Sci. 2005, 9, 75–84. [Google Scholar] [CrossRef]
- Zhou, X.W.; Johnson, R.A.; Wadley, H.N.G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef]
- Cherednichenko, A.I.; Zakharov, P.V.; Starostenkov, M.D.; Eremin, A.M.; Dong, G. Analysis of eam and meam potentials for modeling localized states of Ni3Al and Pt3Al crystals. Basic Probl. Mater. Sci. 2021, 2, 188–195. [Google Scholar] [CrossRef]
- Zakharov, P.V.; Eremin, A.M.; Starostenkov, M.D.; Lutsenko, I.S.; Zakhakova, E.A.; Dmitriev, S.V. Excitation of soliton-type waves in crystals of the A3B stoichiometry. Phys. Solid State 2019, 61, 2160–2166. [Google Scholar] [CrossRef]
- Fu, C.L.; Yoo, M.H. Electronic structure and mechanical behavior of transition-metal aluminides: A first-principles total-energy investigation. Mater. Chem. Phys. 1992, 32, 25–36. [Google Scholar] [CrossRef]
- Shcherbinin, S.A.; Krylova, K.A.; Chechin, G.M.; Soboleva, E.G.; Dmitriev, S.V. Delocalized nonlinear vibrational modes in fcc metals. Commun. Nonlinear Sci. Numer. Simul. 2022, 104, 106039. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Chen, C.Q. Amplitude-dependent boundary modes in topological mechanical lattices. J. Mech. Phys. Solids 2021, 153, 104482. [Google Scholar] [CrossRef]
- Smirnov, V.V.; Manevitch, L.I. Large-amplitude nonlinear normal modes of the discrete sine lattices. Phys. Rev. E 2017, 95, 022212. [Google Scholar] [CrossRef] [PubMed]
- Aero, E.L.; Budygin, A.N. Theory of nonlinear waves in solids undergoing a radical rearrangement of the crystal structure. Vychisl. Mekh. Splosh. Sred. 2009, 2, 19–43. [Google Scholar] [CrossRef][Green Version]
- Kamdoum Kuitche, A.; Togueu Motcheyo, A.B.; Kanaa, T.; Tchawoua, C. Supratransmission in transversely connected nonlinear pendulum pairs. Chaos Solitons Fractals 2022, 160, 112196. [Google Scholar] [CrossRef]
- Born, M.; Kun, H. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1955; 432p. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).