Abstract
This research proposes a new image compression method based on the F1-transform which improves the quality of the reconstructed image without increasing the coding/decoding CPU time. The advantage of compressing color images in the YUV space is due to the fact that while the three bands Red, Green and Blue are equally perceived by the human eye, in YUV space most of the image information perceived by the human eye is contained in the Y band, as opposed to the U and V bands. Using this advantage, we construct a new color image compression algorithm based on F1-transform in which the image compression is accomplished in the YUV space, so that better-quality compressed images can be obtained without increasing the execution time. The results of tests performed on a set of color images show that our color image compression method improves the quality of the decoded images with respect to the image compression algorithms JPEG, F1-transform on the RGB color space and F-transform on the YUV color space, regardless of the selected compression rate and with comparable CPU times.
1. Introduction
YUV is a color model used in the NTSC, PAL, and SECAM color encoding systems, which describes the color space in terms of a brightness component (the Y band called luma) and the two chrominance components (the U and V bands are called chroma).
The YUV model has been used in image processing: its main advantage is that unlike of the Red, Green and Blue (RGB) bands, perceived by the human eye, in YUV space, most of the color image information is contained in the Y band, as opposed to the U and V bands. The main application of the YUV model in image processing is related to the lossy compression of images, which can be performed mainly in the U and V bands, with slight loss of information.
YUV is used in the JPEG color image compression method [1,2] where the Discrete Cosine Transform (DCT) algorithm is executed on the YUV space, sub-sampling and reducing the UV channels in a dynamic range in order to balance the reduction in data and the feel of human eyes. In [3], the DCT algorithm is executed in the YUV space for wireless capsule endoscopy application: the results show that the quality of the reconstructed images is better than that obtained by applying the DCT image compression method in the RGB space.
Many authors proposed image compression and reconstruction algorithms applied on the YUV space in order to improve the quality of the reconstructed images.
In [4,5] an image compression algorithm based on fuzzy relation equations is applied in the YUV space to compress color images: the image is divided into blocks of equal sizes, coding the blocks in the UV channels more strongly than blocks in the Y band. In [6,7], the Fuzzy Transform technique (for short F-transform) [8] is applied to coding color images in the YUV space: the authors show that the quality of color images coded and decoded via F-transform in the YUV space is better than the F-transform method in the RGB space and comparable with the one obtained using JPEG.
A fractal image compression technique applied in the YUV space is proposed in [9]; the authors show that the quality of color images coded/decoded using this approach is better than the one obtained applying the same method in the RGB space.
Furthermore, comparison tests between the RGB and YUV perception-oriented properties in [10] show that compressed images in the YUV space provide better quality than images compressed in the RGB spaces in a human–computer interaction and machine vision applications.
In [11] a technique using Chebyshev bit allocation is applied to compress images in the YUV space: the results show that this method improves the visual quality of color images compressed via JPEG by 42%. A color image compression method applying a subsampling process to the two chroma channels and a modification algorithm to the Y channel is applied to color images in [12] to improve JPEG performances.
An image compression method with a learning-base filter is applied in [13] on color images constructing the filter in YUV space instead of RGB space: the authors show that the quality of the coded images is better than that obtained using the filter in the RGB space. In [14], an image lossy compression algorithm in which quantization and subsampling are executed in the YUV space is applied for wireless capsule endoscopy: the quality of the coded images is better than that obtained by executing quantization and subsampling in the RGB space.
Recently, hybrid lossy color image compression methods based on Neural [15], Fuzzy neural [16,17], Quantum Discrete Cosine Transform [18] and Adaptive Discrete Wavelet Transform [19] have been proposed in the literature. These methods improve the quality of the decoded images, and are robust to the presence of noise, but are computationally too expensive.
In particular, in [20], a wavelet-based color image compression method using trained convolutional neural network in the lifting scheme is applied to the YUV executing the trained CNN in the Y, U, V channels separately: this method improves the quality of the coded images obtained using traditional wavelet-based color image compression algorithms. However, the execution times are much higher than those adopted by applying traditional color image compression algorithms.
In [21] an image reconstruction method performed on the YUV space is applied to prevent data corruption when using adversarial perturbation of the image: the results show that the image can be recovered on the YUV space without distortions and with high visual quality.
In this paper, we propose a novel image compression algorithm in which the bi-dimensional First-Degree F-transform algorithm (for shorts, F1-transform) [22,23] is applied to code/decode color images in the YUV space.
The bi-dimensional F-transform was used recently by various researchers for image and video coding. In [24], the bi-dimensional F-transform is applied to compress massive images: the coded images are used as input images in an image segmentation algorithm.
In [25], an image monitoring model is proposed in which the bi-dimensional F-transform is used to compress gray images.
A hybrid image compression algorithm, which combines the L1-norm and the bi-dimensional F-transform, is proposed in [26]: results executed on a set of gray-level noised images show that this method is more robust in the presence of noise than the canonical F-transform image compression algorithm.
A generalization of the F-transform called high-order F-transform (Fm-transform), has been proposed in [27] in order to reduce the approximation error of the original function approximated with the inverse F-transform. In the Fm-transform, the components of the direct high-order fuzzy transforms are polynomials of degree m, unlike the components of the direct F-transform (labeled as F°-transform), where they were constant values. The greater the degree of the polynomial, the smaller the error of the approximation: however, as the degree of the polynomial increases, the computational complexity of the algorithm increases.
In [18] the bi-dimensional first-order degree F-transform (F1-transform) is used to compress images: the authors show that the quality of the coded/decoded images is better than that obtained executing F-transform, with negligible augments of CPU time. The critical point of this method, unlike the F-transform and JPEG methods, is that it does not require the compressed image to be saved in the memory, but matrices of three coefficients of the same size related to the compressed image itself must be contained in a memory three times greater than that necessary to archive the compressed image.
To solve this problem, we propose a new lossy color image compression algorithm in which is executed the F1-transform algorithm to code/decode color images transformed in the YUV space. The transformed image in each of the three channels is partitioned into blocks and each block is compressed by the bi-dimensional direct F1-transform, compressing the blocks of the chroma channels more. The image is subsequently reconstructed by decomposing the single blocks with the use of the bi-dimensional inverse F1-transform.
The main benefits of this method are as follows:
- ▪
- The use of the bi-dimensional F1-transform represents a trade-off between the quality of the compressed image and the CPU times. It reduces the information loss obtained by compressing the image with the same compression rate using the F-transform algorithm with acceptable coding/decoding CPU time;
- ▪
- The compression of the color images is carried out in the YUV space to guarantee a high visual quality of the color images and solve the criticality of the F1-transform color image compression method in the RGB space [18] having a larger memory to allocate the information of the compressed image. In fact, by performing a high compression of the two chrominance channels, the size of the matrices in which the information of the compressed image is contained, is reduced in these two channels, and this allows us to reduce the memory allocations and CPU times.
We compare our color lossy image compression method with the JPEG method and with the image compression methods based on the bi-dimensional F-transform [7,8] and F1-transform [22] on the RGB space and on the bi-dimensional F-transform in the YUV space [6].
In the next Section, the concepts of F-transform and F1-transform are briefly presented, and the F-transform lossy color image compression method applied in YUV space is shown as well. Our method is presented in Section 3. In Section 4, the comparative results obtained in some datasets of color images are shown and discussed. Conclusive discussions are contained in Section 5.
2. Preliminaries
2.1. The bi-Dimensional F-Transform
Let [a, b] be a closed real interval and let {x1, x2, …, xn} be a set of points of [a, b], called nodes, such that x1 = a < x2 <…< xn = b.
Let {A1,…,An} be a family of fuzzy sets of X, where Ai: [a, b] → [0, 1]: it forms a fuzzy partition of X id the following conditions hold:
- (1)
- Ai(xi) = 1 for every i =1, 2, …, n;
- (2)
- Ai(x) = 0 if x∉(xi − 1, xi + 1), by setting x0 = x1 = a and xn + 1 = xn = b;
- (3)
- Ai(x) is a continuous function over [a, b];
- (4)
- Ai(x) is strictly increasing over [xi − 1, xi] for each i = 2, …, n;
- (5)
- Ai(x) is strictly decreasing over [xi, xi + 1] for each i = 1, …, n−1;
- (6)
- for every x∈[a, b].
Let . The fuzzy partition {A1, …, An} is an uniform fuzzy partition if:
- (7)
- n ≥ 3;
- (8)
- xi =a + h∙(i−1), for i = 1, 2, …, n;
- (9)
- Ai(xi−x) = Ai(xi + x) for every x [0, h] and i = 2, …, n−1;
- (10)
- Ai + 1(x) = Ai(x−h) for every x [xi, xi + 1] and i = 1, 2, …, n−1.
Let f(x) be a continuous function over [a, b] and {A1, A2, …, An} be a fuzzy partition of [a, b]. The n-tuple F = is called uni-dimensional direct F-transform of f with respect to {A1, A2, …, An} if the following holds:
The following function defined for every x∈[a, b] as
is called the uni-dimensional inverse F-transform of the function f.
The following theorem holds (cfr. ([7], Theorem 2)):
Theorem 1.
Let f(x) be a continuous function over [a, b]. For every ε > 0 there exists an integer n(ε) and a fuzzy partition {A1, A2, …, An(ε)} of [a, b] for which holds the inequality for every x [a, b].
Now, consider the discrete case where the function f is known in a set of N points P = {p1, …, pN}, where pj ∈ [a, b], j = 1, 2, …, m. The set {p1, …, pN} is called sufficiently dense with respect to the fixed fuzzy partition {A1, A2, …, An} if for i = 1, …, n, there exists at least an index j {1, …, m} such that Ai(pj) > 0.
If the set P is sufficiently dense with respect to the fuzzy partition, we can define the discrete direct F-transform with components given as
and the discrete inverse F-transform as
The following theorem applied to the discrete inverse F-transform holds (cfr. ([7], Theorem 5)):
Theorem 2.
Let f(x) be a continuous function over [a, b] known in a discrete set of points P = {p1, …, pm}. For every ε > 0, there exists an integer n(ε) and a fuzzy partition {A1, A2, …, An(ε)} of [a, b], with respect to which P is sufficiently dense, for which the following inequality holds for j = 1, …, N.
According to Theorem 2, the inverse fuzzy transform (4) can be used to approximate the function f in a point.
Now, we consider functions in two variables. Let x1, x2, …, xn be a set of n nodes in [a,b] where n > 2 and x1 = a < x2 <…< xn = b, and let y1, y2, …, ym be a set of m nodes in [c,d], where m > 2 and and y1 = c < y2 <…< ym = d. Moreover, let A1,…,An: [a, b] → [0, 1] be a fuzzy partition of [a, b], B1, …, Bm: [c, d] → [0, 1] be a fuzzy partition of [c, d] and let f(x,y) be a function defined in the Cartesian product [a, b] × [c, d].
We suppose that f assumes known values in a set of points (pj, qj)∈[a, b] × [c, d], where i = 1, …, N and j = 1, …, m, where the set P = {p1, …, pN} is sufficiently dense with respect to the fuzzy partition {A1, …, An} and the set Q = {q1, …, qM} is sufficiently dense with respect to the fuzzy partition {B1, …, Bm}.
In this case, we can define the bi-dimensional discrete F-transform of f, given by matrix [Fhk] with entries defined as
and the bi-dimensional discrete inverse F-transform of f with respect to {A1, A2, …, An} and {B1, …, Bm} defined as
2.2. The bi-Dimensional F1-Transform
This paragraph introduces the concept of higher-degree fuzzy transform or F1-transform.
Let Ah, h = 1, …, n, be the hth fuzzy set of the fuzzy partition {A1, …, An} defined in [a, b] and L2([xh − 1,xh + 1]) be the Hilbert space of square-integrable functions f,g: [xh − 1,xh + 1] ⟶ R with the inner product:
Given a integer r ≥ 0, we denote with ([xh−1,xh+1]) a linear subspace of the Hilbert space L2([xh−1,xh+1]) that has as an orthogonal basis the polynomials {, , …,} constructed by applying the Gram–Schmidt ortho-normalization to the linear independent system of polynomials {1, x, x2, …, xr} defined in the interval [xh−1,xh+1]. We have the following:
The following Lemma holds (Cfr. [7], Lemma 1):
Lemma 1.
Let be the orthogonal projection of the function f on ([xh−1,xh+1]). Then,
where
it is the hth component of the direct Fr-transform of f. The inverse Fr-transform of f in a point x ∊ [a, b] is defined as
For r = 0, we have = 1 and the F0-transform is given by the F-transform in one variable ( (x) = ch,0).
For r = 1, we have = (x − xh) and the hth component of the F1-transform is given as
If the function f is known in a set of N points, P = {p1, …, pN}, ch,0 and ch,1 can be discretized in the following formulas:
The F1-transform can be extended in a bi-dimensional space. We consider the Hilbert space L2([xh−1, xh+1] × [yk−1, yk+1]) of square-integrable functions f: [xh − 1, xh + 1] × [yk − 1,yk + 1]→ R with the weighted inner product:
Two functions L2 ([xh−1, xh+1] × [yk−1, yk+1]) are orthogonal if .
Let f: X ⊆ R2 → Y⊆ R be a continuous bi-dimensional function defined in [a, b] × [c, d]. Let {A1, A2, …, An} be a fuzzy partition of [a, b] and {B1, B2, …, Bm} be a fuzzy partition of [c, d]. Moreover, let {(p1,q1),…, (pN,qjN)} a set of N points in which the function f is known, where (pj,qj) [a, b] × [c, d]. Let P = {p1, …, pN} be sufficiently dense with respect to the fuzzy partition {A1, …, An} and Q = {q1, …, qM} be sufficiently dense with respect to the fuzzy partition {B1, …, Bm}.
We can define the bi-dimensional direct F1-transform of f, with components given as
where is the component of the bi-dimensional discrete direct F transform of f, defined via Formula (5). The three coefficients in (17) are given as
The inverse F1-transform of f in a point (x,y) ∊ [a, b] × [c, d] is defined as
where is the (h,k)th component of the bi-dimensional direct F1-transform given from Formula (16).
2.3. Coding/Decoding Images using the Bidimensional F and F1-Transforms
Let I be a gray N × M image. A pixel can be considered a data point with coordinates (i,j), where i = 1, 2, …, N and j = 1, 2, …, M: the value of this data point is given as the pixel value I(i,j). In [8], the image is normalized in [0, 1] according to the formula R(i,j) = I(i,j)/(L-1), where L is the number of gray levels.
We can create a partition of this image in blocks of equal size N(B) × M(B), coded to a block FB of sizes n(B) × m(B), with n(B) << N(B) and m(B) << M(B), using the bi-dimensional direct F-transform.
Let {A1, …, An(B)} be a fuzzy partition of the set [1,N(B)] and let {B1,…,Bm(B)} be a fuzzy partition of the set [1,M(B))]. Each block is compressed by the bi-dimensional direct F-transform:
The coded image is reconstructed by merging all compressed blocks. Each block is decompressed using the bi-dimensional inverse F-transform. The pixel value I(i,j) in the block is approximated with the following value:
The decoded image is reconstructed by merging the decompressed blocks. The F-transform compression and decompression algorithms are shown in the pseudocode as Algorithms 1 and 2, respectively.
| Algorithm 1: F1-transform image compression |
| Input: N × M Image I with L grey levels |
| Size of the blocks of the source image N(B) × M(B) |
| Size of the compressed blocks n(B) × m(B) |
| Output: n × m compressed image IC |
|
| Algorithm 2: F-transform image decompression |
| Input: n × m compressed image Ic |
| Output: N × M decoded image ID |
|
In [22] an improvement in the quality of the decompressed image is accomplished using the bi-dimensional F1-transform. The blocks are compressed by using the bi-dimensional direct F1-transform:
where
The three coefficients , and are constructed by merging the coefficients of each block and finally stored, forming the output of coding process.
During the decompression process, the image is reconstructed by decompressing the block with the following bi-dimensional inverse F1-transform:
where the bi-dimensional direct F1-transform of the block is calculated using (23).
The decompressed blocks are merged to form the decompressed image. The F1-transform compression and decompression algorithms are shown in the pseudocode as Algorithms 3 and 4, respectively.
| Algorithm 3: F1-transform image compression |
| Input: N × M Image I with L grey levels |
| Size of the blocks of the source image N(B) × M(B) |
| Size of the compressed blocks n(B) × m(B) |
| Output: n × m matrices of the direct F1-transform coefficients , and |
|
| Algorithm 4: F1-transform image decompression |
| Input: n × m matrices of the direct F1-transform coefficients coefficients , and |
| Size of the blocks of the decoded image N(B) × M(B) |
| Size of the blocks of the coded image n(B) × m(B) |
| Output: N × M decoded image ID |
|
3. The YUV-Based F1-Transform Color Image Compression Method
Let I be a N × M color image into L gray levels. All pixel values in bands R, G and B are normalized in [0, 1].
Considering a 256 gray levels color image and the scaled and offset version of the YUV color space, the source image is transformed in the YUV space via the formula (cfr. [28]):
Then, the F1-transform image compression algorithm is executed separately to the three normalized images Y, U and V, using a strong compression for the chroma images U and V.
If N(B) and M(B) are the sizes of each block in the three channels, the blocks in the brightness channel are compressed with a compression rate and the blocks in the two chroma channels are compressed with a compression rate , where nUV(B) << nY(B) and mUV(B) << mY(B), so that ρUV << ρY.
The F1-transform image compression algorithm will store in output for each channel the three matrixes of the coefficients of the bi-dimensional direct F1-transform: , and . The size of the three matrices in the brightness channel is ρY (N × M) and the size of the three matrices in each of the two chroma channels is ρUV (N × M).
By choosing suitable brightness and chroma compression rates, it is possible to reduce the memory capacity necessary to store the direct F1-transform coefficients in the RGB space.
For example, suppose we execute the F1-transform image compression algorithm in the RGB space to compress a 256 × 256 color image by partitioning the image into 16 × 16 blocks compressed into 4 × 4 blocks. The compression rate will be ρRGB = 0.0625 and the size of the matrix of each coefficient is 64 × 64. Executing the F1-transform algorithm in the YUV space and compressing the 16 × 16 blocks in the two chroma channels into 2 × 2 blocks (ρUV = 0.016) and the 16 × 16 blocks in the brightness channel into 8 × 8 blocks (ρY = 0.25), the size of the matrix of each coefficient in the U and V channels will be 32 × 32, and the size of the matrix of each coefficient in the Y channel will be 128 × 128. By carrying out the compression of the source image in the YUV space in this way, two advantages are obtained in terms of visual quality of the reconstructed image and in terms of the available memory necessary to archive the coefficients of the direct F1-transforms in the three channels.
Below, the YUV F1-transform color image compression algorithm (Algorithm 5) is shown as pseudocode.
| Algorithm 5: YUV F1-transform color image compression |
| Input: N × M color image I with L grey levels |
| Size of the blocks of the source image N(B) × M(B) |
| Size of the compressed blocks in the Y channel nY(B) × mY(B) |
| Size of the compressed blocks in the U and V channels nUV(B) × mUV(B) |
| Output: n × m matrices of thedirect F1-transform coefficients , and in the Y, U and channels |
|
In Figure 1 we give the flow diagram of the YUV F1-transform image compression algorithm.
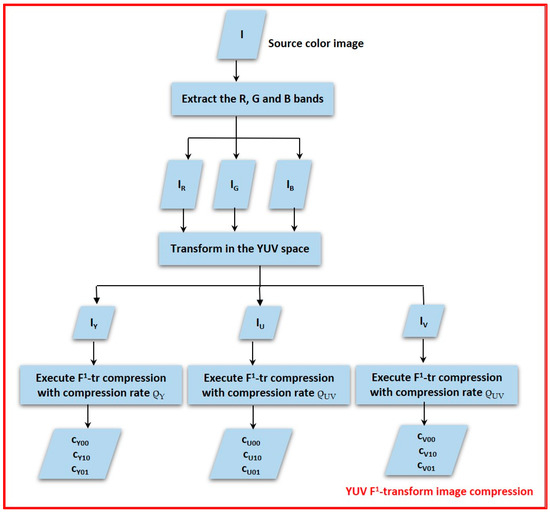
Figure 1.
Flow diagram of the YUV F1-transform image compression algorithm.
The decompression process is performed by executing the F1-transform image decompression algorithm in the brightness and chroma channels; to decompress the image, the F1-transform image decompression algorithm is executed separately for each of the channels Y, U and V, assigning as input the three coefficient matrices of the direct F1-transform and the dimensions of the original and compressed blocks.
Then, the three decoded images IDY, IDU, and IDV are transformed in the RGB space, according to the formula [28]:
Finally, the decoded image in the RGB band (IDR, IDG, IDB) is returned as well. Below, the YUV F1-transform color image decompression algorithm (Algorithm 6) is shown as pseudocode.
| Algorithm 6: YUV F1-transform image decompression |
| Input: n × m matrices of the direct F1-transform coefficients coefficients , and in the Y, U and V channels |
| Size of the blocks of the decoded image N(B) × M(B) |
| Size of the compressed blocks in the Y channel nY(B) × mY(B) |
| Size of the compressed blocks in the U and V channels nUV(B) × mUV(B) |
| Output: N × M decoded image ID |
|
In Figure 2 the flow diagram of the YUV F1-transform image decompression algorithm is schematized as well.
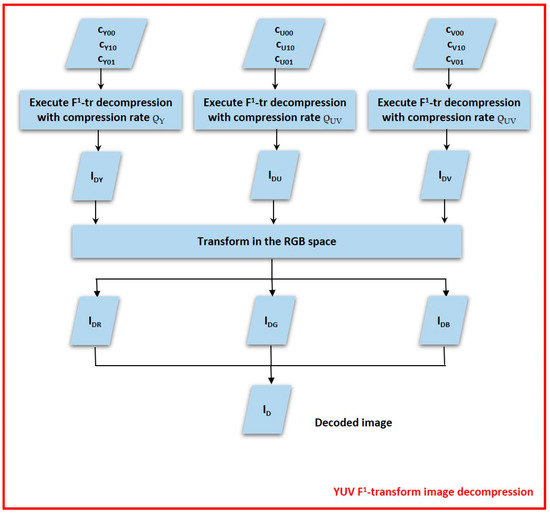
Figure 2.
Flow diagram of the YUV F1-transform image decompression algorithm.
We compare our lossy color image compression report with the JPEG algorithm [1,2] and the color image compression methods based on F-transform on the YUV space [6] and F1-transform on the RGB space [22].
The Peak-Signal-to-Noise index (PSNR) is used to measure the quality of the decoded images. In order to measure the gain obtained executing the YUV F1-transform algorithm with respect to another color image compression method, we measure the PSNR gain, expressed in a percentage and given as follows:
In the next Section, the results applied to the color image dataset are shown and discussed.
4. Results
We test the YUV F1-transform lossy color image compression algorithm on the color image dataset provided by the University of Southern California Signal and Image Processing Institute (USC SIPI) and published on the website http://sipi.usc.edu/database.
The dataset is made up of over 50 color images of different sizes. For brevity, we show in detail the results obtained for 256 × 256 source images 4.1.04 and the 412 × 512 source image 4.2.07 shown in Figure 3.
Figure 3.
Source images: (a) 256 × 256 image 4.1.04; (b): 512 × 512 image 4.2.07.
Each image was compressed and decompressed by performing JPEG [2], YUV F-transform [6], F1-transform [22] and YUV F1-transform lossy image compression algorithms.
We compare the four image compression methods measuring the quality of the reconstructed image as the compression rate changes assuming various values. The compression rate used when executing YUV F-transform and YUV F1-transform is the mean compression rate set for each channel Y, U and V.
In Figure 4 we show, for the original image 4.1.04, the decoded images obtained by executing the four algorithms setting a compression rate ρ ≈ 0.10.

Figure 4.
Decoded image 4.1.04, ρ ≈ 0.10, obtained via: (a) JPEG; (b) F1-transform; (c): YUV F-transform; (d) YUV F1-transform.
Figure 5 shows, for the original image 4.1.04, the decoded images obtained by executing the four algorithms setting a compression rate ρ ≈ 0.25.

Figure 5.
Decoded image 4.1.04, ρ ≈ 0.25, obtained via: (a) JPEG; (b) F1-transform; (c): YUV F-transform; (d) YUV F1-transform.
Figure 6 shows the trend of the PSNR index obtained by varying the compression rate. The trends obtained by executing JPEG and F1-transform are similar. However, for strong compressions (ρ < 0.1), the PSNR value calculated by executing JPEG decreases exponentially as the compression increases: this result shows that the quality of the decoded image obtained using JPEG drops quickly for very high compressions. The highest PSNR values are obtained by performing YUV F-transform and YUV F1-transform. In particular, the PSNR values obtained with the two methods are similar for ρ < 0.2, while, for lower compressions, YUV F1-transform provides decompressed images of better quality than those obtained with YUV F-transform.
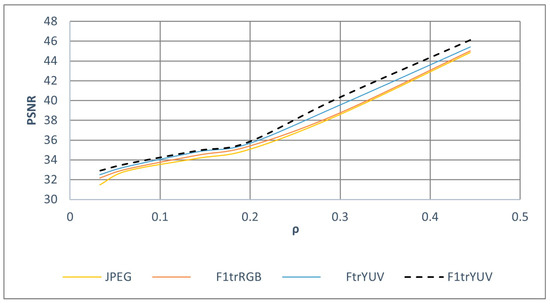
Figure 6.
PSNR trend for the color image 4.1.04 obtained by executing the four color image compressions algorithms.
Table 1 shows the gain index values obtained for different compression rates.

Table 1.
Gain index of YUV F1-transform for the color image 4.1.04.
The gain of YUV-F1-transform compared to JPEG is always greater than 2%, regardless of the compression rate; similarly, the gain of YUV-F1-transform compared to F1-transform in the RGB space is greater than 1% regardless of the compression rate. The gain of YUV-F1-transform compared to YUV-F-transform is always positive and reaches values greater than 1% for strong (ρ < 0.05) and weak compressions (ρ > 025).
Now, we show the results obtained for the color image 4.2.07. In Figure 7, we show the decoded images obtained by executing the four algorithms via a compression rate ρ ≈ 0.10.

Figure 7.
Decoded image 4.2.07, ρ ≈ 0.10, obtained via: (a) JPEG; (b) F1-transform; (c): YUV F-transform; (d) YUV F1-transform.
Figure 8 shows the decoded images of 4.2.07 obtained by executing the four algorithms setting a compression rate ρ ≈ 0.25.

Figure 8.
Decoded image 4.2.07, ρ ≈ 0.25, obtained via: (a) JPEG; (b) F1-transform; (c): YUV F-transform; (d) YUV F1-transform.
In Figure 9, the trend of the PSNR index is plotted obtained by varying the compression rate. The best values of PSNR are obtained by executing YUV F1-transform. The trend of the PSNR obtained by executing the YUV F-transform is better than the one obtained by executing F-transform and JPEG. As the results obtained for the color image 4.1.04 show, the trend of PSNR obtained by executing JPEG for the image 4.2.07 decays rapidly as compression increases (ρ < 0.1).
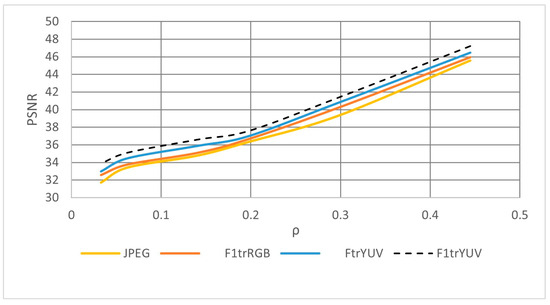
Figure 9.
PSNR trend for the color image 4.2.07 obtained by executing the four color image compression algorithms.
Table 2 shows the gain index values obtained for different compression rates.

Table 2.
Gain index of YUV F1-transform for the color image 4.2.07.
The gain of YUV-F1-transform compared to JPEG is always greater than 3%, regardless of the compression rate: it reaches values above 6% for strong compressions (ρ < 0.04). The gain of YUV-F1-transform compared to F1-transform in the RGB space is greater than 2% regardless of the compression rate: it reaches values above 4% for ρ < 0.15. The gain of YUV-F1-transform compared to YUV-F-transform is always greater than 1%: it reaches values above 2% for strong compressions (ρ < 0.05). In Figure 10, the trends of the gain of the YUV F1-transform algorithm are plotted with respect to the other three color image compression algorithms, where the Gain index is calculated using formula (30) and is averaged for all the images of the dataset used in the comparative tests. The gain of the proposed method with respect to YUV F-transform is approximately equal to 2%, regardless of the compression rate. The gain of YUV F1-transform varies from 3% for small compressions and to 4% for high compressions (ρ < 0.2). The gain of YUV F1-transform with respect to JPEG varies from 3% for small compressions to 5% for medium–high compressions (0.1 < ρ < 0.2). For compression rates lower than 0.1, the Gain index increases quickly as the compression rate reaches about 7%.
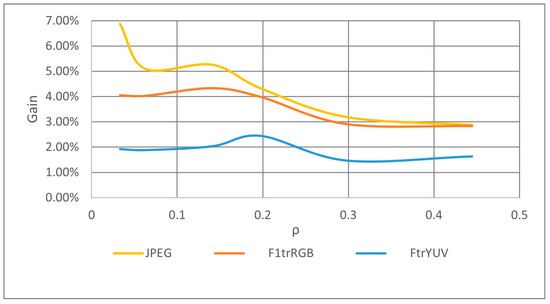
Figure 10.
Trend of the Gain of YUV-F1transform with respect to the other three color image compression methods.
These results show that the quality of the images coded/decoded using the YUV-F1-transform is higher than that obtained using YUV-F-transform, F1-transform and JPEG, regardless of the compression rate.
Finally, in Table 3, we show the mean gain and the coding/decoding CPU time obtained by executing the four color image compression algorithms: in order to compare the quality of the decoded images and the CPU times with recent image compression methods, the tests are also executed with respect to the CNN-based YUV color image compression method [20]. The average values refer to gain and CPU times measured for all images of the same size and for all compression rates.

Table 3.
Mean gain and coding/decoding CPU time obtained for the 256 × 256 and 512 × 512 images executing the four image compression algorithms.
From the results in Table 3, we deduce the following:
- -
- The quality of the decoded images obtained using our method is comparable with those obtained by executing the wavelet-like CNN-based YUV image compression method and better than the ones obtained by executing JPEG, F1-transform and YUV-F-transform, regardless of the image size;
- -
- Both the coding/decoding CPU times measured by executing the YUV- F1-transform are comparable with those obtained via JPEG, F1-transform and YUV-F-transform.
5. Conclusions
A lossy color image compression process employing the bi-dimensional F1-transform in YUV space is proposed. The benefit of this approach is that it improves the quality of the reconstructed image, with acceptable CPU coding/decoding times. In fact, the F1-transform method retains more information from the original image than other image compression methods, but at the expense of a greater amount of allocated memory space and longer execution times. The proposed method, operating in the YUV space, allows us to obtain a high-quality decompressed image without increasing the allocated memory and the CPU times. The results show that this method improves the quality of the decompressed image compared to that obtained with the use of JPEG, the F-transform applied in YUV space and the F1-transform applied in RGB space; moreover, the execution times are compatible with those obtained by executing the other three color image compression methods. Comparisons with the CNN-based wavelet-like color image compression method [20] show that the proposed method provides decoded images of comparable quality to those obtained with this wavelet-like method, but with much shorter execution times.
In the future, we intend to adapt the YUV-F1-transform algorithm to the compression of large color images. Furthermore, we intend to extend the proposed method in order to optimize the lossy compression of multi-band images.
Author Contributions
Conceptualization, B.C., F.D.M. and S.S.; methodology, B.C., F.D.M. and S.S.; software, B.C., F.D.M. and S.S.; validation, B.C., F.D.M. and S.S.; formal analysis, B.C., F.D.M. and S.S.; investigation, B.C., F.D.M. and S.S.; resources, B.C., F.D.M. and S.S.; data curation, B.C., F.D.M. and S.S.; writing—original draft preparation, B.C., F.D.M. and S.S.; writing—review and editing, B.C., F.D.M. and S.S.; visualization, B.C., F.D.M. and S.S.; supervision, B.C., F.D.M. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wallace, G. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, xviii. [Google Scholar] [CrossRef]
- Raid, A.M.; Khedr, W.M.; El-Dosuky, M.A.; Ahmed, W. Jpeg image compression using discrete cosine transform—A survey. Int. J. Comput. Sci. Eng. Surv. (IJCSES) 2014, 5, 39–47. [Google Scholar] [CrossRef]
- Mostafa, A.; Wahid, K.; Ko, S.B. An efficient YUV-based image compression algorithm for Wireless Capsule Endoscopy. In Proceedings of the IEEE CCECE 2011, 24th Canadian Conference on Electrical and Computer Engineering (CCECE), Niagara Falls, ON, Canada, 8-11 May 2011; pp. 943–946. [Google Scholar] [CrossRef]
- Nobuhara, H.; Pedrycz, W.; Hirota, K. Fuzzy Relational Compression: An Optimization by Different Color Spaces. In Proceedings of the Joint 1st International Conference on Soft Computing and Intelligent Systems and 3rd International Symposium on Advanced Intelligent Systems (SCIS & ISIS 2002) (CD-Proceedings), 24B5-6, Tsukuba, Japan, 21–25 October 2002; p. 6. [Google Scholar]
- Nobuhara, H.; Pedrycz, W.; Hirota, K. Relational image compression: Optimizations through the design of fuzzy coders and YUV color space. Soft Comput. 2005, 9, 471–479. [Google Scholar] [CrossRef]
- Di Martino, F.; Loia, V.; Sessa, S. Direct and inverse fuzzy transforms for coding/decoding color images in YUV space. J. Uncertain Syst. 2009, 3, 11–30. [Google Scholar]
- Perfilieva, I. Fuzzy Transform: Theory and Application. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Di Martino, F.; Loia, V.; Perfilieva, I.; Sessa, S. An Image coding/decoding method based on direct and inverse fuzzy transforms. Int. J. Approx. Reason. 2008, 48, 110–131. [Google Scholar] [CrossRef]
- Son, T.N.; Hoang, T.M.; Dzung, N.T.; Giang, N.H. Fast FPGA implementation of YUV-based fractal image compression. In Proceedings of the 2014 IEEE Fifth International Conference on Communications and Electronics (ICCE), Danang, Vietnam, 30 July–1 August 2014; pp. 440–445. [Google Scholar] [CrossRef]
- Podpora, M.; Korbas, G.P.; Kawala-Janik, A. YUV vs. RGB—Choosing a color space for human-machine interaction. In Proceedings of the 2014 Federated Conference on Computer Science and Information Systems, Warsaw, Poland, 29 September 2014; Volume 3, pp. 29–34. [Google Scholar] [CrossRef]
- Ernawan, F.; Kabir, N.; Zamli, K.Z. An efficient image compression technique using Tchebichef bit allocation. Optik 2017, 148, 106–119. [Google Scholar] [CrossRef]
- Zhu, S.; Cui, C.; Xiong, R.; Guo, U.; Zeng, B. Efficient chroma sub-sampling and luma modification for color image compression. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 1559–1563. [Google Scholar] [CrossRef]
- Sun, H.; Liu, C.; Katto, J.; Fan, Y. An image compression framework with learning-based filter. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 152–153. [Google Scholar]
- Malathkar, N.V.; Soni, S.K. High compression efficiency image compression algorithm based on subsampling for capsule endoscopy. Multimed. Tools Appl. 2021, 80, 22163–22175. [Google Scholar] [CrossRef]
- Prativadibhayankaram, S.; Richter, T.; Sparenberg, H.; Fößel, S. Color learning for image compression. arXiv 2023. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, J.; Zhang, T. Fuzzy image processing based on deep learning: A survey. In The International Conference on Image, Vision and Intelligent Systems (ICIVIS 2021); Lecture Notes in Electrical Engineering; Yao, J., Xiao, Y., You, P., Sun, G., Eds.; Springer: Singapore, 2022; Volume 813, pp. 111–120. [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; Zhang, Z.; Jin, X.; Chen, Z. Learned block-based hybrid image compression. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 3978–3990. [Google Scholar] [CrossRef]
- Anju, M.I.; Mohan, J. DWT lifting scheme for image compression with cordic-enhanced operation. Int. J. Pattern Recognit. Artif. Intell. 2022, 36, 2254006. [Google Scholar] [CrossRef]
- Pang, H.-Y.; Zhou, R.-G.; Hu, B.-Q.; Hu, W.W.; El-Rafei, A. Signal and image compression using quantum discrete cosine transform. Inf. Sci. 2019, 473, 121–141. [Google Scholar] [CrossRef]
- Ma, H.; Liu, D.; Yan, N.; Li, H.; Wu, F. End-to-End optimized versatile image compression with wavelet-like transform. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1247–1263. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Chen, L.; Lyu, W.; Luo, B. Reversible attack based on adversarial perturbation and reversible data hiding in YUV colorspace. Pattern Recognit. Lett. 2023, 166, 1–7. [Google Scholar] [CrossRef]
- Di Martino, F.; Sessa, S.; Perfilieva, I. First order fuzzy transform for images compression. J. Signal Inf. Process. 2017, 8, 178–194. [Google Scholar] [CrossRef][Green Version]
- Di Martino, F.; Sessa, S. Fuzzy Transforms for Image Processing and Data Analysis—Core Concepts, Processes and Applications; Springer Nature: Cham, Switzerland, 2020; p. 217. [Google Scholar] [CrossRef]
- Cardone, B.; Di Martino, F. Bit reduced fcm with block fuzzy transforms for massive image segmentation. Information 2020, 11, 351. [Google Scholar] [CrossRef]
- Seifi, S.; Noorossana, R. An integrated statistical process monitoring and fuzzy transformation approach to improve process performance via image data. Arab. J. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Min, H.J.; Jung, H.Y. A study of least absolute deviation fuzzy transform. Int. J. Fuzzy Syst. 2023, 11. [Google Scholar] [CrossRef]
- Perfilieva, I.; Dankova, M.; Bede, B. Towards a higher degree F-transform. Fuzzy Sets Syst. 2011, 180, 3–19. [Google Scholar] [CrossRef]
- ISO/IEC 10918-1:1994; Technology—Digital Compression and Coding of Continuous-Tone Still Images: Requirements and Guidelines. ISO: Geneva, Switzerland, 1994; p. 182.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).