Capacitive Water-Cut Meter with Robust Near-Linear Transfer Function

Abstract

The water content in fuel–water emulsions can vary from 10% to 30%, and is under control during the process of emulsification. The main task of this study was to obtain near-linear static function for a water-cut meter with capacitive sensors, and to provide it with effective type-uncertainty compensation during the process of water–fuel emulsion moisture control. To fulfill the capacitive measurements, two capacitive sensors in the measuring channel and two capacitive sensors in the reference channel were used. The method of least squares and general linear regression instruments were used to obtain robust and near-linear transfer function of the capacitive water-cut meter. The prototype product of the water-cut meter was developed with the purpose of fulfilling multiple moisture measurements and checking the workability of the new transfer function. Values of moisture content for the new transfer function and the closest analog were compared with the help of dispersion analysis. The new transfer function provided minimal dispersions of repeatability and adequacy, and minimal F-test values, proving its better capability for type-uncertainty compensation and better adequacy for the nominal linear transfer function of the water-cut meter.

1. Introduction

Emulsified fuels have a clear effect on the combustion process, and are one of the modern combustible systems that offer prospects for new technologies. This has been exploited recently in diesel engines, which have been used for a long time as the main source of driving power due to their reliable design and high fuel-saving economy [1,2]. Significant results in the toxicity reduction of diesel engines’ exhaust fumes were achieved by the application of fuels with water and alcohol additives [3]. Hence, emulsified fuels are mixtures of a combustible liquid, either oil or fuel as a continuous phase, and a smaller amount of water with or without a surfactant as a dispersed phase. Emulsion of petroleum fuel in water is the most common form of such emulsion [4]. In emulsified diesel fuel, the heat absorption by water vaporization causes a decrease in the local adiabatic flame temperature, and this reduces the chemical reaction in the gas phase to produce thermal NO_x [5]. Moreover, this helps to reduce the formation of soot, PM, CO, and HC [6,7]. Water–fuel emulsion is a system that includes water (dispersed phase with 0.1…10 μm diameter of droplets) and diesel fuel as a dispersion medium [8,9,10], and the volumetric water content in the fuel–water emulsions can vary from 5% to 30%, and is an object of strict control during the process of emulsification [4,11,12,13].

Methods of moisture measurement can be divided into direct—based on dividing the substance under research into free water and dry material—and indirect, where moisture content can be defined based on the values of other measurements functionally connected with moisture [14,15,16]. To identify popular principles of moisture measurement, a detailed analysis of the world moisture meter market, produced in a recent period, was carried out for bulk substances and oil products as objects of measurement. In total, 358 moisture meters for bulk materials and 64 moisture meters for oil products were detected. The dielcometer (capacitive) principle of moisture measurement remains forward-looking among all indirect methods [17].

A large number of factors influence moisture measurement accuracy. Among them, we traditionally emphasize the physicochemical composition of the combustible liquid (oil fuel as a continuous phase of the emulsion) [16,18,19]. It is not only the type of fuel that has an effect on its physicochemical composition, but the conditions of extraction and processing, etc., and obtaining a full list of factors for analytic forecasting is usually complicated.

A list of analytical methods has been developed to determine the moisture content of oils, based on the fact that water has appreciably different bulk physical characteristics than the oil matrix, e.g., density, dielectric permittivity, or refractive index. These methods are usually only suitable for the analysis of substances in which the composition of the oil matrix does not change significantly, but where the water-to-oil ratio of the matrix changes. For example, the water content of an oil-in-water emulsion can be determined by measuring the density or dielectric permittivity, because the density and dielectric permittivity of water are significantly higher than those of oil. If the composition of the oil matrix changes as well as the water content, then it may not be possible to accurately determine the moisture content of the oil, because more than one oil composition may give the same value for the physical property being measured. Unfortunately, it is impossible to obtain an analytic forecast of the chemical composition and different features of all of the emulsified fuels under research. This is why most indirect methods of moisture measurement have local effectiveness, and are not versatile.

At present, approximately 33% of moisture meters are represented by dielcometer measuring instruments with capacitive sensors. Moisture meters of this type have method error (type uncertainty), the value of which directly depends on the dielectric permittivity of the dry oil as a continuous phase of the emulsion under research (oil type, for example) [16,18]. The influence of type uncertainty on the result of moisture measurement is usually significant, and traditional methods of compensation can be effective when we know the composition of a substance. Such compensation, in general, can be fulfilled using a secondary measuring transducer by using complementary reference capacitors, dedicated analytic calculations, reference calibration curves stored in the secondary measuring transducers’ memory, etc. It can all be used for the limited number of materials under research, and does not allow the moisture meter to be versatile for a wide range of fuel substances. In other cases, the effectiveness of traditional compensation methods essentially decreases, because of which further improvement of the existing methods of moisture measurement with a view to solving the problem of type-uncertainty compensation is a relevant and perspective mission [20]. In-depth analysis of modern moisture control approaches with the purpose of further development and improvement is still a relevant task, and the process of searching for new methods of water-cut sensing optimization is under constant continuation [21,22,23].

“Successful” modifications of capacitive moisture meters with capacitive sensors appeared years ago [24,25,26]. An idea to obtain capacitive measurements using two or more positions for one of the capacitor plates, with further direct comparison, seemed to be of special interest [27,28]. This approach helps to eliminate parasitic capacitances almost completely, compensate for leakage currents, and reduce the influence of fringe electric fields. The main task of this research is in achieving robust, near-linear transfer function for the comparison of methods of moisture measurement, as described in [17], and to provide effective type-uncertainty compensation during the process of water–fuel emulsion moisture control.

2. Materials and Methods

In capacitive sensors, where one of the capacitor plates should be placed in two or more positions [27], we first take an empty sensor, where a change in electric capacitance ΔC₀ should be defined before and after the distance between two plates is changed. Then, we define the change in electric capacitance ΔC₁ when a capacitive sensor is filled with a tested substance for the same positions of the capacitor plates. After that, the relation ΔC₁/ΔC₀ should be calculated. In this method, only the accuracy of the capacitor plates’ positioning would influence the uncertainty of the measurements. Thus, the transfer function of the moisture meter should be described with the following formula:

$$W=K\cdot \frac{C_3-C_4}{C_2-C_1},$$

(1)

where K is a normalizing coefficient [17] equal to K = 28.599 when we take the values of electric capacitances, equal to 15 pF for C₁ and C₄, and 50 pF for C₂ and C₃ when the capacitive sensors are empty.

The suggested design of the capacitive instrument measuring transducer is described below (Figure 1). As we can see, both of its sensors consist of a system of flat plates (1), where two pairs of flat plates belong to measuring capacitors C₁ and C₄, and the rest of the flat plates create another pair of measuring capacitors C₂ and C₃. All flat plates of equal length l are assembled inside two fluoroplastic rings (2) at an equal gap, designated as Z.

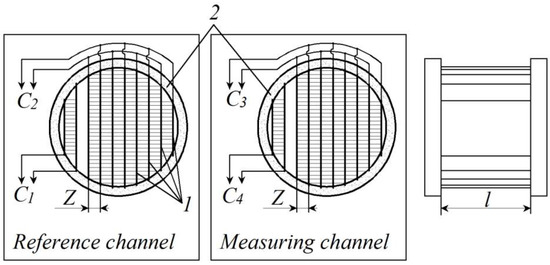
Figure 1. Capacitive instrument measuring transducer for moisture content (1—system of flat electrodes, 2—fluoroplastic rings).

The measuring channel should be filled with a probe of liquid fuel under moisture control, and the reference channel should be filled with the same substance, but previously dehydrated. Using the method mentioned above, it is necessary to measure the values of electric capacitances C₁, C₂, C₃, and C₄, and then to calculate the differences C₂ − C₁ and C₃ − C₄. When this is done, we can calculate the relationship of these differences (C₃ − C₄)/(C₂ − C₁), and this would be an informative parameter for further processing, directly connected with moisture content.

To implement this idea in practice, moisture content measuring instruments should have a structure, as given in Figure 2. As we can see, four capacitive sensors of the measuring transducer are connected to the inputs of corresponding monostable multivibrators MMV1…MMV4, designed to convert values of electric capacitance into a duration of rectangular pulses. The microcontroller CPU controls the monostable multivibrators’ work by generating rectangular pulses of a stable frequency on one of its output pins.

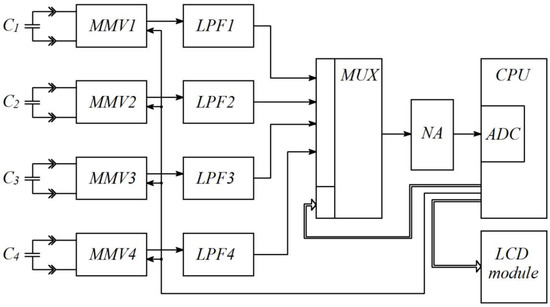
Figure 2. Structural electric circuit of the moisture meter (MMV1…MMV4—monostable multivibrators, LPF1…LPF4—low-pass filters, MUX—multiplexer, NA—normalizing amplifier, ADC—analog-to-digital converter).

Each monostable multivibrator generates a sequence of rectangular pulses, the duration of which is in direct proportion with the value of electric capacitance, connected to its input (diagrams in Figure 3).

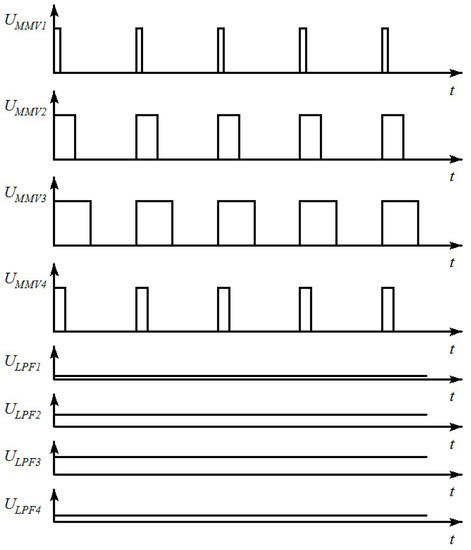
Figure 3. Operating diagrams for the analogue part of the moisture meter.

Low-pass filters convert pulse duration into DC voltage in proportion to the pulse duration amplitude. The multiplexer MUX, controlled by the CPU, commutes the outputs of the low-pass filters LPF1…LPF4 with the input of the normalizing amplifier NA which, in turn, provides levels of DC voltage compatible with the measuring range of the analog-to-digital converter ADC embedded in the CPU. The microcontroller CPU, after having four values of DC voltage proportional to the values of the four electric capacitances C₁, C₂, C₃, and C₄, calculates the moisture content of the substance under research, and displays the results on the LCD module’s screen. To check the behavior of the transfer function (1) with different types of moist substances, we took four values of dielectric permittivity for imaginary dehydrated fuels (ε_n = 2.0; ε_n = 2.5; ε_n = 3.0; ε_n = 3.5) and four values of moisture content (W = 0%; W = 10%; W = 20%; W = 30%). The values of dielectric permittivity for moist substances, necessary to calculate the values of the four sensors’ capacitances, were estimated with the help of the universal Wiener equation [29,30,31,32]. The values of capacitances C₁, C₂, C₃, and C₄, and the calculated values of moisture content defined with the help of the static function (1), are given in Table 1.

Table 1. Calculated values of sensors’ capacitances and moisture content for the transfer function (1).

W, %	Ci, pF	εn
		2.0	2.5	3.0	3.5
0	C1	30	37.5	45	52.5
	C2	100	125	150	175
	C3	100	125	150	175
	C4	30	37.5	45	52.5
	Wcalc	0	0	0	0
		εn
		2.614	3.252	3.885	4.512
	C1	30	37.5	45	52.5
10	C2	100	125	150	175
	C3	130.7	162.6	194.25	225.6
	C4	39.21	48.78	58.28	67.68
	Wcalc	8.78	8.60	8.44	8.23
		εn
		3.368	4.317	4.963	5.741
20	C1	30	37.5	45	52.5
	C2	100	125	150	175
	C3	168.4	215.85	248.15	287.05
	C4	50.52	64.76	74.45	86.12
	Wcalc	19.56	20.78	18.71	18.31
		εn
		4.317	5.324	6.305	7.262
30	C1	30	37.5	45	52.5
	C2	100	125	150	175
	C3	215.85	266.2	315.25	363.1
	C4	64.76	79.86	94.58	108.93
	Wcalc	33.13	32.31	31.51	30.74

Graphs of received transfer functions for different moist substances, and their comparison with an ideal linear transfer function, are given in Figure 4.

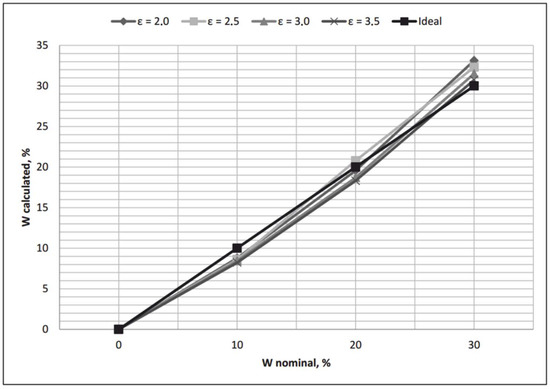
Figure 4. Calculated transfer functions, placed together with an ideal transfer function of the water-cut meter.

As we can see, all transfer functions received with the help of Equation (1) are nonlinear, and the calculated values of moisture content are significantly different from nominal in all points, except for W = 0%. Hence, at first, Equation (1) should be linearized.

To achieve near-linear dependence between moisture content W and the (C₃ − C₄)/(C₂ − C₁) relationship, the method of least squares and instruments of general linear regression were used. The modified transfer function for the water-cut meter is given in Equation (2), where a and b are coefficients preliminarily defined in [33] (a = 0.9622, b = 0.0371):

$$W_m=-1.019+1.269\cdot \frac{\left(\frac{C_3-C_4}{C_2-C_1}-a\right)}{b}-0.00527\cdot {\frac{\left(\frac{C_3-C_4}{C_2-C_1}-a\right)}{b^2}}^2-0.000112\cdot {\frac{\left(\frac{C_3-C_4}{C_2-C_1}-a\right)}{b^3}}^3.$$

(2)

New values of moisture content, calculated using Formula (2), are given in Table 2.

Table 2. Calculated values of a static function (2).

W, %	Wm
	εn = 2.0	εn = 2.5	εn = 3.0	εn = 3.5
0	0.268	0.268	0.268	0.268
10	10.230	10.045	9.859	9.674
20	20.850	20.470	20.085	19.723
30	30.658	30.211	29.476	29.280

The graphs of received transfer functions for different moist substances can be seen in Figure 5. If we compare Figure 4 and Figure 5, it would be possible to say that the modified transfer function (2) is far more effective than the initial transfer function (1).

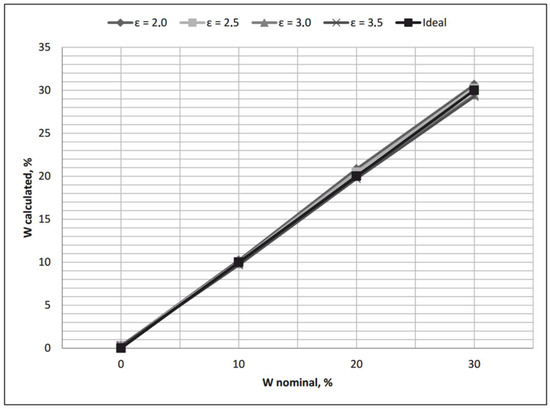
Figure 5. Modified transfer functions together with an ideal transfer function of the water-cut meter.

To prove this analytically, it seemed to be rational to calculate one of the goodness-of-fit parameters, e.g., root mean estimator (Equation (3)):

$$S=\sqrt{\frac{{{\displaystyle \sum \left(W_{inom}-W_{icalc}\right)}}^2}{n}}.$$

(3)

For the data in Table 1, we can write:

$$\begin{gathered} \begin{array}{l}{{\displaystyle \sum \left(W_{inom}-W_{icalc}\right)}}^2={\left(0-0\right)}^2\cdot 4+{\left(10-8.78\right)}^2+{\left(10-8.60\right)}^2+{\left(10-8.44\right)}^2+\\ +{\left(10-8.23\right)}^2+{\left(20-19.56\right)}^2+{\left(20-20.78\right)}^2+{\left(20-18.71\right)}^2+{\left(20-18.31\right)}^2+\\ +{\left(30-31.13\right)}^2+{\left(30-32.31\right)}^2+{\left(30-31.51\right)}^2+{\left(30-30.74\right)}^2=27.2978,\end{array} \\ S=\sqrt{\frac{27.2978}{16}}=1.3062\%. \end{gathered}$$

For the data in Table 2, the result would be S = 0.4158%.

To carry out experimental research with the purpose of checking the workability of a transfer function (2), and to estimate the provided level of uncertainty in the moisture content measurements, it was necessary to obtain stable reference samples of oil products with different dielectric permittivity values ε_n in a dehydrated state, and values of moisture content equal to W = 0%, W = 10%, W = 20%, and W = 30%. We used diesel fuel with ε_n = 2.01 and mazut with ε_n = 2.67 for this purpose. Stable reference samples of diesel fuel and mazut with 10 µm diameter of water particles were obtained by adding appropriate volumes of water, with the help of a second-class precision pipette [34] and 30 min of mechanical mixing at n = 3200 rpm [35,36].

Sensors of a measuring transducer were assembled from four identical fluoroplastic rings with slots to insert flat stainless steel plates, which were glued to the internal surface of the appropriate pair of fluoroplastic rings with the help of superglue gel, and soldered with wires to create four capacitive sensors (Figure 6).

Figure 6. Prototype product of the capacitive measuring transducer: (a,b) in an empty state, (c) filled with diesel fuel (ε_n = 2.01), and (d) filled with mazut (ε_n = 2.67).

The process of moisture measurement was performed following the substitution method, where the value of the quantity being measured is not found directly from a reading of the measuring instrument, but rather from the magnitude of the standard, which is regulated in such a way that the reading of the measuring instrument remains the same when the quantity being measured is replaced by the standard. Commonly known, this method eliminates systematic errors and provides high accuracy, and the substitution method is extensively used in measuring electrical quantities, such as resistance, capacitance, and inductance. The connection scheme of the devices involved in the process of moisture measurement is given in Figure 7.

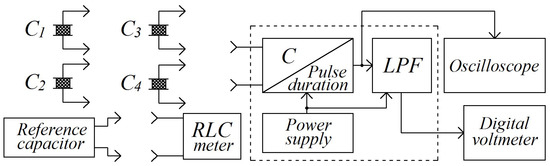
Figure 7. Connection of the devices involved in the moisture measurement: experimental setup.

The setup consists of four capacitive sensors, designated as C₁, C₂, C₃, and C₄, one channeled capacitance into a DC-voltage transducer that performs a sequence of transformations “capacitance–pulse duration–dc voltage”, a variable air capacitor (reference capacitor), an oscilloscope, a digital voltmeter, and an RLC meter.

From the very beginning, a part of the measuring transducer with two capacitive sensors C₁ and C₂ (reference channel) was filled with the original (with traces of water) sample of oil product (Figure 8a). Both capacitive sensors of the reference channel were connected one by one to the input of capacitance into the DC-voltage transducer, and appropriate DC voltage values were taken from the screen of a digital voltmeter and fixed by the operator. Then, the variable air capacitor (reference capacitor or standard) was connected instead of the capacitive sensors. Its capacitance was slowly changed in correspondence with the method of substitution until the moment when the DC voltage value on the voltmeter’s screen became equal to the values detected previously (Figure 8b).

Figure 8. Process of moisture measurement: (a) connection of the first part of the measuring transducer (sensors C₁ and C₂ with dehydrated diesel fuel) to the input of a secondary capacitance into the DC-voltage transducer; (b) the reference capacitor’s connection instead of sensors C₁ and C₂; (c) measuring the capacitance of a reference capacitor with the help of the RLC meter; (d) connection of the second part of the measuring transducer (sensors C₃ and C₄ with moist diesel fuel, W = 20%) to the input of a secondary capacitance into the DC-voltage transducer.

After that, the standard capacitor was disconnected from the transducer, and its capacitance was measured with the help of an accurate RLC meter at a 10 kHz frequency. The same process took place for the capacitive sensors in the measuring channel, filled with moist samples of oil products (Figure 8d). As a result, 10 measurements of electric capacitance were received from each capacitive sensor. The oscilloscope helped to control the correct operation of the capacitance into the pulse duration transducer. At first, this helped to choose the correct operating mode of the secondary transducer, when the duration of rectangular pulses was in direct proportion with the C₁, C₂, C₃, and C₄ capacitance values in the whole range of their variation. Furthermore, the presence of the oscilloscope was necessary to detect possible oscillation stops when measuring high moisture contents (i.e., over 20%).

3. Theory/Calculation

The next step was to check the ability of the new transfer function (2) to retain stability when working with experimental results of measurements with natural random variation. The values of electric capacitances taken from capacitive sensors were not the ideal deterministic values used in Table 1, but would always have some random variation. The presence of random variation (i.e., capacitance measurement uncertainty) influences the uncertainty of the calculated moisture content values; it can decrease the robustness of the transfer function (2) up to the moment when it becomes irrelevant [37,38,39]. To check the robustness of the transfer function (2) theoretically, we introduced symmetric variation into the values of electric capacitance. The range of variation was set at a level of 0.01% from the values of electric capacitance after the analysis of metrological performance for modern capacitance and RLC meters. The calculated values of electric capacitance for capacitive sensors placed in the reference channel are shown in Table 3, while those for the sensors of the measuring channel are shown in Table 4 (initial values of electric capacitance calculated for different substances are marked with bold print).

Table 3. Capacitance values for the sensors in the reference channel, with 0.01% variation.

W	εn = 2.0			εn = 2.5			εn = 3.0			εn = 3.5
0%	$C_{1-}$	$C_1$	$C_{1+}$	$C_{1-}$	$C_1$	$C_{1+}$	$C_{1-}$	$C_1$	$C_{1+}$	$C_{1-}$	$C_1$	$C_{1+}$
	29.7	30.0	30.3	37.125	37.5	37.875	44.55	45.0	45.45	51.975	52.5	53.025
	$C_{2-}$	$C_2$	$C_{2+}$	$C_{2-}$	$C_2$	$C_{2+}$	$C_{2-}$	$C_2$	$C_{2+}$	$C_{2-}$	$C_2$	$C_{2+}$
	99	100	101	123.75	125	126.25	148.5	150	151.5	173.25	175	176.75

Table 4. Capacitance values for the sensors in the measuring channel, with 0.01% variation.

εn	Variation of C	W = 0%	W = 10%	W = 20%	W = 30%
2.0	$C_{3-}$	99	129.393	166.716	213.692
	$C_3$	100	130.7	168.4	215.85
	$C_{3+}$	101	132.007	170.084	218.009
2.5	$C_{3-}$	123.75	160.974	206.564	263.538
	$C_3$	125	162.6	208.65	266.2
	$C_{3+}$	126.25	164.226	210.737	268.862
3.0	$C_{3-}$	148.5	192.308	245.669	312.098
	$C_3$	150	194.25	248.15	315.25
	$C_{3+}$	151.5	196.193	250.632	318.403
3.5	$C_{3-}$	148.5	192.308	245.669	312.098
	$C_3$	150	194.25	248.15	315.25
	$C_{3+}$	151.5	196.193	250.632	318.403
2.0	$C_{4-}$	29.7	38.818	50.015	64.107
	$C_4$	30.0	39.21	50.52	64.755
	$C_{4+}$	30.3	39.602	51.025	65.403
2.5	$C_{4-}$	37.125	48.292	61.969	79.061
	$C_4$	37.5	48.78	62.595	79.86
	$C_{4+}$	37.875	49.268	63.221	80.659
3.0	$C_{4-}$	44.55	57.692	73.701	93.629
	$C_4$	45.0	58.275	74.445	94.575
	$C_{4+}$	45.45	58.858	75.189	95.521
3.5	$C_{4-}$	51.975	67.003	85.254	107.841
	$C_4$	52.5	67.68	86.115	108.93
	$C_{4+}$	53.025	68.357	86.976	110.019

The robustness of the transfer function (2) was checked for the conditions when each value of sensors’ capacitance was the maximum or minimum within the symmetric variation range ±0.01%. The signs “+” and “−” in later designations represent the maximal or minimal values of electric capacitance. As we had four sensors, 16 different combinations were possible (Table 5). For example, the designation “+–++” means that the electric capacitances C₁, C₃, and C₄ take maximal values, while C₂ is minimal [40].

Table 5. Calculated moisture values with 0.01% variation of capacitances C₁, C₂, C₃, and C₄.

W	εn = 2.0				εn = 2.5
	Wnominal, %				Wnominal, %
	0	10	20	30	0	10	20	30
W−−++	0.952	11.038	21.7	31.325	0.952	10.845	21.325	30.884
W+−++	1.252	11.392	22.068	31.601	1.252	11.198	21.694	31.17
W−+++	−0.017	9.89	20.491	30.378	−0.017	9.7	20.115	29.908
W++++	0.268	10.23	20.851	30.666	0.268	10.039	20.475	30.204
W−−−+	−0.026	9.881	20.481	30.37	−0.026	9.69	20.105	30.204
W+−−+	0.268	10.23	20.851	30.666	0.952	10.845	21.325	30.884
W−+−+	−0.973	8.749	19.268	29.364	1.252	11.198	21.694	31.17
W++−+	−0.694	9.083	19.628	29.668	−0.017	9.7	20.115	29.908
W−−+−	1.243	11.382	22.057	30.666	0.268	10.039	20.475	30.204
W+−+−	1.546	11.737	22.424	30.956	−0.026	9.69	20.105	30.204
W−++−	0.268	10.23	20.85	30.666	0.268	10.039	20.475	30.504
W+++−	0.556	10.57	21.209	30.948	−0.973	8.561	18.892	29.19
W−−−−	0.268	10.23	20.85	30.666	-0.694	8.895	19.252	29.497
W+−−−	0.564	10.58	21.22	30.956	1.243	11.188	21.684	31.162
W−+−−	−0.686	9.093	19.639	29.677	1.546	11.543	22.052	31.442
W++−−	−0.405	9.429	19.999	29.977	0.268	10.039	20.475	30.204
	εn = 3.0				εn = 3.5
W−−++	0.952	10.665	20.945	30.439	0.952	10.473	20.583	29.993
W+−++	1.252	11.017	21.315	30.733	1.252	10.833	20.952	30.296
W−+++	−0.017	9.522	19.734	29.437	−0.017	9.341	19.37	28.968
W++++	0.268	9.86	20.094	29.74	0.268	9.678	19.731	29.278
W−−−+	−0.026	9.512	19.724	29.428	−0.026	9.331	19.36	28.959
W+−−+	0.268	9.86	20.094	29.74	0.268	9.678	19.731	29.278
W−+−+	−0.973	8.386	18.511	28.377	−0.973	8.208	18.147	27.888
W++−+	−0.694	8.719	18.871	28.694	−0.694	8.54	18.507	28.211
W−−+−	1.243	11.027	21.304	30.725	1.243	10.823	20.942	30.288
W+−+−	1.546	11.381	21.673	31.015	1.546	11.176	21.311	30.585
W−++−	0.268	9.86	20.094	29.74	0.268	9.678	19.731	29.278
W+++−	0.556	10.199	20.454	30.039	0.556	10.017	20.091	29.583
W−−−−	0.268	9.86	20.094	29.74	0.268	9.678	19.731	29.278
W+−−−	0.564	10.209	20.464	30.047	0.564	10.026	20.101	29.592
W−+−−	−0.686	8.728	18.881	28.703	−0.686	8.55	18.518	28.22
W++−−	−0.405	9.063	19.241	29.016	−0.405	8.883	18.878	28.539

As we can see from Table 5, it would be nearly impossible to use separate random results of capacitance measurements together with Formula (2), because the relative full-scale error of moisture content would be rather large. Here, it would be rational to use such robust estimators as the mean (average), median, and truncated mean—in other words, to increase the accuracy of the moisture measurements, we would have to use some kind of estimator, the uncertainty of which would be many times smaller compared with the uncertainty of separate measurements.

Measured values of capacitances for the sensors C₁, C₂, C₃, and C₄ are given in Table 6.

Table 6. Measured values of capacitance for the sensors C₁, C₂, C₃, and C₄ with diesel fuel and mazut.

№ of Experiment	Moisture Content W, %
	0		10		20		30
	Diesel Fuel, εn = 2.01
	C1, pF	C2, pF	C3, pF	C4, pF	C3, pF	C4, pF	C3, pF	C4, pF
1	30.22	94.69	125.34	40.62	159.45	51.24	202.91	68.36
2	30.61	94.81	125.21	40.30	160.11	50.96	203.26	68.24
3	30.29	95.16	125.64	40.36	159.66	50.84	203.11	67.86
4	30.48	94.73	125.82	40.29	159.74	51.11	202.84	67.91
5	30.41	94.79	125.70	40.32	159.91	51.03	202.89	67.99
6	30.36	94.91	125.49	40.59	159.86	50.91	203.04	68.02
7	30.28	94.98	125.66	40.44	159.72	50.89	203.13	68.17
8	30.31	95.11	125.21	40.26	159.84	51.36	202.94	68.06
9	30.42	94.73	125.32	40.32	159.79	51.01	202.63	68.24
10	30.41	94.85	125.61	40.41	160.03	51.26	202.79	67.93
Mean values	30.58	94.81	125.50	40.39	159.81	51.06	202.95	68.08
Median values	30.39	94.83	125.55	40.34	159.82	51.02	202.93	68.04
№ of Experiment	Mazut, εn = 2.67
	C1, pF	C2, pF	C3, pF	C4, pF	C3, pF	C4, pF	C3, pF	C4, pF
1	41.16	127.56	168.46	54.08	213.86	70.36	270.64	87.52
2	41.29	127.64	168.04	54.21	214.21	70.24	270.99	88.26
3	41.36	128.12	168.54	54.66	214.10	70.08	271.04	87.96
4	41.28	127.74	168.22	54.71	214.36	70.21	270.45	87.71
5	41.40	127.81	168.11	54.32	214.02	69.96	270.93	87.82
6	41.31	127.94	168.01	54.39	213.69	69.91	270.44	87.46
7	41.19	127.90	168.14	54.56	213.76	70.22	270.51	87.56
8	41.22	127.69	168.34	54.38	213.84	70.16	270.72	87.39
9	41.38	127.78	168.21	54.49	213.92	70.28	270.59	87.94
10	41.31	128.09	168.03	54.41	213.90	69.08	270.41	87.62
Mean values	41.29	127.83	168.21	54.42	213.97	70.05	270.67	87.72
Median values	41.30	127.80	168.18	54.40	213.91	70.19	270.62	87.67

Calculated values of moisture content with mean and median values of the sensors’ capacitances for the transfer functions (1) and (2) can be found in Table 7.

Table 7. Calculated results of the transfer functions (1) and (2), with mean and median values.

Wnom, %	Wcalculated, %
	Static Function (1)		Static Function (2)
	with Mean Values of C1, C2, C3 and C4		with Mean Values of C1, C2, C3 and C4
	Diesel Fuel	Mazut	Diesel Fuel	Mazut
0	0.000	0.000	0.268	0.268
10	9.297	9.005	10.784	10.472
20	19.823	18.962	21.080	20.318
30	31.453	31.861	29.708	29.948
	with Median Values of C1, C2, C3 and C4		with Median Values of C1, C2, C3 and C4
0	0.000	0.000	0.268	0.268
10	9.218	9.019	10.700	10.487
20	19.687	18.918	20.961	20.278
30	31.266	31.889	29.597	29.964

To compare the robustness of the results in Table 7, it would be rational to use dispersion analysis. At first, four values of mean square error (dispersions of repeatability) should be calculated (4):

$$S_{rep}^2=\frac{{\displaystyle \sum _{j=1}^m{\displaystyle \sum _{i=1}^n{\left(W_{i,j}-\overline{W_j}\right)}^2}}}{n\cdot m-1}.$$

(4)

Formula (4) requires the mean values of moisture content to be calculated for the results in Table 7. Appropriate calculations are given in Table 8.

Table 8. Arithmetic mean values of moisture content.

Wnom, %	$\mathbf{Mean}\mathbf{Values}{\overline{\mathit{W}}}_{\mathit{j}},\%$
	Function (1), Mean Values	Function (1), Median Values	Function (2), Mean Values	Function (2), Median Values
0	0.000	0.000	0.268	0.268
10	9.151	9.119	10.628	10.594
20	19.393	19.303	20.699	20.620
30	31.657	31.578	29.828	29.781

After the application of Formula (4), we receive:

$$\begin{gathered} S_{rep1}^2=\frac{{\left(0.000-0.000\right)}^2+{\left(9.297-9.151\right)}^2+{\left(19.823-19.393\right)}^2+{\left(31.453-31.657\right)}^2}{2\cdot 4-1}+ \\ +\frac{{\left(0.000-0.000\right)}^2+{\left(9.005-9.151\right)}^2+{\left(18.962-19.393\right)}^2+{\left(31.861-31.657\right)}^2}{2\cdot 4-1}=0.0708, \\ {S}_{rep2}^2=\frac{{\left(0.268-0.268\right)}^2+{\left(9.218-9.119\right)}^2+{\left(19.687-19.303\right)}^2+{\left(31.266-31.578\right)}^2}{2\cdot 4-1}+ \\ +\frac{{\left(0.268-0.268\right)}^2+{\left(9.019-9.119\right)}^2+{\left(18.918-19.303\right)}^2+{\left(31.889-31.578\right)}^2}{2\cdot 4-1}=0.07279, \\ {S}_{rep3}^2=\frac{{\left(0.268-0.268\right)}^2+{\left(10.784-10.628\right)}^2+{\left(21.080-20.699\right)}^2+{\left(29.708-29.828\right)}^2}{2\cdot 4-1}+ \\ +\frac{{\left(0.268-0.268\right)}^2+{\left(10.472-10.628\right)}^2+{\left(20.318-20.699\right)}^2+{\left(29.948-29.828\right)}^2}{2\cdot 4-1}=0.0525, \\ {S}_{rep4}^2=\frac{{\left(0.268-0.268\right)}^2+{\left(10.700-10.594\right)}^2+{\left(20.961-20.620\right)}^2+{\left(29.597-29.781\right)}^2}{2\cdot 4-1}+ \\ +\frac{{\left(0.268-0.268\right)}^2+{\left(10.487-10.594\right)}^2+{\left(20.278-20.620\right)}^2+{\left(29.964-29.781\right)}^2}{2\cdot 4-1}=0.0462, \end{gathered}$$

where $S_{rep1}^2$ is a dispersion of repeatability for the transfer function (1) with mean values of C₁, C₂, C₃, and C₄; $S_{rep2}^2$ is a dispersion of repeatability for the transfer function (1) with median values; $S_{rep3}^2$ is a dispersion of repeatability for the transfer function (2) with mean values; and $S_{rep4}^2$ is a dispersion of repeatability for the transfer function (2) with median values.

Then four dispersions of adequacy (for the data in Table 8) should be calculated as follows (5):

$$S_{ad}^2=\frac{{\displaystyle \sum _{j=1}^m{\left(\overline{W_j}-{\overline{W}}_{jnom}\right)}^2}}{N-\left(m+1\right)},$$

(5)

where N is the total number of moisture content values W_calculated; and m is the number of nominal points of moisture content W_nom.

$$\begin{gathered} S_{ad1}^2=\frac{{\left(0-0\right)}^2+{\left(9.151-10\right)}^2+{\left(19.393-20\right)}^2+{\left(31.657-30\right)}^2}{8-\left(4+1\right)}=1.302, \\ {S}_{ad2}^2=\frac{{\left(0-0\right)}^2+{\left(9.119-10\right)}^2+{\left(19.303-20\right)}^2+{\left(31.578-30\right)}^2}{8-\left(4+1\right)}=1.275, \\ {S}_{ad3}^2=\frac{{\left(0.268-0\right)}^2+{\left(10.628-10\right)}^2+{\left(20.699-20\right)}^2+{\left(29.828-30\right)}^2}{8-\left(4+1\right)}=0.328, \\ {S}_{ad4}^2=\frac{{\left(0.268-0\right)}^2+{\left(10.594-10\right)}^2+{\left(20.620-20\right)}^2+{\left(29.781-30\right)}^2}{8-\left(4+1\right)}=0.286, \end{gathered}$$

where $S_{ad1}^2$ is a dispersion of adequacy for the transfer function (1) with mean values; $S_{ad2}^2$ is a dispersion of adequacy for the transfer function (1) with median values; $S_{ad3}^2$ is a dispersion of adequacy for the transfer function (2) with mean values; and $S_{ad4}^2$ is a dispersion of adequacy for the transfer function (2) with median values.

To compare the dispersions of adequacy with the dispersions of repeatability, we used the following F-test: $F=S_{ad}^2/S_{rep}^2.$ All calculations for the results given in Table 7 and Table 8 can be found in Table 9.

Table 9. Results of robustness verification for the transfer functions (1) and (2).

Data Source	${\mathit{S}}_{\mathit{r}\mathit{e}\mathit{p}}^2$	${\mathit{S}}_{\mathit{a}\mathit{d}}^2$	$\mathit{F}$
Function (1), mean values	0.0708	1.302	18.39
Function (1), median values	0.0728	1.275	17.51
Function (2), mean values	0.0525	0.328	6.25
Function (2), median values	0.0462	0.286	6.19

4. Results/Discussion

As mentioned in the “Materials and Methods” section, the first attempt to provide effective “type uncertainty” compensation for capacitive moisture meters was described in [8], and transfer function (1) is the result.

The calculated values of the sensors’ capacitances and moisture content for the transfer function (1) were received with a help of the universal Wiener equation as one of the most popular dielectric mixture models (6):

$${\epsilon }_{mix}={\epsilon }_n\left(1+\frac{3W}{\left({\epsilon }_W+2{\epsilon }_n\right)/\left({\epsilon }_W-{\epsilon }_n\right)-W}\right),$$

(6)

where ε_mix is the dielectric permittivity of a binary material–water mixture; ε_n is the dielectric permittivity of dry material; ε_W = 80, and is the dielectric permittivity of water; and W is the volumetric moisture content, taken in absolute values.

If we apply the universal Wiener equation to the values of dielectric permittivity given in Table 1, and use it as the water-cut meter’s transfer function, we obtain a family of curves (Figure 9).

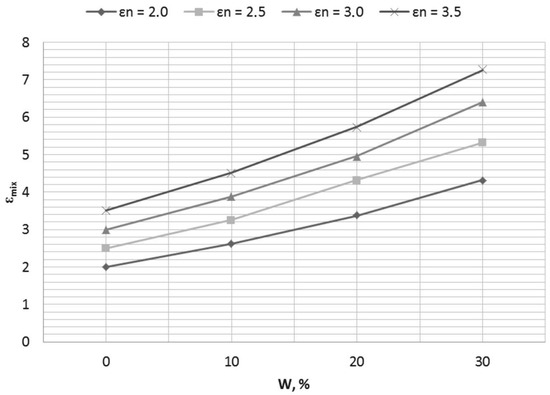
Figure 9. Influence of the changes in the composition of a dry substance ε_n on the value of the dielectric permittivity of a binary mixture ε_mix.

Figure 9 illustrates the situation when the oil matrix composition changes as well as the water content (oil type uncertainty). If no type-uncertainty compensation happens, we have a family of transfer functions for the water-cut meter instead of one, taken as a nominal.

The transfer function (1) helps to solve this problem, and provides the possibility of measurements in emulsified fuels, where the dielectric permittivity of a dry oil ε_n varies in a wide range from 2 to 3.5, without any preliminary calibration.

However, Figure 1 illustrates that a transfer function received with the help of Equation (1) is still nonlinear, the influence of fuel type uncertainty remains significant, and the calculated values of moisture content do not correspond to the nominal linear model.

To determine the linear dependence between moisture content W and the (C₃ − C₄)/(C₂ − C₁) relationship, we used the method of least squares:

$$a+b\cdot W=\frac{C_3-C_4}{C_2-C_1},$$

(7)

where a and b are unknown coefficients of a first-order polynomial (7).

To build a system of conditional equations, we had to choose average values of the (C₃ − C₄)/(C₂ − C₁) relationship (Table 10).

Table 10. Average values for the (C₃ − C₄)/(C₂ − C₁) relationship.

Wnom, %	(C3 − C4)/(C2 − C1)
	εn = 2.0	εn = 2.5	εn = 3.0	εn = 3.5	Average
0	1	1	1	1	1
10	1.307	1.301	1.295	1.289	1.298
20	1.684	1.669	1.654	1.640	1.662
30	2.158	2.130	2.102	2.075	2.116

A system of linear conditional equations, based on the first-order polynomial (7), is given below.

$$\left\{\begin{array}{l}a+b\cdot 0=1,\\ a+b\cdot 10=1.298,\\ a+b\cdot 20=1.662,\\ a+b\cdot 30=2.116\end{array}\right.$$

.

It was solved in a traditional way:

$$\begin{gathered} Q=\left|\begin{array}{cc}\left[XX\right]& \left[XY\right]\\ \left[YX\right]& \left[YY\right]\end{array}\right|=\left|\begin{array}{cc}4& 60\\ 60& 1400\end{array}\right|=2000,Q_a=\left|\begin{array}{cc}\left[XL\right]& \left[XY\right]\\ \left[YL\right]& \left[YY\right]\end{array}\right|=\left|\begin{array}{cc}6.076& 60\\ 109.7& 1400\end{array}\right|=1924.4, \\ {Q}_b=\left|\begin{array}{cc}\left[XX\right]& \left[XL\right]\\ \left[YX\right]& \left[YL\right]\end{array}\right|=\left|\begin{array}{cc}4& 6.076\\ 60& 109.7\end{array}\right|=74.24, \\ a=\frac{Q_a}{Q}=\frac{1924.4}{2000}=0.9622,b=\frac{Q_b}{Q}=\frac{74.24}{2000}=0.0371 \end{gathered}$$

.

Calculated values of moisture W_calc, received from a first-order polynomial (7):

$$W_{calc}=\frac{C_3-C_4}{\left(C_2-C_1\right)\cdot 0.0371}-25.9353,$$

are given in Table 11.

Table 11. Values of moisture content W’ obtained from a first-order polynomial (7).

Wnom, %	Wcalc, %
	εn = 2.0	εn = 2.5	εn = 3.0	εn = 3.5
0	1.019	1.019	1.019	1.019
10	9.294	9.132	8.970	8.809
20	19.456	19.051	18.647	18.270
30	32.232	31.477	30.722	29.995

After obtaining the results of Table 11, it was possible to conclude that the least squares method is not effective for our case, as it was expected to obtain the linear transfer function of the water-cut meter (Figure 10). The next step of the linearization was to calculate the discrepancies ΔW between nominal points of moisture content and values from Table 11, and to approximate them by applying the instruments of general linear regression. Discrepancies between nominal points of moisture content and values from Table 11, taken for ε_n = 3.0, are given in Table 12.

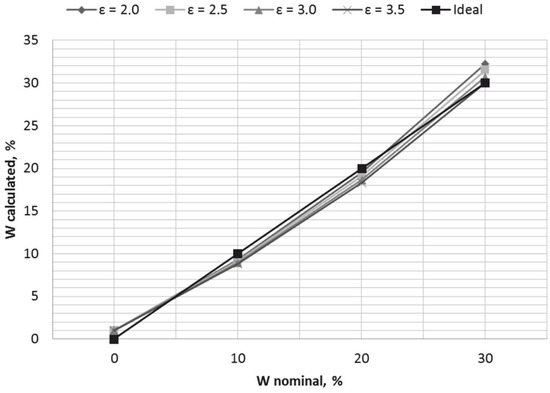
Figure 10. Graphs of a first-order polynomial (7), placed together with an ideal transfer function of the water-cut meter.

Table 12. Values of moisture content W’ obtained from a first-order polynomial (7).

	εn = 3.0
Wnominal, %	0	10	20	30
Wcalc, %	1.019	8.970	18.647	30.722
ΔW = Wcalc − Wnominal, %	1.019	−1.030	−1.353	0.722

To approximate the values of discrepancies ΔW from Table 11, a sum of four functions (1, W, W ², and W ³) was taken with appropriate coefficients, defined with the help of Mathcad software (linfit function (x, y, Y)):

$$\mathsf{\Delta }W=1.019-0.269\cdot W+0.00527\cdot W^2+0.000112\cdot W^3,$$

(8)

where W is a volumetric moisture content taken from the first-order polynomial (7). Formula (8) provides an ideal approximation of the discrepancies ΔW, as can be seen in Table 13.

Table 13. Approximated values of discrepancies ΔW_calc.

	εn = 3.0
ΔW	1.019	−1.030	−1.353	0.722
ΔWcalc	1.019	−1.030	−1.353	0.722

Taking into account Equations (7) and (8), we received a modified transfer function of a water-cut meter (function 2), as displayed in Figure 5.

During the comparison of the water-cut meter’s transfer functions (1) and (2), it was necessary to estimate how both of them compensated for the type uncertainty, and how close both of them were to the nominal linear transfer function. Dispersions of repeatability, calculated for transfer function (1) and transfer function (2) with mean and median values, describe a possible variation in the measured moisture values for two chosen substances (diesel fuel and mazut). We can see that the values of $S_{rep1}^2$ and $S_{rep2}^2$ are approximately 1.35 times greater in comparison with $S_{rep3}^2$ and $S_{rep4}^2$. This means that transfer function (2) provides a lower level of variability of the measured values, depending on the type of oil fuel under research. In other words, transfer function (2) is not as sensitive to fuel type as transfer function (1).

Dispersions of adequacy reflect the correspondence of experimental transfer functions (1) and (2) (taken for diesel fuel and mazut as dielectric substances with a significant difference in relative permittivity) with the nominal linear transfer function of a water-cut meter (the ideal transfer function given in Figure 4 and Figure 5). Again, it is possible to see that dispersions of adequacy calculated for the transfer function (2) give us values that are approximately 4.5 times smaller in comparison with the dispersions of transfer function (1). This means that Equation (2) provides 4.5 times better adequacy to the ideal than Equation (1).

As a general result, we can conclude that it would be rational to choose transfer function (2) with median values of moisture content as a nominal transfer function of the water-cut meter, because it has the smallest F-test value (F = 6.19).

Moisture measurement uncertainty can be estimated by using the method of mathematical programing [41]. If the function f(x) is continuous, it is possible to find maximal and minimal values of f(x) within the limit value of the function’s argument error. Absolute uncertainty of moisture measurement can be calculated as a half difference Δf = (f_max(x) − f_min(x))/2. Maximal and minimal capacitance values were taken from the results of 10 random measurements in mazut with 30% moisture content: C_1min = 41.16 pF, C_1max = 41.40 pF, C_2min = 127.56 pF, C_2max = 128.09 pF, C_3min = 270.41 pF, C_3max = 271.04 pF, C_4min = 87.39 pF, and C_4max = 88.26 pF. After substituting these capacitances into Formula (2), we received the following maximal and minimal values of moisture content: W_max = 30.235%, and W_min = 29.633%. The value of absolute moisture measurement’s extended uncertainty was equal to U(W) = (30.235 − 29.633)/2 = 0.3%, which is very good for a capacitive water-cut meter, because modern accuracy limits are mostly no lower than 0.5% (in [20,24], we have 1%; in [26], −0.67%; in [21], −3%...)

5. Conclusions

At first, the workability of a transfer function suggested in [17] with different types of oil fuels was checked. Four values of dielectric permittivity for dehydrated substances (ε_n = 2.0; ε_n = 2.5; ε_n = 3.0; ε_n = 3.5) and four values of moisture content (W = 0%; W = 10%; W = 20%; W = 30%) were taken for that purpose. The obtained graphs of transfer functions for the mentioned substances happened to be nonlinear, and the calculated values of moisture content were significantly different from the nominal at all points, except for W = 0%. To achieve near-linear transfer function of the capacitive water-cut meter, the method of least squares was used. The next step of linearization was in calculating discrepancies between the nominal points of moisture content and values received after the application of the LS method, with their approximation using general linear regression instruments.

Analyzing the graphs of the modified transfer functions for different moist substances, it was possible to say that they happened to be far more effective than the initial transfer function suggested in [17]. The root mean estimator was calculated for the initial transfer function, and the static function—received after general linear regression—as an integral difference between the nominal and calculated values of moisture content. The corresponding root mean estimator values were 1.3062% and 0.4158%, proving the effectiveness of transfer function (2), modified with the help of general linear regression instruments.

To check the workability of the modified transfer function in real conditions, two different fuels were taken: diesel fuel and mazut. The values of moisture content for two transfer functions, calculated for the mean and median values of C₁, C₂, C₃, and C₄, were compared with the help of dispersion analysis. After the dispersions of repeatability and adequacy had been calculated and compared, it was possible to conclude that the modified transfer function of a water-cut meter, calculated for median values of C₁, C₂, C₃, and C₄, provided minimal dispersions of repeatability and adequacy, and a minimal F-test value. Values of both dispersions for the modified transfer function were significantly smaller, as were the F-test values, proving its more robust properties (i.e., capacity for type-uncertainty compensation) and better adequacy to the nominal linear transfer function of the water-cut meter.