Numerical Analysis of Deformation Characteristics of Elastic Inhomogeneous Rotational Shells at Arbitrary Displacements and Rotation Angles
Abstract
:1. Introduction
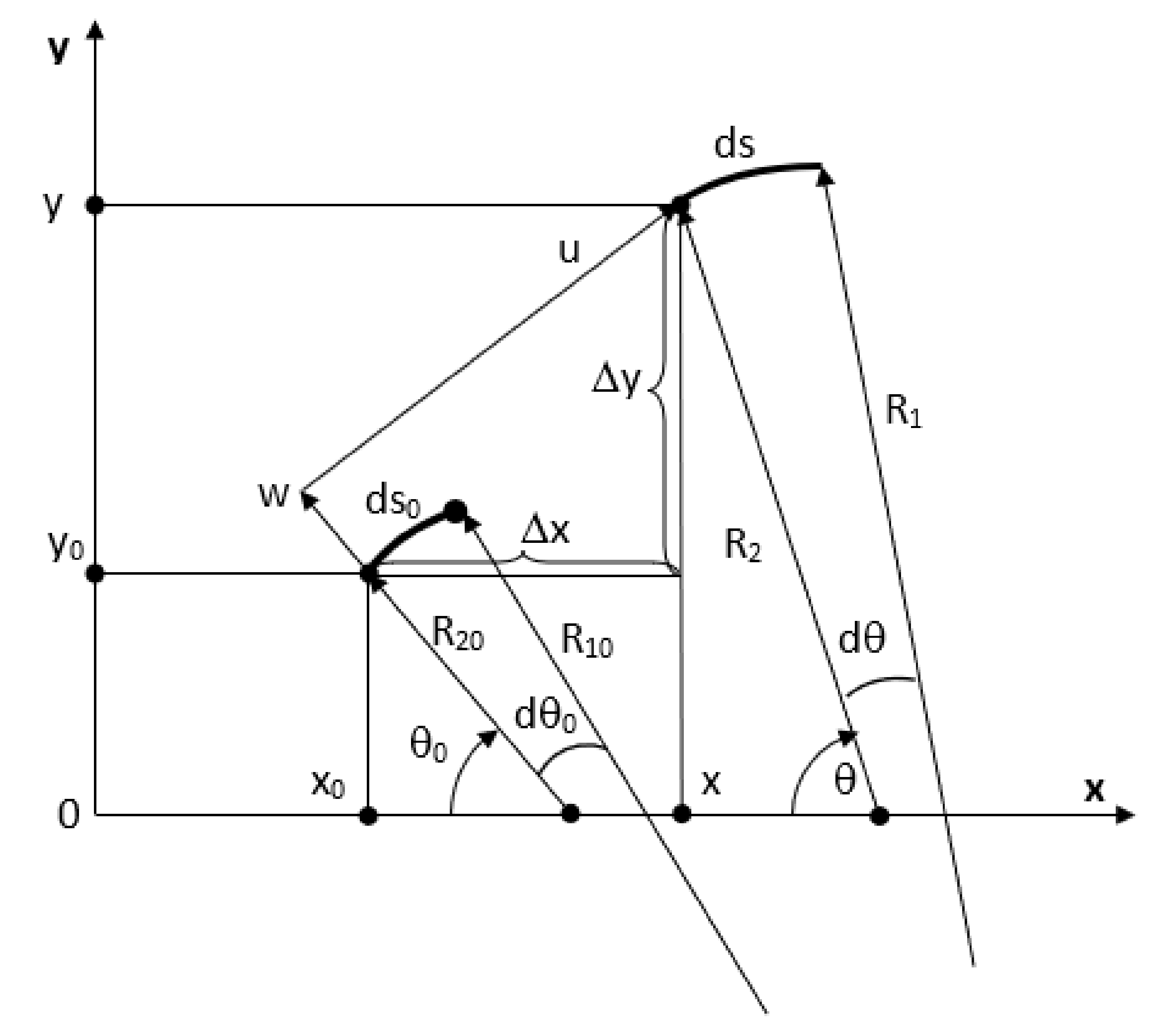
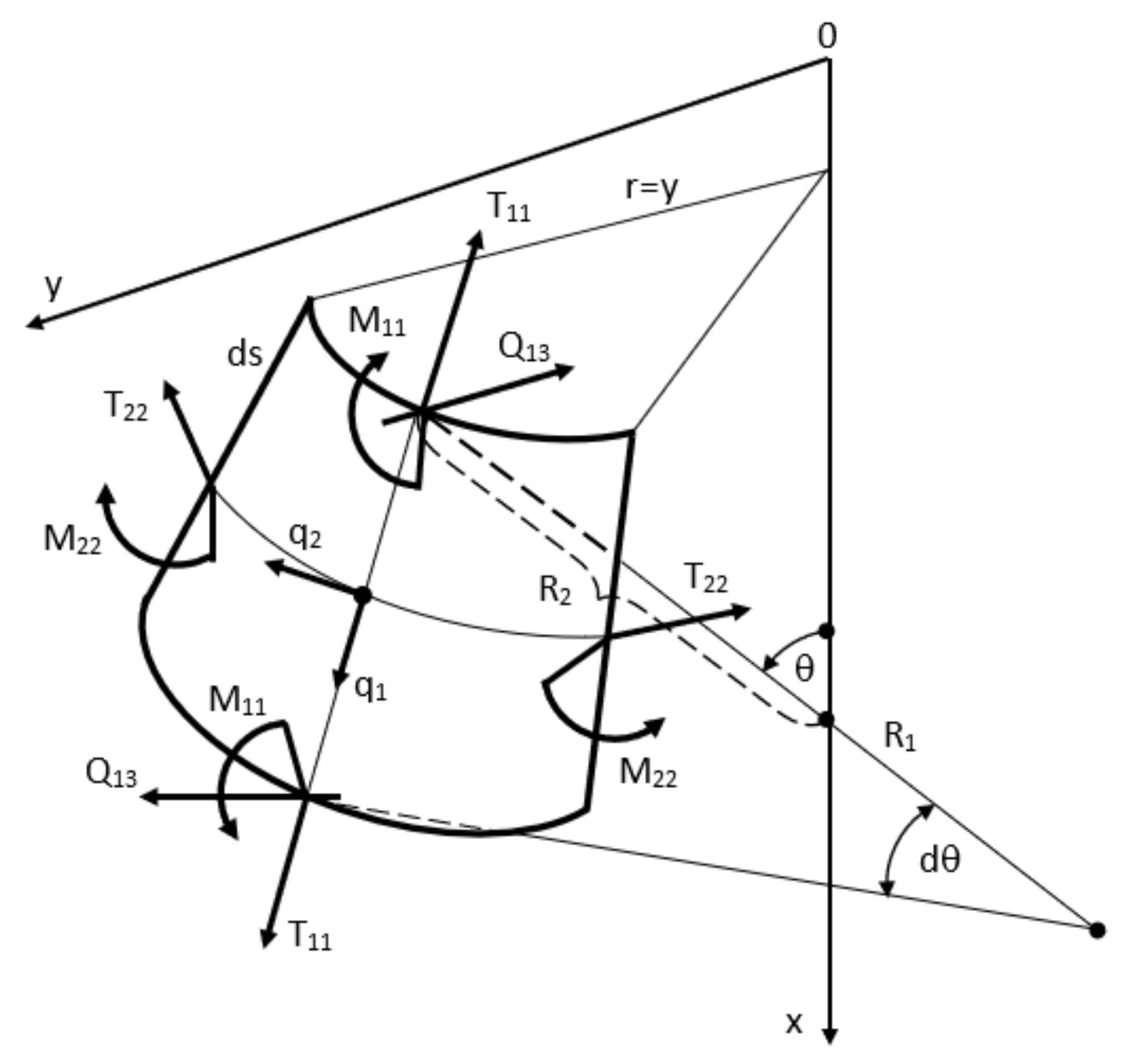
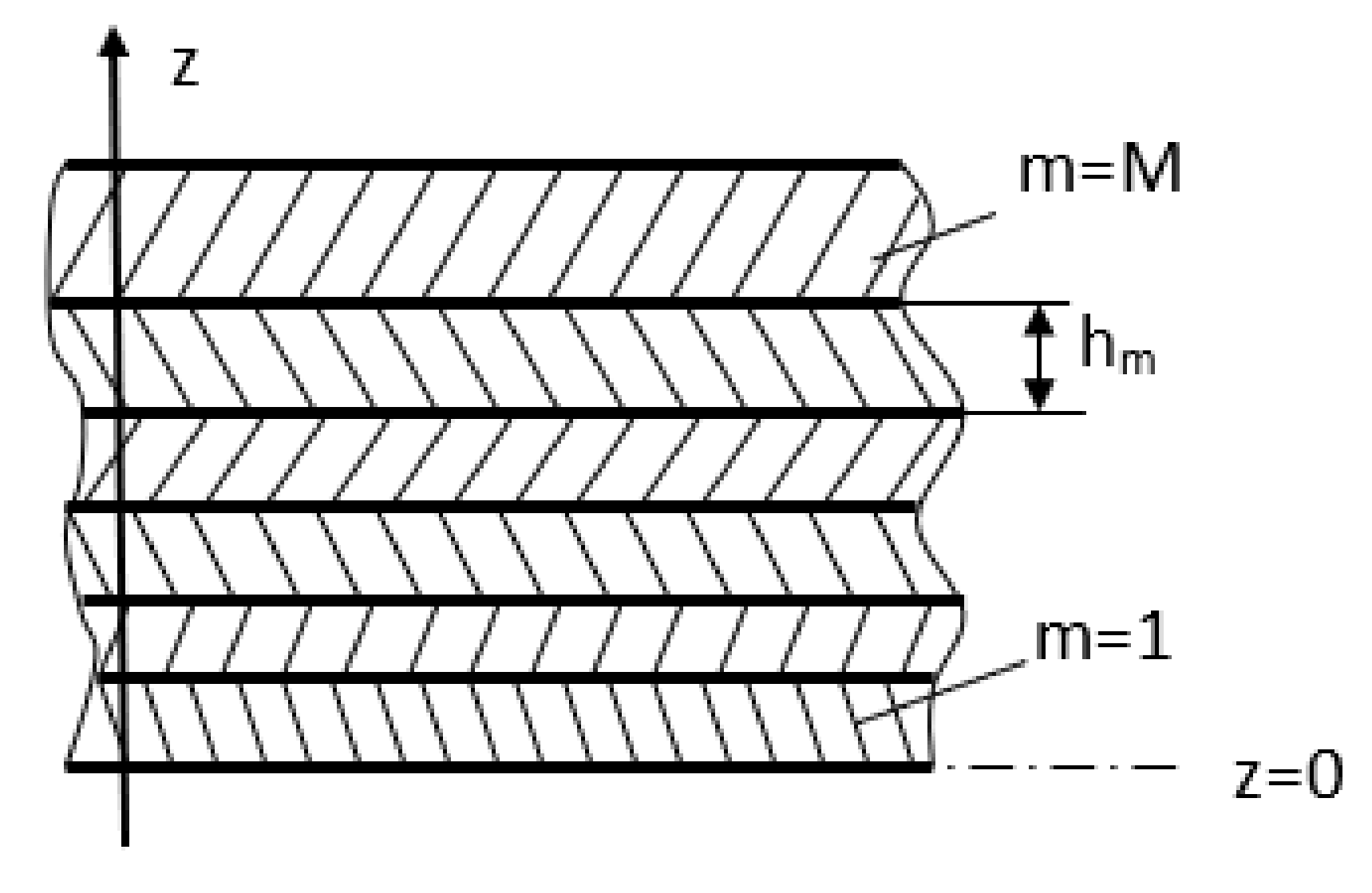
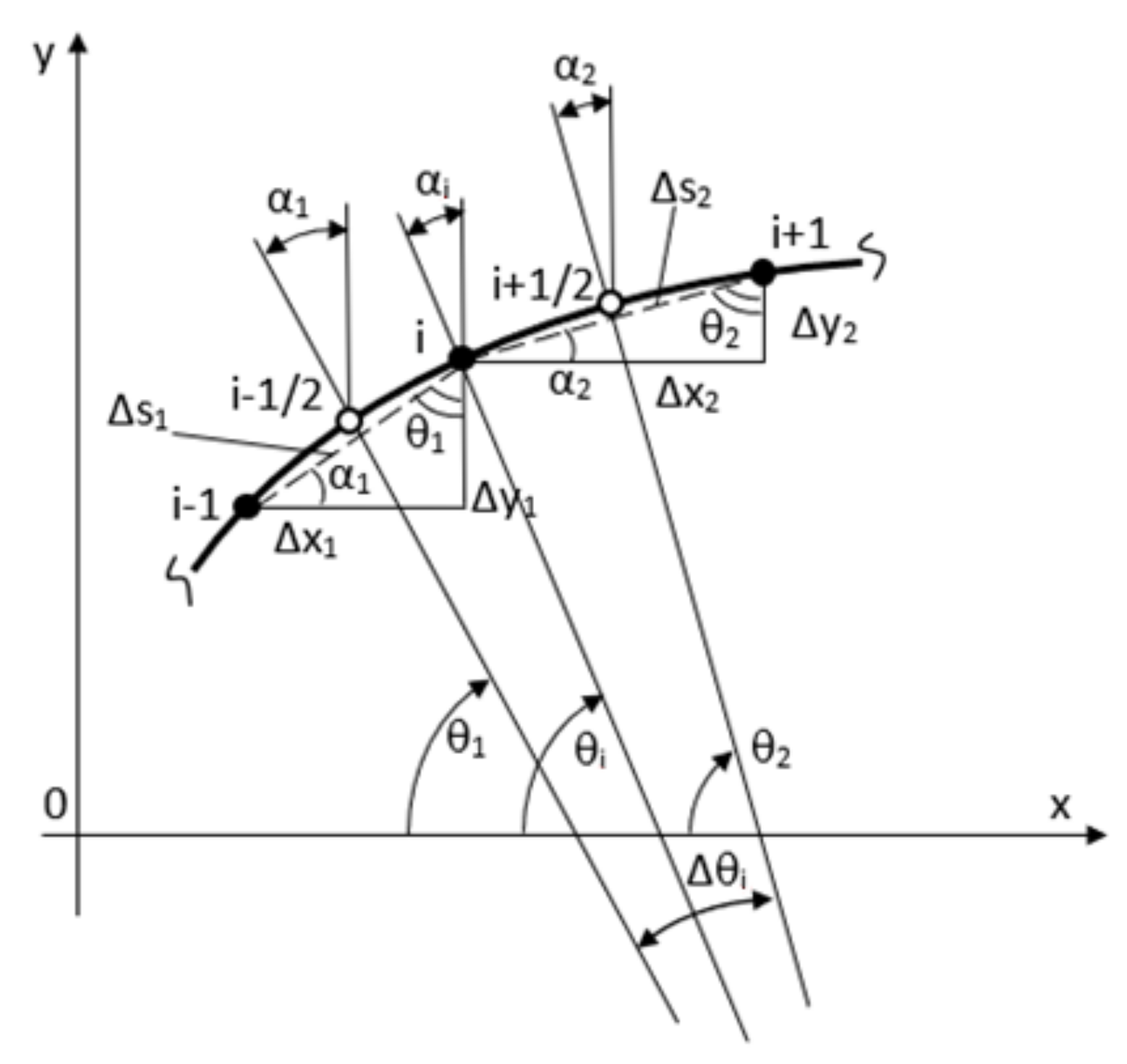
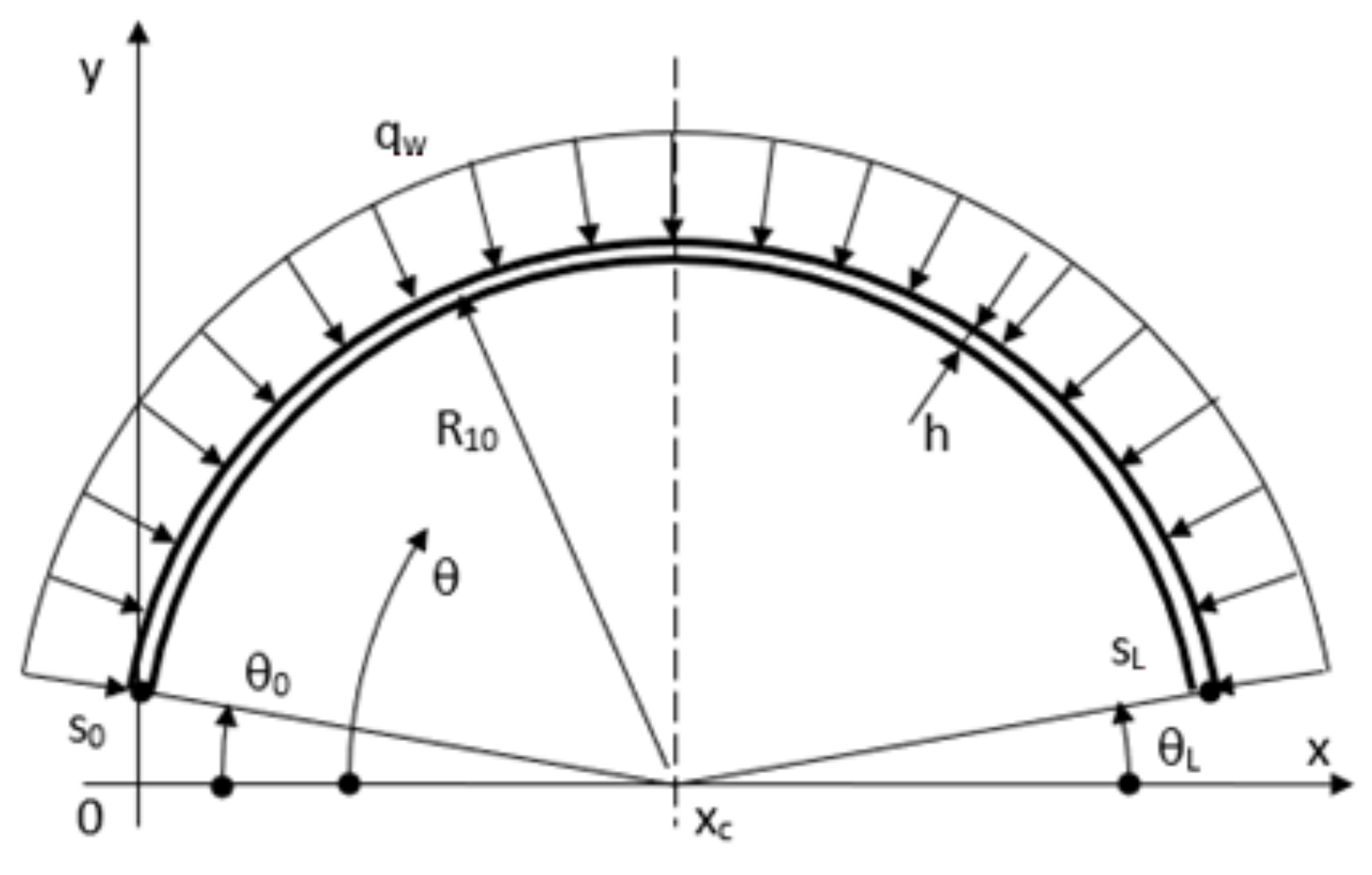
2. Materials and Methods
- rigid fixing (12):
- pin-edge fixing (13):
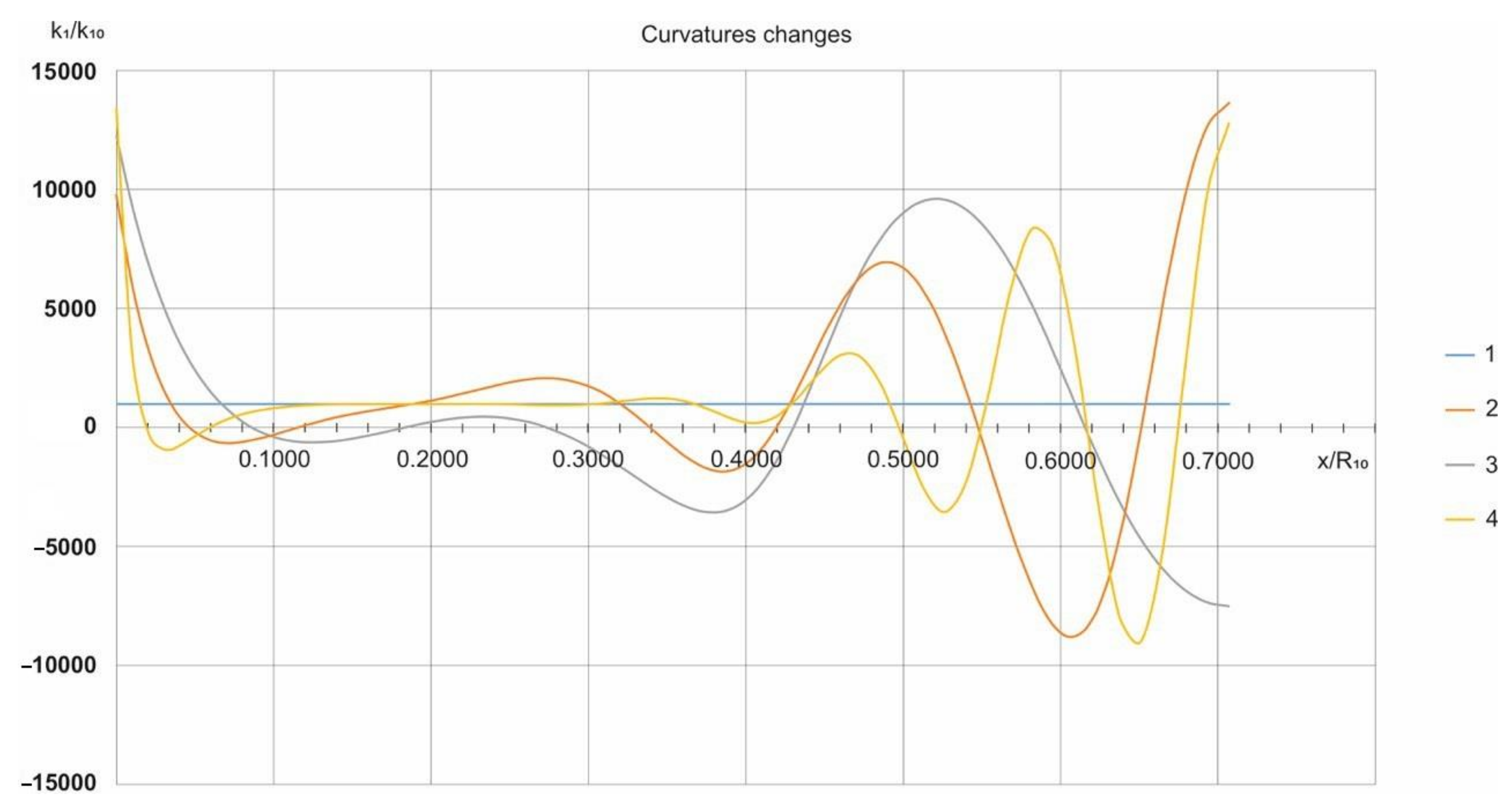
3. Results and Discussion
- the smallest eigenvalues (29):
- the largest eigenvalues (30):
E1 < E2: E1 = 0.083·E2; ν12 = 0.289.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Babaytsev, A.V.; Rabinskiy, L.N.; Thu Aung, K. Investigation of the contact zone of a cylindrical shell located between two parallel rigid plates with a gap. INCAS Bull. 2020, 12, 43–52. [Google Scholar] [CrossRef]
- Babaytsev, A.V.; Zotov, A.A. Designing and calculation of extruded sections of an inhomogeneous composition. Russ. Met. 2019, 2019, 1452–1455. [Google Scholar] [CrossRef]
- Lomakin, E.; Rabinskiy, L.; Radchenko, V.; Solyaev, Y.; Zhavoronok, S.; Babaytsev, A. Analytical estimates of the contact zone area for a pressurized flat-oval cylindrical shell placed between two parallel rigid plates. Meccanica 2018, 53, 3831–3838. [Google Scholar] [CrossRef]
- Dmitriev, V.G.; Egorova, O.V.; Starovoitov, E.I. Particularities of mathematical modeling of deformation processes for arched and panel designs of composites with large displacements and rotation angles. INCAS Bull. 2020, 12, 53–66. [Google Scholar] [CrossRef]
- Dmitriev, V.G.; Biryukov, V.I.; Egorova, O.V.; Zhavoronok, S.I.; Rabinskii, L.N. Nonlinear deforming of laminated composite shells of revolution under finite deflections and normal’s rotation angles. Russ. Aeronaut. 2017, 60, 169–176. [Google Scholar] [CrossRef]
- Grigolyuk, E.I.; Shalashilin, V.I. The method of parameter continuation in problems of nonlinear deformation of rods, plates and shells. Stud. Theory Plat Shells 1984, 17, 3–58. [Google Scholar]
- Grigolyuk, E.I.; Shalashilin, V.I. Problems of Nonlinear Deformation: A Method for Continuing the Solution by Parameter in Nonlinear Problems of Mechanics of a Solid Deformable Body; Science: Moscow, Russia, 1988. [Google Scholar]
- Dmitriev, V. Applied mathematics technologies in nonlinear mechanics of thin-walled constructions. In Mathematics Applied to Engineering and Management; Routledge: London, UK, 2019; pp. 71–116. [Google Scholar]
- Babaytsev, A.V.; Rabinskiy, L.N. Design calculation technique for thick-walled composite constructions operating under high-speed loading. Period. Tche Quim. 2019, 16, 480–489. [Google Scholar] [CrossRef]
- Bakhvalov, N.S.; Zhidkov, N.P.; Kobelkov, G.M. Numerical Methods; Nauka: Moscow, USSR, 1987. [Google Scholar]
- Dmitriev, V.G.; Preobrazhensky, I.N. Deformation of flexible shells with cutouts. News USSR Ac. Sci. 1988, 1, 177–184. [Google Scholar]
- Dmitriev, V.G.; Egorova, O.V.; Zhavoronok, S.I.; Rabinsky, L.N. Investigation of buckling behavior for thin-walled bearing aircraft structural elements with cutouts by means of numerical simulation. Russ. Aer. 2018, 61, 165–174. [Google Scholar] [CrossRef]
- Babaytsev, A.V.; Orekhov, A.; Rabinskiy, L.N. Properties and microstructure of AlSi10Mg samples obtained by selective laser melting. Nanosci. Technol. Int. J. 2020, 11, 213–222. [Google Scholar] [CrossRef]
- Dudkin, K.K.; Alifanov, O.M.; Babaitsev, A.V. Determination of the thermophysical characterisitics of the Moon soil with depthed thermoprobes. J. Phys. Conf. Ser. 2020, 1683, 032023. [Google Scholar] [CrossRef]
- Kyaw, Y.K.; Pronina, P.F.; Polyakov, P.O. Mathematical modelling of the effect of heat fluxes from external sources on the surface of spacecraft. J. Appl. Eng. Sci. 2020, 18, 732–736. [Google Scholar]
- Astapov, A.N.; Kuznetsova, E.L.; Rabinskiy, L.N. Operating capacity of anti-oxidizing coating in hypersonic flows of air plasma. Surf. Rev. Lett. 2019, 26, 1850145. [Google Scholar] [CrossRef]
- Egorova, O.V.; Kyaw, Y.K. Solution of inverse non-stationary boundary value problems of diffraction of plane pressure wave on convex surfaces based on analytical solution. J. Appl. Eng. Sci. 2020, 18, 676–680. [Google Scholar] [CrossRef]
- Zagovorchev, V.A.; Tushavina, O.V. Selection of temperature and power parameters for multi-modular lunar jet penetrator. INCAS Bull. 2019, 11, 231–241. [Google Scholar] [CrossRef]
- Zagovorchev, V.A.; Tushavina, O.V. The use of jet penetrators for movement in the lunar soil. INCAS Bull. 2019, 11, 121–130. [Google Scholar] [CrossRef]
- Vahterova, Y.A.; Fedotenkov, G.V. The inverse problem of recovering an unsteady linear load for an elastic rod of finite length. J. Appl. Eng. Sci. 2020, 18, 687–692. [Google Scholar] [CrossRef]
- Fedotenkov, G.V.; Tarlakovsky, D.V.; Vahterova, Y.A. Identification of non-stationary load upon timoshenko beam. Lobachevskii J. Math. 2019, 40, 439–447. [Google Scholar] [CrossRef]
- Ivannikov, S.I.; Vahterova, Y.A.; Utkin, Y.A.; Sun, Y. Calculation of strength, rigidity, and stability of the aircraft fuselage frame made of composite materials. INCAS Bull. 2021, 13, 77–86. [Google Scholar] [CrossRef]
- Vahterova, Y.A.; Min, Y.N. Effect of shape of armoring fibers on strength of composite materials. Turk. J. Comp. Math. Educ. 2021, 12, 2703–2708. [Google Scholar]
- Starovoitov, E.I.; Zakharchuk, Y.V.; Kuznetsova, E.L. Elastic circular sandwich plate with compressible filler under axially symmetrical thermal force load. J. Balk. Tribol. Assoc. 2021, 27, 175–188. [Google Scholar]
- Kuznetsova, E.L.; Makarenko, A.V. Mathematical model of energy efficiency of mechatronic modules and power sources for prospective mobile objects. Period. Tche Quim. 2019, 16, 529–541. [Google Scholar] [CrossRef]
- Bulychev, N.A.; Kuznetsova, E.L. Ultrasonic application of nanostructured coatings on metals. Russ. Eng. Res. 2019, 39, 809–812. [Google Scholar] [CrossRef]
- Kuznetsova, E.L.; Rabinskiy, L.N. Heat transfer in nonlinear anisotropic growing bodies based on analytical solution. Asia Life Sci. 2019, 2, 837–846. [Google Scholar]
- Kuznetsova, E.L.; Rabinskiy, L.N. Numerical modeling and software for determining the static and linkage parameters of growing bodies in the process of non-stationary additive heat and mass transfer. Period. Tche Quim. 2019, 16, 472–479. [Google Scholar]
- Kuznetsova, E.L.; Rabinskiy, L.N. Linearization of radiant heat fluxes in the mathematical modeling of growing bodies by the action of high temperatures in additive manufacturing. Asia Life Sci. 2019, 2, 943–954. [Google Scholar]
- Babaytsev, A.V.; Kuznetsova, E.L.; Rabinskiy, L.N.; Tushavina, O.V. Investigation of permanent strains in nanomodified composites after molding at elevated temperatures. Period. Tche Quim. 2020, 17, 1055–1067. [Google Scholar] [CrossRef]
- Rabinsky, L.N.; Kuznetsova, E.L. Simulation of residual thermal stresses in high-porous fibrous silicon nitride ceramics. Powd. Metall. Met. Ceram. 2019, 57, 663–669. [Google Scholar] [CrossRef]
- Sun, Y.; Kolesnik, S.A.; Kuznetsova, E.L. Mathematical modeling of coupled heat transfer on cooled gas turbine blades. INCAS Bull. 2020, 12, 193–200. [Google Scholar] [CrossRef]
- Antufev, B.A.; Kuznetsova, E.L.; Rabinskiy, L.N.; Tushavina, O.V. Investigation of a complex stress-strain state of a cylindrical shell with a dynamically collapsing internal elastic base under the influence of temperature fields of various physical nature. Asia Life Sci. 2019, 2, 689–696. [Google Scholar]
- Antufev, B.A.; Kuznetsova, E.L.; Rabinskiy, L.N.; Tushavina, O.V. Complex stressed deformed state of a cylindrical shell with a dynamically destructive internal elastic base under the action of temperature fields of various physical nature. Asia Life Sci. 2019, 2, 775–782. [Google Scholar]
- Kuznetsova, L.E.; Fedotenkov, V.G. Dynamics of a spherical enclosure in a liquid during ultrasonic cavitation. J. Appl. Eng. Sci. 2020, 18, 681–686. [Google Scholar] [CrossRef]
- Makarenko, A.V.; Kuznetsova, E.L. Energy-efficient actuator for the control system of promising vehicles. Russ. Eng. Res. 2019, 39, 776–779. [Google Scholar] [CrossRef]
- Kuznetsova, E.L.; Makarenko, A.V. Mathematic simulation of energy-efficient power supply sources for mechatronic modules of promising mobile objects. Period. Tche Quim. 2018, 15, 330–338. [Google Scholar]
- Kuznetsova, E.L.; Fedotenkov, G.V.; Starovoitov, E.I. Methods of diagnostic of pipe mechanical damage using functional analysis, neural networks and method of finite elements. INCAS Bull. 2020, 12, 79–90. [Google Scholar] [CrossRef]
- Rabinskiy, L.N.; Tushavina, O.V. Problems of land reclamation and heat protection of biological objects against contamination by the aviation and rocket launch site. J. Environ. Manag. Tour. 2019, 10, 967–973. [Google Scholar]
- Dobryanskiy, V.N.; Rabinskiy, L.N.; Tushavina, O.V. Validation of methodology for modeling effects of loss of stability in thin-walled parts manufactured using SLM technology. Period. Tche Quim. 2019, 16, 650–656. [Google Scholar] [CrossRef]
- Rabinskiy, L.N.; Tushavina, O.V.; Starovoitov, E.I. Study of thermal effects of electromagnetic radiation on the environment from space rocket activity. INCAS Bull. 2020, 12, 141–148. [Google Scholar] [CrossRef]
- Rabinskiy, L.N.; Sitnikov, S.A. Development of technologies for obtaining composite material based on silicone binder for its further use in space electric rocket engines. Period. Tche Quim. 2018, 15, 390–395. [Google Scholar]
- Kyaw, Y.K.; Kuznetsova, E.L.; Makarenko, A.V. Complex mathematical modelling of mechatronic modules of promising mobile objects. INCAS Bull. 2020, 12, 91–98. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dmitriev, V.G.; Danilin, A.N.; Popova, A.R.; Pshenichnova, N.V. Numerical Analysis of Deformation Characteristics of Elastic Inhomogeneous Rotational Shells at Arbitrary Displacements and Rotation Angles. Computation 2022, 10, 184. https://doi.org/10.3390/computation10100184
Dmitriev VG, Danilin AN, Popova AR, Pshenichnova NV. Numerical Analysis of Deformation Characteristics of Elastic Inhomogeneous Rotational Shells at Arbitrary Displacements and Rotation Angles. Computation. 2022; 10(10):184. https://doi.org/10.3390/computation10100184
Chicago/Turabian StyleDmitriev, Vladimir G., Alexander N. Danilin, Anastasiya R. Popova, and Natalia V. Pshenichnova. 2022. "Numerical Analysis of Deformation Characteristics of Elastic Inhomogeneous Rotational Shells at Arbitrary Displacements and Rotation Angles" Computation 10, no. 10: 184. https://doi.org/10.3390/computation10100184
APA StyleDmitriev, V. G., Danilin, A. N., Popova, A. R., & Pshenichnova, N. V. (2022). Numerical Analysis of Deformation Characteristics of Elastic Inhomogeneous Rotational Shells at Arbitrary Displacements and Rotation Angles. Computation, 10(10), 184. https://doi.org/10.3390/computation10100184




