Inversion Theory Leveling as a New Methodological Approach to Antioxidant Thermodynamics: A Case Study on Phenol
Abstract
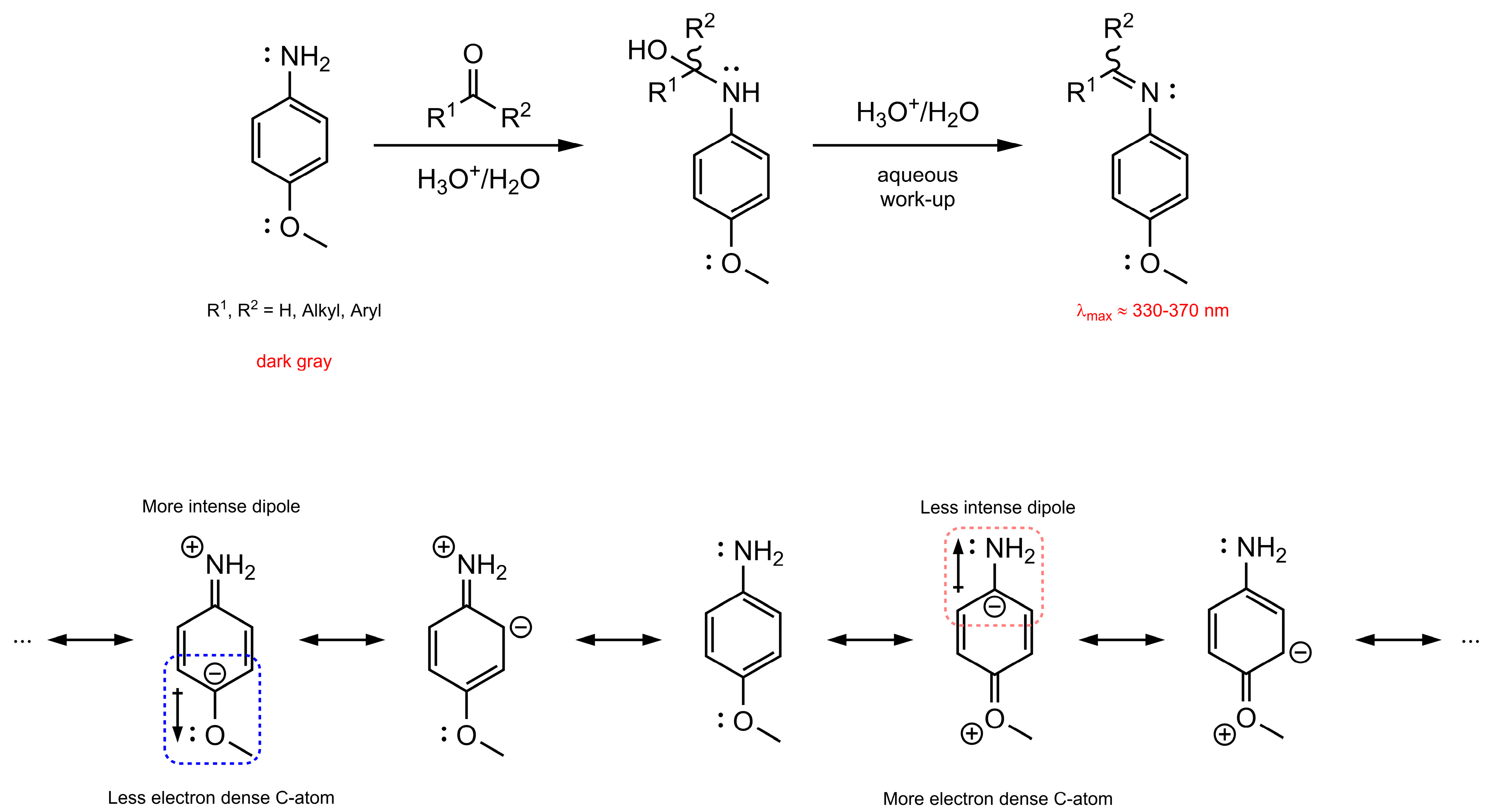
1. Introduction
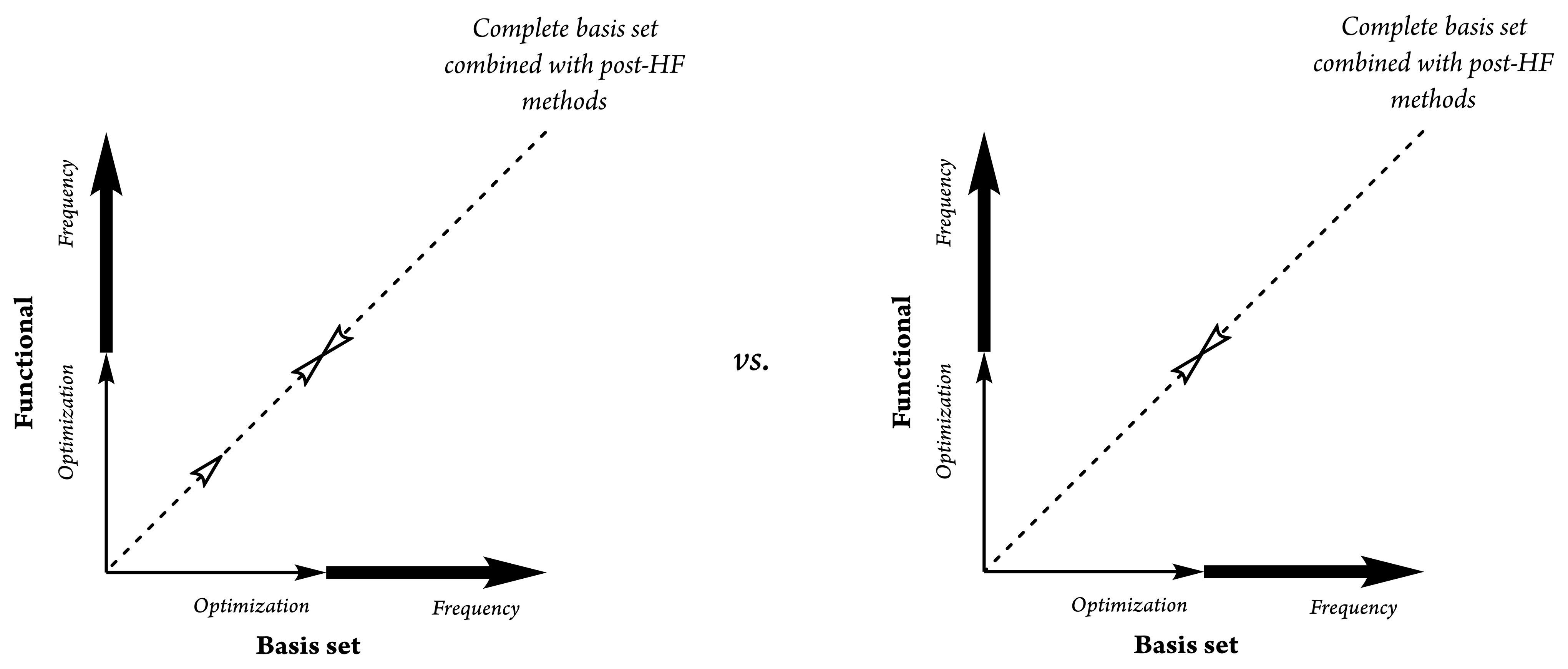
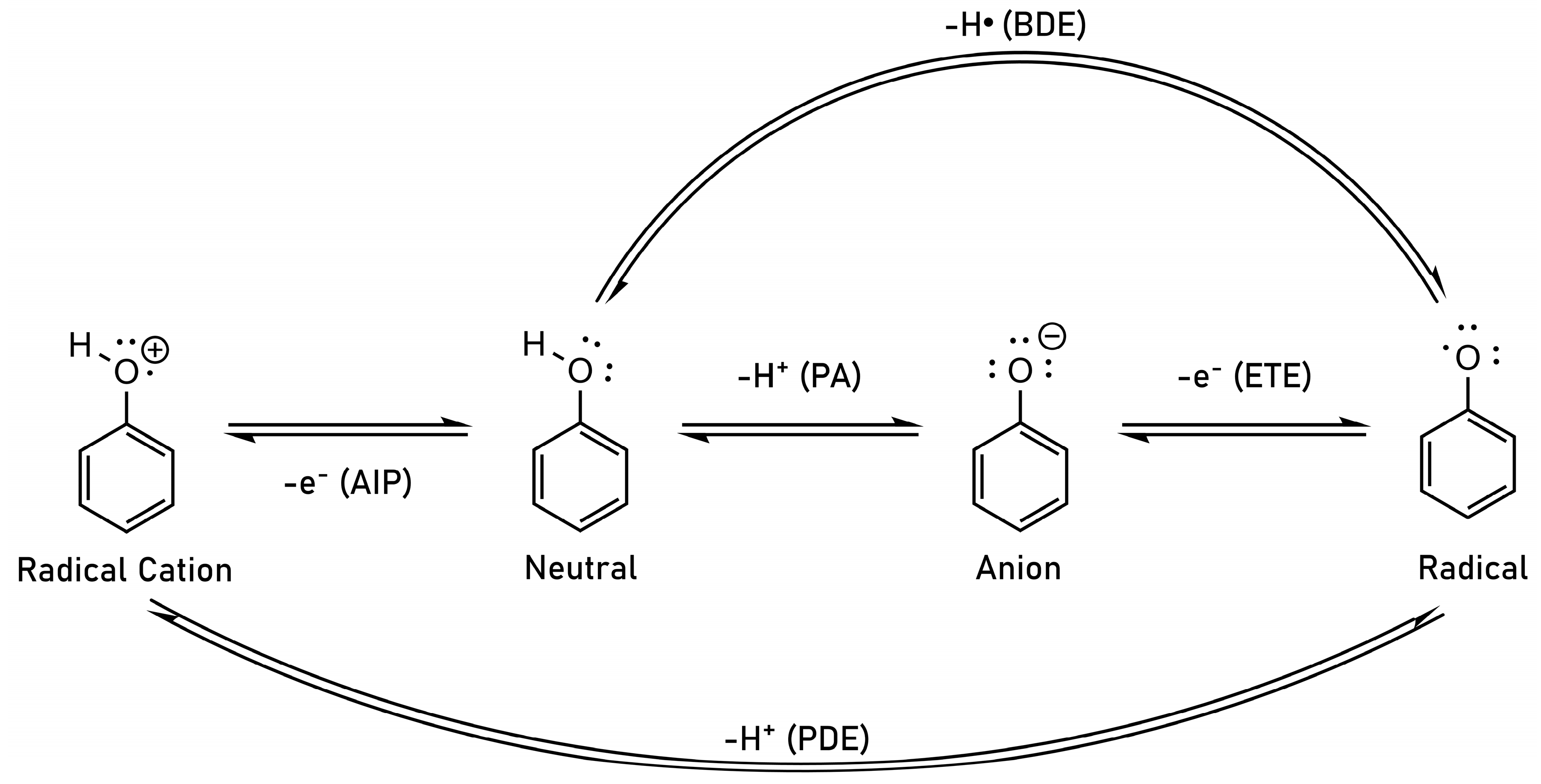
2. Theoretical Background and Concept Description
- Step 1:
- Use more complex functionals with higher quality (i.e., triple or quadruple ζ-valence levels) for the MEP procedure;
- Step 2:
- Apply moderately complex theories to obtain a good estimate of the frequencies and hence the thermodynamics. In the case of ITL, the refined differentiation of functionals had to be rewritten and improved. Moderately complex theories should include at least two complementary effect-parameterized terms in the mathematical structure of a specific function (i.e., the dispersion forces, BSSE correction for vicarious orbital radii, long-range treatment, etc.).
3. Results and Discussion
- 1.
- M08HX performed almost as well as the reference method and provided the antioxidant parameters mentioned here. A similar line could be drawn for the total wall times, which are almost twice as fast as the reference method.
- 2.
- Apart from the leveling effect, the ITL method improved results in usually low-cost methods, such as the three-component composite methods presented in this manuscript.
4. Conclusions and Outlook
5. Computational Details
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chiorcea-Paquim, A.-M.; Enache, T.A.; De Souza Gil, E.; Oliveira-Brett, A.M. Natural phenolic antioxidants electrochemistry: Towards a new food science methodology. Compr. Rev. Food Sci. Food Saf. 2020, 19, 1680–1726. [Google Scholar] [CrossRef]
- Munteanu, I.G.; Apetrei, C. Analytical Methods Used in Determining Antioxidant Activity: A Review. Int. J. Mol. Sci. 2021, 22, 3380. [Google Scholar] [CrossRef] [PubMed]
- Salehi, B.; Martorell, M.; Arbiser, J.L.; Sureda, A.; Martins, N.; Maurya, P.K.; Sharifi-Rad, M.; Kumar, P.; Sharifi-Rad, J. Antioxidants: Positive or Negative Actors? Biomolecules 2018, 8, 124. [Google Scholar] [CrossRef] [PubMed]
- Apak, R. Current Issues in Antioxidant Measurement. J. Agric. Food Chem. 2019, 67, 9187–9202. [Google Scholar] [CrossRef]
- Hernandez, I.; Alegre, L.; Van Breusegem, F.; Munné-Bosch, S. How relevant are flavonoids as antioxidants in plants? Trends Plant Sci. 2009, 14, 125–132. [Google Scholar] [CrossRef]
- Agati, G.; Brunetti, C.; Fini, A.; Gori, A.; Lucia Guidi, L.; Landi, M.; Sebastiani, M.; Tattini, M. Are Flavonoids Effective Antioxidants in Plants? Twenty Years of Our Investigation. Antioxidants 2020, 9, 1098. [Google Scholar] [CrossRef] [PubMed]
- Gulcin, I. Antioxidants and antioxidant methods: An updated overview. Arch. Toxicol. 2020, 94, 651–715. [Google Scholar] [CrossRef]
- Neha, K.; Haider, M.R.; Pathak, A.; Yar, M.S. Medicinal prospects of antioxidants: A review. Eur. J. Med. Chem. 2019, 178, 687–704. [Google Scholar] [CrossRef]
- Xu, X.; You, Y.; Liu, X.; Wei, D.; Guan, Y.; Zheng, A. Experimental and density functional theory investigations on the antioxidant mechanism of carbon nanotubes. Carbon 2021, 177, 189–198. [Google Scholar] [CrossRef]
- Shang, Y.; Zhou, H.; Li, X.; Zhou, J.; Chen, K. Theoretical studies on the antioxidant activity of viniferifuran. New J. Chem. 2019, 43, 15736–15742. [Google Scholar] [CrossRef]
- Ma, Y.; Fengb, Y.; Diaoa, T.; Zenga, W.; Zuoc, Y. Experimental and theoretical study on antioxidant activity of the four anthocyanins. J. Mol. Struc. 2020, 1204, 127509. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Y.; Zhang, L.; An, L.; Chen, R.; Liu, Y.; Luo, Q.; Li, Y.; Wang, H.; Xue, Y. Computational study on the antioxidant property of coumarin-fused coumarins. Food Chem. 2020, 304, 125446. [Google Scholar] [CrossRef]
- Young Lee, C.; Sharma, A.; Semenya, J.; Anamoah, C.; Chapman, K.N.; Barone, V. Computational Study of Ortho-Substituent Effects on Antioxidant Activities of Phenolic Dendritic Antioxidants. Antioxidants 2020, 9, 189. [Google Scholar] [CrossRef]
- Vuong, T.V. Natural Products and Their Derivatives with Antibacterial, Antioxidant and Anticancer Activities. Antibiotics 2021, 10, 70. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, J.; Xiao, C.; Harqin, C.; Mab, M.; Long, T.; Lib, Z.; Yang, Y.; Liu, J.; Zhao, L. Structural characterization of a low-molecular-weight polysaccharide from Angelica pubescens Maxim f. biserrata Shan et Yuan root and evaluation of its antioxidant activity. Carbohydr. Polym. 2020, 236, 116047. [Google Scholar] [CrossRef]
- Wang, M.; Sun, X.; Luo, W.; Božović, S.; Gong, C.; Ren, J. Characterization and analysis of antioxidant activity of walnut-derived pentapeptide PW5 via nuclear magnetic resonance spectroscopy. Food Chem. 2021, 339, 128047. [Google Scholar] [CrossRef]
- Zhou, S.; Huang, G.; Chen, G. Extraction, structural analysis, derivatization and antioxidant activity of polysaccharide from Chinese yam. Food Chem. 2021, 361, 130089. [Google Scholar] [CrossRef]
- Thummajitsakul, S.; Samaikam, S.; Tacha, S.; Silprasit, K. Study on FTIR spectroscopy, total phenolic content, antioxidant activity and anti-amylase activity of extracts and different tea forms of Garcinia schomburgkiana leaves. LWT 2020, 134, 110005. [Google Scholar] [CrossRef]
- Oracz, J.; Zyzelewicz, D. In Vitro Antioxidant Activity and FTIR Characterization of High-Molecular Weight Melanoidin Fractions from Different Types of Cocoa Beans. Antioxidants 2019, 8, 560. [Google Scholar] [CrossRef]
- Hamden, Z.; El-Ghoul, Y.; Alminderej, F.M.; Saleh, S.M.; Majdoub, H. High-Quality Bioethanol and Vinegar Production from Saudi Arabia Dates: Characterization and Evaluation of Their Value and Antioxidant Efficiency. Antioxidants 2022, 11, 1155. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Gegechkori, V.; Petrovich, D.S.; Ilinichna, K.T.; Morton, D.W. HPTLC and FTIR Fingerprinting of Olive Leaves Extracts and ATR-FTIR Characterisation of Major Flavonoids and Polyphenolics. Molecules 2021, 26, 6892. [Google Scholar] [CrossRef]
- Song, X.-C.; Canellas, E.; Asensio, E.; Nerín, C. Predicting the antioxidant capacity and total phenolic content of bearberry leaves by data fusion of UV–Vis spectroscopy and UHPLC/Q-TOF-MS. Talanta 2020, 213, 120831. [Google Scholar] [CrossRef]
- Serdaroglu, G.; Elik, M. (-)-Tubifolidine as strychnos indole alkaloid: Spectroscopic charactarization (FT-IR, NMR, UV-Vis), antioxidant activity, molecular docking, and DFT studies. J. Mol. Struc. 2021, 1244, 130978. [Google Scholar] [CrossRef]
- Singh, R.; Hano, C.; Nath, G.; Sharma, B. Green Biosynthesis of Silver Nanoparticles Using Leaf Extract of Carissa carandas L. and Their Antioxidant and Antimicrobial Activity against Human Pathogenic Bacteria. Biomolecules 2021, 11, 299. [Google Scholar] [CrossRef] [PubMed]
- Pisani, M.; Astolfi, P.; Sabbatini, S.; Carloni, P. Antioxidant Activity Level, Bioactive Compounds, Colour and Spectroscopic Analysis (UV-Vis and FT-IR) of Flavoured Drinks Made with Wine and Sour Cherries (Prunuscerasus Var. austera). Foods 2021, 10, 1953. [Google Scholar] [CrossRef]
- Della Vedova, L.; Ferrario, G.; Gado, F.; Altomare, A.; Carini, M.; Morazzoni, P.; Aldini, G.; Baron, G. Liquid Chromatography–High-Resolution Mass Spectrometry (LC-HRMS) Profiling of Commercial Enocianina and Evaluation of Their Antioxidant and Anti-Inflammatory Activity. Antioxidants 2022, 11, 1187. [Google Scholar] [CrossRef]
- Shabana, S.; Prasansha, C.; Kalinina, I.; Potoroko, I.; Bagale, U.; Shirisha, S.H. Ultrasound assisted acid hydrolyzed structure modification and loading of antioxidants on potato starch nanoparticles. Ultrason. Sonochem. 2019, 51, 444–450. [Google Scholar] [CrossRef]
- Buldurun, K.; Turan, N.; Bursal, E.; Aras, A.; Mantarcı, A.; Çolak, N.; Türkan, F.; Gülçin, I. Synthesis, characterization, powder X-ray diffraction analysis, thermal stability, antioxidant properties and enzyme inhibitions of M(II)-Schiff base ligand complexes. J. Biomol. Struct. Dyn. 2021, 39, 6480–6487. [Google Scholar] [CrossRef] [PubMed]
- Khaliq, G.; Ramzan, M.; Baloch, A.H. Effect of Aloe vera gel coating enriched with Fagonia indica plant extract on physicochemical and antioxidant activity of sapodilla fruit during postharvest storage. Food Chem. 2019, 286, 346–353. [Google Scholar] [CrossRef] [PubMed]
- Rastegar, S.; Khankahdani, H.H.; Rahimzadeh, M. Effectiveness of alginate coating on antioxidant enzymes and biochemical changes during storage of mango fruit. J. Food Biochem. 2019, 43, e12990. [Google Scholar] [CrossRef]
- Muzykiewicz-Szymańska, A.; Nowak, A.; Wira, D.; Klimowicz, A. The Effect of Brewing Process Parameters on Antioxidant Activity and Caffeine Content in Infusions of Roasted and Unroasted Arabica Coffee Beans Originated from Different Countries. Molecules 2021, 26, 3681. [Google Scholar] [CrossRef] [PubMed]
- Garazhian, M.; Gharaghani, A.; Eshghi, S. Genetic diversity and inter-relationships of fruit bio-chemicals and antioxidant activity in Iranian wild blackberry species. Sci. Rep. 2020, 10, 18983. [Google Scholar] [CrossRef]
- Wang, L.; Luo, Y.; Wu, Y.; Xia, F.; Wua, Z. Quickly verifying the antioxidant contribution of the individual composition in natural antioxidants by HPLC-free radical scavenging detection. LWT 2018, 96, 461–468. [Google Scholar] [CrossRef]
- Xia, J.-X.; Zhao, B.-B.; Zan, J.-F.; Wang, P.; Chen, L.-L. Simultaneous determination of phenolic acids and flavonoids in Artemisiae Argyi Folium by HPLC-MS/MS and discovery of antioxidant ingredients based on relevance analysis. J. Pharm. Biomed. Anal. 2019, 175, 112734. [Google Scholar] [CrossRef]
- Hossain, M.A.; Arafat, M.Y.; Alam, M.; Hossain, M.M. Effect of solvent types on the antioxidant activity and total flavonoids of some Bangladeshi legumes. Food Res. 2021, 5, 329–335. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Yao, S.; Zhang, Y.; Liu, Q.; Xu, F.; Wu, G.; Dong, W.; Tan, L. Effects of in vitro saliva, gastric and intestinal digestion on the chemical properties, antioxidant activity of polysaccharide from Artocarpus heterophyllus Lam. (Jackfruit) Pulp. Food Hydrocoll. 2019, 87, 952–959. [Google Scholar] [CrossRef]
- Borahan, T.; Girgin, A.; Atsever, N.; Zaman, B.T.; Chormey, D.S.; Bakırdere, S. Development of a double-monitoring method for the determination of total antioxidant capacity as ascorbic acid equivalent using CUPRAC assay with RP-HPLC and digital image-based colorimetric detection. Eur. Food Res. Technol. 2022, 248, 707–713. [Google Scholar] [CrossRef]
- Bayarsaikhan, G.; Avan, A.N.; Çekiç, S.D.; Apak, R. Use of modified CUPRAC and dinitrophenylhydrazine colorimetric methods for simultaneous measurement of oxidative protein damage and antioxidant defense against oxidation. Talanta 2019, 204, 613–625. [Google Scholar] [CrossRef]
- Sethi, S.; Joshi, A.; Arora, B.; Bhowmik, A.; Sharma, R.R.; Kumar, P. Significance of FRAP, DPPH, and CUPRAC assays for antioxidant activity determination in apple fruit extracts. Eur. Food Res. Technol. 2020, 246, 591–598. [Google Scholar] [CrossRef]
- Perez-Lamela, C.; Franco, I.; Falque, E. Impact of High-Pressure Processing on Antioxidant Activity during Storage of Fruits and Fruit Products: A Review. Molecules 2021, 26, 5265. [Google Scholar] [CrossRef]
- Skroza, D.; Šimat, V.; Vrdoljak, L.; Jolić, N.; Skelin, A.; Čagalj, M.; Frleta, R.; Mekinić, I.G. Investigation of Antioxidant Synergisms and Antagonisms among Phenolic Acids in the Model Matrices Using FRAP and ORAC Methods. Antioxidants 2022, 11, 1784. [Google Scholar] [CrossRef] [PubMed]
- Gregorio, B.J.R.; Ramos, I.I.; Magalhães, L.M.; Silva, E.M.P.; Reis, S.; Segundo, M.A. Microplate ORAC-pyranine spectrophotometric assay for high-throughput assessment of antioxidant capacity. Microchem. J. 2020, 158, 105156. [Google Scholar] [CrossRef]
- Ansar, M.; Qu, Y.; Ivanciuc, T.; Garofalo, R.P.; Casola, A. Lack of Type I Interferon Signaling Ameliorates Respiratory Syncytial Virus-Induced Lung Inflammation and Restores Antioxidant Defenses. Antioxidants 2022, 11, 67. [Google Scholar] [CrossRef] [PubMed]
- Ni, D.; Jiang, D.; Kutyreff, C.J.; Lai, J.; Yan, Y.; Barnhart, T.E.; Yu, B.; Im, H.-J.; Kang, L.; Cho, S.Y.; et al. Molybdenum-based nanoclusters act as antioxidants and ameliorate acute kidney injury in mice. Nat. Commun. 2018, 9, 5421. [Google Scholar] [CrossRef] [PubMed]
- Xiao, C.; Toldrá, F.; Zhao, M.; Zhou, F.; Luo, D.; Jia, R.; Mora, L. In vitro and in silico analysis of potential antioxidant peptides obtained from chicken hydrolysate produced using Alcalase. Food Res. Int. 2022, 157, 111253. [Google Scholar] [CrossRef] [PubMed]
- Romani, V.P.; Martins, V.G.; Goddard, J.M. Radical scavenging polyethylene films as antioxidant active packaging materials. Food Control 2020, 109, 106946. [Google Scholar] [CrossRef]
- Ilyasov, I.R.; Beloborodov, V.L.; Selivanova, I.A.; Terekhov, R.P. ABTS/PP Decolorization Assay of Antioxidant Capacity Reaction Pathways. Int. J. Mol. Sci. 2020, 21, 1131. [Google Scholar] [CrossRef] [PubMed]
- Sridhar, K.; Charles, A.L. In vitro antioxidant activity of Kyoho grape extracts in DPPH radical dot and ABTS radical dot assays: Estimation methods for EC50 using advanced statistical programs. Food Chem. 2019, 275, 41–49. [Google Scholar] [CrossRef]
- Karton, A.; Tarnopolsky, A.; Lamère, J.-F.; Schatz, G.C.; Martin, J.M.L. Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A 2008, 112, 12868–12886. [Google Scholar] [CrossRef]
- Casanova-Paez, M.; Goerigk, L. Time-Dependent Long-Range-Corrected Double-Hybrid Density Functionals with Spin-Component and Spin-Opposite Scaling: A Comprehensive Analysis of Singlet–Singlet and Singlet–Triplet Excitation Energies. J. Chem. Theory Comput. 2021, 17, 5165–5186. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291–309. [Google Scholar] [CrossRef]
- Safna Hussan, K.P.; Thayyil, M.S.; Vijisha, K.; Rajan, V.K.; Muraleedharan, K. DFT studies on global parameters, antioxidant mechanism and molecular docking of amlodipine besylate. Comput. Biol. Chem. 2019, 80, 46–53. [Google Scholar] [CrossRef]
- Uludag, N.; Serdaroğlu, G.; Sugumar, P.; Rajkumar, P.; Colak, N.; Ercag, E. Synthesis of thiophene derivatives: Substituent effect, antioxidant activity, cyclic voltammetry, molecular docking, DFT, and TD-DFT calculations. J. Mol. Struc. 2022, 1257, 132607. [Google Scholar] [CrossRef]
- Sridhar, K.; Charles, A.L. Grape skin extracts as a sustainable source of antioxidants in an oil-in-water emulsion: An alternate natural approach to synthetic antioxidants using principal component analysis. Int. J. Food Sci. Technol. 2021, 56, 1937–1945. [Google Scholar] [CrossRef]
- Jacobsen, C. Oxidative Rancidity. In Encyclopedia of Food Chemistry; Melton, L., Shahidi, F., Varelis, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 261–269. ISBN 978-0-12-814045-1. [Google Scholar]
- Abeyrathne, E.D.N.S.; Nam, K.; Ahn, D.U. Analytical Methods for Lipid Oxidation and Antioxidant Capacity in Food Systems. Antioxidants 2021, 10, 1587. [Google Scholar] [CrossRef] [PubMed]
- Tran, H.; Nikzad, S.; Chiong, J.A.; Schuster, N.J.; Peña-Alcántara, A.E.; Feig, V.R.; Zheng, Y.-Q.; Bao, Z. Modular Synthesis of Fully Degradable Imine-Based Semiconducting p-Type and n-Type Polymers. Chem. Mater. 2021, 33, 7465–7474. [Google Scholar]
- Kumosinski, T.F.; Brown, E.M.; Farrell, H.M., Jr. Molecular modeling in food research: Technology and techniques. Trends Food. Sci. Technol. 1991, 2, 110–115. [Google Scholar] [CrossRef]
- Palheta, I.C.; Ferreira, L.R.; Joyce, K.L.; Vale, J.K.L.; Osmarina, P.P.; Silva, O.P.P.; Herculano, A.M.; Oliveira, K.R.H.M.; Chaves Neto, A.M.J.; Joaquín, M.; et al. Alkylated Sesamol Derivatives as Potent Antioxidants. Molecules 2020, 25, 3300. [Google Scholar] [CrossRef]
- Galano, A.; Francisco-Márquez, M.; Rául Alvarez-Idaboy, J. Mechanism and kinetics studies on the antioxidant activity of sinapinic acid. Phys. Chem. Chem. Phys. 2011, 13, 11199–11205. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.; Ma, L.; Li, J.; Shahzad, N.; Kim, C.K. Structure-antioxidant activity relationship of methoxy, phenolic hydroxyl, and carboxylic acid groups of phenolic acids. Sci. Rep. 2020, 10, 2611. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Dehkordi, M.M.; Asgarshamsi, M.H. Density functional theory studies of the antioxidants—A review. J. Mol. Model. 2021, 27, 271–284. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xu, X.; Goddard III, W.A. Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics. Proc. Natl. Acad. Sci. USA 2009, 106, 4963–4968. [Google Scholar] [CrossRef] [PubMed]
- Görling, A.; Levy, M. Correlation-energy functional and its high-density limit obtained from a coupling-constant perturbation expansion. Phys. Rev. B 1993, 47, 13105–13113. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected double-hybrid density functionals. J. Chem. Phys. 2009, 131, 174105. [Google Scholar] [CrossRef]
- Casanova-Páez, M.; Dardis, M.B.; Goerigk, L. ωB2PLYP and ωB2GPPLYP: The First Two Double-Hybrid Density Functionals with Long-Range Correction Optimized for Excitation Energies. J. Chem. Theory Comput. 2019, 15, 4735–4744. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Exchange-correlation functional with broad accuracy for metallic and nonmetallic compounds, kinetics, and noncovalent interactions. J. Chem. Phys. 2005, 123, 161103. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Double-hybrid density functionals with long-range dispersion corrections: Higher accuracy and extended applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef] [PubMed]
- Brémond, E.; Sancho-García, J.C.; Pérez-Jiménez, A.J.; Adamo, C. Communication: Double-hybrid functionals from adiabatic-connection: The QIDH model. J. Chem. Phys. 2014, 141, 031101. [Google Scholar] [CrossRef] [PubMed]
- Ernzerhof, M.; Perdew, J.P. Generalized gradient approximation to the angle- and system-averaged exchange hole. J. Chem. Phys. 1998, 109, 3313–3320. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Austin, A.; Peterson, G.A.; Frisch, M.J.; Dobek, F.J.; Scalmani, G.; Throssell, K. A Density Functional with Spherical Atom Dispersion Terms. J. Chem. Theory Comput. 2012, 8, 4989–5007. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. Exploring the Limit of Accuracy of the Global Hybrid Meta Density Functional for Main-Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Grimme, S.; Brandenburg, J.G.; Bannwarth, C.; Hansen, A. Consistent structures and interactions by density functional theory with small atomic orbital basis sets. J. Chem. Phys. 2015, 143, 054107. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Bannwarth, C.; Hansen, A.; Grimme, S. B97-3c: A revised low-cost variant of the B97-D density functional method. J. Chem. Phys. 2018, 148, 064104. [Google Scholar] [CrossRef]
- Furness, J.M.; Kaplan, A.D.; Ning, J.; Perdew, J.P.; Sun, J. Accurate and Numerically Efficient r2SCAN Meta-Generalized Gradient Approximation. J. Phys. Chem. Lett. 2020, 11, 8208–8215. [Google Scholar] [CrossRef]
- Jensen, F. Unifying General and Segmented Contracted Basis Sets. Segmented Polarization Consistent Basis Sets. J. Chem. Theory Comput. 2014, 10, 1074–1085. [Google Scholar] [CrossRef] [PubMed]
- Henderson, T.M.; Izmaylov, A.F.; Scalmani, G.; Scuseria, G.E. Can short-range hybrids describe long-range-dependent properties? J. Chem. Phys. 2009, 131, 044108. [Google Scholar] [CrossRef] [PubMed]
- Najibi, A.; Goerigk, L. The non-local kernel in van-der-Waals density functionals as an additive correction—An extensive analysis with special emphasis on the B97M-V and ωB97M-V approaches. J. Chem. Theory Comput. 2018, 14, 5725–5738. [Google Scholar] [CrossRef] [PubMed]
- Curtiss, L.A.; Raghavachar, K.; Pople, J.A. Gaussian-2 theory using reduced MølIer-Plesset orders. J. Chem. Phys. 1993, 98, 1293–1298. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Galano, A.; Mazzone, G.; Alvarez-Diduk, R.; Marino, T.; Alvarez-Idaboy, J.R.; Russo, N. Food Antioxidants: Chemical Insights at the Molecular Level. Annu. Rev. Food Sci. Technol. 2016, 7, 335–352. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Ryzhova, O.N. Enthalpy of Formation and O−H Bond Dissociation Enthalpy of Phenol: Inconsistency between Theory and Experiment. J. Phys. Chem. A 2016, 120, 2471–2479. [Google Scholar] [CrossRef]
- Lucarini, M.; Pedulli, G.F. Free radical intermediates in the inhibition of the autoxidation reaction. Chem. Soc. Rev. 2010, 39, 2106–2119. [Google Scholar] [CrossRef]
- Angel, L.A.; Ervin, K.M. Gas-Phase Acidities and O-H Bond Dissociation Enthalpies of Phenol, 3-Methylphenol, 2,4,6-Trimethylphenol, and Ethanoic Acid. J. Phys. Chem. A 2006, 110, 10392–10403. [Google Scholar] [CrossRef]
- Klein, E.; Lukeš, V. DFT/B3LYP Study of the Substituent Effect on the Reaction Enthalpies of the Individual Steps of Single Electron Transfer-Proton Transfer and Sequential Proton Loss Electron Transfer Mechanisms of Phenols Antioxidant Action. J. Phys. Chem. A 2006, 110, 12312–12320. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Peterson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.02; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2017, 8, e1327. [Google Scholar] [CrossRef]

| Original Method | BDE | PA | ETE | |||
|---|---|---|---|---|---|---|
| GP | ISM/CPCM | GP | ISM/CPCM | GP | ISM/CPCM | |
| B97(D3BJ) | 81.033 | 80.996 | 348.769 | 261.125 | 47.928 | 76.262 |
| ωB97 | 81.657 | 81.715 | 348.983 | 260.808 | 47.664 | 76.624 |
| M08HX | 87.462 | 87.571 | 346.680 | 258.620 | 56.408 | 85.302 |
| APFD | 82.045 | 82.168 | 348.185 | 260.147 | 49.376 | 78.263 |
| PBEh0 | 81.341 | 81.467 | 347.802 | 259.740 | 48.564 | 77.478 |
| mPW2PLYPD | 84.195 | 84.107 | 349.035 | 261.079 | 48.048 | 76.642 |
| B97-3c | 77.206 | 81.492 | 346.759 | 258.697 | 49.298 | 78.019 |
| r2SCAN-3c | 81.961 | 80.331 | 345.474 | 256.885 | 49.274 | 78.670 |
| PBEh-3c | 80.275 | 79.011 | 349.590 | 261.013 | 43.207 | 73.223 |
| M052X/6-311+G(d,p) | 87.695 | 87.537 | 347.570 | 259.038 | 54.130 | 83.228 |
| G4(MP2) | 85.696 | 85.209 | 346.795 | 258.797 | 53.967 | 82.951 |
| Experimental | 88.340 a | 87.200 b | 347.99 c | - | 52.10 d | - |
| Original Method | RAD | Wall Time | |||||||
|---|---|---|---|---|---|---|---|---|---|
| BDE (GP) | BDE (ISM) | PA (GP) | PA (ISM) | ETE (GP) | ETE (ISM) | GP | ISM/ CPCM | Total | |
| B97(D3BJ) | 8.27 | 7.12 | 0.22 | - | 8.01 | - | 1989.00 | 716.00 | 2705.00 |
| ωB97 | 7.57 | 6.29 | 0.29 | - | 8.51 | - | 1123.00 | 1059.00 | 2182.00 |
| M08HX | 0.99 | 0.42 | 0.38 | - | 8.27 | - | 1233.00 | 1457.00 | 2690.00 |
| APFD | 7.13 | 5.77 | 0.06 | - | 5.23 | - | 700.00 | 914.00 | 1614.00 |
| PBEh0 | 7.92 | 6.57 | 0.05 | - | 6.79 | - | 940.00 | 838.00 | 1778.00 |
| mPW2PLYPD | 4.69 | 3.55 | 0.30 | - | 7.78 | - | 1970.00 | 2084.00 | 4054.00 |
| B97-3c | 12.60 | 6.55 | 0.35 | - | 5.38 | - | 1571.48 | 1882.67 | 3454.15 |
| r2SCAN-3c | 7.22 | 7.88 | 0.72 | - | 5.42 | - | 1936.52 | 2113.98 | 4050.50 |
| PBEh-3c | 9.13 | 9.39 | 0.46 | - | 17.07 | - | 971.52 | 900.32 | 1871.84 |
| M052X/6-311+G(d,p) | 0.73 | 0.39 | 0.12 | - | 3.90 | - | 3816.00 | 5150.00 | 8966.00 |
| G4(MP2) | 2.99 | 2.28 | 0.34 | - | 3.58 | - | 9915.00 | 31827.00 | 41742.00 |
| Original Method\\LC-ωHPBE | BDE | PA | ETE | RAD | Wall Time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GP | ISM | GP | ISM | GP | ISM | BDE (GP) | BDE (ISM) | PA (GP) | PA (ISM) | ETE (GP) | ETE (ISM) | GP | ISM | Total | |
| B97(D3BJ) | 81.501 | 81.663 | 350.713 | 262.402 | 48.697 | 77.896 | 7.74 | 6.35 | 0.78 | - | 6.53 | - | 1202.00 | 1505.00 | 2707.00 |
| ωB97 | 81.560 | 81.695 | 350.672 | 262.363 | 48.797 | 77.966 | 7.68 | 6.31 | 0.77 | - | 6.34 | - | 1420.00 | 1178.00 | 2598.00 |
| M08HX | 81.548 | 81.681 | 350.681 | 262.374 | 48.776 | 77.942 | 7.69 | 6.33 | 0.77 | - | 6.38 | - | 1100.00 | 1092.00 | 2192.00 |
| APFD | 81.585 | 81.723 | 350.653 | 262.350 | 48.841 | 78.008 | 7.65 | 6.28 | 0.77 | - | 6.26 | - | 904.00 | 1011.00 | 1915.00 |
| PBEh0 | 81.624 | 81.754 | 350.656 | 262.347 | 48.877 | 78.041 | 7.60 | 6.25 | 0.77 | - | 6.19 | - | 805.00 | 1060.00 | 1865.00 |
| mPW2PLYPD | 81.582 | 81.718 | 350.681 | 262.372 | 48.810 | 77.981 | 7.65 | 6.29 | 0.77 | - | 6.31 | - | 2400.00 | 2537.00 | 4937.00 |
| B97-3c * | 78.920 | 78.920 | 347.833 | 259.434 | 48.996 | 78.122 | 10.66 | 9.49 | 0.05 | - | 5.96 | - | 1213.89 | 1323.30 | 2537.19 |
| r2SCAN-3c * | 78.796 | 78.796 | 347.882 | 259.455 | 48.823 | 77.976 | 10.80 | 9.64 | 0.03 | - | 6.29 | - | 1420.54 | 1597.42 | 3017.96 |
| PBEh-3c * | 78.792 | 78.760 | 347.834 | 259.388 | 48.867 | 78.006 | 10.81 | 9.68 | 0.04 | - | 6.21 | - | 777.95 | 612.29 | 1390.24 |
| Original Method\\ω-B97X-V(D3BJ) | BDE | PA | ETE | RAD | Wall Time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GP | ISM | GP | ISM | GP | I SM | BDE(GP) | BDE (ISM) | PA (GP) | PA (ISM) | ETE (GP) | ETE (ISM) | GP | ISM | Total | |
| M08HX | 85.301 | 85.502 | 352.981 | 263.967 | 48.885 | 79.635 | 3.44 | 1.95 | 1.43 | - | 6.17 | - | 1886.86 | 2387.85 | 4274.71 |
| PBEh0 | 85.252 | 85.448 | 352.948 | 263.907 | 48.869 | 79.641 | 3.50 | 2.01 | 1.42 | - | 6.20 | - | 1701.47 | 1810.67 | 3512.14 |
| mPW2PLYPD | 85.296 | 85.500 | 352.976 | 263.924 | 48.885 | 79.675 | 3.45 | 1.95 | 1.43 | - | 6.17 | - | 2706.85 | 2580.22 | 5287.07 |
| B97-3c * | 82.010 | 82.103 | 350.201 | 261.038 | 48.375 | 79.164 | 7.17 | 5.85 | 0.64 | - | 7.15 | - | 2005.54 | 2279.77 | 4285.31 |
| r2SCAN-3c * | 82.573 | 82.671 | 350.270 | 261.106 | 48.867 | 79.665 | 6.53 | 5.19 | 0.66 | - | 6.21 | - | 2272.68 | 2492.85 | 4765.53 |
| PBEh-3c * | 81.851 | 81.940 | 350.194 | 261.078 | 48.223 | 78.962 | 7.35 | 6.03 | 0.63 | - | 7.44 | - | 1991.85 | 1574.31 | 3566.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamenković, N.; Cerkovnik, J.; Poklar Ulrih, N. Inversion Theory Leveling as a New Methodological Approach to Antioxidant Thermodynamics: A Case Study on Phenol. Antioxidants 2023, 12, 282. https://doi.org/10.3390/antiox12020282
Stamenković N, Cerkovnik J, Poklar Ulrih N. Inversion Theory Leveling as a New Methodological Approach to Antioxidant Thermodynamics: A Case Study on Phenol. Antioxidants. 2023; 12(2):282. https://doi.org/10.3390/antiox12020282
Chicago/Turabian StyleStamenković, Nikola, Janez Cerkovnik, and Nataša Poklar Ulrih. 2023. "Inversion Theory Leveling as a New Methodological Approach to Antioxidant Thermodynamics: A Case Study on Phenol" Antioxidants 12, no. 2: 282. https://doi.org/10.3390/antiox12020282
APA StyleStamenković, N., Cerkovnik, J., & Poklar Ulrih, N. (2023). Inversion Theory Leveling as a New Methodological Approach to Antioxidant Thermodynamics: A Case Study on Phenol. Antioxidants, 12(2), 282. https://doi.org/10.3390/antiox12020282








