Subject Combination and Electrode Selection in Cooperative Brain-Computer Interface Based on Event Related Potentials
Abstract
:1. Introduction
2. BCI Issues
3. Cooperative BCI
3.1. Extending the Notion of BCI
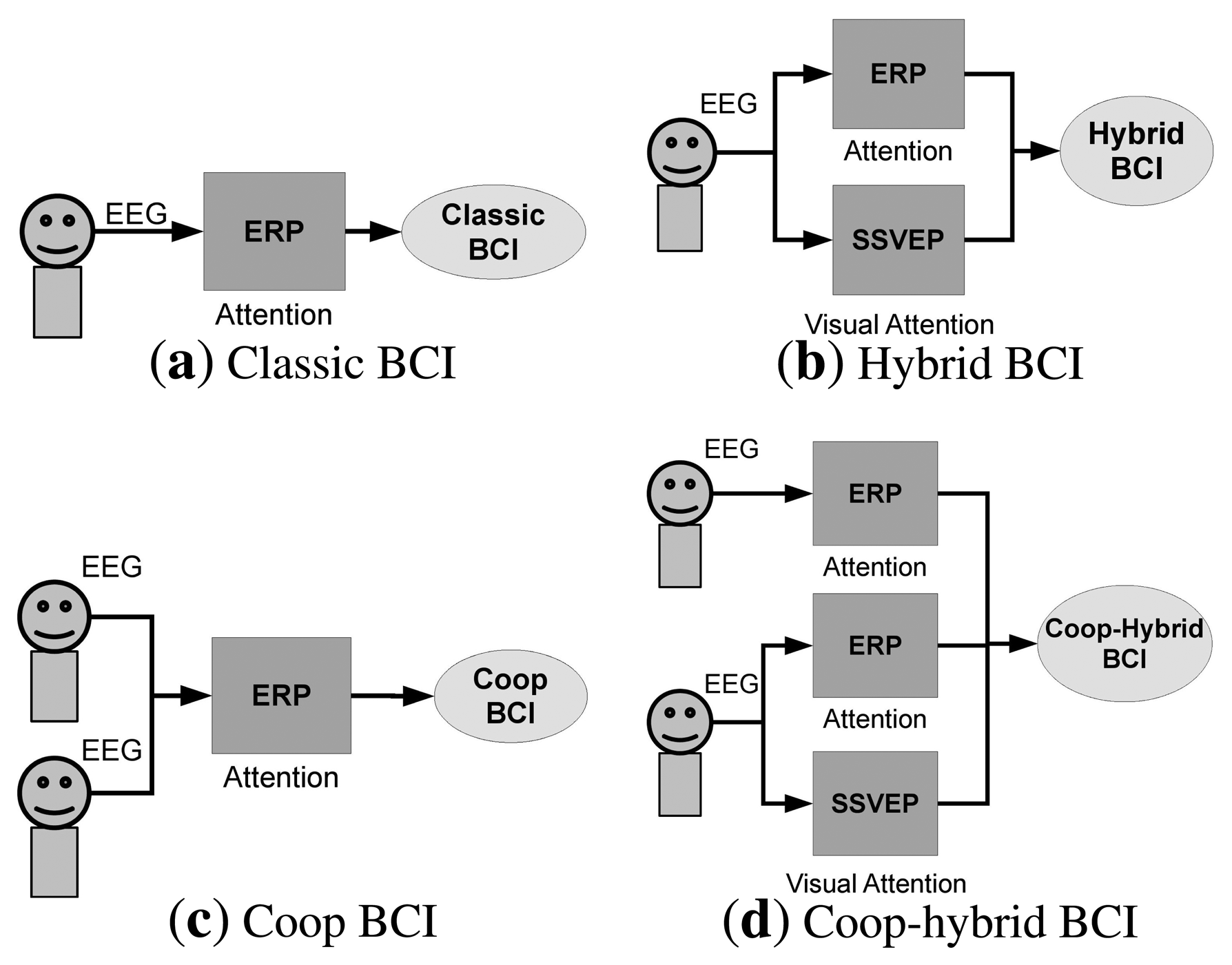
- The classical BCI: it involves a single person and a single brain modality, i.e., a single type of brain response (ERP or SSVEP, motor imagery, …) (see Figure 1a).
- The hybrid BCI: it involves a single person, and the possibility to consider several brain modalities (see Figure 1b).
- The cooperative BCI: it involves a group of people, and a single brain modality (see Figure 1c).
- The cooperative-hybrid BCI: it involves a group of people, and the possibility to consider several brain modalities. The type of brain response can depend on the subject, i.e., the BCI can be hybrid only for some subjects (see Figure 1d).

3.2. Combination Strategies
- The sum of the classifier outputs (Osum):
- The weighted sum of the classifier outputs (Ow_sum):
- The product of classifier outputs (Oprod):
- The selection of the maximum score (Omax):
- The selection of the minimum score (Omin):
- The voting (Ov(k)):where Di(α) is the binary decision associated with the i-th subject defined byand α is a threshold for the decision to assign the input signal to the target or non-target class. Two particular cases of voting can be distinguished: the majority vote where k = Nsub/2, and the consensus vote where k = Nsub, which are denoted Omaj and Ocons, respectively.
3.3. Performance Evaluation
4. Single-Event ERP Detection
4.1. Participants and Study Design
4.2. Signal Processing and Classification
4.3. Results
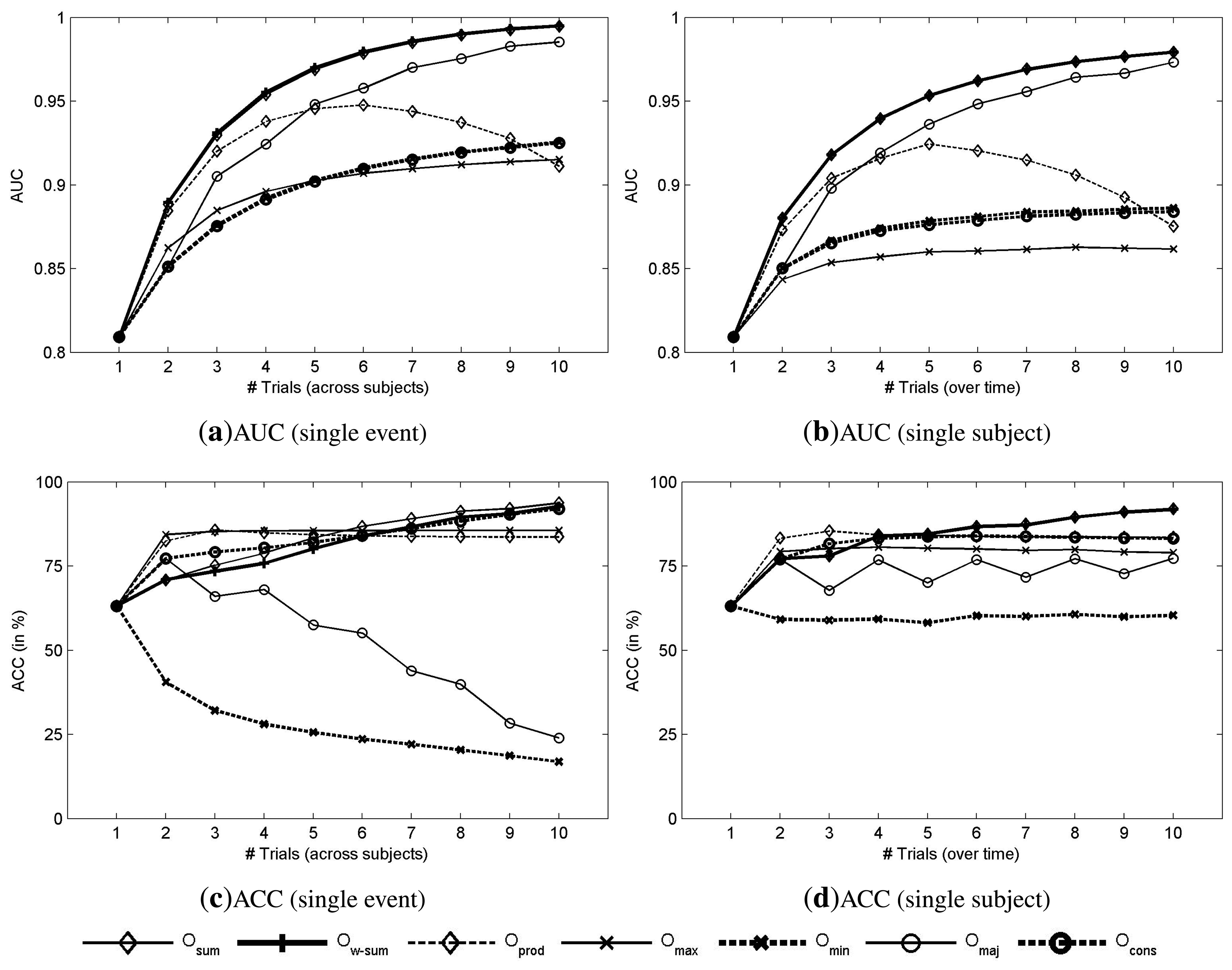
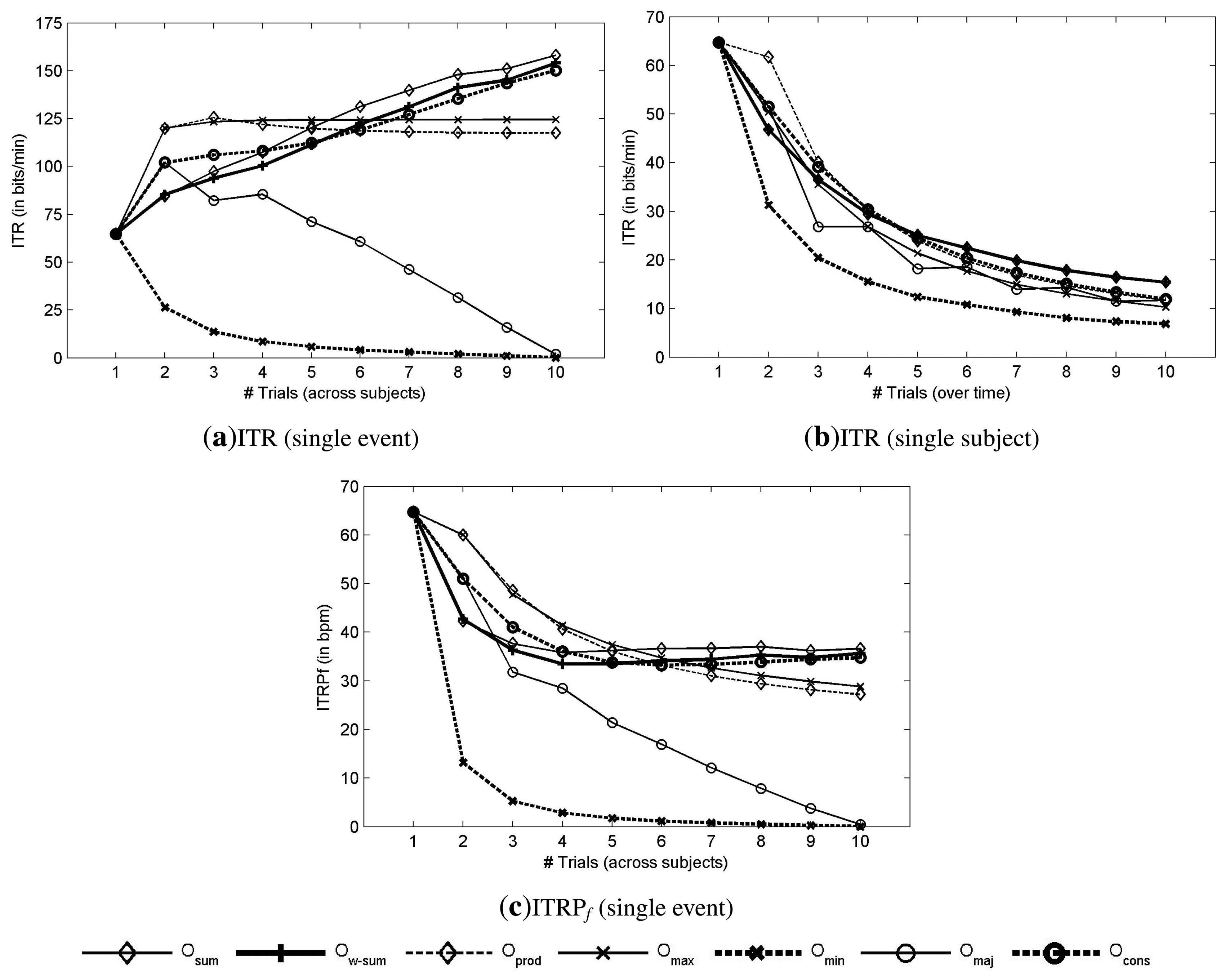
5. Electrode Selection in Cooperative BCIs
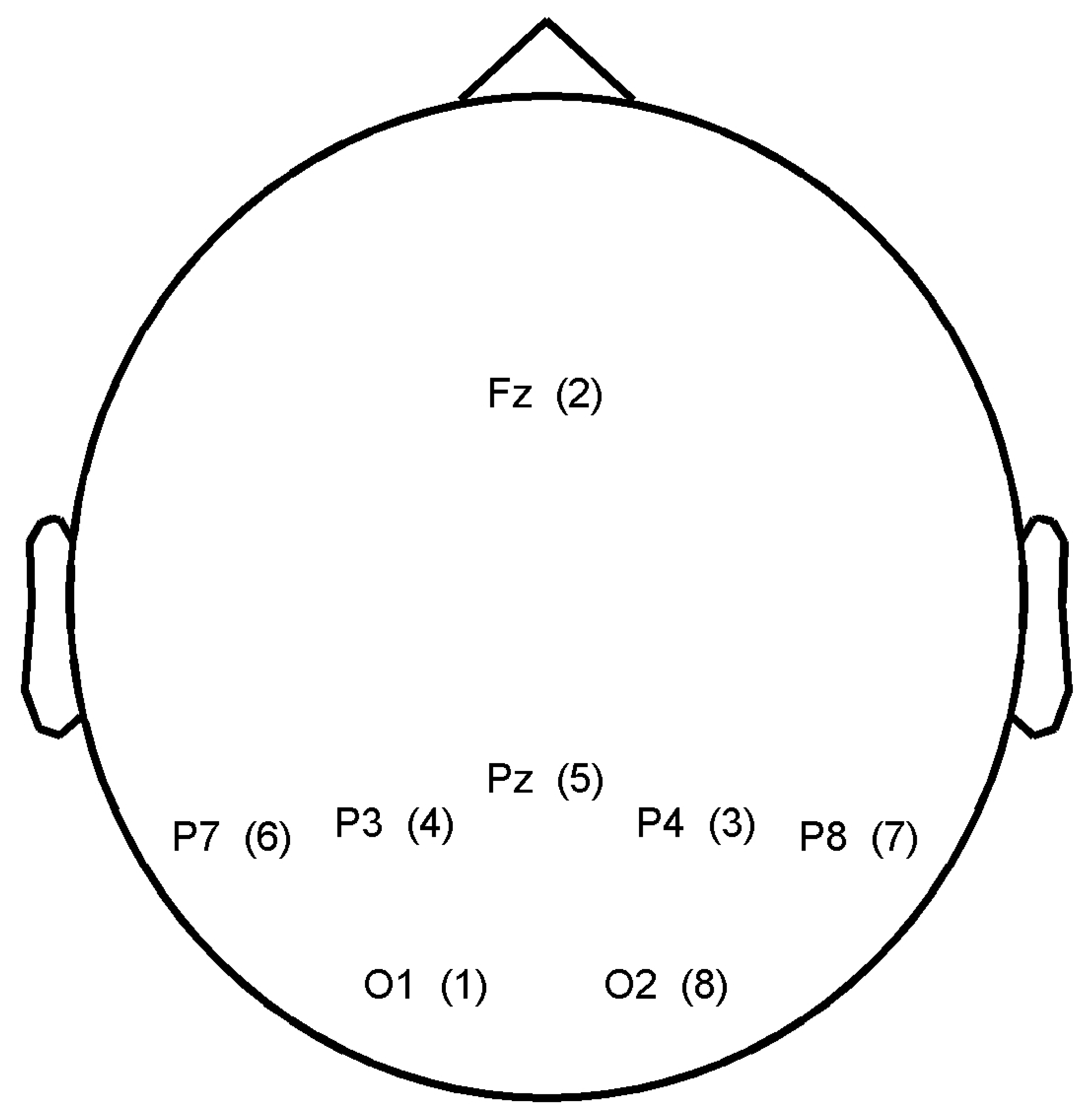
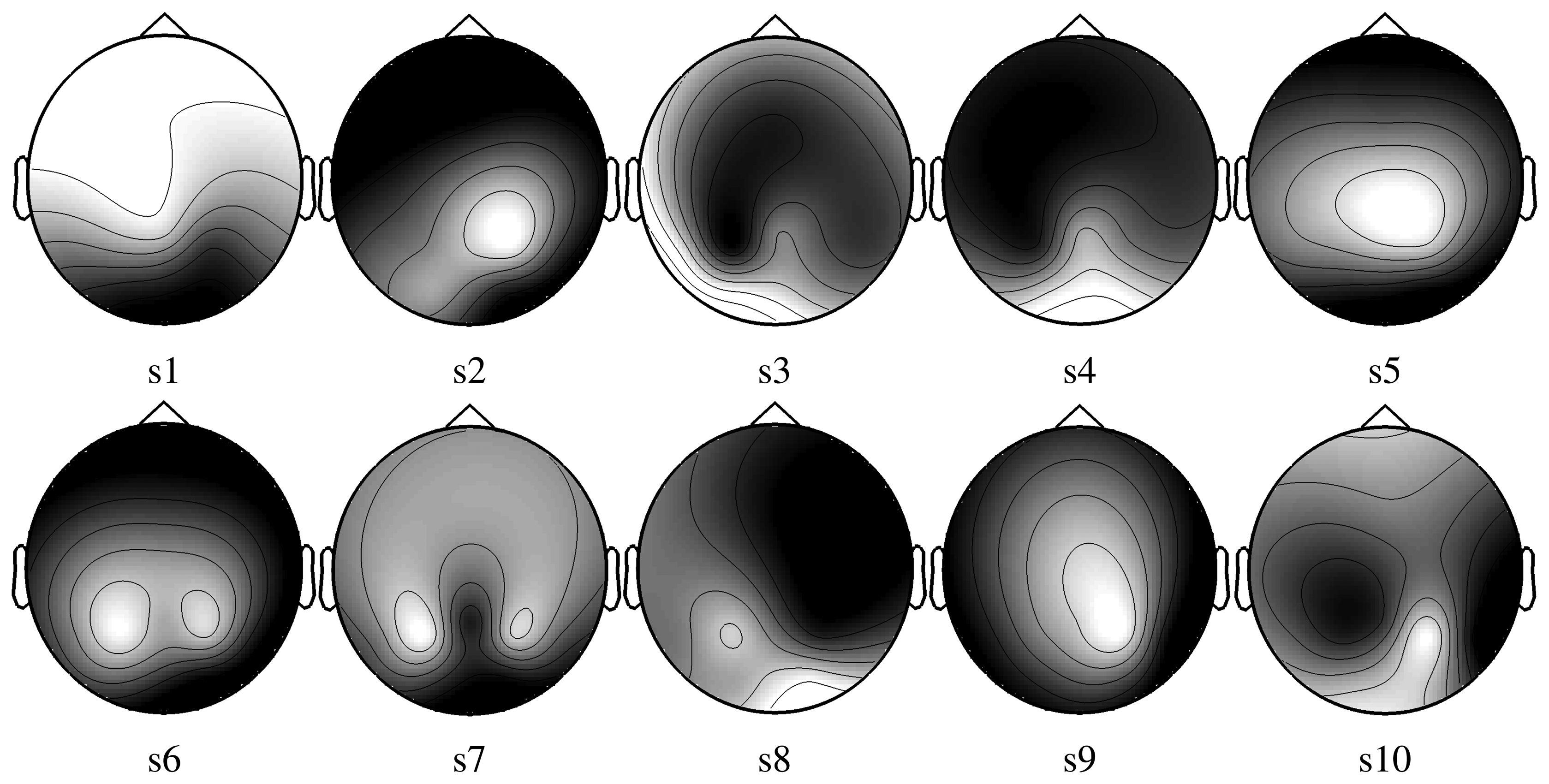
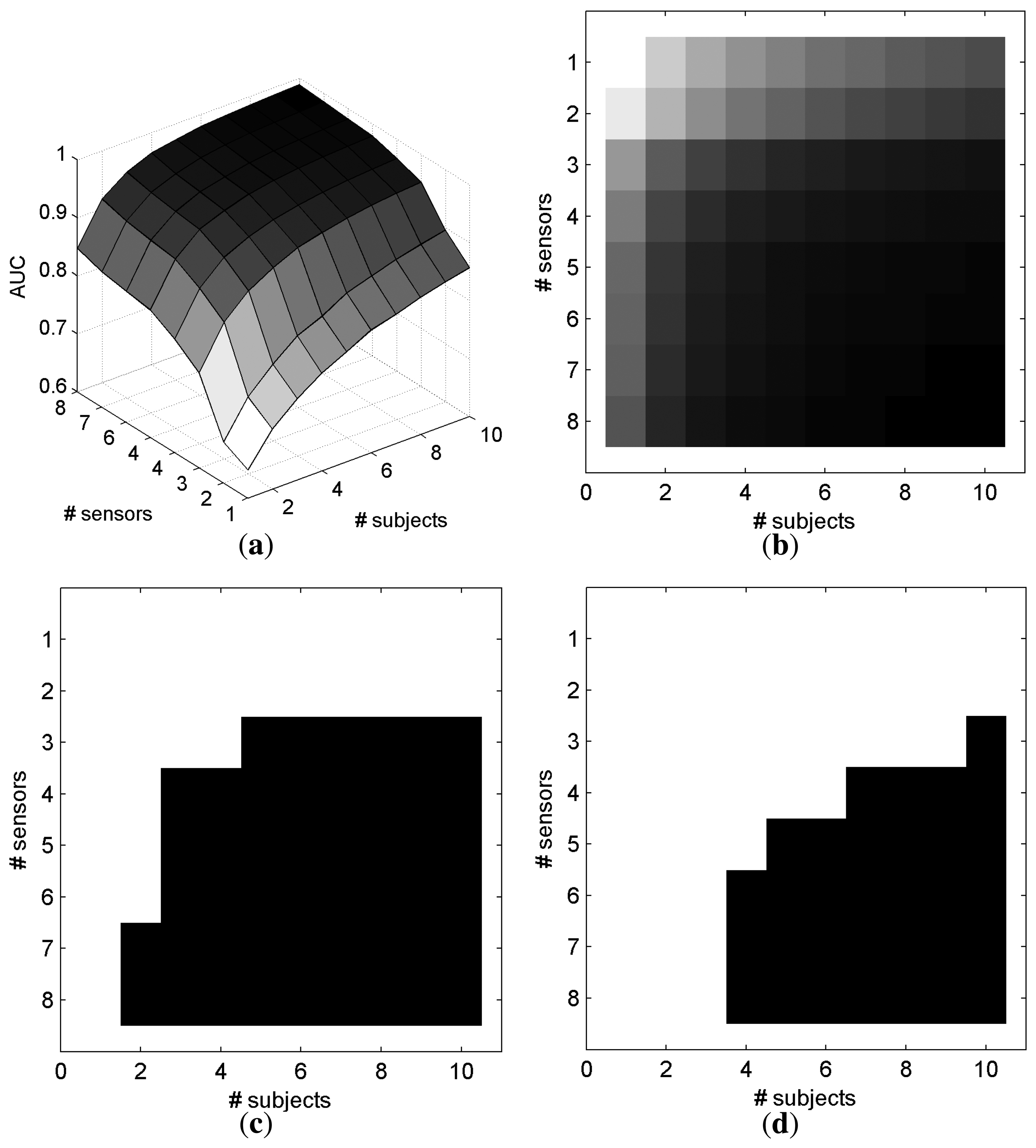
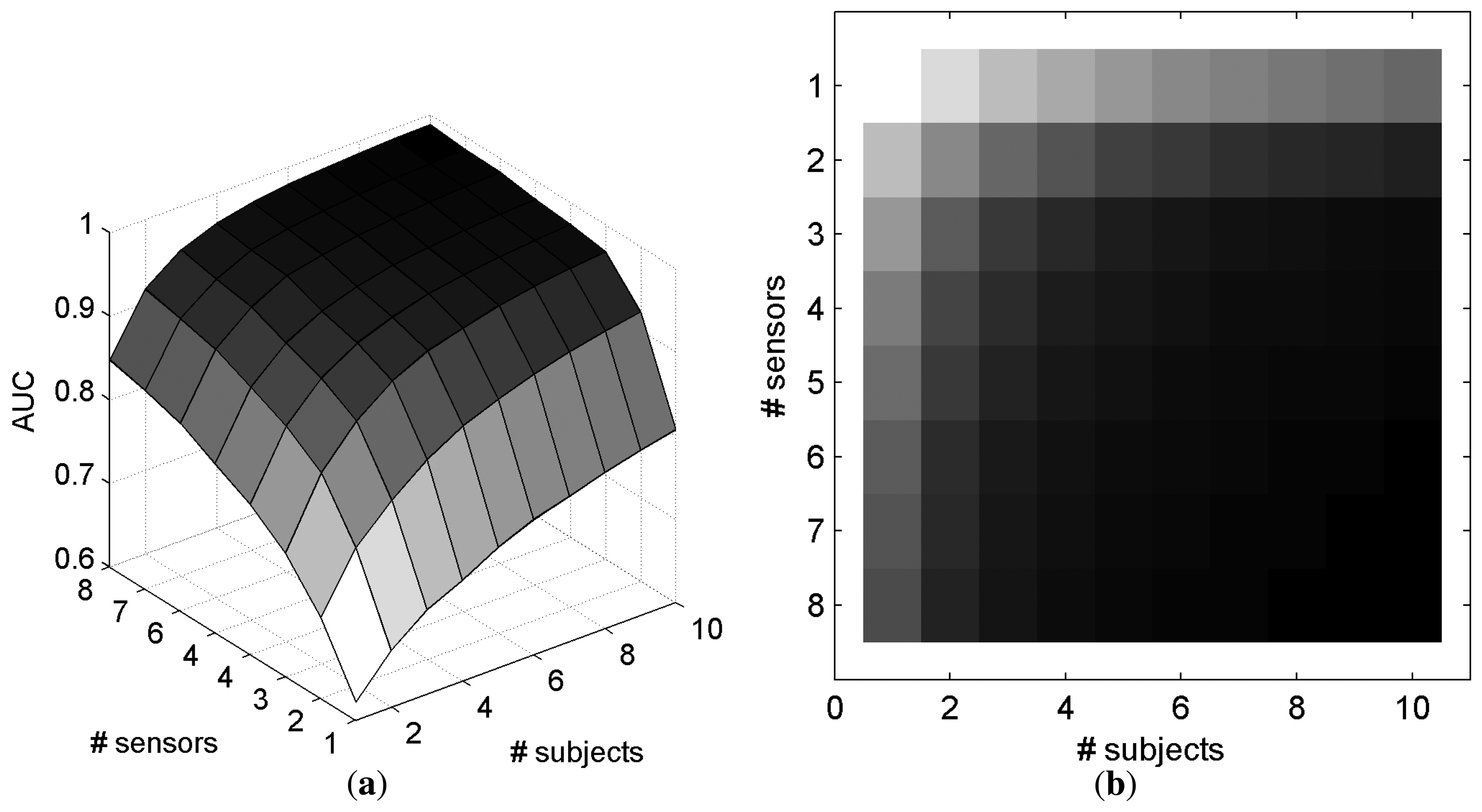
6. Discussion
6.1. Social Psychology
6.2. Entertainment and Education
6.3. Materials and Technical Issues
7. Conclusions
Conflicts of Interest
References
- Farwell, L.; Donchin, E. Talking off the top of your head: Toward a mental prosthesis utilizing event-related brain potentials. Electroencephalogr. Clin. Neurophysiol. 1988, 70, 510–523. [Google Scholar]
- Cecotti, H. Spelling with Non-Invasive Brain-Computer Interfaces—Current and future trends. J. Physiol. Paris. 2011, 105, 106–114. [Google Scholar]
- Millán, J.R.; Rupp, R.; Müller-Putz, G.R.; Murray-Smith, R.; Giugliemma, C.; Tangermann, M.; Vidaurre, C.; Cincotti, F.; Kübler, A.; Leeb, R. Combining brain-computer interfaces and assistive technologies: State-of-the-art and challenges. Front. Neurosci. 2010, 4, 1–15. [Google Scholar]
- Townsend, G.; LaPallo, B.K.; Boulay, C.B.; Krusienski, D.J.; Frye, G.E.; Hauser, C.K.; Schwartz, N.E.; Vaughan, T.M.; Wolpaw, J.R.; Sellers, E.W. A novel P300-based brain-computer interface stimulus presentation paradigm: Moving beyond rows and columns. Clin. Neurophysiol. 2010, 121, 1109–1120. [Google Scholar]
- Yuan, P.; Wang, Y.; Wu, W.; Xu, H.; Gao, X.; Gao, S. Study on an online collaborative BCI to accelerate response to visual targets. Proceedings of the 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), San Diego, CA, USA, 28 August–1 September 2012; pp. 1736–1739.
- Yuan, P.; Wang, Y.; Gao, X.; Jung, T.P.; Gao, S. A collaborative brain-computer interface for accelerating human decision making. Proceedings of the 7th International Conference on Universal Access in Human-Computer Interaction: Design Methods, Tools, and Interaction Techniques for eInclusion, UAHCI 2013, Las Vegas, NV, USA, 21–26 July 2013; pp. 672–681.
- Poli, R.; Cinel, C.; Matran-Fernandez, A.; Sepulveda, F.; Stoica, A. Some Steps towards Realtime Control of a Space-craft Simulator via a Brain-computer Interface; Technical Report CES-525; University of Essex: Colchester, UK, 2012; pp. 1–23. [Google Scholar]
- Babiloni, F.; Cincotti, F.; Mattia, D.; Mattiocco, M.; Fallani, D.V.F.; Tocci, A.; Bianchi, L.; Marciani, M.G.; Astolfi, L. Hypermethods for EEG hyperscanning. Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), New York, NY, USA, 30 August–3 September 2006; Volume 1, pp. 3666–3669.
- Eckstein, M.; Das, K.; Pham, B.T.; Peterson, M.; Abbey, C.; Sy, J.; Giesbrecht, B. Neural decoding of collective wisdom with multi-brain computing. NeuroImage 2012, 59, 94–108. [Google Scholar]
- Poli, R.; Cinel, C.; Sepulveda, F.; Stoica, A. A Preliminary Study of a Collaborative Brain-computer Interface in a Visual Matching Task; Technical Report CES-524; University of Essex: Colchester, UK, 2012; pp. 1–22. [Google Scholar]
- Poli, R.; Cinel, C.; Sepulveda, F.; Stoica, A. Improving decision-making based on visual perception via a collaborative brain-computer interface. Proceedings of the IEEE International Multi-Disciplinary Conference on Cognitive Methods in Situation Awareness and Decision Support CogSIMA 2013, San Diego, CA, USA, 25–28 February 2013; pp. 1–8.
- Allison, B.Z.; Lüth, T.; Valbuena, D.; Teymourian, A.; Volosyak, I.; Gräser, A. BCI Demographics: How Many (and What Kinds of) People Can Use an SSVEP BCI? IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 107–116. [Google Scholar]
- Guger, C.; Daban, S.; Sellers, E.; Holznera, C.; Krausza, G.; Carabalonac, R.; Gramaticac, F.; Edlinger, G. How many people are able to control a P300-based brain.computer interface (BCI)? Neurosci. Lett. 2009, 462, 94–98. [Google Scholar]
- Samek, W.; Vidaurre, C.; Müller, K.R.; Kawanabe, M. Stationary common spatial patterns for brain-computer interfacing. J. Neural Eng. 2012, 9, 026013. [Google Scholar] [CrossRef]
- Lu, S.; Guan, C.; Zhang, H. Unsupervised Brain Computer Interface based on Inter-Subject Information and Online Adaptation. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 1–11. [Google Scholar]
- Cecotti, H.; Rivet, B.; Congedo, M.; Jutten, C.; Bertrand, O.; Maby, E.; Mattout, J. A robust sensor selection method for P300 Brain-Computer Interfaces. J. Neural Eng. 2011, 8, 016001. [Google Scholar] [CrossRef]
- Rivet, B.; Cecotti, H.; Maby, E.; Mattout, J. Impact of Spatial Filters During Sensor Selection in a Visual P300 Brain-Computer Interface. Brain Topogr. 2012, 12, 55–63. [Google Scholar]
- Thulasidas, M.; Guan, C. Optimization of BCI Speller Based on P300 Potential. Proceedings of the 27th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Shanghai, China, 1–4 September 2005; Volume 5, pp. 5396–5399.
- Ryan, D.B.; Frye, G.E.; Townsend, G.; Berry, D.R.; Mesa-G, S.; Gates, N.A.; Sellers, E.W. Predictive Spelling With a P300-Based Brain-Computer Interface: Increasing the Rate of Communication. Int. J. Hum. Comput. Interact. 2011, 27, 69–84. [Google Scholar]
- Allison, B.Z.; Leeb, R.; Brunner, C.; Müller-Putz, G.R.; Bauernfeind, G.; Kelly, J.W.; Neuper, C. Toward smarter BCIs: Extending BCIs through hybridization and intelligent control. J. Neural Eng. 2012, 9, 1–7. [Google Scholar]
- Pfurtscheller, G.; Allison, B.Z.; Bauernfeind, G.; Brunner, C.; Escalante, T.S.; Scherer, R.; Zander, T.O.; Mueller-Putz, G.; Neuper, C.; Birbaumer, N. The hybrid BCI. Front. Neurosci. 2010, 4, 1–11. [Google Scholar]
- Sullivan, T.J.; Deiss, S.R.; Jung, T.P.; Cauwenberghs, G. A Brain-Machine Interface using Dry-Contact, Low-Noise EEG Sensors. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Seattle, WA, USA, 18–21 May 2008; pp. 1986–1989.
- Gargiulo, G.; Calvo, R.A.; Bifulco, P.; Cesarelli, M.; Jin, C.; Mohamed, A.; Schaik, A. A new EEG recording system for passive dry electrodes. Clin. Neurophysiol 2010, 121, 686–693. [Google Scholar]
- Wang, Y.T.; Wang, Y.; Jung, T.P. Measuring steady-state visual evoked potentials from non-hair-bearing areas. Proceedings of the 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), San Diego, CA, USA, 28 August–1 September 2012; pp. 1806–1809.
- Estepp, J.R.; Christensen, J.C.; Monnin, J.W.; Davis, I.M.; Wilson, G.F. Validation of a Dry Electrode System for EEG. Proceedings of the Human Factors and Ergonomics Society, 53rd Annual Meeting, San Antonio, TX, USA, 19–23 October 2009; pp. 1171–1175.
- Lin, C.T.; Ko, L.W.; Chang, C.J.; Wang, Y.T.; Chung, C.H.; Yang, F.S.; Duann, J.R.; Jung, T.P.; Chiou, J.C. Wearable and Wireless Brain-Computer Interface and Its Applications. Proceedings of the 5th International Conference on Foundations of Augmented Cognition, San Diego, CA, USA, 19–24 July 2009; pp. 741–748.
- Wang, Y.; Jung, T.P. A Collaborative Brain-Computer Interface for Improving Human Performance. PLoS One 2011, 6, e20422. [Google Scholar]
- Wang, Y.; Wang, Y.T.; Jung, T.P.; Gao, X.; Gao, S. A collaborative brain computer interface. Proceedings of the 4th International Conference on BioMedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; pp. 583–586.
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Fumera, G.; Roli, F. Performance Analysis and Comparison of Linear Combiners for Classifier Fusion. 6–9 August 2002; pp. 424–432.
- Kittler, J.; Alkoot, F.M. Sum Versus Vote Fusion in Multiple Classifier Systems. IEEE Trans. Pattern Anal. Mach. Intell 2003, 25, 110–115. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1964. [Google Scholar]
- Rivet, B.; Souloumiac, A.; Attina, V.; Gibert, G. xDAWN algorithm to enhance evoked potentials: Application to brain-computer interface. IEEE Trans. Biomed. Eng. 2009, 56, 2035–2043. [Google Scholar]
- Rivet, B.; Souloumiac, A. Optimal linear spatial filters for event-related potentials based on a spatio-temporal model: Asymptotical performance analysis. Signal Process 2013, 93, 387–398. [Google Scholar]
- Cecotti, H.; Kasper, R.; Elliott, J.C.; Eckstein, M.P.; Giesbrecht, B. Multimodal target detection using single trial evoked EEG responses in single and dual-tasks. 6311–6314.
- Hoffmann, U.; Vesin, J.; Diserens, K.; Ebrahimi, T. An efficient P300-based brain-computer interface for disabled subjects. J. Neurosci. Methods 2008, 167, 115–125. [Google Scholar]
- Luck, S.J. A Introduction to the Event-Related Potential Technique; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Astolfi, L.; Toppi, J.; Fallani, F.D.V.; Vecchiato, G.; Salinari, S.; Mattia, D.; Cincotti, F.; Babiloni, F. Neuroelectrical hyperscanning measures simultaneous brain activity in humans. Brain Topogr. 2010, 23, 243–256. [Google Scholar]
- Astolfi, L.; Toppi, J.; Fallani, F.D.V.; Vecchiato, G.; Cincotti, F.; Wilke, C.T.; Yuan, H.; Mattia, D.; He, B.; Babiloni, F. Imaging the Social Brain by Simultaneous Hyperscanning During Subject Interaction. IEEE Intell. Syst. 2011, 26, 38–45. [Google Scholar]
- Krepki, R.; Blankertz, B.; Curio, G.; Müller, K.R. The Berlin brain-computer interface (BBCI): towards a new communication channel for online control in gaming applications. J. Multimed. Tools Appl. 2007, 33, 73–90. [Google Scholar]
- Tangermann, M.; Krauledat, M.; Grzeska, K.; Sagebaum, M.; Blankertz, B.; Vidaurre, C.; Müller, K.R. Playing Pinball with non-invasive BCI. Proceedings of the Conference of Neural Information Processing Systems (NIPS’08), Vancouver, Canada, 8–10 December 2008; pp. 1641–1648.
- Finke, A.; Lenhards, A.; Ritter, H. The MindGame: A P300-based brain-computer interface game. Neural Netw. 2009, 22, 1329–1333. [Google Scholar]
- Mül, C.; Görkök, H.; Plass-Oude Bos, D.; Thurlings, M.E.; Scherffig, L.; Duvinage, M.; Elbakyan, A.A.; Kang, S.; Poel, M.; Heylen, D. Bacteria Hunt: A multimodal, multiparadigm BCI game. J. Multimodal User Interfaces 2010, 4, 11–25. [Google Scholar]
- Huang, L.; Pashler, H. Attention capacity and task difficulty in visual search. Cognition 2005, 94, 101–111. [Google Scholar]
- Pashler, H.; Johnston, J.C. Attentional limitations in dual-task performance. In Attention; Psychology Press: Hove, UK, 1998; pp. 155–189. [Google Scholar]
- Schalk, G.; McFarland, D.J.; Hinterberger, T.; Birbaumer, N.; Wolpaw, J. BCI2000: A general-purpose brain-computer interface (BCI) system. IEEE Trans. Biomed. Eng. 2004, 51, 1034–1043. [Google Scholar]
- Renard, Y.; Lotte, F.; Gibert, G.; Congedo, M.; Maby, E.; Delannoy, V.; Bertrand, O.; Lecuyer, A. OpenViBE: An Open-Source Software Platform to Design, Test, and Use Brain-Computer Interfaces in Real and Virtual Environments. Presence Teleoperators Virtual Environ. 2010, 19, 35–53. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cecotti, H.; Rivet, B. Subject Combination and Electrode Selection in Cooperative Brain-Computer Interface Based on Event Related Potentials. Brain Sci. 2014, 4, 335-355. https://doi.org/10.3390/brainsci4020335
Cecotti H, Rivet B. Subject Combination and Electrode Selection in Cooperative Brain-Computer Interface Based on Event Related Potentials. Brain Sciences. 2014; 4(2):335-355. https://doi.org/10.3390/brainsci4020335
Chicago/Turabian StyleCecotti, Hubert, and Bertrand Rivet. 2014. "Subject Combination and Electrode Selection in Cooperative Brain-Computer Interface Based on Event Related Potentials" Brain Sciences 4, no. 2: 335-355. https://doi.org/10.3390/brainsci4020335
APA StyleCecotti, H., & Rivet, B. (2014). Subject Combination and Electrode Selection in Cooperative Brain-Computer Interface Based on Event Related Potentials. Brain Sciences, 4(2), 335-355. https://doi.org/10.3390/brainsci4020335