Anti-Disturbance of Scale-Free Spiking Neural Network against Impulse Noise
Abstract
1. Introduction
2. Construction of SFSNN
2.1. Generation of a Scale-Free Network
- (1)
- Scale-free property
- (2)
- Clustering coefficient
2.2. Izhikevich Neuron Model
2.3. Synaptic Plasticity Model
2.4. Construction Process of the SFSNN
| Algorithm 1 The construction algorithm of the SFSNN |
| Input: Adjacency matrix of the scale-free network at Output: The high-clustering SFSNN
|
3. Anti-Disturbance of the SFSNN
3.1. External Disturbance and Anti-Disturbance Indexes
- Impulse noiseImpulse noise is an irregular discontinuous signal composed of pulse spikes, which is characterized by short duration, large amplitude and burst. It can be described as follows:where is the intensity of impulse noise, is the start time of the stimulus and T is the duration of the stimulus. In this study, impulse noise , as current disturbance, is applied to in Equation (3) of all neurons in the SFSNN.
- The indexes of anti-disturbance
- (1)
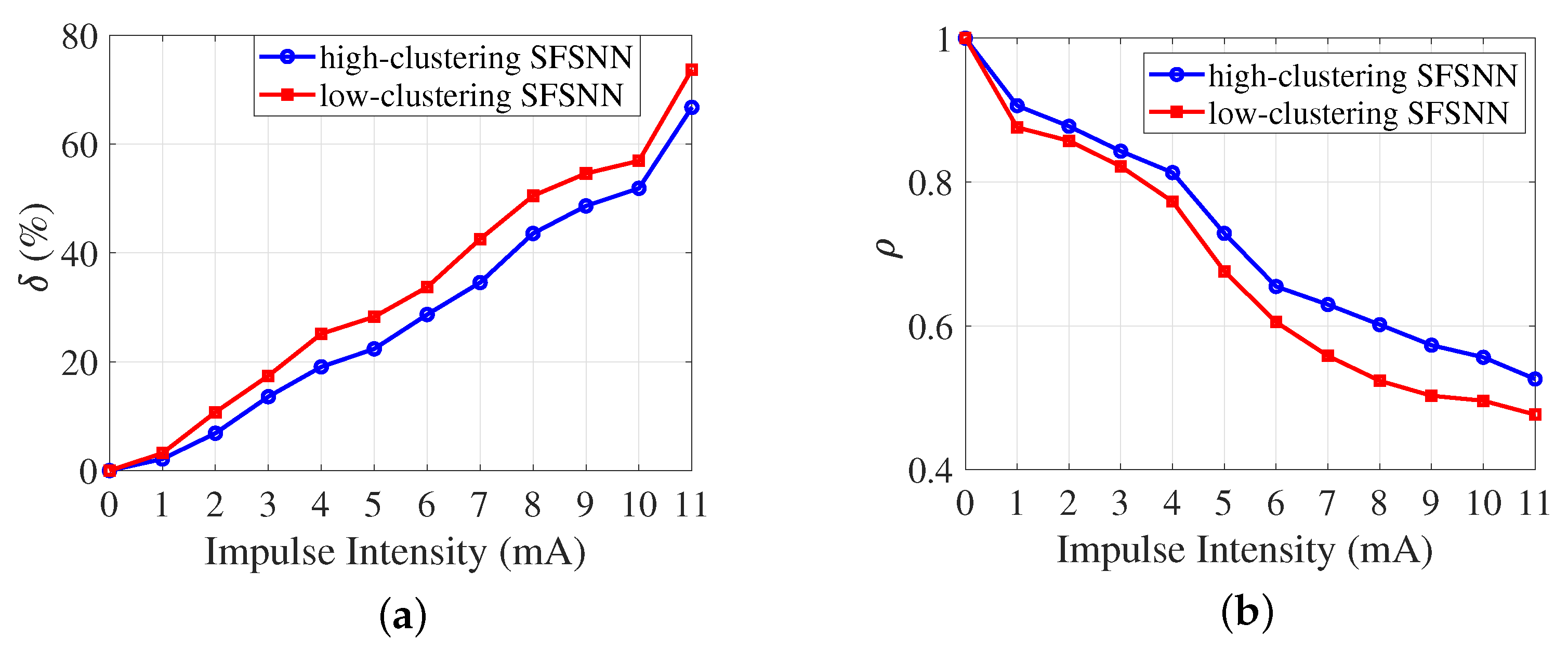
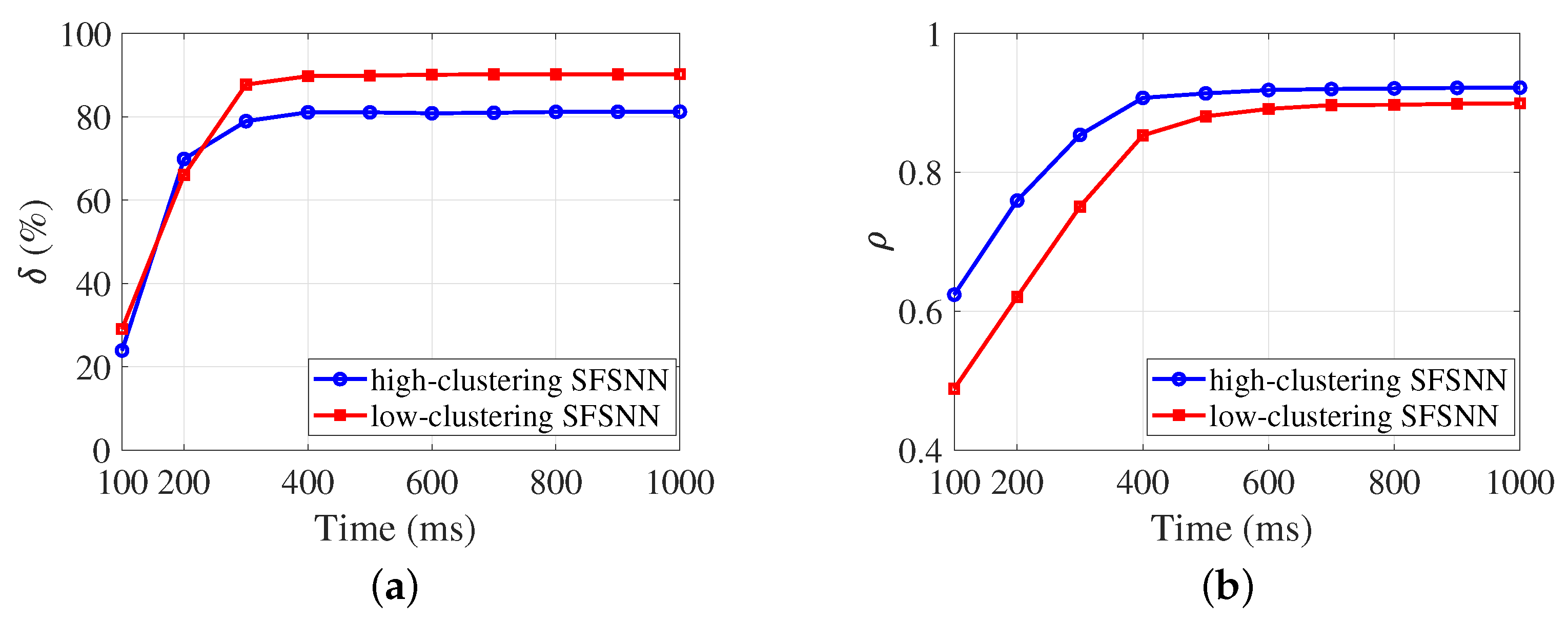
- The relative change rate of the firing rateThe firing rate of a neuron reflects the frequency of action potentials per unit of time in a neuron. The relative change rate of the firing rate can characterize the change degree of the neuronal firing rate before and after disturbance, which is defined as follows:where and are the mean firing rates of the SFSNN before and after disturbance, respectively. The smaller the value of , the smaller the changes in the neuronal firing rate before and after disturbance, and the better the anti-disturbance ability of the SFSNN.
- (2)
- The correlation between membrane potentialThe correlation between membrane potential reflects the degree of similarity between the membrane potentials of the neurons before and after disturbance, which is defined as follows:where and are the mean membrane potential of neurons in the SFSNN before and after disturbance, respectively, and is the simulation time. The larger the value of , the smaller the changes in the neuronal membrane potential before and after disturbance, and the better the anti-disturbance ability of the SFSNN.
3.2. Anti-Disturbance Ability of the SFSNN
3.3. Comparison of Anti-Disturbance Ability
- (1)
- Calculate the difference w between two samples. If w is a positive number, denote it as a positive sign; otherwise, w is a negative number, denoted it as a negative sign.
- (2)
- Calculate the corresponding order by sorting the absolute value of w.
- (3)
- Calculate the sum order of the positive and negative signs w, denoted as and , respectively.
4. Discussion
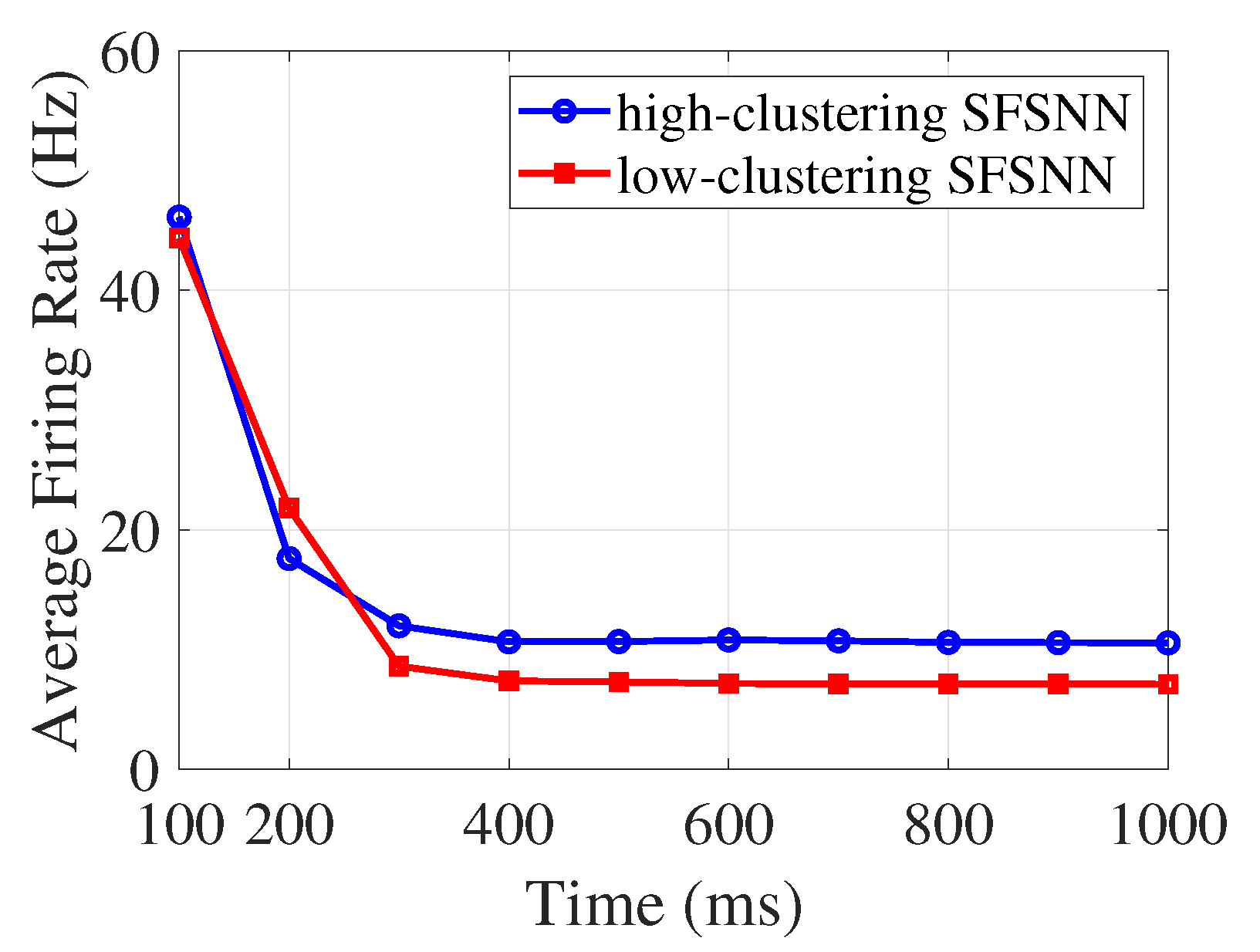
4.1. Firing Rate
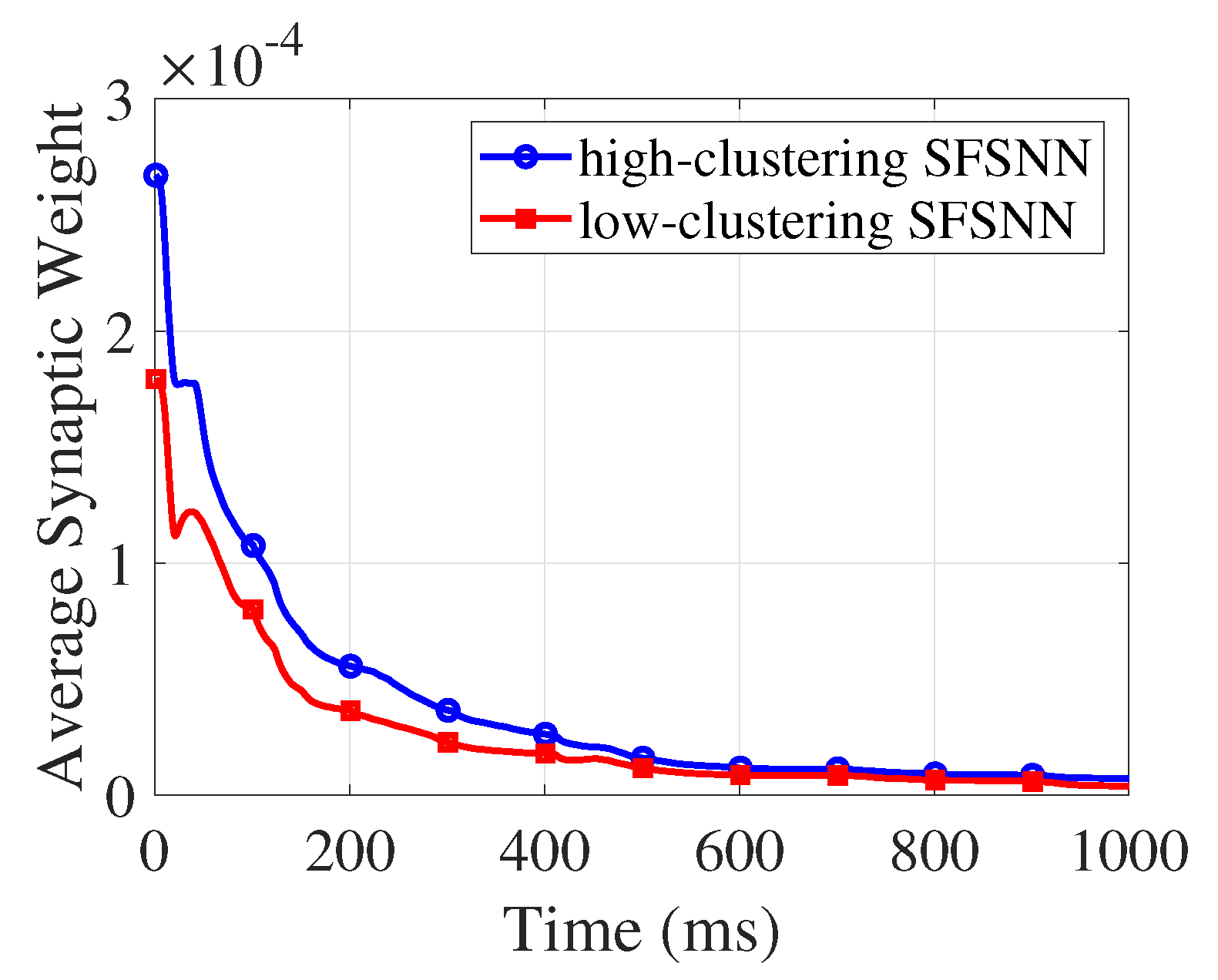
4.2. Synaptic Weight
4.3. Relevance between the Synaptic Plasticity and the Anti-Disturbance Ability
4.3.1. Pearson Correlation Coefficient and t-Test
4.3.2. Evolution Process of the Anti-Disturbance Ability
4.3.3. Relevance Analysis
4.4. Effect of Network Topology on the Anti-Disturbance Ability
4.4.1. Weighted Clustering Coefficient
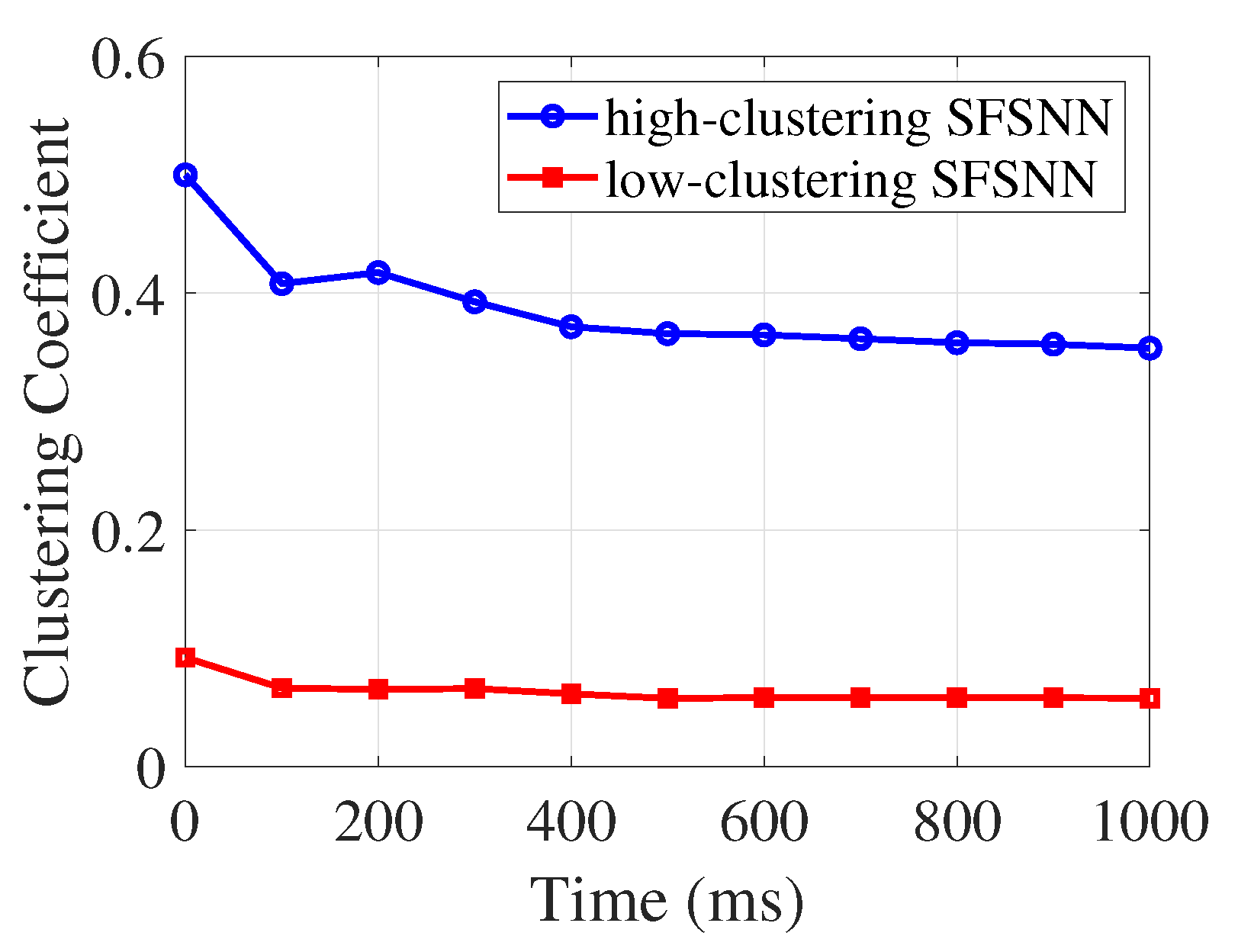
4.4.2. Evolution Process of the Weighted Clustering Coefficient
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Wang, Y.; Zhang, N.; Li, X. An accurate and robust method for spike sorting based on convolutional neural networks. Brain Sci. 2020, 10, 835. [Google Scholar] [CrossRef]
- Zhang, Y.; Lee, T.S.; Li, M.; Tang, S. Convolutional neural network models of V1 responses to complex patterns. J. Comput. Neurosci. 2019, 46, 33–54. [Google Scholar] [CrossRef]
- Maryam, H.; Michael, A.N.; Maryam, Z.; Shapour, J. Determination of anodal tDCS duration threshold for reversal of corticospinal excitability: An investigation for induction of counter-regulatory mechanisms. Brain Stimul. 2020, 13, 832–839. [Google Scholar]
- Yang, X.; Lei, Y.; Wang, M.; Cai, J.; Wang, M.; Huan, Z.; Lin, X. Evaluation of the Effect of the Dynamic Behavior and Topology Co-Learning of Neurons and Synapses on the Small-Sample Learning Ability of Spiking Neural Network. Brain Sci. 2022, 12, 139. [Google Scholar] [CrossRef]
- He, H.; Shang, Y.J.; Yang, X.; Di, Y.Z.; Lin, J.J.; Zhu, Y.M.; Zheng, W.H. Constructing an associative memory system using spiking neural network. Front. Neurosci. 2019, 13, 650. [Google Scholar] [CrossRef]
- Yamazaki, K.; Vo-Ho, V.K.; Bulsara, D.; Le, N. Spiking neural networks and their applications: A Review. Brain Sci. 2022, 12, 863. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Brette, R.; Gerstner, W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 2005, 94, 3637–3642. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1560–1572. [Google Scholar] [CrossRef]
- Sohn, W.J.; Sanger, T.D. Constraint-induced intervention as an emergent phenomenon from synaptic competition in biological systems. J. Comput. Neurosci. 2021, 49, 175–188. [Google Scholar] [CrossRef]
- Leigh, A.J.; Mirhassani, M.; Muscedere, R. An efficient spiking neuron hardware system based on the hardware-oriented modified Izhikevich neuron (HOMIN) model. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3377–3381. [Google Scholar]
- Oliveira, L.; Gomes, R.M.; Santos, B.A.; Borges, H.E. Effects of the parameters on the oscillation frequency of Izhikevich spiking neural networks. Neurocomputing 2019, 337, 251–261. [Google Scholar] [CrossRef]
- Nicola, W.; Campbell, S.A. Bifurcations of large networks of two-dimensional integrate and fire neurons. J. Comput. Neurosci. 2013, 35, 87–108. [Google Scholar] [CrossRef]
- Qu, W.R.; Yuan, B.M.; Liu, J.; Liu, Q.Q.; Zhang, X.; Cui, R.J.; Yang, W.; Li, B.J. Emerging role of AMPA receptor subunit GluA1 in synaptic plasticity: Implications for Alzheimer’s disease. Cell Prolif. 2021, 54, e12959. [Google Scholar] [CrossRef]
- Fernandes, M.; Dobrachinski, F.; Silva, H.B.; Lopes, J.P.; Goncalves, F.Q.; Soares, F.A.; Porciuncula, L.O.; Andrade, G.M.; Cunha, R.A.; Tome, A.R. Neuromodulation and neuroprotective effects of chlorogenic acids in excitatory synapses of mouse hippocampal slices. Sci. Rep. 2021, 11, 10488. [Google Scholar] [CrossRef]
- Mannan, Z.I.; Adhikari, S.P.; Yang, C.J.; Budhathoki, R.K.; Hyongsuk, K.; Chua, L. Memristive imitation of synaptic transmission and plasticity. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3458–3470. [Google Scholar] [CrossRef] [PubMed]
- Dargaei, Z.; Liang, X.; Serranilla, M.; Santos, J.; Woodin, M.A. Alterations in hippocampal inhibitory synaptic transmission in the R6/2 mouse model of Huntington’s disease. Neuroscience 2019, 404, 130–140. [Google Scholar] [CrossRef]
- Zhang, Q.; Dai, Y. A modeling study of spinal motoneuron recruitment regulated by ionic channels during fictive locomotion. J. Comput. Neurosci. 2020, 48, 409–428. [Google Scholar] [CrossRef]
- Pena, R.F.O.; Zaks, M.A.; Roque, A.C. Dynamics of spontaneous activity in random networks with multiple neuron subtypes and synaptic noise. J. Comput. Neurosci. 2018, 45, 1–28. [Google Scholar] [CrossRef]
- Hodkinson, D.J.; Lee, D.; Becerra, L.; Borsook, D. Scale-free amplitude modulation of low-frequency fluctuations in episodic migraine. Pain 2019, 160, 2298–2304. [Google Scholar] [CrossRef]
- Bin, S.; Sun, G.; Chen, C. Analysis of functional brain network based on electroencephalography and complex network. Microsyst. Technol. 2021, 27, 1525–1533. [Google Scholar] [CrossRef]
- Muhammet, U. Firing dynamics in hybrid coupled populations of bistable neurons. Neurocomputing 2019, 367, 328–336. [Google Scholar]
- Zeraati, R.; Priesemann, V.; Levina, A. Self-organization toward criticality by synaptic plasticity. Front. Phys. 2021, 9, 619661. [Google Scholar] [CrossRef]
- Galli, G.; Vadillo, M.A.; Sirota, M.; Feurrad, M.; Medvedevaa, A. A systematic review and meta-analysis of the effects of transcranial direct current stimulation (tDCS) on episodic memory. Brain Stimul. 2019, 12, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Gellner, A.K.; Reis, J.; Fiebich, B.L.; Fritsch, B. Electrified microglia: Impact of direct current stimulation on diverse properties of the most versatile brain cell. Brain Stimul. 2021, 14, 1248–1258. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, B.; Qin, Y.; Cong, M.; Sun, J. Weak electric fields detectability in a noisy neural network. Cogn. Neurodyn. 2017, 11, 81–90. [Google Scholar] [CrossRef]
- Etémé, S.A.; Tabi, C.B.; Mohamadou, A. Firing and synchronization modes in neural network under magnetic stimulation. Commun. Nonlinear Sci 2019, 72, 432–440. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Wang, R.B.; Zhu, F.Y. The energy coding of a structural neural network based on the Hodgkin-Huxley model. Front. Neurosci. 2018, 12, 122. [Google Scholar] [CrossRef]
- Guo, W.Z.; Fouda, M.E.; Eltawil, A.M.; Salama, K.N. Neural coding in spiking neural networks: A comparative study for robust neuromorphic systems. Front. Neurosci. 2021, 15, 638474. [Google Scholar] [CrossRef]
- Barrat, A.; Barthelemy, M.; Vespignani, A. Weighted evolving networks: Coupling topology and weight dynamics. Phys. Rev. Lett. 2004, 92, 228701. [Google Scholar] [CrossRef]
- Wang, D.; Jin, X.Z. On weighted scale-free network model with tunable clustering and congestion. Acta Phys. Sin. 2012, 61, 228901. [Google Scholar] [CrossRef]
- He, B.Y.; Zempel, J.M.; Snyder, A.Z.; Raichle, M.E. The temporal structures and functional significance of scale-free brain activity. Neuron 2010, 66, 353–369. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2020, 3, 919–926. [Google Scholar]
- Vogels, T.P.; Sprekeler, H.; Zenke, F.; Clopath, C.; Gerstner, W. Inhibitory plasticity balances excitation and inhibition in sensory pathways and memory networks. Science 2011, 334, 1569–1573. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
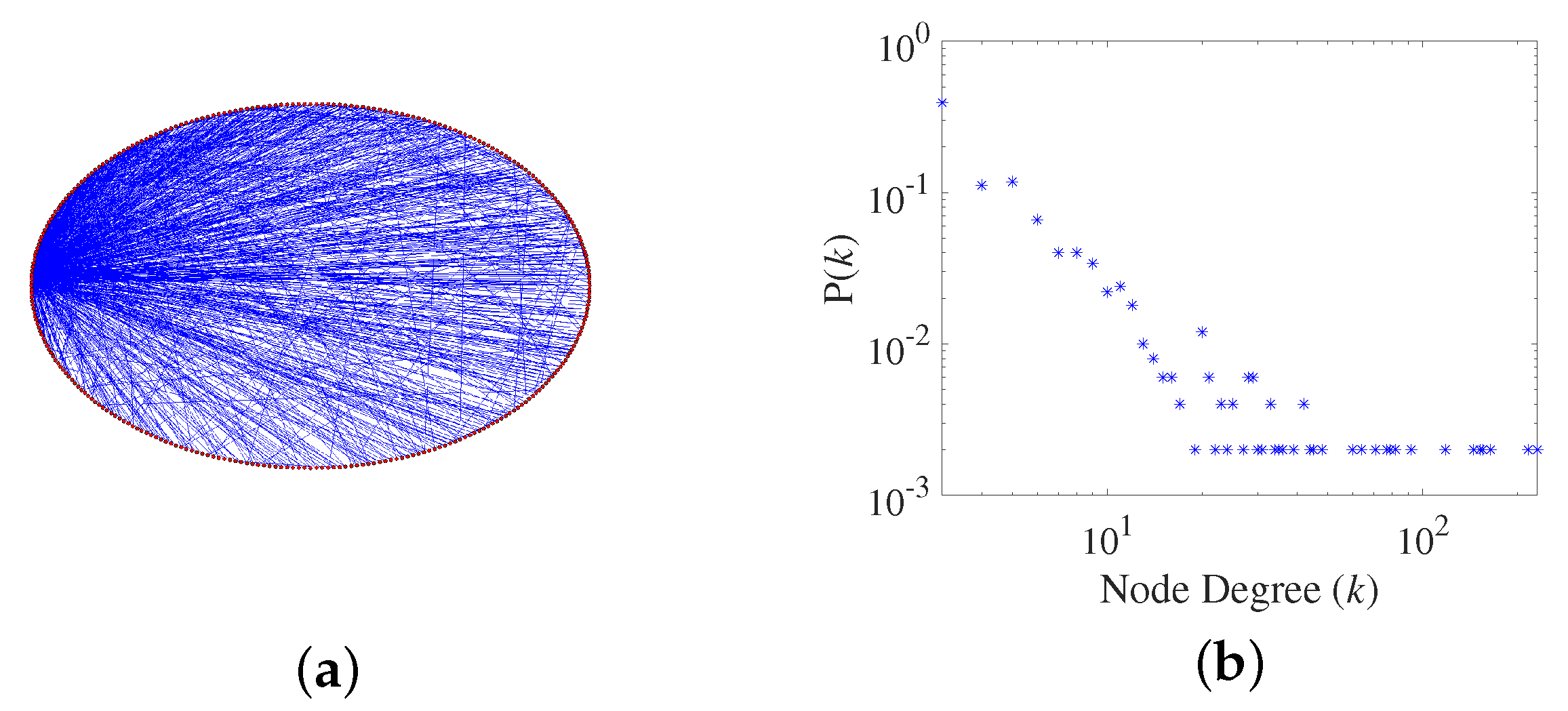



| p | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.55 | 1.82 | 2.15 | 2.41 | 2.51 | 2.76 | 2.86 | 2.87 | 2.98 | 3.18 | |
| C | 0.7028 | 0.6236 | 0.5001 | 0.4707 | 0.4180 | 0.3884 | 0.3133 | 0.2524 | 0.1889 | 0.1643 |
| Types of SFSNN | High-Clustering | Low-Clustering |
|---|---|---|
| −0.915 ** | −0.988 ** | |
| −0.970 ** | −0.963 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Guo, M.; Wu, Y.; Xu, G. Anti-Disturbance of Scale-Free Spiking Neural Network against Impulse Noise. Brain Sci. 2023, 13, 837. https://doi.org/10.3390/brainsci13050837
Guo L, Guo M, Wu Y, Xu G. Anti-Disturbance of Scale-Free Spiking Neural Network against Impulse Noise. Brain Sciences. 2023; 13(5):837. https://doi.org/10.3390/brainsci13050837
Chicago/Turabian StyleGuo, Lei, Minxin Guo, Youxi Wu, and Guizhi Xu. 2023. "Anti-Disturbance of Scale-Free Spiking Neural Network against Impulse Noise" Brain Sciences 13, no. 5: 837. https://doi.org/10.3390/brainsci13050837
APA StyleGuo, L., Guo, M., Wu, Y., & Xu, G. (2023). Anti-Disturbance of Scale-Free Spiking Neural Network against Impulse Noise. Brain Sciences, 13(5), 837. https://doi.org/10.3390/brainsci13050837






