Aeolian Ripple Migration and Associated Creep Transport Rates
Abstract
:1. Introduction
2. Previous Studies
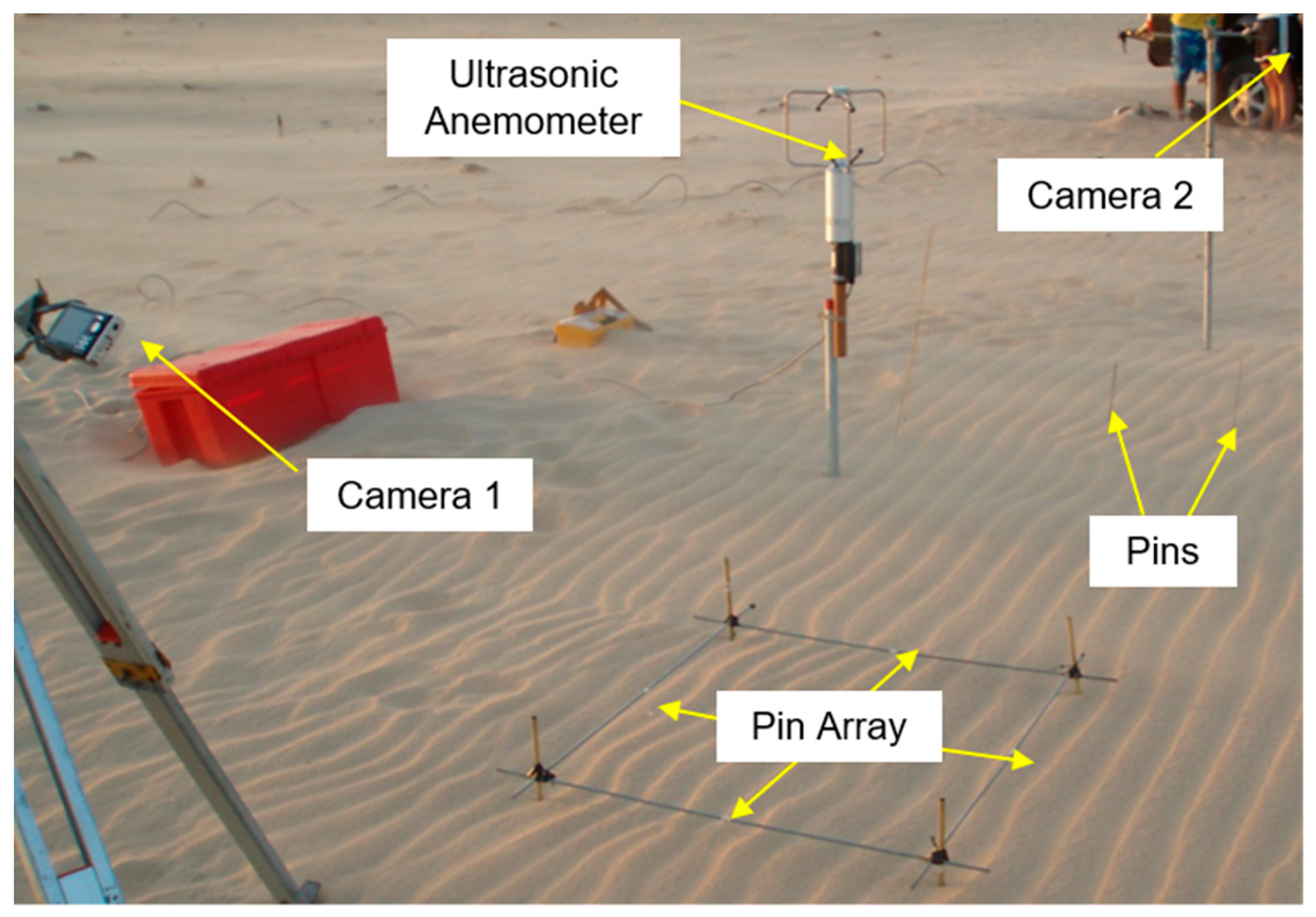
3. Study Sites and Field Methods
4. Data Analysis
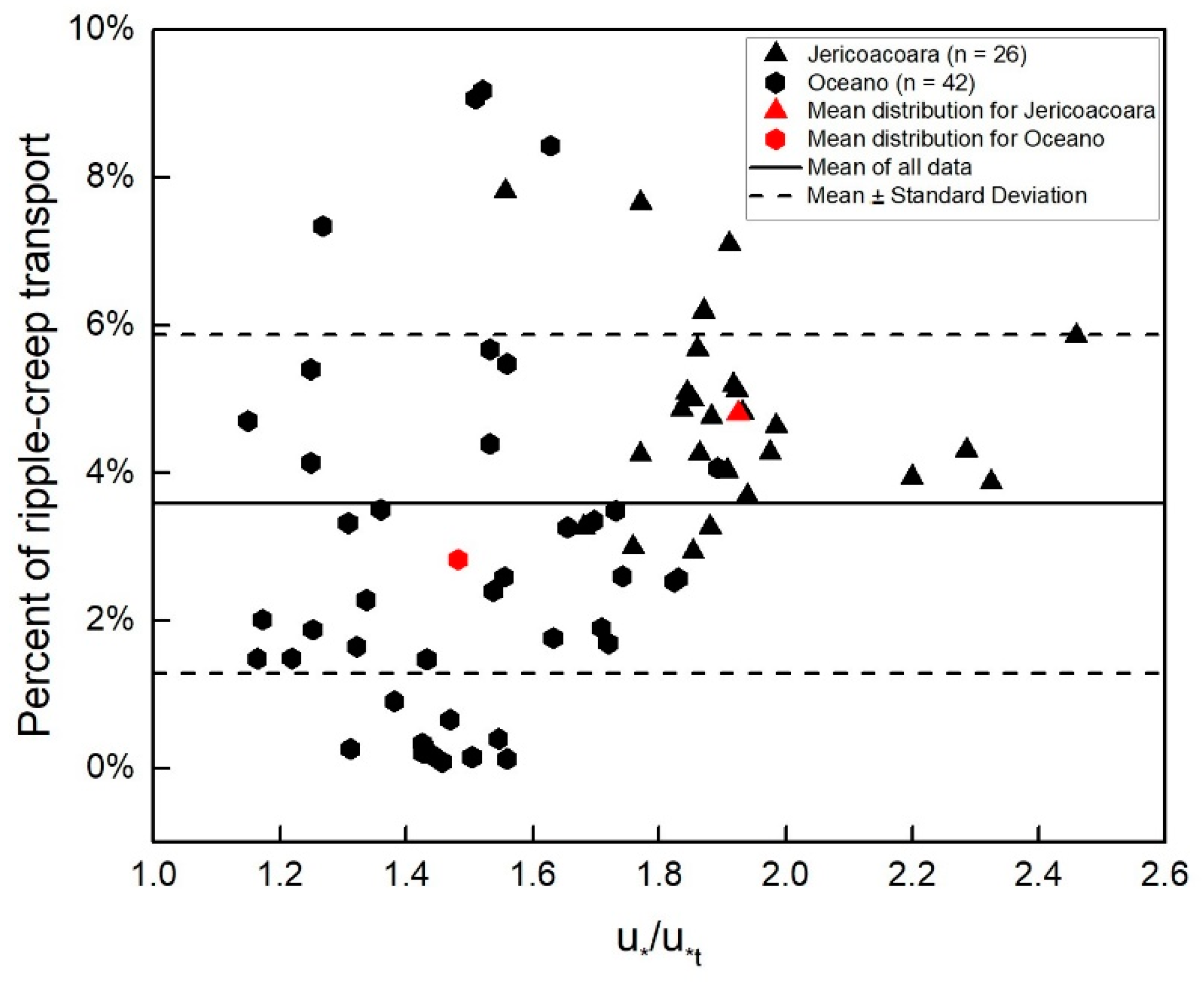
5. Results
6. Discussion
7. Conclusions
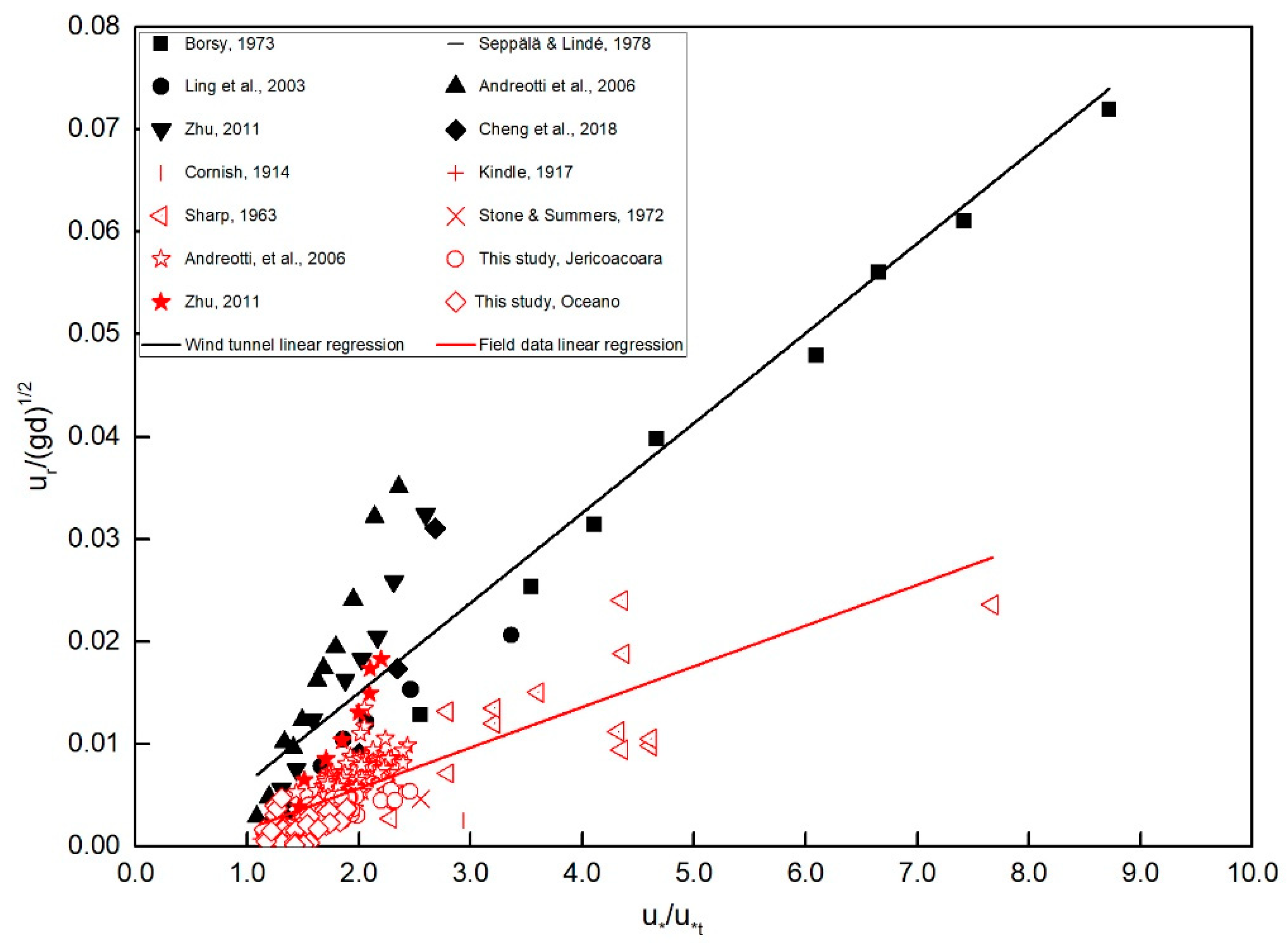
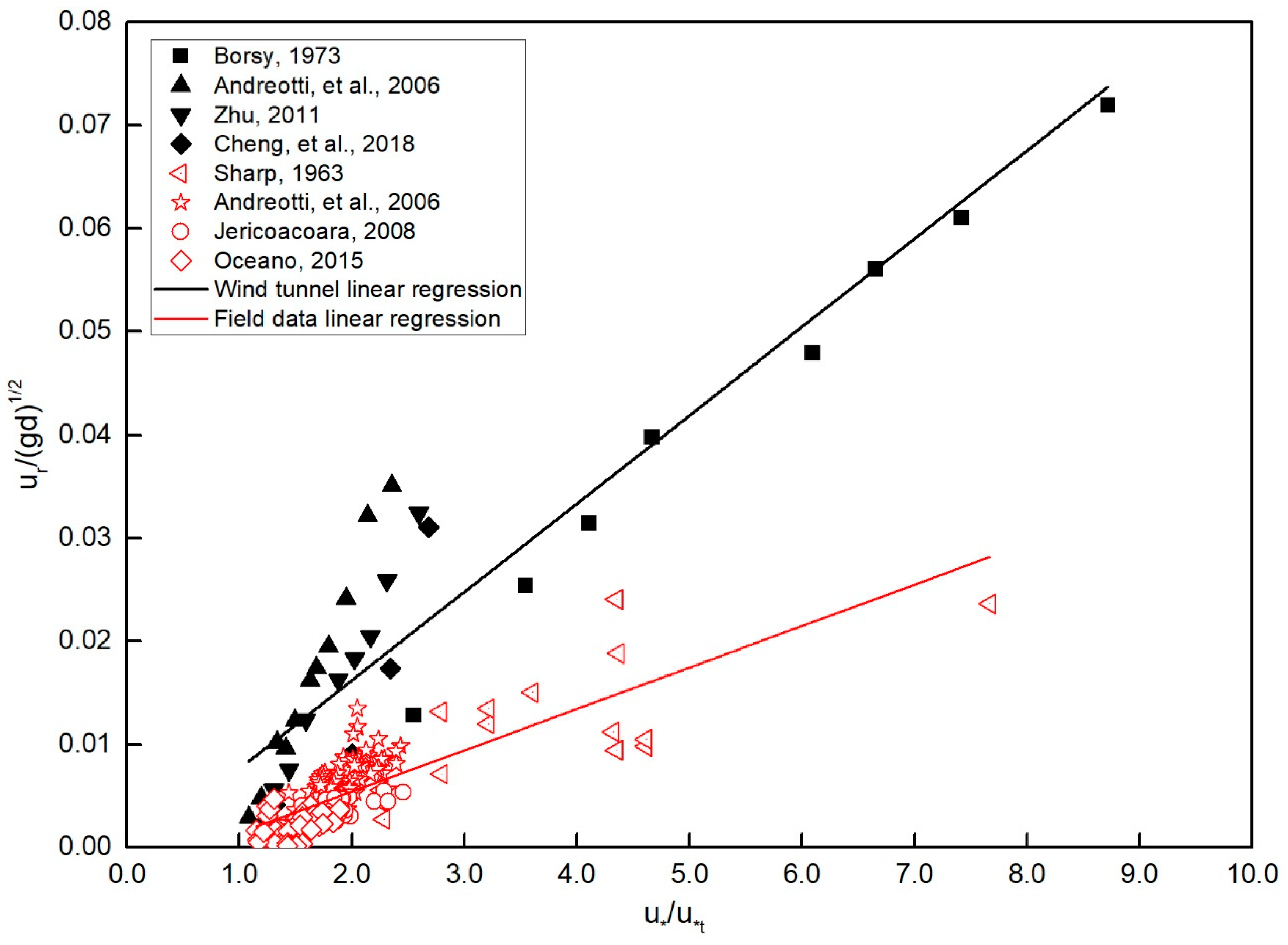
- There is a linear relationship between shear velocity and ripple migration rate. This is evidenced in the regression analyses performed with the dimensionless variable pairs u*/ut and ur/(gd)1/2, and for the dimensional variable pairs and .
- The dimensionless and dimensional migration rates from wind tunnel studies are statistically distinct from those found in field experiments. For a given shear velocity, ripple migration rates in wind tunnels are about two to three times faster than those found in the field.
- The proportion of total sand transport that can be attributed to ripple migration (creep) averages 3.6% in our field studies, comparable to findings in other field studies. We found evidence that increases weakly with shear velocity.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
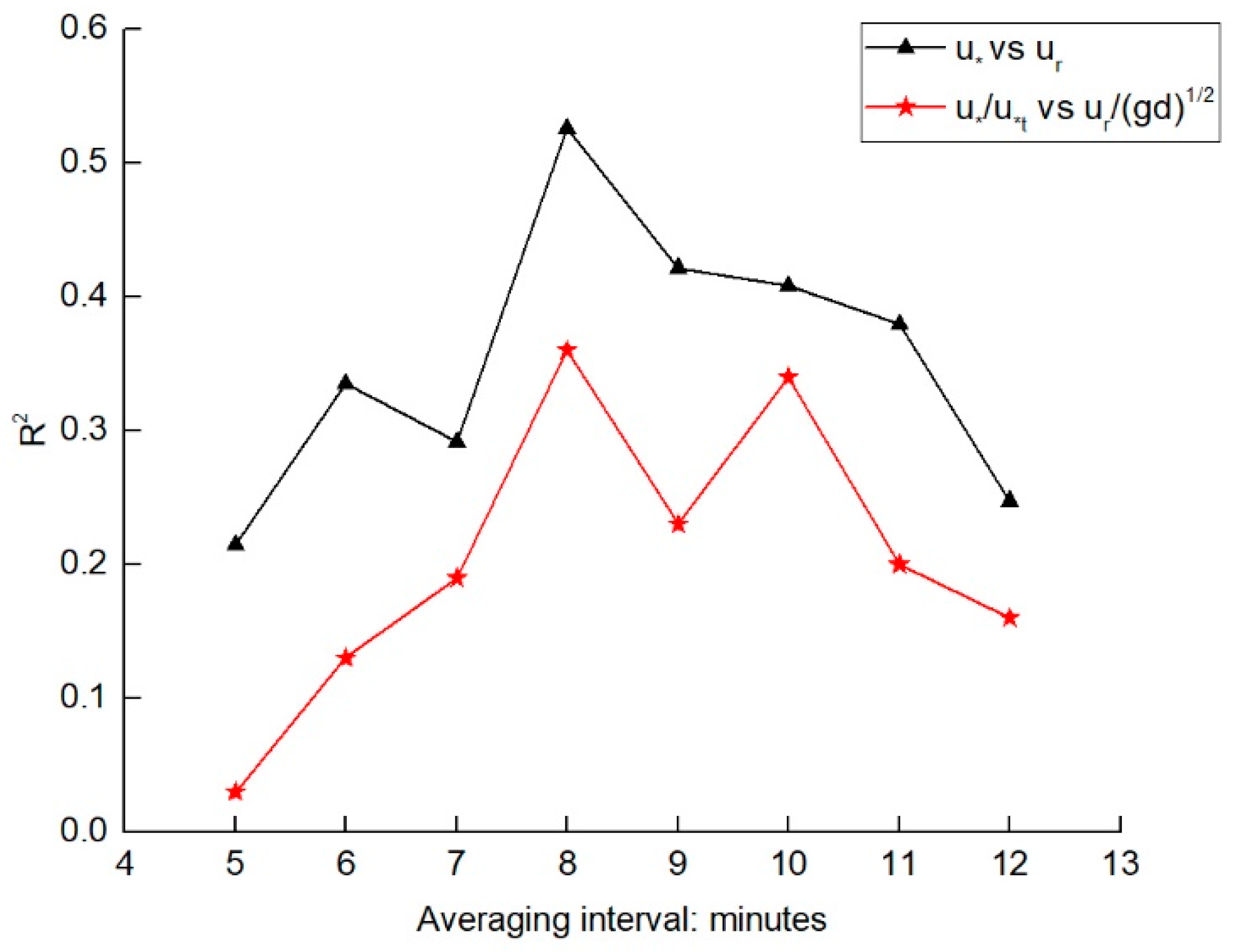
Appendix A. Assessing Ripple Measurement Accuracy and Optimal Averaging Intervals for Linking Ripple Migration Rates with Shear Velocity Estimates
Appendix B. Processing the Laser Distance Sensor (Sick Dt35) Time Series to Resolve Ripple Heights and Migration Rates
References
- Walker, J.D. An Experimental Study of Wind Ripples. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, January 1981. [Google Scholar]
- Ungar, J.E.; Haff, P.K. Steady state saltation in air. Sedimentology 2006, 34, 289–299. [Google Scholar] [CrossRef]
- Mitha, S.; Tran, M.Q.; Werner, B.T.; Haff, P.K. The grain-bed impact process in aeolian saltation. Acta Mech. 1986, 63, 267–278. [Google Scholar] [CrossRef]
- Werner, B.T.; Haff, P.K. The impact process in aeolian saltation: Two-dimensional simulations. Sedimentology 2010, 35, 189–196. [Google Scholar] [CrossRef]
- Welland, M. Sediment transport by wind and water: The pioneering work of ralph bagnold. In Macro-engineering Seawater in Unique Environments; Badescu, V., Cathcart, R.B., Eds.; Springer-Verlag: Berlin, Germany, 2010; pp. 399–429. [Google Scholar]
- Lämmel, M.; Rings, D.; Kroy, K. A two-species continuum model for aeolian sand transport. New J. Phys. 2012, 14, 093037. [Google Scholar] [CrossRef]
- Willets, B.; Rice, M. Collisions in aeolian transport: the saltation/creep link. In Proceedings of The Binghamton Symposium in Geomorphology. Aeolian Geomorphology; Nicking, W.G., Ed.; Allen & Unwin: London, UK, 1986; Volume 18, pp. 1–17. [Google Scholar]
- Manukyan, E.; Prigozhin, L. Formation of aeolian ripples and sand sorting. Phys. Rev. E 2009, 79, 031303. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, D.; Wang, L.; Zhang, Y. Measurement of sand creep on a flat sand bed using a high-speed digital camera. Sedimentology 2009, 56, 1705–1712. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, C.; Zou, X.; Li, J.; He, J.; Liu, B.; Wu, Y.; Kang, L.; Fang, Y. Aeolian creeping mass of different grain sizes over sand beds of varying length. J. Geophys. Res. Earth Surf. 2015, 120, 1404–1417. [Google Scholar] [CrossRef] [Green Version]
- Brookfield, M.E. The origin of bounding surfaces in ancient aeolian sandstones. Sedimentology 1977, 24, 303–332. [Google Scholar] [CrossRef]
- Lapotre, M.; Ewing, R.; Lamb, M.; Fischer, W.; Grotzinger, J.; Rubin, D.; Lewis, K.; Ballard, M.; Day, M.; Gupta, S. Large wind ripples on Mars: A record of atmospheric evolution. Science 2016, 353, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Wessely, J. Der Europaische Flugsand Und Seine Kultur: Besprochen Im Hinblike Auf Ungarn Und Die Banater Wuste Insbesondere; Faesy & Frick: Wien, Österreich-Ungarn, 1873; pp. 48–72. [Google Scholar]
- Sokolow, N.A. Die Dünen: Bildung, Entwickelung und innerer Bau; Julius Springer: Berlin, Germany, 1894. [Google Scholar]
- Cornish, V. On the formation of sand-dunes. Geogr. J. 1897, 9, 278–302. [Google Scholar] [CrossRef]
- Joly, J. Formation of sand-ripples. Sci. Proc. R. Dublin Soc. 1904, 10, 328–330. [Google Scholar]
- Ayrton, H.; Ayrton, W.E. The origin and growth of ripple-mark. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1910, 84, 285–310. [Google Scholar] [CrossRef] [Green Version]
- Free, E.E.; Stuntz, S.C. The Movement of Soil Material by the Wind; US Government Printing Office: Washington, DC, USA, 1911. [Google Scholar]
- King, W.H. The nature and formation of sand ripples and dunes. Geogr. J. 1916, 189–207. [Google Scholar] [CrossRef]
- Yizhaq, H.; Isenberg, O.; Wenkart, R.; Tsoar, H.; Karnieli, A. Morphology and dynamics of aeolian mega-ripples in Nahal Kasuy, southern Israel. Israel J. Earth Sci. 2009, 57, 149–165. [Google Scholar] [CrossRef]
- Lämmel, M.; Meiwald, A.; Yizhaq, H.; Tsoar, H.; Katra, I.; Kroy, K. Aeolian sand sorting and megaripple formation. Nat. Phys. 2018, 14, 22–30. [Google Scholar] [CrossRef]
- Yizhaq, H.; Bel, G.; Silvestro, S.; Elperin, T.; Kok, J.F.; Cardinale, M.; Provenzale, A.; Katra, I. The origin of the transverse instability of aeolian megaripples. Earth Planet. Sci. Lett. 2019, 512, 59–70. [Google Scholar] [CrossRef]
- Balme, M.; Berman, D.C.; Bourke, M.C.; Zimbelman, J.R. Transverse Aeolian Ridges (TARs) on Mars. Geomorphology 2008, 101, 703–720. [Google Scholar] [CrossRef] [Green Version]
- Foroutan, M.; Zimbelman, J.R. Mega-ripples in Iran: A new analog for transverse aeolian ridges on Mars. Icarus 2016, 274, 99–105. [Google Scholar] [CrossRef]
- Geissler, P.E. The birth and death of transverse aeolian ridges on Mars. J. Geophys. Res. Planets 2014, 119, 2583–2599. [Google Scholar] [CrossRef]
- Sharp, R.P. Wind ripples. J. Geol. 1963, 71, 617–636. [Google Scholar] [CrossRef]
- Wilson, I.G. Aeolian bedforms—their development and origins. Sedimentology 1972, 19, 173–210. [Google Scholar] [CrossRef]
- Seppälä, M.; Lindé, K. Wind tunnel studies of ripple formation. Geogr. Ann. Ser. A Phys. Geogr. 1978, 60, 29–42. [Google Scholar] [CrossRef]
- Durán, O.; Claudin, P.; Andreotti, B. Direct numerical simulations of aeolian sand ripples. Proc. Natl. Acad. Sci. 2014, 111, 15665–15668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siminovich, A.; Elperin, T.; Katra, I.; Kok, J.; Sullivan, R.; Silvestro, S.; Yizhaq, H. Numerical study of shear stress distribution over sand ripples under terrestrial and Martian conditions. J. Geophys. Res. Planets 2019, 124, 175–185. [Google Scholar] [CrossRef]
- Anderson, R.S. A theoretical model for aeolian impact ripples. Sedimentology 1987, 34, 943–956. [Google Scholar] [CrossRef]
- Valance, A.; Rioual, F. A nonlinear model for aeolian sand ripples. Eur. Phys. J. B-Condensed Matter Complex Syst. 1999, 10, 543–548. [Google Scholar] [CrossRef]
- Pelletier, J.D. Controls on the height and spacing of eolian ripples and transverse dunes: A numerical modeling investigation. Geomorphology 2009, 105, 322–333. [Google Scholar] [CrossRef]
- Qian, G.; Dong, Z.; Zhang, Z.; Luo, W.; Lu, J. Granule ripples in the Kumtagh Desert, China: Morphology, grain size and influencing factors. Sedimentology 2012, 59, 1888–1901. [Google Scholar] [CrossRef]
- Ewing, R.C.; Mcdonald, G.D.; Hayes, A.G. Geomorphology Multi-spatial analysis of aeolian dune-field patterns. Geomorphology 2015, 240, 44–53. [Google Scholar] [CrossRef]
- Field, J.P.; Pelletier, J.D. Controls on the aerodynamic roughness length and the grain-size dependence of aeolian sediment transport. Earth Surf. Process. Landf. 2018, 43, 2616–2626. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, J.; Huang, N. A theoretical model for aeolian polydisperse-sand ripples. Geomorphology 2019, 335, 28–36. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, C.; Li, J.; Liu, B.; Zheng, Z.; Zou, X.; Kang, L.; Fang, Y. Experimental study of aeolian sand ripples in a wind tunnel. Earth Surf. Process. Landf. 2018, 43, 312–321. [Google Scholar] [CrossRef]
- Hunter, R.E. Basic types of stratification in small eolian dunes. Sedimentology 1977, 24, 361–387. [Google Scholar] [CrossRef]
- Fryberger, S.G.; Schenk, C. Wind sedimentation tunnel experiments on the origins of aeolian strata. Sedimentology 1981, 28, 805–821. [Google Scholar] [CrossRef]
- Bristow, C.; Mountney, N. Aeolian stratigraphy. In Treatise on Geomorphology; Shroder, J., Lancaster, N., Sherman, D.J., Baas, A.C.W., Eds.; Academic Press: San Diego, CA, USA, 2013; Volume 11, pp. 246–268. [Google Scholar]
- Sullivan, R.; Banfield, D.; Bell III, J.F.; Calvin, W.; Fike, D.; Golombek, M.; Greeley, R.; Grotzinger, J.; Herkenhoff, K.; Jerolmack, D. Aeolian processes at the Mars exploration rover Meridiani Planum landing site. Nature 2005, 436, 58. [Google Scholar] [CrossRef] [PubMed]
- Bridges, N.; Geissler, P.; Silvestro, S.; Banks, M. Bedform migration on Mars: Current results and future plans. Aeolian Res. 2013, 9, 133–151. [Google Scholar] [CrossRef]
- Weitz, C.M.; Sullivan, R.J.; Lapotre, M.G.; Rowland, S.K.; Grant, J.A.; Baker, M.; Yingst, R.A. Sand grain sizes and shapes in eolian bedforms at Gale Crater, Mars. Geophys. Res. Lett. 2018, 9471–9479. [Google Scholar] [CrossRef]
- Lapotre, M.; Ewing, R.; Weitz, C.; Lewis, K.; Lamb, M.; Ehlmann, B.; Rubin, D. Morphologic diversity of Martian ripples: Implications for large-ripple formation. Geophys. Res. Lett. 2018, 45, 10229–10239. [Google Scholar] [CrossRef]
- Vinent Durán, O.; Andreotti, B.; Claudin, P.; Winter, C. A unified model of ripples and dunes in water and planetary environments. Nat. Geosci. 2019, 12, 345. [Google Scholar] [CrossRef]
- Evier, E.L.; Landry, W.; Werner, B.T. Computer simulations of self-organized wind ripple pattern. Physica D Nonlinear Phenom. 1994, 77, 238–260. [Google Scholar]
- Jerolmack, D.J.; Mohrig, D.; Grotzinger, J.P.; Fike, D.A.; Watters, W.A. Spatial grain size sorting in eolian ripples and estimation of wind conditions on planetary surfaces: Application to Meridiani Planum, Mars. J. Geophys. Res. Planets 2006, 111, 1–14. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Valdez, A. Variable wind ripple migration at Great Sand Dunes National Park and Preserve, observed by timelapse imaging. Geomorphology 2011, 133, 1–10. [Google Scholar] [CrossRef]
- Bridges, N.T.; Ayoub, F.; Avouac, J.-p.; Leprince, S.; Lucas, A.; Mattson, S. Earth-like sand fluxes on Mars. Nature 2012, 485, 339–342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lorenz, R.D. Observations of wind ripple migration on an Egyptian seif dune using an inexpensive digital timelapse camera. Aeolian Res. 2011, 3, 229–234. [Google Scholar] [CrossRef]
- Bagnold, R. The physics of blown sand and desert dunes: New York. William Morrow Co. 1941, 1, 91–96. [Google Scholar]
- Louge, M.Y.; Valance, A.; Ould el-Moctar, A.; Dupont, P. Packing variations on a ripple of nearly monodisperse dry sand. J. Geophys. Res. Earth Surf. 2010, 115, F02001. [Google Scholar] [CrossRef]
- Wang, Z.T.; Zheng, X.J. Theoretical prediction of creep flux in aeolian sand transport. Powder Technol. 2004, 139, 123–128. [Google Scholar] [CrossRef]
- Cheng, H.; Zou, X.; Liu, C.; He, J.; Wu, Y. Transport mass of creeping sand grains and their movement velocities. J. Geophys. Res. Atmos. 2013, 118, 6374–6382. [Google Scholar]
- Bagnold, R.A. The size-garding of sand by wind. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1937, 163, 250–264. [Google Scholar]
- Bagnold, R.A. The measurement of sand storms. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1938, 167, 282–291. [Google Scholar] [Green Version]
- Sherman, D.J.; Zhang, P.; Martin, R.L.; Ellis, J.T.; Kok, J.F.; Farrell, E.J.; Li, B. Data for Aeolian Ripple Migration and Associated Creep Transport Rates (Dataset). Zenodo, 2019. Available online: https://doi.org/10.5281/zenodo.3378825 (accessed on 4 September 2019).
- Sherman, D.J.; Farrell, E.J. Aerodynamic roughness lengths over movable beds: Comparison of wind tunnel and field data. J. Geophys. Res. Earth Surf. 2008, 113, F02S08. [Google Scholar] [CrossRef]
- Bagnold, R.A. The movement of desert sand. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1936, 157, 594–620. [Google Scholar] [CrossRef]
- Kindle, E.M. Recent and fossil ripple-mark; Canada Department of Mines, Geological Survey: Ottawa, ON, Canada, 1917; pp. 9–29. [Google Scholar]
- Strickland, W.W. Notes and Observations on Forms of Sand; Smithson, R.H., Ed.; Blanchard: London, UK, 1915; pp. 16–20. [Google Scholar]
- Wentworth, C.K. A scale of grade and class terms for clastic sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Stone, R.O.; Summers, H.J. Study of Subaqueous and Subaerial Sand Ripples; University of Southern California: Los Angeles, CA, USA, 1972. [Google Scholar]
- Borsy, Z. A homokfodrok. Fldrajzi rtesito 1973, 22, 109–115. [Google Scholar]
- Ling, Y.; Qu, J.; Li, C. Study on sand ripple movement with close shoot method. J. Desert Res. 2003, 23, 118–120. [Google Scholar]
- Ling, Y.; Wu, Z.; Liu, S. A wind tunnel simulation of aeolian sand ripple formation. Acta Geogr. Sin. 1998, 53, 527–534. [Google Scholar]
- Andreotti, B.; Claudin, P.; Pouliquen, O. Aeolian sand ripples: experimental study of fully developed states. Phys. Rev. Lett. 2006, 96, 028001. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W. Investigations on the Formation and Evolution of Aeolian Sand Ripples. Ph.D. Thesis, Lanzhou University, Lanzhou, China, June 2011. [Google Scholar]
- Farrell, E.; Sherman, D.; Ellis, J.; Li, B. Vertical distribution of grain size for wind blown sand. Aeolian Res. 2012, 7, 51–61. [Google Scholar] [CrossRef]
- Barrineau, C.P.; Ellis, J. Sediment transport and wind flow around hummocks. Aeolian Res. 2013, 8, 19–27. [Google Scholar] [CrossRef]
- Jimenez, J.A.; Maia, L.P.; Serra, J.; Morais, J. Aeolian dune migration along the Ceara coast, north-eastern Brazil. Sedimentology 1999, 46, 689–701. [Google Scholar] [CrossRef]
- Maia, L.; Freire, G.; Lacerda, L. Accelerated dune migration and aeolian transport during El Nino events along the NE Brazilian coast. J. Coast. Res. 2005, 1121–1126. [Google Scholar] [CrossRef]
- Pease, P.; Lecce, S.; Gares, P.; Lange, M. Suggestions for low-cost equipment for physical geography II: field equipment. J. Geogr. 2002, 105, 199–206. [Google Scholar] [CrossRef]
- Sherman, D.J.; Swann, C.; Barron, J.D. A high-efficiency, low-cost aeolian sand trap. Aeolian Res. 2014, 13, 31–34. [Google Scholar] [CrossRef]
- Martin, R.L.; Kok, J.F.; Hugenholtz, C.H.; Barchyn, T.E.; Chamecki, M.; Ellis, J.T. High-frequency measurements of aeolian saltation flux: Field-based methodology and applications. Aeolian Res. 2018, 30, 97–114. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.L.; Kok, J.F. Wind-invariant saltation heights imply linear scaling of aeolian saltation flux with shear stress. Sci. Adv. 2017, 3, e1602569. [Google Scholar] [CrossRef] [PubMed]
- Fryrear, D.W. A field dust sampler. J. Soil Water Conserv. 1986, 41, 117–120. [Google Scholar]
- Martin, R.L.; Kok, J.F. Aeolian saltation fieldwork 30-minute wind and saltation values (Dataset). Zenodo, 2017. Available online: https://doi.org/10.5281/zenodo.291798 (accessed on 4 September 2019).
- Martin, R.L.; Kok, J.F. Distinct thresholds for the initiation and cessation of aeolian saltation from field measurements. J. Geophys. Res. Earth Surf. 2018, 123, 1546–1565. [Google Scholar] [CrossRef]
- Stout, J.; Zobeck, T. Intermittent saltation. Sedimentology 1997, 44, 959–970. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.S.; Baas, A.C.W. Streamline correction for the analysis of boundary layer turbulence. Geomorphology 2012, 171, 69–82. [Google Scholar] [CrossRef]
- Blott, S.J.; Pye, K. GRADISTAT: a grain size distribution and statistics package for the analysis of unconsolidated sediments. Earth Surf. Process. Landf. 2001, 26, 1237–1248. [Google Scholar] [CrossRef]
- Martin, R.L.; Jerolmack, D.J. Origin of hysteresis in bed form response to unsteady flows. Water Resour. Res. 2013, 49, 1314–1333. [Google Scholar] [CrossRef] [Green Version]
- Sherman, D.J. An equilibrium relationship for shear velocity and apparent roughness lenght in aeolian saltation. Geomorphology 1992, 5, 419–431. [Google Scholar] [CrossRef]
- Sterk, G.; Jacobs, A.; Van Boxel, J. The effect of turbulent flow structures on saltation sand transport in the atmospheric boundary layer. J. Br. Geomorphol. Group 1998, 23, 877–887. [Google Scholar] [CrossRef]
- Baas, A.C. Wavelet power spectra of aeolian sand transport by boundary layer turbulence. Geophys. Res. Lett. 2006, 33, L05403. [Google Scholar] [CrossRef]
- Spies, P.-J.; McEwan, I.K.; Butterfield, G.R. On wind velocity profile measurements taken in wind tunnels with saltating grains. Sedimentology 1995, 42, 515–521. [Google Scholar] [CrossRef]
- Butterfield, G.R. Near-bed mass flux profiles in aeolian sand transport: high-resolution measurements in a wind tunnel. J. Br. Geomorphol. Res. Group 1999, 24, 393–412. [Google Scholar] [CrossRef]
- Bauer, B.; Houser, C.; Nickling, W. Analysis of velocity profile measurements from wind-tunnel experiments with saltation. Geomorphology 2004, 59, 81–98. [Google Scholar] [CrossRef]
- Mikami, M.; Yamada, Y.; Ishizuka, M.; Ishimaru, T.; Gao, W.; Zeng, F. Measurement of saltation process over gobi and sand dunes in the Taklimakan desert, China, with newly developed sand particle counter. J. Geophys. Res. Atmos. 2005, 110, D18S02. [Google Scholar] [CrossRef]
- Creyssels, M.; Dupont, P.; El Moctar, A.O.; Valance, A.; Cantat, I.; Jenkins, J.T.; Pasini, J.M.; Rasmussen, K.R. Saltating particles in a turbulent boundary layer: experiment and theory. J. Fluid Mech. 2009, 625, 47–74. [Google Scholar] [CrossRef] [Green Version]
- McKenna Neuman, C.; Bédard, O. A wind tunnel study of flow structure adjustment on deformable sand beds containing a surface-mounted obstacle. J. Geophys. Res. Earth Surf. 2015, 120, 1824–1840. [Google Scholar] [CrossRef]
- Pähtz, T.; Valyrakis, M.; Zhao, X.-H.; Li, Z.-S. The critical role of the boundary layer thickness for the initiation of aeolian sediment transport. Geosciences 2018, 8, 314. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, X.; Wang, X.; Li, F.; Zhao, A. Experimental investigation of the velocity of a sand cloud blowing over a sandy surface. Earth Surf. Process. Landf. 2004, 29, 343–358. [Google Scholar] [CrossRef]
- Dong, Z.; Qian, G.; Luo, W.; Wang, H. Analysis of the mass flux profiles of an aeolian saltating cloud. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
- Liu, X.; Dong, Z. Experimental investigation of the concentration profile of a blowing sand cloud. Geomorphology 2004, 60, 371–381. [Google Scholar] [CrossRef]
- Rasmussen, K.R.; Valance, A.; Merrison, J. Laboratory studies of aeolian sediment transport processes on planetary surfaces. Geomorphology 2015, 244, 74–94. [Google Scholar] [CrossRef]
- Shao, Y.; Raupach, M. The overshoot and equilibration of saltation. J. Geophys. Res. Atmos. 1992, 97, 20559–20564. [Google Scholar] [CrossRef]
- Liu, B.; Qu, J.; Zhang, W.; Tan, L.; Gao, Y. Numerical evaluation of the scale problem on the wind flow of a windbreak. Sci. Rep. 2014, 4, 6619. [Google Scholar] [CrossRef]
- Farrell, E. Characterizing vertical mass flux profiles in aeolian saltation systems. PhD Thesis, Texas A & M University, College Station, TX, USA, May 2012. [Google Scholar]
- Mckenna Neuman, C.; Maljaars, M. Wind tunnel measurement of boundary-layer response to sediment transport. Bound. Layer Meteorol. 1997, 84, 67–83. [Google Scholar] [CrossRef]
- Chepil, W. Dynamics of wind erosion: II. Initiation of soil movement. Soil Sci. 1945, 60, 397. [Google Scholar] [CrossRef]
- Horikawa, K.; Shen, H.W. Sand Movement by Wind Action: on the Characteristics of Sand Traps; USACE, Beach Erosion Board: Denver, CO, USA, 1960. [Google Scholar]
- Ishihara, T.; Iwagaki, Y. Studies on the counter-measures to prevent ajiro-harbour from filling up with sand-drift. Bull. Comm. Count. -Meas. Sand Drift, Tot tori Prefect. 1950, 2, 1–32. [Google Scholar]
- Dong, Z.; Liu, X.; Wang, H.; Zhao, A.; Wang, X. The flux profile of a blowing sand cloud: A wind tunnel investigation. Geomorphology 2002, 49, 219–230. [Google Scholar] [CrossRef]
- Nickling, W. Eolian sediment transport during dust storms: Slims River valley, Yukon Territory. Can. J. Earth Sci. 1978, 15, 1069–1084. [Google Scholar] [CrossRef]
- Kang, Y.; He, Q.; Yang, X.; Yang, F.; Ali, M.; Huo, W. Research on saltation and creeping laws of wind-blown currents based on field observations. J. Arid Land Resour. Environ. 2017, 31, 119–127. [Google Scholar]
- Yizhaq, H.; Kok, J.F.; Katra, I. Basaltic sand ripples at Eagle Crater as indirect evidence for the hysteresis effect in martian saltation. Icarus 2014, 230, 143–150. [Google Scholar] [CrossRef]
- Kok, J.F.; Renno, N.O. A comprehensive numerical model of steady state saltation (COMSALT). J. Geophys. Res. Atmos. 2009, 114, D17204. [Google Scholar] [CrossRef]
- Runyon, K.D.; Bridges, N.T.; Newman, C.E. Martian sand sheet characterization and implications for formation: A case study. Aeolian Res. 2017, 29, 1–11. [Google Scholar] [CrossRef]
- Van Boxel, J.; Sterk, G.; Arens, S. Sonic anemometers in aeolian sediment transport research. Geomorphology 2004, 59, 131–147. [Google Scholar] [CrossRef] [Green Version]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sherman, D.J.; Zhang, P.; Martin, R.L.; Ellis, J.T.; Kok, J.F.; Farrell, E.J.; Li, B. Aeolian Ripple Migration and Associated Creep Transport Rates. Geosciences 2019, 9, 389. https://doi.org/10.3390/geosciences9090389
Sherman DJ, Zhang P, Martin RL, Ellis JT, Kok JF, Farrell EJ, Li B. Aeolian Ripple Migration and Associated Creep Transport Rates. Geosciences. 2019; 9(9):389. https://doi.org/10.3390/geosciences9090389
Chicago/Turabian StyleSherman, Douglas J., Pei Zhang, Raleigh L. Martin, Jean T. Ellis, Jasper F. Kok, Eugene J. Farrell, and Bailiang Li. 2019. "Aeolian Ripple Migration and Associated Creep Transport Rates" Geosciences 9, no. 9: 389. https://doi.org/10.3390/geosciences9090389
APA StyleSherman, D. J., Zhang, P., Martin, R. L., Ellis, J. T., Kok, J. F., Farrell, E. J., & Li, B. (2019). Aeolian Ripple Migration and Associated Creep Transport Rates. Geosciences, 9(9), 389. https://doi.org/10.3390/geosciences9090389





