Developing an Optimal Spatial Predictive Model for Seabed Sand Content Using Machine Learning, Geostatistics, and Their Hybrid Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region and Sediment Samples
2.2. Predictive Variables
- Two location variables: latitude (lat) and longitude (long),
- Bathymetry (bathy),
- Twenty-seven backscatter (bs) variables (bs10 to bs36): a diffused reflection of acoustic energy due to scattering process back to the direction from which it was generated, measured as the ratio of the acoustic energy sent to a seabed to that returned from the seabed, normalized to incidence angles between 10° and 36°,
- Seventeen backscatter-derived variables from bs25 based on object and spatial windows (i.e., window size of 30, 50, and 70 m) approach:
- bs_o,
- homogeneity (bs_homo_o, bs_homo3, bs_homo5, and bs_homo7),
- entropy (bs_entro_o, bs_entro3, bs_entro5, and bs_entro7),
- local Moran I (bs_lmi_o, bs_lmi3, bs_lmi5, and bs_lmi7), and
- variance (bs_var_o, bs_var3, bs_var5, and bs_var7).
- Twenty-nine derived variables from bathy using object and spatial windows (i.e., window size of 30, 50, and 70 m) approach:
- bathy_o,
- lmi_o, lmi3, lmi5, lmi7,
- topographic position index (tpi_o, tpi3, tpi5, and tpi7),
- seabed slope (slope_o, slope3, slope5, and slope7),
- planar curvature (plan_cur_o, plan_cur3, plan_cur5, and plan_cur7),
- profile curvature (prof_cur_o, prof_cur3, prof_cur5, and prof_cur7),
- topographic relief (relief_o, relief3, relief5, and relief7), and
- seabed rugosity (rugosity_o, rugosity3, rugosity5, and rugosity7).
- Distance to coast (dist.coast).
2.3. Preliminary Selection of Predictive Variables
2.4. Predictive Methods
2.5. Variable Selection for Random Forest (RF)
2.6. Variable Selection for Generalized Boosted Regression Modelling (GBM)
2.7. Model Validation
2.8. Model Comparison and Generation of Spatial Predictions
3. Results
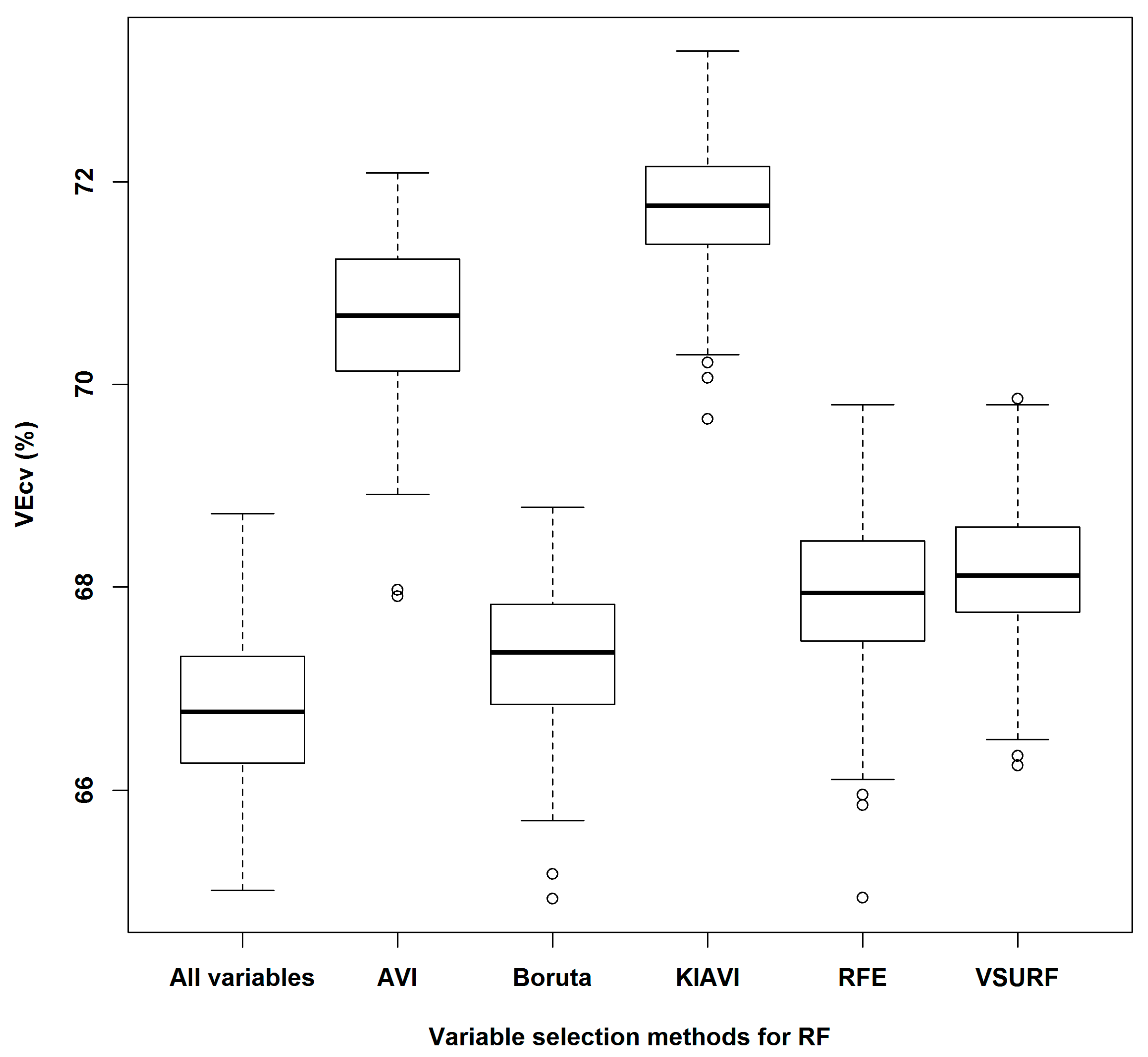
3.1. Variable Selection Methods for RF
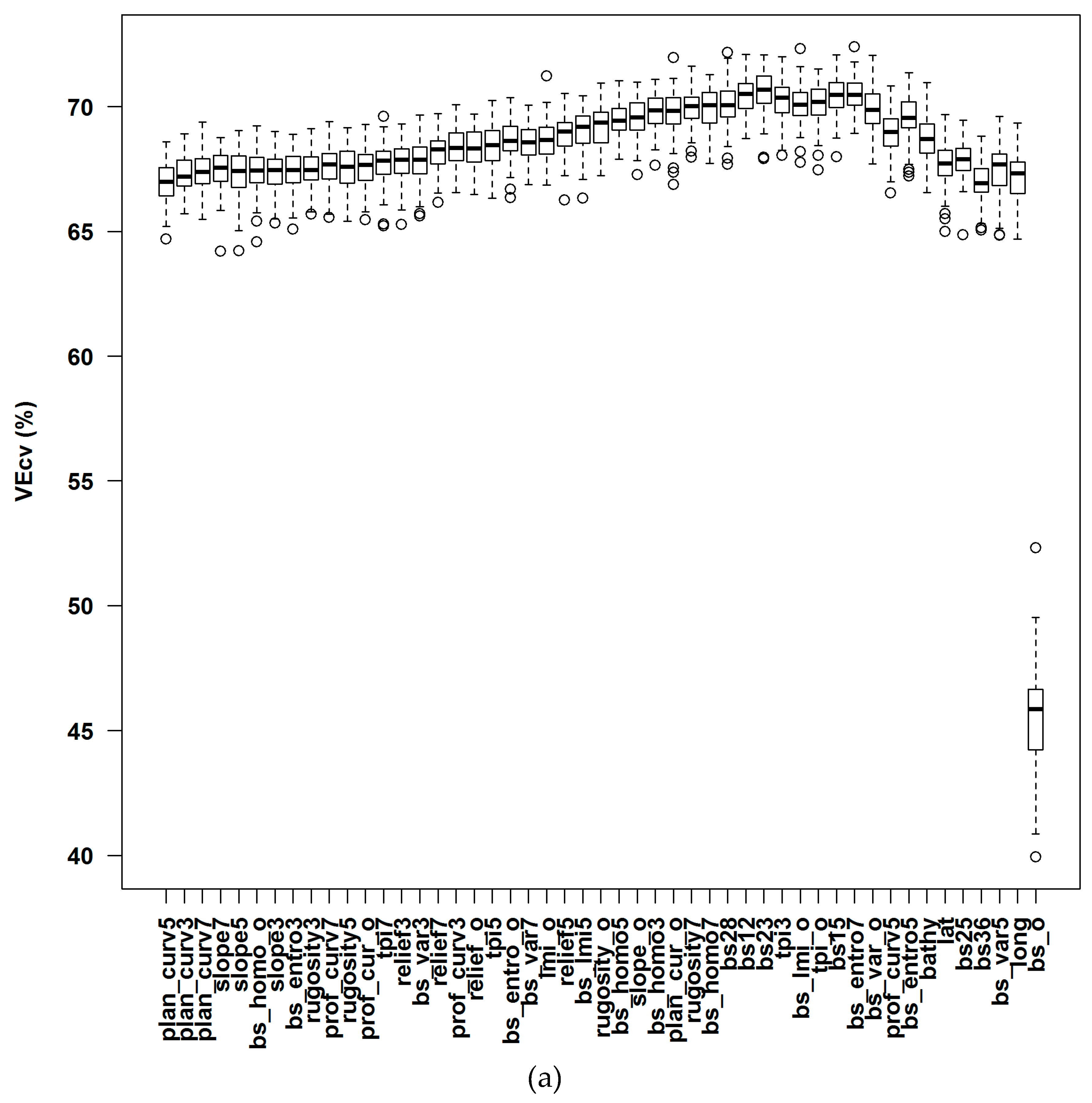
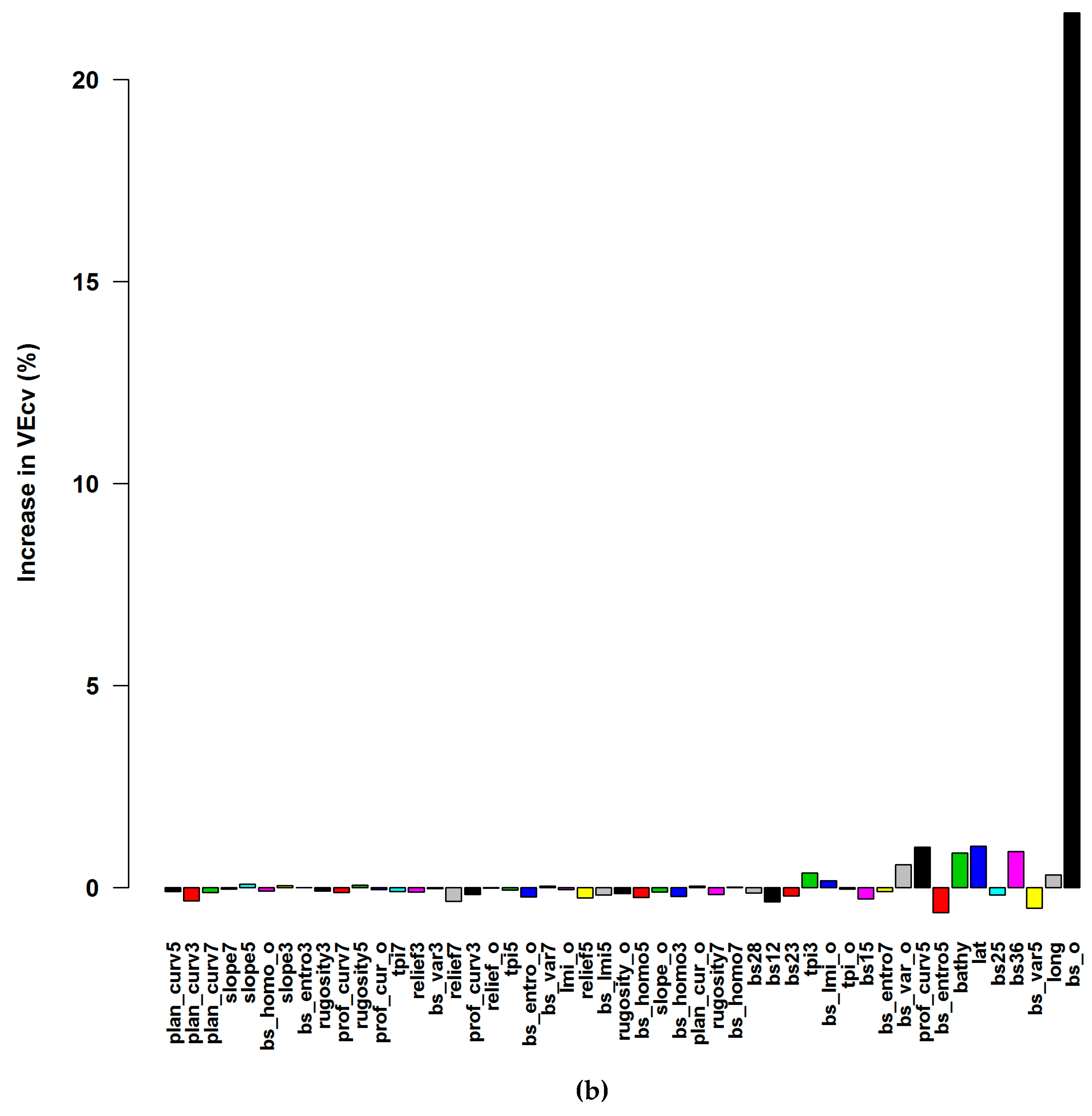
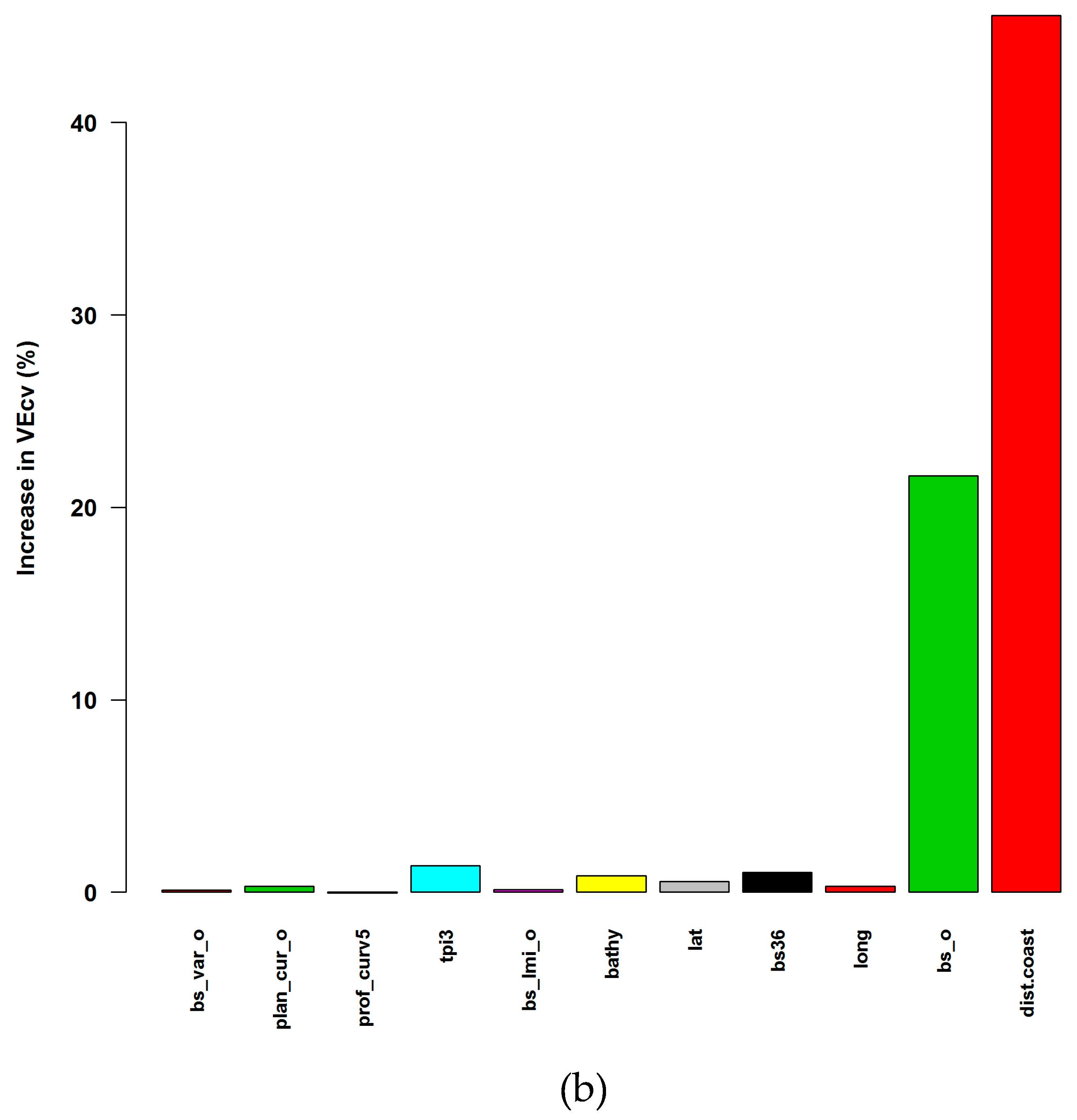
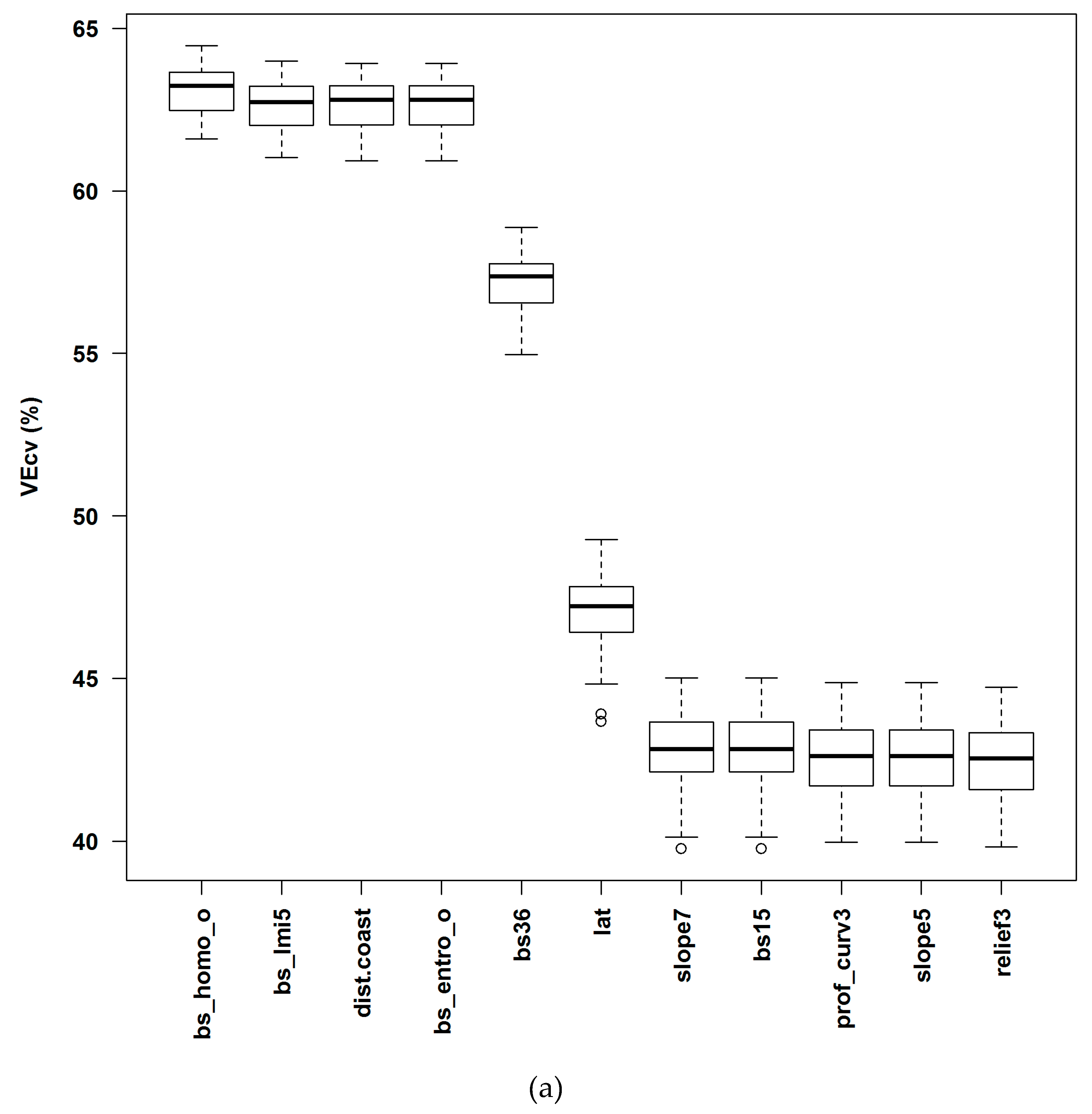
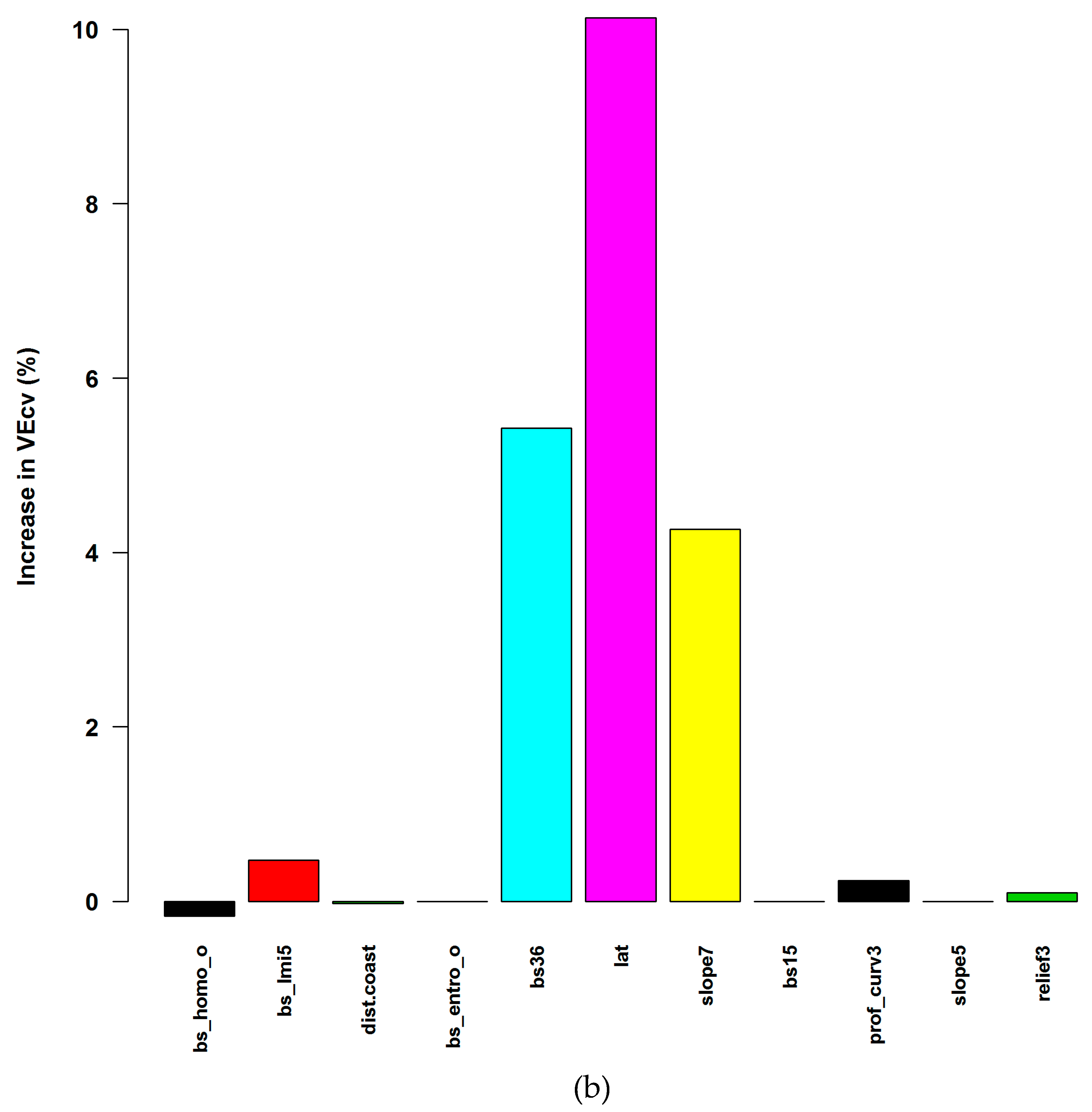
3.1.1. Averaged Variable Importance (AVI)
3.1.2. Knowledge-Informed AVI (KIAVI2)
3.1.3. Boruta, Recursive Feature Selection (RFE), and Variable Selection Using RF (VSURF) and their Comparisons with AVI and KIAVI2
3.2. Variable Selection Methods for GBM
3.3. Comparison of Predictive Methods in Spm
3.4. Predictions of Seabed Sand Content
4. Discussion
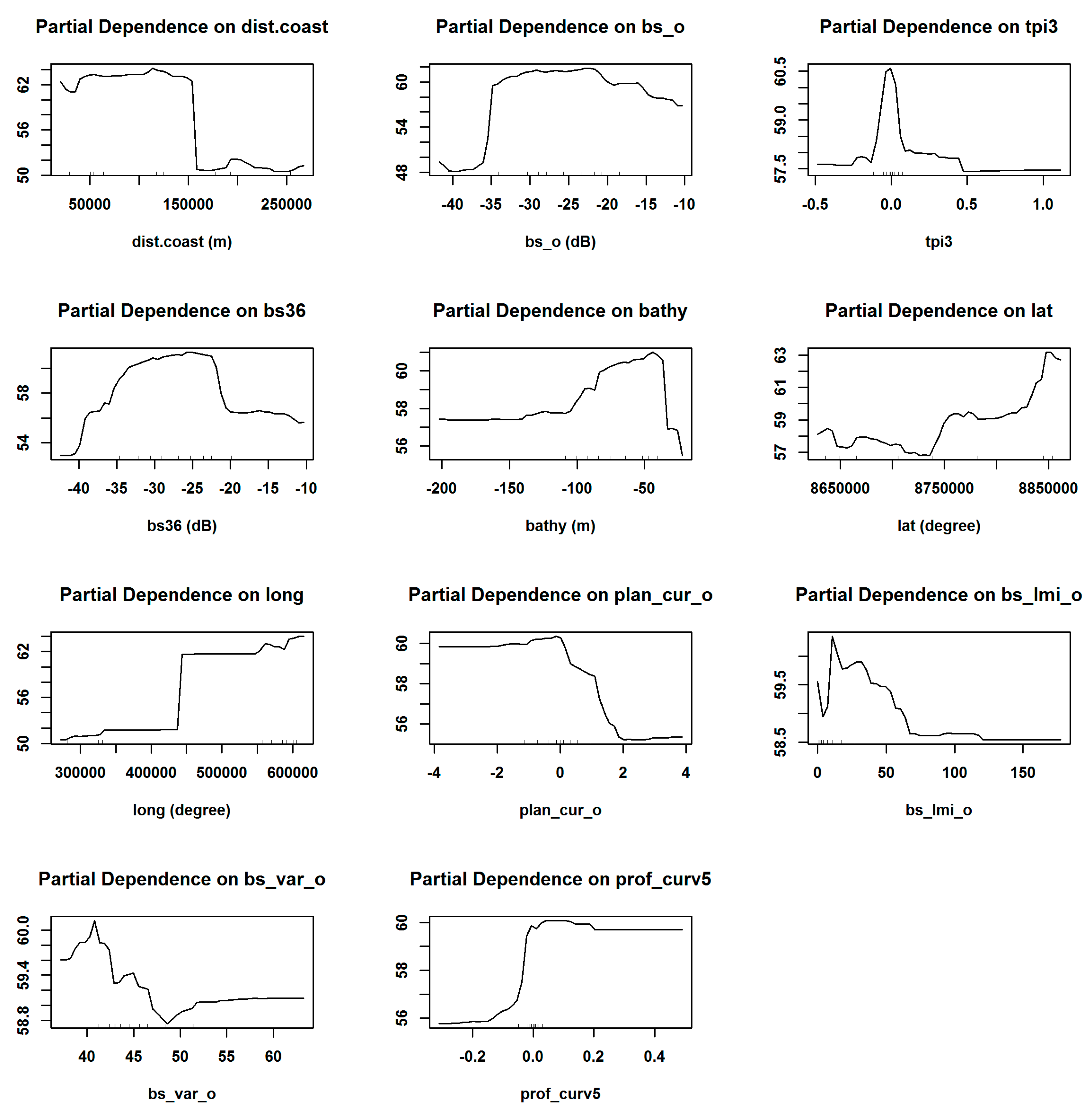
4.1. Bathymetry-Related Variables vs Backscatter-Related Variables for Predictions of Seabed Sand Content
4.2. Highly Correlated Predictive Variables
4.3. Variable Importance and Initial Input Predictive Variables for RF
4.4. Accuracy Contribution and Initial Input Predictive Variables for RF
4.5. Variable Selection Methods for RF
4.6. Issues with Model Valuation and Selection Criteria for GBM
4.7. Predictive Accuracy of Seabed Sand Content
4.8. Predictions of Seabed Sand Content and their Application
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Verfaillie, E.; Van Lancker, V.; Van Meirvenne, M. Multivariate geostatistics for the predictive modelling of the surficial sand distribution in shelf seas. Cont. Shelf Res. 2006, 26, 2454–2468. [Google Scholar] [CrossRef]
- Verfaillie, E.; Du Four, I.; Van Meirvenne, M.; Van Lancker, V. Geostatistical modeling of sedimentological parameters using multi-scale terrain variables: Application along the Belgian Part of the North Sea. Int. J. Geogr. Inf. Sci. 2008. [Google Scholar] [CrossRef]
- Stephens, D.; Diesing, M. Towards quantitative spatial models of seabed sediment composition. PLoS ONE 2015, 10, e0142502. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Nichol, S.; Siwabessy, P.J.W.; Daniell, J.; Brooke, B.P. Predictive Modelling of Seabed Sediment Parameters Using Multibeam Acoustic Data: A Case Study on the Carnarvon Shelf, Western Australia. Int. J. Geogr. Inf. Sci. 2012, 26, 283–307. [Google Scholar] [CrossRef]
- McArthur, M.A.; Brooke, B.P.; Przeslawski, R.; Ryan, D.A.; Lucieer, V.L.; Nichol, S.; McCallum, A.W.; Mellin, C.; Cresswell, I.D.; Radke, L.C. On the use of abiotic surrogates to describe marine benthic biodiversity. Estuar. Coast. Shelf Sci. 2010, 88, 21–32. [Google Scholar] [CrossRef]
- Przeslawski, R.; Daniell, J.; Anderson, T.; Vaughn Barrie, J.; Heap, A.; Hughes, M.; Li, J.; Potter, A.; Radke, L.; Siwabessy, J.; et al. Seabed Habitats and Hazards of the Joseph Bonaparte Gulf and Timor Sea, Northern Australia; Geoscience Australia, Record 2008/23; Geoscience Australia: Canberra, ACT, Australia, 2011; 69p.
- Li, J.; Potter, A.; Huang, Z.; Daniell, J.J.; Heap, A. Predicting Seabed Mud Content across the Australian Margin: Comparison of Statistical and Mathematical Techniques Using a Simulation Experiment; Geoscience Australia, Record 2010/11; Geoscience Australia: Canberra, ACT, Australia, 2010; 146p.
- Li, J.; Potter, A.; Huang, Z.; Heap, A. Predicting Seabed Sand Content across the Australian Margin Using Machine Learning and Geostatistical Methods; Geoscience Australia, Record 2012/48; Geoscience Australia: Canberra, ACT, Australia, 2012; 115p.
- Li, J.; Heap, A.; Potter, A.; Daniell, J.J. Predicting Seabed Mud Content across the Australian Margin II: Performance of Machine Learning Methods and Their Combination with Ordinary Kriging and Inverse Distance Squared; Geoscience Australia, Record 2011/07; Geoscience Australia: Canberra, ACT, Australia, 2011; 69p.
- Li, J. Predicting the spatial distribution of seabed gravel content using random forest, spatial interpolation methods and their hybrid methods. In Proceedings of the International Congress on Modelling and Simulation (MODSIM) 2013, Adelaide, Australia, 1–6 December 2013; pp. 394–400. [Google Scholar]
- Li, J.; Heap, A.; Potter, A.; Huang, Z. Seabed sand content across the Australian continental EEZ 2011. GEOCAT: 71982. Data format: Digital ArcGIS-grid (ArcInfo grid) in 0.01 decimal degree resolution in WGS84 and digital ASCII text in 0.01 decimal degree resolution in WGS84. 2011. Available online: http://pid.geoscience.gov.au/dataset/ga/71982 (accessed on 17 April 2019).
- Li, J. Predicted seabed sand content in the north-northwest region of the Australian continental EEZ 2013. GEOCAT: 76999. Data format: Digital ArcGIS-grid (ArcInfo grid) in 0.0025 decimal degree resolution in WGS84. 2013. Available online: http://pid.geoscience.gov.au/dataset/ga/76999 (accessed on 17 April 2019).
- Diesing, M.; Mitchell, P.; Stephens, D. Image-based seabed classification: What can we learn from terrestrial remote sensing? ICES J. Mar. Sci. 2016, fsw 118. [Google Scholar] [CrossRef]
- Lark, R.M.; Marchant, B.P.; Dove, D.; Green, S.L.; Stewart, H.; Diesing, M. Combining observations with acoustic swath bathymetry and backscatter to map seabed sediment texture classes: The empirical best linear unbiased predi. Sediment. Geol. 2015, 328, 17–32. [Google Scholar] [CrossRef]
- Heap, A.D.; Przeslawski, R.; Radke, L.; Trafford, J.; Battershill, C.; Party, S. Seabed Environments of the Eastern Joseph Bonaparte Gulf, Northern Australia. Sol4934—Post-survey Report; Geoscience Australia, Record 2010/09; Geoscience Australia: Canberra, ACT, Australia, 2010; 78p.
- Anderson, T.J.; Nichol, S.; Radke, L.; Heap, A.D.; Battershill, C.; Hughes, M.; Siwabessy, P.J.; Barrie, V.; Alvarez de Glasby, B.; Tran, M.; et al. Seabed Environments of the Eastern Joseph Bonaparte Gulf, Northern Australia: GA0325/Sol5117—Post-Survey Report; Geoscience Australia, Record 2011/08; Geoscience Australia: Canberra, ACT, Australia, 2011; 59p.
- Nichol, S.; Howard, F.; Kool, J.; Stowar, M.; Bouchet, P.; Radke, L.; Siwabessy, J.; Przeslawski, R.; Picard, K.; Alvarez de Glasby, B.; et al. Oceanic Shoals Commonwealth Marine Reserve (Timor Sea) Biodiveristy Survey: GA0339/SOL5650 Post-Survey Report; Geoscience Australia, Record 2013/38; Geoscience Australia: Canberra, ACT, Australia, 2013.
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Li, J.; Heap, A. A Review of Spatial Interpolation Methods for Environmental Scientists; Geoscience Australia, Record 2008/23; Geoscience Australia: Canberra, ACT, Australia, 2008; 137p.
- Li, J.; Heap, A. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Li, J. Predicted seabed gravel content in the north-northwest region of the Australian continental EEZ 2013. GEOCAT: 76997. Data format: Digital ArcGIS-grid (ArcInfo grid) in 0.0025 decimal degree resolution in WGS84. 2013. Available online: http://pid.geoscience.gov.au/dataset/ga/76997 (accessed on 17 April 2019).
- Cutler, D.R.; Edwards, T.C.J.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecography 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Diaz-Uriarte, R.; de Andres, S.A. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Shan, Y.; Paull, D.; McKay, R.I. Machine learning of poorly predictable ecological data. Ecol. Model. 2006, 195, 129–138. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Drake, J.M.; Randin, C.; Guisan, A. Modelling ecological niches with support vector machines. J. Appl. Ecol. 2006, 43, 424–432. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Marmion, M.; Parviainen, M.; Luoto, M.; Heikkinen, R.K.; Thuiller, W. Evaluation of consensus methods in predictive species distribution modelling. Divers. Distrib. 2009, 15, 59–69. [Google Scholar] [CrossRef]
- Li, J.; Alvarez, B.; Siwabessy, J.; Tran, M.; Huang, Z.; Przeslawski, R.; Radke, L.; Howard, F.; Nichol, S. Application of random forest, generalised linear model and their hybrid methods with geostatistical techniques to count data: Predicting sponge species richness. Environ. Model. Softw. 2017, 97, 112–129. [Google Scholar] [CrossRef]
- Sanabria, L.A.; Qin, X.; Li, J.; Cechet, R.P.; Lucas, C. Spatial interpolation of McArthur’s forest fire danger index across Australia: Observational study. Environ. Model. Softw. 2013, 50, 37–50. [Google Scholar] [CrossRef]
- Sanabria, L.A.; Cechet, R.P.; Li, J. Mapping of Australian Fire Weather Potential: Observational and modelling studies. In Proceedings of the 20th International Congress on Modelling and Simulation (MODSIM2013), Adelaide, Australia, 1–6 December 2013; pp. 242–248. [Google Scholar]
- Appelhans, T.; Mwangomo, E.; Hardy, D.R.; Hemp, A.; Nauss, T. Evaluating machine learning approaches for the interpolation of monthly air temperature at Mt. Kilimanjaro, Tanzania. Spat. Stat. 2015, 14, 91–113. [Google Scholar] [CrossRef]
- Tadić, J.M.; Ilić, V.; Biraud, S. Examination of geostatistical and machine-learning techniques as interpolaters in anisotropic atmospheric environments. Atmos. Environ. 2015, 111, 28–38. [Google Scholar] [CrossRef]
- Li, J. A new R package for spatial predictive modelling: spm. In Proceedings of the useR! 2018, Brisbane, Australia, 10–13 July 2018. [Google Scholar]
- Li, J.; Tran, M.; Siwabessy, J. Selecting optimal random forest predictive models: A case study on predicting the spatial distribution of seabed hardness. PLoS ONE 2016, 11, e0149089. [Google Scholar] [CrossRef]
- Li, J. Predictive Modelling Using Random Forest and Its Hybrid Methods with Geostatistical Techniques in Marine Environmental Geosciences. In Proceedings of the Eleventh Australasian Data Mining Conference (AusDM 2013), Canberra, Australia, 13–15 November 2013. [Google Scholar]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Li, J.; Potter, A.; Heap, A. Irrelevant Inputs and Parameter Choices: Do They Matter to Random Forest for Predicting Marine Environmental Variables? In Proceedings of the Australian Statistical Conference 2012, Adelaide, Australia, 9–12 July 2012. [Google Scholar]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. VSURF: Variable Selection Using Random Forests, R Package Version 1.0.2; 2015. Available online: https://CRAN.R-project.org/package=VSURF (accessed on 17 April 2019).
- Li, J.; Alvarez, B.; Siwabessy, J.; Tran, M.; Huang, Z.; Przeslawski, R.; Radke, L.; Howard, F.; Nichol, S. Selecting predictors to form the most accurate predictive model for count data. In Proceedings of the International Congress on Modelling and Simulation (MODSIM) 2017, Hobart, Australia, 3–8 December 2017. [Google Scholar]
- Li, J.; Siwabessy, J.; Tran, M.; Huang, Z.; Heap, A. Predicting Seabed Hardness Using Random Forest in R. In Data Mining Applications with R; Zhao, Y., Cen, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 299–329. [Google Scholar]
- Radke, L.C.; Li, J.; Douglas, G.; Przeslawski, R.; Nichol, S.; Siwabessy, J.; Huang, Z.; Trafford, J.; Watson, T.; Whiteway, T. Characterising sediments for a tropical sediment-starved shelf using cluster analysis of physical and geochemical variables. Environ. Chem. 2015, 12, 204–226. [Google Scholar] [CrossRef]
- Radke, L.; Nicholas, T.; Thompson, P.; Li, J.; Raes, E.; Carey, M.; Atkinson, I.; Huang, Z.; Trafford, J.; Nichol, S. Baseline biogeochemical data from Australia’s continental margin links seabed sediments to water column characteristics. Mar. Freshw. Res. 2017. [Google Scholar] [CrossRef]
- De Moustier, C.P.; Alexandrou, D. Angular dependence of 12-kHz seafloor acoustic backscatter. J. Acoust. Soc. Am. 1991, 90, 522–531. [Google Scholar] [CrossRef]
- Siwabessy, P.J.W.; Gavrilov, A.N.; Duncan, A.N.; Parnum, I.M. Analysis of statistics of backscatter strength from different seafloor habitats. In Proceedings of the Conference of the Australasian Acoustical Societies, Acoustics 2006, Christchurch, New Zealand, 20–22 November 2006; pp. 507–514. [Google Scholar]
- Siwabessy, P.J.W.; Daniell, J.; Li, J.; Huang, Z.; Heap, A.D.; Nichol, S.; Anderson, T.J.; Tran, M. Methodologies for Seabed Substrate Characterisation Using Multibeam Bathymetry, Backscatter and Video Data: A Case Study from the Carbonate Banks of the Timor Sea, Northern Australia; Geoscience Australia, Record 2013/11; Geoscience Australia: Canberra, ACT, Australia, 2013; 82p.
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M. caret: Classification and Regression Training. R package version 60-30. 2014. Available online: http://CRAN.R-project.org/package=caret (accessed on 17 April 2019).
- Li, J.; Alvarez, B.; Siwabessy, J.; Tran, M.; Huang, Z.; Przeslawski, R.; Radke, L.; Howard, F.; Nichol, S. Spatial distribution of sponge species richness: Lessons learned from spatial predictive modelling and pattern predictions. In Proceedings of the Australian Marine Sciences Association (AMSA) Conference, Adelaide, Australia, 1–5 July 2018. [Google Scholar]
- Smith, S.J.; Ellis, N.; Pitcher, C.R. Conditional variable importance in R package extendedForest. Available online: http://gradientforest.r-forge.r-project.org/Conditional-importance.pdf (accessed on 17 April 2019).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; p. 763. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143. [Google Scholar]
- Li, J. Assessing spatial predictive models in the environmental sciences: Accuracy measures, data variation and variance explained. Environ. Model. Softw. 2016, 80, 1–8. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Ridgeway, G. gbm: Generalized Boosted Regression Models, R package version 2.1.3. 2017. Available online: https://CRAN.R-project.org/package=gbm (accessed on 17 April 2019).
- Li, J.; Heap, A.D.; Potter, A.; Huang, Z.; Daniell, J. Can we improve the spatial predictions of seabed sediments? A case study of spatial interpolation of mud content across the southwest Australian margin. Cont. Shelf Res. 2011, 31, 1365–1376. [Google Scholar] [CrossRef]
- Huang, Z.; Brooke, B.; Li, J. Performance of predictive models in marine benthic environments based on predictions of sponge distribution on the Australian continental shelf. Ecol. Inform. 2011, 6, 205–216. [Google Scholar] [CrossRef]
- Stephens, D.; Diesing, M. A Comparison of Supervised Classification Methods for the Prediction of Substrate Type Using Multibeam Acoustic and Legacy Grain-Size Data. PLoS ONE 2014, 9, e93950. [Google Scholar]
- Diesing, M.; Green, S.L.; Stephens, D.; Lark, R.M.; Stewart, H.A.; Dove, D. Mapping seabed sediments: Comparison of manual, geostatistical, object-based image analysis and machine learning approaches. Cont. Shelf Res. 2014, 84, 107–109. [Google Scholar] [CrossRef]
- Li, J. spm: Spatial Predictive Modelling, R package version 1.1.0. 2018. Available online: https://CRAN.R-project.org/package=spm (accessed on 17 April 2019).
- Hengl, T.; Heuvelink, G.B.M.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; de Jesus, J.M.; Tamene, L.; et al. Mapping Soil Properties of Africa at 250 m Resolution: Random Forests Significantly Improve Current Predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef] [PubMed]
- Reinhardt, K.; Samimi, C. Comparison of different wind data interpolation methods for a region with complex terrain in Central Asia. Clim. Dyn. 2018, 51, 3635–3652. [Google Scholar] [CrossRef]
- Przeslawski, R.; Glasby, C.; Nichol, S. Polychaetes (Annelida) of the Oceanic Shoals region, northern Australia: Considering small macrofauna in marine management. Mar. Freshw. Res. 2019, 70, 307–321. [Google Scholar] [CrossRef]
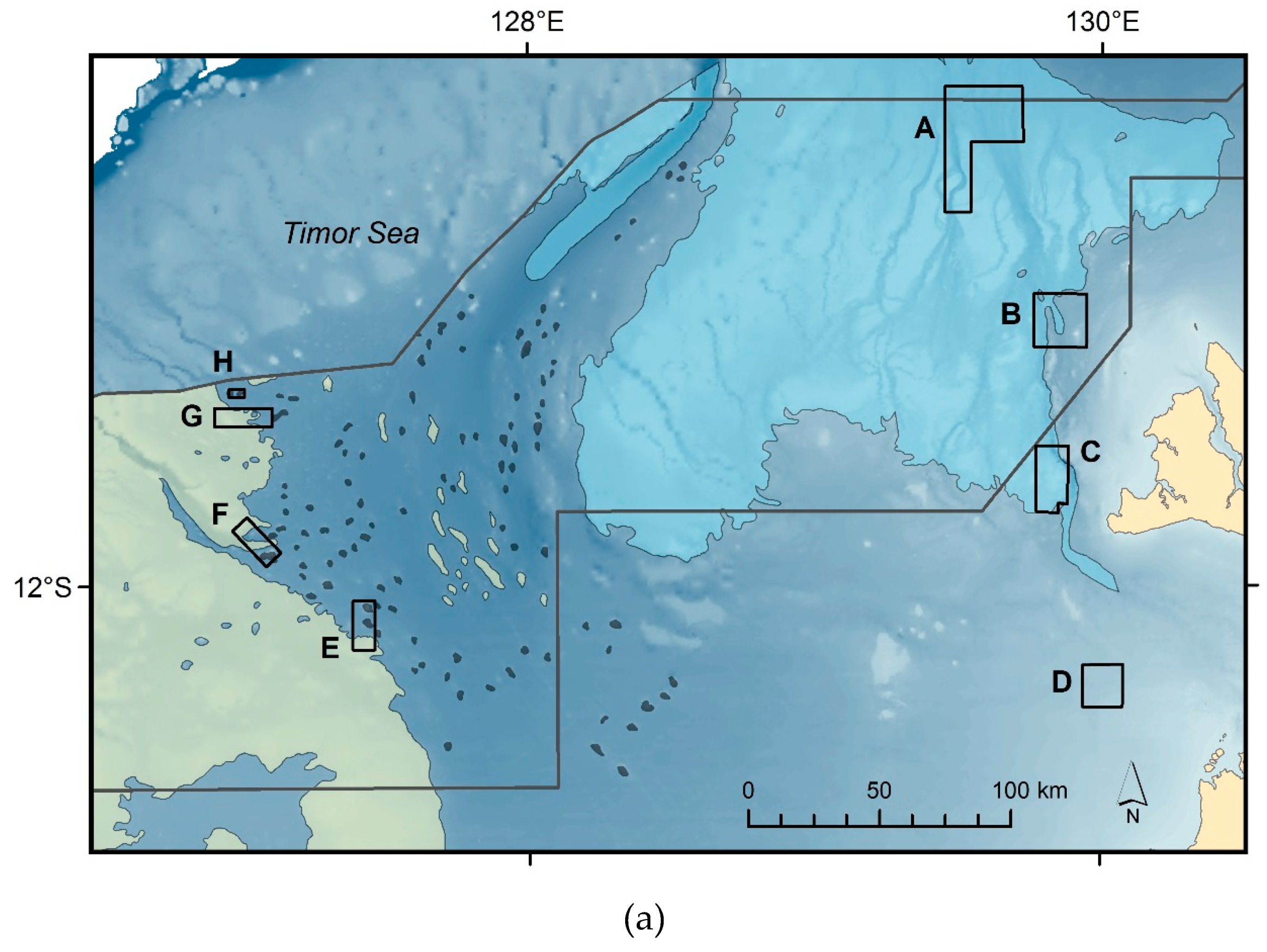
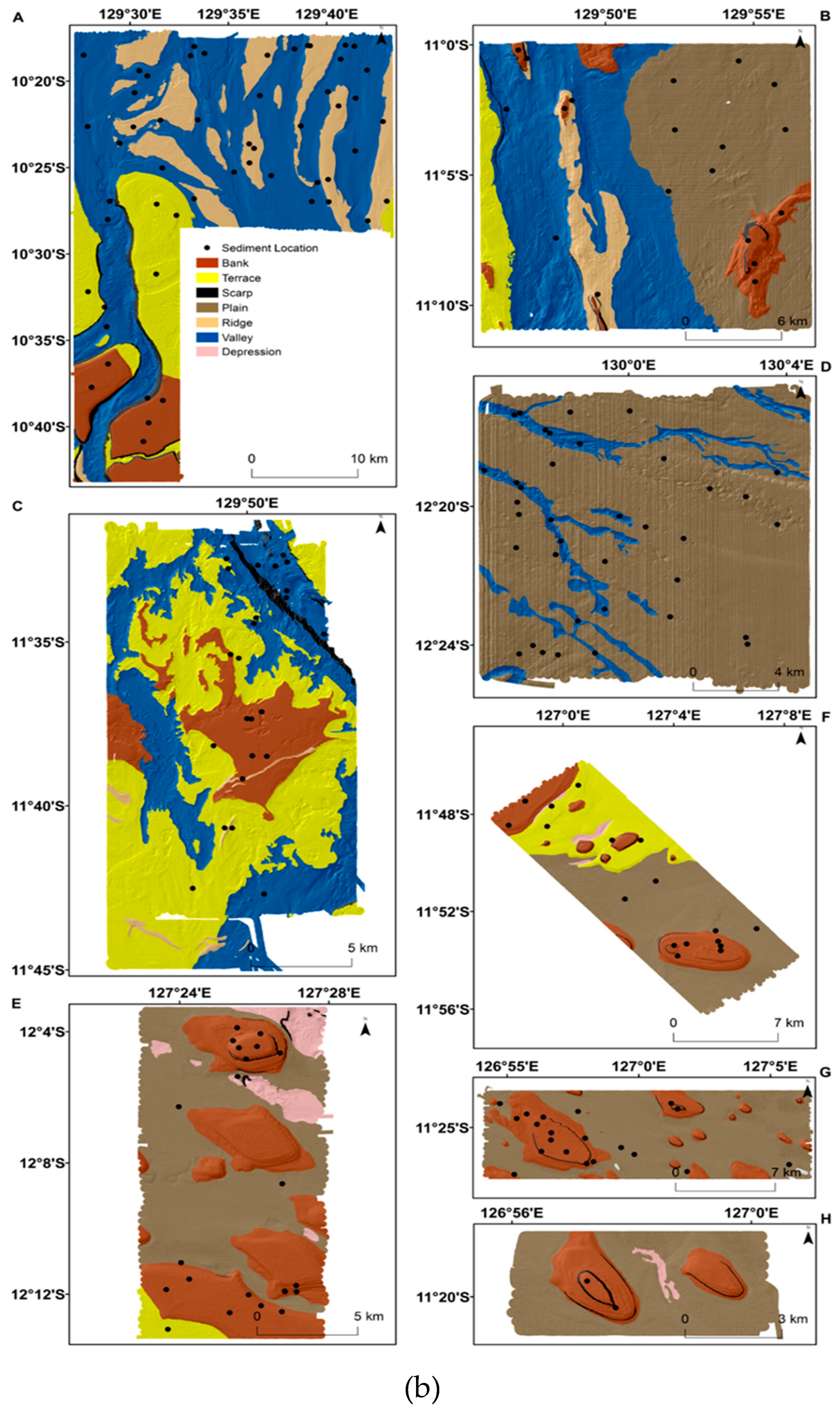

| No. | Predictive Variable | Unit | No. | Predictive Variable | Unit |
|---|---|---|---|---|---|
| 1 | long | degree | 26 | slope7 | degree |
| 2 | lat | degree | 27 | rugosity3 | |
| 3 | bs25 | dB | 28 | rugosity5 | |
| 4 | bs_entro_o3 | 29 | rugosity7 | ||
| 5 | bs_entro_o5 | 30 | tpi3 | ||
| 6 | bs_entro_o7 | 31 | tpi5 | ||
| 7 | bs_homo3 | 32 | tpi7 | ||
| 8 | bs_homo5 | 33 | bs12 | ||
| 9 | bs_homo7 | 34 | bs15 | ||
| 10 | bs_var3 | 35 | bs23 | ||
| 11 | bs_var5 | 36 | bs28 | ||
| 12 | bs_var7 | 37 | bs36 | ||
| 13 | bs_lmi5 | 38 | dist.coast | m | |
| 14 | bathy | m | 39 | bs_o | dB |
| 15 | plan_curv3 | 40 | bs_homo_o | ||
| 16 | plan_curv5 | 41 | bs_entro_o | ||
| 17 | plan_curv7 | 42 | bs_var_o | ||
| 18 | prof_curv3 | 43 | bs_lmi_o | ||
| 19 | prof_curv5 | 44 | lmi_o | ||
| 20 | prof_curv7 | 45 | tpi_o | ||
| 21 | relief3 | m | 46 | slope_o | |
| 22 | relief5 | m | 47 | plan_cur_o | |
| 23 | relief7 | m | 48 | prof_cur_o | |
| 24 | slope3 | degree | 49 | relief_o | m |
| 25 | slope5 | degree | 50 | rugosity_o |
| Abbreviation | Full Name | Type |
|---|---|---|
| IDW | Inverse distance weighting | Modelling methods |
| OK | Ordinary kriging | |
| GBM | Generalized boosted regression modelling | |
| RF | Random forest | |
| RFIDW | The hybrid of RF with IDW | |
| RFOK | The hybrid of RF with OK | |
| RFOKRFIDW | The average of RFOK and RFIDW | |
| AVI | Averaged variable importance | Selection methods |
| KIAVI | Knowledge-informed AVI | |
| RVI | Relative variable influence | |
| KIRVI | Knowledge-informed RVI (KIRVI) | |
| RFE | Recursive feature selection | |
| VSURF | Variable selection using RF | |
| VEcv | Variance explained by predictive models | Accuracy measure |
| Distance Power (idp) | Window Size (nmax) | Variogram Model (vgm.args) | |
|---|---|---|---|
| IDW default | 2 | 12 | |
| IDW optimal | 0.6 | 19 | |
| OK default | 12 | Sph | |
| OK optimal | 19 | Sph | |
| RFIDW | 0.1 | 11 | |
| RFOK | 17 | Lin |
| Step | Method | Description |
|---|---|---|
| 1.1 | AVI | Apply RFcv to all predictive variables and repeat it 100 times to produce an averaged predictive accuracy (i.e., averaged VEcv). |
| 1.2 | Calculate the importance of each variable in the RF model and repeat it 100 times to produce an averaged variable importance (AVI) and find the variable with the lowest AVI. | |
| 1.3 | Remove the variable with the lowest AVI and repeat step 1.1 by applying RFcv to the remaining predictive variables. | |
| 1.4 | Repeat step 1.2 and 1.3 until only one predictive variable is retained in the model. | |
| 1.5 | Calculate the contribution of each predictive variable removed to predictive accuracy by sequentially subtracting the averaged VEcv of the model with and without the variable for each variable. | |
| 1.6 | Find the model with the highest averaged VEcv. | |
| 1.7 | KIAVI2 | Remove variables with negative contribution (i.e., unimportant variable based on the predictive accuracy) derived in step 1.5 from all available predictive variables and then repeat steps 1.1 to 1.6 using the remaining variables. |
| 1.8 | Repeat step 1.7 if the model with the highest averaged VEcv identified in step 1.7 is more accurate than the model identified in step 1.6 or previous repetition, until no further improvement in accuracy can be achieved. Then select the model with the highest averaged VEcv. |
| RF | GBM | ||||||
|---|---|---|---|---|---|---|---|
| Predictive variable | AVI | Boruta | KIAVI2 | RFE | VSURF | No. of selection | KIRVI |
| long | ✔ | ✔ | ✔ | ✔ | 4 | ||
| lat | ✔ | ✔ | ✔ | ✔ | 4 | ✔ | |
| bs25 | ✔ | ✔ | ✔ | ✔ | 4 | ||
| bs_entro_o3 | ✔ | ✔ | 2 | ||||
| bs_entro_o5 | ✔ | ✔ | 2 | ||||
| bs_entro_o7 | ✔ | ✔ | 2 | ||||
| bs_homo3 | ✔ | 1 | |||||
| bs_homo5 | ✔ | 1 | |||||
| bs_homo7 | ✔ | 1 | |||||
| bs_var3 | ✔ | ✔ | 2 | ||||
| bs_var5 | ✔ | ✔ | 2 | ||||
| bs_var7 | ✔ | 1 | |||||
| bs_lmi5 | ✔ | 1 | ✔ | ||||
| bathy | ✔ | ✔ | ✔ | 3 | |||
| plan_curv3 | ✔ | 1 | |||||
| prof_curv3 | ✔ | 1 | ✔ | ||||
| prof_curv5 | ✔ | ✔ | 2 | ✔ | |||
| relief3 | 0 | ✔ | |||||
| relief5 | ✔ | 1 | |||||
| relief7 | 0 | ✔ | |||||
| rugosity7 | ✔ | 1 | |||||
| slope5 | 0 | ✔ | |||||
| slope7 | 0 | ✔ | |||||
| tpi3 | ✔ | ✔ | ✔ | 3 | |||
| tpi5 | ✔ | 1 | |||||
| bs12 | ✔ | 1 | |||||
| bs15 | ✔ | ✔ | 2 | ✔ | |||
| bs23 | ✔ | 1 | |||||
| bs28 | ✔ | 1 | |||||
| bs36 | ✔ | ✔ | ✔ | 3 | ✔ | ||
| dist.coast | ✔ | ✔ | ✔ | ✔ | ✔ | 5 | ✔ |
| bs_o | ✔ | ✔ | ✔ | ✔ | ✔ | 5 | |
| bs_entro_o | 0 | ✔ | |||||
| bs_homo_o | ✔ | 1 | ✔ | ||||
| bs_var_o | ✔ | ✔ | 2 | ||||
| bs_lmi_o | ✔ | ✔ | ✔ | ✔ | 4 | ||
| lim_o | ✔ | 1 | |||||
| tpi_o | ✔ | ✔ | 2 | ||||
| slope_o | ✔ | ✔ | 2 | ||||
| plan_curv_o | ✔ | 1 | |||||
| relief_o | ✔ | 1 | |||||
| rugosity_o | ✔ | 1 | |||||
| No. of variables selected | 16 | 31 | 11 | 4 | 11 | 13 | |
| Variable Selection Method | VEcv (%) | p-Value | ||||
|---|---|---|---|---|---|---|
| All Variables | AVI | Boruta | KIAVI2 | RFE | ||
| All variables | 66.86 | |||||
| AVI | 70.63 | 0.0000 | ||||
| Boruta | 67.30 | 0.0000 | 0.0000 | |||
| KIAVI2 | 71.75 | 0.0000 | 0.0000 | 0.0000 | ||
| RFE | 67.93 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| VSURF | 68.14 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0959 |
| Model | VEcv (%) | p-Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
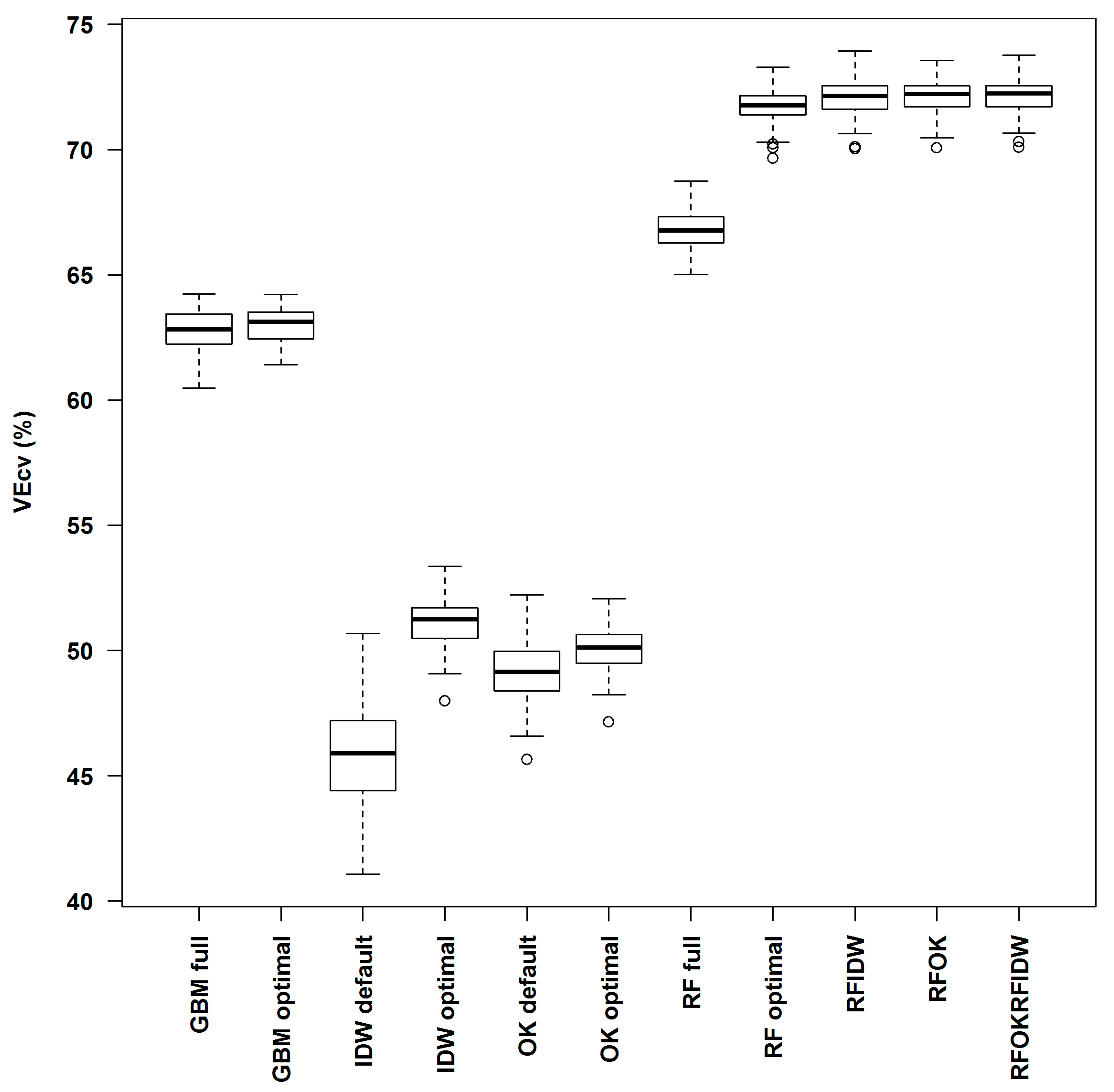
| IDW Default | IDW Optimal | OK Default | OK Optimal | GBM Full | GBM Optimal | RF Full | RF Optimal | RFOK | RFIDW | ||
| IDW default | 45.89 | ||||||||||
| IDW optimal | 51.19 | 0.0000 | |||||||||
| OK default | 49.12 | 0.0000 | 0.0000 | ||||||||
| OK optimal | 50.10 | 0.0000 | 0.0000 | 0.0000 | |||||||
| GBM full | 62.79 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||||||
| GBM optimal | 62.95 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.1199 | |||||
| RF full | 66.86 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||||
| RF optimal | 71.75 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |||
| RFOK | 72.15 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||
| RFIDW | 72.12 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0003 | 0.6433 | |
| RFOKRFIDW | 72.16 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.9795 | 0.6294 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Siwabessy, J.; Huang, Z.; Nichol, S. Developing an Optimal Spatial Predictive Model for Seabed Sand Content Using Machine Learning, Geostatistics, and Their Hybrid Methods. Geosciences 2019, 9, 180. https://doi.org/10.3390/geosciences9040180
Li J, Siwabessy J, Huang Z, Nichol S. Developing an Optimal Spatial Predictive Model for Seabed Sand Content Using Machine Learning, Geostatistics, and Their Hybrid Methods. Geosciences. 2019; 9(4):180. https://doi.org/10.3390/geosciences9040180
Chicago/Turabian StyleLi, Jin, Justy Siwabessy, Zhi Huang, and Scott Nichol. 2019. "Developing an Optimal Spatial Predictive Model for Seabed Sand Content Using Machine Learning, Geostatistics, and Their Hybrid Methods" Geosciences 9, no. 4: 180. https://doi.org/10.3390/geosciences9040180
APA StyleLi, J., Siwabessy, J., Huang, Z., & Nichol, S. (2019). Developing an Optimal Spatial Predictive Model for Seabed Sand Content Using Machine Learning, Geostatistics, and Their Hybrid Methods. Geosciences, 9(4), 180. https://doi.org/10.3390/geosciences9040180






