Bayesian Variable Selection for Pareto Regression Models with Latent Multivariate Log Gamma Process with Applications to Earthquake Magnitudes
Abstract
1. Introduction
2. Methodology
2.1. Pareto Regression with Spatial Random Effects
2.2. Bayesian Model Assessment Criteria
2.2.1. DIC
2.2.2. LPML
2.3. Analytic Connections between Bayesian Variable Selection Criteria with Conditional AIC for the Normal Linear Regression with Spatial Random Effects
3. MCMC Scheme
4. Simulation Study
4.1. Simulation for the Connection between Multivariate Log Gamma and Multivariate Normal Distribution
4.2. Simulation for Estimation Performance
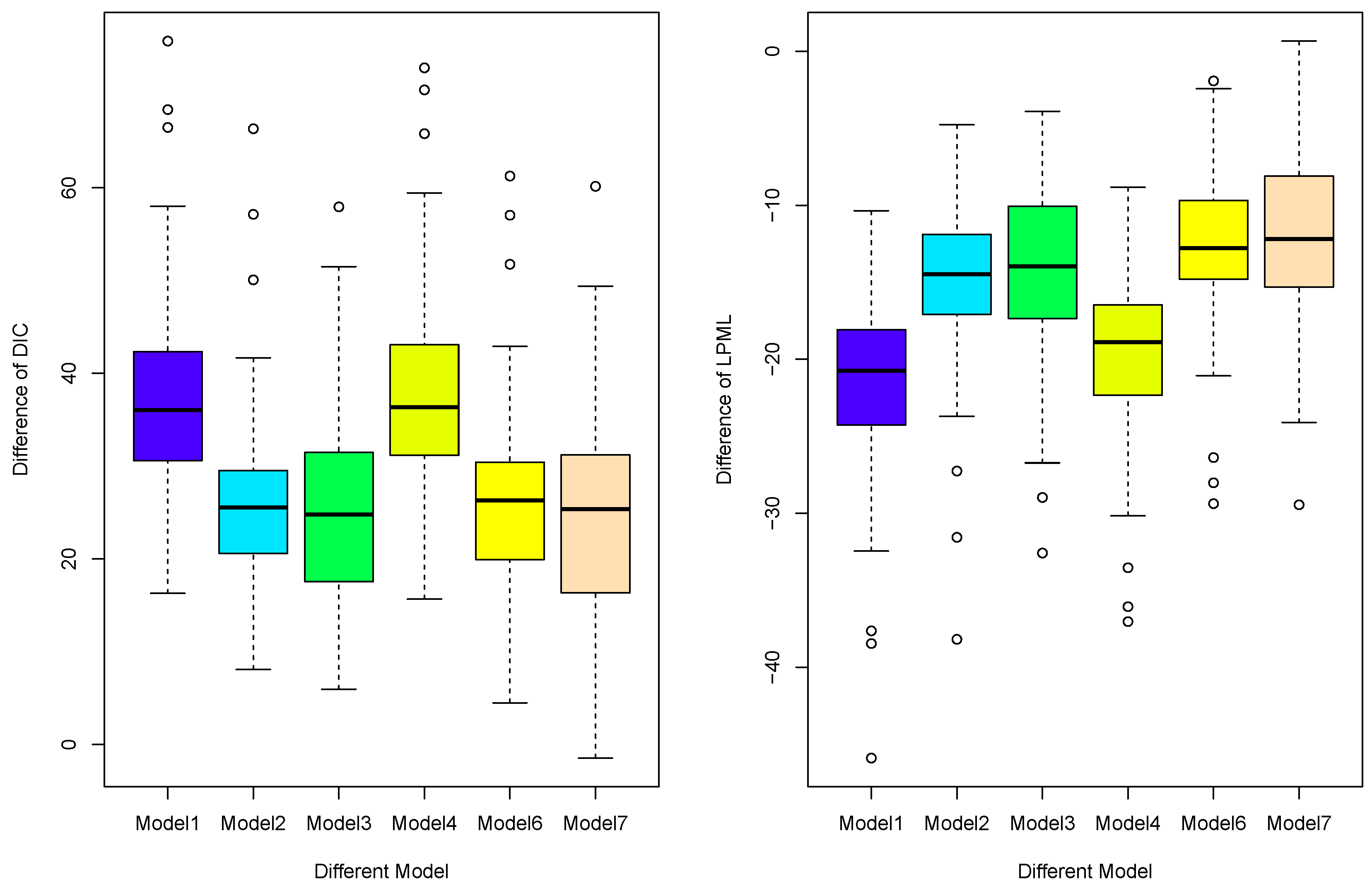
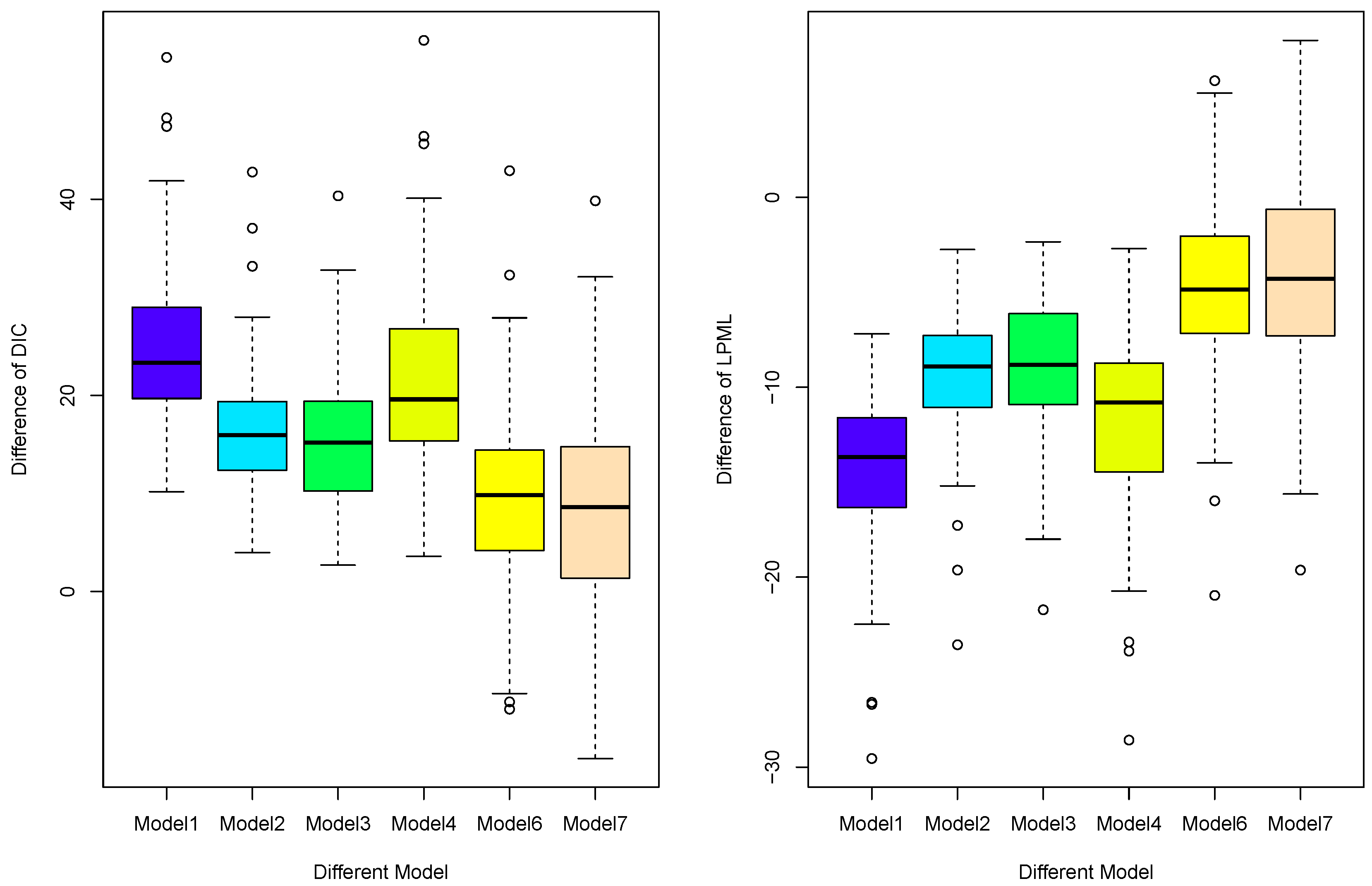
4.3. Simulation for Model Selection
4.4. Simulation for Model Comparison
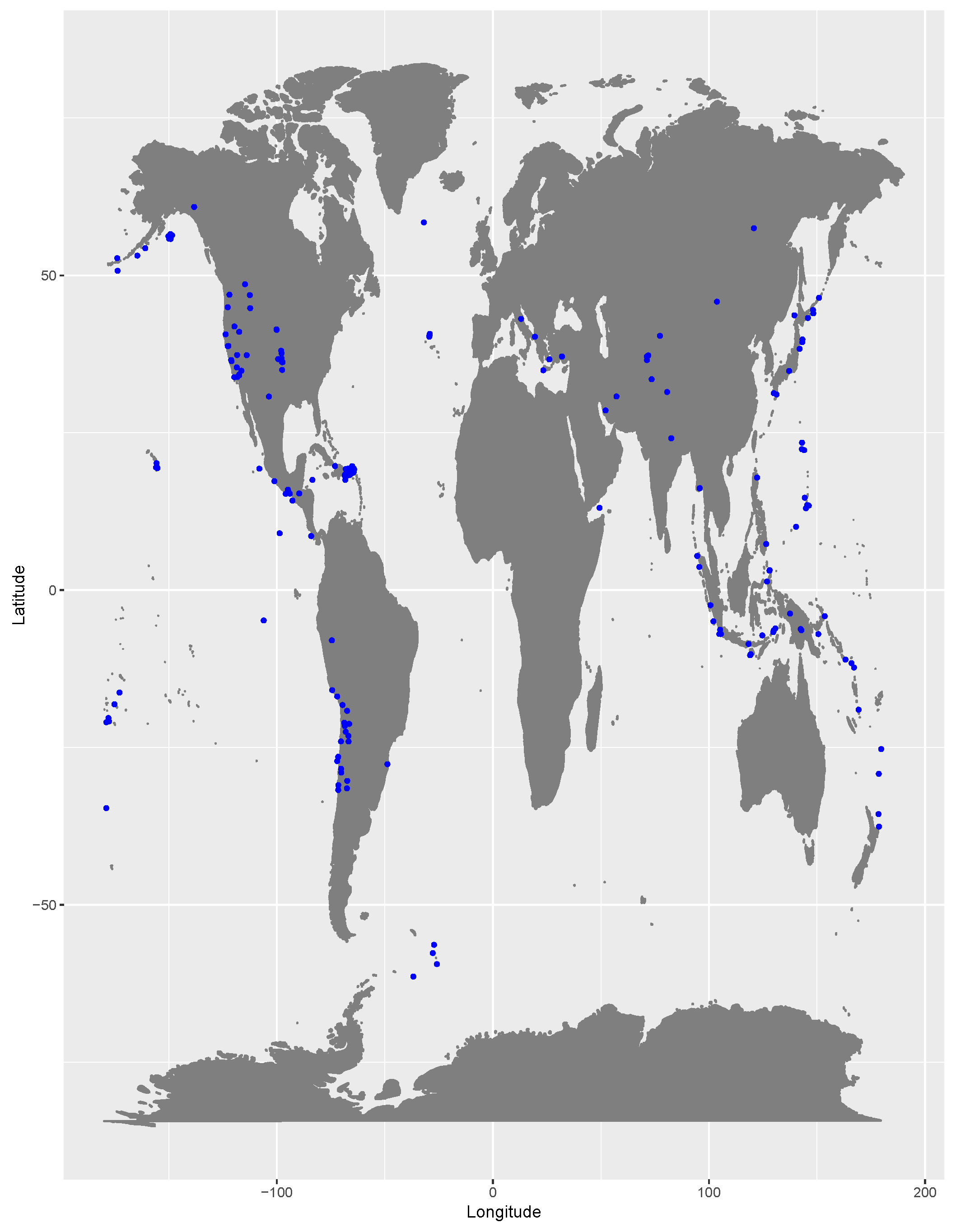
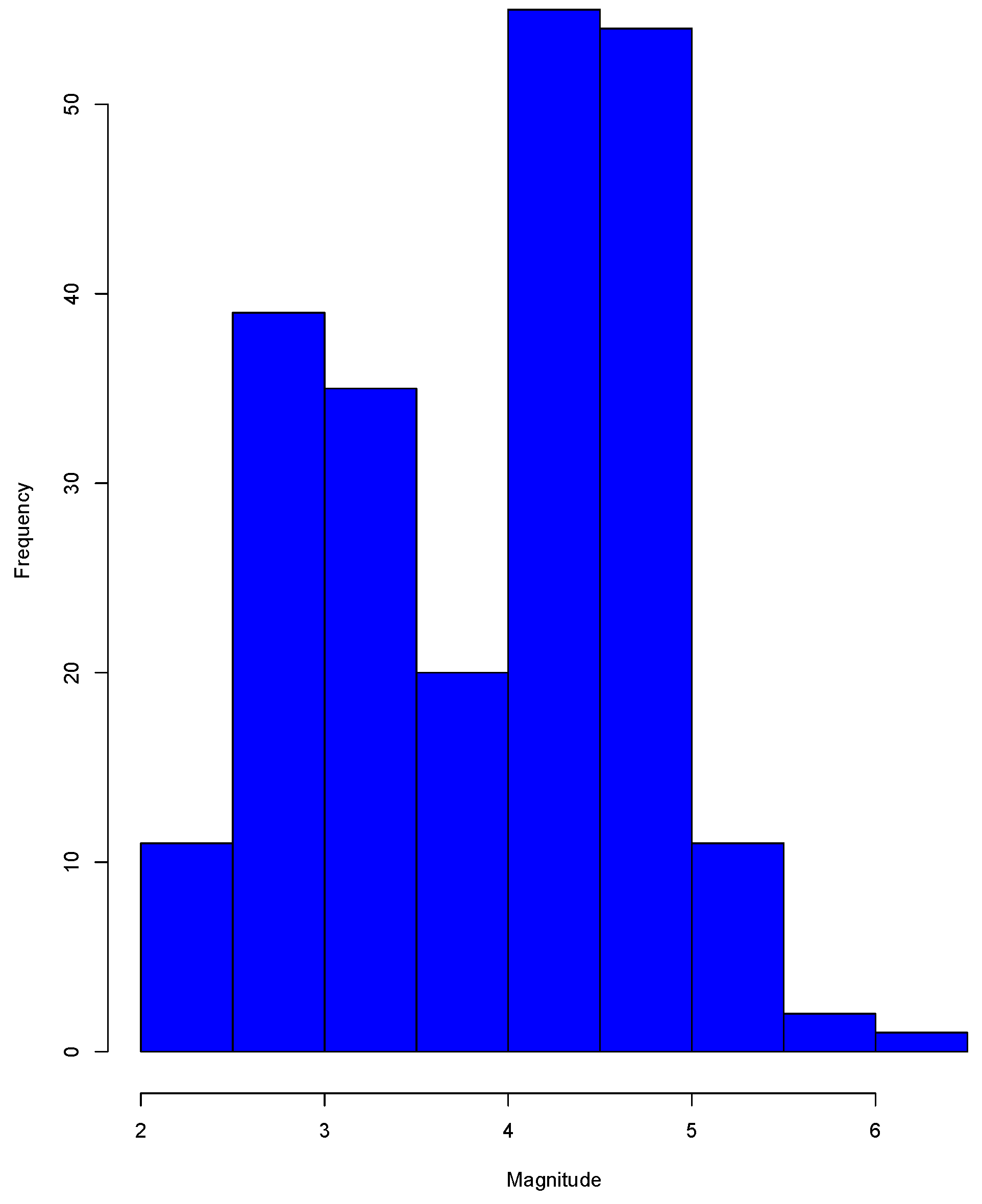
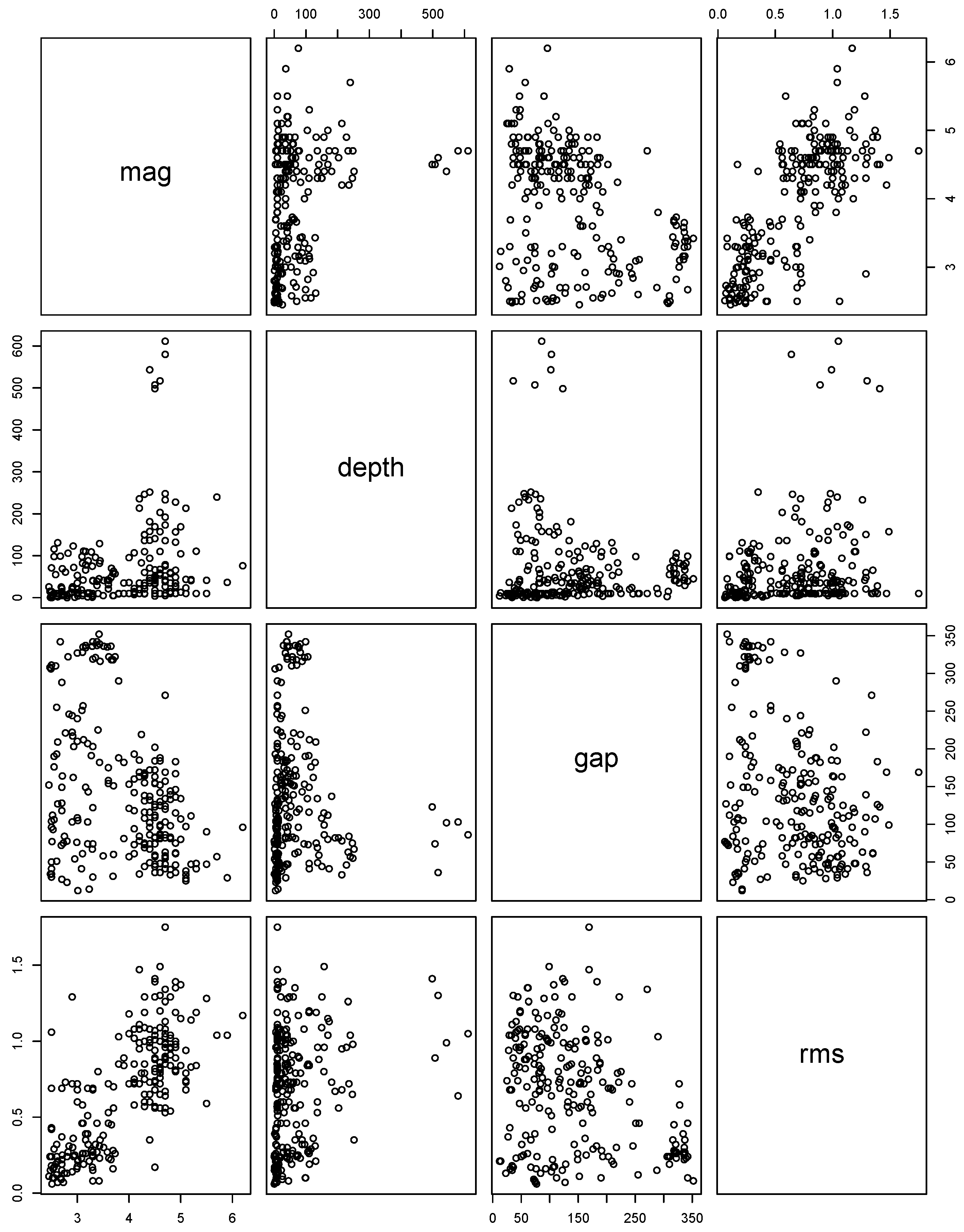
5. A Real Data Example
5.1. Data Description
5.2. Analysis
6. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A. Full Conditionals Distributions for Pareto Data with Latent Multivariate Log-Gamma Process Models
| Parameter | Form |
|---|---|
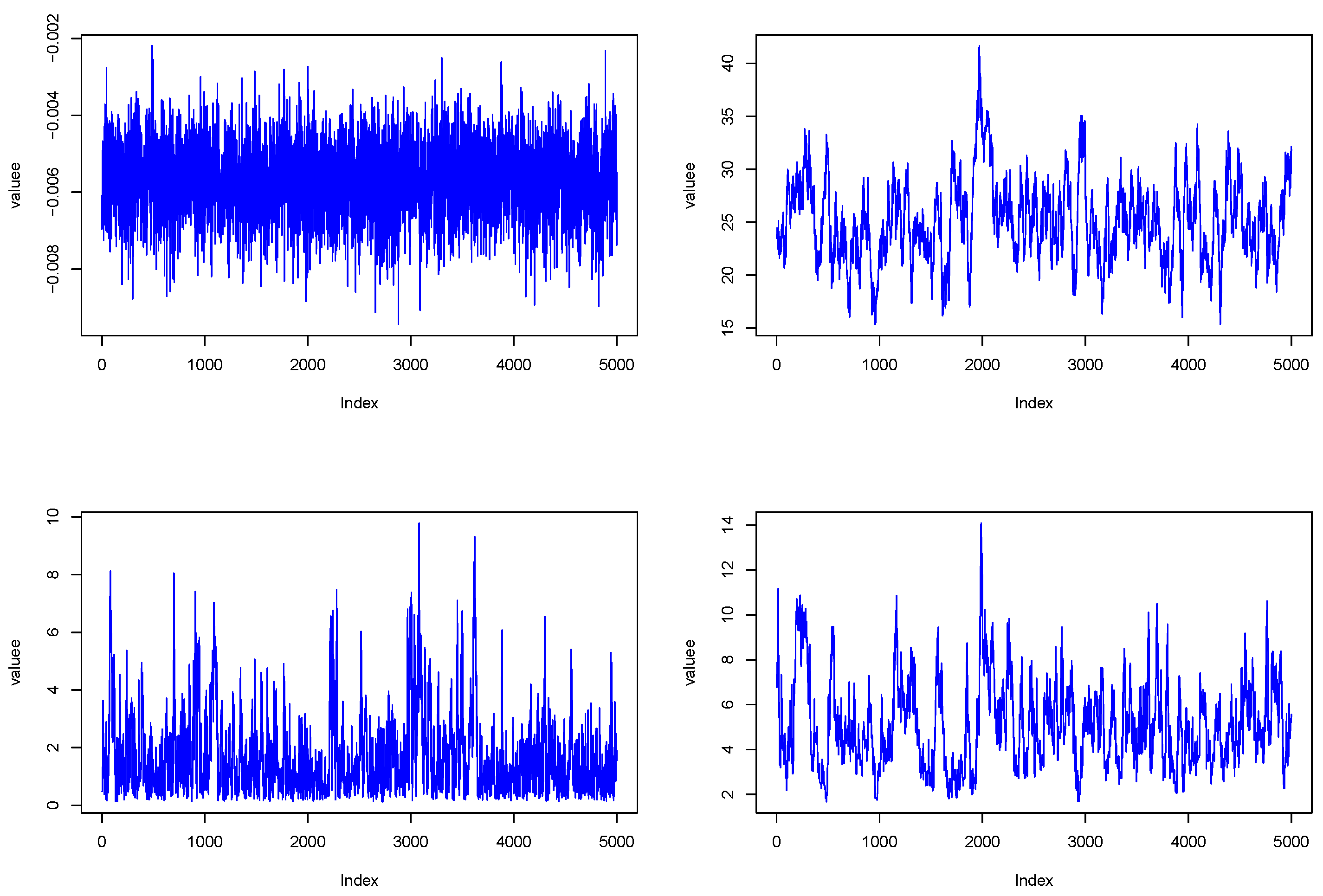
Appendix B. Trace Plot in Real Data Analysis
References
- Mega, M.S.; Allegrini, P.; Grigolini, P.; Latora, V.; Palatella, L.; Rapisarda, A.; Vinciguerra, S. Power-law time distribution of large earthquakes. Phys. Rev. Lett. 2003, 90, 188501. [Google Scholar] [CrossRef] [PubMed]
- Kijko, A. Estimation of the maximum earthquake magnitude, m max. Pure Appl. Geophys. 2004, 161, 1655–1681. [Google Scholar] [CrossRef]
- Vere-Jones, D.; Robinson, R.; Yang, W. Remarks on the accelerated moment release model: Problems of model formulation, simulation and estimation. Geophys. J. Int. 2001, 144, 517–531. [Google Scholar] [CrossRef]
- Charpentier, A.; Durand, M. Modeling earthquake dynamics. J. Seismol. 2015, 19, 721–739. [Google Scholar] [CrossRef]
- Hu, G.; Bradley, J. A Bayesian spatial—Temporal model with latent multivariate log-gamma random effects with application to earthquake magnitudes. Stat 2018, 7, e179. [Google Scholar] [CrossRef]
- Johnson, J.B.; Omland, K.S. Model selection in ecology and evolution. Trends Ecol. Evol. 2004, 19, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Cressie, N.; Calder, C.A.; Clark, J.S.; Hoef, J.M.V.; Wikle, C.K. Accounting for uncertainty in ecological analysis: The strengths and limitations of hierarchical statistical modeling. Ecol. Appl. 2009, 19, 553–570. [Google Scholar] [CrossRef] [PubMed]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: Berlin, Germany, 1973; pp. 199–213. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Dey, D.K. Bayesian model choice: Asymptotics and exact calculations. J. R. Stat. Soc. Ser. B (Methodol.) 1994, 56, 501–514. [Google Scholar] [CrossRef]
- Geisser, S. Predictive Inference; Routledge: Abingdon, UK, 1993. [Google Scholar]
- Ibrahim, J.G.; Laud, P.W. A predictive approach to the analysis of designed experiments. J. Am. Stat. Assoc. 1994, 89, 309–319. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B Stat. Methodol. 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Chen, M.H.; Huang, L.; Ibrahim, J.G.; Kim, S. Bayesian variable selection and computation for generalized linear models with conjugate priors. Bayesian Anal. 2008, 3, 585. [Google Scholar] [CrossRef] [PubMed]
- Bradley, J.R.; Holan, S.H.; Wikle, C.K. Bayesian Hierarchical Models with Conjugate Full-Conditional Distributions for Dependent Data from the Natural Exponential Family. arXiv, 2017; arXiv:1701.07506. [Google Scholar]
- Chen, M.H.; Ibrahim, J.G. Conjugate priors for generalized linear models. Stat. Sin. 2003, 13, 461–476. [Google Scholar]
- Geisser, S.; Eddy, W.F. A predictive approach to model selection. J. Am. Stat. Assoc. 1979, 74, 153–160. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Schliep, E.M. Spatial statistics and Gaussian processes: A beautiful marriage. Spat. Stat. 2016, 18, 86–104. [Google Scholar] [CrossRef]
- Bradley, J.R.; Holan, S.H.; Wikle, C.K. Computationally Efficient Distribution Theory for Bayesian Inference of High-Dimensional Dependent Count-Valued Data. arXiv, 2015; arXiv:1512.07273. [Google Scholar]
- Chen, M.H.; Shao, Q.M.; Ibrahim, J.G. Monte Carlo Methods in Bayesian Computation; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Liang, H.; Wu, H.; Zou, G. A note on conditional AIC for linear mixed-effects models. Biometrika 2008, 95, 773–778. [Google Scholar] [CrossRef] [PubMed]
- Baringhaus, L.; Franz, C. On a new multivariate two-sample test. J. Multivar. Anal. 2004, 88, 190–206. [Google Scholar] [CrossRef]
- Ogata, Y. Statistical models for earthquake occurrences and residual analysis for point processes. J. Am. Stat. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
- Neal, R.M. Slice sampling. Ann. Stat. 2003, 31, 705–741. [Google Scholar] [CrossRef]
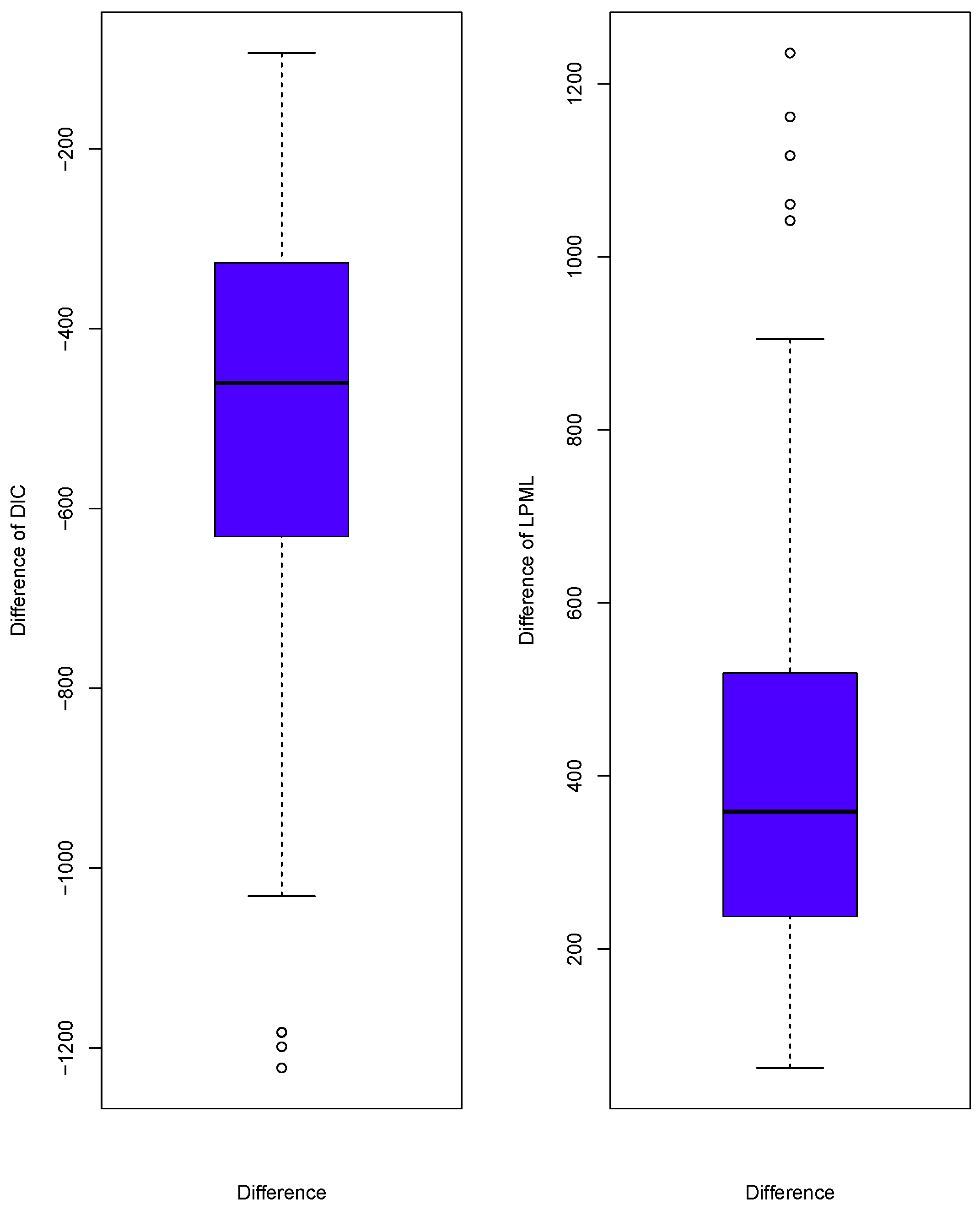
| Parameter | True Value | Bias | SE | MSE | Coverage Probability |
|---|---|---|---|---|---|
| 1 | −0.0272 | 0.2903 | 0.085 | 0.94 | |
| 1 | −0.0024 | 0.2939 | 0.0863 | 0.94 | |
| 1 | −0.0102 | 0.3369 | 0.1135 | 0.94 |
| Model | DIC | LPML | LPD | DIC | LPML | LPD |
|---|---|---|---|---|---|---|
| 3058.71 | −1535.68 | −1528.58 | 3325.47 | −1669.44 | −1661.86 | |
| 2936.72 | −1472.54 | −1469.38 | 3130.42 | −1569.94 | −1564.33 | |
| 3037.96 | −1522.69 | −1516.97 | 3258.84 | −1633.79 | −1628.54 | |
| 3056.02 | −1533.71 | −1526.38 | 3322.33 | −1666.84 | −1660.28 | |
| 2890.80 | −1446.60 | −1445.789 | 2958.61 | −1480.68 | −1478.42 | |
| 2908.10 | −1457.28 | −1452.35 | 3073.28 | −1540.16 | −1535.76 | |
| 3034.67 | −1519.84 | −1518.62 | 3896.29 | −1951.31 | −1947.27 |
| Posterior Mean | Standard Error | 95% Credible Interval | |
|---|---|---|---|
| −0.00568 | 0.0009616 | (−0.00763, −0.00389) | |
| 24.8693 | 4.5693 | (17.5827, 35.1427) | |
| 2.1620 | 2.4563 | (0.2642, 9.1086) | |
| 4.9304 | 1.7632 | (2.1670, 8.8958) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.-C.; Hu, G.; Chen, M.-H. Bayesian Variable Selection for Pareto Regression Models with Latent Multivariate Log Gamma Process with Applications to Earthquake Magnitudes. Geosciences 2019, 9, 169. https://doi.org/10.3390/geosciences9040169
Yang H-C, Hu G, Chen M-H. Bayesian Variable Selection for Pareto Regression Models with Latent Multivariate Log Gamma Process with Applications to Earthquake Magnitudes. Geosciences. 2019; 9(4):169. https://doi.org/10.3390/geosciences9040169
Chicago/Turabian StyleYang, Hou-Cheng, Guanyu Hu, and Ming-Hui Chen. 2019. "Bayesian Variable Selection for Pareto Regression Models with Latent Multivariate Log Gamma Process with Applications to Earthquake Magnitudes" Geosciences 9, no. 4: 169. https://doi.org/10.3390/geosciences9040169
APA StyleYang, H.-C., Hu, G., & Chen, M.-H. (2019). Bayesian Variable Selection for Pareto Regression Models with Latent Multivariate Log Gamma Process with Applications to Earthquake Magnitudes. Geosciences, 9(4), 169. https://doi.org/10.3390/geosciences9040169





