Modelling External Magnetic Fields of Magnetite Particles: From Micro- to Macro-Scale
Abstract
1. Introduction
2. Theoretical Models
2.1. Micromagnetism Algorithm
2.2. Numerical Calculation of the Magnetic Stray Field of Large Irregular Magnetic Structures
3. Results and Discussion
4. Conclusions
- (1)
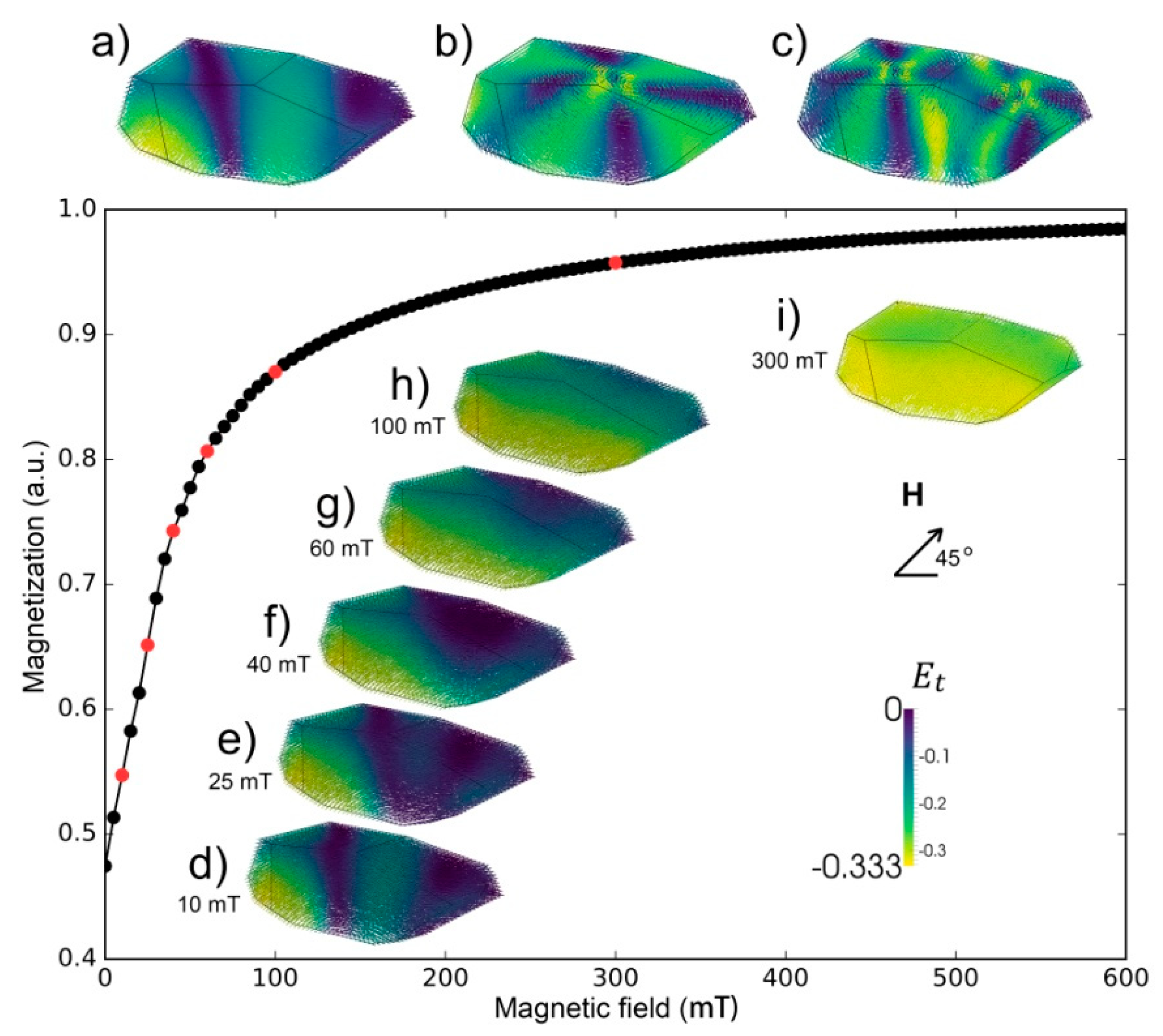
- Two-domain, single- or double-vortex configurations were found in the magnetite particle (297.8 nm) without an external field. The non-uniformity gradually changed with increasing applied fields; at 100 mT the magnetic structure becomes approximately uniform. For larger particles, fields of <100 mT are likely required to saturate the magnetic structures.
- (2)
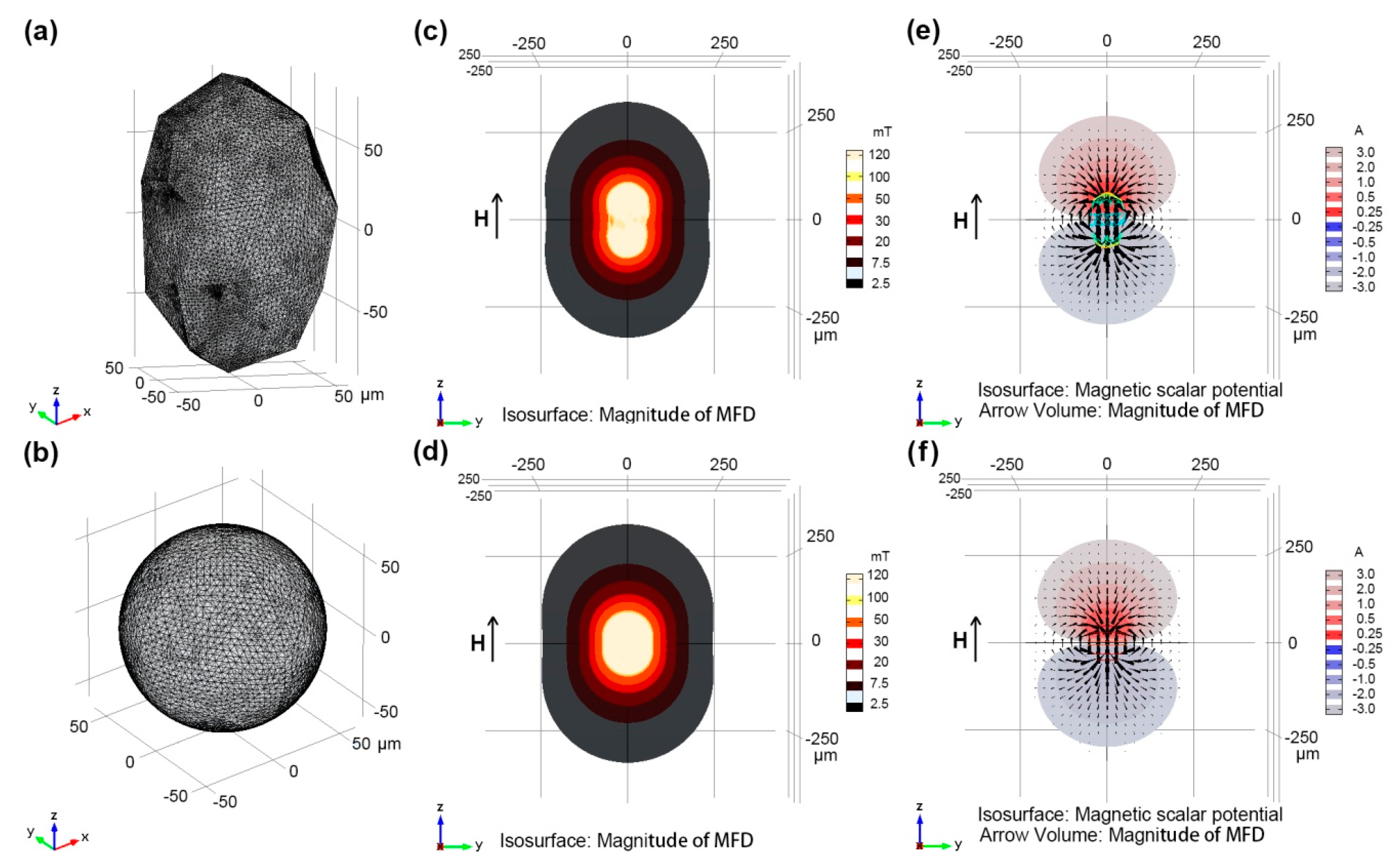
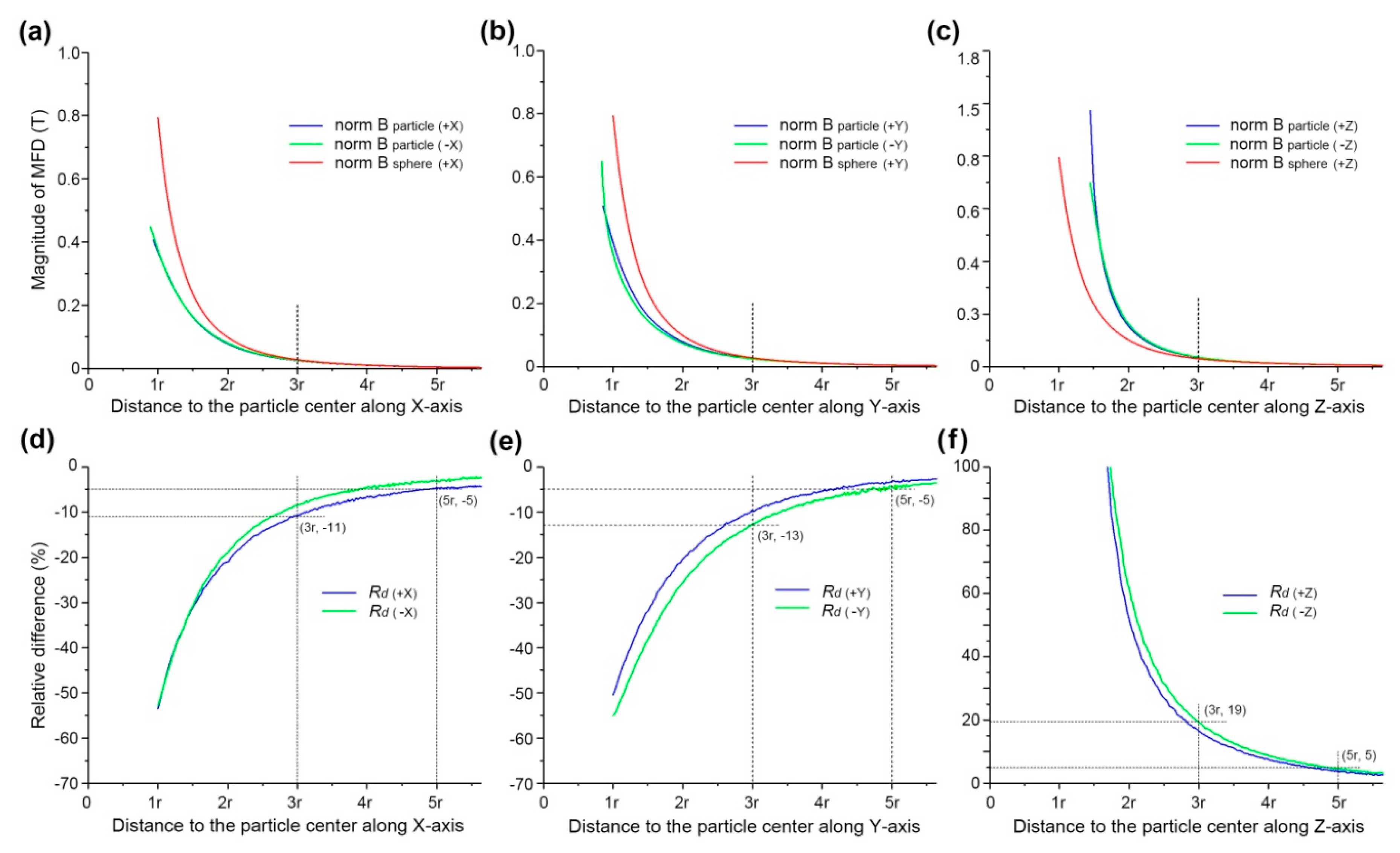
- Magnitude of MFD of a particle and the corresponding sphere drop rapidly with increasing distance before reaching a plateau. The magnitude of MFD differs significantly between the particle and sphere when the distance is relatively small, e.g., close to the surface of the particle; however, when the distance is >3r, the magnitude of MFD of the particle and sphere are nearly equal.
- (3)
- Relative differences between particle and sphere MFD vary significantly with an increase in distance from the particles.
- (4)
- The ideas developed in this paper have the potential to improve magnetic mineral extraction yield, critical to mineral processing.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Smolkin, M.R.; Smolkin, R.D. Calculation and analysis of the magnetic force acting on a particle in the magnetic field of separator. Analysis of the equations used in the magnetic methods of separation. IEEE Trans. Magn. 2006, 42, 3682–3693. [Google Scholar] [CrossRef]
- van Netten, K.; Zhou, J.; Galvin, K.P.; Moreno-Atanasio, R. Influence of magnetic and hydrodynamic forces on chain-aggregation and motion of magnetisable particles and composites. Chem. Eng. Sci. 2013, 93, 229–237. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, Y.; Lu, D. Study on capture radius and efficiency of fine weakly magnetic minerals in high gradient magnetic field. Miner. Eng. 2015, 74, 79–85. [Google Scholar] [CrossRef]
- Fischer, P.; Ghosh, A. Magnetically actuated propulsion at low Reynolds numbers: towards nanoscale control. Nanoscale 2011, 3, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Martinez, H.A.; Song, S.; Lopez-Valdivieso, A. In situ observation of quartz particles entrained into magnetite coagulates in a uniform magnetic field. Miner. Eng. 2011, 24, 963–966. [Google Scholar] [CrossRef]
- Ku, J.; Chen, H.; He, K.; Xu, L.; Yan, Q. Numerical simulation of agglomeration process dynamics offerromagnetic mineral particles in a weak magnetic field. Int. J. Miner. Process. 2014, 133, 46–51. [Google Scholar] [CrossRef]
- Dimova, T.; Aprahamian, B.; Marinova, M.; Streblau, M. Increasing the efficiency of permanent magnet separators by maintenance of certain functional state of the object of separation. In Proceedings of the 18th International Symposium on Electrical Apparatus and Technologies, Bourgas, Bulgaria, 29–31 May 2014; pp. 1–4. [Google Scholar]
- Ku, J.; Chen, H.; He, K.; Yan, Q. Simulation and observation of magnetic mineral particles aggregatinginto chains in a uniform magnetic field. Miner. Eng. 2015, 79, 10–16. [Google Scholar] [CrossRef]
- Sand, A.; Stener, J.F.; Toivakka, M.O.; Carlson, J.E.; Pålsson, B.I. A stokesian dynamics approach for simulation of magnetic particle suspensions. Miner. Eng. 2016, 79, 70–76. [Google Scholar] [CrossRef]
- Petruska, A.J.; Abbott, J.J. Optimal permanent-magnet geometries for dipole field approximation. IEEE Trans. Magn. 2013, 49, 811–819. [Google Scholar] [CrossRef]
- Zhou, N.N.; Xue, G.Q.; Gelius, L.J.; Wang, H.Y.; Yan, S. Analysis of the near-source error in TEM due to the dipole hypothesis. J. Appl. Geophys. 2015, 116, 75–83. [Google Scholar] [CrossRef]
- Muxworthy, R.A.; Williams, W.; Virdee, D. Effect of magnetostatic interactions on the hysteresis parameters of single-domain and pseudo-single-domain grains. J. Geophys. Res. 2003, 108, 2517. [Google Scholar] [CrossRef]
- Zhao, C.W. Research of Mechanics Behavior of MRFs Based on Microstructure. Ph.D. Thesis, Chongqing University, Chongqing, China, 2014. [Google Scholar]
- Ku, J.G.; Liu, X.Y.; Chen, H.H.; Deng, R.D.; Yan, Q.X. Interaction between two magnetic dipoles in a uniform magnetic field. AIP Adv. 2016, 6, 025004. [Google Scholar] [CrossRef]
- Schabes, M.E.; Bertram, H.N. Magnetization processes in ferromagnetic cubes. J. Appl. Phys. 1988, 64, 1347–1357. [Google Scholar] [CrossRef]
- Nagy, L.; Williams, W.; Muxworthy, A.R.; Fabian, K.; Almeida, T.P.; Conbhuí, P.Ó.; Shcherbakov, V.P. Stability of equidimensional pseudo–single-domain magnetite over billion-year timescales. Proc. Natl. Acad. Sci. USA 2017, 114, 10356–10360. [Google Scholar] [CrossRef] [PubMed]
- Ó Conhuí, P.; Williams, W.; Fabian, K.; Ridley, P.; Nagy, L.; Muxworthy, A.R. MERRILL: Micromagnetic earth related robust interpreted language laboratory. Geochem. Geophys. Geosyst. 2018, 19, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Williams, W.; Dunlop, D.J. Three-dimensional micromagnetic modelling of ferromagnetic domain structure. Nature 1989, 337, 634–637. [Google Scholar] [CrossRef]
- Williams, W.; Muxworthy, A.R.; Evans, M.E. A micromagnetic investigation of magnetite grains in the form of Platonic polyhedra with surface roughness. Geochem. Geophys. Geosyst. 2011, 12, Q10Z31. [Google Scholar] [CrossRef]
- Wightman, W.E.; Jalinoos, F.; Sirles, P.; Hanna, K. Application of Geophysical Methods to Highway Related Problems; Federal Highway Administration: Washington, DC, USA, 2004.
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, J.; Valdez-Grijalva, M.A.; Deng, R.; Zuo, W.; Chen, Q.; Lin, H.; Muxworthy, A.R. Modelling External Magnetic Fields of Magnetite Particles: From Micro- to Macro-Scale. Geosciences 2019, 9, 133. https://doi.org/10.3390/geosciences9030133
Ku J, Valdez-Grijalva MA, Deng R, Zuo W, Chen Q, Lin H, Muxworthy AR. Modelling External Magnetic Fields of Magnetite Particles: From Micro- to Macro-Scale. Geosciences. 2019; 9(3):133. https://doi.org/10.3390/geosciences9030133
Chicago/Turabian StyleKu, Jiangang, Miguel A. Valdez-Grijalva, Rongdong Deng, Weiran Zuo, Qidi Chen, Hua Lin, and Adrian R. Muxworthy. 2019. "Modelling External Magnetic Fields of Magnetite Particles: From Micro- to Macro-Scale" Geosciences 9, no. 3: 133. https://doi.org/10.3390/geosciences9030133
APA StyleKu, J., Valdez-Grijalva, M. A., Deng, R., Zuo, W., Chen, Q., Lin, H., & Muxworthy, A. R. (2019). Modelling External Magnetic Fields of Magnetite Particles: From Micro- to Macro-Scale. Geosciences, 9(3), 133. https://doi.org/10.3390/geosciences9030133





