2. Overview of Tested Systems
All valid ETAssessments of the 66 flexible rockfall protection systems tested according to ETAG 027 are listed on the EOTA website [
19]. It is known that there are more protection systems available on the market, but that do not have a valid ETA.
During the period when ETAG 027 was used for approval or assessment, ten different manufacturers/producers of flexible rockfall protection systems obtained approval or assessment. This means that, on average, 6.6 different systems per manufacturer were tested. Some manufactures had a single system tested, whereas the maximum number of tested systems from a single manufacturer was 17.
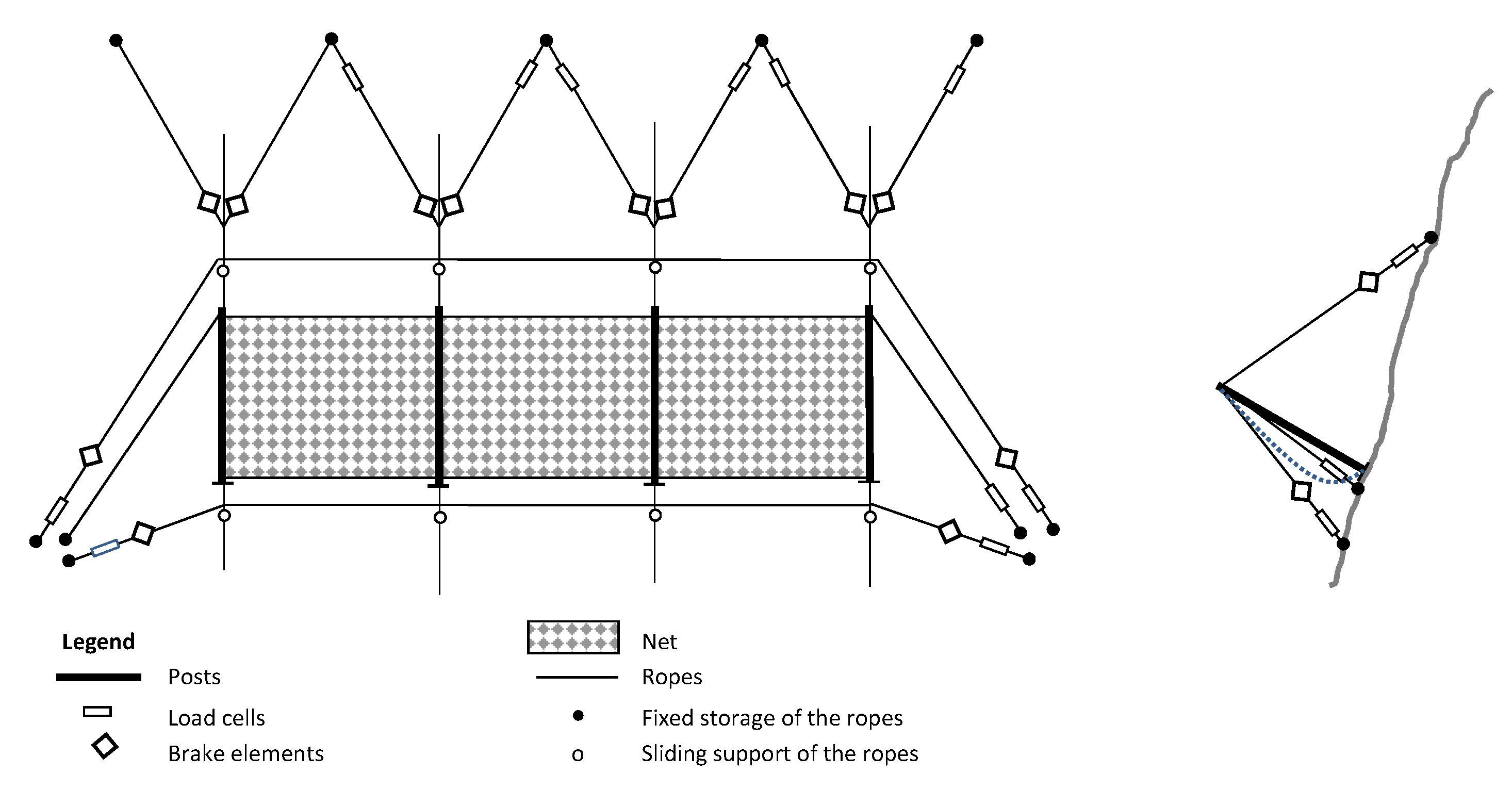
When speaking of tested systems, the mentioned tests are usually related to the impact of a single block within the center of the middle field of a barrier consisting of three fields, as sketched in
Figure 1. The block’s shape, density, size, and minimum impact speed are defined in the corresponding regulations. A test usually is quantified by the level of the kinetic energy of the impacting block. The ETAG 027 distinguishes between a Maximum Energy Level (MEL) and a Service Energy Level (SEL). The SEL test foresees two subsequent impacts of the same block without any repair works in between. The classification of the tested systems into the energy classes defined in ETAG 027 are shown in
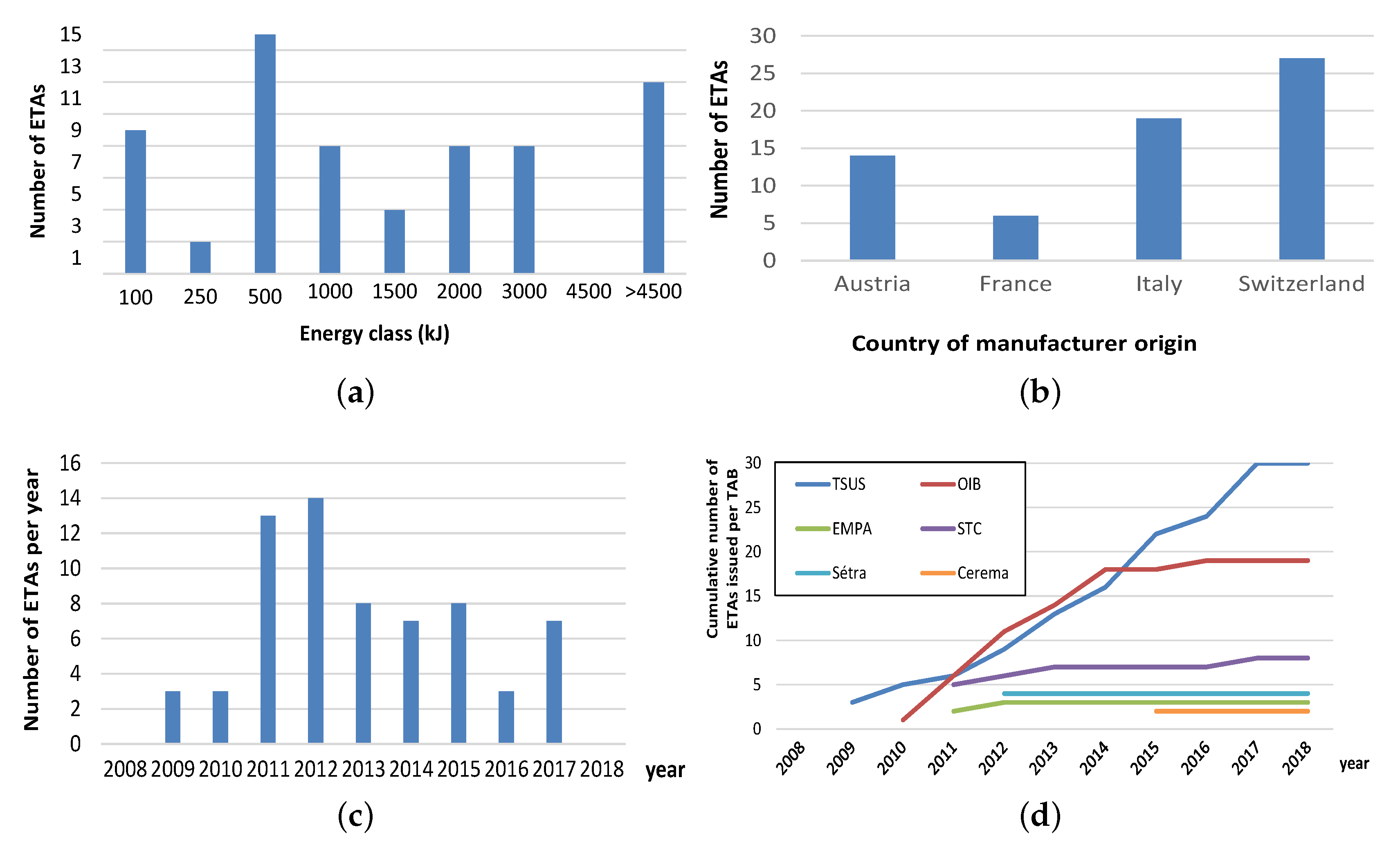
Figure 2. Most of the systems have an MEL of 500 kJ. The energy class “>4500 kJ” has 12 members because it covers a wide energy spectrum with different impact MELs, ranging from 5040 kJ to 10,400 kJ. There is no system listed in the class “4500 kJ” because, on the one hand, no manufacturer asked for an assessment of its barrier within this class and, on the other hand, as soon as the MEL is even slightly greater than 4500 kJ, the system can be listed within the highest energy class “>4500 kJ”. Therefore, the class “4500 kJ” has been rated in this context as non-existent and there are, on average, 8.3 systems tested per energy class. This gives an impression of the large variety of systems the market offers to the clients.
The geographical distribution of the manufacturers of the tested systems, which ranged from 6 (France) to 27 (Switzerland) per country, is shown in
Figure 2b. All systems originate from only four European countries, i.e., so far, there are no barriers from overseas tested for CE marking. The years when ETAs were issued are presented in
Figure 2c, where year corresponds to the official document number of the ETAs [
19], in which the first two digits indicate the reference year. Most of the systems received their ETA during 2011 or 2012.
In principle, every member state of EOTA has at least one designated TAB that can issue an ETA if the TAB is nominated for product area 34 (see [
9] Annex IV for a list of product areas). However, manufacturers are also free to choose TABs in other countries, and this is visible in
Figure 2d: ETAs are issued by six TABs located in five countries. The “Building Testing and Research Institute” (TSUS) from Slovakia issued the most ETAs even though no manufacturer is situated there, and four of the TABs issued only a few ETAs.
Aiming for an ETA is a technical procedure that requires a large administrative effort. Therefore, a relatively long time can pass before a manufacturer receives a valid ETA even if the product itself would be ready to be sold sooner.
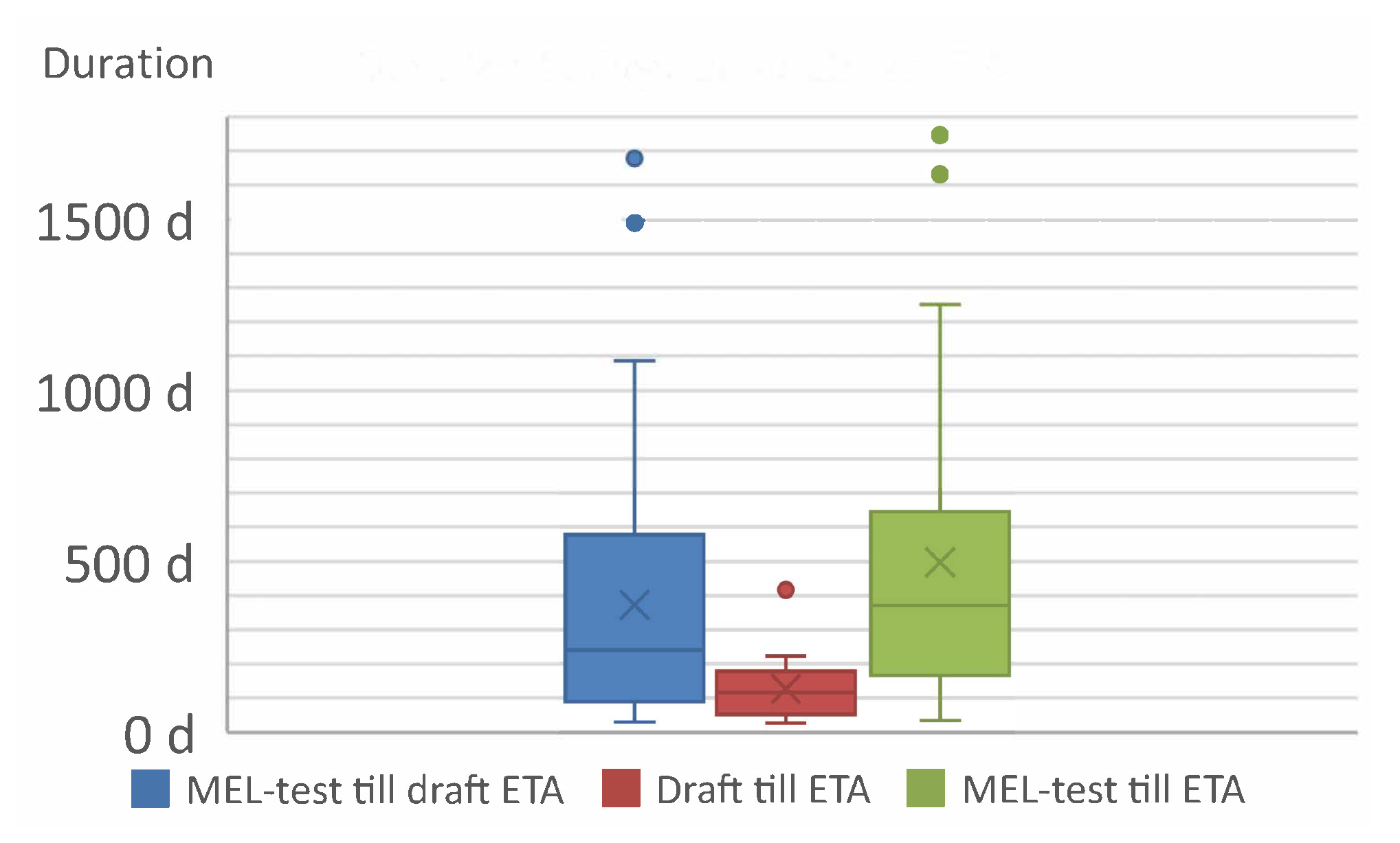
Figure 3 features three boxplots indicating the time needed to have a first draft of an ETA ready for circulation, for all EOTA members, and the time required for the circulation and iterations. The median value for circulation is 116 days, and there are 1.35 iterations on average. A maximum of three iterations was observed. The median time between a successful MEL test and the issuing of an ETA is 371 days. The fastest approval/assessment procedure took 35 days, including four weeks for the commenting period. The longest durations were more than four years. The reason for such long periods is mostly that the MEL test took place long before the manufacturer decided to apply for an ETA for the corresponding system. Witnessing of the test by a TAB still has to be solved in such a case.
2.1. System Specifications
A total of 55 tested systems were set up using simply supported posts in combination with an upslope suspension, whereas 10 systems had clamped posts. Apart from a few, all systems had a length of 30 m, covering three fields and four posts.
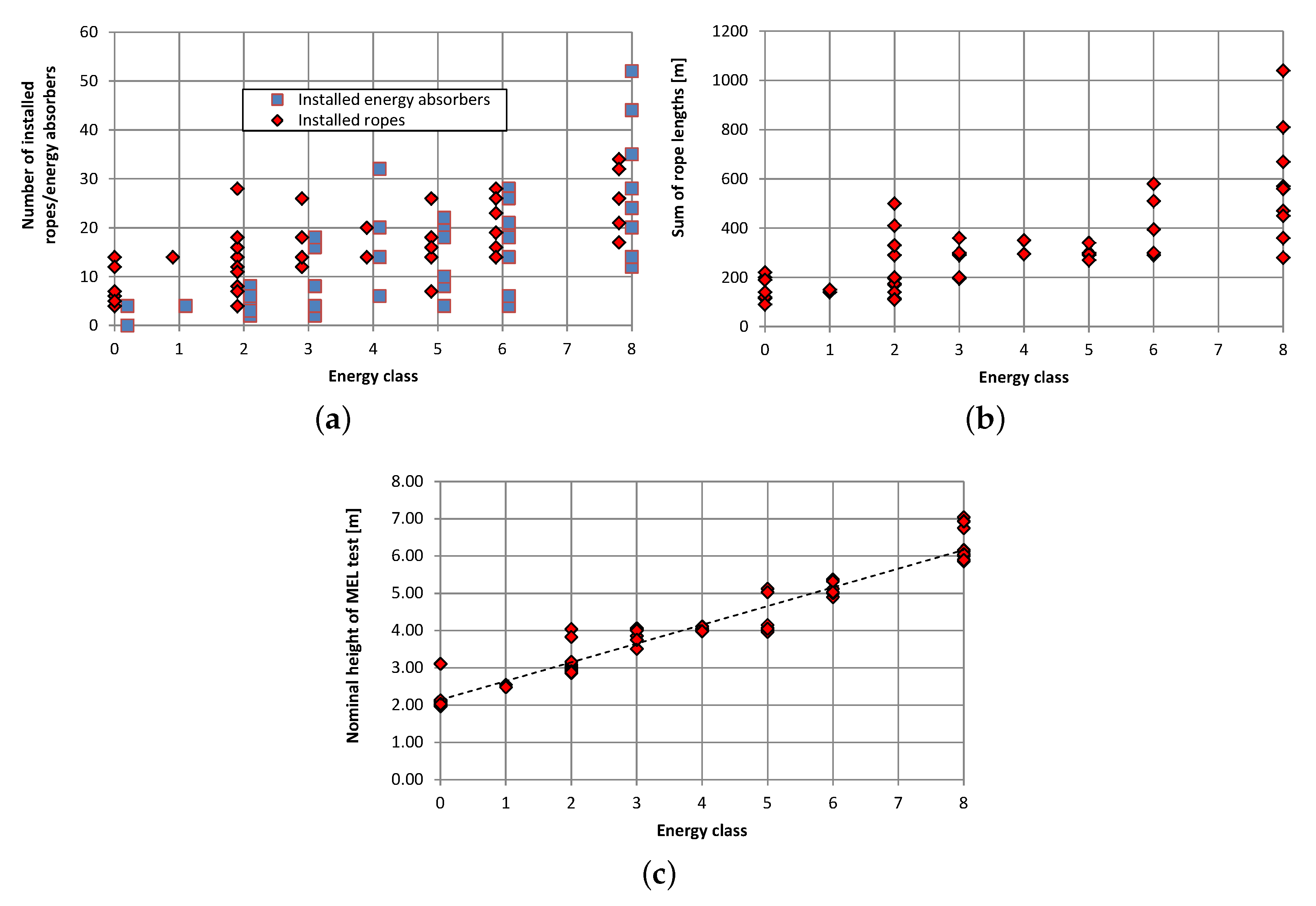
Figure 4a gives an impression of the number of energy-absorbing elements and ropes used for such a system, depending on the energy class. If the single rope lengths are estimated based on their function/position within a system, the sum of all rope lengths can be calculated; this total length ranges from about 100–1050 m, as shown in
Figure 4b. The total length within a single energy class varies by up to 500%.
The nominal height of a system is defined as the minimum distance of the upper net edge or support rope to the base line of the system close to the ground, projected orthogonally to a so-called reference slope upslope of the barrier. The nominal height of the barriers was between 1.97 m and 7.05 m and usually increased with increasing energy class, as shown in
Figure 4c for all MEL tests. Within a single energy class, nominal height varied by up to about 1 m. The nominal height of the corresponding SEL tests (for all energy classes except Class 0) differed from the MEL nominal height maximum of 0.37 m by an average of 0.03 m. This corresponds to an average deviation of the tested SEL and MEL nominal heights of 1%.
2.2. Testing Conditions
ETAG 027 allows testing of the barriers at different angles of the block’s trajectory with respect to the horizon. Of the test setups known within this framework, a vertically free-falling test specimen was used in 74% and inclined trajectories impacted the nets in 26% of the test. If barrier inclination is defined as the inclination of the steel posts with respect to the horizon, the falling blocks entered the different barriers with an impact angle between 57 and 89
(average 73
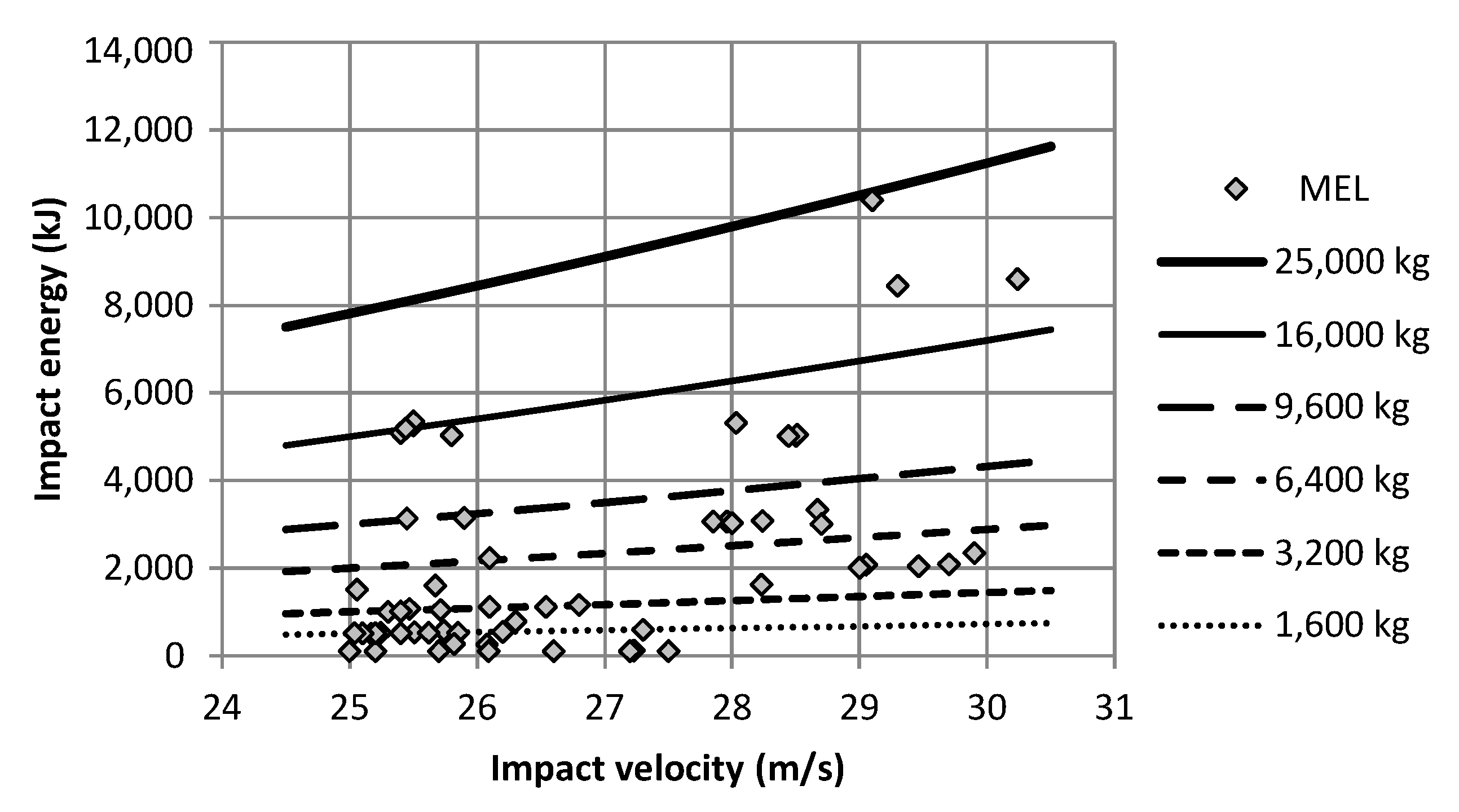
). The impacting blocks weighed between 260 and 24,900 kg, entering the barriers with impact velocities generally ranging from 25.0–30.2 m/s to achieve the necessary kinetic impact energies.
Figure 5 gives an impression of which combination of block mass and impact velocity led to a certain impact energy and which combination was used for the different MEL tests.
The block dimensions (
) varied between 0.5 and 2.3 m. According ETAG 027, block density has to be between 2500 and 3000 kg/m
. Density is estimated by calculating the block’s volume (
V) from its average extension
:
Block densities ranged from 2500–2997 kg/m
, with an average value of 2741 kg/m
.
3. Performance of Barriers
In this section, results about the deceleration processes of the falling blocks and the measured rope forces and residual useful heights of the barriers are presented (measured after the impact without removing the block).
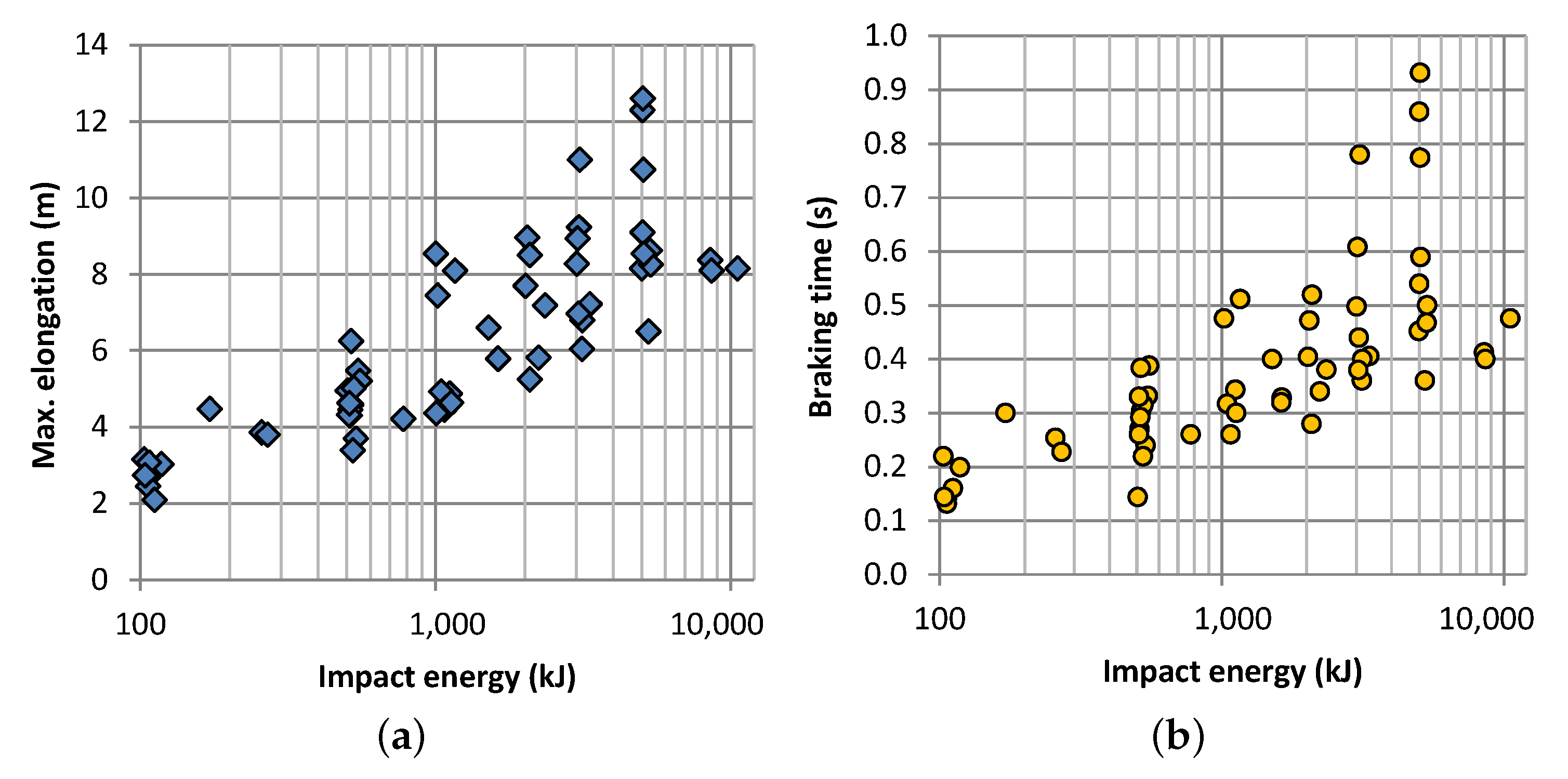
As a result of the different testing conditions and different constructions of barriers, different braking distances and times occurred. Based on the impact energy, shorter braking distances were more likely for low impact energies and larger ones for higher impact energies. However, there were also differences within the individual energy classes. For example, in the energy class 500 kJ, maximum braking distances of 3.7–6.2 m were measured. This is a relatively large range and overlaps with the braking distances of 4.5–8.5 m in the 1000-kJ energy class. Minimum braking distances of 2.5 m were measured for the 100 kJ class, and a maximum of 12.5 m was measured for 5000 kJ of impact energy (
Figure 6a).
Braking time also varied widely, with values ranging from 0.13–0.22 s for the 100-kJ class and from 0.35–0.95 s for 5000 kJ of impact energy. The braking distances and braking times had much narrower ranges for 8000 kJ of impact energy, with braking distances of 8.1–8.4 m and braking times of 0.4–0.41 s (
Figure 6b).
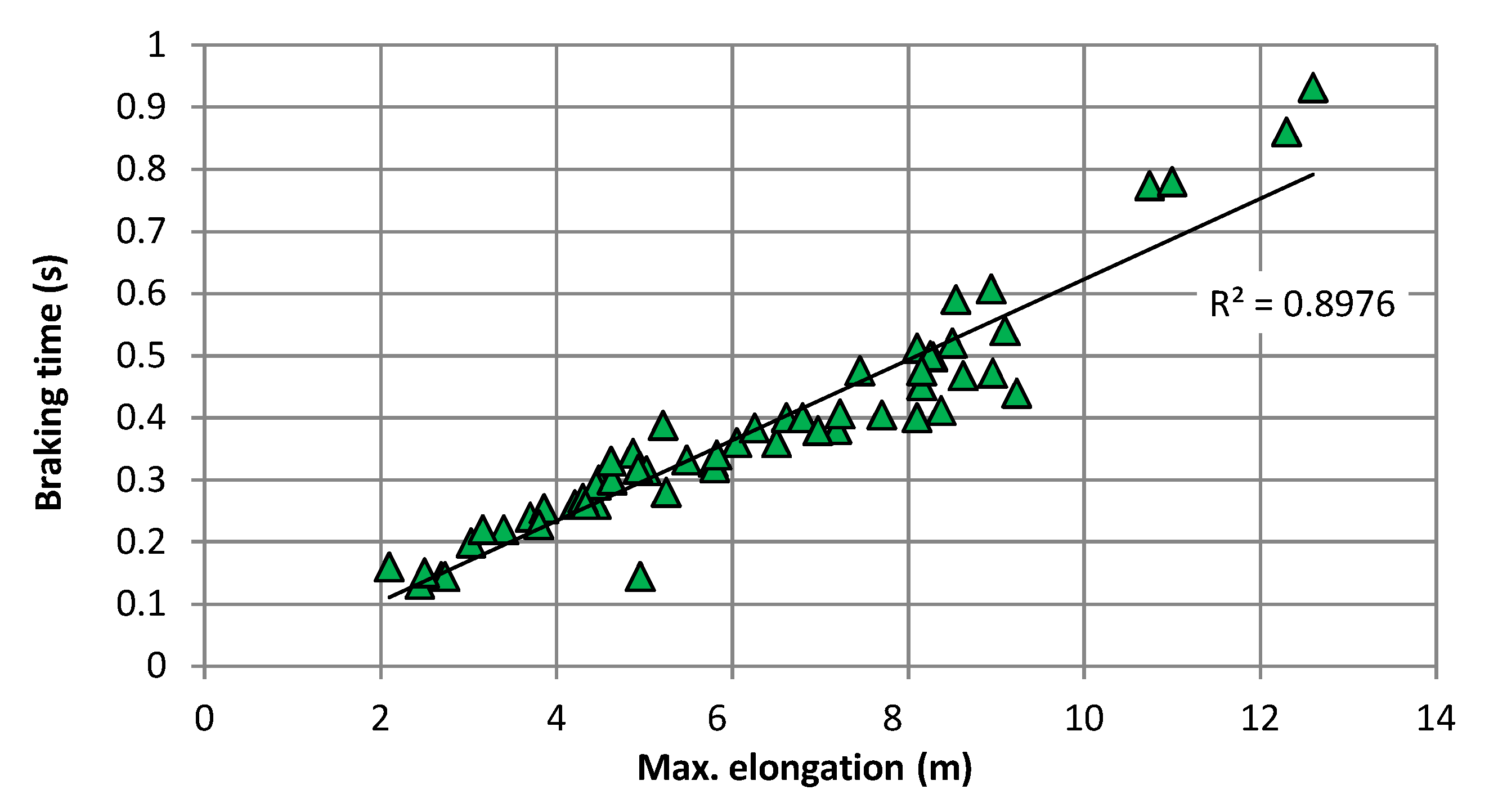
Based on the similar point distributions of braking distances and braking times in
Figure 6, it seems that there is a relationship between these two variables. To examine this relationship in more detail, braking time was plotted as a function of braking distance, and the correlation was shown to be almost 90% (R
= 0.898). For braking distances of 2–12.5 m, the braking times were 0.14–0.93 s (
Figure 7). However, this representation of the individual values also suggests that errors have crept into the data. For example, the “normal” braking times for a braking distance of approximately 5 m were between 0.28 and 0.35 s. The value (0.14 s/5 m) does not fit into this correlation and seems to be clearly wrong, recommending a check of the corresponding testing report.
When braking a falling weight, it always experiences a braking force. This braking force is zero during free fall and reaches a maximum during the braking process. Today, such a maximum braking force and its development can be measured as for example shown in [
20] or derived from a deflection-time-curve that has been extracted from video records. However, such procedures are not prescribed by the current testing guidelines for rockfall protection nets, and therefore, no such information is available for further analyses. Instead, the given braking times and distances can be used to formulate average braking forces, i.e., a braking force that is assumed to be constant during the braking process or along the braking distance. It must be clear that such an assumption of constancy does not reflect reality; especially because of the different structural behavior of each system: some of them produce a curve of the braking force over time that stays rather low for a longer time after first net contact ending up with a high peak just before standstill; others, in turn, build up a significant resistance force almost immediately after net contact with a lower maximum force. Both variants could show the same average braking force. Different thinkable evolutions of braking forces over time are discussed in [
21].
For an average force
, two approaches are thinkable. One calculates the magnitude based on the impact energy of the block
corresponding to the work that has been done by the average braking force
along the braking distance
s by:
Another approach assumes the force
to be constant until the block’s momentum
has been absorbed during the braking time
by:
Both approaches to calculate an average braking force neglect the influence of gravity. To include this correctly, the vertical component of the braking force has to be modified accordingly.
Figure 8a visualizes both
and
for all MEL tests. Both approaches follow a polynomial trend with increasing impact energy. As stated above, the diagrams shown in
Figure 8a do not inform about the maximum peak forces to be expected, but the magnitude of the average forces. This information can be used for single manufacturers to classify the performance of their barriers to the competitors’ ones. Both approaches for
deliver similar results for an averaging braking force: the relation between
and
mostly is between 1.0 and 1.5, as is visible in
Figure 8b. The outlier visible in this figure recommends a check of the corresponding testing reports.
A barrier has to absorb not only the impact energy, but also the potential energy of the impacting block along its braking distance (see [
22] and
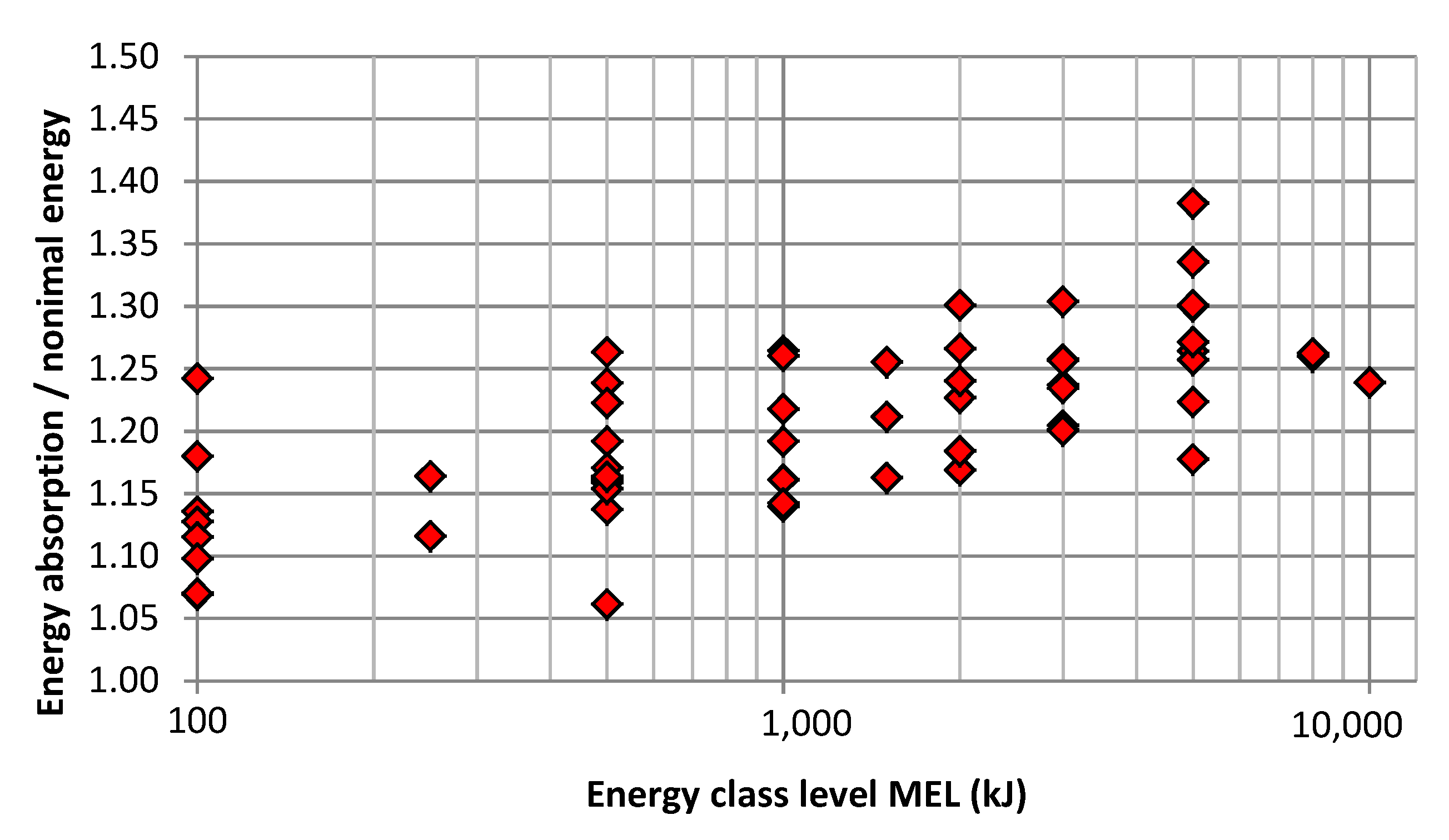
Figure 9). This means that a barrier absorbs more energy than represented by its energy class. The procedure for determining the magnitude of this increase and the total energy dissipated by a barrier is explained here. The potential energy directly corresponds to the braking distance for vertically-falling blocks. For inclined impact trajectories, only the vertical portion of the braking distance contributes to the potential energy. Therefore, the potential energy of the impacting block along its braking distance has to be added to the kinetic impact energy. This new value corresponds to the total work performed by the barrier with regard to the lowest position of the block in the net. A comparison of the resulting values with the nominal energy values of the individual energy classes is presented in
Figure 10. This comparison indicates an average conversion factor of 1.20, which means that the barriers absorb about 20% more energy than minimally required in the respective energy class. Within the lowest energy class (100 kJ), the values are scattered over a relatively wide range of 7–24%, in contrast to in the energy class 3000 kJ, where 20–30% more energy was dissipated. Data from the energy class >4500 kJ were presented not together within a single energy line, but split into the effectively-aimed impact energies of 5000 kJ, 8000 kJ, and 10,000 kJ. It is noteworthy that in this energy class, the energy effectively absorbed at 5000 kJ increases by up to 38% relative to the impact energy.
The barriers not only have to absorb energy, but also have to comply with certain conditions regarding the position of the barrier height after a test. According to [
12], the residual height, i.e., the distance between the suspension ropes projected orthogonally to the reference slope, must be at least 70% of the original nominal height after the first test with a block impacting at the service energy level (SEL1). The residual height after the MEL defines the quality class into which a barrier is categorized: if the 50% limit is exceeded in the MEL test, the barrier is assigned to Quality Class A; for values more than 30 and up to 50%, Class B; and for values equal to or less than 30%, Class C.
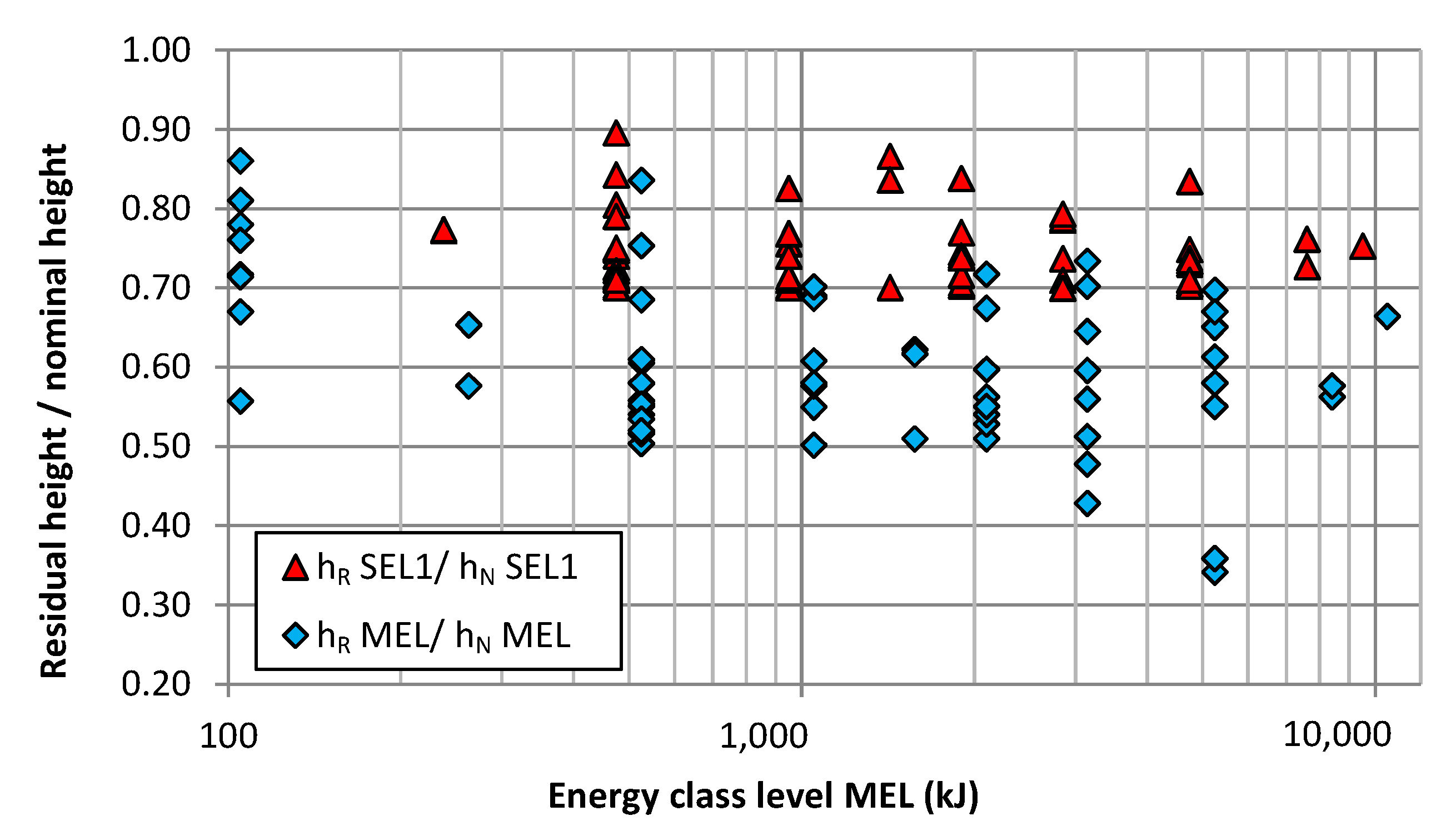
Because of the residual height requirement of 70% after SEL1, all tested barriers fulfil this criterion (
Figure 11). For the energy class 500 kJ, a value of 90% was even measured, which means that the height of the barrier is only reduced by 10% after SEL1 impact. Values of over 80% were measured in other energy classes, as well.
After the MEL test, almost all barriers reached a residual height of 50% and therefore were categorized as Quality Class A. Only the energy classes 3000 kJ and 5000 kJ each had two barriers that were classified as Quality Class B. No barrier was categorized into Class C; this might be related to the correlation prescribed in ETAG 027 between the size of the impacting block L and the minimum nominal height h, i.e., h > 3 L. In other words, if the block size is about 33% and it is assumed that the minimum residual height of the barrier is located at the impact position, the residual height automatically is greater than 30% and therefore belongs to Class B.
Overall, many barriers show residual heights of over 70% after the MEL test, especially in the low energy classes of 100 kJ and 500 kJ. This ensures continuing protection against any subsequent falling rocks.
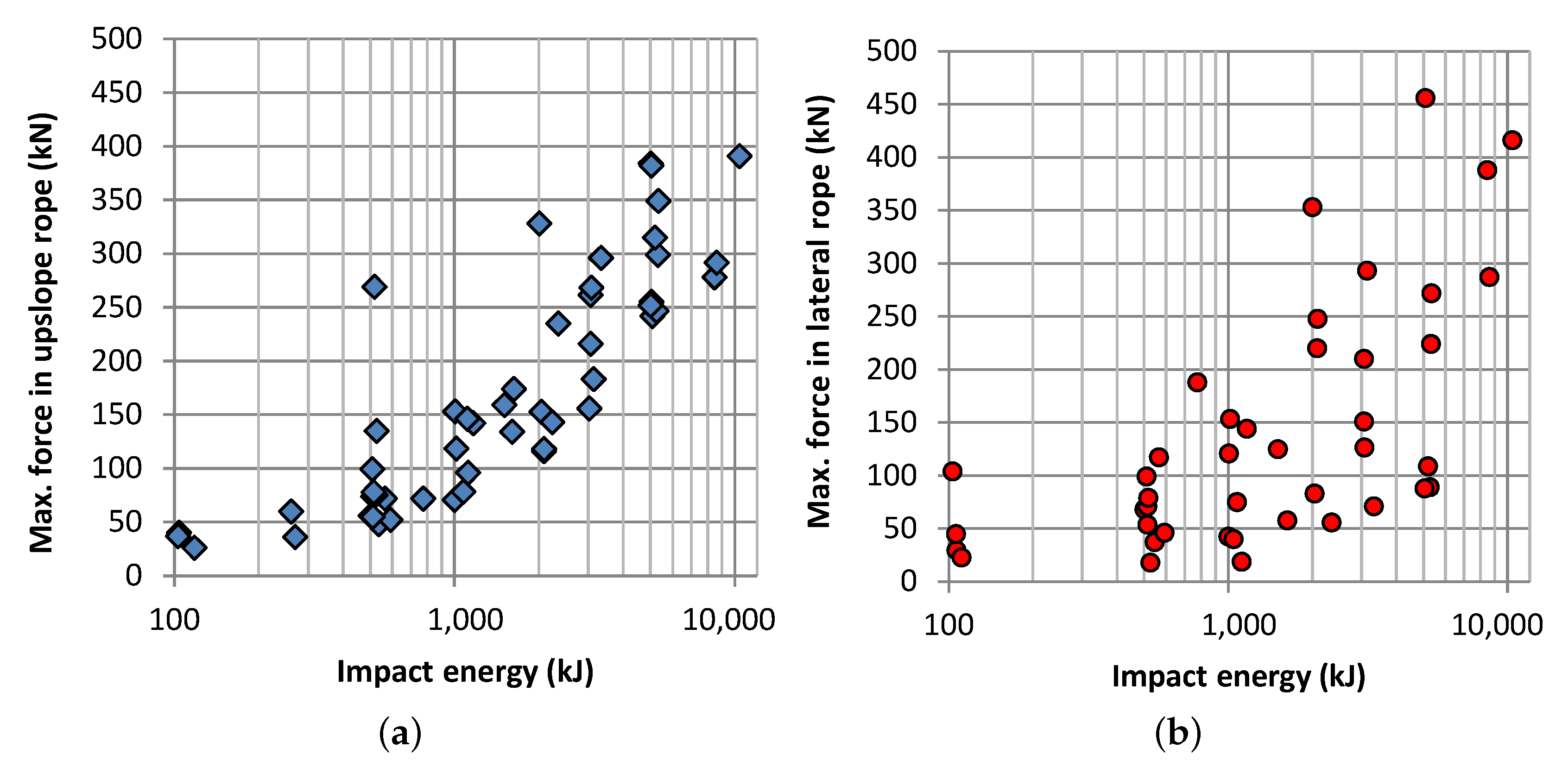
A relatively large scatter of the data within a single energy class and among the different energy classes was also apparent for the measured rope forces. The barriers are constructed in many different ways, and thus, uniform functioning cannot be expected. Especially the different structural constellations regarding the longitudinal net supporting ropes cause differing loads on anchorages. The only components that are common to almost all systems and that were measured during the tests are upslope retention ropes and lateral suspension ropes. Therefore, only the results of the maximum forces in the upslope ropes and those in the lateral ropes are presented here and shown in
Figure 12.
The maximum forces in the upslope ropes (
Figure 12a) basically show strong dependence on the impact energy. With increasing energy, the forces in the upslope ropes also increase. However, these forces are decisively influenced by the presence of energy-absorbing elements (so-called braking elements). The braking elements dampen and limit the maximum force within the ropes, allowing the forces to remain at a lower level. However, this influence could not be analyzed in detail. The relatively large forces (230 kN and 330 kN) at the impact energies of 500 kJ and 2000 kJ therefore only suggest the absence of braking elements.
An increase in the maximum forces in the lateral ropes was also detected with increasing impact energy (see
Figure 12b). The dispersion of the forces by a factor of 3–4 in the individual classes, however, is much greater than that observed for the upslope ropes. These data are therefore only of limited use, but further point out the existing variety of different systems regarding their performance.
In principle, one would assume that a longer braking distance reduces the loads within a system or the single ropes, respectively. However, when looking at
Figure 13a, it seems to be the reverse. Here, the measured maximum forces of the upslope and lateral ropes are plotted against the braking distance. The higher the braking distance, the higher the loads are. However,
Figure 13a fully neglects the different impact energies. Usually, higher impact energies result in higher braking distances, and this in turn explains the higher maximum rope forces. To propose a consideration of the impact energies,
Figure 13b plots the rope forces against the braking distance divided by the impact energy. A clear trend is visible that the highest loads are measured for the lowest abscissa values, i.e., highest impact energies. The upslope force of the system with an abscissa value of about 0.012 does not follow this trend. In fact, when checking the system’s structure in the ETA, it had a clearly different structural setup compared to other systems.
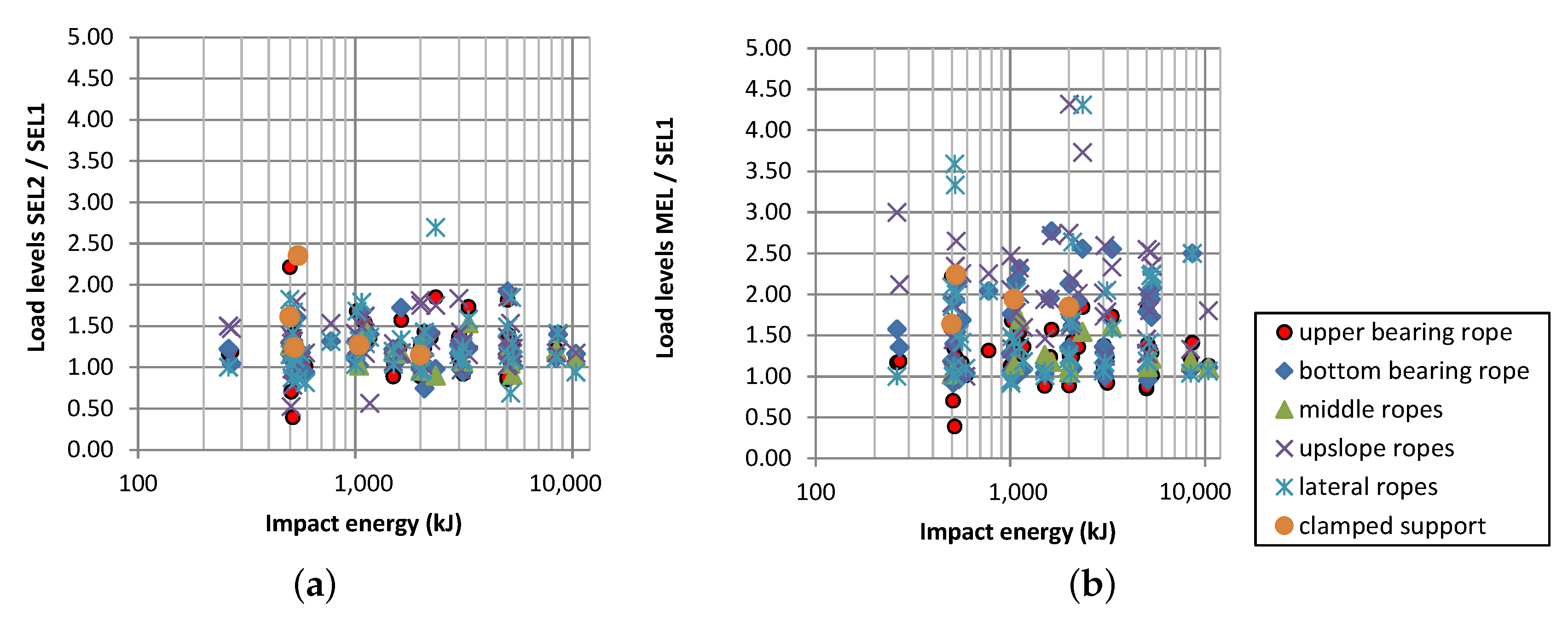
Another approach studying the maximum forces acting within the ropes is to evaluate the different loads within the same system during the SEL1, SEL2, and MEL tests. These loads are directly comparable because they are usually measured at the same location within a barrier during all tests. If the maximum load achieved during SEL1 test serves as a reference level, the corresponding loads during the SEL2 test increased by 20% on average. This increase is usually observed because the SEL1 impact degrades all existing pre-tension within an unloaded barrier; the SEL2 impact then enters a more or less loose system, resulting in larger peak loads during braking. The loads detected during the MEL test, i.e., 300% impact energy, were 53% larger on average. The factor by which the measured loads changed in the SEL2 and MEL tests relative to the SEL1 test is displayed in
Figure 14. In most cases, the load increased by a factor of less than 2.0 for the SEL2 test and less than 3.0 for the MEL test. Many loads had change factors around 1.0. In most cases, this finding is related to the existence of braking elements, which dampen and limit the rope forces transferred to the anchorage. Cases where forces for SEL2 or MEL are smaller than those for SEL1 (i.e., change factors clearly less than 1.0) can be explained by the behavior of brake elements: the activation force of some brake elements, i.e., the load at which the brake starts elongating, is not always the same. If there is a large scatter for the activation force of a brake element and an element is not activated at all during SEL1, the corresponding values of SEL2 or MEL might remain below.
There are other post-test criteria that have to be reported in the ETA, for example how much the mesh width is reduced at the outer posts. The lateral inward movement of the mesh edge at the outer posts (lateral gaps) reached up to 2.01 m after the SEL1 test or 6.7 m after the MEL test. In the median, 0.31 m openings are observed after the MEL test. The more recently developed barriers usually show no lateral gaps after testing.
To gain insight into the residual energy-absorbing capabilities of a system after an impact (mostly after the MEL test), the potential residual capacity of the energy-absorbing elements has to be determined. If an energy absorber has been fully activated, the system has no reserves left. The maximum remaining capacity was observed to be 68%, i.e., only 32% of the barrier’s capacity have been exploited. On average, the tested barriers had a residual capacity of 19.9% after testing.
4. Evaluation and Known Issues
It can be seen from
Figure 2c that a total of six TABs actively handle ETAs regarding ETAG 027. However, four of them are responsible for only a small number of ETAs, whereas two cover a continuously-increasing number of ETAs. Looking at the evolution over time, it is apparent that most of the TABs started with ETAG 027-ETAs at about the same time: around the beginning of the second decade of this millennium. However, most of them did not cover additional ETAs, and the number of institutions that handle ETAs actually declined over time. This is advantageous in that the remaining two institutions gain much experience and can guarantee consistent quality of the ETAs for the investigated product area. On the other hand, if all the other TABs do not cover new ETAs, their knowledge and expertise within this field diminishes over time. This increases the risk that they cannot sufficiently evaluate the ETAs that are sent for circulation among the EOTA members.
ETAG 027 allows barriers with different inclinations of the impacting block’s trajectory to be tested. This makes it difficult to compare the performance of different barriers within, e.g., one energy class. Volkwein [
22] and Heiss [
23] studied the influence of an inclined versus a vertical trajectory test setup, and both studies led to the conclusion that especially the residual height after a rockfall event is affected significantly. However, commonly-accepted methods to cover such differences do not exist. For example, it is not yet defined how barrier characteristics such as residual height or residual capacity of energy absorbers have to be adjusted if the reference slope of a tested system differs too much from the slope angle in the field.
Certainly, any standardization of construction product testing neglects the variability in product loading under (natural) field conditions, owing to differences in block shape, rotational movements, impact speed, or impact location. In particular, certain impact locations have the potential to harm a barrier more than the tested standard load cases or even cause the failure of a barrier. Further, if small blocks with high impact velocities are expected, the mesh might suffer from puncturing loads, as studied by [
24,
25,
26]. One would hope, therefore, that market competition not only favors the least expensive systems, but also helps resolve quality issues. Numerical simulations, such as those presented in [
27], might help evaluate barriers for non-standardized performance.
ETAG 027 defines reasonable boundary conditions for type testing. For example, the block’s mass, shape and density are limited. Setting a maximum density results in a minimum block size, and this in turn causes a minimum barrier nominal height within a certain energy class. Defining a minimum density prevents situations where very large blocks avoid the inverse of the “bullet effect” with smaller loads in the mesh.
Checks for corrosion protection of the barrier components are also part of the testing process. However, it has been observed that energy-absorbing elements behave differently if corrosion protection is applied. Therefore, it should be kept in mind that applying corrosion protection might influence the steel properties of a barrier component. Procedures for considering specific corrosion protection are, however, not handled consequently so far.
One drawback of following an existing guideline is that it is difficult to include new measurement procedures in the evaluation and to incorporate their results into the ETA of a system. For example, determining the deceleration of the block within the net is standard today (e.g., [
20,
28,
29]), but is not to be included in the ETA.