Application of Sensitivity Analysis for Process Model Calibration of Natural Hazards
Abstract
1. Introduction
2. Materials and Methods
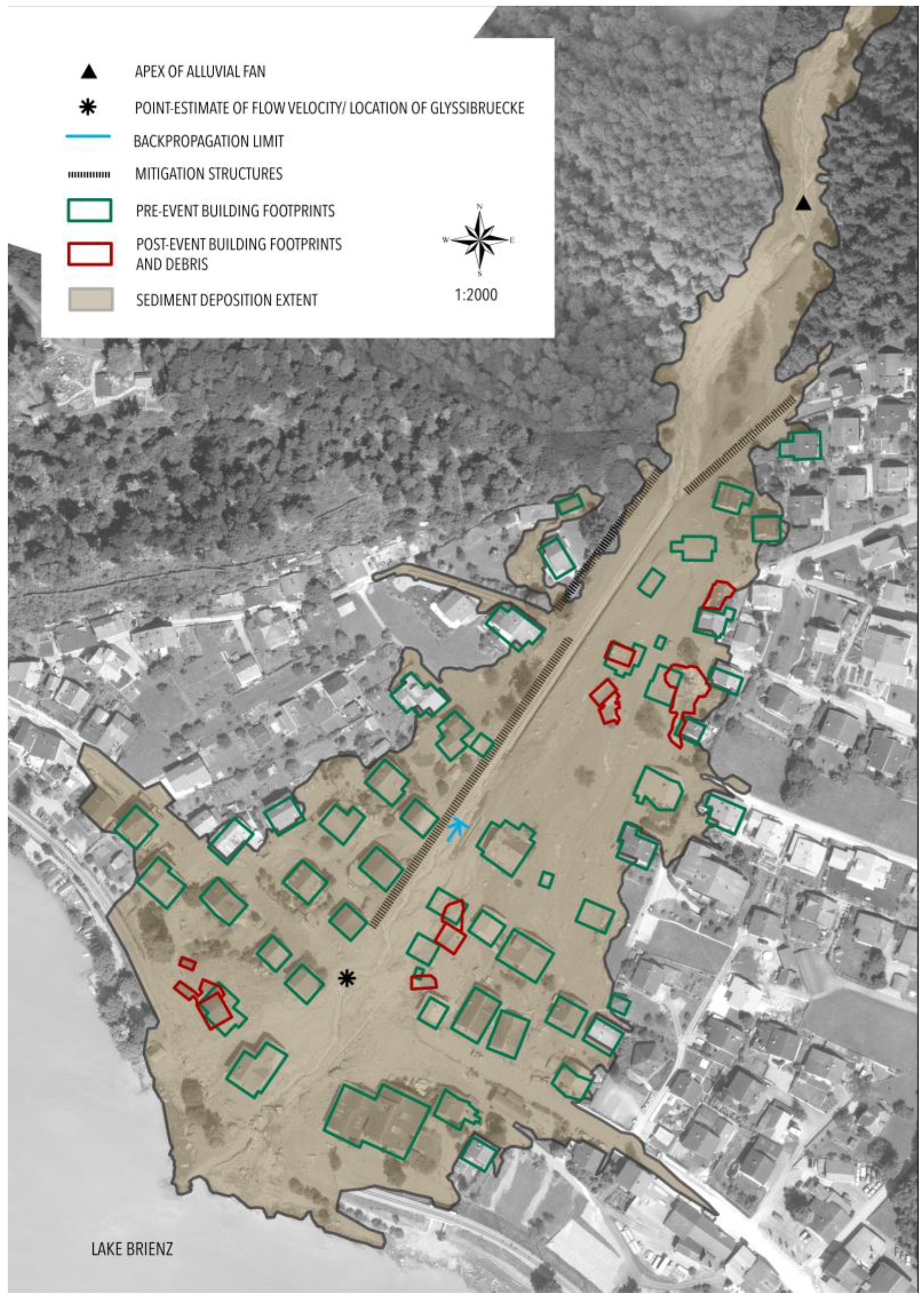
2.1. Site Description
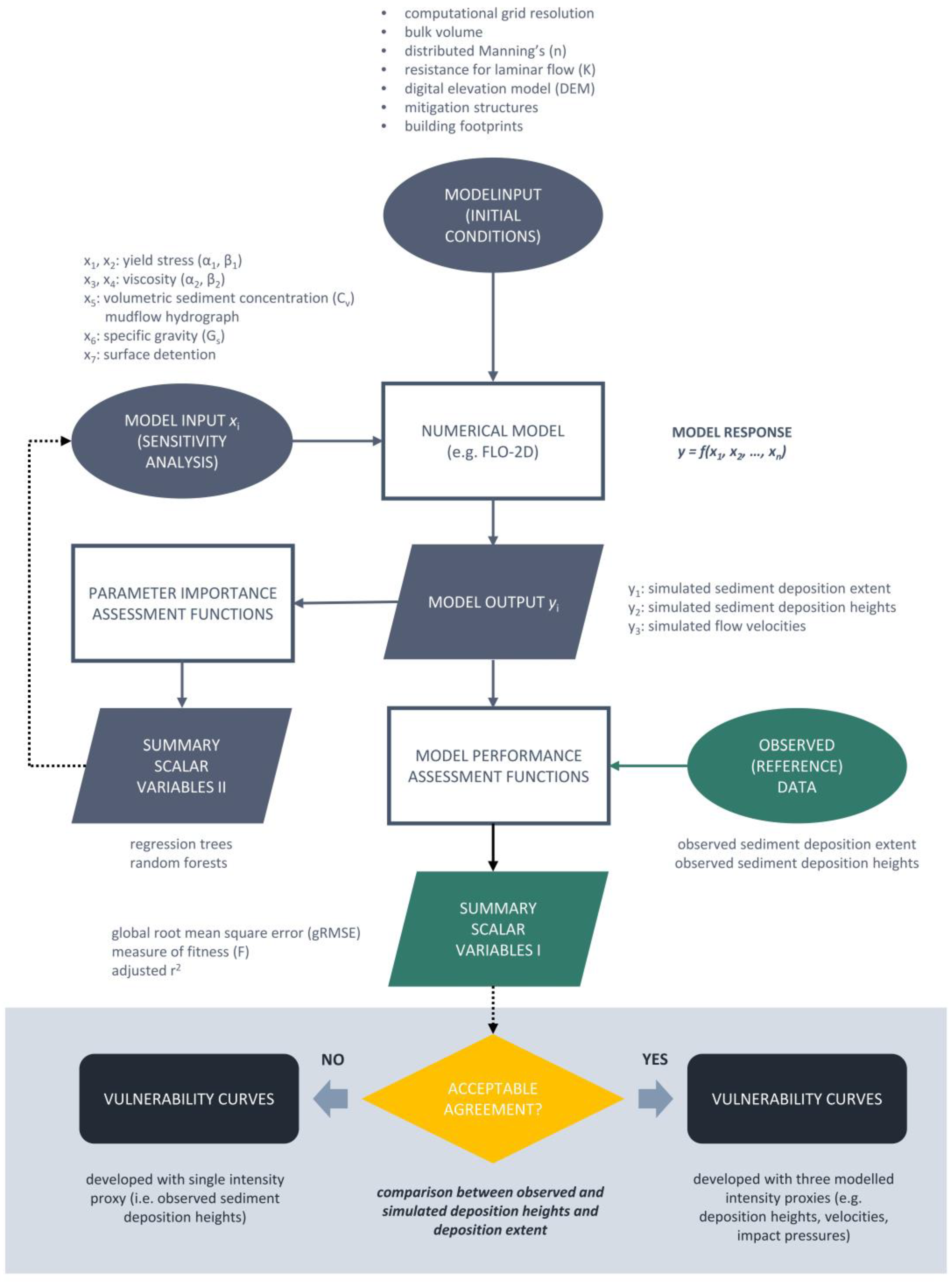
2.2. Methods
2.3. Data Sources
2.3.1. Initial Conditions and Fixed Parameters
2.3.2. Input Factors for Calibration
2.3.3. Calibration of Rheological Values
2.3.4. Observed Reference Data for Model Verification
2.4. Model Description
2.5. Performance Metrics
3. Results
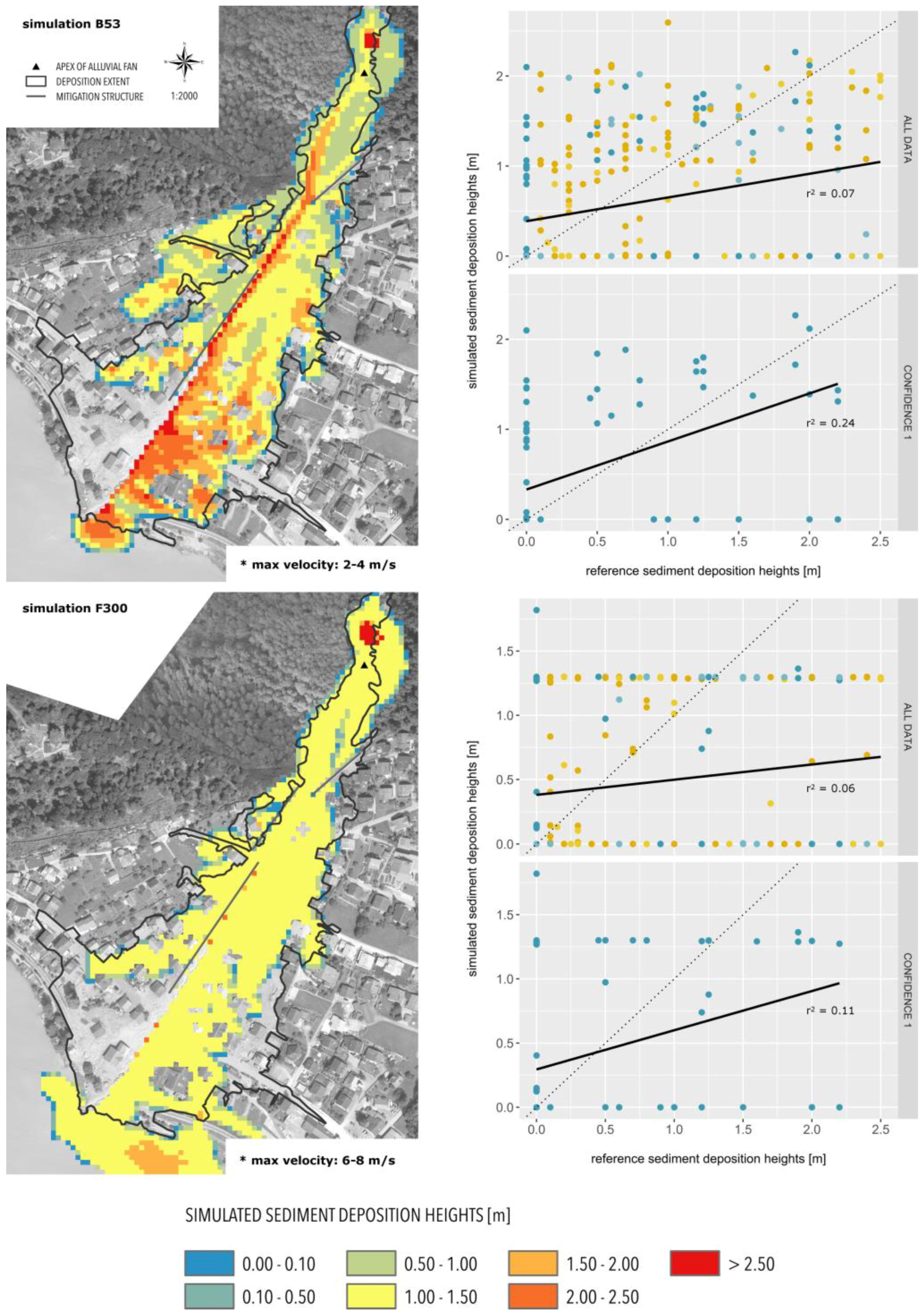
3.1. Model Performance Assessments
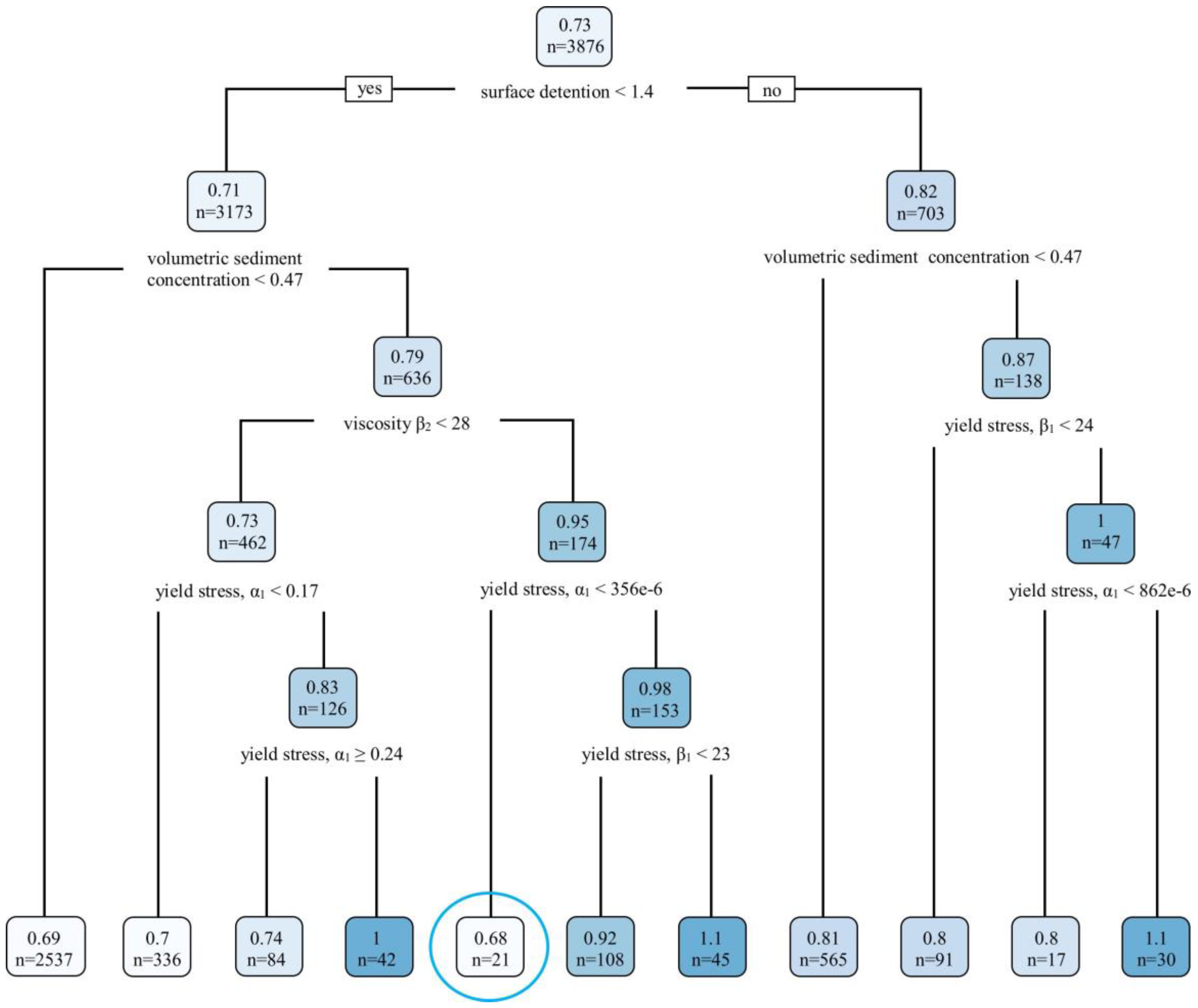
3.2. Parameter Importance and Model Behaviour Assessments
4. Discussion
4.1. Sensitivity Analysis for Model Calibration
4.2. Model Performance Assessment: Potentials and Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eisbacher, G. Mountain torrents and debris flows. Episodes 1982, 4, 12–17. [Google Scholar]
- Varnes, D. Slope movement types and processes. In Landslides: Analysis and Control, TRB Special Report 176: Transportation Research Board; National Academy of Sciences: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Hungr, O.; Evans, S.; Bovis, M.; Hutchinson, J. A review of the classification of landslides of the flow type. Environ. Eng. Geosci. 2001, 7, 221–238. [Google Scholar] [CrossRef]
- Costa, J. Physical Geomorphology of Debris Flows. In Developments and Applications of Geomorphology; Springer: Berlin, Germany, 1984; pp. 268–317. [Google Scholar]
- Takahashi, T.; Sawada, T.; Suwa, H.; Mizuyama, T.; Mizuhara, K.; Wu, J.; Tang, B.; Kang, Z.; Zhou, B. Japan-China joint research on the prevention from debris flow hazards. In Research Report; Japanese Ministry of Education, Science and Culture, International Scientific Research Program No. 03044085; Japanese Ministry of Education: Tokyo, Japan, 1994. [Google Scholar]
- Wan, Z.; Wang, Z. Hyperconcentrated flow. In IAHR Monograph Series; Balkema: Rotterdam, The Netherlands, 1994. [Google Scholar]
- Scheidl, C.; Rickenmann, D. Empirical Prediction of Debris-Flow Mobility and Deposition on Fans. Earth Surf. Process. Landf. 2010, 35, 157–173. [Google Scholar] [CrossRef]
- Jakob, M.; Hungr, O. Debris-flow Hazards and Related Phenomena; Praxis Publishing Limited: Chichester, UK, 2005; p. 14. [Google Scholar]
- Bradley, J.; McCutcheon, S. The effects of high sediment concentration on transport processes and flow phenomena. In International Symposium on Erosion, Debris Flow and Disaster Prevention; Toshindo: Tsukuba, Japan, 1985; pp. 219–225. [Google Scholar]
- Papathoma-Köhle, M.; Kappes, M.; Keiler, M.; Glade, T. Physical vulnerability assessment for alpine hazards: State of the art and future needs. Nat. Hazards 2011, 58, 645–680. [Google Scholar] [CrossRef]
- Totschnig, R.; Fuchs, S. Mountain torrents: Quantifying vulnerability and assessing uncertainties. Eng. Geol. 2013, 155, 31–44. [Google Scholar] [CrossRef] [PubMed]
- Mazzorana, B.; Simoni, S.; Scherer, C.; Gems, B.; Fuchs, S.; Keiler, M. A physical approach on flood risk vulnerability of buildings. Hydrol. Earth Syst. Sci. 2014, 18, 3817–3836. [Google Scholar] [CrossRef]
- Papathoma-Köhle, M.; Zischg, A.; Fuchs, S.; Glade, T.; Keiler, M. Loss estimation for landslides in mountain areas—An integrated toolbox for vulnerability assessment and damage documentation. Environ. Model. Softw. 2015, 63, 156–169. [Google Scholar] [CrossRef]
- Hübl, J.; Kienholz, H.; Loipersberger, A. DOMODIS—Documentation of Mountain Disasters. Available online: http://www.baunat.boku.ac.at/fileadmin/data/H03000/H87000/H87100/Downloads/Domodis_Deutsch.pdf (accessed on 14 June 2018).
- Scheidl, C.; Rickenmann, D.; Chiari, M. The use of airborne LiDAR data for the analysis of debris flow events in Switzerland. Nat. Hazards Earth Syst. Sci. 2008, 8, 1113–1127. [Google Scholar] [CrossRef]
- Quan Luna, B.; Blahut, J.; van Westen, C.; Sterlacchini, S.; van Asch, T.; Akbas, S. The application of numerical debris modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 2011, 11, 2047–2060. [Google Scholar] [CrossRef]
- Jakob, M.; Stein, D.; Ulmi, M. Vulnerability of buildings to debris flow impact. Nat. Hazards 2012, 60, 241–261. [Google Scholar] [CrossRef]
- Scheidegger, A. On the prediction of the reach and velocity of catastrophic landslides. Rock Mech. 1973, 5, 231–236. [Google Scholar] [CrossRef]
- Körner, H. Reichweite und Geschwindigkeit von Bergstürzen und Fliesslawinen. Rock Mech. 1976, 8, 225–256. [Google Scholar] [CrossRef]
- Rickenmann, D. Empirical relationships for debris flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Legros, F. The mobility of long runout landslides. Eng. Geol. 2002, 63, 301–331. [Google Scholar] [CrossRef]
- Berti, M.; Simoni, A. Prediction of debris flow inundation areas using empirical mobility relationships. Geomorphology 2007, 90, 144–161. [Google Scholar] [CrossRef]
- Magirl, C.; Griffiths, P.; Webb, R. Analyzing debris flows with the statistically calibrated empirical model LAHARZ in southeastern Arizona, USA. Geomorphology 2010, 119, 111–124. [Google Scholar] [CrossRef]
- Scheidl, C.; Rickenmann, D. TopFlowDf—A simple GIS based model to simulate debris-flow runout on the fan. In Proceedings of the 5th International Conference on Debris-Flow Hazards: Mitigation, Mechanics, Prediction and Assessment, Padua, Italy, 14–17 June 2011; pp. 253–262. [Google Scholar]
- Gruber, S. A mass-conserving fast algorithm to parameterize gravitational transport and deposition using digital elevation models. Water Resour. Res. 2007, 43, W06412. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flows: Mechanics, Prediction and Countermeasures; CRC Press: Rotterdam, The Netherlands, 1991. [Google Scholar]
- O’Brien, J.; Julien, P.; Fullerton, W. Two-dimensional water flood and mudflow simulation. J. Hydraul. Eng. 1993, 119, 244–261. [Google Scholar] [CrossRef]
- Hungr, O. A model for the runout analysis of rapid flow slide, debris flow, and avalanches. Can. Geotech. J. 1995, 32, 610–623. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P.; Ghilardi, R.; Natale, L.; Savi, F. 1-D mathematical modelling of debris flow. J. Hydraul. Res. 2000, 38, 435–446. [Google Scholar] [CrossRef]
- Medina, V.; Hurlimann, M.; Bateman, A. Application of FLATModel, a 2D finite volume code, to debris flows in the Northeastern part of Iberian Peninsula Experimental evidences and numerical modelling of debris flow initiated by channel runoff. Landslide 2008, 5, 127–142. [Google Scholar] [CrossRef]
- Liu, K.; Wang, M. Numerical modelling of debris-flow with application on hazard area mapping. Comput. Geosci. 2006, 10, 221–240. [Google Scholar] [CrossRef]
- Rickenmann, D.; Laigle, D.; McArdell, B.M.; Hübl, J. Comparison of 2D debris-flow simulation models with field events. Comput. Geosci. 2006, 10, 241–264. [Google Scholar] [CrossRef]
- Armanini, A.; Fraccarollo, L.; Rosatti, G. Two-dimensional simulation of debris flows in erodible channels. Comput. Geosci. 2009, 35, 993–1006. [Google Scholar] [CrossRef]
- Begueira, S.; Van Asch, T.; Malet, J.; Grondahl, S. A GIS-based numerical model for simulating the kinematics of mud and debris flows over complex terrain. Nat. Hazards Earth Syst. Sci. 2009, 9, 1897–1909. [Google Scholar] [CrossRef]
- Christen, M.; Bartelt, P.; Kowalski, J. Back calculation of the In den Arelen avalanche with RAMMS: Interpretation of model results. Ann. Glaciol. 2010, 51, 161–168. [Google Scholar] [CrossRef]
- Christen, M.; Kowalski, J.; Bartelt, P. RAMMS: Numerical simulation of dense snow avalanches in three-dimensional terrain. Cold Reg. Sci. Technol. 2010, 63, 1–14. [Google Scholar] [CrossRef]
- Pirulli, M. On the use of the calibration-based approach for debris-flow forward-analyses. Nat. Hazards Earth Syst. Sci. 2010, 10, 1009–1019. [Google Scholar] [CrossRef]
- De Blasioa, F.; Elverhbia, A.; Isslera, D.; Harbitzb, C.; Brync, P.; Lienc, R. Flow models of natural debris flows originating from overconsolidated clay materials. Mar. Geol. 2004, 213, 439–455. [Google Scholar] [CrossRef]
- Mergili, M.; Schratz, K.; Ostermann, L.; Fellin, W. Physically-based modelling of granular flows with Open Source GISNat. Nat. Hazards Earth Syst. Sci. 2012, 12, 187–200. [Google Scholar] [CrossRef]
- Pudasaini, S. A general two-phase debris flow model. J. Geophys. Res. 2012, 117, F03010. [Google Scholar] [CrossRef]
- Rosatti, G.; Begnudelli, L. Two dimensional simulations of debris flows over mobile beds: Enhancing the TRENT2D model by using a well-balanced generalized Roe-type solver. Comput. Fluids 2013, 71, 179–185. [Google Scholar] [CrossRef]
- McDougall, S.; Hungr, O. A model for the analysis of rapid landslide motion across three-dimensional terrain. Can. Geotech. J. 2004, 41, 1084–1097. [Google Scholar] [CrossRef]
- Pastor, M.; Haddad, B.; Sorbino, G.; Cuomo, S.; Demptric, V. A depth integrated-coupled SPH model for flow like landslides and related phenomena. Int. J. Numer. Anal. Methods Geomech. 2008, 33, 143–172. [Google Scholar] [CrossRef]
- Deangeli, C.; Segre, E. Cellular automaton for realistic modelling of landslides. Nonlinear Process. Geophys. 1995, 2, 1–15. [Google Scholar]
- D’Ambrosio, D.; Di Gregorio, S.; Iovine, G.; Lupiano, V.; Rongo, R.; Spataro, W. First simulations of the Sarno debris flows through Cellular Automata modelling. Geomorphology 2003, 54, 91–117. [Google Scholar] [CrossRef]
- Deangeli, C. Laboratory granular flows generated by slope failures. Rock Mech. Rock Eng. 2008, 41, 199–217. [Google Scholar] [CrossRef]
- Gregoretti, C.; Degetto, M.; Boreggio, M. GIS-based cell model for simulating debris flow runout on a fan. J. Hydrol. 2016, 534, 326–340. [Google Scholar] [CrossRef]
- Schraml, K.; Thomschitz, B.; McArdell, B.; Kaitna, R. Modeling debris-flow runout patterns on two alpine fans with different dynamic simulation models. Nat. Hazards Earth Syst. Sci. 2015, 15, 1483–1492. [Google Scholar] [CrossRef]
- Naef, D.; Rickenmann, D.; Rutschmann, P.; McArdell, B. Comparison of flow resistance relations for debris flows using a one-dimensional finite element simulation model. Nat. Hazards Earth Syst. Sci. 2006, 6, 155–165. [Google Scholar] [CrossRef]
- Rickenmann, D. Debris-flow hazard assessment and methods applied in engineering practice. Int. J. Eros. Control Eng. 2016, 9, 80–90. [Google Scholar] [CrossRef]
- Mannschatz, T.; Dietrich, P. Chapter 2—Model Input Data Uncertainty and Its Potential Impact on Soil Properties. In Sensitivity Analysis in Earth Observation Modelling; Elsevier: Amsterdam, The Netherlands, 2017; pp. 25–52. [Google Scholar]
- Hürlimann, M.; Rickenmann, D.; Medina, V.; Bateman, A. Evaluation of approaches to calculate debris-flow parameters for hazard assessment. Eng. Geol. 2008, 102, 152–163. [Google Scholar] [CrossRef]
- Hussin, H.; Quan Luna, B.; Van Westen, C.; Christen, M.; Malet, J.-P.; van Asch, T. Parameterization of a numerical 2-D debris flow model with entrainment: A case study of the Faucon catchment, Southern French Alps. Nat. Hazards Earth Syst. Sci. 2012, 12, 3075–3090. [Google Scholar] [CrossRef]
- D’Aniello, A.; Cozzolino, L.; Cimorelli, L.; Della Morte, R.; Pianese, D. A numerical model for the simulation of debris flow triggering, propagation and arrest. Nat. Hazards 2015, 75, 1403–1433. [Google Scholar] [CrossRef]
- Iverson, R. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- McDougall, S.; Hungr, O. Modelling of landslides which entrain material from the path, Can. Geotech. J. 2005, 42, 1437–1448.
- Frank, F.; McArdell, B.; Huggel, C.; Vieli, A. The importance of entrainment and bulking on debris flow runout modeling: Examples from the Swiss Alps. Nat. Hazards Earth Syst. Sci. 2015, 15, 2569–2583. [Google Scholar] [CrossRef]
- Bertolo, P.; Wieczorek, G. Calibration of numerical models for small debris flows in Yosemite Valley, California, USA. Nat. Hazards Earth Syst. Sci. 2005, 5, 993–1001. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.; Rougier, J.; Stephenson, D.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical frameworks. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Beven, K.; Aspinall, W.; Bates, P.; Borgomeo, E.; Goda, K.; Hall, J.; Page, T.; Phillips, J.; Simpson, M.; Smith, P.; et al. Epistemic uncertainties and natural hazard risk assessment. 2. What should constitute good practice? Nat. Hazards Earth Syst. Sci. Discuss. 2017. [Google Scholar] [CrossRef]
- Rougier, J.; Sparks, S.; Hill, L. Risk and Uncertainty Assessment for Natural Hazards; University Press: Cambridge, UK, 2013. [Google Scholar]
- Stancanelli, L.; Foti, E. A comparative assessment of two different debris flow propagation approaches—Blind simulations on a real debris flow event. Nat. Hazards Earth Syst. Sci. 2015, 15, 735–746. [Google Scholar] [CrossRef]
- Von Boetticher, A.; Turowski, J.; McArdell, B.; Rickenmann, D.; Kirchner, J. DebrisInterMixing-2.3: A finite volume solver for three-dimensional debris-flow simulations with two calibration parameters—Part 1: Model description. Geosci. Model Dev. 2016, 9, 2909–2923. [Google Scholar] [CrossRef]
- Huang, Y.; Qin, X. Uncertainty analysis for flood inundation modelling with random floodplain roughness field. Environ. Syst. Res. 2014, 3, 9. [Google Scholar] [CrossRef]
- Swisstopo. swissALTI3D. Available online: https://shop.swisstopo.admin.ch/en/products/height_models/alti3D (accessed on 14 June 2018).
- Sosio, R.; Crosta, G.; Frattini, P. Field observations, rheological testing and numerical modelling of a debris-flow event. Earth Surf. Process. Landf. 2007, 32, 290–306. [Google Scholar] [CrossRef]
- Lin, M.; Wang, K.; Huang, J. Debris flow run off simulation and verification? Case study of Chen-You-Lan Watershed, Taiwan. Nat. Hazards Earth Syst. Sci. 2005, 5, 439–445. [Google Scholar] [CrossRef]
- D’Agostino, V.; Tecca, P. Some considerations on the application of FLO-2D model for debris flow hazard assessment. WIT Trans. Ecol. Environ. 2006, 90, 159–170. [Google Scholar]
- Boniello, M.; Calligaris, C.; Lapasin, R.; Zini, L. Rheological investigation and simulation of a debris-flow event in the Fella watershed. Nat. Hazards Earth Sci. 2010, 10, 989–997. [Google Scholar] [CrossRef]
- NDR Consulting Zimmermann/Niederer + Pozzi Umwelt AG. Lokale Lösungsorientierte Ereignisanalyse Glyssibach. Bericht zum Vorprojekt; Tiefbauamt des Kantons Bern: Thun, Switzerland, 2006. [Google Scholar]
- Swisstopo. Orthophotos. Available online: https://shop.swisstopo.admin.ch/en/products/images/ortho_images/SWISSIMAGE_RS (accessed on 14 June 2018).
- Chow, V. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Ziliani, L.; Surian, N.; Coultard, T.; Tarantola, S. Reduced-complexity modeling of braided rivers: Assessing model performance by sensitivity analysis, calibration, and validation. J. Geophys. Res. Earth Surf. 2013, 118, 2243–2262. [Google Scholar] [CrossRef]
- Skinner, C.; Coulthard, T.; Schwanghart, W.; Van De Wiel, M.; Hancock, G. Global Sensitivity Analysis of Parameter Uncertainty in Landscape Evolution Models. Geosci. Model Dev. Discuss. 2017. [Google Scholar] [CrossRef]
- Yin, P.; Fan, X. Estimating R2 shrinkage in multiple regression: A comparison of different analytical methods. J. Exp. Educ. 2001, 69, 203–224. [Google Scholar] [CrossRef]
- Sikuli/SikuliX Documentation for version 1.1+ (2014 and Later). Available online: http://www.sikuli.org/ (accessed on 18 June 2016).
- FLO-2D. FLO-2D Reference Manual. Available online: http://www.flo-2d.com/wp-content/uploads/2014/04/Manuals-Pro.zip (accessed on 11 February 2016).
- Hsu, S.; Chiou, L.; Lin, G.; Chao, C.; Wen, H.; Ku, C. Applications of simulation technique on debris-flow hazard zone delineation: A case study in Hualien County, Taiwan. Nat. Hazards Earth Syst. Sci. 2010, 10, 535–545. [Google Scholar] [CrossRef]
- Arcement, G.; Schneider, V. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains. In United States Geological Survey Water-Supply Paper 2339; United States Government Printing Office: Washington, DC, USA, 1989. [Google Scholar]
- Cagnoli, B.; Piersanti, A. Combined effects of grain size, flow volume and channel width on geophysical flow mobility: Three-dimensional discrete element modeling of dry and dense flows of angular rock fragments. Solid Earth 2017, 8, 177–188. [Google Scholar] [CrossRef]
- Di Santolo, A.; Pellegrino, A.; Evangelista, A. Experimental study on the rheological behaviour of debris flow. Nat. Hazards Earth Syst. Sci. 2010, 10, 2507–2514. [Google Scholar] [CrossRef]
- O’Brien, J.; Julien, P. Laboratory analysis of mudflow properties. J. Hydraul. Eng. 1988, 114, 877–887. [Google Scholar] [CrossRef]
- Major, J.; Pierson, T. Debris flow rheology: Experimental analysis of fine-grained slurries. Water Resour. Res. 1992, 28, 841–857. [Google Scholar] [CrossRef]
- Coussot, P.; Piau, J. The effects of an addition of force-free particles on the rheological properties of fine suspensions. Can. Geotech. J. 1995, 32, 263–270. [Google Scholar] [CrossRef]
- FLO-2D. Data Input Manual PRO. Available online: http://www.flo-2d.com/wp-content/uploads/2014/04/Manuals-Pro.zip (accessed on 11 February 2016).
- Bates, P.; De Roo, A. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Pappenberger, F.; Iorgulescu, I.; Beven, K. Sensitivity analysis based on regional splits and regression trees (SARS-RT). Environ. Model. Softw. 2006, 21, 976–990. [Google Scholar] [CrossRef]
- Hofer, E. Sensitivity analysis in the context of uncertainty analysis for computationally intensive models. Comput. Phys. Commun. 1999, 117, 21–34. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Iorgulescu, I.; Beven, K. Nonparametric direct mapping of rainfall-runoff relationships: An alternative approach to data analysis and modeling? Water Resour. Res. 2004, 40, W08403. [Google Scholar] [CrossRef]
- Ancey, C.; Meunier, M. Estimating bulk rheological properties of flowing snow avalanches from field data. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Sosio, R.; Crosta, G. Rheology of concentrated granular suspensions and possible implications for debris flow modeling. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Ancey, C. Plasticity and geophysical flows: A review. J. Non-Newton. Fluid Mech. 2007, 142, 4–35. [Google Scholar] [CrossRef]
- Iverson, R. The debris flow rheology myth. In Third International Conference on Debris-Flow Hazard Mitigation: Mechanics; Prediction and Assessment, American Society of Civil Engineers: Reston, VA, USA, 2003. [Google Scholar]
- Bertolo, P.; Bottino, G. Debris-flow event in the Frangerello Stream-Susa Valley (Italy)—Calibration of numerical models for the back analysis of the 16 October, 2000 rainstorm. Landslides 2008, 5, 19–30. [Google Scholar] [CrossRef]
- Sosio, R.; Crosta, G.; Frattini, P.; Valbuzzi, E. Caratterizzazione reologica e modellazione numerica di un debris flow in ambiente alpino. G. Geol. Appl. 2006, 3, 263–268. [Google Scholar]
- Tiranti, D.; Deangeli, C. Modeling of debris flow depositional patterns according to the catchments and source areas characteristics. Front. Earth Sci. 2015, 3, 1–14. [Google Scholar] [CrossRef]
- Cavalli, M.; Goldin, B.; Comiti, F.; Brardinoni, F.; Marchi, L. Assessment of erosion and deposition in steep mountain basins by differencing sequential digital terrain models. Geomorphology 2017, 291, 4–16. [Google Scholar] [CrossRef]
- Iverson, R.; Denlinger, R. Flow of variably fluidized granular masses across three-dimensional terrain 1. Coulomb mixture theory. J. Geophys. Res. 2001, 106, 537–552. [Google Scholar] [CrossRef]
- McCoy, S.; Tucker, G.; Kean, J.; Coe, J. Field measurement of basal forces generated by erosive debris flows. J. Geophys. Resour. Earth Surf. 2013, 118, 589–602. [Google Scholar] [CrossRef]



| Sources of Rheology Values | Model Validation | Reference Data | |||||
|---|---|---|---|---|---|---|---|
| Cases from Literature | Lab Analyses of Post-Event Field Samples | From Literature | Visual Comparison | Quantification | Sediment Deposition Extent | Sediment Deposition Heights | Number of Sample Points |
| Sosio et al. [67] | √ | √ | √ | √ | √ | √ | 18 |
| Quan Luna et al. [16] | √ | √ | √ | √ | 13 | ||
| Lin et al. [68] | √ | √ | √ | √ | √ | √ | 8 |
| D’Agostino et al. [69] | √ | √ | √ | √ | √ | ||
| Boniello et al. [70] | √ | √ | √ | √ | √ | ||
| Rickenmann et al. [32] | √ | √ | √ | ||||
| Feasible Ranges of Values | ||||||
|---|---|---|---|---|---|---|
| Initial Conditions | Input Factors for Calibration | Description | Symbol | Units | for FLO-2D Model | for 2005 Debris Flow in Brienz |
| √ | computational grid resolution | m | 5 | |||
| √ | sediment volume | m3 | 70,000–72,000 | |||
| √ | (distributed) Manning’s values | n | m−⅓·s | forested areas (0.33), channels and streets (0.01), sparsely vegetated settlement areas (0.08) | ||
| √ | resistance parameter for laminar flow | K | 24–50,000 | determined based on floodplain grid element’s Manning’s n value | ||
| x1 | yield stress, α1 | τy | Pa | 0–∞ | unknown; see Table 3 for potentially applicable values | |
| x2 | yield stress, β2 | 0–∞ | ||||
| x3 | viscosity, α1 | η | Pa·s | 0–∞ | ||
| x4 | viscosity, β2 | 0–∞ | ||||
| x5 | volumetric sediment concentration (determines mud hydrograph) | Cv | 0.03–0.90 | 0.30–0.70 | ||
| x6 | specific gravity | Gs | 2.5–2.8 | 2.5–2.8 | ||
| x7 | surface detention | m | 0.01–0.50 | model-specific input factor; calibrated with feasible model ranges | ||
| Yield Stress (Ty) | Viscosity (n) | |||||
|---|---|---|---|---|---|---|
| ID | Sources from Literature | Sample Name | α1 | β1 | α2 | β2 |
| Dynes/cm2 | Poises | |||||
| A | O’Brien and Julien [83] | Glenwood 4 | 0.00172 | 29.5 | 0.000602 | 33.1 |
| Glenwood 1 | 0.0345 | 20.1 | 0.00283 | 23 | ||
| Glenwood 3 | 0.0765 | 16.9 | 0.648 | 6.2 | ||
| Glenwood 2 | 0.000707 | 29.8 | 0.00632 | 19.9 | ||
| B | O’Brien and Julien [83] | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 |
| Aspen pit 2 | 2.72 | 10.4 | 0.0538 | 14.5 | ||
| Aspen natural soil | 0.152 | 18.7 | 0.00136 | 28.4 | ||
| Aspen mine fill | 0.0473 | 21.1 | 0.128 | 12 | ||
| Aspen natural soil source | 0.0383 | 19.6 | 0.000495 | 27.1 | ||
| Aspen mine fill source | 0.291 | 14.3 | 0.000201 | 33.1 | ||
| C | Sosio et al. [67] | Scenario A | 0.0013 | 23 | 0.0000283 | 19 |
| Scenario B | 0.000093 | 23.5 | 0.000183 | 19 | ||
| Scenario C | 0.0011 | 21.8 | 0.0000283 | 18.2 | ||
| L1 (deposit sample) | 0.000127 | 22.8 | 0.0000297 | 18.8 | ||
| L2 (source area sample) | 0.0004 | 22 | 0.000203 | 18 | ||
| D | D’Agostino and Tecca [69] | Rio Dona | 0.05 | 22 | 0.0015 | 22 |
| Fiames | 0.152 | 18.7 | 0.0075 | 14.39 | ||
| E | Lin et al. [68] | Nan-Ping-Kern | 0.2433 | 4.116 | 0.001386 | 3.372 |
| Jun-Kern; Err-Bu | 0.7299 | 12.348 | 0.004158 | 10.116 | ||
| Shan-Bu | 0.4055 | 6.86 | 0.00231 | 5.62 | ||
| Fong-Chu | 0.85155 | 14.406 | 0.004851 | 11.802 | ||
| Tung-Fu Community | 0.811 | 13.72 | 0.00462 | 11.24 | ||
| Her-Ser 1 | 1.0543 | 17.836 | 0.006 | 14.612 | ||
| Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | ||
| F | Boniello et al. [70] | Fella sx debris flow 1 | 0.000005 | 42.01 | 0.00000002 | 42.23 |
| Fella sx debris flow 2 | 0.0383 | 19.6 | 0.000495 | 27.1 | ||
| Input Factors for Model Calibration | Summary Scalar Variables I | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1, x2: Yield Stress | x3, x4: Viscosity | x5: Volumetric Sediment Concentration | x6: Specific Gravity | x7: Surface Detention | F | gRMSE1 | gRMSE4 | |||||
| Rank | Simulation Run ID | α1 | β1 | α2 | β2 | (%) | Very Certain Data Points (m) | All Data Points (m) | ||||
| 1 | B53 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.45 | 2.8 | 0.80 | 53.42 | 0.71 | 0.92 |
| 2 | B54 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.45 | 2.8 | 1.00 | 53.34 | 0.72 | 0.92 |
| 3 | B52 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.45 | 2.8 | 0.60 | 53.22 | 0.71 | 0.92 |
| 4 | E48 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.50 | 2.5 | 1.40 | 53.15 | 0.87 | 0.94 |
| 5 | B34 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.45 | 2.65 | 1.00 | 53.02 | 0.72 | 0.93 |
| 6 | E103 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.50 | 2.65 | 1.40 | 52.99 | 0.87 | 0.94 |
| 7 | B41 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.45 | 2.8 | 0.50 | 52.98 | 0.71 | 0.92 |
| 8 | E158 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.50 | 2.8 | 1.40 | 52.97 | 0.87 | 0.93 |
| 9 | B33 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.45 | 2.65 | 0.80 | 52.96 | 0.71 | 0.93 |
| 10 | E49 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.50 | 2.5 | 1.50 | 52.95 | 0.84 | 0.92 |
| Input Factors for Model Calibration | Summary Scalar Variables I | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1, x2: Yield Stress | x3, x4: Viscosity | x5: Volumetric Sediment Concentration | x6: Specific Gravity | x7: Surface Detention | F | gRMSE1 | gRMSE4 | |||||
| Rank | Simulation Run ID | α1 | β1 | α2 | β2 | (%) | Very Certain Data Points (m) | All Data Points (m) | ||||
| 1 | E112 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.30 | 2.80 | 1.00 | 44.66 | 0.60 | 0.88 |
| 2 | A6 | Glenwood 4 | 0.00172 | 29.5 | 0.000602 | 33.1 | 0.35 | 2.50 | 1.00 | 42.71 | 0.60 | 0.90 |
| 3 | E2 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.30 | 2.50 | 1.00 | 44.72 | 0.60 | 0.87 |
| 4 | E57 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.30 | 2.65 | 1.00 | 44.81 | 0.60 | 0.87 |
| 5 | B1 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.30 | 2.50 | 0.80 | 42.84 | 0.61 | 0.89 |
| 6 | B21 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.30 | 2.65 | 0.80 | 42.69 | 0.61 | 0.89 |
| 7 | B41 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.30 | 2.80 | 0.80 | 42.58 | 0.61 | 0.89 |
| 8 | A26 | Glenwood 4 | 0.00172 | 29.5 | 0.000602 | 33.1 | 0.35 | 2.65 | 1.00 | 42.57 | 0.61 | 0.90 |
| 9 | B26 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.35 | 2.65 | 1.00 | 43.18 | 0.61 | 0.92 |
| 10 | B46 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.35 | 2.80 | 1.00 | 43.29 | 0.61 | 0.92 |
| Model Inputs for Calibration | |||||||||
| x1, x2: Yield Stress | x3, x4: Viscosity | x5: Volumetric Sediment Concentration | x6: Specific Gravity | x7: Surface Detention | |||||
| Rank | Simulation Run ID | α1 | β1 | α2 | β2 | ||||
| 1 | B53 | Aspen pit 1 | 0.181 | 25.7 | 0.036 | 22.1 | 0.45 | 2.80 | 0.80 |
| 2 | E48 | Chui-Sue River | 1.2652 | 16.464 | 0.924 | 14.612 | 0.50 | 2.50 | 1.40 |
| 3 | A55 | Glenwood 4 | 0.00172 | 29.5 | 0.000602 | 33.1 | 0.45 | 2.80 | 1.50 |
| 4 | D50 | Rio Dona | 0.05 | 22 | 0.0015 | 22 | 0.30 | 2.80 | 1.30 |
| 5 | F300 | Fella sx debris flow 2 | 0.0383 | 19.6 | 0.000495 | 27.1 | 0.30 | 2.65 | 1.30 |
| 6 | C60 | Scenario A | 0.0013 | 23 | 2.83 × 10−5 | 19 | 0.30 | 2.80 | 1.30 |
| Summary Scalar Variables I | |||||||||
| F | gRMSE1 | gRMSE4 | Adjusted r2 | ||||||
| Rank | Simulation Run ID | (%) | Very Certain Data Points (m) | All Data Points (m) | Very Certain Data Points | All Data | Simulated Maximum Velocity (m/s) | ||
| 1 | B53 | Aspen pit 1 | 53.42 | 0.71 | 0.92 | 0.24 | 0.07 | 2–4 | |
| 2 | E48 | Chui-Sue River | 53.15 | 0.87 | 0.94 | 0.08 | 0.04 | 0.5–1 | |
| 3 | A55 | Glenwood 4 | 52.03 | 0.86 | 0.93 | 0.11 | 0.06 | 1–2 | |
| 4 | D50 | Rio Dona | 46.27 | 0.72 | 0.96 | 0.10 | 0.06 | 2–8 | |
| 5 | F300 | Fella sx debris flow 2 | 46.11 | 0.72 | 0.95 | 0.11 | 0.06 | 6–8 | |
| 6 | C60 | Scenario A | 45.73 | 0.72 | 0.97 | 0.09 | 0.01 | 6–8 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chow, C.; Ramirez, J.; Keiler, M. Application of Sensitivity Analysis for Process Model Calibration of Natural Hazards. Geosciences 2018, 8, 218. https://doi.org/10.3390/geosciences8060218
Chow C, Ramirez J, Keiler M. Application of Sensitivity Analysis for Process Model Calibration of Natural Hazards. Geosciences. 2018; 8(6):218. https://doi.org/10.3390/geosciences8060218
Chicago/Turabian StyleChow, Candace, Jorge Ramirez, and Margreth Keiler. 2018. "Application of Sensitivity Analysis for Process Model Calibration of Natural Hazards" Geosciences 8, no. 6: 218. https://doi.org/10.3390/geosciences8060218
APA StyleChow, C., Ramirez, J., & Keiler, M. (2018). Application of Sensitivity Analysis for Process Model Calibration of Natural Hazards. Geosciences, 8(6), 218. https://doi.org/10.3390/geosciences8060218




