Modelling Ephemeral Gully Erosion from Unpaved Urban Roads: Equifinality and Implications for Scenario Analysis
Abstract
:1. Introduction
2. Materials and Methods
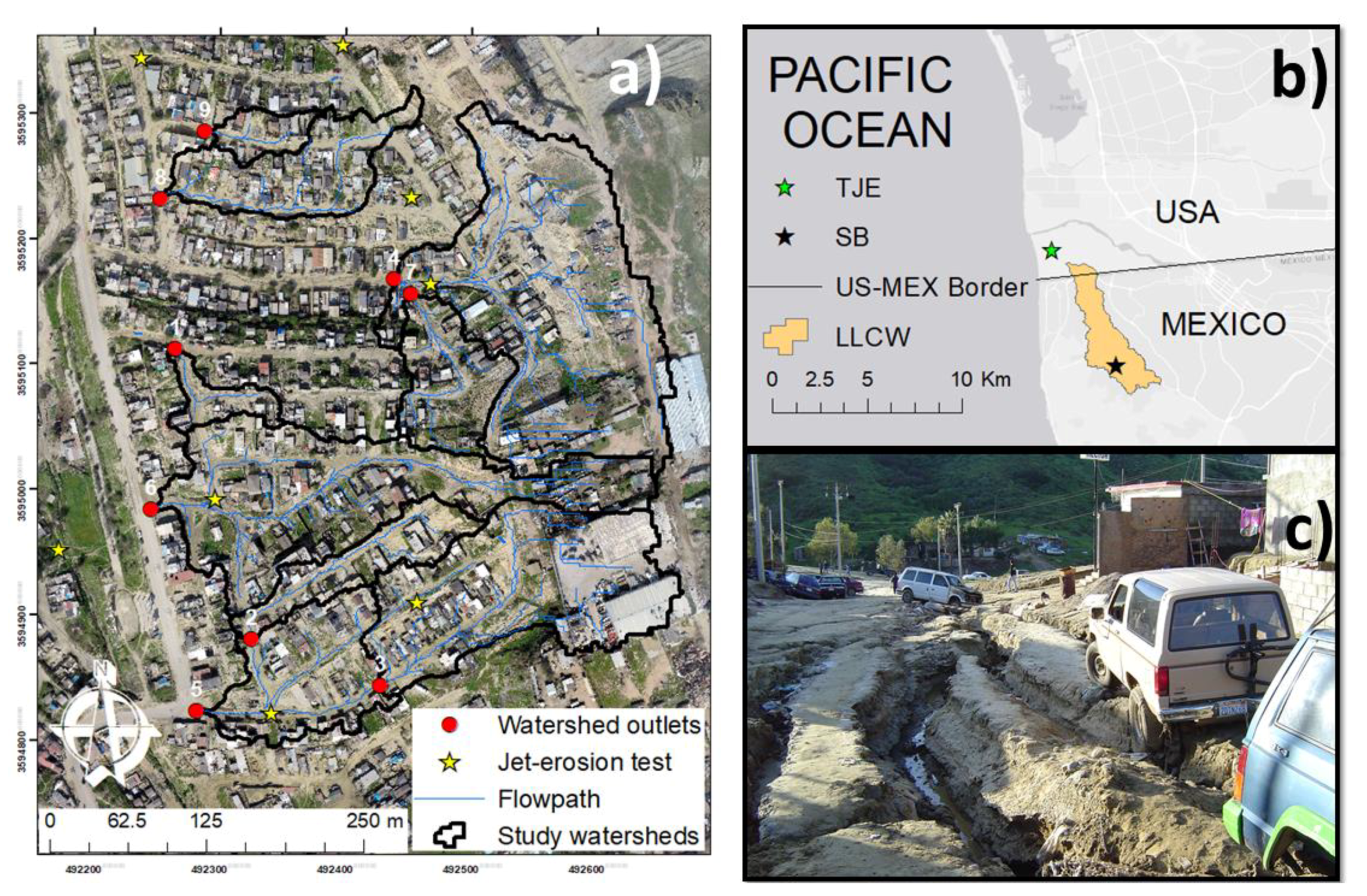
2.1. Study Area
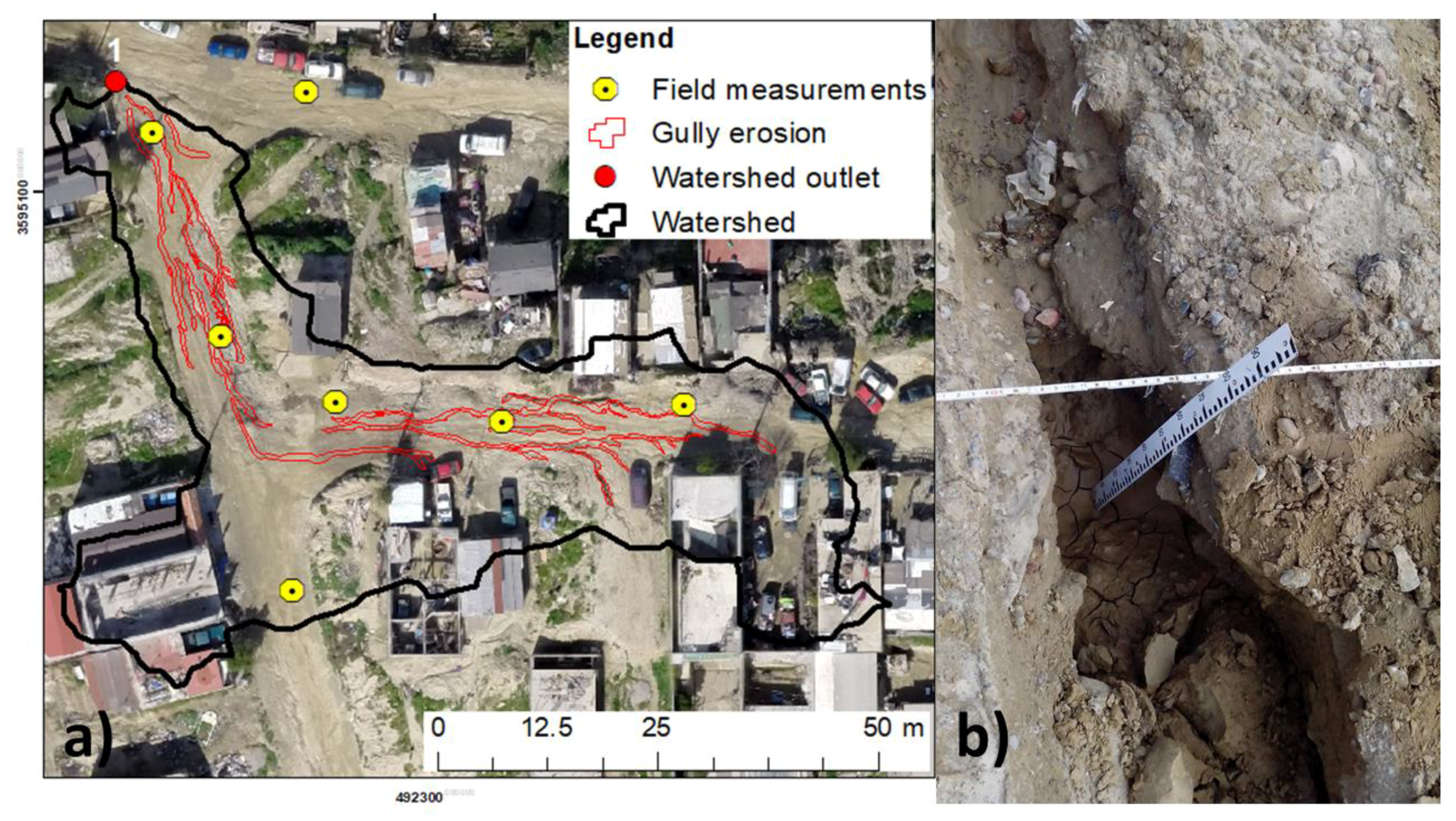
2.2. Observed Gully Erosion
2.3. AnnAGNPS Model
2.4. Model Setup
2.5. Sensitivity Analysis
2.6. Model Equifinality and Scenario Analysis
3. Results
3.1. Sensitivity Analysis
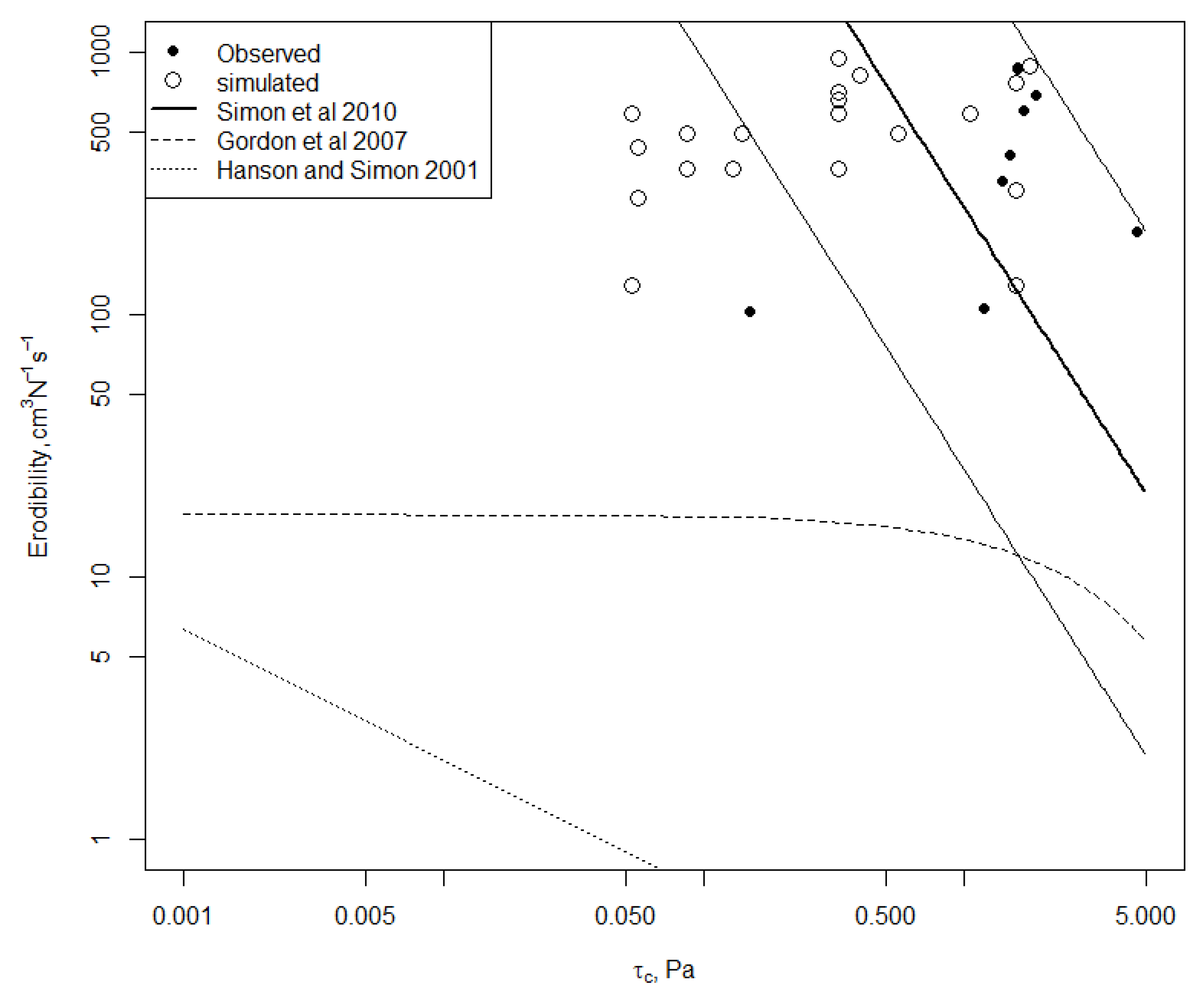
3.2. Behavioural Models and Parameter Identification
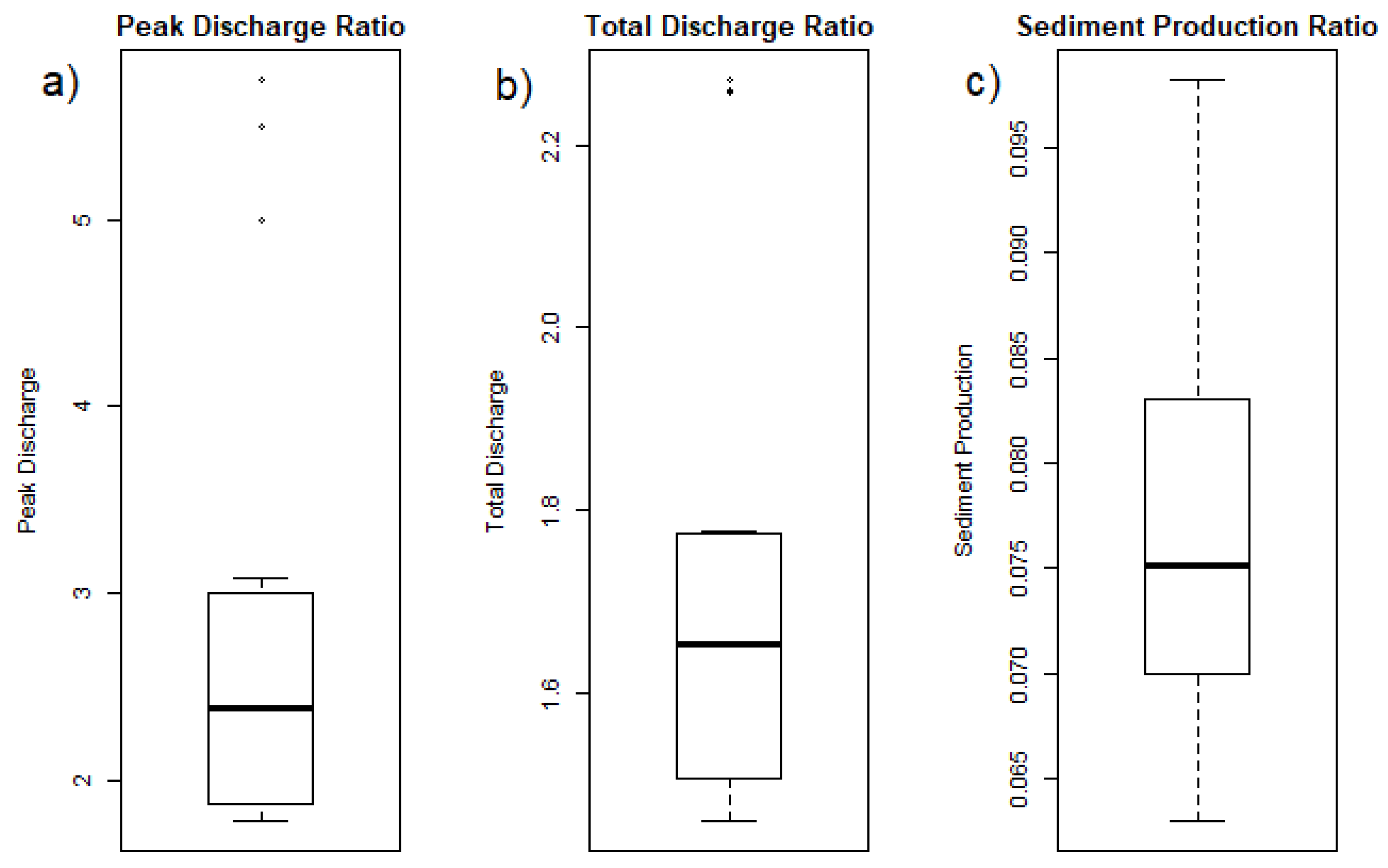
3.3. Scenario Analysis: Equifinality
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Montgomery, D.R. Road surface drainage, channel initiation, and slope instability. Water Resour. Res. 1994, 30, 1925–1932. [Google Scholar] [CrossRef]
- Ziegler, A.D.; Giambelluca, T.W. Importance of rural roads as source areas for runoff in mountainous areas of northern Thailand. J. Hydrol. 1997, 196, 204–229. [Google Scholar] [CrossRef]
- Poesen, J.; Govers, G. Gully erosion in the loam belt of Belgium. In Soil Erosion on Agricultural Land, Proceedings of a Workshop Sponsored by the British Geomorphological Research Group, Coventry, Chicester, UK, January 1989; Boardman, J., Foster, I.D.L., Dearing, J., Eds.; Wiley: Chicester, UK, 1989; pp. 513–530. [Google Scholar]
- Momm, H.G.; Bingner, R.L.; Wells, R.R.; Wilcox, D. AGNPS GIS-based tool for watershed-scale identification and mapping of cropland potential ephemeral gullies. Appl. Eng. Agric. 2012, 28, 17–29. [Google Scholar] [CrossRef]
- Bingner, R.L.; Czajkowski, K.; Palmer, M.; Coss, J.; Davis, S.; Stafford, J.; Widman, N.; Theurer, F.; Koltum, G.; Richards, P.; et al. Upper Auglaize Watershed AGNPS Modelling Project: Final Report; Research Report No. 51; USDA-ARS National Sedimentation Laboratory: Oxford, MS, USA, 2006. [Google Scholar]
- Guerra, A.J.T.; Hoffman, H. Urban gully erosion in Brazil. Geography 2006, 19, 26–29. [Google Scholar]
- Adediji, A.; Jeje, L.K.; Ibitoye, M.O. Urban development and informal drainage patterns: Gully dynamics in Southwestern Nigeria. Appl. Geogr. 2013, 40, 90–102. [Google Scholar] [CrossRef]
- Trimble, S.W. Contribution of stream channel erosion to sediment yield from an urbanizing watershed. Science 1997, 278, 1442–1444. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, K.; Biggs, T.W. Regional impacts of urbanization on stream channel geometry: A case study in semi-arid southern California. Geomorphology 2015, 248, 228–236. [Google Scholar] [CrossRef]
- Gudino-Elizondo, N.; Biggs, T.; Castillo, C.; Bingner, R.; Langendoen, E.; Taniguchi, K.; Kretzschmar, T.; Yuan, Y.; Liden, D. Ephemeral gully erosion rates and topographical thresholds in an urban watershed using Unmanned Aerial Systems and structure from motion photogrammetric techniques. Land Degrad. Dev. 2018, in press. [Google Scholar]
- Wemple, B.C.; Browning, T.; Ziegler, A.D.; Celi, J.; Chun, K.P.; Jaramillo, F.; Leite, N.; Ramchunder, S.J.; Negishi, J.N.; Palomeque, X.; et al. Ecohydrological disturbances associated with roads: Current knowledge, research needs, and management concerns with reference to the Tropics. Ecohydrology 2017. [Google Scholar] [CrossRef]
- Reid, L.M.; Dunne, T. Sediment production from forest road surfaces. Water Resour. Res. 1984, 20, 1753–1761. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. Where do channels begin? Nature 1988, 336, 232–234. [Google Scholar] [CrossRef]
- Ramos-Scharrón, C.E.; MacDonald, L.H. Runoff and suspended sediment yields from an unpaved road segment, St. John, US Virgin Islands. Hydrol. Process. 2007, 21, 35–50. [Google Scholar] [CrossRef]
- Castillo, C.; Gómez, J.A. A century of gully erosion research: Urgency, complexity and study approaches. Earth-Sci. Rev. 2016, 160, 300–319. [Google Scholar] [CrossRef]
- Merkel, W.H.; Woodward, D.E.; Clarke, C.D. Ephemeral gully erosion model (EGEM). In Modeling Agricultural, Forest, and Rangeland Hydrology, Proceedings of the International Symposium, Chicago, IL, USA, 12–13 December 1988; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1988; pp. 315–323. [Google Scholar]
- Woodward, D.E. Method to predict cropland ephemeral gully erosion. Catena 1999, 37, 393–399. [Google Scholar] [CrossRef]
- Bingner, R.L.; Theurer, F.D. Physics of suspended sediment transport in AnnAGNPS. In Proceedings of the 2nd Federal Interagency Hydrologic Modeling Conference, Las Vegas, NV, USA, 28 July–1 August 2002. [Google Scholar]
- Bingner, R.L.; Theurer, F.D.; Yuan, Y.P. AnnAGNPS Technical Processes. Washington, D.C. US Department of Agriculture (USDA)—Agricultural Research Service (ARS). 2015. Available online: https://www.wcc.nrcs.usda.gov/ftpref/wntsc/H&H/AGNPS/downloads/AnnAGNPS_Technical_Documentation.pdf (accessed on 5 July 2017).
- Taguas, E.V.; Yuan, Y.; Bingner, R.L.; Gomez, J.A. Modeling the contribution of ephemeral gully erosion under different soil managements: A case study in an olive orchard microcatchment using the AnnAGNPS model. Catena 2012, 98, 1–16. [Google Scholar] [CrossRef]
- Merritt, W.S.; Letcher, R.A.; Jakeman, A.J. A review of erosion and sediment transport models. Environ. Model. Softw. 2003, 18, 761–799. [Google Scholar] [CrossRef]
- Bull, L.J.; Kirkby, M.J. Gully processes and modelling. Progress Phys. Geogr. 1997, 21, 354–374. [Google Scholar] [CrossRef]
- Casali, J.; Gimenez, R.; Bennett, S. Gully erosion processes: Monitoring and modelling. Earth Surf. Process. Landf. 2009, 34, 1839–1840. [Google Scholar] [CrossRef]
- Nachtergaele, J.; Poesen, J.; Vandekerckhove, L.; Oostwould-Wijdenes, D.J.; Roxo, M. Testing the ephemeral gully erosion model (EGEM) for two Mediterranean environments. Earth Surf. Process. Landf. 2001, 26, 17–30. [Google Scholar] [CrossRef]
- Yuan, Y.; Bingner, R.L.; Rebich, R.A. Evaluation of AnnAGNPS on Mississippi Delta MSEA watersheds. Trans. ASAE 2001, 44, 1673–1682. [Google Scholar] [CrossRef]
- Yuan, Y.; Bingner, R.L.; Rebich, R.A. Evaluation of AnnAGNPS nitrogen loading in an agricultural watershed. J. Am. Water Resour. Assoc. 2003, 39, 457–466. [Google Scholar] [CrossRef]
- Yuan, Y.; Bingner, R.L.; Theurer, F.D.; Rebich, R.A.; Moore, P.A. Phosphorus component in AnnAGNPS. Trans. ASAE 2005, 48, 2145–2154. [Google Scholar] [CrossRef]
- Baginska, B.; Milne-Home, W.A. Parameter sensitivity in calibration and validation of an annualized agricultural non-point source model. Water Sci. Appl. 2003, 6, 331–345. [Google Scholar] [CrossRef]
- Suttles, J.B.; Vellidis, G.; Bosch, D.; Lowrance, R.; Sheridan, J.M.; Usery, E.L. Watershed-scale simulation of sediment and nutrient loads in Georgia Coastal Plain streams using the Annualized AGNPS model. Trans. ASAE 2003, 46, 1325–1335. [Google Scholar] [CrossRef]
- Licciardello, F.; Zema, D.A.; Zimbone, S.M.; Bingner, R.L. Runoff and soil erosion evaluation by the AnnAGNPS Model in a small Mediterranean watershed. Trans. ASAE 2007, 50, 1585–1593. [Google Scholar] [CrossRef]
- Shamshad, A.; Leow, C.S.; Ramlah, A.; Wan Hussin, W.M.A.; Mohd Sanusi, S.A. Applications of AnnAGNPS model for soil loss estimation and nutrient loading for Malaysian conditions. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 239–252. [Google Scholar] [CrossRef]
- Gordon, L.M.; Bennett, S.J.; Bingner, R.L.; Theurer, F.D.; Alonso, C.V. Simulating ephemeral gully erosion in AnnAGNPS. Trans. ASAE 2007, 50, 857–866. [Google Scholar] [CrossRef]
- Alonso, C.V.; Bennett, S.J.; Stein, O.R. Predicting headcut erosion and migration in concentrated flows typical of upland areas. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Beven, K.J.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Hornberger, G.M.; Spear, R.C. An approach to the preliminary analysis of environmental systems. J. Environ. Manag. 1981, 12, 7–18. [Google Scholar]
- Beven, K.J. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service Soils. 2018. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/main/soils/survey/ (accessed on 4 February 2018).
- Grover, R. Local Perspectives on Environmental Degradation and Community Infrastructure in Los Laureles Canyon, Tijuana. Master’s Thesis, San Diego State University, San Diego, CA, USA, 2011. [Google Scholar]
- CalEPA, California Environmental Protection Agency. 2018. Available online: https://www.waterboards.ca.gov/sandiego/water_issues/programs/tmdls/TijuanaRiverValley.shtml (accessed on 4 February 2018).
- Liden, T.D.; US Environmental Protection Agency, San Diego, CA, USA. Personal communication, 2016.
- Biggs, T.W.; Taniguchi, K.T.; Gudino-Elizondo, N.; Yongping, Y.; Bingner, R.L.; Langendoen, E.J.; Liden, D. Field Measurements to Support Sediment and Hydrological Modelling in Los Laureles Canyon; U.S. Environmental Protection Agency: Washington, DC, USA, 2018.
- SCS. Hydrology, National Engineering Handbook; Natural Resources Conservation Service, US Department of Agriculture: Washington, DC, USA, 1972; Chapter 4. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detailfull/national/water/?&cid=stelprdb1043063 (accessed on 15 November 2017).
- SCS. Technical Release 55: Urban Hydrology for Small Watersheds; Natural Resources Conservation Service, US Department of Agriculture: Washington, DC, USA, 1986. Available online: https://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb1044171.pdf (accessed on 15 November 2017).
- Wells, R.R.; Momm, H.G.; Rigby, J.R.; Bennett, S.J.; Bingner, R.L.; Dabney, S.M. An empirical investigation of gully widening rates in upland concentrated flows. Catena 2013, 101, 114–121. [Google Scholar] [CrossRef]
- Bingner, R.L.; Wells, R.R.; Momm, H.G.; Rigby, J.R.; Theurer, F.D. Ephemeral gully channel width and erosion simulation technology. Nat. Hazards 2016, 80, 1949–1966. [Google Scholar] [CrossRef]
- Garbrecht, J.; Martz, L.W. TOPAGNPS, An Automated Digital Landscape Analysis Tool for Topographic Evaluation, Drainage Identification Watershed Segmentation and Subcatchment Parameterization for AGNPS. Watershed Modelling Technology; Agricultural Research Service: Beltsville, MD, USA, 1999. Available online: https://www.ars.usda.gov/ARSUserFiles/60600505/AGNPS/Dataprep/TOPAGNPS_userman.pdf (accessed on 1 June 2017).
- Biggs, T.W.; Taniguchi, K.T.; Gudino-Elizondo, N.; Yongping, Y.; Bingner, R.L.; Langendoen, E.J.; Liden, D. Geology, soil properties and erosion on marine terraces along the US-Mexico Border. Manuscript in preparation. 2018. [Google Scholar]
- Hanson, G.J. Surface erodibility of earthen channels at high stresses part II—Developing an in situ testing device. Trans. ASAE 1990, 33, 132–137. [Google Scholar] [CrossRef]
- Biggs, T.W.; Atkinson, E.; Powell, R.; Ojeda-Revah, L. Land cover following rapid urbanization on the US-Mexico border: Implications for conceptual models of urban watershed processes. Lands. Urban Plan. 2010, 96, 78–87. [Google Scholar] [CrossRef]
- Taniguchi, K.T.; Biggs, T.W.; Langendoen, E.J.; Castillo, C.; Gudino-Elizondo, N.; Yongping, Y.; Liden, D. Stream channel erosion in a rapidly urbanizing region of the US–Mexico border: Documenting the importance of channel hardpoints with Structurefrom-Motion photogrammetry. Earth Surf. Process. Landf. 2018. [Google Scholar] [CrossRef]
- Dunne, T.; Leopold, L.B. Water in Environmental Planning; W.H. Freeman and Company: New York, NY, USA, 1987; p. 818. ISBN 0-71670079-4. [Google Scholar]
- Hanson, G.J.; Cook, K.R. Procedure to estimate soil erodibility for water management purposes. In Proceeding of the Mini-Conference Advance in Water Quality Modeling, Toronto, ON, Canada, 18–21 July 1999; ASAE 1999, Paper No. 992133; ASAE: St. Joseph, MI, USA, 1999. [Google Scholar]
- Das, S.; Rudra, R.P.; Gharabaghi, B.; Gebremeskel, V.; Goel, P.K.; Dickinson, W.T. Applicability of AnnAGNPS for Ontario conditions. Can. Biosyst. Eng. 2008, 50, 1.1–1.11. [Google Scholar]
- Zema, D.A.; Bingner, R.L.; Denisi, P.; Govers, G.; Licciardello, F.; Zimbone, S.M. Evaluation of runoff, peak flow and sediment yield for events simulated by the AnnAGNPS model in a Belgian agricultural watershed. Land Degrad. Dev. 2012, 23, 205–215. [Google Scholar] [CrossRef]
- Chahor, Y.; Casalí, J.; Giménez, R.; Bingner, R.L.; Campo, M.A.; Goñi, M. Evaluation of the AnnAGNPS model for predicting runoff and sediment yield in a small Mediterranean agricultural watershed in Navarre (Spain). Agric. Water Manag. 2014, 134, 24–37. [Google Scholar] [CrossRef]
- Kim, S.H.; Yi, S. Understanding relationship between sequence and functional evolution in yeast proteins. Genetica 2007, 131, 151–156. [Google Scholar] [CrossRef] [PubMed]
- Momm, H.G.; Bingner, R.L.; Yuan, Y.; Locke, M.A.; Wells, R.R. Spatial Characterization of Riparian Buffer Effects on Sediment Loads from Watershed Systems. J. Environ. Qual. 2014, 43, 1736–1753. [Google Scholar] [CrossRef] [PubMed]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Am. Stat. Assoc. 1979, 21, 239–245. [Google Scholar] [CrossRef]
- U.S. GEOLOGICAL SURVEY, Scientific Investigations Report 2008–5093, Table 7. 2018. Available online: https://pubs.usgs.gov/sir/2008/5093/table7.html (accessed on 5 January 2018).
- Engman, E.T. Roughness coefficients for routing surface runoff. J. Irrig. Drain. Eng. 1986, 112, 39–53. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multi-level expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Beven, K.J.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.L.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Parajuli, P.B.; Nelson, N.O.; Frees, L.D.; Mankin, K.R. Comparison of AnnAGNPS and SWAT model simulation results in USDA-CEAP agricultural watersheds in south-central Kansas. Hydrol. Process. 2009, 23, 748–763. [Google Scholar] [CrossRef]


| Parameter | Default Values | Parameter Range | LHS-Derived Parameter Range, All Models (N = 500) | Behavioural Models Parameter Range, (N = 21) | |||
|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | ||
| Smax | 55.75 mm | 27.87 | 83.63 | 27.93 | 80.84 | 35.18 | 56.85 |
| Saturated conductivity | 50 mm·d−1 | 5 | 500 | 5.51 | 438 | 5.51 | 438 |
| Critical shear stress | 1 N·m−2 | 0.04 | 4 | 0.05 | 3.25 | 0.05 | 1.79 |
| Manning’s n | 0.15 | 0.015 | 0.3 | 0.017 | 0.29 | 0.017 | 0.22 |
| Tillage depth | 0.60 m | 0.3 | 2.4 | 0.33 | 2.31 | 0.63 | 0.95 |
| Head-cut erodibility | 1000 g·N−1·s−1 | 150 | 1750 | 213 | 1713 | 213 | 1562 |
| Variable | LCC | PCC |
|---|---|---|
| Smax | −0.58 * | −0.77 * |
| Tillage depth | 0.44 * | 0.72 * |
| Critical shear stress | −0.48 * | −0.71 * |
| Headcut erodibility | −0.10 | −0.03 |
| Manning’s n | 0.01 | 0.05 |
| Saturated conductivity | 0.02 | 0.01 |
| Parameter | Smax | Head Cut Erodibility | Saturated Conductivity | Critical Shear Stress | Manning’s n | Tillage Depth |
|---|---|---|---|---|---|---|
| Smax | 1 | 0.03 | 0.05 | −0.51 * | −0.18 | −0.31 |
| Head cut erodibility | 1 | −0.42 † | 0.14 | −0.27 | 0.24 | |
| Saturated conductivity | 1 | 0.11 | 0.11 | 0.10 | ||
| Critical shear stress | 1 | −0.21 | 0.43 † | |||
| Manning’s n | 1 | −0.44 † | ||||
| Tillage depth | 1 |
| Peak (L/s) | Q (m3) | Sediment (tons) | |
|---|---|---|---|
| Unpaved | |||
| min | 4 | 148 | 513 |
| mean | 50 | 500 | 787 |
| max | 101 | 739 | 1048 |
| Paved | |||
| min | 20 | 337 | 49 |
| mean | 105 | 799 | 59 |
| max | 181 | 1078 | 67 |
| Ratio of Paved: Unpaved | |||
| min | 1.78 | 1.46 | 0.06 |
| mean | 2.73 | 1.70 | 0.08 |
| max | 5.75 | 2.27 | 0.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gudino-Elizondo, N.; Biggs, T.W.; Bingner, R.L.; Yuan, Y.; Langendoen, E.J.; Taniguchi, K.T.; Kretzschmar, T.; Taguas, E.V.; Liden, D. Modelling Ephemeral Gully Erosion from Unpaved Urban Roads: Equifinality and Implications for Scenario Analysis. Geosciences 2018, 8, 137. https://doi.org/10.3390/geosciences8040137
Gudino-Elizondo N, Biggs TW, Bingner RL, Yuan Y, Langendoen EJ, Taniguchi KT, Kretzschmar T, Taguas EV, Liden D. Modelling Ephemeral Gully Erosion from Unpaved Urban Roads: Equifinality and Implications for Scenario Analysis. Geosciences. 2018; 8(4):137. https://doi.org/10.3390/geosciences8040137
Chicago/Turabian StyleGudino-Elizondo, Napoleon, Trent W. Biggs, Ronald L. Bingner, Yongping Yuan, Eddy J. Langendoen, Kristine T. Taniguchi, Thomas Kretzschmar, Encarnacion V. Taguas, and Douglas Liden. 2018. "Modelling Ephemeral Gully Erosion from Unpaved Urban Roads: Equifinality and Implications for Scenario Analysis" Geosciences 8, no. 4: 137. https://doi.org/10.3390/geosciences8040137
APA StyleGudino-Elizondo, N., Biggs, T. W., Bingner, R. L., Yuan, Y., Langendoen, E. J., Taniguchi, K. T., Kretzschmar, T., Taguas, E. V., & Liden, D. (2018). Modelling Ephemeral Gully Erosion from Unpaved Urban Roads: Equifinality and Implications for Scenario Analysis. Geosciences, 8(4), 137. https://doi.org/10.3390/geosciences8040137







