Downscaling Africa’s Drought Forecasts through Integration of Indigenous and Scientific Drought Forecasts Using Fuzzy Cognitive Maps
Abstract
1. Introduction
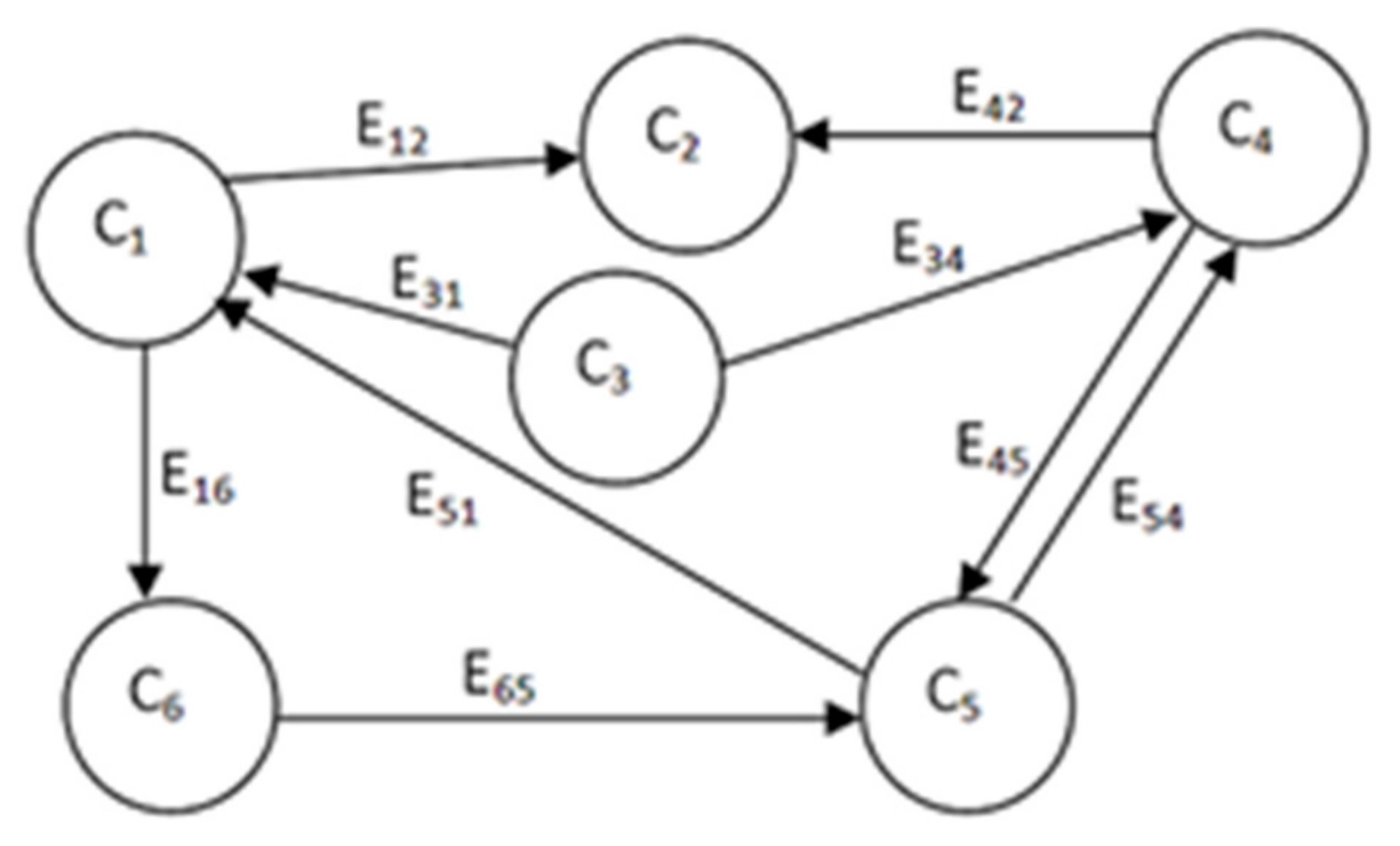
- Eij = 0 indicates no causality;
- Eij > 0 indicates causal increase, i.e., Cj increases as Ci increases;
- Eij < 0 indicates causal decrease or negative causality i.e., Cj decreases as Ci increases.
2. Materials and Methods
2.1. Data Sources
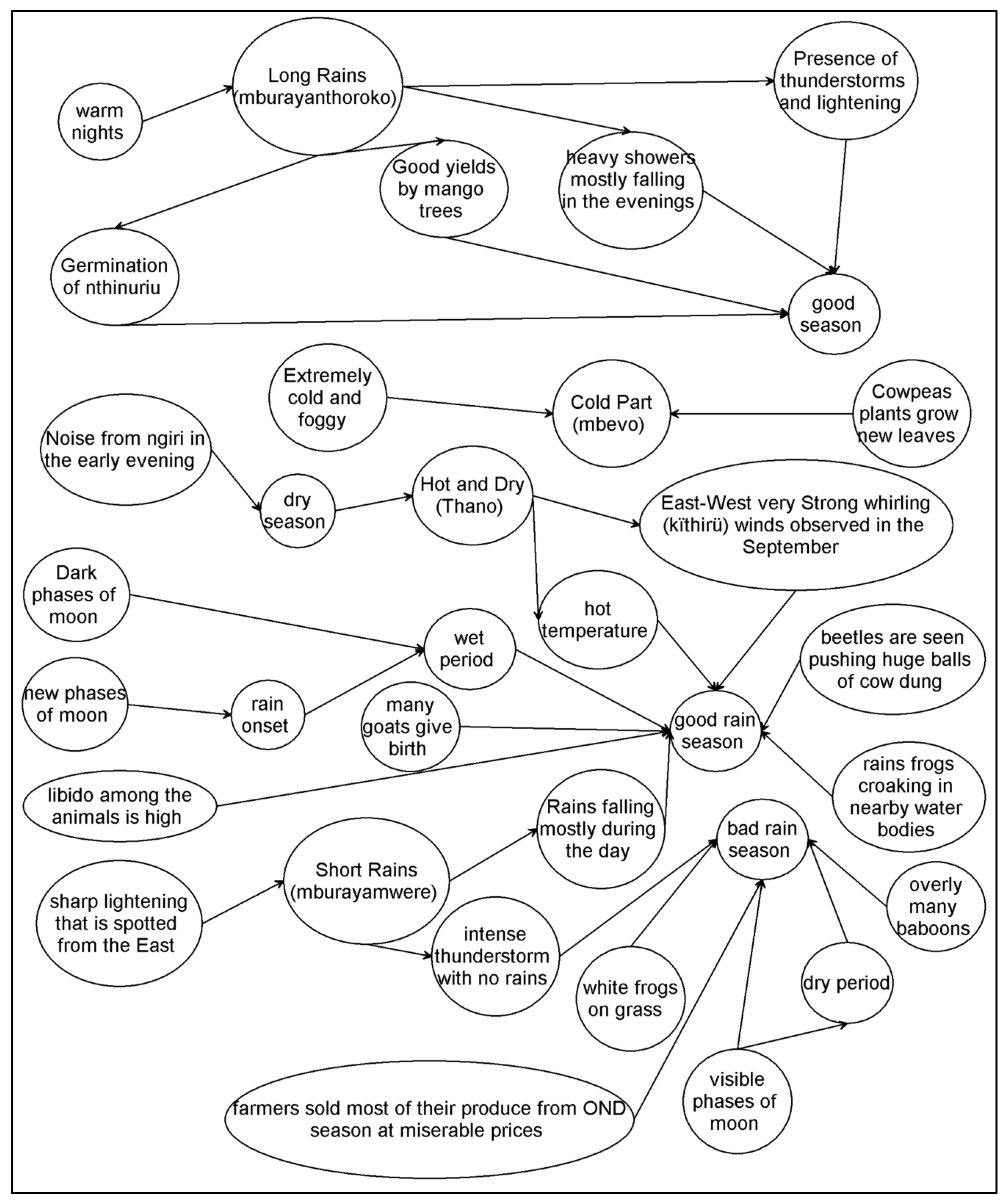
2.1.1. Source 1: Indigenous Knowledge on Drought Forecast Indicators from the Literature
Monze and Sinazonmgwe, Zambia
Lupane and Lower Gweru, Zimbabwe
Rakai District, Uganda
Wajir in Kenya
- Failure of the out of season showers expected on the 56th day (towards the end of February) is an indicator of a bad season and
- Failure of the out of season showers expected on the 70th day (second week of March) is an indicator of a bad season.
- When a drought is looming in the coming season, cattle take on excessive water and refuse, or are reluctant to, move away from the watering point;
- When cattle take water and run around jovially as if in a celebration mood, this predicts a good season (rain) on the way;
- When cows give birth to female calves, the community should prepare for a bad season (drought);
- Cattle bulls become “arrogantly playful” when the coming season is going to be good;
- Female camels urinate while sitting as if to express hopelessness for the future; and
- A sudden increase in libido, mating and general excitement of livestock symbolizes the rain season approaching.
- If rain starts early in the morning, the community should prepare their cattle and land as it symbolizes good seasonal harvest and plenty of pasture for livestock during that season;
- Failure of mid-season showers expected on the 90th day is an indicator of a bad season
- Failure of peak season showers expected on the 90th day (which is on 15th of April) is an indicator of a bad season and
- One astronomical indicator states that if there is a shooting star on a Tuesday, camels will soon get stuck in mud, and this symbolizes heavy (adequate) rain on the way.
- The jovial mood of camels is an indication that the coming season will be good;
- Grunting of camel bulls (making mating calls) symbolizes a good rainy season;
- If the cattle refuse to go back to home and run away while facing different directions, it is a sign of a bad season;
- If cattle run towards their home around 3 o’clock in the afternoon, this shows that a good season (rain) is coming and
- When cattle make specific throat vocal sounds when sleeping at night, this is an indicator that the coming season is going to be good; other vocals represent a bad season.
- When camels run away browsing haphazardly and appear to have lost their hearing senses, this depicts a bad season;
- When camels brush their legs together, this is a good indication of a bumper season and
- When moles throw up soil, making the sand loose for aeration, this depicts a very hot season.
Common Features of IK on Drought Forecasting
2.1.2. Source 2: Primary Data Collection
Case Study 1: Mbeere, Kenya
- Moderate temperatures (less than 25 °C) are considered good because this ensures that the annual crops (cotton and pigeon peas) survive until the MAM rains.
- Good yields by mango trees that produce large fruits (e.g., ndoto) are a good sign, the opposite indicates a poor season, and
- Good yields from some wild fruits such as ngaa are a bad sign.
- Many goats giving birth is a good sign; the sign is stronger when twins are born;
- If movement of the Mindithu (Playing Mantis) is as if they are ‘kissing’ the ground is noticed in late February, then the rains are less than a month away.
- A poor MAM season is predicted if many farmers sell most of their produce from OND season at ‘throw-away’ prices; this is a ‘punishment from God’
- Presence of thunderstorms and lightening is a sign of a good season;
- Intense heavy showers, mostly falling in the evenings and early parts of the night, is a good sign and
- Very warm nights are a sign of rain within 24 h.
- Germination of nthinuriu is a sign of a good season and
- Flourishing of edible wild tubers (mbaku) and some wild fruits, such as ngawa and Njiara, is a sign of a poor season. These fruits and tubers are seen as God’s provision in place of food.
- Sounds from a bird called kivutambura (means rain puller) is a sign of good harvest;
- When young bulls jump up and down as they return home, it is a sign that rains will fall in less than 2 weeks;
- The presence of many baboons is a sign of a poor season—the rains are not adequate to support their wild sources of food and water;
- If, after about two weeks of rain, frogs are heard croaking in nearby water bodies, then the harvest will be good;
- If beetles are seen pushing huge balls of cow dung (or human waste), the season will be good. The beetles are said to be preparing homes for their offspring
- If Bugvare are observed filling their nests to the brim after about 2 weeks of rain, this signifies a good season—it is an analogy of a full granary and
- The presence of white frogs on grass is a bad sign. These frogs are known to kill cows if they (cows) ingest them during grazing.
- Rain onset is predicted to occur around the time of a new moon. Visible phases of full moon signify a drier period. Dark phases of moon dictate a wet period
- When older people experience congested chests in early March; this means that rain is less than a week away. Scientifically, this is related to increased humidity in the atmosphere.
- Night temperatures drop to 15 °C or below;
- Intense cold implies abundant rainfall in the rainy season;
- The cold, sometimes accompanied by drizzle, retains the moisture from the MAM rains and gives late (planted) crops a chance to grow. Late and annual maturing crops such as pigeon peas also benefit from the cool temperature and so do animals because the water bodies retain water for longer and the fodder does not wither fast;
- Cowpea plants grow new leaves that are used as vegetables;
- Interruption of the cold season by days of warm temperature implies drought spells during the rainy season, and
- Strong and destructive winds are a bad omen at this time—they carry away stock (of crops) that is used as fodder for animals.
- Intense hot temperature predicts abundant rainfall. The community believes that these temperatures ‘cook’ the rain;
- East–west, very strong, whirling (kïthirü) winds observed in September are a sign of favorable season. Since there are many water bodies in the east, this movement is translated to mean that the wind is carrying the water to go and ‘make’ the rains, and
- Very warm nights are a sign of rains within 24 h.
- Production of secondary leaves by cowpeas is a good sign—there is still moisture in the soil), and
- Very leafy migaa is a good sign—the trees branches are usually cut and used as fodder for goats and sheep.
- Maturity of wild fruits of the Mutiru (ndiru) is a sign that the OND rains will be starting in less than 2 weeks;
- Flowering of muramba (oak trees) is a sign of rain onset;
- Germination of karambakanthi is a sign of rain onset;
- Flowering of mugaa, mutororo, mukuu and muthigira means rain is 2 weeks away. This is true when there is shedding of seeds by muthuri and gakega.
- Low nesting by the ngoco bird along water bodies is a sign that rain will be poor and vice versa for favorable rain;
- When cows are unwilling to leave (they are forced) the water points, this is a sign of poor OND rains, and
- When the Mindithu (Playing Mantis) starts moving southwards this is a sign that OND rains will be inadequate for crop production.
- The presence of an intense thunderstorm with no rain is a sign of a bad season. A moderate start (not storms) is a good sign;
- Rain falling mostly during the day (from 11 a.m. onwards) is a sign of a good season;
- Storms and hailstones are considered bad omens; they bring down millet stocks which are generally weaker than maize; and
- Dew in the morning is a sign of dry spell onset.
- Flowering and fruiting of drought-category mango trees is a sign of a bad season and
- Flowering and fruiting of large category mango trees is a sign of a good season.
- Flocks of the thari bird seen migrating from the west to Mbeere is a bad sign. The bird’s name means ‘snatch’ (ku-thara) and it is interpreted that the birds are coming to snatch the little crops (millet and sorghum) from the farmers;
- When thari birds invade maize crops, an extreme drought is predicted;
- A good season is predicted if the libido among animals is high;
- Hopelessness expressed by bulls that refuse to plough (and lie down instead) is a sign of a poor season. It is interpreted that these bulls are telling the farmers that they are wasting their time planting becausethe crops will not mature, and
- Noise from ngiri (crickets) in the early evening is a sign of the onset of a dry season. Farmers still planting should be alarmed because their seeds may not germinate.
- Rain onset is predicted to be around the time of a new moon;
- Visible phases of full moon signify a drier period, and
- Dark phases of the moon indicate wet periods.
Case Study 2—KwaZulu-Natal, South Africa
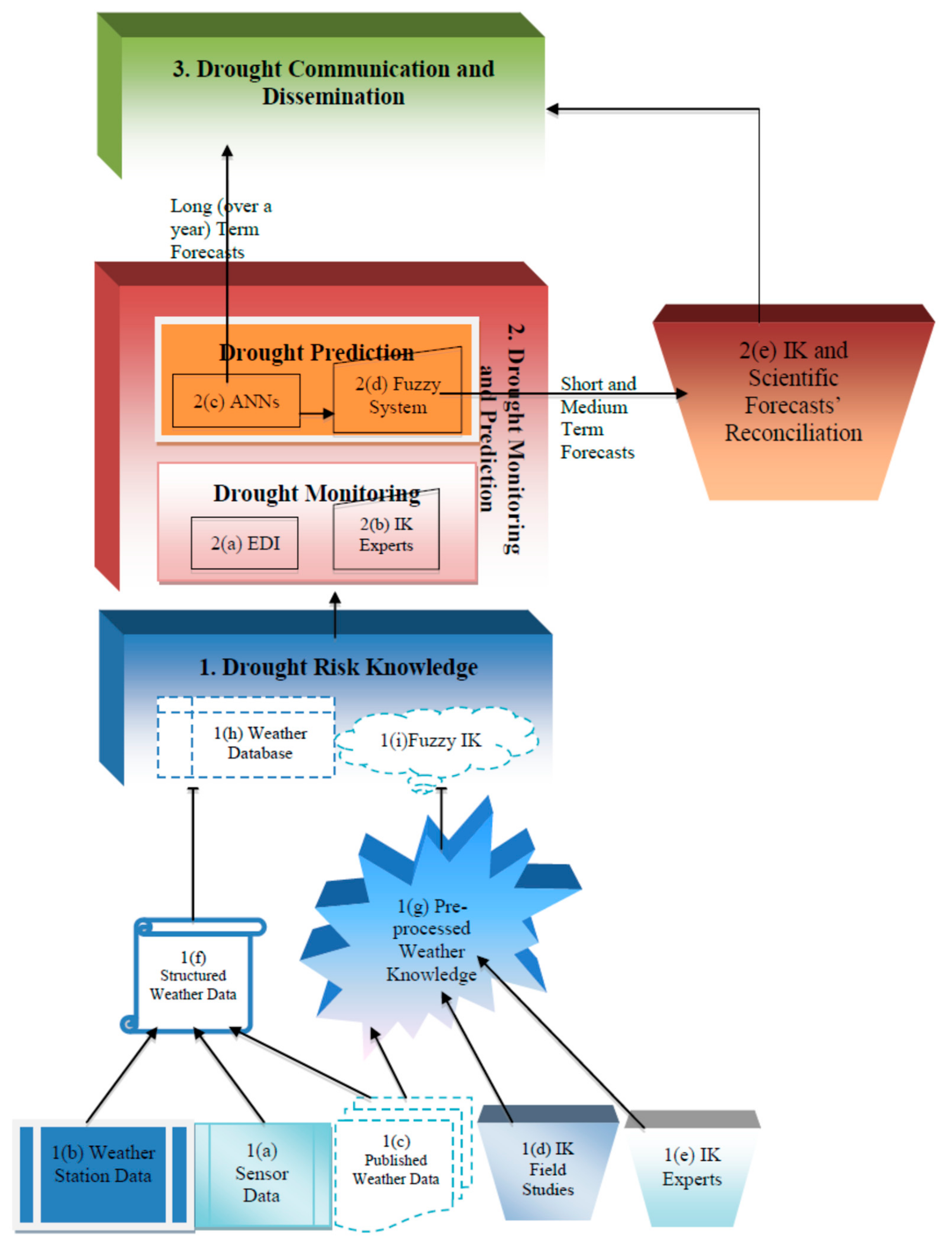
2.2. Integration Framework Design
2.3. Layer 1: Drought Knowledge
2.4. Layer 2: Drought Monitoring and Prediction
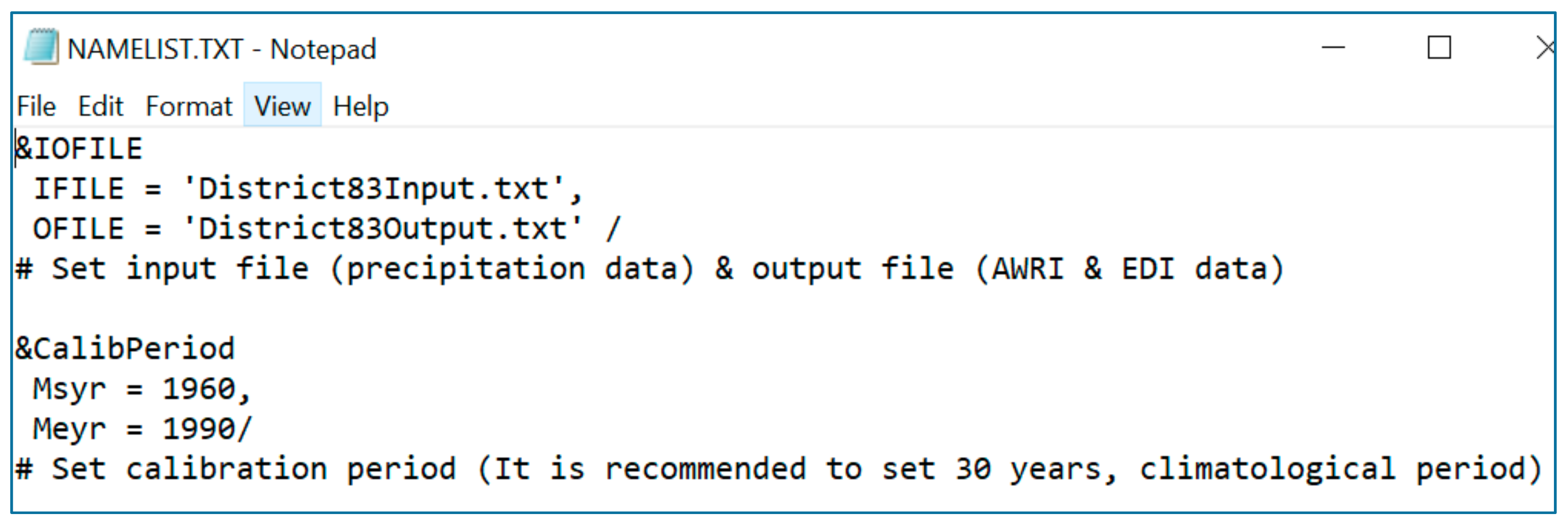
2.4.1. Drought Monitoring Using the Effective Drought Index (EDI)
The normal precipitation for November is the mean of the precipitations for November 1979, November 1980, November 28, 1980, …, November 2009.
2.4.2. Drought Forecasting: Artificial Neural Networks (ANNs)
2.4.3. Drought Forecasting: Fuzzy System
3. Results
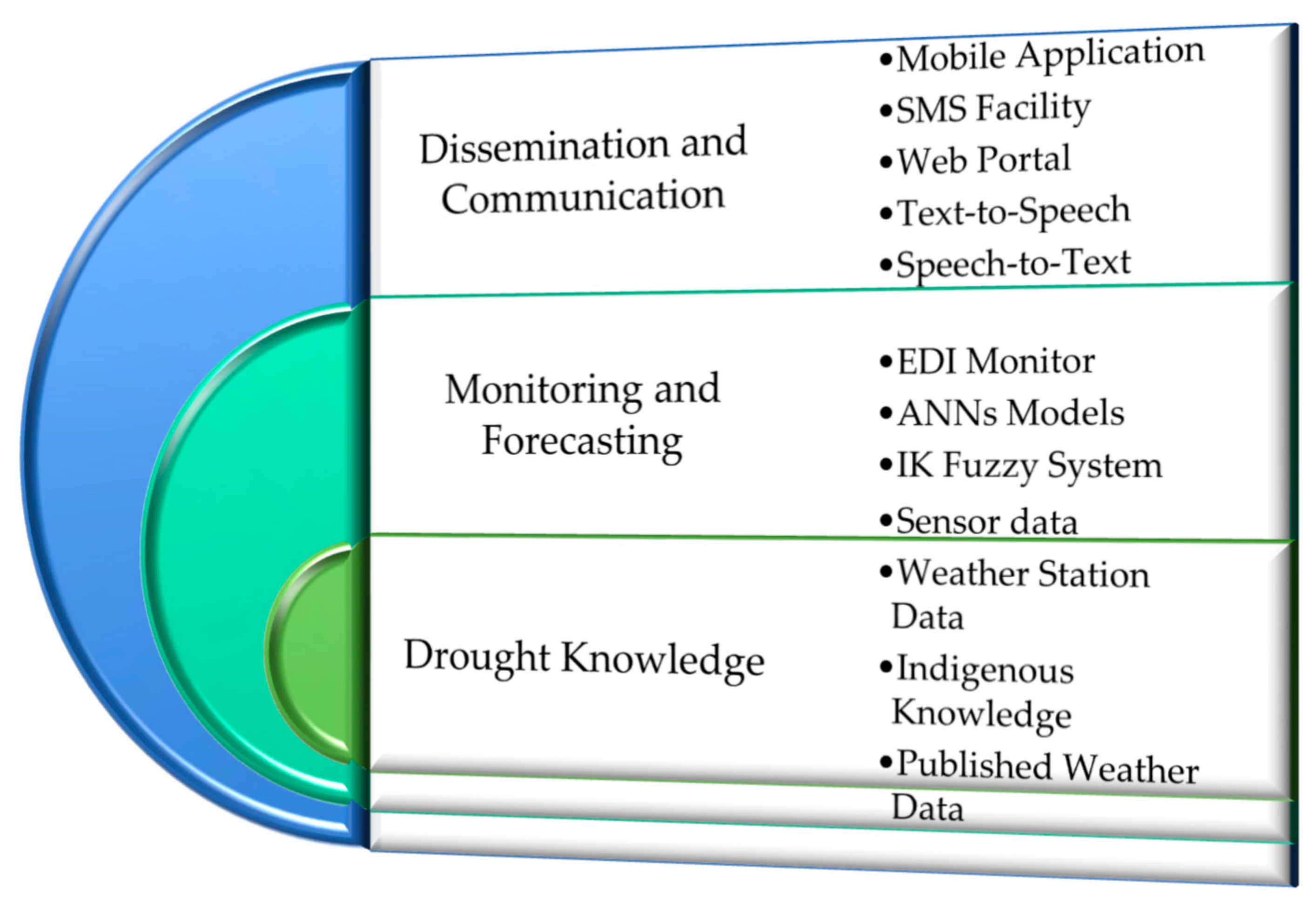
3.1. Integrated Drought Early Warning System
3.1.1. Drought Knowledge
3.1.2. Monitoring and Forecasting
- (a)
- The EDI monitor that handled the ‘monitoring’ aspect. Here, the stand-alone FORTRAN program developed by [57] was used.
- (b)
- Artificial Neural Networks (ANNs) were in charge of the ‘forecasting’ aspect. These were implemented in MATLAB and used to predict future values (EDI and AWRI) of droughts.
- (c)
- A Fuzzy Logic System handled the monitoring and forecasting of droughts using indigenous knowledge. This was also implemented using MATLAB; its output was uploaded to the MySQL database from where it was linked to the ANN models’ output.
3.1.3. Dissemination and Communication
3.2. EDI Monitor
3.3. IK Fuzzy Logic System
4. Conclusions and Further Work
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Wilhite, D.A.; Glantz, M.H. Understanding the Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- ISDR; ECA; UNDP. 3rd African Drought Adaptation Forum Report September, 2008; ISDR, ECA, UNDP: Addis Ababa, Ethiopia, 2008. [Google Scholar]
- Zwaagstra, L.; Sharif, Z.; Wambile, A.; Leeuw, J.D.; Said, M.Y.; Johnson, N.; Njuki, J.; Ericksen, P.; Herrero, M. An Assessment of the Response to the 2008–2009 Drought in Kenya. Available online: https://cgspace.cgiar.org/bitstream/handle/10568/2057/assessment_drought_2010.pdf?sequence=3 (accessed on 10 November 2017).
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Branstator, G.W.; Karoly, D.; Kumar, A.; Lau, N.C.; Ropelewski, C. Progress during TOGA in understanding and modeling global teleconnections associated with tropical sea surface temperatures. J. Geophys. Res. Oceans 1998, 103, 14291–14324. [Google Scholar] [CrossRef]
- Masinde, M. Artificial neural networks models for predicting effective drought index: Factoring effects of rainfall variability. Mitig. Adapt. Strat. Glob. Chang. 2014, 19, 1139–1162. [Google Scholar] [CrossRef]
- Marshall, N.A.; Gordon, I.J.; Ash, A.J. The reluctance of resource-users to adopt seasonal climate forecasts to enhance resilience to climate variability on the rangelands. Clim. Chang. 2011, 107, 511–529. [Google Scholar] [CrossRef]
- Mwagha, S.M.; Masinde, M. Scientific Verification of Weather Lore for Drought Forecasting—The Role of Fuzzy Cognitive Mapping. In Proceedings of the IST-Africa 2015 Conference, Lilongwe, Malawi, 6–8 May 2015; Cunningham, P., Cunningham, M., Eds.; IIMC International Information Management Corporation: Dublin, Ireland, 2015. ISBN 978-1-905824-50-2. [Google Scholar]
- Mugabe, F.T.; Mubaya, C.P.; Nanja, D.; Gondwe, P.; Munodawafa, A.; Mutswangwa, E.; Chagonda, I.; Masere, P.; Dimes, J.; Murewi, C. Use of Indigenous Knowledge Systems and Scientific Methods for Climate Forecasting in Southern Zambia and North-Western Zimbabwe. Zimb. J. Technol. Sci. 2010, 1, 19–30. [Google Scholar] [CrossRef]
- Ziervogel, G.; Bithell, M.; Washington, R.; Downing, T. Agent-based social simulation: A method for assessing the impact of seasonal climate forecast applications among smallholder farmers. Agric. Syst. 2005, 83, 1–26. [Google Scholar] [CrossRef]
- Enock, C.M. Indigenous Knowledge Systems and Modern Weather Forecasting: Exploring the Linkages. J. Agric. Sustain. 2013, 2, 98–141. [Google Scholar]
- Anandaraja, N.; Rathakrishnan, T. Indigenous weather and forecast practices of Coimbatore district farmers of Tamil Nadu. Indian J. Tradit. Knowl. 2008, 7, 630–633. [Google Scholar]
- Masinde, M.; Bagula, A. ITIKI: Bridge between African indigenous knowledge and modern science of drought prediction. Knowl. Manag. Dev. J. 2011, 7, 274–290. [Google Scholar] [CrossRef]
- Warren, D.M. Information and Communication Technologies, Knowledge Management and Indigenous Knowledge: Implications to Livelihood of Communities in Ethiopia; World Bank Discussion Paper 127; The World Bank: Washington, DC, USA, 1991; pp. 1–12. [Google Scholar]
- Risiro, J.; Mashoko, D.; Tshuma, T.; Rurinda, E. Weather Forecasting and Indigenous Knowledge Systems in Chimanimani District of Manicaland. Zimb. J. Emerg. Trends Educ. Res. Policy Stud. 2012, 3, 561–566. [Google Scholar]
- Xue, S. Neural Fuzzy Inference System-Based Weather Prediction Model and Its Precipitation Predicting Experiment. Atmosphere 2014, 5, 788–805. [Google Scholar] [CrossRef]
- Ziervogel, G.; Downing, T.E. Stakeholder networks: improving seasonal climate forecasts. Clim. Chang. 2004, 65, 73–101. [Google Scholar] [CrossRef]
- Masinde, M. An innovative drought early warning system for sub-Saharan Africa: Integrating modern and indigenous approaches. Afr. J. Sci. Technol. Innov. Dev. 2015, 7, 8–25. [Google Scholar] [CrossRef]
- Mercer, J.; Kelman, I.; Taranis, L.; Suchet-Pearson, S. Framework for integrating indigenous and scientific knowledge for disaster risk reduction. Disasters 2010, 34, 214–239. [Google Scholar] [CrossRef] [PubMed]
- Roncoli, C. Ethnographic and participatory approaches to research on farmers’ responses to climate predictions. Clim. Res. 2006, 33, 81. [Google Scholar] [CrossRef]
- Stigter, C.J.; Dawei, Z.; Onyewotu, L.O.Z.; Xurong, M. Using traditional methods and indigenous technologies for coping with climate variability. Clim. Chang. 2005, 70, 255–271. [Google Scholar] [CrossRef]
- Brokensha, D.W.; Warren, D.M.; Werner, O. Indigenous Knowledge Systems and Development; University Press of America: Lanham, MD, USA, 1980. [Google Scholar]
- Flora, C.B. Reconstructing agriculture: The case for local knowledge. Rural Sociol. 1992, 57, 92–97. [Google Scholar] [CrossRef]
- Sillitoe, P. The development of indigenous knowledge: A new applied anthropology 1. Curr. Anthropol. 1998, 39, 223–252. [Google Scholar] [CrossRef]
- Thrupp, L.A. Legitimizing local knowledge: From displacement to empowerment for Third World people. Agric. Hum. Values 1989, 6, 13–24. [Google Scholar] [CrossRef]
- Virji, H.; Cory, F.; Amy, F.; Mayuri, S. Climate Variability, Water Resources and Agricultural Productivity: Food Security Issues in Tropical Sub-Saharan Africa; World Food Programme: Rome, Italy, 1997. [Google Scholar]
- Krupnik, I.; Ray, G.C. Pacific walruses, indigenous hunters, and climate change: Bridging scientific and indigenous knowledge. Deep Sea Res. Part II Top. Stud. Oceanogr. 2007, 54, 2946–2957. [Google Scholar] [CrossRef]
- Lauer, M.; Aswani, S. Integrating indigenous ecological knowledge and multi-spectral image classification for marine habitat mapping in Oceania. Ocean Coast. Manag. 2008, 51, 495–504. [Google Scholar] [CrossRef]
- Voinov, A.; Bousquet, F. Modelling with stakeholders. Environ. Modell. Softw. 2010, 25, 1268–1281. [Google Scholar] [CrossRef]
- Voinov, A.; Gaddis, E.J.B. Lessons for successful participatory watershed modelling: A perspective from modeling practitioners. Ecol. Model. 2008, 216, 197–207. [Google Scholar] [CrossRef]
- Giordano, R.; Liersch, S. A fuzzy GIS-based system to integrate local and technical knowledge in soil salinity monitoring. Environ. Model. Softw. 2012, 36, 49–63. [Google Scholar] [CrossRef]
- Sicat, R.S.; Carranza, E.J.M.; Nidumolu, U.B. Fuzzy modeling of farmers’ knowledge for land suitability classification. Agric. Syst. 2005, 83, 49–75. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy Cognitive Maps. Int. J. Man-Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Maitra, S.; Banerjee, D. Application of Fuzzy Cognitive Mapping for Cognitive Task Analysis in Mechanised Mines. IOSR J. Mech. Civ. Eng. 2014, 11, 20–28. [Google Scholar] [CrossRef]
- Chinlampianga, M. Traditional knowledge, weather prediction and bioindicators: A case study in Mizoram, Northeastern India. Indian J. Tradit. Knowl. 2011, 10, 207–211. [Google Scholar]
- Guerram, T.; Maamri, R.; Sahnoun, Z. A Tool for Qualitative Causal Reasoning on Complex Systems. Int. J. Comput. Sci. Issues 2010, 7, 120–125. [Google Scholar]
- Mago, V.K.; Morden, H.K.; Fritz, C.; Wu, T.; Namazi, S.; Geranmayeh, P. Analyzing the impact of social factors on homelessness: A Fuzzy Cognitive Map approach. BMC Med. Inform. Decis. Mak. 2013, 13, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Xirogiannis, G.; Glykas, M. Fuzzy Cognitive Maps in Business Analysis and Performance-Driven Change. IEEE Trans. Eng. Manag. 2004, 51, 334–351. [Google Scholar] [CrossRef]
- Chrysostomos, S.; Peter, G. Mathematical Formulation of Fuzzy Cognitive Maps. In Proceedings of the 7th Mediterranean Conference on Control and Automation, Haifa, Israel, 28–30 June 1999; pp. 2251–2261. [Google Scholar]
- Karagiannis, I.; Groumpos, P. Input-Sensitive Fuzzy Cognitive Maps. Int. J. Comput. Sci. Issues 2013, 10, 143–151. [Google Scholar]
- Carvalho, J.P. On the Semantics and the Use of Fuzzy Cognitive Maps in Social Sciences. In Proceedings of the 2010 IEEE World Congress on Computational Intellige nce (WCCI), Barcelona, Spain, 18–23 July 2010; pp. 18–23. [Google Scholar]
- Chrysafiadi, K.; Virvou, M. A knowledge representation approach using fuzzy cognitive maps for better navigation support in an adaptive learning system. Springerplus 2013, 2, 81. [Google Scholar] [CrossRef] [PubMed]
- Din, M.A.; Cretan, G.C. Causal modelling of the higher education determinants regarding the labour market absorption of graduates: A Fuzzy Cognitive Maps approach. Int. J. Fuzzy Syst. Adv. Appl. 2014, 1, 1–6. [Google Scholar]
- Yousef, O.M.S. Causality analysis of the technology strategy maps using the fuzzy cognitive strategy map. Afr. J. Bus. Manag. 2014, 8, 191–210. [Google Scholar] [CrossRef]
- Aguilar, J. A Survey about Fuzzy Cognitive Maps Papers. Int. J. Comput. Cognit. 2005, 3, 27–33. [Google Scholar]
- Papageorgiou, E.; Kontogianni, A. Using Fuzzy Cognitive Mapping in Environmental Decision Making and Management: A Methodological Primer and an Application. In International Perspectives on Global Environmental Change; Young, S., Ed.; InTech: London, UK, 2012; pp. 427–450. ISBN 978-953-307-815-1. Available online: http://www.intechopen.com/books/international-perspectives-on-global-environmental-change/using-fuzzy-cognitive-mapping-in-environmental-decision-making-and-management-a-methodological-prime (accessed on 10 November 2017).
- Văidianu, M.N. Fuzzy cognitive maps: Diagnosis and scenarios for a better management process of visitors flows in Romanian Danube Delta Biosphere Reserve. J. Coast. Res. 2013, 65, 1063–1068. [Google Scholar] [CrossRef]
- Kwon, S.J.; Mustapha, E.E. Exploring the Effect of Cognitive Map on Decision Makers’ Perceived Equivocality and Usefulness in the Context of Task Analyzability and Representation. In Proceedings of the Fifth International Conference on Information, Process, and Knowledge Management, Nice, France, 24 February–1 March 2013; pp. 117–122. [Google Scholar]
- Rangarajan, K.; Jayasudha, S.; Ramanathan, K. Fuzzy Petri Nets and Fuzzy Cognitive Maps. Int. J. Comput. Appl. 2012, 46, 5–9. [Google Scholar]
- Orlove, B.; Roncoli, C.; Merit, K.; Abushen, M. Indigenous climate knowledge in southern Uganda: The multiple components of a dynamic regional system. Clim. Chang. 2009, 100, 243–265. [Google Scholar] [CrossRef]
- Morton, J.; Barton, D.; Collinson, C.; Heath, B. Comparing Drought Mitigation Interventions in the Pastoral Livestock Sector; University of Greenwich, Natural Resource Institute: Chatham, UK, 2006. [Google Scholar]
- The Arid Lands Resource Management Project (ALRMP). Wajir District Vision and Strategy: 2005–2015; Government of Kenya: Nairobi, Kenya, 2005.
- The Kenya Census 2009: Population and Housing Census Highlights. Available online: https://www.knbs.or.ke/2009-kenya-population-and-housing-census-analytical-reports/ (accessed on 10 November 2017).
- Duan, N.; Hoagwood, K. Purposeful Sampling for Qualitative Data Collection and Analysis in Mixed Method Implementation Research. Adm. Policy Ment. Health Serv. Res. 2015, 42, 533–544. [Google Scholar] [CrossRef]
- Preist, C.; Massung, E.; Coyle, D. Competing or aiming to be average?: Normification as a means of engaging digital volunteers. In Proceedings of the 17th ACM Conference on Computer Supported Cooperative Work and Social Computing, Baltimore, MD, USA, 15–19 February 2014; pp. 1222–1233. [Google Scholar]
- Byun, H.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Svoboda, M.D. Drought Early Warning Systems in the Context of Drought Preparedness and Mitigation; World Meteorological Organization: Geneva, Switzerland, 2000; pp. 1–16. [Google Scholar]
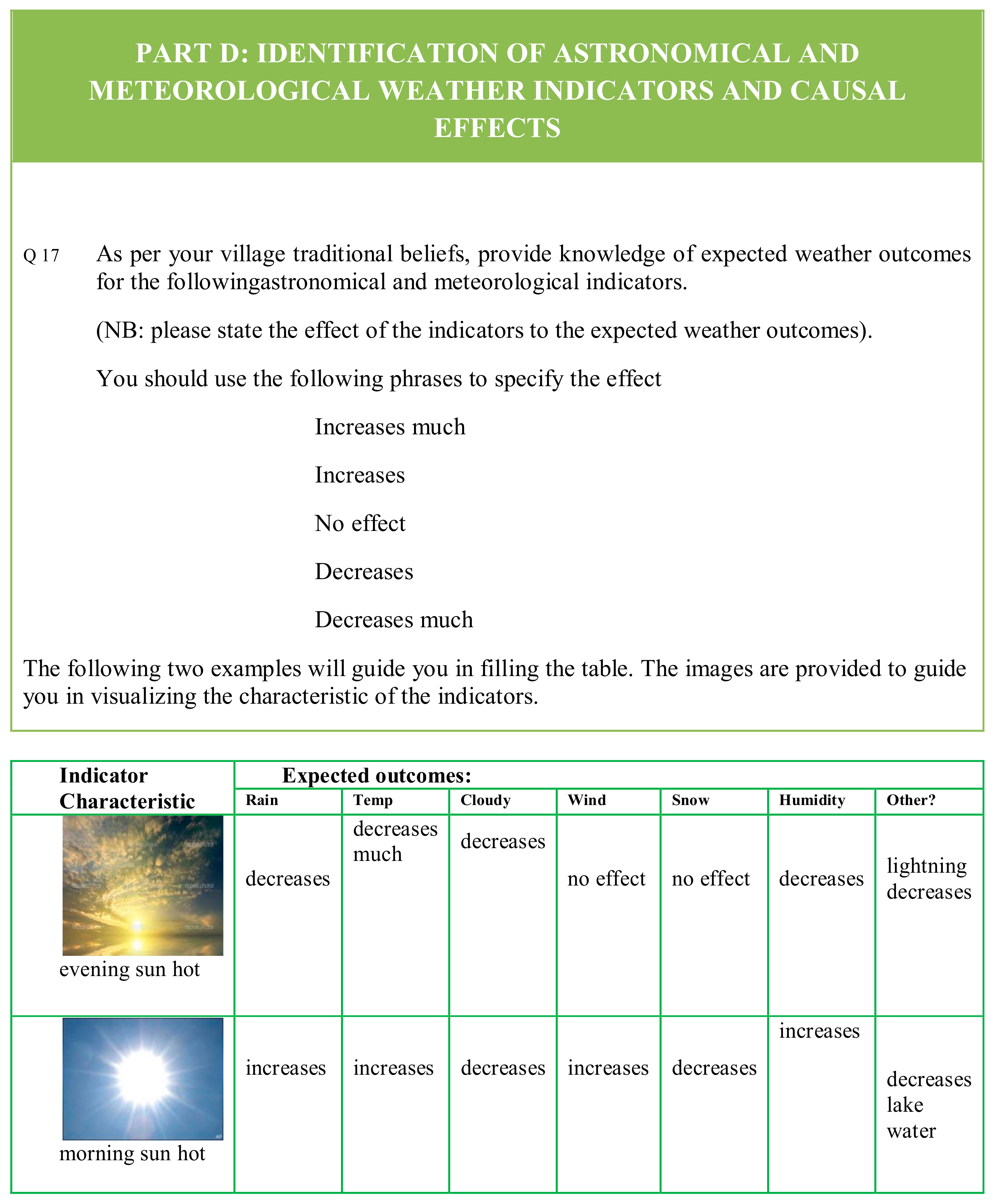
| Season | Local Name | Onset Signs | Cessation Signs |
|---|---|---|---|
| Summer | Ihlobo (October–February) | Lightening Very hot Daytime rain | Cold Winds Temperature lowers Rain stops |
| Autumn | Intwasabusika (March–May) | Trees shed leaves Grass changes color | Very cold |
| Winter | Ubusika (May–July) | Mists | Clear sky in the morning Birds build new nests Trees look dry |
| Spring | Intwasahlo (August–October) | Lots of wind | Very hot |
| Drought Class Description | Drought Index Values |
|---|---|
| Extreme Flood | EDI > 2 |
| Severe Flood | 1.5 < EDI < 1.99 |
| Moderate Flood | 1 < EDI < 1.49 |
| Wet–Near Normal | 0.01 < EDI < 0.99 |
| Drought–Near Normal | −0.99 < EDI < 0.00 |
| Moderate Drought | −1 < EDI < −1.49 |
| Severe Drought | −1.5 < EDI < −1.99 |
| Extreme Drought | EDI < −2 |
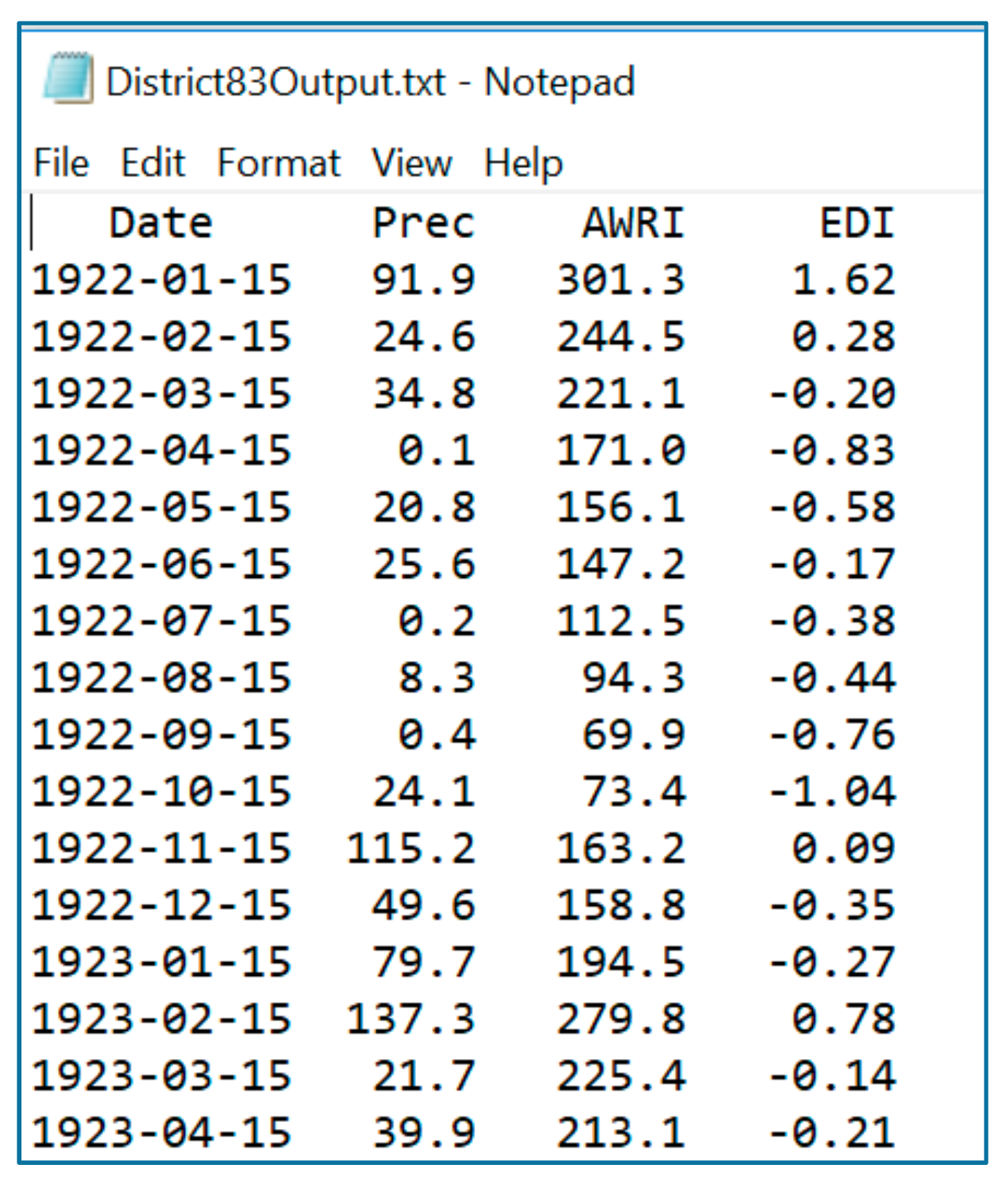
| Date | Total Precipitation | AWRI | EDI |
|---|---|---|---|
| 15 June 1980 | 70.80 | 230.0 | −0.51 |
| 15 February 1980 | 13.0 | 179.7 | −0.65 |
| 15 March 1980 | 37.9 | 170.1 | −0.86 |
| 15 April 1980 | 105.9 | 229.8 | −1.35 |
| 15 December 1980 | 33.5 | 460.8 | 1.05 |
| 15 June 1981 | 14.6 | 364.9 | 0.37 |
| 15 December 2009 | 121.10 | 297.5 | −0.27 |
| Concepts | High Clouds | Low Clouds | Medium Clouds | Clear Sky | Many Stars | Rainbow | Lightning | Partial/Dark Moon | Full/Visible Moon | Rain | Dry | Hot | Cold |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| High clouds | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | −1.00 | 0.00 | 0.00 | −0.75 | 0.75 | 0.75 | −1.00 |
| Low clouds | 0.00 | 0.00 | 0.00 | −1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | −0.50 | 0.50 |
| Medium clouds | 0.00 | 0.00 | 0.00 | −0.50 | 0.00 | 0.00 | 0.00 | 0.00 | −0.50 | 0.00 | 0.00 | 0.00 | 0.50 |
| Clear sky | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −1.00 | 0.00 | 0.00 | −0.75 | 0.75 | 1.00 | −1.00 |
| Many stars | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −1.00 | 0.75 | 0.75 | −1.00 |
| Rainbow | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.50 | 0.00 | 0.50 | 0.00 |
| Lightning | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | −1.00 | −0.75 | 0.75 |
| Partial/dark moon | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.50 | −0.75 | −0.50 | 0.50 |
| Full/visible moon | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.75 | −0.25 | 0.75 | −0.75 |
| Rain | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Dry | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Hot | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Cold | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Concepts | Out Degree | In Degree | Centrality |
|---|---|---|---|
| High clouds | 4.75 | 0.00 | 4.75 |
| Low clouds | 2.50 | 0.00 | 2.50 |
| Medium clouds | 1.50 | 0.00 | 1.50 |
| Clear sky | 4.50 | 2.00 | 6.50 |
| Many stars | 3.50 | 0.00 | 3.50 |
| Rainbow | 1.00 | 0.00 | 1.00 |
| Lightning | 3.50 | 2.00 | 5.50 |
| Partial/dark moon | 2.25 | 0.00 | 2.25 |
| Full/visible moon | 2.50 | 0.50 | 3.00 |
| Rain | 0.00 | 5.75 | 5.75 |
| Dry | 0.00 | 4.25 | 4.25 |
| Hot | 0.00 | 5.50 | 5.50 |
| Cold | 0.00 | 6.00 | 6.00 |
| Spring | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In degree | 0 | 0 | 0 | 3 | 0 | 0 | 2 | 0 | 1 | 9 | 9 | 9 | 8 |
| Out degree | 6 | 5 | 6 | 5 | 4 | 4 | 4 | 3 | 4 | 0 | 0 | 0 | 0 |
| Centrality | 6 | 5 | 6 | 8 | 4 | 4 | 6 | 3 | 5 | 9 | 9 | 9 | 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masinde, M.; Mwagha, M.; Tadesse, T. Downscaling Africa’s Drought Forecasts through Integration of Indigenous and Scientific Drought Forecasts Using Fuzzy Cognitive Maps. Geosciences 2018, 8, 135. https://doi.org/10.3390/geosciences8040135
Masinde M, Mwagha M, Tadesse T. Downscaling Africa’s Drought Forecasts through Integration of Indigenous and Scientific Drought Forecasts Using Fuzzy Cognitive Maps. Geosciences. 2018; 8(4):135. https://doi.org/10.3390/geosciences8040135
Chicago/Turabian StyleMasinde, Muthoni, Mwanjele Mwagha, and Tsegaye Tadesse. 2018. "Downscaling Africa’s Drought Forecasts through Integration of Indigenous and Scientific Drought Forecasts Using Fuzzy Cognitive Maps" Geosciences 8, no. 4: 135. https://doi.org/10.3390/geosciences8040135
APA StyleMasinde, M., Mwagha, M., & Tadesse, T. (2018). Downscaling Africa’s Drought Forecasts through Integration of Indigenous and Scientific Drought Forecasts Using Fuzzy Cognitive Maps. Geosciences, 8(4), 135. https://doi.org/10.3390/geosciences8040135






