A Database for Climatic Conditions around Europe for Promoting GSHP Solutions
Abstract
:1. Introduction
- a Decision Support System (DSS) to help expert and non-expert users in assessing a first feasibility study on GSHP systems;
- an LCA tool to calculate the overall impact of a GSHP system and comparing it with standard HVAC solutions.
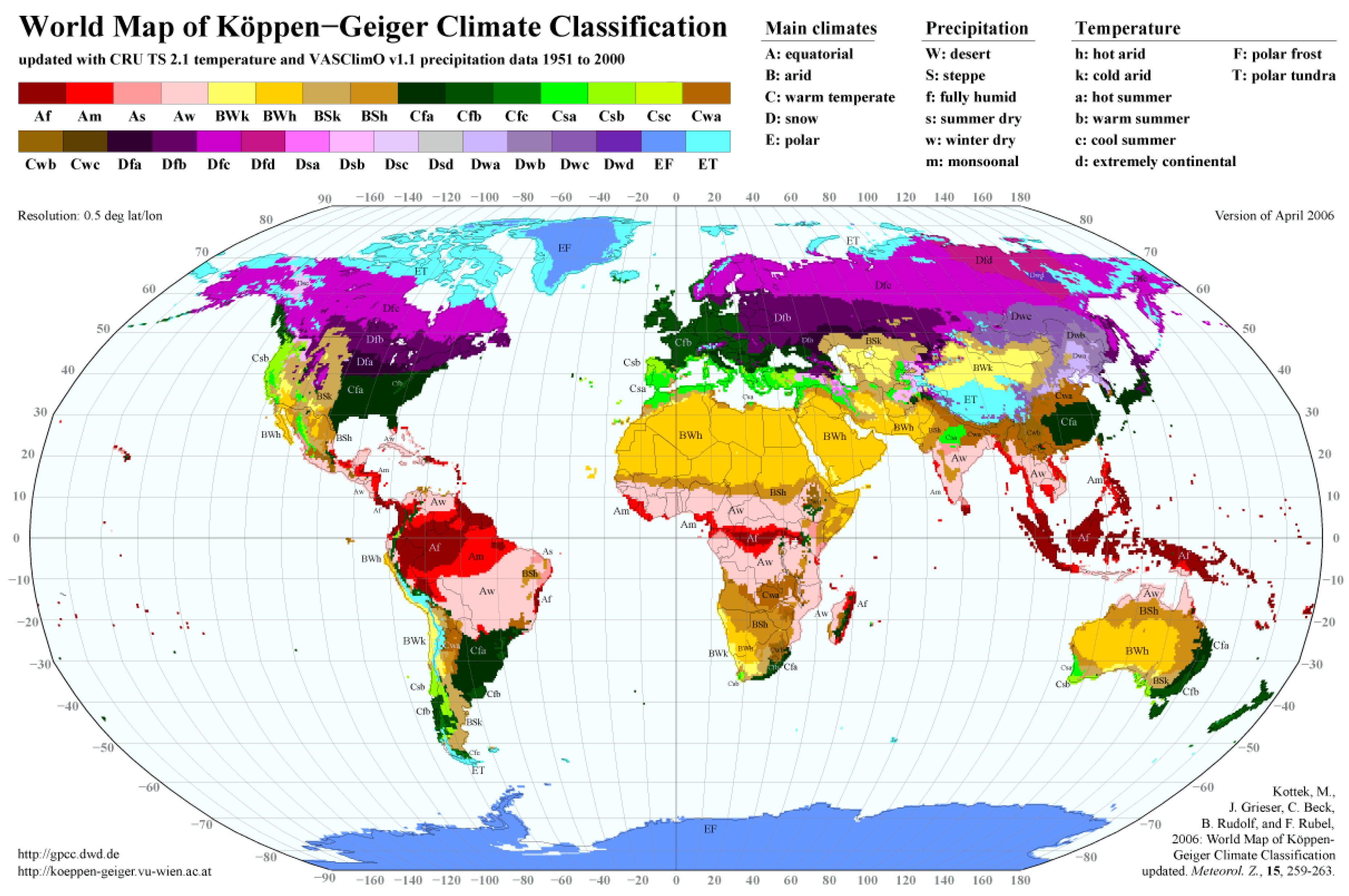
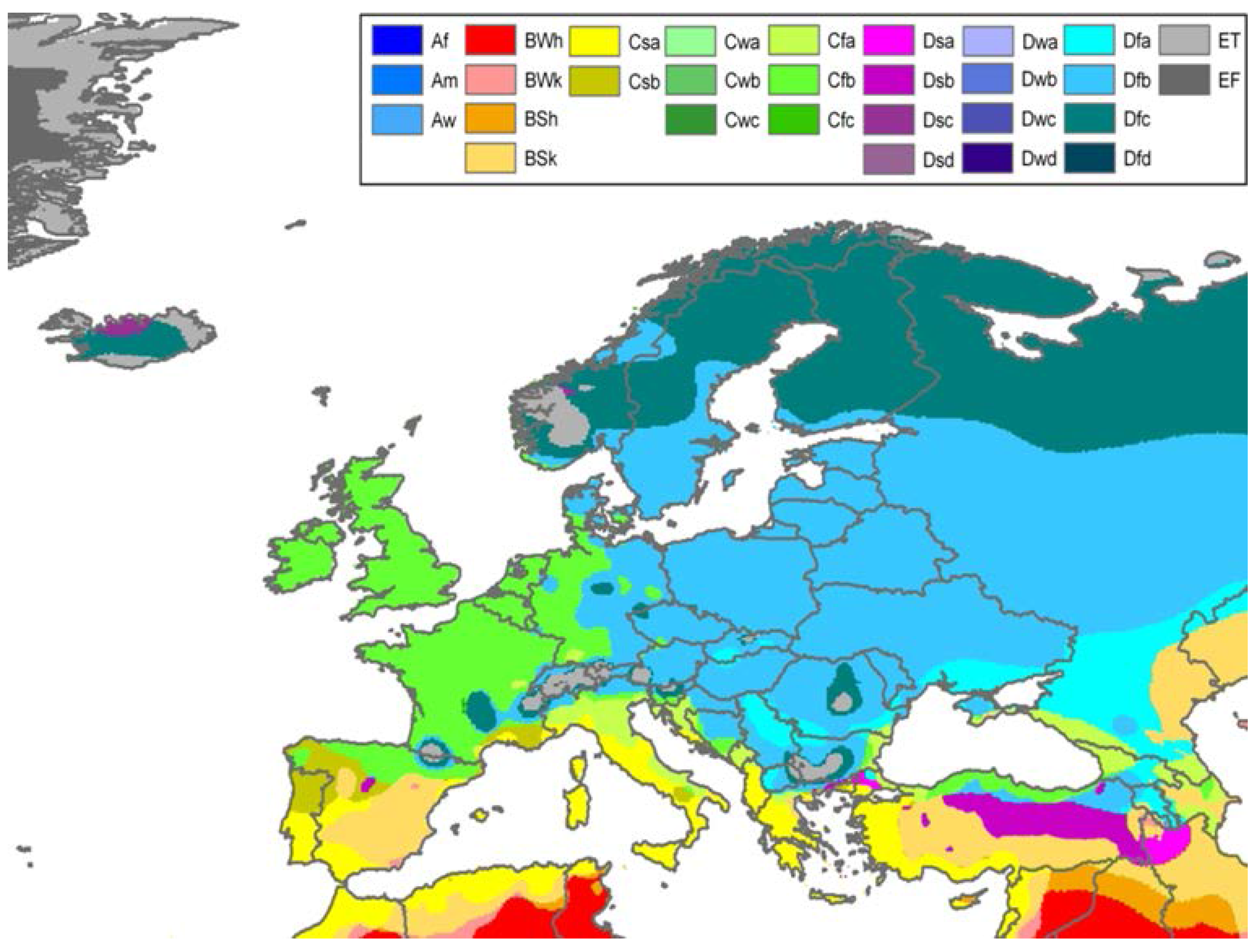
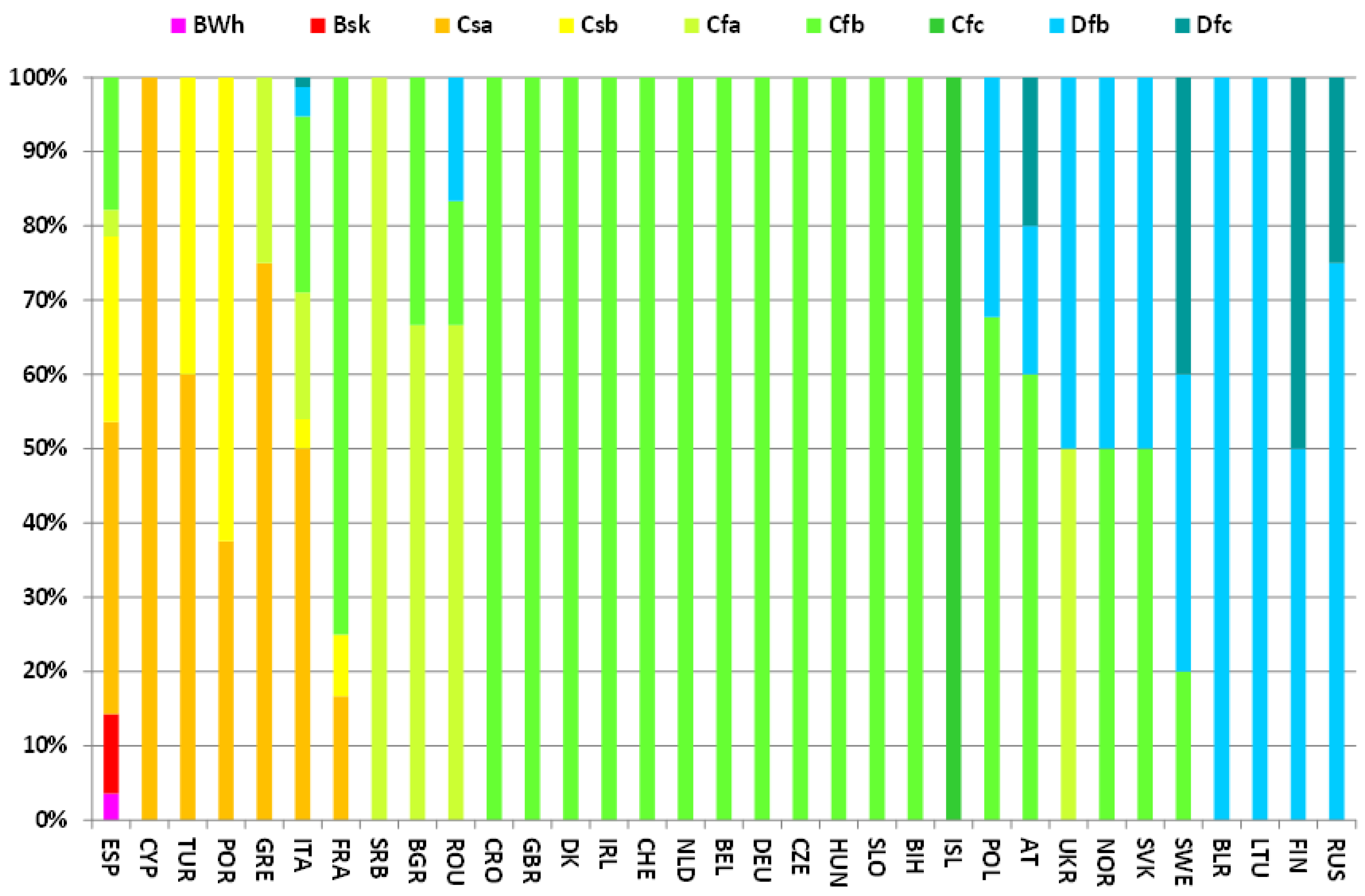
1.1. Köppen Scale
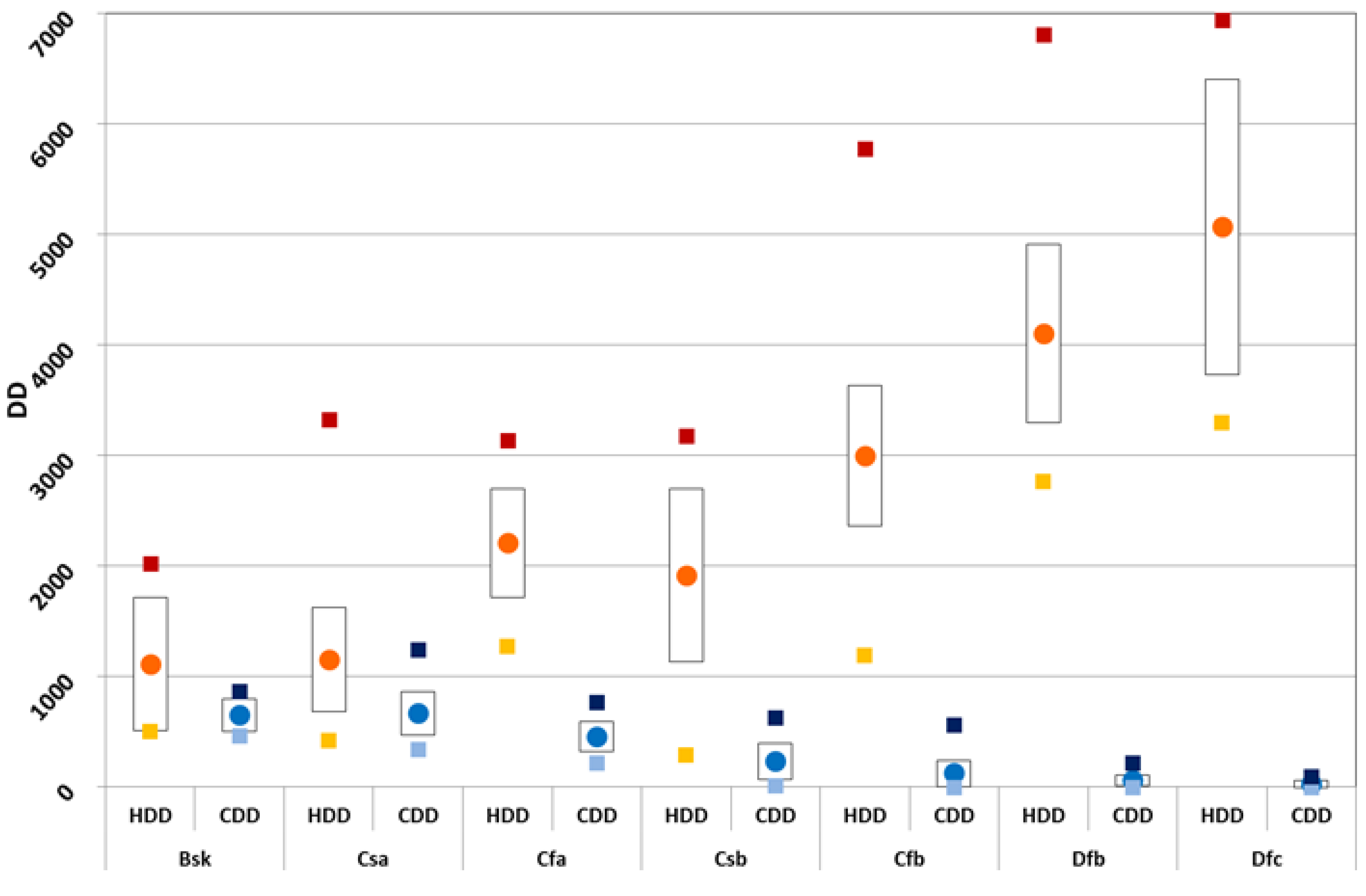
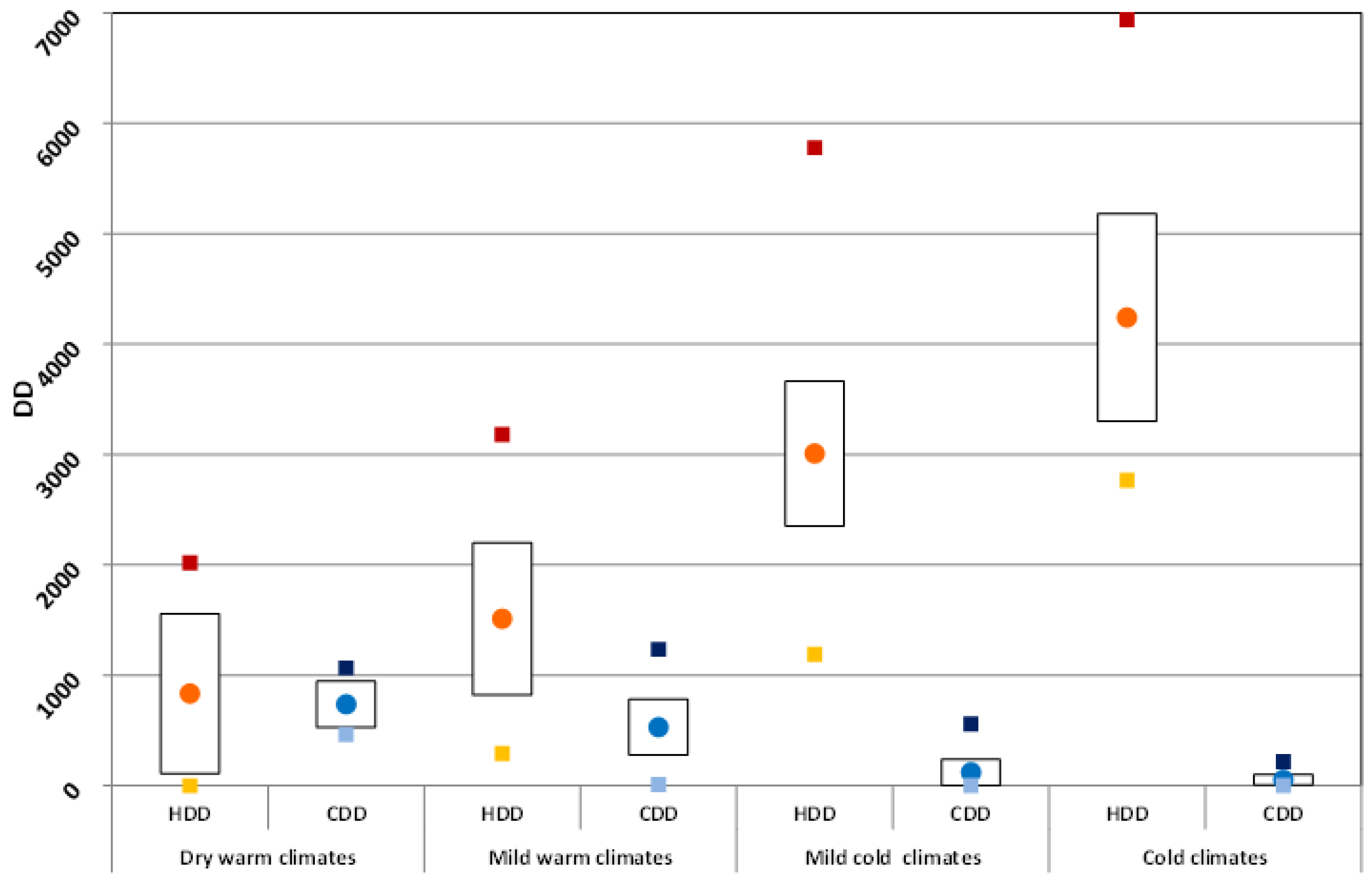
1.2. Degree Day for Heating and Cooling
2. Material and Methods
2.1. Data Analysis
- The Köppen-Geiger scale helps to select the climate similar to the location being investigated.
- The degree-day (DD) for heating (HDD) and cooling (CDD) shows an expert user if the location requires mostly heating or cooling or both.
- Dry warm climates, including BWh and BSk
- Mild warm climates, including Csa, Csb, Cfa
- Mild cold climates, including Cfb and Cfc
- Cold climates, including Dfb and Dfc
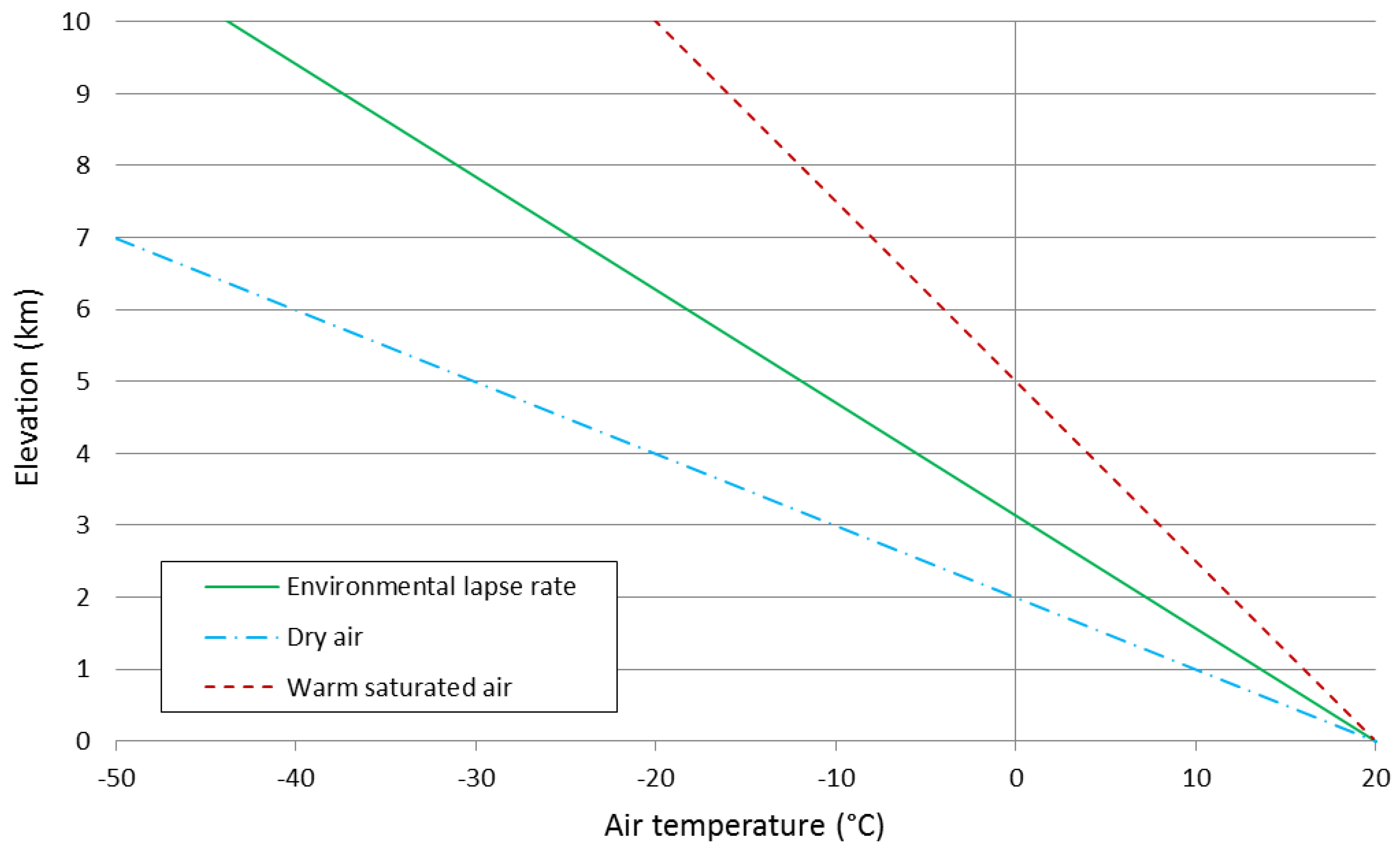
2.2. Altitude Correlation
2.3. Air Temperature Modeling
- Non geostatistical;
- Geostatistical (Univariate and Multivariate);
- Combined methods;
2.4. Proposed Algorithm to Obtain Temperature Data in Unknown Locations from Nearby Weather Stations at Different Altitude
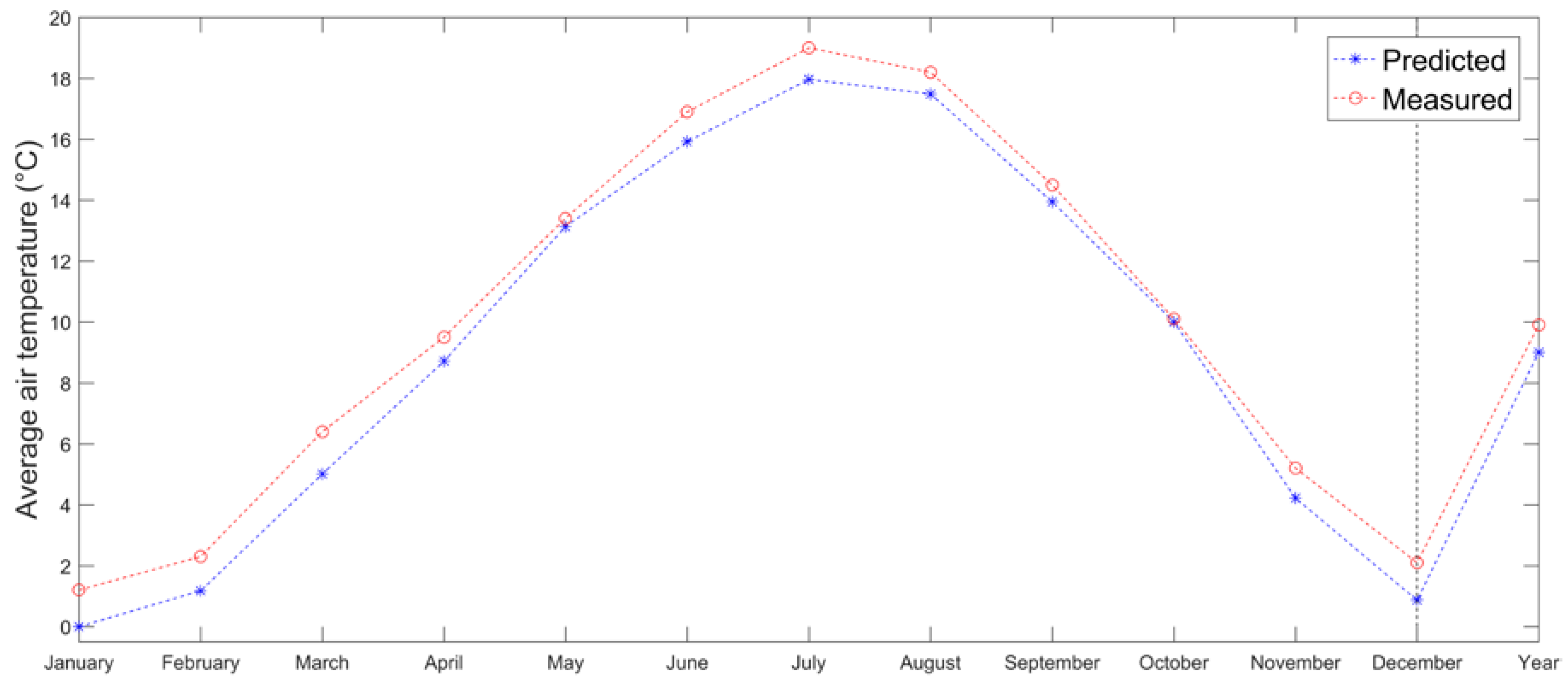
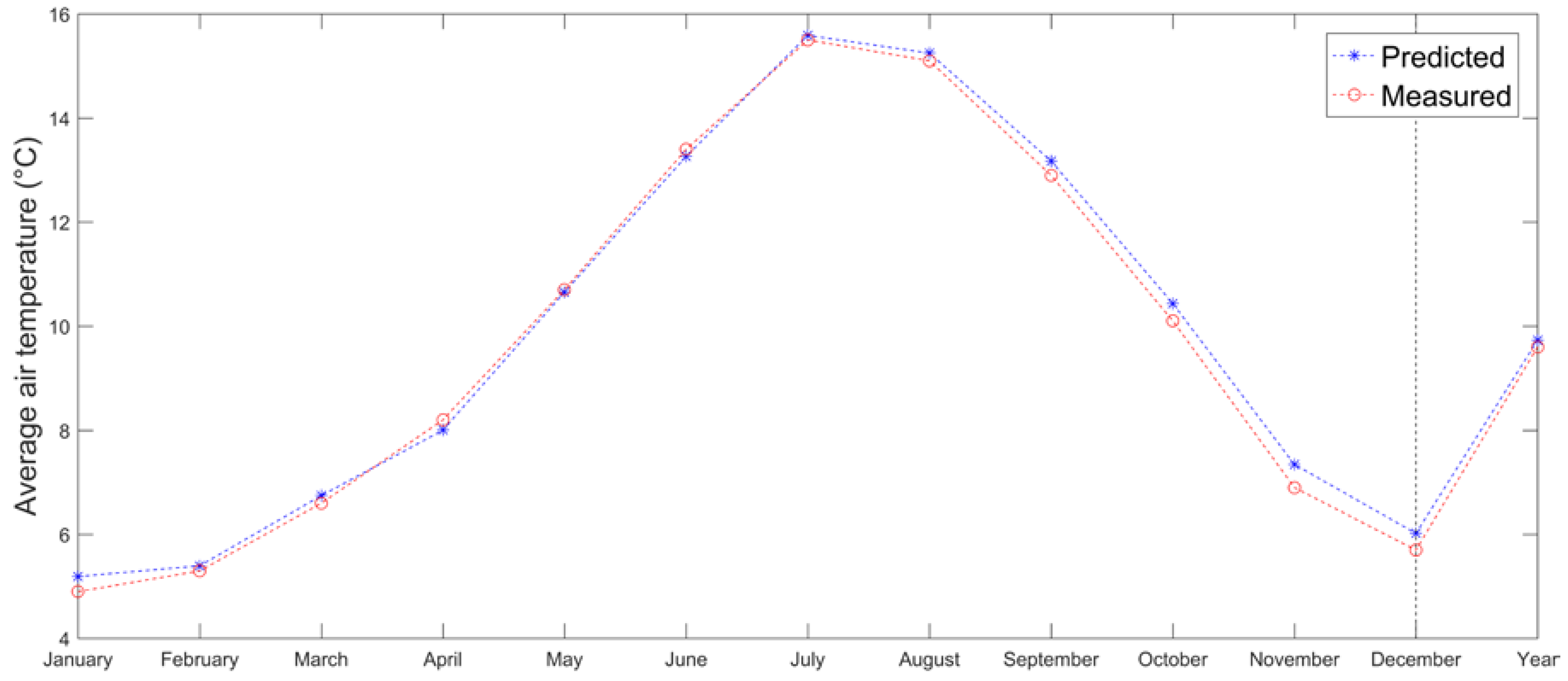
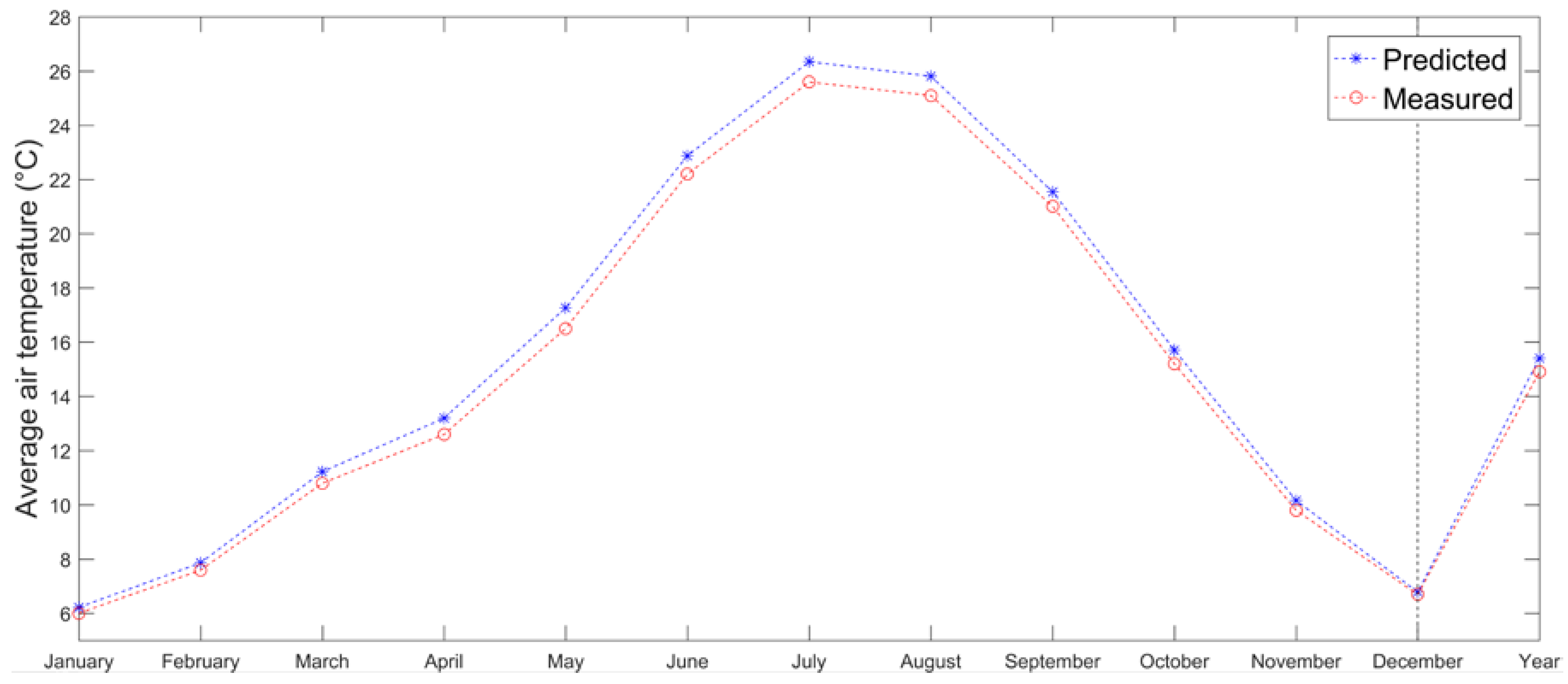
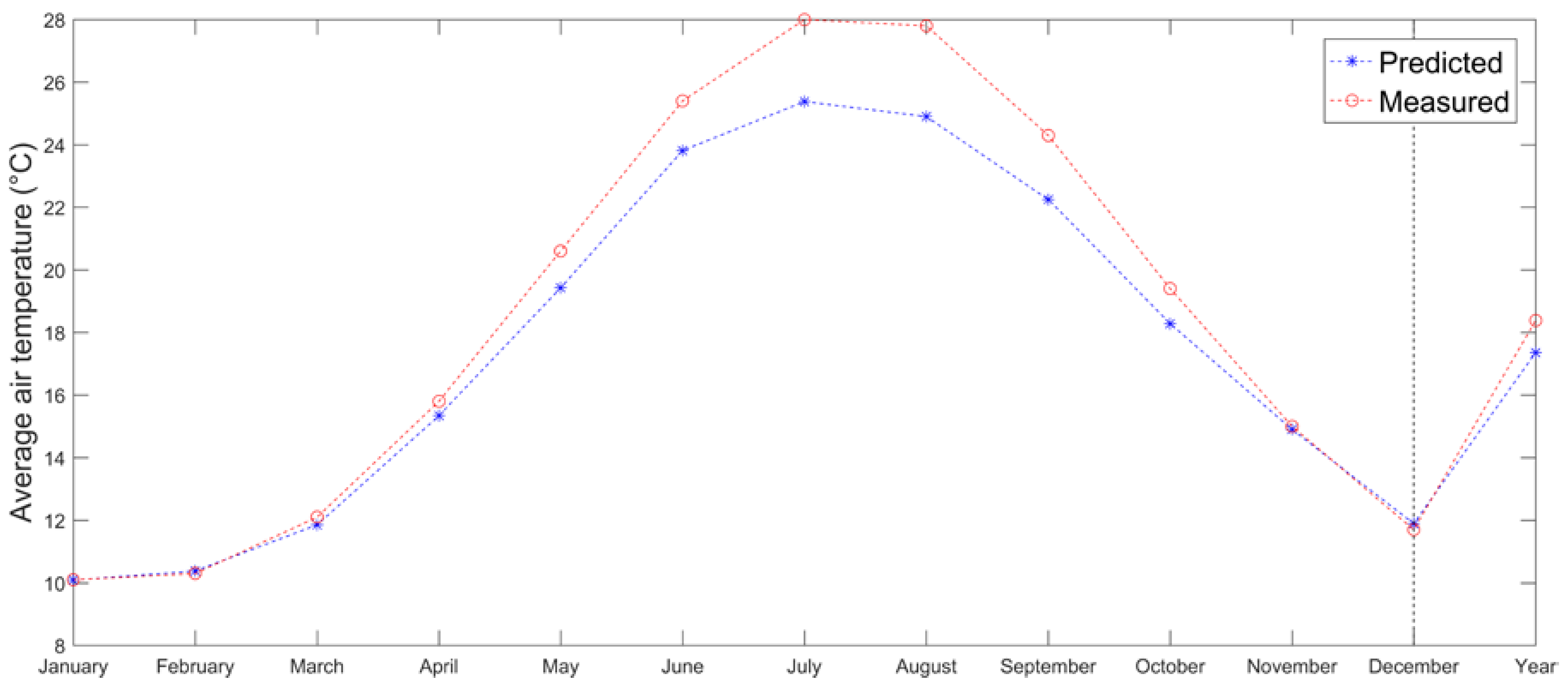
2.5. Testing of the Proposed Method and Results
3. Discussion and Conclusions
- TRY from ENERGYPLUS and METEONORM data sets;
- Data set of calculated degree-days for heating and cooling;
- Köppen-Geiger climate classification;
- Macro-climatic subdivision
- Data input from the user;
- Estimation of temperatures at unknown locations.
- The user provides the coordinates and altitude of the location of interest with unknown climatic information;
- The tool should search within increasing radius from the provided coordinates to get at least one pair of meteorological stations being one below and the other above the altitude provided by the user. The research for meteorological stations should be stopped at a fixed distance from the location proposed by the user (e.g., 300 km, a proposal to be tested during tool development), or when a fixed number of suitable pairs are reached (e.g., 10 pairs, proposed value);
- Pairs of stations being both at lower or both at higher altitudes than one of the user input should be discarded;
- The tool performs the calculation of the monthly lapse rates using only pairs of stations placed one at lower and one at higher altitude from the user input;
- If more than one pair of stations is available, the tool calculates the mean lapse rate for each month to obtain monthly mean temperature at the user location.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kavanaugh, S.P.; Rafferty, K.D. Ground Source Heat Pumps—Design of Geothermal Systems for Commercial and Institutional Buildings; Parsons, R., Ed.; ASHRAE Handbook, Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 1997; ISBN 978-1-883413-45-3. [Google Scholar]
- De Carli, M.; Tonon, M.; Zarrella, A.; Zecchin, R. A computational capacity resistance model (CaRM) for vertical ground-coupled heat exchangers. Renew. Energy 2010, 35, 1537–1550. [Google Scholar] [CrossRef]
- Di Sipio, E.; Bertermann, D. Influence of different moisture and load conditions on heat transfer within soils in very shallow geothermal application: An overview of ITER project. In Proceedings of the 42nd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 13–15 February 2017. [Google Scholar]
- Bruno, D.E.; Lombardo, G.; Di Sipio, E.; Galgaro, A.; D’Arpa, S.; Destro, E.; Passarella, G.; Barca, E.; Uricchio, V.F.; Manzella, A. Mo.nalis.a: A methodological approach to identify how to meet thermal industrial needs using already available geothermal resources. Energy Effic. 2017, 10, 639–655. [Google Scholar] [CrossRef]
- Di Sipio, E.; Chiesa, S.; Destro, E.; Galgaro, A.; Giaretta, A.; Gola, G.; Manzella, A. Rock Thermal Conductivity as Key Parameter for Geothermal Numerical Models. Energy Procedia 2013, 40, 87–94. [Google Scholar] [CrossRef]
- Bernardi, A.; De Carli, M.; Di Tuccio, M.; Emmi, G.; Galgaro, A.; Graci, S.; Pera, S.; Zarrella, A. A data base for European climatic data for energy potentials and mapping. In Proceedings of the 12th REHVA World Congress (CLIMA 2016), Aalborg, Denmark, 22–25 May 2016; Heiselberg, P.K., Ed.; Aalborg University: Aalborg, Denmark, 2016; Volume 9. [Google Scholar]
- Wilcock, A.A. Köppen after fifty years. Ann. Assoc. Am. Geogr. 1968, 58, 12–28. [Google Scholar] [CrossRef]
- Belda, M.; Holtanová, E.; Halenka, T.; Kalvová, J. Climate classification revisited: From Köppen to Trewartha. Clim. Res. 2014, 59, 1–13. [Google Scholar] [CrossRef]
- Sanderson, M. The classification of climates from Pythagoras to Koeppen. Bull. Am. Meteorol. Soc. 1999, 80, 669–673. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. Problems in the Classification of Climates. Geogr. Rev. 1943, 33, 233. [Google Scholar] [CrossRef]
- Essenwanger, O.M. World Survey of Climatology, General Climatology, 1C: Classification of Climates; Elsevier: Amsterdam, The Netherlands, 2001; ISBN 0-444-88278-2. [Google Scholar]
- Jacobeit, J. Classifications in climate research. Phys. Chem. Earth Parts ABC 2010, 35, 411–421. [Google Scholar] [CrossRef]
- Deliège, A.; Nicolay, S. Köppen–Geiger Climate Classification for Europe Recaptured via the Hölder Regularity of Air Temperature Data. Pure Appl. Geophys. 2016, 173, 2885–2898. [Google Scholar] [CrossRef]
- Lier, J. Köppen revised and conjugated. J. Geogr. 1980, 79, 13–22. [Google Scholar] [CrossRef]
- Kalvová, J.; Halenka, T.; Bezpalcová, K.; Nemešová, I. Köppen climate types in observed and simulated climates. Stud. Geophys. Geod. 2003, 47, 185–202. [Google Scholar] [CrossRef]
- Gnanadesikan, A.; Stouffer, R.J. Diagnosing atmosphere-ocean general circulation model errors relevant to the terrestrial biosphere using the Köppen climate classification. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Fraedrich, K.; Gerstengarbe, F.-W.; Werner, P.C. Climate shifts during the last century. Clim. Chang. 2001, 50, 405–417. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Institute for Veterinary Public Health World Maps of Köppen-Geiger Climate Classification. Available online: http://koeppen-geiger.vu-wien.ac.at/ (accessed on 10 January 2017).
- Global Precipitation Climatology Centre Global Precipitation Climatology Centre (GPCC). Available online: http://www.dwd.de/EN/ourservices/gpcc/gpcc.html (accessed on 14 February).
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Brown, N.; Wright, A.J.; Shukla, A.; Stuart, G. Longitudinal analysis of energy metering data from non-domestic buildings. Build. Res. Inf. 2010, 38, 80–91. [Google Scholar] [CrossRef]
- Roltsch, W.J.; Zalom, F.G.; Strawn, A.J.; Strand, J.F.; Pitcairn, M.J. Evaluation of several degree-day estimation methods in California climates. Int. J. Biometeorol. 1999, 42, 169–176. [Google Scholar] [CrossRef]
- Gaitani, N.; Lehmann, C.; Santamouris, M.; Mihalakakou, G.; Patargias, P. Using principal component and cluster analysis in the heating evaluation of the school building sector. Appl. Energy 2010, 87, 2079–2086. [Google Scholar] [CrossRef]
- Hor, C.-L.; Watson, S.J.; Majithia, S. Analyzing the Impact of weather variables on monthly electricity demand. IEEE Trans. Power Syst. 2005, 20, 2078–2085. [Google Scholar] [CrossRef]
- Chartered Institution of Building Services Engineer (CIBSE). Degree-Days—Theory and Application; TM41: 2006; CIBSE: London, UK, 2006; ISBN 1-903287-76-6. [Google Scholar]
- Rodrigues, C.M.; Barnes, J.; Farebrother, D.; Gaddas, R. Degree Days for Energy Management—A Practical Introduction; Energy Efficiency Good Practice Guide; Chartered Institution of Building Services Engineers: London, UK, 2002. [Google Scholar]
- Oughton, D.; Martin, P.L. Faber and Kell’s Heating and Air Conditioning of Buildings; Routledge: Abingdon-on-Thames, UK, 1997; ISBN 978-0-7506-3778-7. [Google Scholar]
- Valor, E.; Meneu, V.; Caselles, V. Daily air temperature and electricity load in Spain. J. Appl. Meteorol. 2001, 40, 1413–1421. [Google Scholar] [CrossRef]
- Salisu, A.A.; Ayinde, T.O. Modeling energy demand: Some emerging issues. Renew. Sustain. Energy Rev. 2016, 54, 1470–1480. [Google Scholar] [CrossRef]
- Oughton, D.R.; Hodkinson, S.; Faber, O. Faber & Kell’s Heating and Air-Conditioning of Buildings; Oughton, D.R., Hodkinson, S.L., Eds.; Butterworth-Heinemann: Amsterdam, The Netherlands; London, UK, 2008; ISBN 978-0-7506-8365-4. [Google Scholar]
- Badens, B.; Bellieardi, M.; Bernardi, A.; De Carli, M.; Di Tuccio, M.; Emmi, G.; Galgaro, A.; Graci, S.; Pockelè, L.; Vivarelli, A.; et al. Definition of standardized energy profiles for heating and cooling of buildings. In Proceedings of the 12th REHVA World Congress, Aalborg, Denmark, Aalborg, Denmark, 22–25 May 2016; Heiselberg, P.K., Ed.; Aalborg University: Aalborg, Denmark, 2016; Volume 6. [Google Scholar]
- Zarrella, A.; Emmi, G.; Graci, S.; De Carli, M.; Cultrera, M.; Santa, G.; Galgaro, A.; Bertermann, D.; Mueller, J.; Pockele’, L.; et al. Thermal Response Testing Results of Different Types of Borehole Heat Exchangers: An Analysis and Comparison of Interpretation Methods. Energies 2017, 10, 801. [Google Scholar] [CrossRef]
- Galgaro, A.; Dalla Santa, G.; Cultrera, M.; Bertermann, D.; Müller, J.; De Carli, M.; Emmi, G.; Zarrella, A.; Di Tuccio, M.; Pockelè, L.; et al. EU project “Cheap-GSHPs”: The geoexchange field laboratory. Energy Procedia 2017, 125, 511–519. [Google Scholar] [CrossRef]
- Dalla Santa, G.; Peron, F.; Galgaro, A.; Cultrera, M.; Bertermann, D.; Müller, J.; Bernardi, A. Laboratory Measurements of Gravel Thermal Conductivity: A New Methodological Approach. Energy Procedia 2017, 125, 671–677. [Google Scholar] [CrossRef]
- Turban, E.; Rainer, R.K.; Potter, R.E. Introduction to Information Technology, 3rd ed.; Wiley: New York, NY, USA, 2004; ISBN 978-0-471-34780-4. [Google Scholar]
- Sun, R.; Zhang, B. Topographic effects on spatial pattern of surface air temperature in complex mountain environment. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Wu, W.; Tang, X.-P.; Ma, X.-Q.; Liu, H.-B. A comparison of spatial interpolation methods for soil temperature over a complex topographical region. Theor. Appl. Climatol. 2016, 125, 657–667. [Google Scholar] [CrossRef]
- Barry, R.G.; Blanken, P.D. Microclimate and Local Climate; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Barry, R.G.; Chorley, R.J. Atmosphere, Weather, and Climate; Routledge: London, UK; New York, NY, USA, 2003; ISBN 978-0-203-42823-8. [Google Scholar]
- World Meteorological Organization. Guide to Meteorological Instruments and Methods of Observation; WMO-No. 8, 2008 Edition Updated in 2010; WMO: Geneva, Switzerland, 2012; Volume 8, ISBN 978-92-63-10008-5. [Google Scholar]
- Burrough, P.A.; McDonnell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems, 2nd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Holdaway, M.R. Spatial modeling and interpolation of monthly temperature using kriging. Clim. Res. 1996, 6, 215–225. [Google Scholar] [CrossRef]
- Cao, X.; Okhrin, O.; Odening, M.; Ritter, M. Modelling spatio-temporal variability of temperature. Comput. Stat. 2015, 30, 745–766. [Google Scholar] [CrossRef]
- Dodson, R.; Marks, D. Daily air temperature interpolated at high spatial resolution over a large mountainous region. Clim. Res. 1997, 8, 1–20. [Google Scholar] [CrossRef]
- Wu, T.; Li, Y. Spatial interpolation of temperature in the United States using residual kriging. Appl. Geogr. 2013, 44, 112–120. [Google Scholar] [CrossRef]
- You, J.; Hubbard, K.G.; Goddard, S. Comparison of methods for spatially estimating station temperatures in a quality control system. Int. J. Climatol. 2008, 28, 777–787. [Google Scholar] [CrossRef]
- Andrade-Bejarano, M. Monthly Average Temperature Modeling in an Intertropical Region. Weather Forecast. 2013, 28, 1099–1115. [Google Scholar] [CrossRef]
- Frei, C. Interpolation of temperature in a mountainous region using nonlinear profiles and non-Euclidean distances: Interpolation of temperature in a mountainous region. Int. J. Climatol. 2014, 34, 1585–1605. [Google Scholar] [CrossRef]
- Hamann, A.; Wang, T.L. Models of climatic normals for genecology and climate change studies in British Columbia. Agric. For. Meteorol. 2005, 128, 211–221. [Google Scholar] [CrossRef]
- Gray, L.K.; Rweyongeza, D.; Hamann, A.; John, S.; Thomas, B.R. Developing management strategies for tree improvement programs under climate change: Insights gained from long-term field trials with lodgepole pine. For. Ecol. Manag. 2016, 377, 128–138. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Saz-Sánchez, M.A.; Cuadrat, J.M. Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): Application to annual precipitation and temperature. Clim. Res. 2003, 24, 161–180. [Google Scholar] [CrossRef]
- Kisi, O.; Sanikhani, H. Modelling long-term monthly temperatures by several data-driven methods using geographical inputs. Int. J. Climatol. 2015, 35, 3834–3846. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T.; Simolo, C.; Spinoni, J. High-resolution temperature climatology for Italy: Interpolation method intercomparison. Int. J. Climatol. 2014, 34, 1278–1296. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Smart Interpolation of Annually Averaged Air Temperature in the United States. J. Appl. Meteorol. 1995, 34, 2577–2586. [Google Scholar] [CrossRef]
- Glotter, M.J.; Moyer, E.J.; Ruane, A.C.; Elliott, J.W. Evaluating the Sensitivity of Agricultural Model Performance to Different Climate Inputs. J. Appl. Meteorol. Climatol. 2016, 55, 579–594. [Google Scholar] [CrossRef] [PubMed]
- Stahl, K.; Moore, R.D.; Floyer, J.A.; Asplin, M.G.; McKendry, I.G. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Li, J. A Review of Spatial Interpolation Methods for Environmental Scientists; Geoscience Australia: Canberra, Australia, 2008; ISBN 978-1-921498-30-5.
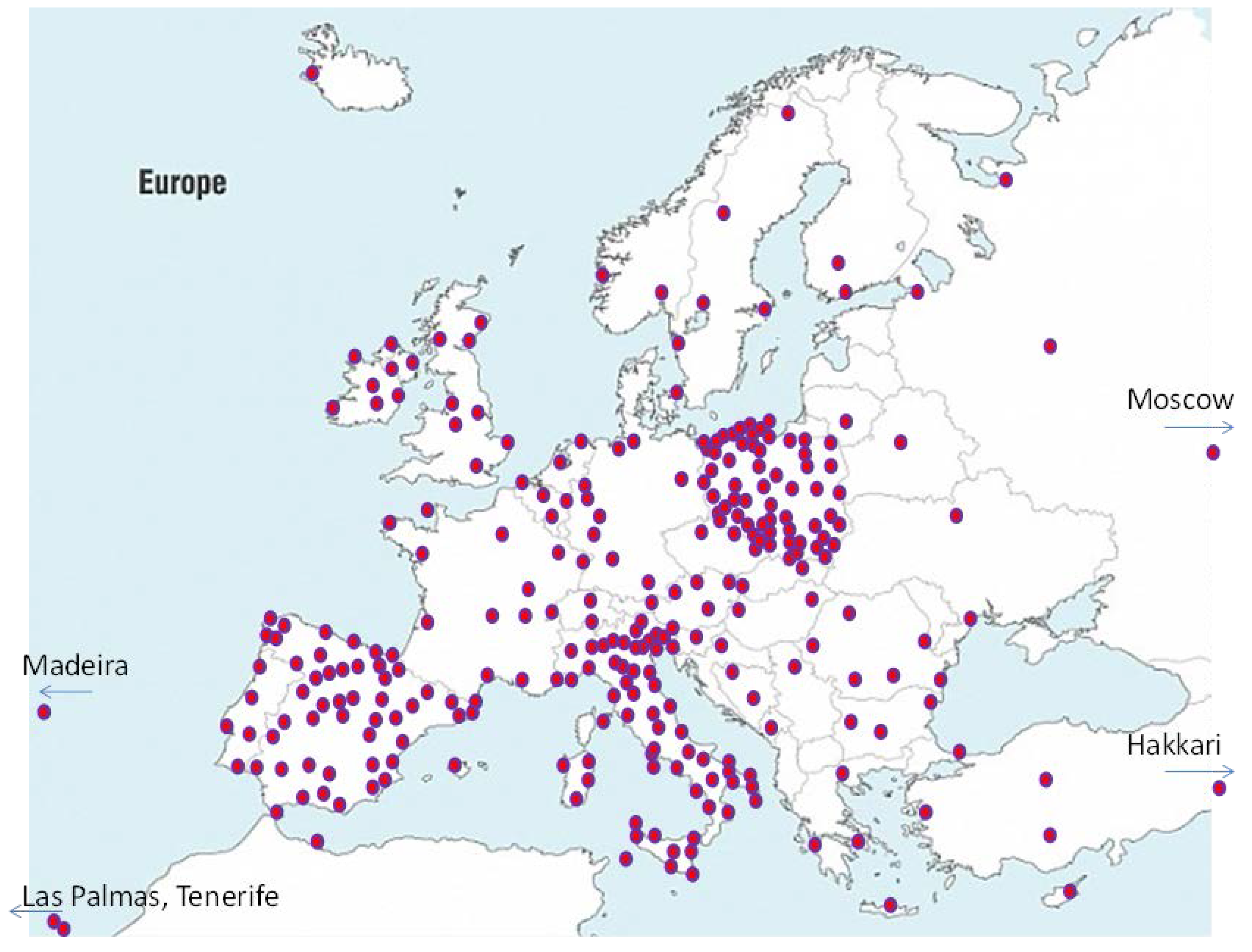
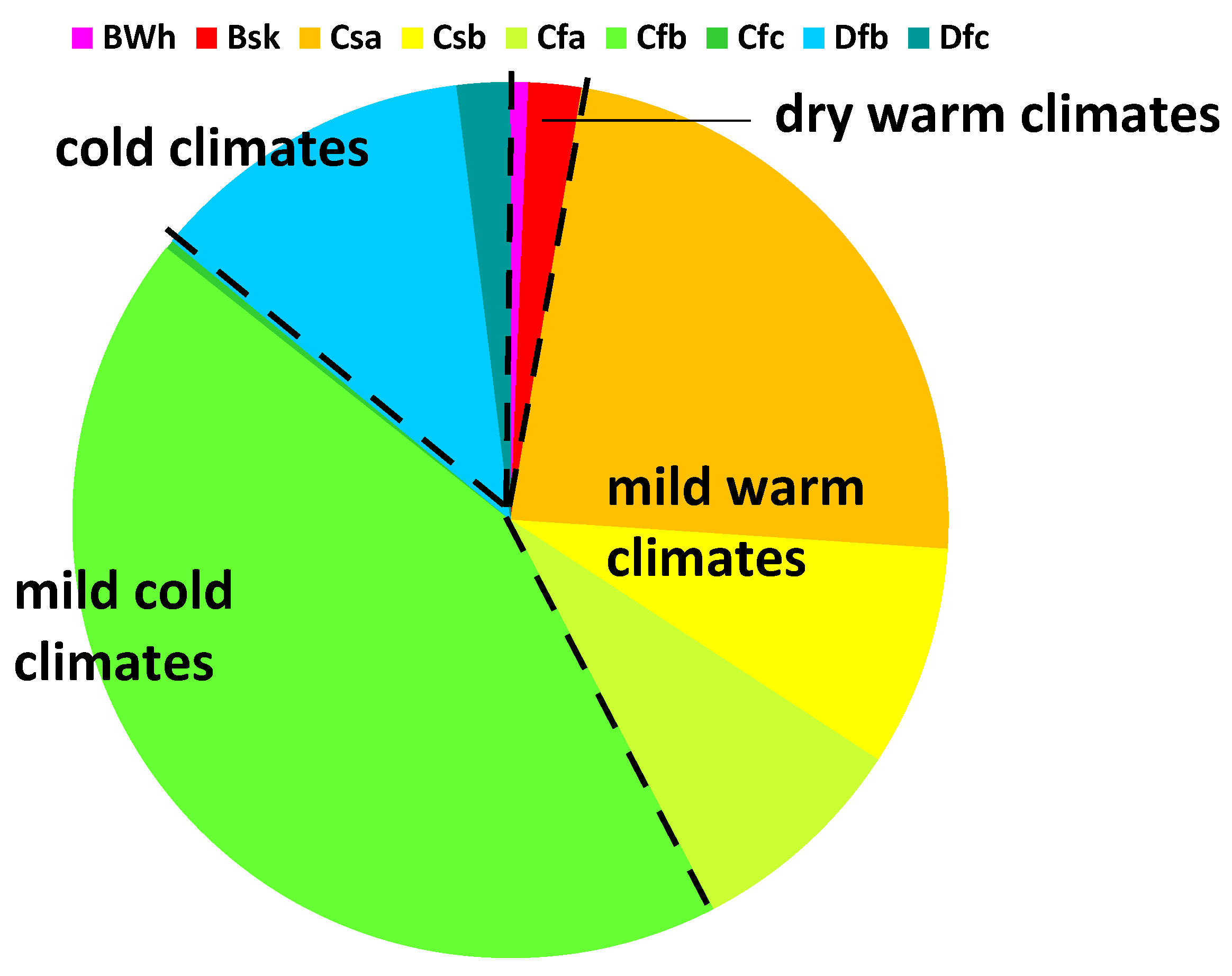
| Type of Climate | Description | Amount of Locations |
|---|---|---|
| BSk | Arid, summer dry, cold air | 6 |
| BWh | Arid, desert, cold air | 2 |
| Cfa | warm temperature, fully humid, hot summer | 25 |
| Cfb | warm temperature, fully humid, warm summer | 133 |
| Cfc | warm temperature, fully humid, cool summer | 1 |
| Csa | warm temperature, summer dry, hot summer | 72 |
| Csb | warm temperature, summer dry, warm summer | 25 |
| Dfa | Snow, fully humid, warm summer | 37 |
| Dfb | Snow, fully humid, cool summer | 6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Carli, M.; Bernardi, A.; Cultrera, M.; Dalla Santa, G.; Di Bella, A.; Emmi, G.; Galgaro, A.; Graci, S.; Mendrinos, D.; Mezzasalma, G.; et al. A Database for Climatic Conditions around Europe for Promoting GSHP Solutions. Geosciences 2018, 8, 71. https://doi.org/10.3390/geosciences8020071
De Carli M, Bernardi A, Cultrera M, Dalla Santa G, Di Bella A, Emmi G, Galgaro A, Graci S, Mendrinos D, Mezzasalma G, et al. A Database for Climatic Conditions around Europe for Promoting GSHP Solutions. Geosciences. 2018; 8(2):71. https://doi.org/10.3390/geosciences8020071
Chicago/Turabian StyleDe Carli, Michele, Adriana Bernardi, Matteo Cultrera, Giorgia Dalla Santa, Antonino Di Bella, Giuseppe Emmi, Antonio Galgaro, Samantha Graci, Dimitrios Mendrinos, Giulia Mezzasalma, and et al. 2018. "A Database for Climatic Conditions around Europe for Promoting GSHP Solutions" Geosciences 8, no. 2: 71. https://doi.org/10.3390/geosciences8020071
APA StyleDe Carli, M., Bernardi, A., Cultrera, M., Dalla Santa, G., Di Bella, A., Emmi, G., Galgaro, A., Graci, S., Mendrinos, D., Mezzasalma, G., Pasquali, R., Pera, S., Perego, R., & Zarrella, A. (2018). A Database for Climatic Conditions around Europe for Promoting GSHP Solutions. Geosciences, 8(2), 71. https://doi.org/10.3390/geosciences8020071










