Modeling Dry-Snow Densification without Abrupt Transition
Abstract
1. Introduction
1.1. Time-Varying Conditions
1.2. Stage 1 and Stage 2 Densification
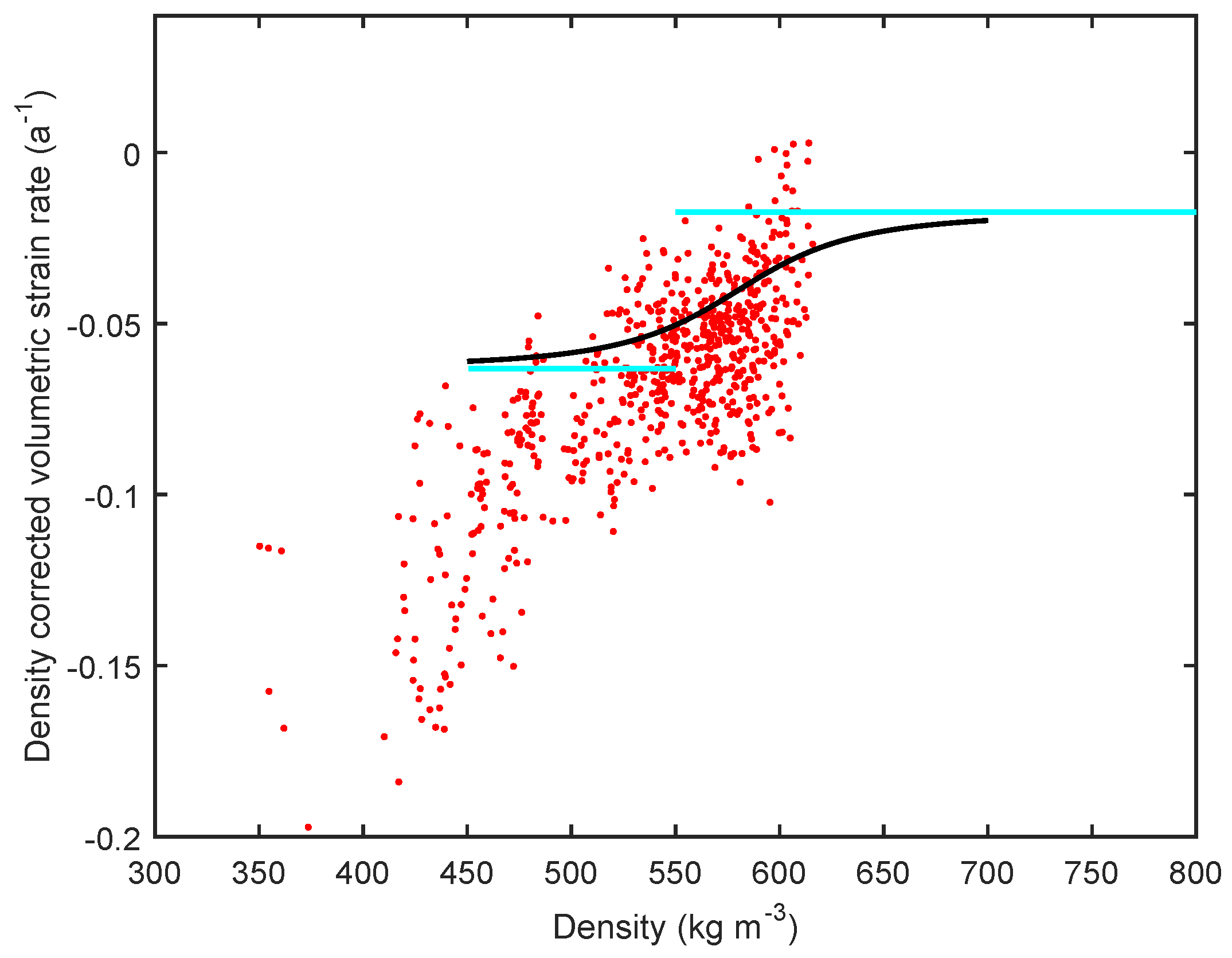
2. Transition Model
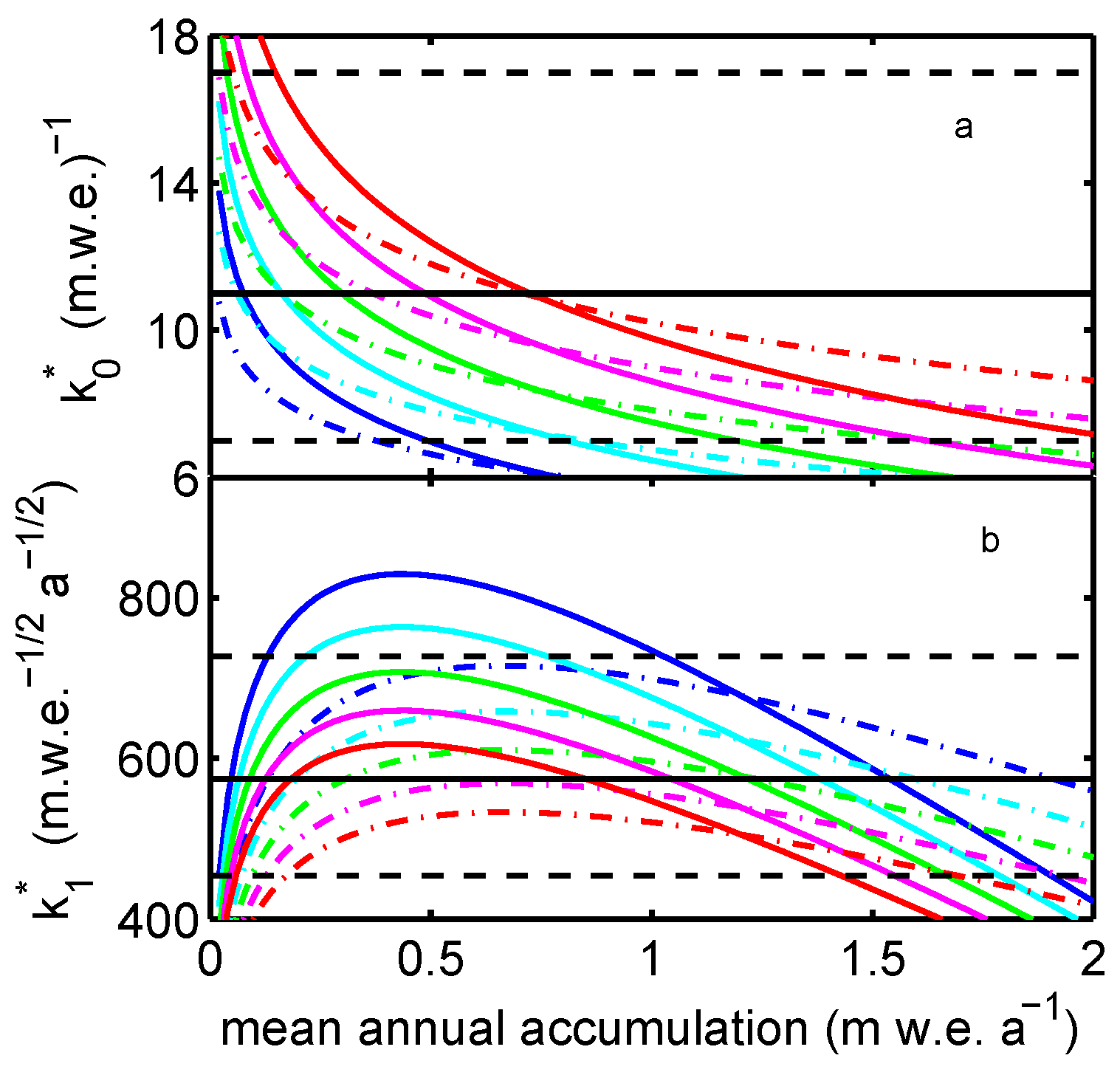
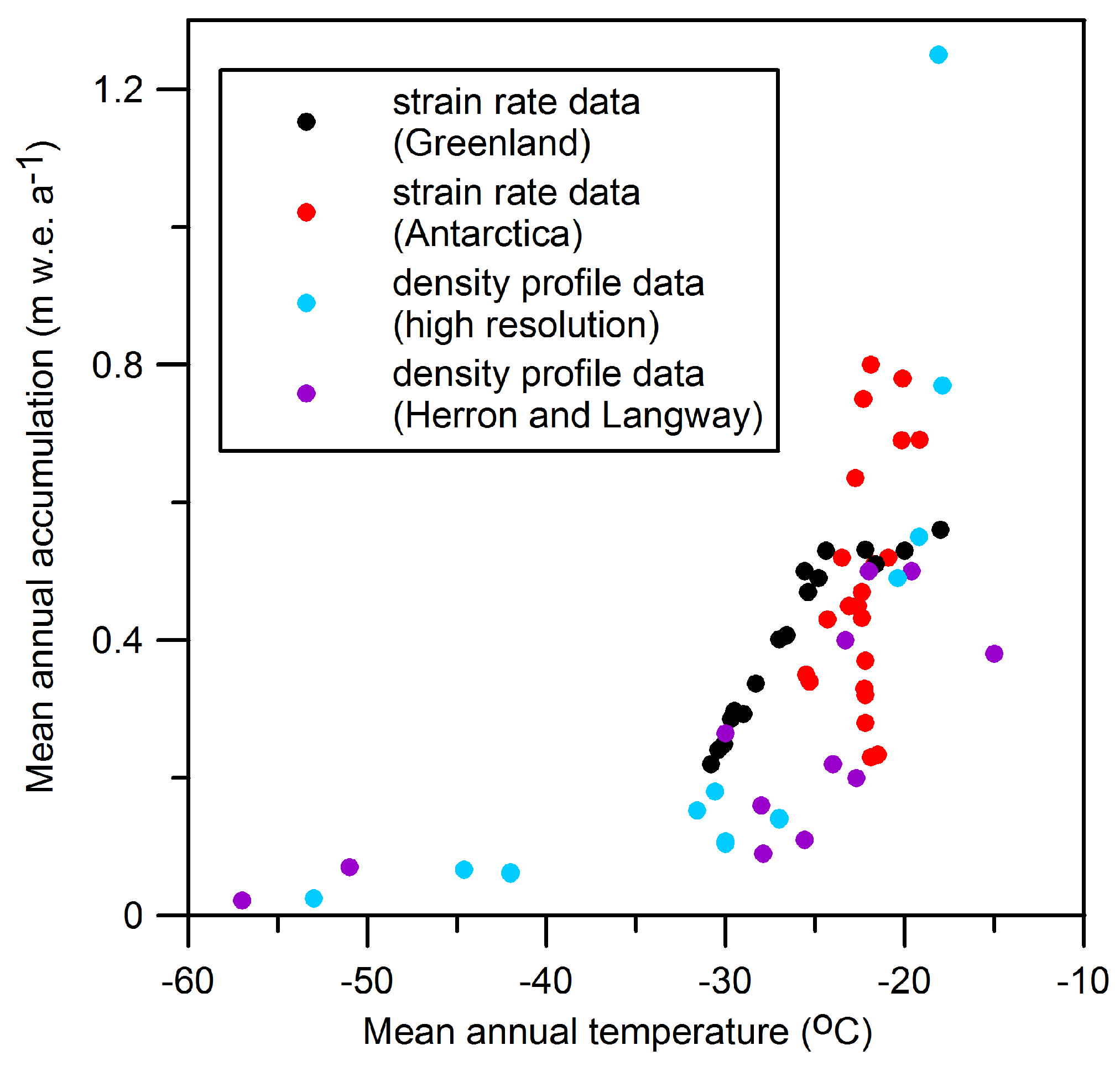
2.1. Calibration and Validation
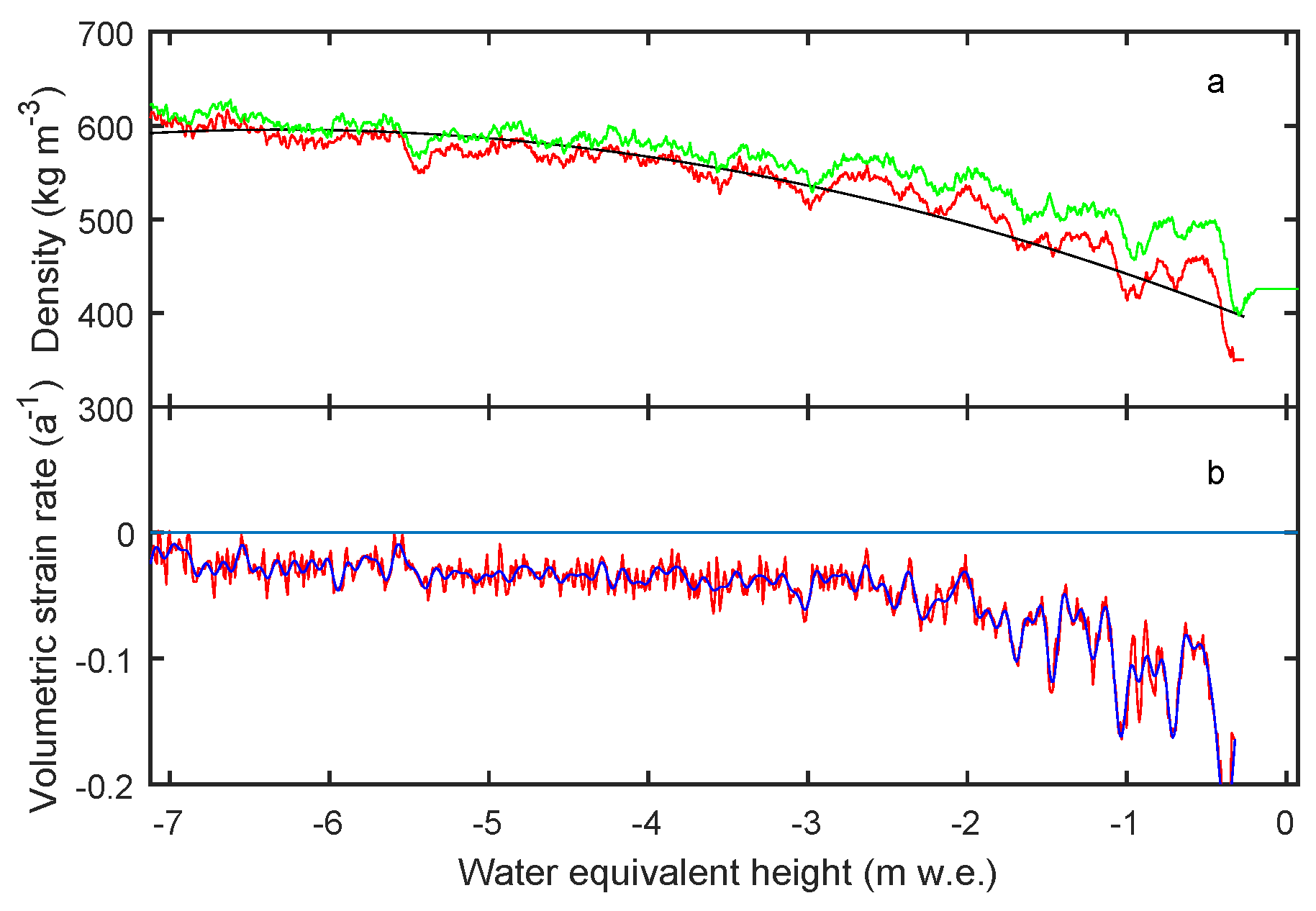
2.2. Strain-Rate Profiles
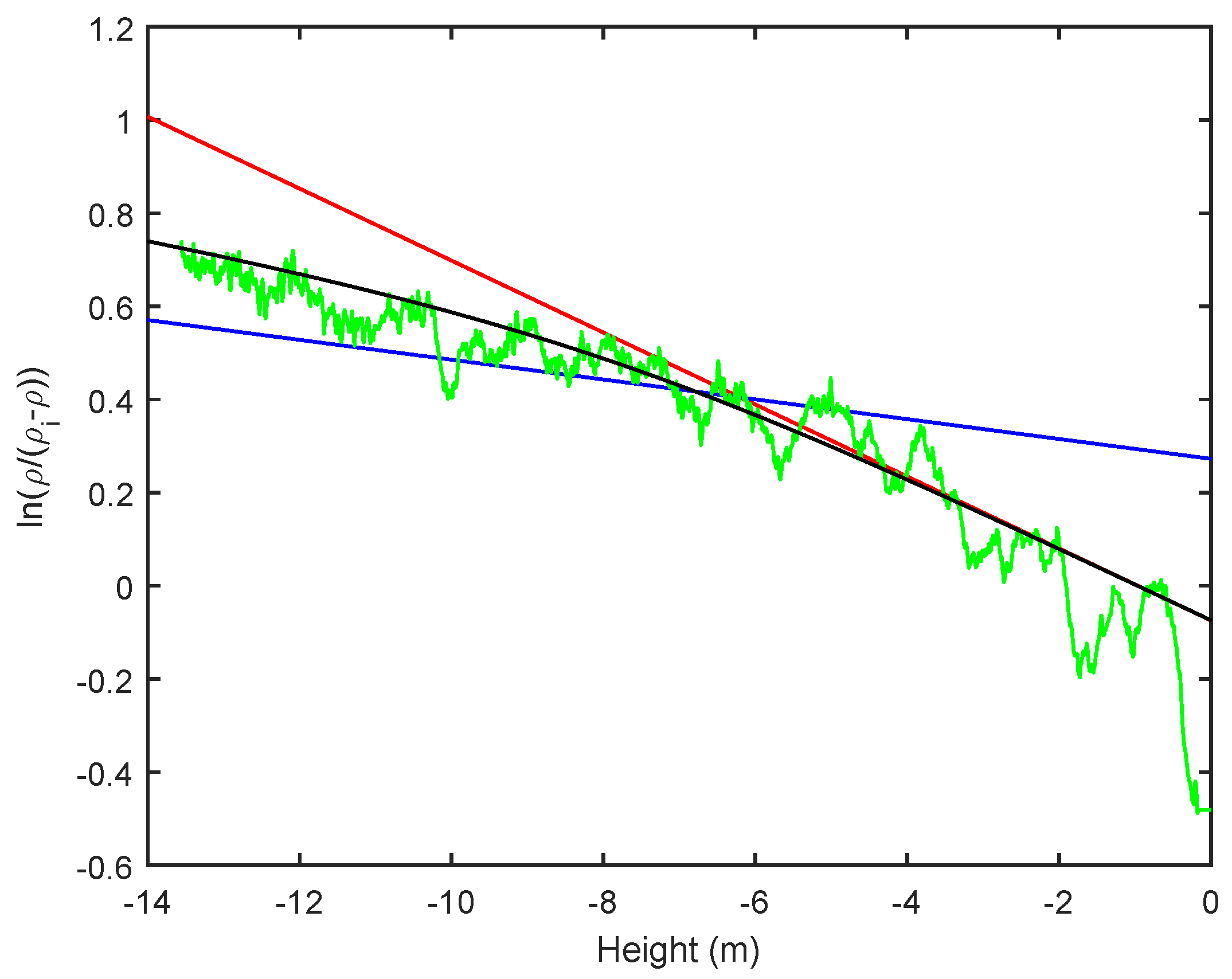
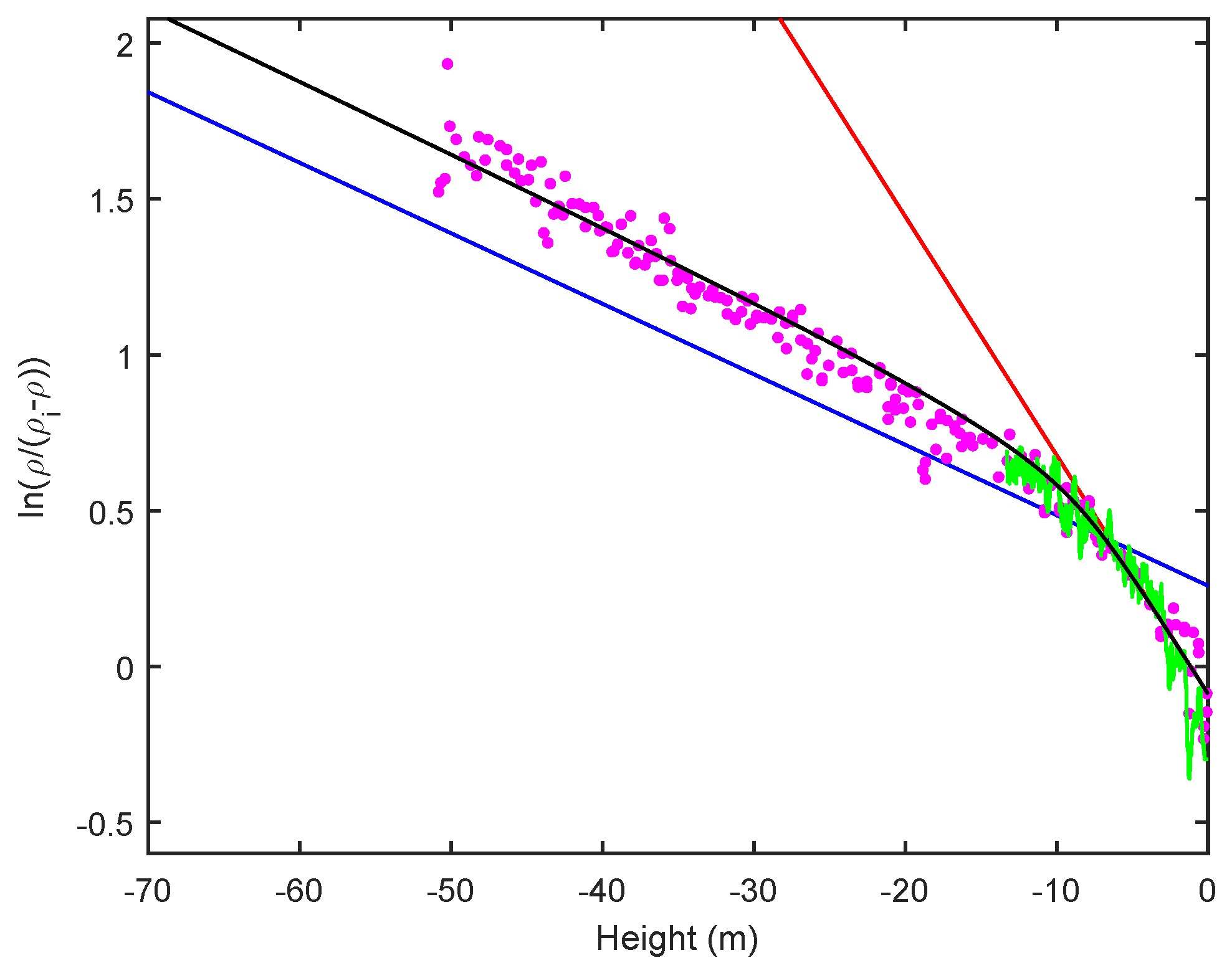
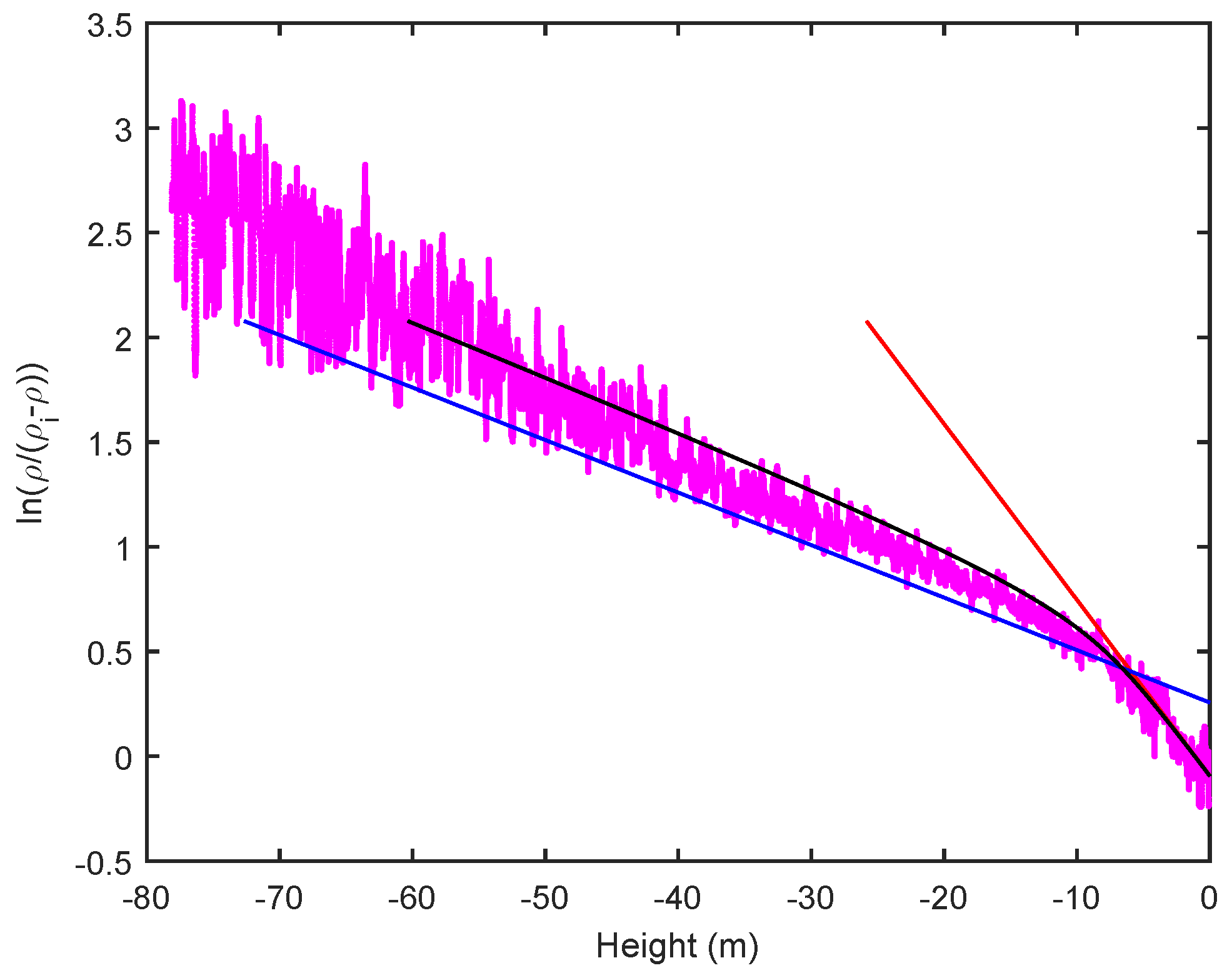
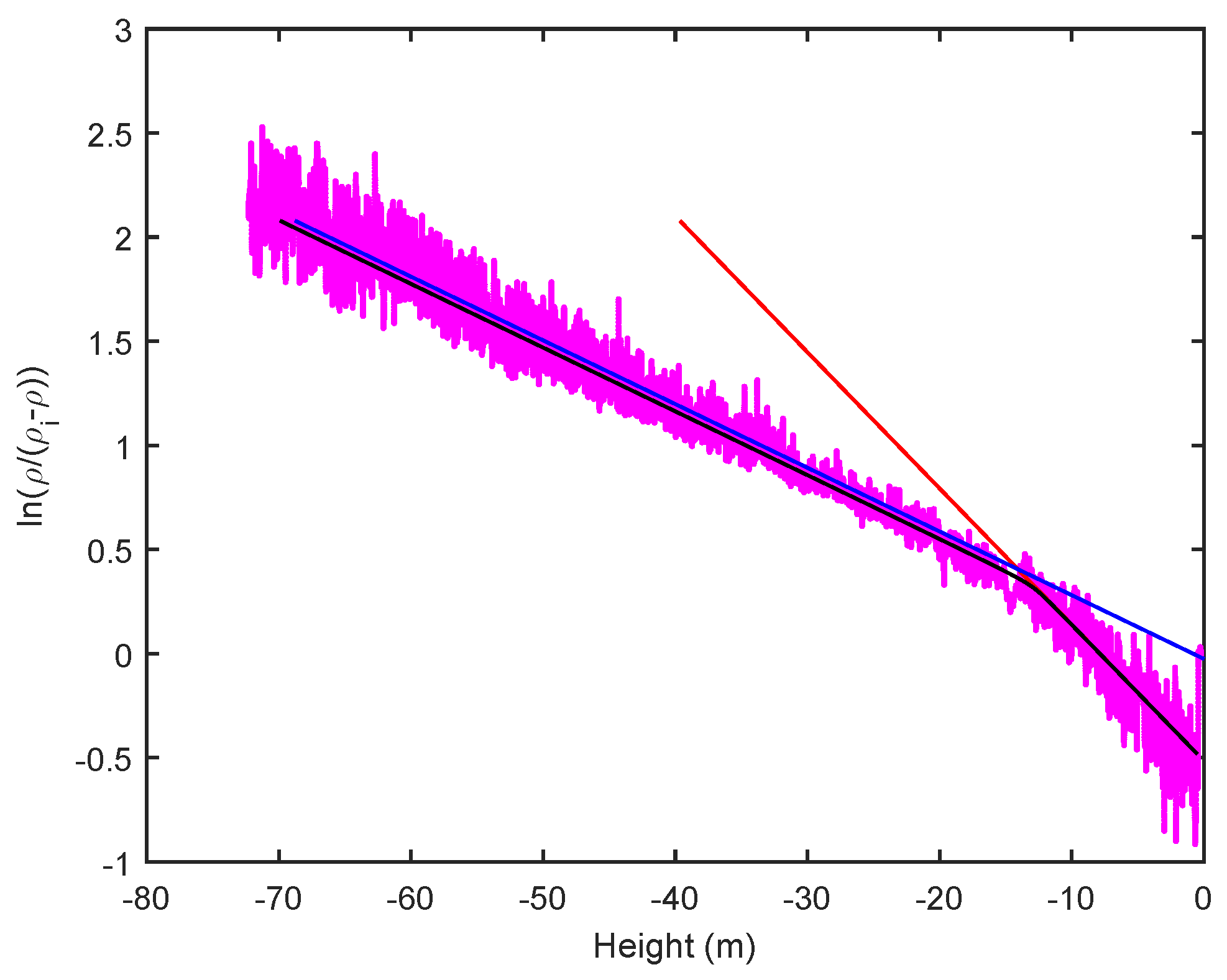
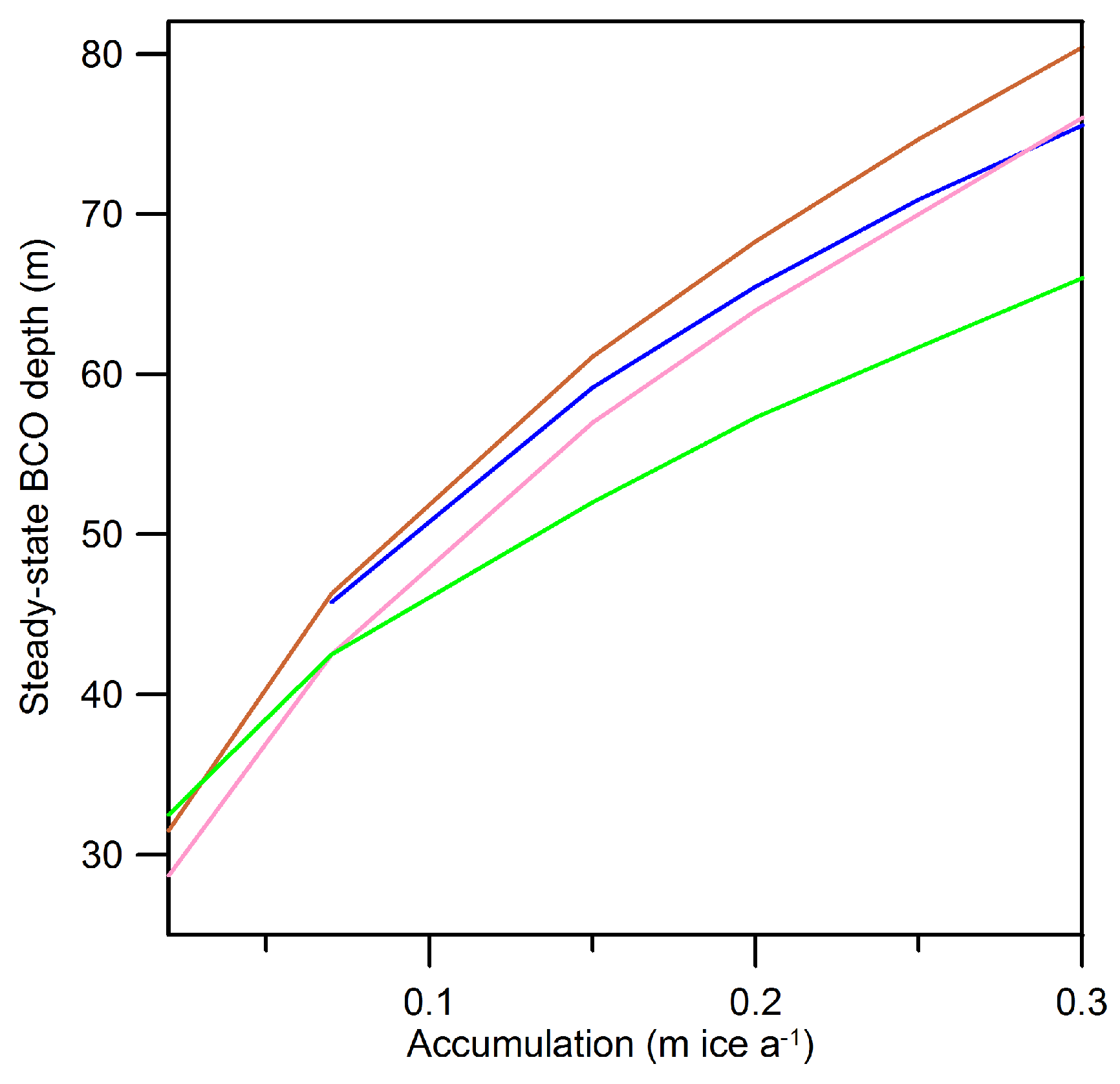
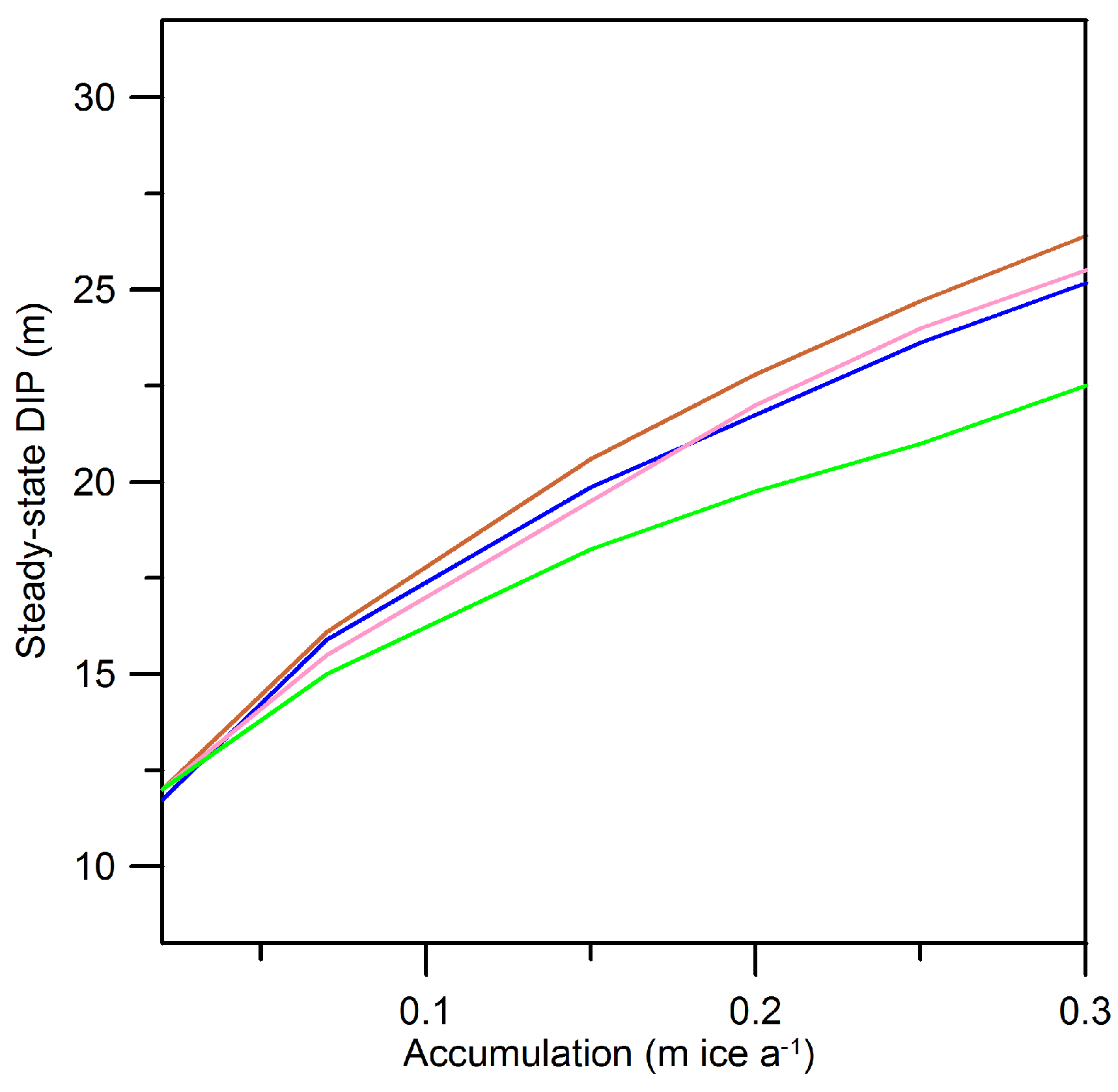
2.3. Density Profiles
3. Discussion
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| mean annual accumulation rate, m w.e. a or kg m a | |
| constant in activation equation, a | |
| constant in activation equation, kg m | |
| c | density-corrected volumetric strain rate, a |
| constant in activation equation, kg m | |
| constant in activation equation, a | |
| E | activation energy, J mol |
| parameter in Simonsen model | |
| parameter in Simonsen model | |
| F | average density-corrected volumetric strain rate, a |
| I | integral |
| k | local vertical densification rate, m w.e. |
| global vertical densification rate, m w.e. | |
| constant in transition model equation | |
| q | water equivalent height, m w.e. |
| Q | mass of section of profile, m w.e. |
| gas constant, 8.314 J mol K | |
| t | time, a |
| T | temperature, K |
| mean annual temperature, K | |
| w | vertical velocity, m a |
| X | scaled density, kg m |
| z | vertical co-ordinate, m |
| Z | length of section of profile, m |
| time between measurements at a given site, a | |
| volumetric strain rate, a | |
| horizontal velocity divergence, a | |
| vertical strain rate, a | |
| density, kg m | |
| density of ice, 917 kg m | |
| transition density, kg m | |
| vertically-smoothed density, kg m | |
| stress, Pa | |
| time since deposition of snow, a | |
| cost function |
Appendix A. Analytical Solution for Depth as a Function of Density
Appendix B. Analytical Solution for Depth-Integrated Porosity as a Function of Density
References
- Lundin, J.; Stevens, C.; Arthern, R.J.; Buizert, C.; Orsi, A.J.; Ligtenberg, S.R.M.; Simonsen, S.B.; Cummings, E.; Essery, R.; Leahy, W.; et al. Firn Model Intercomparison Experiment (FirnMICE). J. Glaciol. 2017, 63, 401–422. [Google Scholar] [CrossRef]
- Vionnet, V.; Brun, E.; Morin, S.; Boone, A.; Faroux, S.; Le Moigne, P.; Martin, E.; Willemet, J. The detailed snowpack scheme Crocus and its implementation in SURFEX v7. 2. Geosci. Model Dev. 2012, 5, 773–791. [Google Scholar] [CrossRef]
- Wever, N.; Schmid, L.; Heilig, A.; Eisen, O.; Fierz, C.; Lehning, M. Verification of the multi-layer SNOWPACK model with different water transport schemes. Cryosphere 2015, 9, 2271–2293. [Google Scholar] [CrossRef]
- Steger, C.; Reijmer, C.; Van den Broeke, M.; Wever, N.; Forster, R.; Koenig, L.; Lehning, M.; Lhermitte, S.; Ligtenberg, S.; Miège, C.; et al. Firn Meltwater Retention on the Greenland Ice Sheet: A Model Comparison. Front. Earth Sci. 2017, 5, 1–16. [Google Scholar] [CrossRef]
- Robin, G.d.Q. Glaciology. III. Seismic shooting and related investigations. In Norwegian-British-Swedish Antarctic Expedition, 1949-52; Norsk Polarinstitutt: Oslo, Norway, 1958; Volume 5. [Google Scholar]
- Herron, M.M.; Langway, C.C. Firn densification: An empirical model. J. Glaciol. 1980, 25, 373–385. [Google Scholar] [CrossRef]
- Hörhold, M.W.; Kipfstuhl, S.; Wilhelms, F.; Freitag, J.; Frenzel, A. The densification of layered polar firn. J. Geophys. Res. 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Morris, E.M.; Mulvaney, R.; Arthern, R.J.; Davies, D.; Gurney, R.J.; Lambert, P.; De Rydt, J.; Smith, A.M.; Tuckwell, R.; Winstrup, M. Snow Densification and Recent Accumulation Along the iSTAR Traverse, Pine Island Glacier, Antarctica. J. Geophys. Res. Earth Surf. 2017, 122, 2284–2301. [Google Scholar] [CrossRef]
- Arthern, R.J.; Wingham, D.J. The natural fluctuations of firn densification and their effect on the geodetic determination of ice sheet mass balance. Clim. Chang. 1998, 40, 605–624. [Google Scholar] [CrossRef]
- Brown, R.L. A volumetric constitutive law for snow based on a neck growth model. J. Appl. Phys. 1980, 51, 161–165. [Google Scholar] [CrossRef]
- Hörhold, M.W.; Laepple, T.; Freitag, J.; Bigler, M.; Fischer, H.; Kipfstuhl, S. On the impact of impurities on the densification of polar firn. Earth Planet. Sci. Lett. 2012, 325–326, 93–99. [Google Scholar] [CrossRef]
- Arthern, R.J.; Vaughan, D.G.; Rankin, A.M.; Mulvaney, R.; Thomas, E.R. In-situ measurements of Antarctic snow compaction compared with predictions of models. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Ligtenberg, S.R.M.; Helsen, M.M.; van den Broeke, M.R. An improved semi-empirical model for the densification of Antarctic firn. Cryosphere 2011, 5, 809–819. [Google Scholar] [CrossRef]
- Kuipers Munneke, P.; Ligtenberg, S.R.; Noël, B.P.Y.; Howat, I.; Box, J.E.; Mosley-Thompson, E.; McConnell, J.R.; Steffen, K.; Harper, J.; Das, S.B.; et al. Elevation change of the Greenland Ice Sheet due to surface mass balance and firn processes, 1960–2014. Cryosphere 2015, 9, 2009–2025. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Stenseng, L.; Adalgeirsdottir, G.; Fausto, R.S.; Hvidberg, C.S.; Lucas-Picher, P. Assessing a multilayered dynamic firn-compaction model for Greenland with ASIRAS radar measurements. J. Glaciol. 2013, 59, 545–558. [Google Scholar] [CrossRef]
- Morris, E.; Wingham, D.J. The effect of fluctuations in surface density, accumulation and compaction on elevation change rates along the EGIG line, central Greenland. J. Glaciol. 2011, 57, 416–430. [Google Scholar] [CrossRef]
- Morris, E.M.; Wingham, D.J. Densification of polar snow: measurements, modelling and implications for altimetry. JGR Earth Surf. 2014, 119, 349–365. [Google Scholar] [CrossRef]
- Morris, E.M.; Wingham, D.J. Uncertainty in mass balance trends derived from altimetry; a case study along the EGIG line, Central Greenland. J. Glaciol. 2015, 61, 345–356. [Google Scholar] [CrossRef]
- Wilhelms, F. Density of Firn Core DML96C07_ 39. 2007. Available online: https://doi.pangaea.de/10.1594/PANGAEA.615238 (accessed on 23 October 2018).
- Miller, H.; Schwager, M. Density of Ice Core ngt37C95.2 from the North Greenland Traverse. 2000. Available online: https://doi.pangaea.de/10.1594/PANGAEA.57798 (accessed on 23 October 2018).

| Site | Herron and Langway | Ligtenberg | Transition | |
|---|---|---|---|---|
| m w.e. a | ||||
| 1 | 0.35 | 0.202 | 0.185 | 0.097 |
| 2 | 0.34 | 0.186 | 0.148 | 0.036 |
| 3 | 0.43 | 0.154 | 0.098 | 0.053 |
| 4 | 0.58 | 0.212 | 0.162 | 0.037 |
| 5 | 0.45 | 0.237 | 0.217 | 0.094 |
| 6 | 0.45 | 0.125 | 0.076 | 0.072 |
| 7 | 0.33 | 0.275 | 0.250 | 0.204 |
| 8 | 0.32 | 0.169 | 0.133 | 0.094 |
| 9 | 0.37 | 0.149 | 0.125 | 0.064 |
| 10 | 0.23 | 0.167 | 0.083 | 0.128 |
| 11 | 0.23 | 0.135 | 0.060 | 0.086 |
| 12 | 0.28 | 0.209 | 0.155 | 0.134 |
| 13 | 0.43 | 0.164 | 0.129 | 0.030 |
| 14 | 0.47 | 0.186 | 0.162 | 0.035 |
| 15 | 0.80 | 0.202 | 0.284 | 0.105 |
| 16 | 0.51 | 0.143 | 0.110 | 0.045 |
| 17 | 0.52 | 0.192 | 0.140 | 0.013 |
| 18 | 0.69 | 0.164 | 0.163 | 0.132 |
| 19 | 0.69 | 0.258 | 0.219 | 0.019 |
| 20 | 0.64 | 0.195 | 0.156 | 0.042 |
| 21 | 0.75 | 0.214 | 0.181 | 0.042 |
| 22 | 0.78 | 0.198 | 0.170 | 0.041 |
| Site | Herron and Langway | Ligtenberg | Transition | |
|---|---|---|---|---|
| m w.e. a | ||||
| 1 | 0.35 | 0.264 | 0.145 | 0.097 |
| 4 | 0.58 | 0.228 | 0.092 | 0.088 |
| 6 | 0.45 | 0.205 | 0.106 | 0.093 |
| 7 | 0.33 | 0.291 | 0.287 | 0.270 |
| 8 | 0.32 | 0.182 | 0.114 | 0.093 |
| 10 | 0.23 | 0.168 | 0.116 | 0.147 |
| 15 | 0.80 | 0.293 | 0.186 | 0.155 |
| 18 | 0.69 | 0.222 | 0.137 | 0.103 |
| 20 | 0.64 | 0.297 | 0.184 | 0.072 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morris, E. Modeling Dry-Snow Densification without Abrupt Transition. Geosciences 2018, 8, 464. https://doi.org/10.3390/geosciences8120464
Morris E. Modeling Dry-Snow Densification without Abrupt Transition. Geosciences. 2018; 8(12):464. https://doi.org/10.3390/geosciences8120464
Chicago/Turabian StyleMorris, Elizabeth. 2018. "Modeling Dry-Snow Densification without Abrupt Transition" Geosciences 8, no. 12: 464. https://doi.org/10.3390/geosciences8120464
APA StyleMorris, E. (2018). Modeling Dry-Snow Densification without Abrupt Transition. Geosciences, 8(12), 464. https://doi.org/10.3390/geosciences8120464





