Analysis of QualitySpec Trek Reflectance from Vertical Profiles of Taiga Snowpack
Abstract
1. Introduction
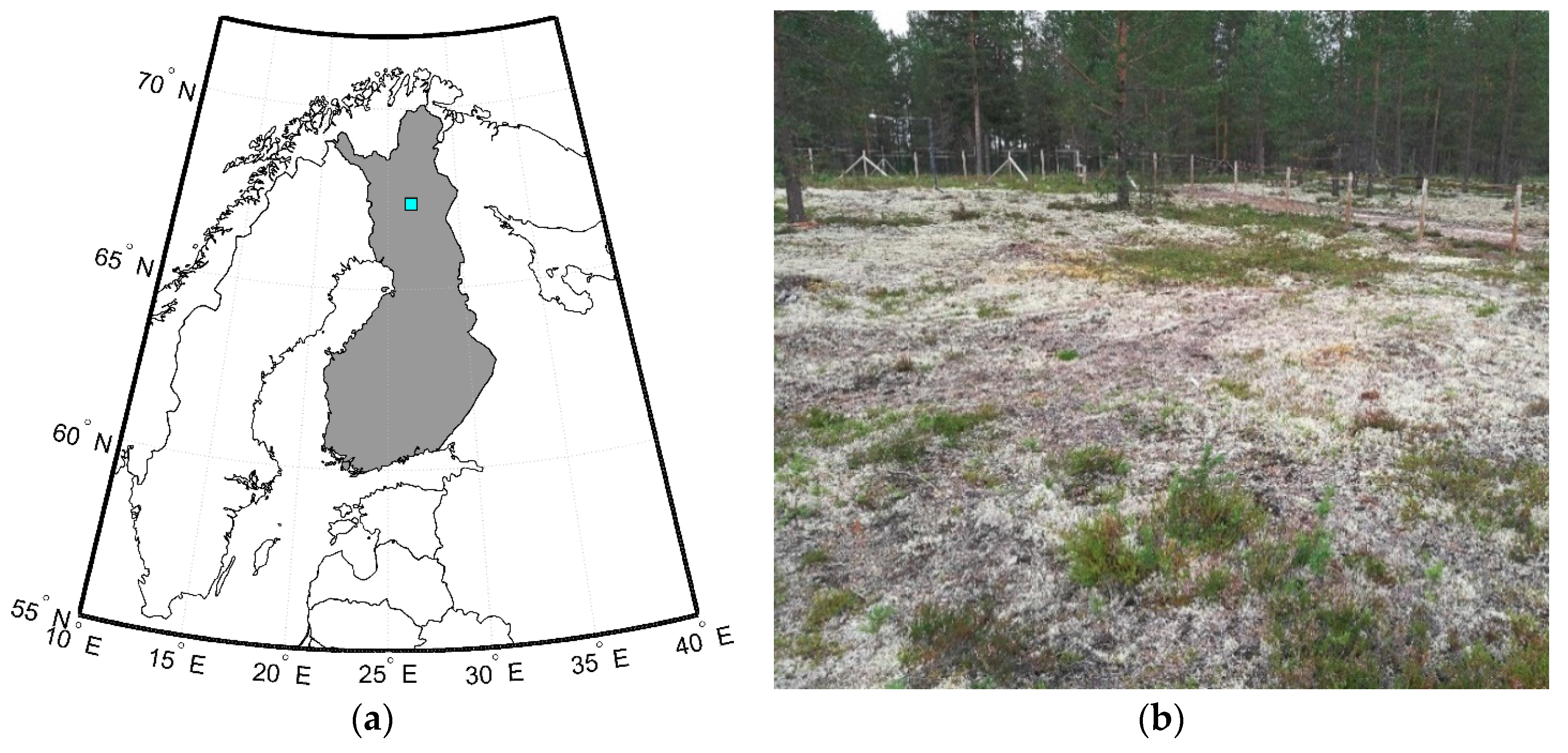
2. Materials and Methods
2.1. Layers, Traditional Grain Size, and Density
2.2. SSA with IceCube
2.3. Reflectance with QualitySpec Trek
2.4. Methods for Comparison of QST and IceCube Measurements
3. Results
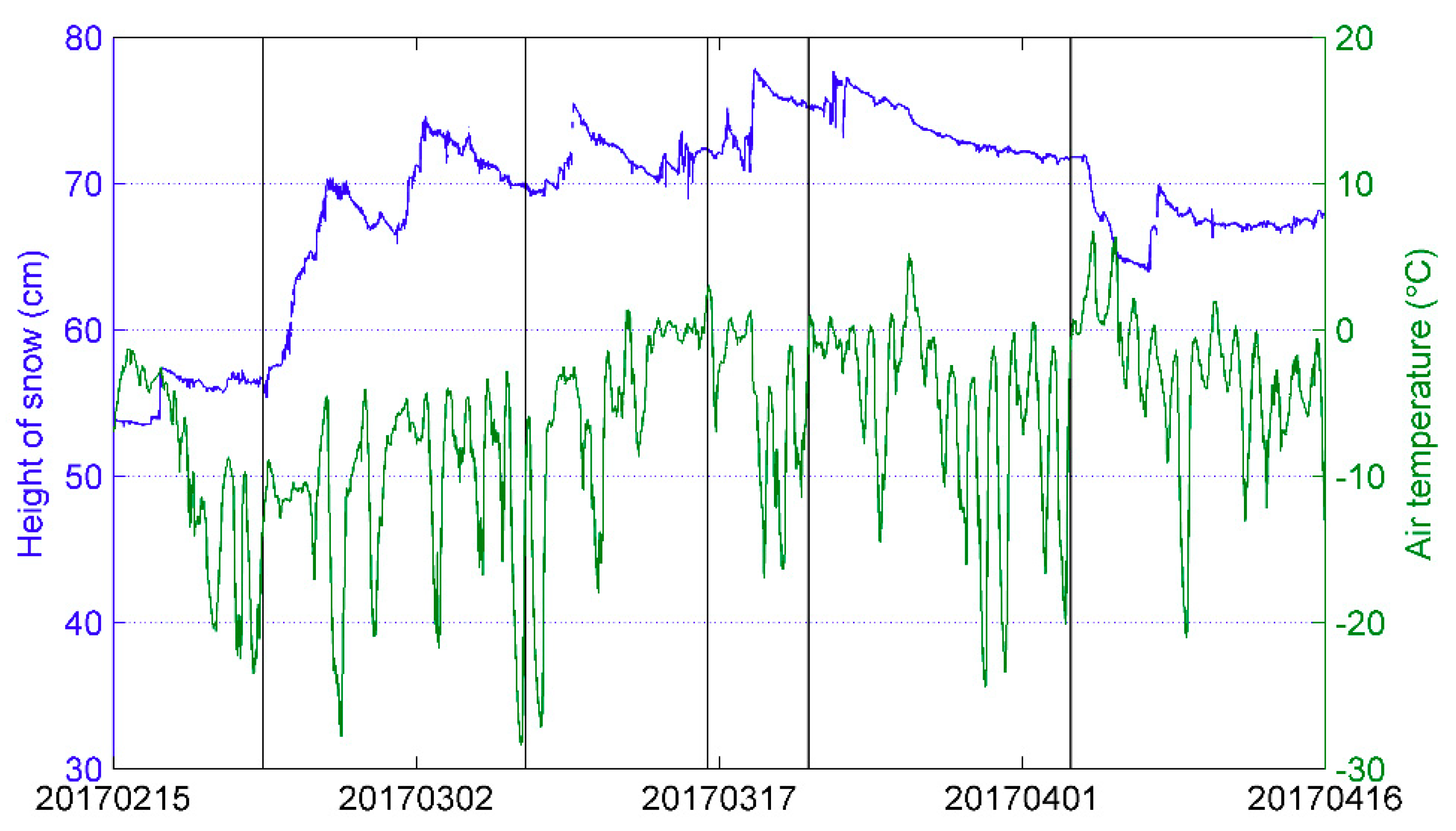
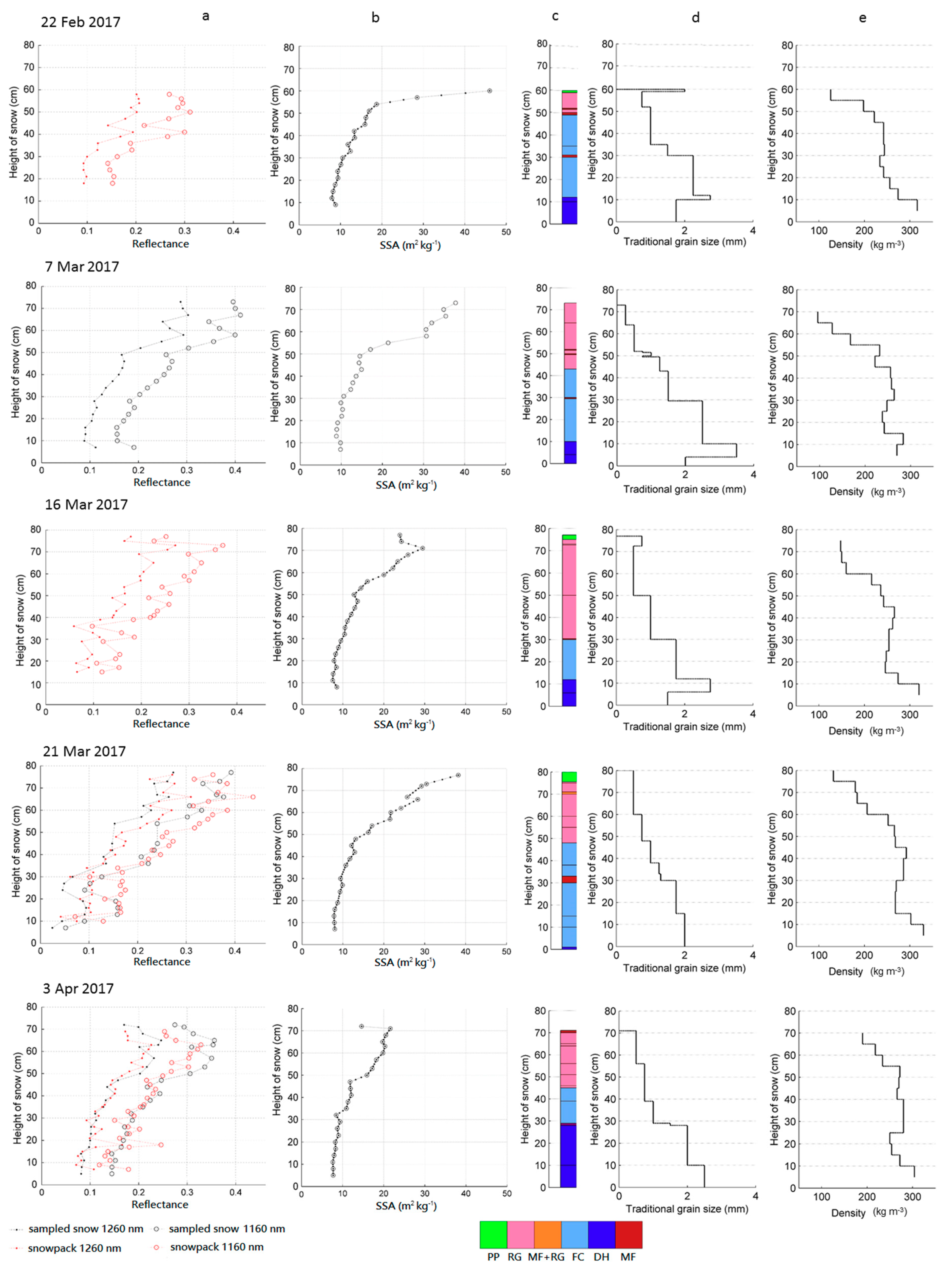
3.1. Snowpack Properties
3.2. Repeatability of SSA Measurements
3.3. Comparison of QST Reflectance Profiles
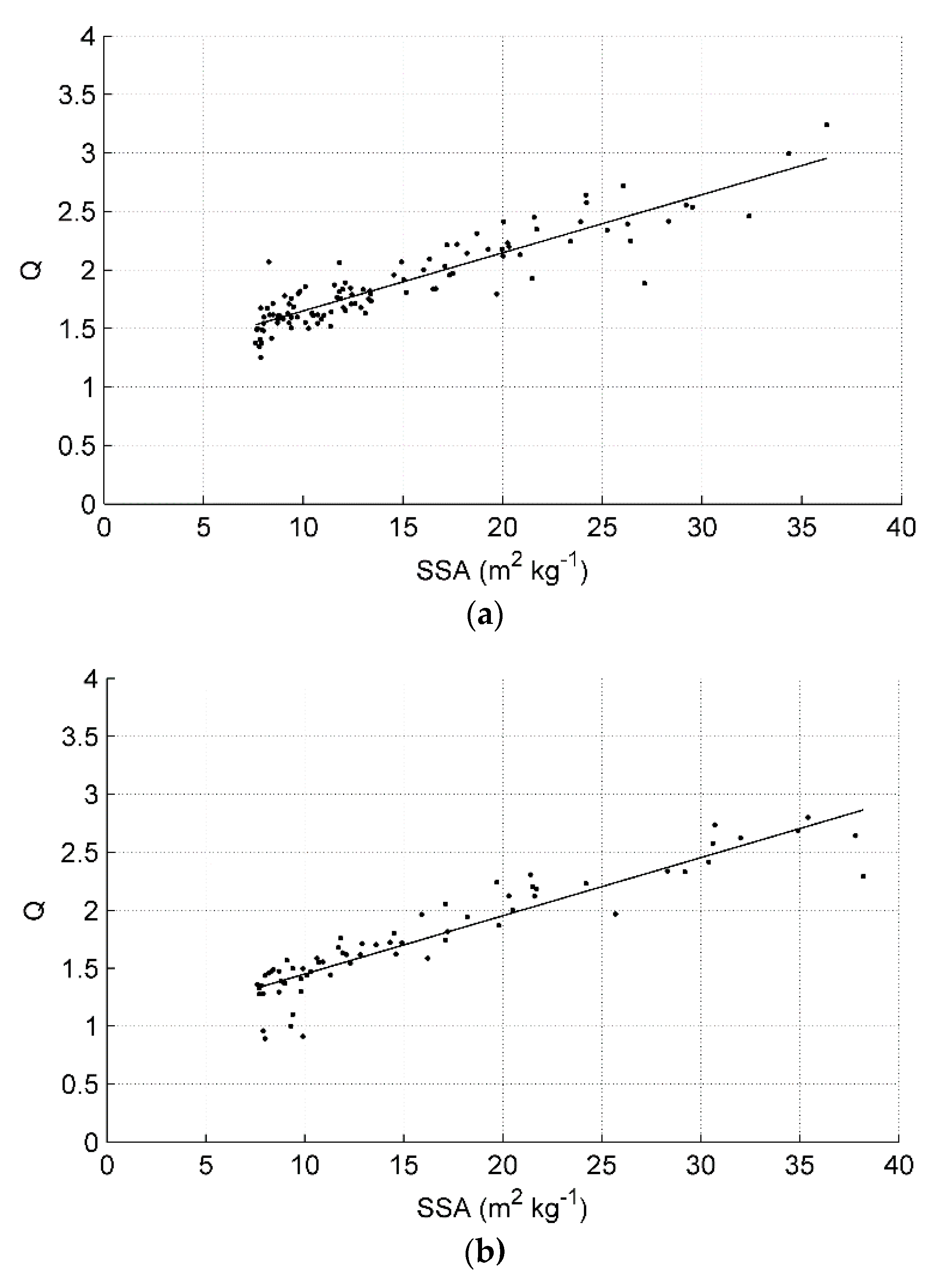
3.4. Empirical Relationship between SSA and Reflectance
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pulliainen, J.; Grandell, J.; Hallikainen, M. HUT snow emission model and its applicability to snow water equivalent retrieval. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1378–1390. [Google Scholar] [CrossRef]
- Nolin, A.W.; Dozier, J. A hyperspectral method for remotely sensing the grain size of snow. Remote Sens. Environ. 2000, 74, 207–216. [Google Scholar] [CrossRef]
- Mätzler, C. MATLAB functions for Mie scattering and absorption, version 2. IAP Res. Rep. 2002, 8, 1–24. [Google Scholar]
- Fierz, C.; Armstrong, R.L.; Durand, Y.; Etchevers, P.; Greene, E.; McClung, D.M.; Nishimura, K.; Satyawali, P.K.; Sokratov, S.A. The International Classification for Seasonal Snow on the Ground; IHP-VII Technical Documents in Hydrology N°83, IACS Contribution N°1; UNESCO-IHP: Paris, France, 2009. [Google Scholar]
- Debye, P.; Anderson, H.R.; Brumberger, H. Scattering by an inhomogeneous solid. II. The correlation function and its application. J. Appl. Phys. 1957, 28, 679–683. [Google Scholar] [CrossRef]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Painter, T.H.; Molotch, N.P.; Cassidy, M.; Flanner, M.; Steffen, K. Contact spectroscopy for determination of stratigraphy of snow optical grain size. J. Glaciol. 2007, 53, 121–127. [Google Scholar] [CrossRef]
- Domine, F.; Salvatori, R.; Legagneux, L.; Salzano, R.; Fily, M.; Casacchia, R. Correlation between the specific surface area and the short wave infrared (SWIR) reflectance of snow. Cold Reg. Sci. Technol. 2006, 46, 60–68. [Google Scholar] [CrossRef]
- Legagneux, L.; Cabanes, A.; Dominé, F. Measurement of the specific surface area of 176 snow samples using methane adsorption at 77 K. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Grenfell, T.C.; Warren, S.G. Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation. J. Geophys. Res. Atmos. 1999, 104, 31697–31709. [Google Scholar] [CrossRef]
- Dominé, F.; Cabanes, A.; Taillandier, A.S.; Legagneux, L. Specific surface area of snow samples determined by CH4 adsorption at 77 K and estimated by optical microscopy and scanning electron microscopy. Environ. Sci. Technol. 2001, 35, 771–780. [Google Scholar] [CrossRef] [PubMed]
- Kokhanovsky, A.A.; Zege, E.P. Scattering optics of snow. Appl. Opt. 2004, 43, 1589–1602. [Google Scholar] [CrossRef] [PubMed]
- Gallet, J.C.; Domine, F.; Zender, C.S.; Picard, G. Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm. Cryosphere 2009, 3, 167–182. [Google Scholar] [CrossRef]
- Neshyba, S.P.; Grenfell, T.C.; Warren, S.G. Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation: 2. Hexagonal columns and plates. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Grenfell, T.C.; Neshyba, S.P.; Warren, S.G. Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation: 3. Hollow columns and plates. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Picard, G.; Brucker, L.; Fily, M.; Gallée, H.; Krinner, G. Modeling time series of microwave brightness temperature in Antarctica. J. Glaciol. 2009, 55, 537–551. [Google Scholar] [CrossRef]
- Gallet, J.C.; Domine, F.; Dumont, M. Measuring the specific surface area of wet snow using 1310 nm reflectance. Cryosphere 2014, 8, 1139–1148. [Google Scholar] [CrossRef]
- Arnaud, L.; Picard, G.; Champollion, N.; Domine, F.; Gallet, J.-C.; Lefebvre, E.; Fily, M.; Barnola, J.-M. Measurement of vertical profiles of snow specific surface area with a 1 cm resolution using infrared reflectance: Instrument description and validation. J. Glaciol. 2011, 57, 17–29. [Google Scholar] [CrossRef]
- Matzl, M.; Schneebeli, M. Measuring specific surface area of snow by near-infrared photography. J. Glaciol. 2006, 52, 558–564. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Hyvärinen, T.; Lammasniemi, J. Infrared Measurement of Grain Size and Melting Degree of Snow; Infrared Technology XI; International Society for Optics and Photonics: San Diego, CA, USA, 1985; Volume 572, pp. 158–166. [Google Scholar]
- Picard, G.; Libois, Q.; Arnaud, L.; Verin, G.; Dumont, M. Development and calibration of an automatic spectral albedometer to estimate near-surface snow SSA time series. Cryosphere 2016, 10, 1297–1316. [Google Scholar] [CrossRef]
- Painter, T.H.; Dozier, J. Measurements of the hemispherical-directional reflectance of snow at fine spectral and angular resolution. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Carmagnola, C.M.; Dominé, F.; Dumont, M.; Wright, P.; Strellis, B.; Bergin, M.; Dibb, J.; Picard, G.; Libois, Q.; Arnaud, L.; et al. Snow spectral albedo at Summit, Greenland: Measurements and numerical simulations based on physical and chemical properties of the snowpack. Cryosphere 2013, 7, 1139–1160. [Google Scholar] [CrossRef]
- Langlois, A.; Royer, A.; Montpetit, B.; Picard, G.; Brucker, L.; Arnaud, L.; Harvey-Collardard, P.; Fily, M.; Goïta, K. On the relationship between snow grain morphology and in-situ near infrared calibrated reflectance photographs. Cold Reg. Sci. Technol. 2010, 61, 34–42. [Google Scholar] [CrossRef]
- Aoki, T.; Aoki, T.; Fukabori, M.; Hachikubo, A.; Tachibana, Y.; Nishio, F. Effects of snow physical parameters on spectral albedo and bidirectional reflectance of snow surface. J. Geophys. Res. Atmos. 2000, 105, 10219–10236. [Google Scholar] [CrossRef]
- Pirazzini, R.; Räisänen, P.; Vihma, T.; Johansson, M.; Tastula, E.M. Measurements and modelling of snow particle size and shortwave infrared albedo over a melting Antarctic ice sheet. Cryosphere 2015, 9, 2357–2381. [Google Scholar] [CrossRef]
- Tanikawa, T.; Aoki, T.; Hori, M.; Hachikubo, A.; Abe, O.; Aniya, M. Monte Carlo simulations of spectral albedo for artificial snowpacks composed of spherical and nonspherical particles. Appl. Opt. 2006, 45, 5310–5319. [Google Scholar] [CrossRef] [PubMed]
- Tanikawa, T.; Aoki, T.; Hori, M.; Hachikubo, A.; Aniya, M. Snow bidirectional reflectance model using non-spherical snow particles and its validation with field measurements. EARSeL eProc. 2006, 5, 137–145. [Google Scholar]
- Peng, J.; Ji, W.; Ma, Z.; Li, S.; Chen, S.; Zhou, L.; Shi, Z. Predicting total dissolved salts and soluble ion concentrations in agricultural soils using portable visible near-infrared and mid-infrared spectrometers. Biosyst. Eng. 2016, 152, 94–103. [Google Scholar] [CrossRef]
- Hu, B.; Chen, S.; Hu, J.; Xia, F.; Xu, J.; Li, Y.; Shi, Z. Application of portable XRF and VNIR sensors for rapid assessment of soil heavy metal pollution. PLoS ONE 2017, 12, e0172438. [Google Scholar] [CrossRef] [PubMed]
- Bartelt, P.; Lehning, M. A physical SNOWPACK model for the Swiss avalanchewarning: Part I: Numerical model. Cold Reg. Sci. Technol. 2002, 35, 123–145. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Fierz, C.; Satyawali, P. A physical SNOWPACK model for the Swiss avalanche warning. Part II: Snow microstructure. Cold Reg. Sci. Technol. 2002, 35, 147–167. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Fierz, C. A physical SNOWPACK model for the Swiss avalanche warning: Part III: Meteorological forcing, thin layer formation and evaluation. Cold Reg. Sci. Technol. 2000, 35, 169–184. [Google Scholar] [CrossRef]
- Leppänen, L.; Kontu, A.; Hannula, H.-R.; Sjöblom, H.; Pulliainen, J. Sodankylä manual snow survey program. Geosci. Instrum. Methods Data Syst. 2016, 5, 163–179. [Google Scholar] [CrossRef]
- Kontu, A.; Lemmetyinen, J.; Vehviläinen, J.; Leppänen, L.; Pulliainen, J. Coupling SNOWPACK-modeled grain size parameters with the HUT snow emission model. Remote Sens. Environ. 2017, 194, 33–47. [Google Scholar] [CrossRef]
- Sandells, M.; Essery, R.; Rutter, N.; Wake, L.; Leppänen, L.; Lemmetyinen, J. Microstructure representation of snow in coupled snowpack and microwave emission models. Cryosphere 2017, 11, 229. [Google Scholar] [CrossRef]
- Jordan, R. A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM.89; Special Report 91-16; Cold Regions Research and Engineering Laboratory (U.S.): Hanover, NH, USA; Engineer Research and Development Center (U.S.): Vicksburg, MS, USA, 1991. [Google Scholar]
- Flanner, M.G.; Zender, C.S. Linking snowpack microphysics and albedo evolution. J. Geophys. Res. 2006, 111, D12208. [Google Scholar] [CrossRef]
- Essery, R.; Best, M.; Cox, P. MOSES 2.2 Technical Documentation; Technical Report, Hadley Centre Technical Note 30; Hadley Centre, Met Office: Exeter, UK, 2001; p. 31. [Google Scholar]
- Salminen, M.; Pulliainen, J.; Metsämäki, S.; Kontu, A.; Suokanerva, H. The behaviour of snow and snow-free surface reflectance in boreal forests: Implications to the performance of snow covered area monitoring. Remote Sens. Environ. 2009, 113, 907–918. [Google Scholar] [CrossRef]
- Meinander, O.; Kazadzis, S.; Arola, A.; Riihelä, A.; Räisänen, P.; Kivi, R.; Kontu, A.; Kouznetsov, R.; Sofiev, M.; Svensson, J.; et al. Spectral albedo of seasonal snow during intensive melt period at Sodankylä, beyond the Arctic Circle. Atmos. Chem. Phys. 2013, 13, 3793–3810. [Google Scholar] [CrossRef]
- Peltoniemi, J.I.; Kaasalainen, S.; Näränen, J.; Matikainen, L.; Piironen, J. Measurement of directional and spectral signatures of light reflectance by snow. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2294–2304. [Google Scholar] [CrossRef]
- Peltoniemi, J.; Hakala, T.; Suomalainen, J.; Puttonen, E. Polarised bidirectional reflectance factor measurements from soil, stones, and snow. J. Quant. Spectrosc. Radiat. 2009, 110, 1940–1953. [Google Scholar] [CrossRef]
- Leppänen, L.; Leinss, S.; Suokanerva, H. Growth of Forest Floor Vegetation Observed from Snow Depth Measurements in Sodankylä, Finland, Snow an Ecological Phenomenon, Smolenice, Slovakia, 19–21 September 2017. Available online: http://www.sbks.sk/smolenice/Leppanen%20et%20al.pdf (accessed on 5 November 2018).
- Leppänen, L.; Kontu, A.; Vehviläinen, J.; Lemmetyinen, J.; Pulliainen, J. Comparison of traditional and optical grain-size field measurements with SNOWPACK simulations in a taiga snowpack. J. Glaciol. 2015, 61, 151–162. [Google Scholar] [CrossRef]



| Density (kg m−3) | SSA (m2 kg−1) | STD | RSD (%) | |
|---|---|---|---|---|
| 225.0 | 39.8 | |||
| Surface | 309.9 | 41.6 | 1.04 | 2.53 |
| 352.4 | 41.6 | |||
| 338.2 | 7.9 | |||
| Bottom | 409.0 | 8.2 | 0.25 | 3.17 |
| 394.9 | 7.7 | |||
| Average | 0.65 | 2.85 |
| Date | Wavelength (nm) | Bias | RMSE | R |
|---|---|---|---|---|
| 1160 | −0.0204 | 0.040 | 0.92 | |
| 21 March 2017 | 1260 | −0.0202 | 0.031 | 0.94 |
| 1310 | −0.0230 | 0.034 | 0.93 | |
| 1160 | 0.0160 | 0.033 | 0.92 | |
| 3 April 2017 | 1260 | 0.0055 | 0.022 | 0.92 |
| 1310 | 0.0068 | 0.023 | 0.92 |
| Date | Profile | R |
|---|---|---|
| 22 February 2017 | Snowpack | 0.95 |
| 7 March 2017 | Sampled Snow | 0.98 |
| 16 March 2017 | Snowpack | 0.89 |
| 21 March 2017 | Sampled Snow | 0.89 |
| 21 March 2017 | Snowpack | 0.94 |
| 3 April 2017 | Sampled Snow | 0.96 |
| 3 April 2017 | Snowpack | 0.85 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leppänen, L.; Kontu, A. Analysis of QualitySpec Trek Reflectance from Vertical Profiles of Taiga Snowpack. Geosciences 2018, 8, 404. https://doi.org/10.3390/geosciences8110404
Leppänen L, Kontu A. Analysis of QualitySpec Trek Reflectance from Vertical Profiles of Taiga Snowpack. Geosciences. 2018; 8(11):404. https://doi.org/10.3390/geosciences8110404
Chicago/Turabian StyleLeppänen, Leena, and Anna Kontu. 2018. "Analysis of QualitySpec Trek Reflectance from Vertical Profiles of Taiga Snowpack" Geosciences 8, no. 11: 404. https://doi.org/10.3390/geosciences8110404
APA StyleLeppänen, L., & Kontu, A. (2018). Analysis of QualitySpec Trek Reflectance from Vertical Profiles of Taiga Snowpack. Geosciences, 8(11), 404. https://doi.org/10.3390/geosciences8110404






