A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water
Abstract
:1. Introduction
2. Methodology
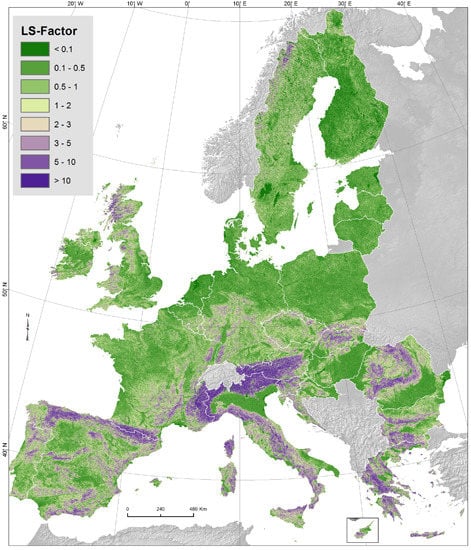
3. Results and Discussion
| Country Name | Code | Mean | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|
| Austria | AT | 5.20 | 5.91 | 1.14 |
| Belgium | BE | 0.68 | 0.95 | 1.40 |
| Bulgaria | BG | 2.34 | 3.00 | 1.28 |
| Cyprus | CY | 2.31 | 2.72 | 1.18 |
| Czech Rep. | CZ | 1.36 | 1.57 | 1.15 |
| Germany | DE | 1.05 | 1.64 | 1.57 |
| Denmark | DK | 0.32 | 0.34 | 1.07 |
| Estonia | EE | 0.32 | 0.31 | 0.96 |
| Spain | ES | 2.24 | 2.97 | 1.33 |
| Finland | FI | 0.41 | 0.64 | 1.56 |
| France | FR | 1.72 | 3.12 | 1.81 |
| Greece | GR | 3.79 | 4.05 | 1.07 |
| Croatia | HR | 1.89 | 2.56 | 1.36 |
| Hungary | HU | 0.59 | 0.99 | 1.69 |
| Ireland | IE | 1.01 | 1.54 | 1.52 |
| Italy | IT | 3.63 | 4.86 | 1.34 |
| Lithuania | LT | 0.35 | 0.38 | 1.09 |
| Luxembourg | LU | 1.62 | 1.68 | 1.04 |
| Latvia | LV | 0.39 | 0.36 | 0.93 |
| Malta | MT | 1.34 | 1.97 | 1.46 |
| Netherlands | NL | 0.19 | 0.20 | 1.05 |
| Poland | PL | 0.52 | 0.86 | 1.67 |
| Portugal | PT | 1.80 | 2.25 | 1.25 |
| Romania | RO | 2.09 | 2.82 | 1.35 |
| Sweden | SE | 0.99 | 1.51 | 1.52 |
| Slovenia | SI | 3.87 | 4.21 | 1.09 |
| Slovakia | SK | 2.57 | 2.84 | 1.11 |
| United Kingdom | UK | 1.40 | 2.02 | 1.45 |
4. Conclusions
Acknowledgments
Author Contributions
Supplementary Materials
Conflicts of Interest
References
- Panagos, P.; Meusburger, K.; van Liedekerke, M.; Alewell, C.; Hiederer, R.; Montanarella, L. Assessing soil erosion in Europe based on data collected through a European Network. Soil Sci. Plant Nutr. 2014, 60, 15–29. [Google Scholar] [CrossRef]
- Risse, L.M.; Nearing, M.A.; Nicks, A.; Leaflen, J.M. Application of radioactive fallout celsium-137 for measuring soil erosion and sediment accumulation rates and patterns: A review. J. Environ. Qual. 1993, 9, 215–233. [Google Scholar]
- Mukherjee, S.; Joshi, P.K.; Mukherjee, S.; Ghosh, A.; Garg, R.D.; Mukhopadhyay, A. Evaluation of vertical accuracy of open source Digital Elevation Model (DEM). Int. J. Appl. Earth Observ. Geoinf. 2014, 21, 205–217. [Google Scholar] [CrossRef]
- Van Rompaey, A.; Krasa, J.; Dostal, T.; Govers, G. Modelling sediment supply to rivers and reservoirs in Eastern Europe during and after the collectivisation period. Hydrobiologia 2003, 494, 169–176. [Google Scholar]
- Van der Knijff, J.M.; Jones, R.J.A.; Montanarella, L. Soil erosion risk assessment in Europe. Available online: http://139.191.1.96/ESDB_Archive/pesera/pesera_cd/pdf/ereurnew2.pdf (accessed on 15 December 2014).
- Desmet, P.; Govers, G. A GIS procedure for automatically calculating the ULSE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Eurostat. Digital Elevation Model (DEM) at 25 m Resolution Dataset. 2014. Available online: http://ec.europa.eu/eurostat/web/gisco/geodata/reference-data/digital-elevation-model (accessed on 15 December 2014).
- European Environmental Agency. EU-DEM Statistical Validation. Available online: http://ec.europa.eu/eurostat/documents/4311134/4350046/Report-EU-DEM-statistical-validation-August2014.pdf/508200d9-b52d-4562-b73b-edb64eedfb93 (accessed on 10 December 2014).
- Borrelli, P.; Marker, M.; Panagos, P.; Schutt, B. Modeling soil erosion and river sediment yield for an intermountain drainage basin of the Central Apennines, Italy. Catena 2014, 114, 45–58. [Google Scholar] [CrossRef]
- Wang, L.; Huang, Y.; Du, Y.; Han, P. Dynamic Assessment of Soil Erosion Risk Using Landsat TM and HJ Satellite Data in Danjiangkou Reservoir Area, China. Remote Sens. 2013, 5, 3826–3848. [Google Scholar] [CrossRef]
- Molnar, D.; Julien, P. Estimation of upland erosion using GIS. Comput. Geosci. 1998, 24, 183–192. [Google Scholar] [CrossRef]
- McCool, D.K.; Foster, G.R.; Mutchler, C.K.; Meyer, L.D. Revised slope steepness factor for the universal Soil Loss Equation. Trans. ASAE 1987, 30, 1387–1399. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Agricultural Handbook 703; U.S. Government Printing Office: Washington, DC, USA, 1997.
- Liu, B.Y.; Zhang, K.L.; Xie, Y. An empirical soil loss equation. In Proceedings of 12th International Soil Conservation, Beijing, China, 26–31 May 2002; pp. 21–25.
- Wischmeier, W.; Smith, D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Agricultural Handbook No. 537; USDA, Science and Education Administration: Hyattsville, MD, USA, 1978.
- Foster, G.R.; Wischmeier, W. Evaluating irregular slopes for soil loss prediction. Trans. Am. Soc. Agric. Eng. 1974, 17, 305–309. [Google Scholar] [CrossRef]
- McCool, D.K.; Foster, G.R.; Mutchler, C.K.; Meyer, L.D. Revised slope length factor for the Universal Soil Loss Equation. Trans. Am. Soc. Agric. Eng. 1989, 32, 1571–1576. [Google Scholar] [CrossRef]
- Mitasova, H.; Hofierka, J.; Zlocha, M.; Iverson, L.R. Modelling topographic potential for erosion and deposition using GIS. Int. J. Geogr. Inf. Syst. 1996, 10, 629–641. [Google Scholar] [CrossRef]
- Desmet, P.; Govers, G. Comment on ‘Modelling topographic potential for erosion and deposition using GIS’. Int. J. Geogr. Inf. Sci. 1997, 11, 603–610. [Google Scholar] [CrossRef]
- Griffin, M.L.; Beasley, D.B.; Fletcher, J.J.; Foster, G.R. Estimating soil loss on topographically nonuniform field and farm units. J. Soil Water Conserv. 1988, 43, 326–331. [Google Scholar]
- Wilson, J.P. Estimating the topographic factor in the universal soil loss equation for watersheds. J. Soil Water Conserv. 1986, 41, 179–184. [Google Scholar]
- McCool, D.K.; George, G.O.; Freckleton, M.; Papendick, R.I.; Douglas, C.L., Jr. Topographic effect on erosion from cropland in the northwestern wheat region. Trans. ASAE 1993, 36, 1067–1071. [Google Scholar] [CrossRef]
- Liu, B.Y.; Nearing, M.A.; Shi, P.J.; Jia, Z.W. Slope length effects on soil loss for steep slopes. Soil Sci. Soc. Am. J. 2000, 64, 1759–1763. [Google Scholar] [CrossRef]
- Mashimbye, Z.E.; de Clercq, W.P.; van Niekerk, A. An evaluation of digital elevation models (DEMs) for delineating land components. Geoderma 2014, 213, 312–319. [Google Scholar] [CrossRef]
- Olaya, V.; Conrad, O. Geomorphometry in SAGA. In Geomorphometry: Concepts, Software, Applications; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 293–308. [Google Scholar]
- SAGA. System for Automated Geoscientific Analyses. 2011. Available online: http://www.saga-gis.org (accessed on 10 December 2014).
- Pilesjö, P.; Hasan, A. A Triangular Form-based Multiple Flow Algorithm to Estimate Overland Flow Distribution and Accumulation on a Digital Elevation Model. Trans. GIS 2014, 18, 108–124. [Google Scholar] [CrossRef]
- Schwanghart, W.; Scherler, D. TopoToolbox 2–MATLAB-based software for topographic analysis and modeling in Earth surface sciences. Earth Surf. Dynam. 2014, 2, 1–7. [Google Scholar] [CrossRef]
- Panagos, P.; Karydas, C.G.; Ballabio, C.; Gitas, I.Z. Seasonal monitoring of soil erosion at regional scale: An application of the G2 model in Crete focusing on agricultural land uses. Int. J. Appl. Earth Observ. Geoinf. 2014, 27B, 147–155. [Google Scholar] [CrossRef]
- Bosco, C.; de Rigo, D.; Dewitte, O.; Poesen, J.; Panagos, P. Modelling soil erosion at European scale: Towards harmonization and reproducibility. Nat. Hazards Earth Syst. Sci. 2015, 15, 225–245. [Google Scholar] [CrossRef] [Green Version]
- Hickey, R. Slope Angle and Slope Length Solutions for GIS. Cartography 2000, 29, 1–8. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G. An evaluation of grid size uncertainty in empirical soil loss modeling with digital elevation models. Environ. Model. Assess. 2005, 10, 33–42. [Google Scholar] [CrossRef]
- Panagos, P.; van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre: Response to European policy support and public data requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Alewell, C. Soil erodibility in Europe: A high-resolution dataset based on LUCAS. Sci. Total Environ. 2014, 479–480, 189–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Panagos, P.; Borrelli, P.; Meusburger, K.; van der Zanden, E.H.; Poesen, J.; Alewell, C. Modelling the effect of support practices (P-factor) on the reduction of soil erosion by water at European Scale. Environ. Sci. Policy 2015. [Google Scholar] [CrossRef] [Green Version]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagos, P.; Borrelli, P.; Meusburger, K. A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences 2015, 5, 117-126. https://doi.org/10.3390/geosciences5020117
Panagos P, Borrelli P, Meusburger K. A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences. 2015; 5(2):117-126. https://doi.org/10.3390/geosciences5020117
Chicago/Turabian StylePanagos, Panos, Pasquale Borrelli, and Katrin Meusburger. 2015. "A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water" Geosciences 5, no. 2: 117-126. https://doi.org/10.3390/geosciences5020117
APA StylePanagos, P., Borrelli, P., & Meusburger, K. (2015). A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences, 5(2), 117-126. https://doi.org/10.3390/geosciences5020117