Evaluation of a Soviet-Era Gravimetric Survey Using Absolute Gravity Measurements and Global Gravity Models: Toward the First National Geoid of Kazakhstan
Abstract
1. Introduction
- –
- Possible systematic errors of analog instruments;
- –
- Mismatches in standards and reference frames;
- –
- Lack of homogeneous georeferencing;
- –
- Coarse determination of survey-point elevations;
- –
- Errors in digitization and map interpretation [1].
- –
- Omission errors, caused by limited spatial resolution,
- –
- Commission errors, arising from random and systematic (including correlated) noise,
- –
- Representativity error, i.e., the inability of the survey to fully capture short-wavelength gravity variations, especially in mountainous and geologically complex regions.
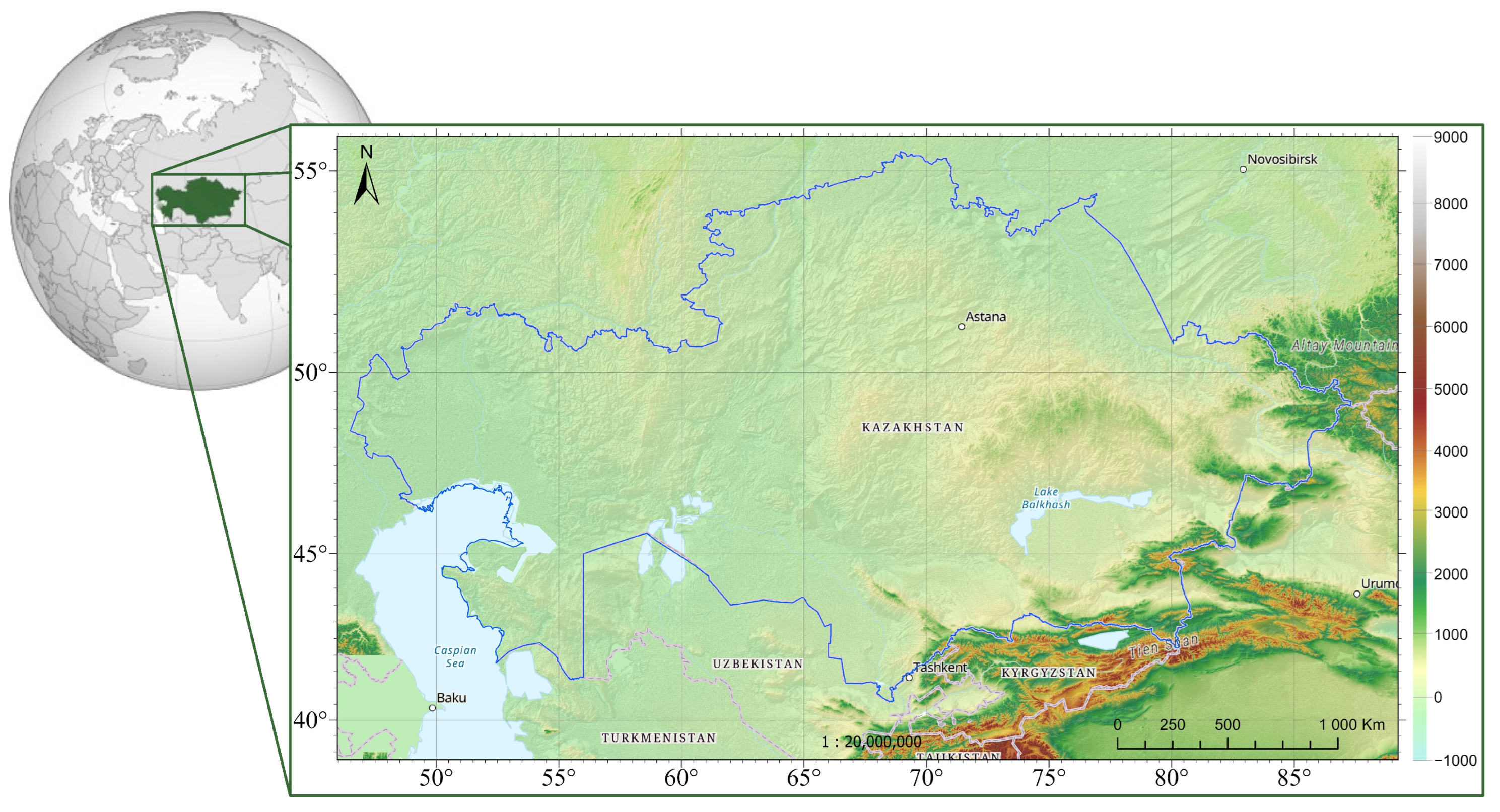
2. Study Area
3. Data Used
3.1. Historical Gravimetric Data
- –
- 1955–1969—surveys at a scale of 1:200,000 conducted with SN-3, Norgard, GAK-3M, GNU-KS, and KNU-KV gravimeters [21], with a density of 3–4 stations per 2 km2 and an isoanomaly contour interval of 1–2 mGal.
- –
- 1970–1990s—more detailed surveys at scales of 1:100,000 and 1:50,000, covering priority geological–industrial zones. In these areas, station density reached 1 per 0.25 km2, and the isoanomaly interval was 0.5–1 mGal.
- –
- About 100 first-order stations (accuracy ≈ 0.03–0.04 mGal),
- –
- A total of 750 second-order stations (≈0.06 mGal),
- –
- And 3500 third-order stations (≈0.02–0.04 mGal).
3.2. Global Geopotential Models
3.3. Modern Gravimetric Reference Frame (QazGRF)
4. Methods
4.1. Corrections to Gravimetric Surveys
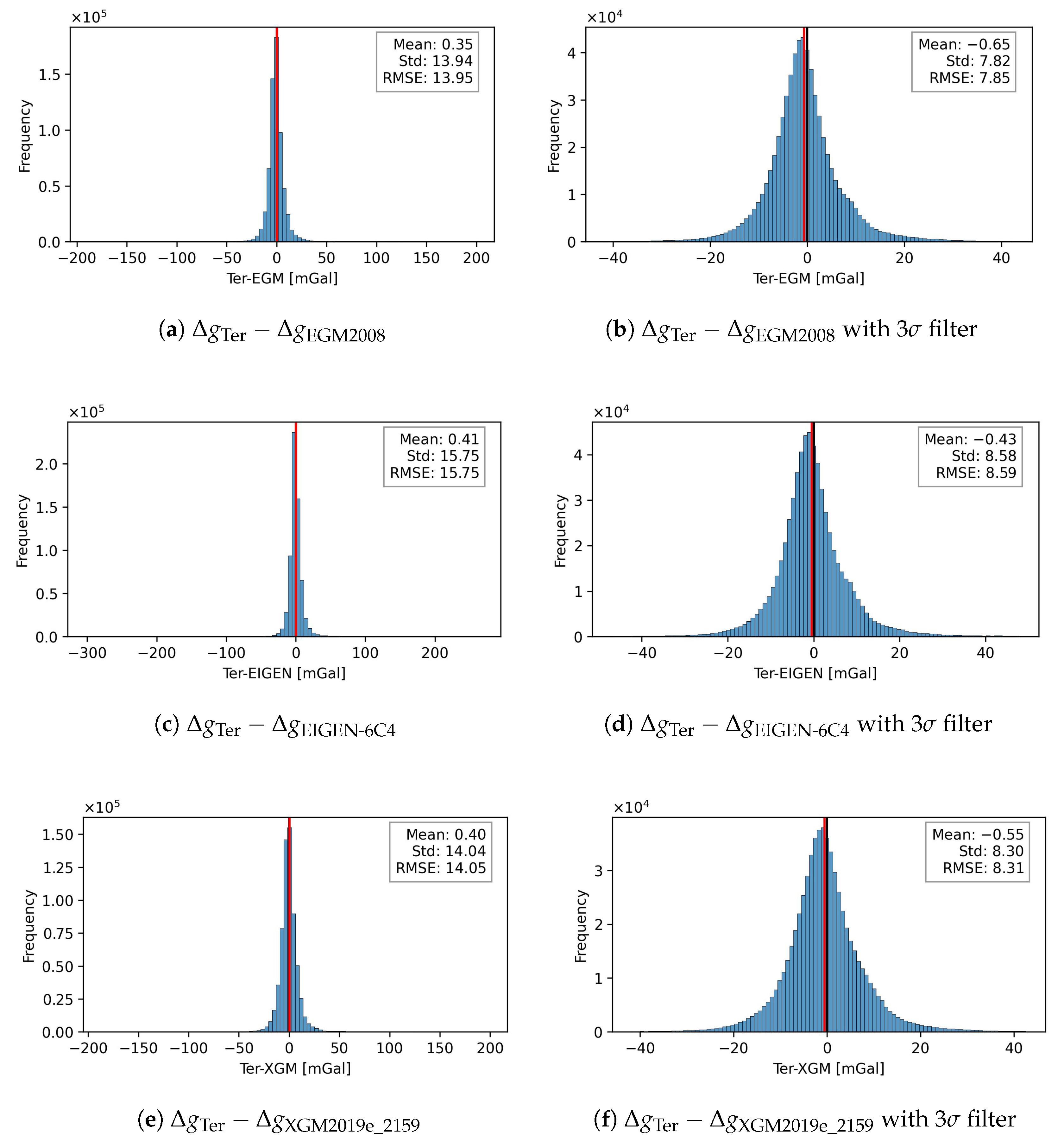
4.2. Accuracy Assessment Against Global Gravity Models
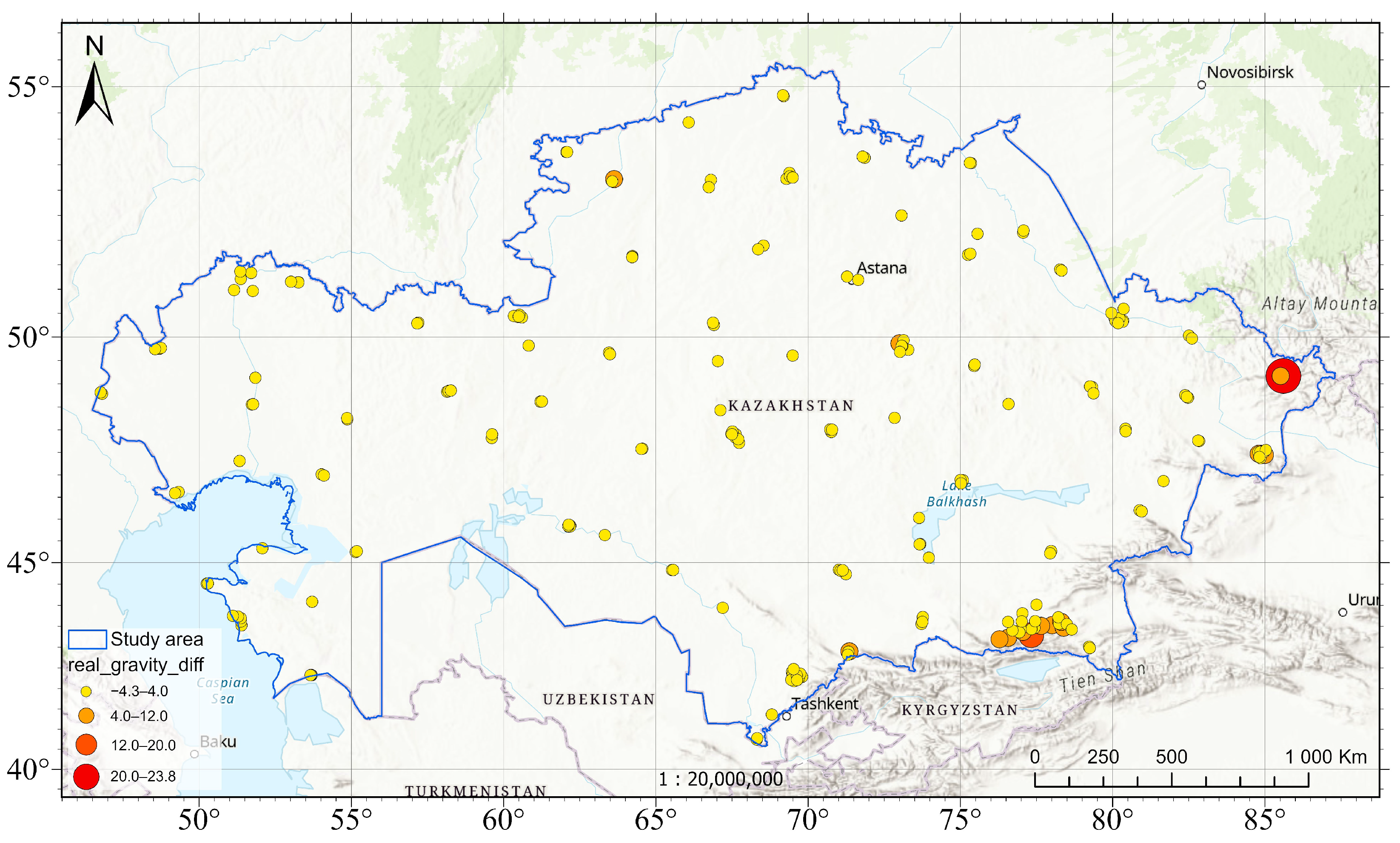
4.3. Assessment Based on Gravity Measurements
5. Results
6. Conclusions
- –
- Use Soviet gravimetric measurements in plains and foothill regions with verification against modern measurements;
- –
- Carry out priority gravimetric surveys in zones with mGal, especially in mountainous areas and at locations of identified artifacts;
- –
- Integrate the updated data into the refinement of the national geoid model and the vertical geodetic framework.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Torge, W.; Müller, J.; Pail, R. Geodesy; De Gruyter: Berlin, Germany, 2023. [Google Scholar] [CrossRef]
- Sideris, M.G. Geoid Determination, Theory and Principles. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 476–482. [Google Scholar] [CrossRef]
- Sermiagin, R.; Kemerbaev, N.; Kassymkanova, K.K.; Kalen, E.; Mussina, G.; Shkiyeva, M.K.; Samarkhanov, K.; Batalova, A.; Rakhimzhanov, A.; Zhumakanov, A.; et al. A historical overview of gravimetric surveys in Kazakhstan. Geod. Cartogr. 2024, 85, 53–64. (In Russian) [Google Scholar] [CrossRef]
- Makedonskii, E.L.; Balmino, G.; Galazin, V.F.; Kogan, M.G.; McNutt, M.K.; Fairhead, J.D. Gravity Field over the Former Soviet Union Mapped. Eos Trans. Am. Geophys. Union 1994, 75, 463–464. [Google Scholar] [CrossRef]
- Gerlach, C.; Ophaug, V.; Omang, O.C.D.; Idžanović, M. Quality and Distribution of Terrestrial Gravity Data for Precise Regional Geoid Modeling: A Generalized Setup. In IX Hotine-Marussi Symposium on Mathematical Geodesy; Novák, P., Crespi, M., Sneeuw, N., Sansò, F., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 151, pp. 209–215. [Google Scholar] [CrossRef]
- Oja, T.; Ellmann, A.; Märdla, S. Gravity Anomaly Field over Estonia. Est. J. Earth Sci. 2019, 68, 55. [Google Scholar] [CrossRef]
- Catalão, J.; Bos, M. Sensitivity Analysis of the Gravity Geoid Estimation: A Case Study on the Azores Plateau. Phys. Earth Planet. Inter. 2008, 168, 113–124. [Google Scholar] [CrossRef]
- Jekeli, C.; Yang, H.J.; Kwon, J.H. Using Gravity and Topography-Implied Anomalies to Assess Data Requirements for Precise Geoid Computation. J. Geod. 2009, 83, 1193–1202. [Google Scholar] [CrossRef]
- Jiang, T.; Dang, Y.; Zhang, C. Gravimetric Geoid Modeling from the Combination of Satellite Gravity Model, Terrestrial and Airborne Gravity Data: A Case Study in the Mountainous Area, Colorado. Earth Planets Space 2020, 72, 189. [Google Scholar] [CrossRef]
- Vergos, G.; Tziavos, I.; Andritsanos, V. Gravity Data Base Generation and Geoid Model Estimation Using Heterogeneous Data. In Gravity, Geoid and Space Missions; Jekeli, C., Bastos, L., Fernandes, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 129, pp. 155–160. [Google Scholar] [CrossRef]
- Ellmann, A.; All, T.; Oja, T. Towards Unification of Terrestrial Gravity Data Sets in Estonia. Est. J. Earth Sci. 2009, 58, 229. [Google Scholar] [CrossRef]
- Lücke, O.H.; Vega Fernández, A.; Varela Sánchez, M.; Barboza, L.A.; Garbanzo-León, J. The Improvements of the Costa Rican Ground-Based Gravity Dataset as a Result of a Comprehensive Attribute and Spatial Assessment of the Historical Databases. Appl. Geomat. 2021, 13, 401–413. [Google Scholar] [CrossRef]
- Vergos, G.S.; Natsiopoulos, D.A.; Mamagiannou, E.G.; Tzanou, E.A.; Triantafyllou, A.I.; Tziavos, I.N.; Ramnalis, D.; Polychronos, V. A Regional Gravimetric and Hybrid Geoid Model in Northern Greece from Dedicated Gravity Campaigns. Remote Sens. 2025, 17, 197. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Alexander, K.; Sideriss, M.G. Gravimetric Geoid Refinement Using High Resolution Gravity and Terrain Data. Geomat. Res. Australas. 1996, 61, 75–99. [Google Scholar]
- Farahani, H.H.; Klees, R.; Slobbe, C. Data Requirements for a 5-Mm Quasi-Geoid in the Netherlands. Stud. Geophys. Geod. 2017, 61, 675–702. [Google Scholar] [CrossRef]
- Jekeli, C. Omission Error, Data Requirements, and the Fractal Dimension of the Geoid. In VII Hotine-Marussi Symposium on Mathematical Geodesy; Sneeuw, N., Novák, P., Crespi, M., Sansò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 137, pp. 181–187. [Google Scholar] [CrossRef]
- Makarenko, N.L.; Gusev, N.A.; Lokhov, V.V. About the state gravimetric network of the USSR. Geod. Cartogr. 1990, 1–5. (In Russian) [Google Scholar]
- Gusev, N.A.; Scheglov, N.S. Reference gravity networks. In Gravimetry and Geodesy; Nauchniy Mir: Moscow, Russia, 2010; pp. 319–332. (In Russian) [Google Scholar]
- Gusev, N.A. Agat Pendulum System. In The Interdepartmental Geophysical Committee Under the Presidium of the Academy of Sciences of the USSR; Results of High-Precision Gravimetric Measurements; Soviet Radio: Moscow, Russia, 1977; pp. 57–71, (In Russian). [Google Scholar] [CrossRef]
- Demyanov, G.; Sermyagin, R.; Basmanov, A.; Oshchepkov, I.; Popadyov, V.; Pozdnyakov, A. Development of the State Gravity Network in Russia. In Proceedings of the 4th IAG Symposium on Terrestrial Gravimetry: Static and Mobile Measurements (TG-SMM 2013), Saint Petersburg, Russia, 17–20 September 2013; pp. 152–157. [Google Scholar]
- Evdokimov, Y.S.; Zemlemerov, B.M.; Vorob’ev, L.S. GOST 13017-83; Surface Gravimeters. General Specifications. Standards Publishing House: Moscow, Russia, 1985. (In Russian)
- Boikov, V.; Galazin, V.; Kaplan, B.; Maksimov, V.; Bazlov, Y.A. Experience in creating the geocentric coordinate system PZ-90. Geod. Cartogr. 1993, 54, 17–21. (In Russian). Available online: https://geocartography.ru/en/scientific_article/1993_11_17-21 (accessed on 14 October 2025).
- Shoganbekova, D.; Urazaliyev, A.; Kassymkanova, K.; Kozhakhmetov, M. Evaluation of the Effectiveness of Global Geopotential Models for the Turkestan Region. Bull. Almaty Univ. Power Eng. Telecommun. 2024, 2, 96–105. (In Russian) [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef]
- Klokočník, J.; Kostelecký, J.; Kalvoda, J.; Eppelbaum, L.; Bezek, A. Gravity disturbances, marussi tensor, invariants and other functions of the geopotential represented by EGM 2008. Earth Sci. Res. 2014, 2, 88–101. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.; Abrikosov, O.; Lemoine, J.; Schaller, T.; Götze, H.; Ebbing, J.; Marty, J.; Flechtner, F.; Balmino, G.; et al. EIGEN6C4–The Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order. 2015. Available online: https://dataservices.gfz-potsdam.de/icgem/showshort.php?id=escidoc:1119897 (accessed on 14 October 2025).
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The Combined Global Gravity Field Model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Tazhedinov, D.; Islyamova, A.; Merkulov, M. Technical Report on the Mathematical Processing (Adjustment) of the Stations of the State Fundamental Gravimetric Network. Project Code: K.04.00086; Technical Report; RSE National Centre of Geodesy and Spatial Information: Astana, Kazakhstan, 2024. (In Russian) [Google Scholar]
- Tazhedinov, D.; Islyamova, A.; Merkulov, M. Technical Report on the Results of the Mathematical Processing (Adjustment) of the Stations of the State First-Order Gravimetric Network. Project Code: K.04.00087; Technical Report; RSE National Centre of Geodesy and Spatial Information: Astana, Kazakhstan, 2024. (In Russian) [Google Scholar]
- Sermiagin, R. Dataset from Processing the 2023–2024 Campaigns to Establish Kazakhstan’s Gravity Reference Frame (QazGRF24). Zenodo 2025. [Google Scholar] [CrossRef]
- Pellinen, L. Higher Geodesy (Theoretical Geodesy); Nedra: Mosow, Russia, 1978. (In Russian) [Google Scholar]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd ed.; Springer: Vienna, Austria, 2006. [Google Scholar] [CrossRef]
- Caputo, M. Review of Formulas for the Space Normal Gravity Field Of The Earth. In Geophysical Monograph Series; Orlin, H., Ed.; American Geophysical Union: Washington, DC, USA, 2013; pp. 121–126. [Google Scholar] [CrossRef]
- Helmert, F. Der normale Theil der Schwerkraft im Meeresniveau. In Sitzungsberichte der Königlich Preussi schen Akademie der Wissenschaften zu Berlin; Reimer: Berlin, Germany, 1901; pp. 327–336. [Google Scholar]
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–133. [Google Scholar] [CrossRef]
- Ladynin, A. Potential Geophysical Fields in Geological Problems; Textbook; Novosibirsk State University: Novosibirsk, Russia, 2008. (In Russian) [Google Scholar]
- Veselov, K.; Varlamov, A.; Kastalskiy, E.; Stepanov, P. (Eds.) Gravity Survey Manual; Number 5 in Unified Technical Requirements; Nedra: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- Šlikas, D.; Paršeliūnas, E.; Birvydienė, R.; Obuchovski, R. The Countrywide Historical Gravity Dataset of Lithuanian Territory. Preprint 2025. [Google Scholar] [CrossRef]
- Honkasalo, T. On the Tidal Gravity Correction. Boll. Geofis. Teor. Appl. 1964, 4, 34–36. [Google Scholar]
- Morelli, C.; Gantar, C.; Mcconnell, R.K.; Szabo, B.; Uotila, U.A. The International Gravity Standardization Net 1971 (I.G.S.N.71); International Association of Geodesy: Paris, France, 1972. [Google Scholar]
- Šimon, Z. A Comment on Honkasalo’s Correction. Stud. Geophys. Geod. 1980, 24, 92–96. [Google Scholar] [CrossRef]
- Guidelines on the Development of the State Gravimetric Network of the USSR (Fundamental and First Order); GUGK: Moscow, Russia, 1988. (In Russian)
- Guidelines for the Development of the High-Precision State Gravimetric Network of Russia; TsNIIGAiK: Moscow, Russia, 2004; (In Russian). Available online: https://meganorm.ru/Data2/1/4293855/4293855517.pdf (accessed on 14 October 2025).
- Odumosu, J.O.; Nnam, V.C. Gravity data requirements for decimetre accuracy regional geoid using Stokes’ Remove Compute Restore technique in Nigeria. Contrib. Geophys. Geod. 2020, 50, 325–346. [Google Scholar] [CrossRef]



| Points | Mean | StD | Min | 25% | 50% | 75% | Max | RMSE | |
|---|---|---|---|---|---|---|---|---|---|
| Count | mGal | mGal | mGal | mGal | mGal | mGal | mGal | mGal | |
| Before | |||||||||
| Ter–EGM2008 | |||||||||
| Ter–EIGEN-6C4 | |||||||||
| Ter–XGM2019e_2159 | |||||||||
| EGM2008–XGM2019e_2159 | 651,862 | ||||||||
| After -filter | |||||||||
| Ter–EGM2008 | |||||||||
| Ter–EIGEN-6C4 | |||||||||
| Ter–XGM2019e_2159 | |||||||||
| Terrain | Station | Mean | StD | Min | 25% | 50% | 75% | Max | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Type | Count | mGal | mGal | mGal | mGal | mGal | mGal | mGal | mGal |
| Flat | 179 | 0.3 | 1.6 | −4.3 | −0.5 | 0.1 | 0.8 | 7.4 | 1.6 |
| Hilly | 33 | 1.2 | 2.1 | −1.8 | −0.3 | 0.7 | 2.0 | 6.1 | 2.4 |
| Mountainous | 6 | 8.6 | 8.9 | 1.0 | 1.9 | 5.6 | 12.5 | 23.8 | 11.8 |
| Overall | 218 | 0.7 | 2.5 | −4.3 | −0.5 | 0.2 | 1.1 | 23.8 | 2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoganbekova, D.; Urazaliyev, A.; Sermiagin, R.; Nurakynov, S.; Kozhakhmetov, M.; Zhaksygul, N.; Islyamova, A. Evaluation of a Soviet-Era Gravimetric Survey Using Absolute Gravity Measurements and Global Gravity Models: Toward the First National Geoid of Kazakhstan. Geosciences 2025, 15, 404. https://doi.org/10.3390/geosciences15100404
Shoganbekova D, Urazaliyev A, Sermiagin R, Nurakynov S, Kozhakhmetov M, Zhaksygul N, Islyamova A. Evaluation of a Soviet-Era Gravimetric Survey Using Absolute Gravity Measurements and Global Gravity Models: Toward the First National Geoid of Kazakhstan. Geosciences. 2025; 15(10):404. https://doi.org/10.3390/geosciences15100404
Chicago/Turabian StyleShoganbekova, Daniya, Asset Urazaliyev, Roman Sermiagin, Serik Nurakynov, Magzhan Kozhakhmetov, Nailya Zhaksygul, and Anel Islyamova. 2025. "Evaluation of a Soviet-Era Gravimetric Survey Using Absolute Gravity Measurements and Global Gravity Models: Toward the First National Geoid of Kazakhstan" Geosciences 15, no. 10: 404. https://doi.org/10.3390/geosciences15100404
APA StyleShoganbekova, D., Urazaliyev, A., Sermiagin, R., Nurakynov, S., Kozhakhmetov, M., Zhaksygul, N., & Islyamova, A. (2025). Evaluation of a Soviet-Era Gravimetric Survey Using Absolute Gravity Measurements and Global Gravity Models: Toward the First National Geoid of Kazakhstan. Geosciences, 15(10), 404. https://doi.org/10.3390/geosciences15100404






