Influence of Groundwater on the Very Shallow Geothermal Potential (vSGP) in the Area of a Large-Scale Geothermal Collector System (LSC)
Abstract
:1. Introduction
1.1. The Significance of the Very Shallow Geothermal Potential (vSGP) in the Context of the Large-Scale Geothermal Collector System (LSC) in Bad Nauheim
1.2. High Groundwater Level as an Influencing Factor on Moisture Content
1.3. Aim of This Study
2. Materials and Methods
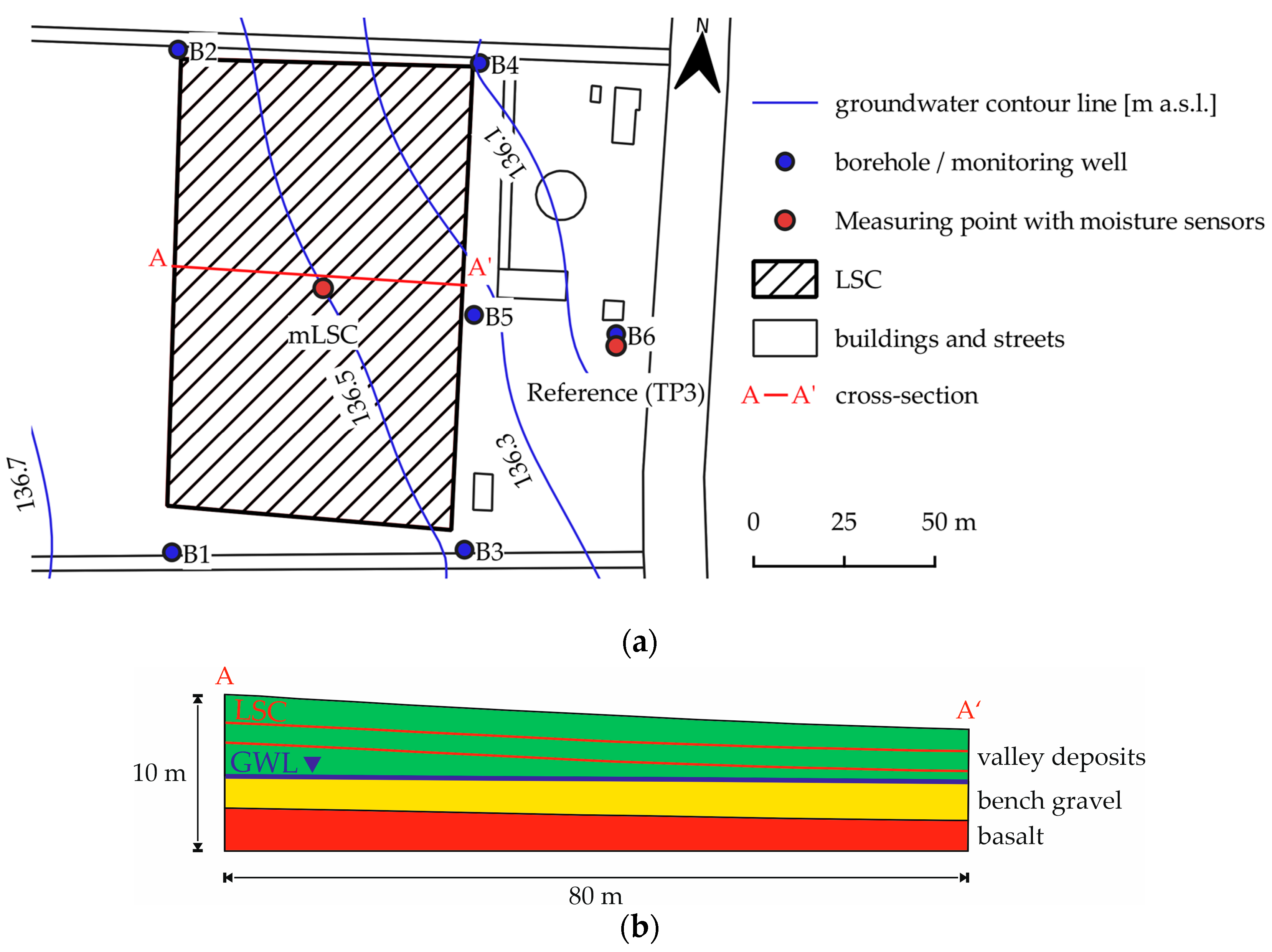
2.1. Hydrogeological Conditions at the LSC in Bad Nauheim
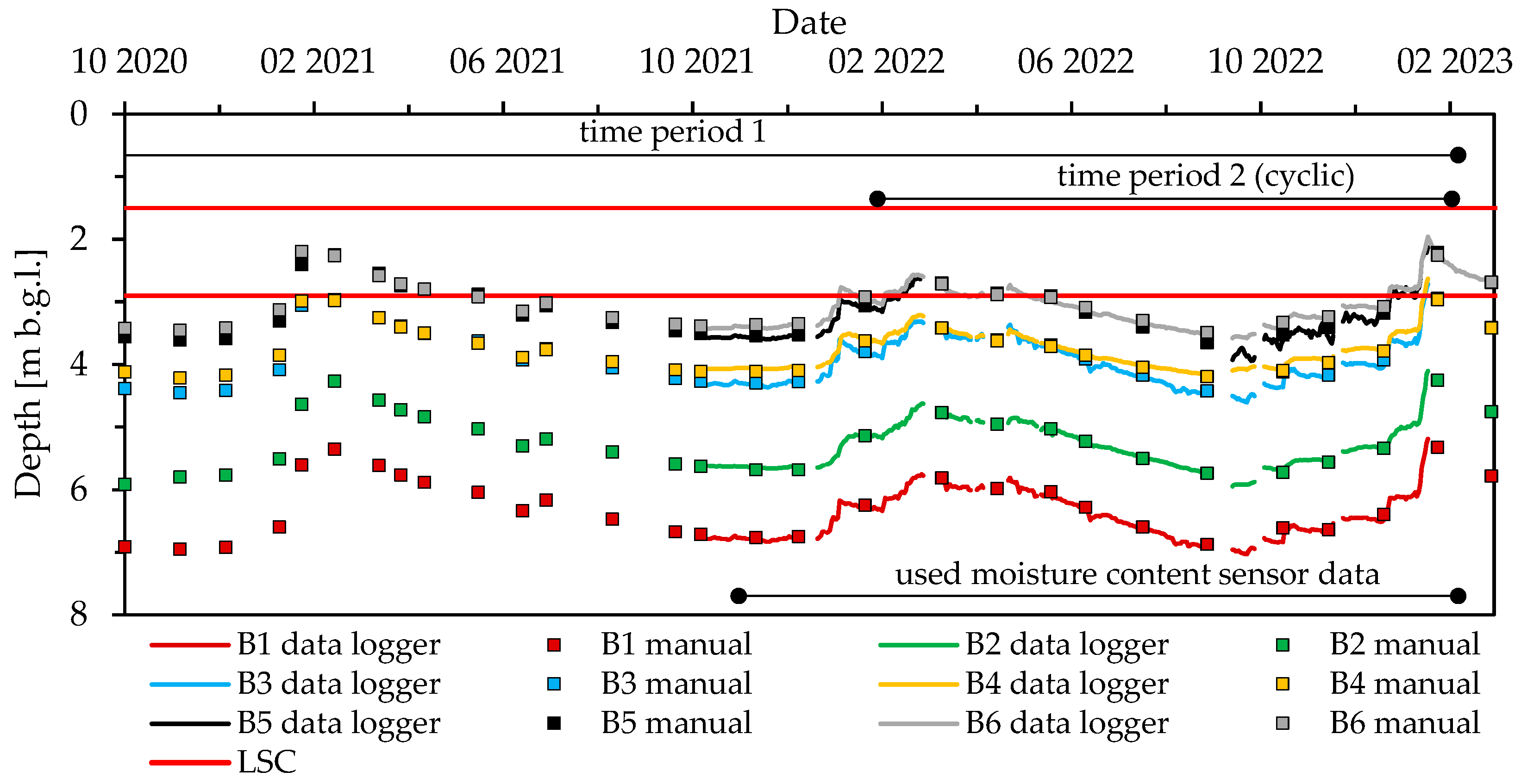
2.2. Monitoring of Moisture Content, Groundwater Table and Weather Data
2.3. Quasi-One-Dimensional Simulations with FEFLOW®
2.3.1. Material Properties and Model Layer Structure
2.3.2. Aquifer and Surface Boundary Conditions
2.4. Derivation of Thermal Conductivities from Simulated Moisture Contents and Exemplary Simulations of Heat Extraction
3. Results
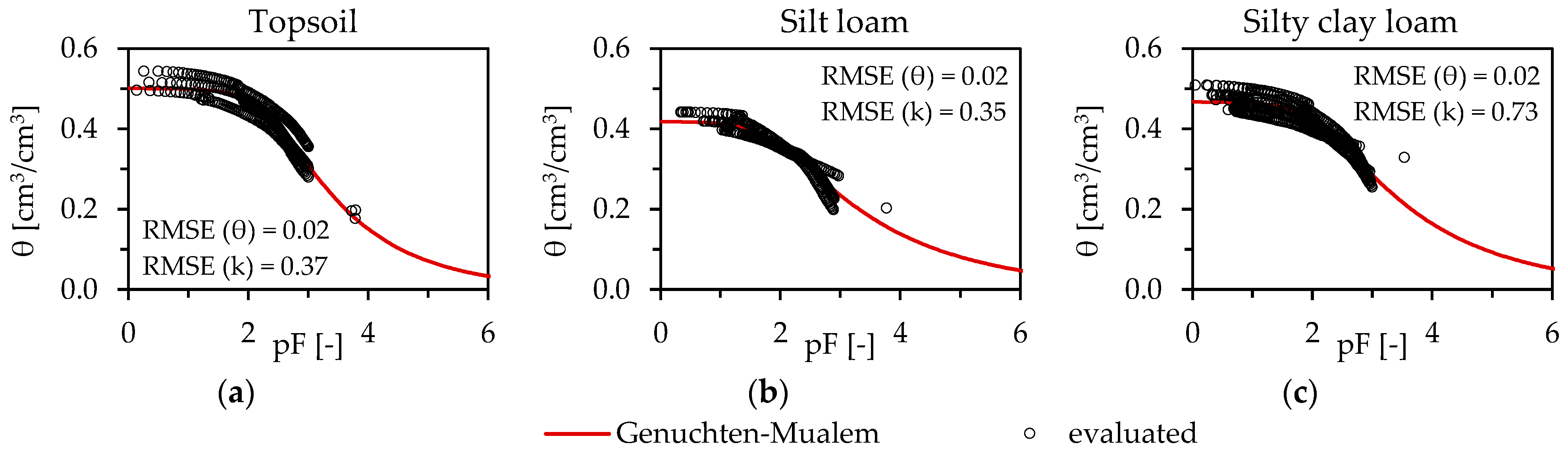
3.1. Parameter Estimation and Model Validation at “Reference” Measuring Point
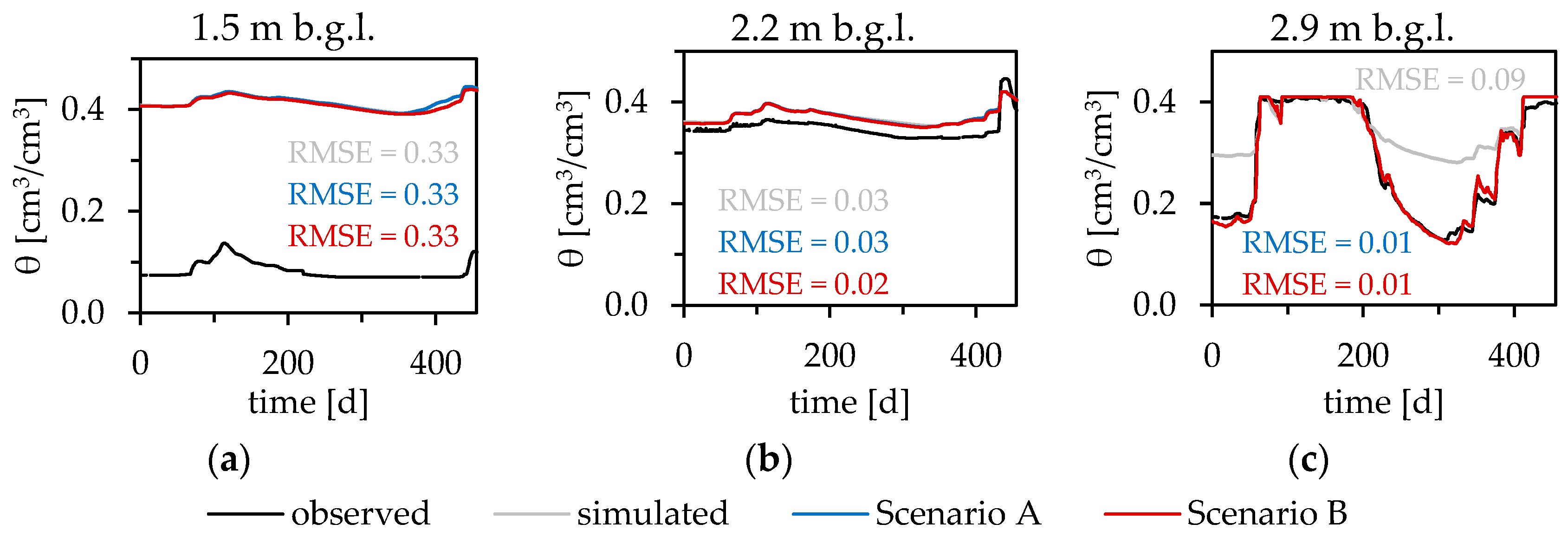
3.2. Model Validation at Measuring Point “mLSC”
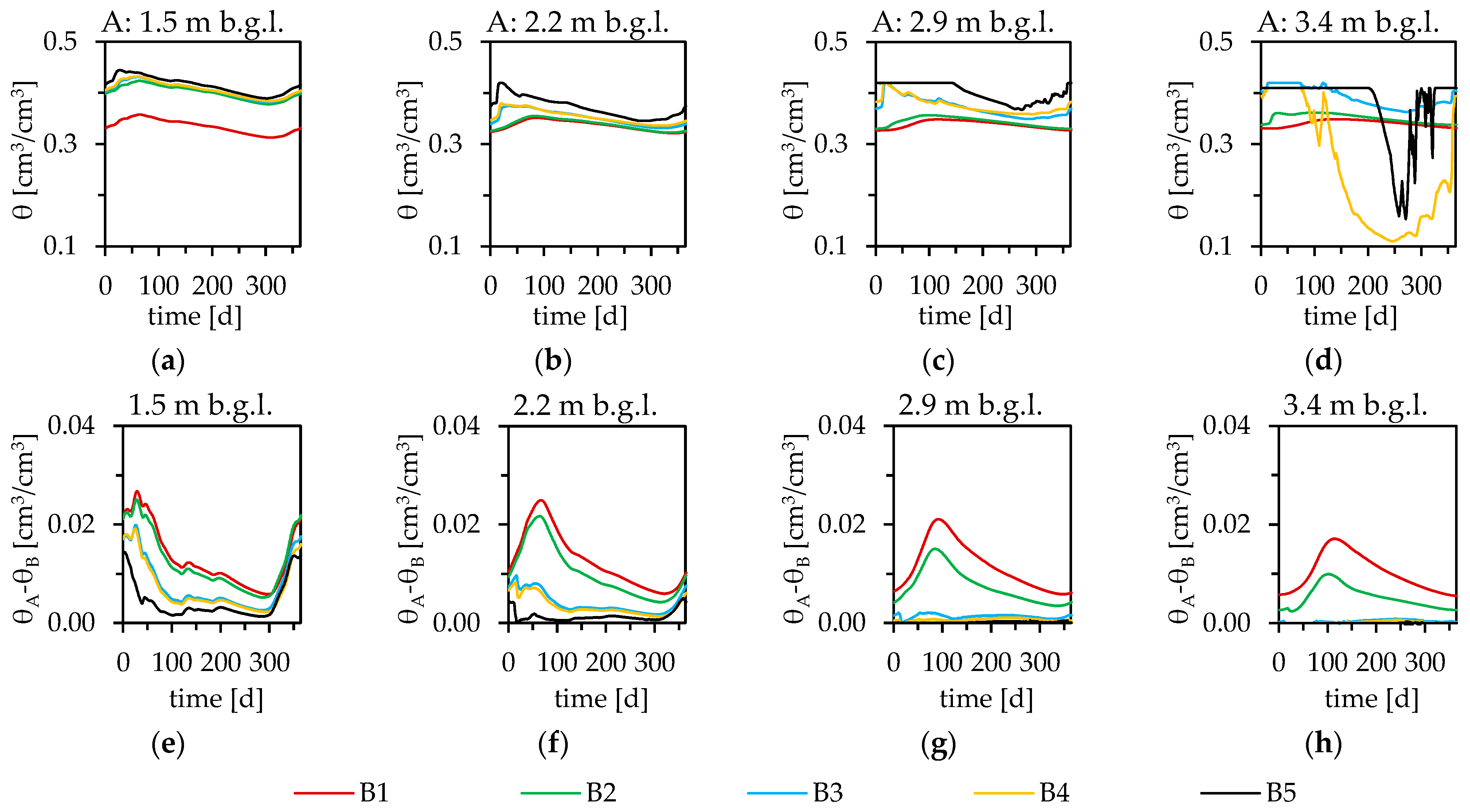
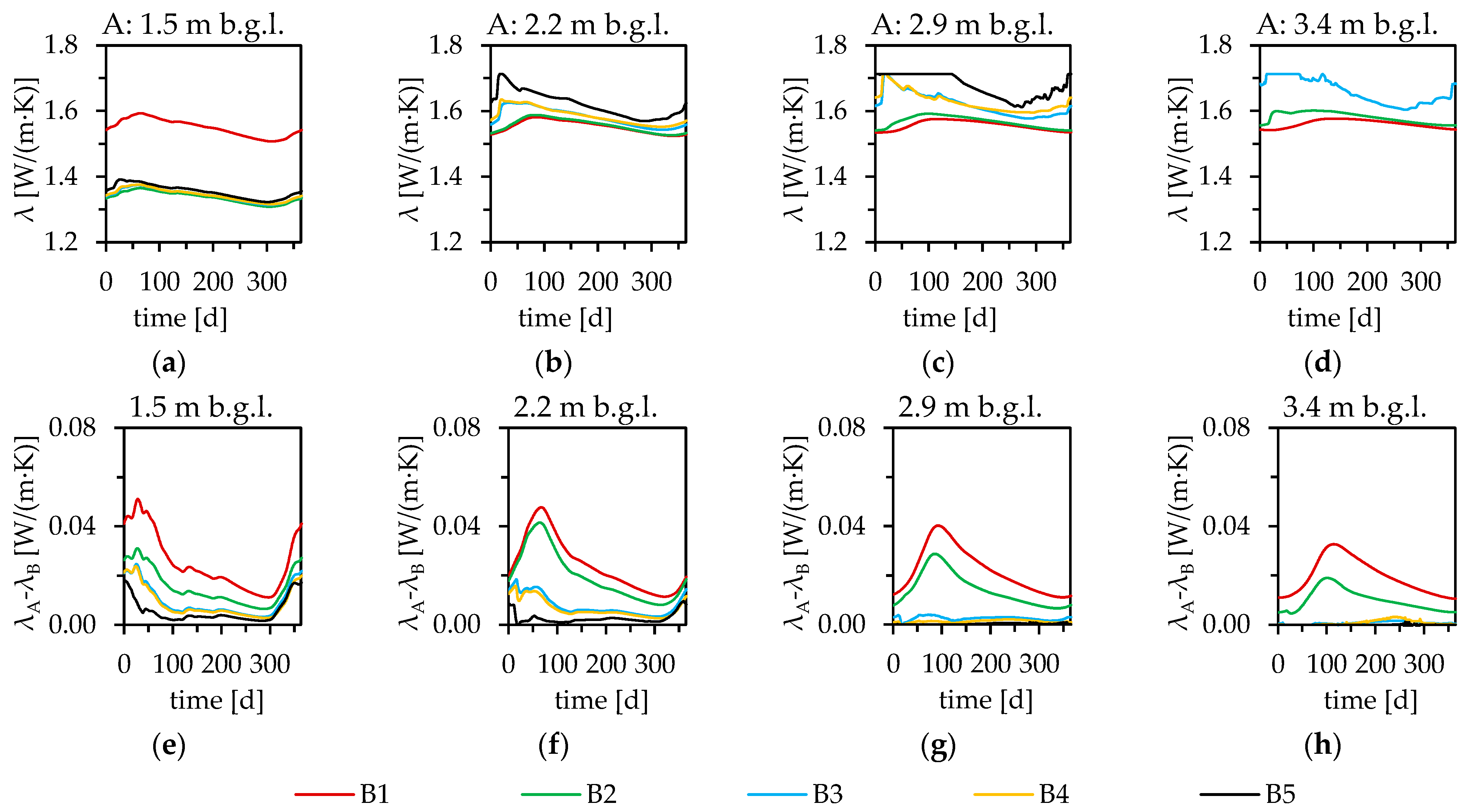
3.3. Simulated Moisture Contents with Different Groundwater Levels at Monitoring Wells B1 to B5
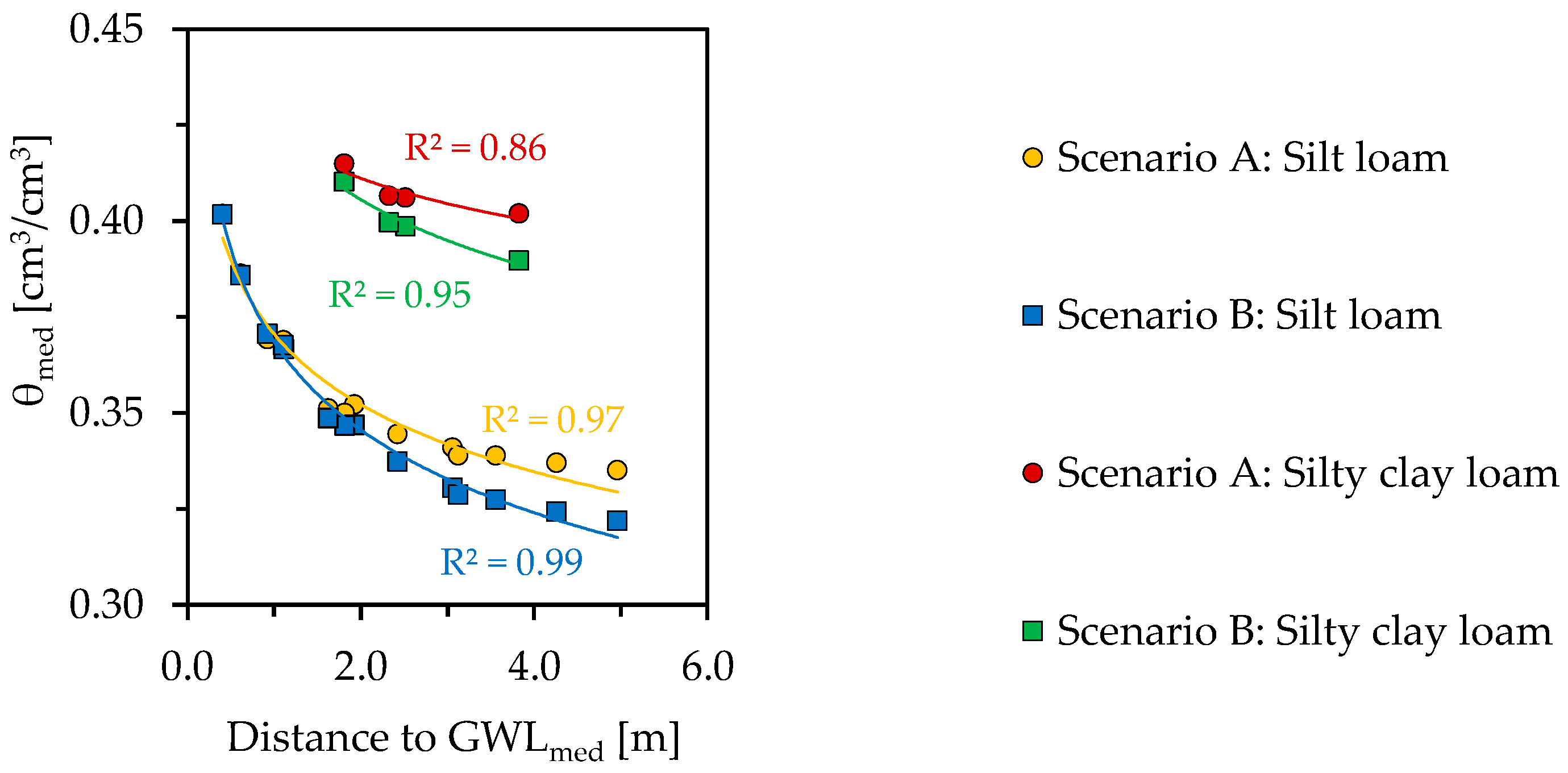
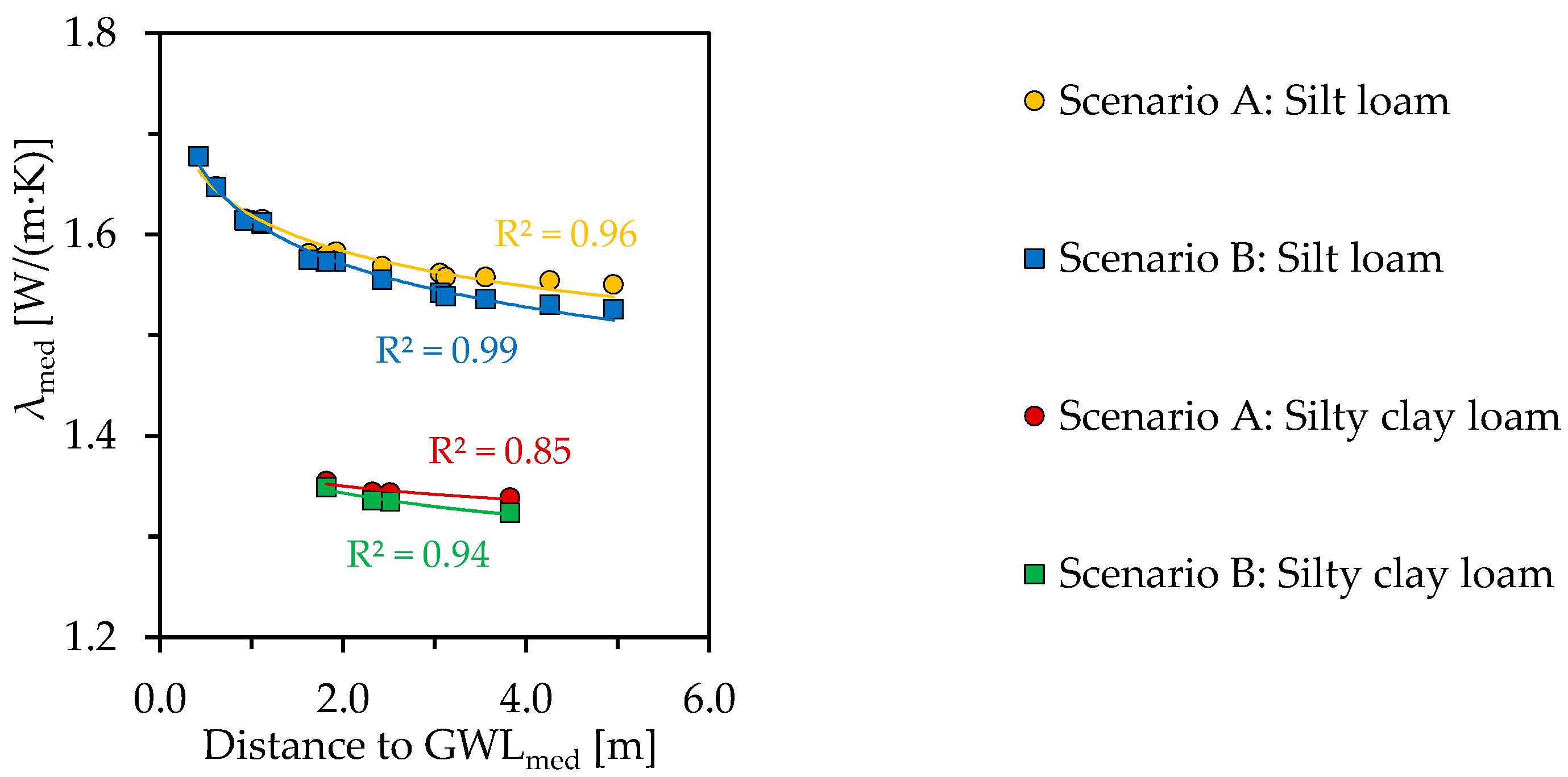
3.4. Influence of Spatial Differences in Groundwater Distance on Moisture Contents
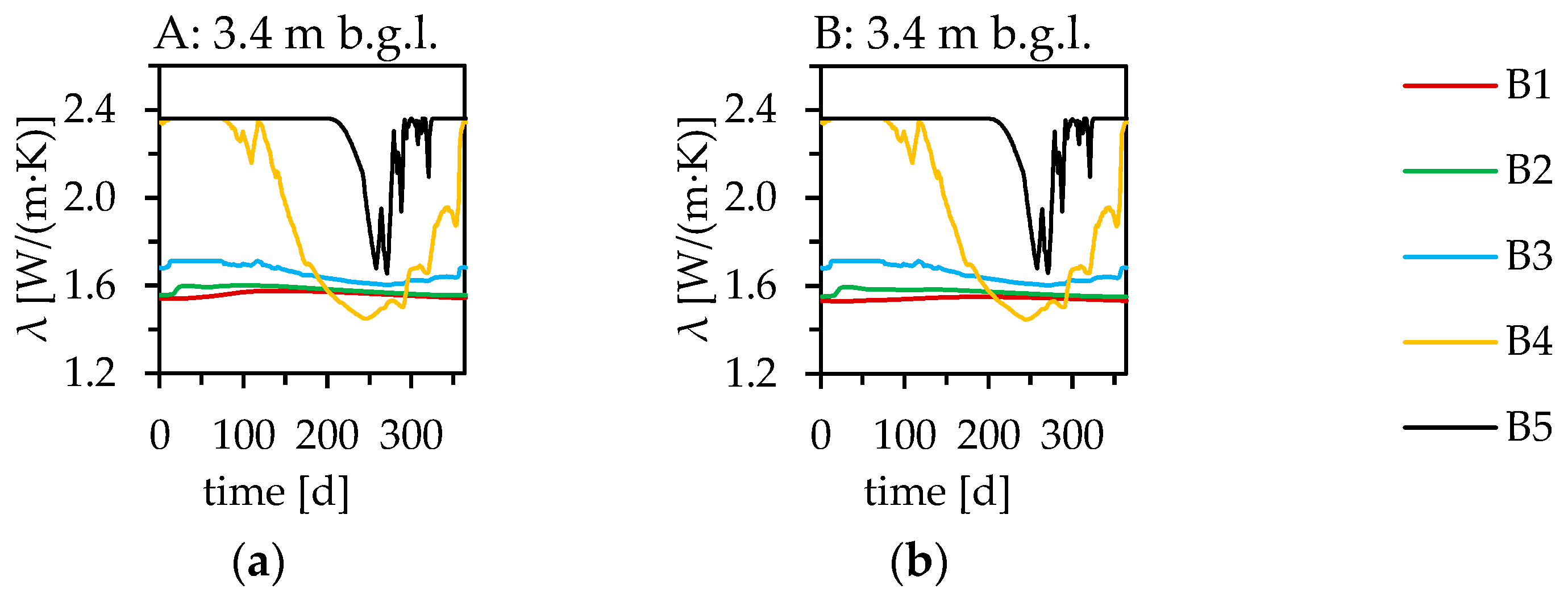
3.5. Influence of Groundwater on the Seasonal Variation in Moisture Content
4. Discussion
4.1. Derived Thermal Conductivities from Simulated Moisture Contents at Monitoring Wells B1 to B5
4.2. Influence of Spatial Differences in Groundwater Distance on the Very Shallow Geothermal Potential (vSGP)
4.3. Influence of Groundwater on the Seasonal Variation in the Very Shallow Geothermal Potential (vSGP)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Layer/Soil Texture Class | Sample Point | Depth [m b.g.l.] | Sampling | ρb_ini [g/cm3] |
|---|---|---|---|---|
| Topsoil | Distributed around the LSC | 0.0 | Repacked | 1.26 |
| 0.0 | Repacked | 1.46 | ||
| 0.0 | Repacked | 1.41 | ||
| 0.0 | Repacked | 1.45 | ||
| Silt loam | East of the LSC | 0.3 | Undisturbed | 1.60 |
| 0.3 | Undisturbed | 1.53 | ||
| 0.3 | Undisturbed | 1.64 | ||
| Silty clay loam | East of the LSC | 0.3 | Undisturbed | 1.46 |
| RCD1 | 1.1–1.5 | Repacked | 1.28 | |
| RCD2 | 1.3–1.5 | Repacked | 1.37 | |
| RCD3 + RCD4 | 1.5 | Repacked | 1.37 | |
| TP5 | 1.4 | Undisturbed | 1.43 |

References
- Zeh, R.; Ohlsen, B.; Philipp, D.; Bertermann, D.; Kotz, T.; Jocic, N.; Stockinger, V. Large-Scale Geothermal Collector Systems for 5th Generation District Heating and Cooling Networks. Sustainability 2021, 13, 6035. [Google Scholar] [CrossRef]
- Zeh, R.; Stockinger, V. Monitoring of a large-scale geothermal collector system and a 5GDHC in Bad Nauheim. In Proceedings of the Eurpean Geothermal Congress 2022, Berlin, Germany, 17–21 October 2022. [Google Scholar]
- Schwarz, H.; Jocic, N.; Bertermann, D. Development of a Calculation Concept for Mapping Specific Heat Extraction for Very Shallow Geothermal Systems. Sustainability 2022, 14, 4199. [Google Scholar] [CrossRef]
- Bertermann, D.; Klug, H.; Morper-Busch, L.; Bialas, C. Modelling vSGPs (very shallow geothermal potentials) in selected CSAs (case study areas). Energy 2014, 71, 226–244. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H. Thermal Properties of Soils as affected by Density and Water Content. Biosyst. Eng. 2003, 86, 97–102. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Reeder, R.C. Soil Thermal Conductivity Effects of Density, Moisture, Salt Concentration, and Organic Matter. Soil Sci. Soc. Am. J. 2000, 64, 1285–1290. [Google Scholar] [CrossRef]
- Farouki, O.T. Thermal Properties of Soils; Cold Regions Research and Engineering Lab: Hanover, NH, USA, 1981. [Google Scholar]
- Yun, T.S.; Santamarina, J.C. Fundamental study of thermal conduction in dry soils. Granul. Matter 2008, 10, 197–207. [Google Scholar] [CrossRef]
- Chen, X.; Hu, Q. Groundwater influences on soil moisture and surface evaporation. J. Hydrol. 2004, 297, 285–300. [Google Scholar] [CrossRef]
- Connolly, R.D. Modelling effects of soil structure on the water balance of soil–crop systems: A review. Soil Tillage Res. 1998, 48, 1–19. [Google Scholar] [CrossRef]
- Ma, L.; Hoogenboom, G.; Saseendran, S.A.; Bartling, P.N.S.; Ahuja, L.R.; Green, T.R. Effects of Estimating Soil Hydraulic Properties and Root Growth Factor on Soil Water Balance and Crop Production. Agron. J. 2009, 101, 572–583. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Y.; Yang, Y.; Wang, J. Evaluation of the Influence of Jiangxiang Reservoir Immersion on Corp and Residential Areas. Geofluids 2018, 2018, 9720970. [Google Scholar] [CrossRef]
- Wessolek, G.; Bohne, K.; Duijnisveld, W.; Trinks, S. Development of hydro-pedotransfer functions to predict capillary rise and actual evapotranspiration for grassland sites. J. Hydrol. 2011, 400, 429–437. [Google Scholar] [CrossRef]
- DIN 4220:2020-11; Pedologic Site Assessment—Designation, Classification and Deduction of Soil Parameters (Normative and Nominal Scaling). Beuth Verlag GmbH: Berlin, Germany, 2020.
- Awan, U.K.; Tischbein, B.; Martius, C. A GIS-based approach for up-scaling capillary rise from field to system level under soil–crop–groundwater mix. Irrig. Sci. 2014, 32, 449–458. [Google Scholar] [CrossRef]
- Widomski, M.; Lagod, G.; Suchorab, Z.; Pavlíková, M.; Pavlik, Z.; Záleská, M. Application of the Darcy and Richards equations for modelling of water capillary rise in building materials. J. Phys. Conf. Ser. 2021, 1736, 012042. [Google Scholar] [CrossRef]
- Smit, Y.; Donker, J.J.A.; Ruessink, G. Spatiotemporal Surface Moisture Variations on a Barred Beach and their Relationship with Groundwater Fluctuations. Hydrology 2019, 6, 8. [Google Scholar] [CrossRef]
- Danyar, S.; Yudong, S.; Jumakeld, M. Influence of groundwater level change on vegetation coverage and their spatial variation in arid regions. J. Geogr. Sci. 2004, 14, 323–329. [Google Scholar] [CrossRef]
- Pirastru, M.; Niedda, M. Evaluation of the soil water balance in an alluvial flood plain with a shallow groundwater table. Hydrol. Sci. J. 2013, 58, 898–911. [Google Scholar] [CrossRef]
- Kümmerle, E. Erläuterungen zur Geologischen Karte von Hessen 1: 25,000 Blatt Nr. 5618 Friedberg; Hessisches Landesamt für Bodenforschung: Wiesbaden, Germany, 1976; p. 247. [Google Scholar]
- Kümmerle, E. Geologische Karte von Hessen 1:25,000 5618 Friedberg; Hessisches Landesamt für Bodenforschung: Wiesbaden, Germany, 1976. [Google Scholar]
- Rammler, M.; Schwarz, H.; Wagner, J.; Bertermann, D. Comparison of Measured and Derived Thermal Conductivities in the Unsaturated Soil Zone of a Large-Scale Geothermal Collector System (LSC). Energies 2023, 16, 1195. [Google Scholar] [CrossRef]
- Scheytt, T.; Hengelhaupt, F. Auffüllversuche in der wassergesättigten und ungesättigten Zone—Ein Vergleich unterschiedlicher Verfahren. Grundwasser 2001, 6, 71–80. [Google Scholar] [CrossRef]
- DIN EN ISO 22282-5; Geotechnical Investigation and Testing—Geohydraulic Testing—Part 5: Infiltrometer Tests (ISO 22282-5:2012); German Version EN ISO 22282-5:2012. Beuth Verlag GmbH: Berlin, Germany, 2012.
- Bertermann, D.; Rammler, M. Suitability of Screened Monitoring Wells for Temperature Measurements Regarding Large-Scale Geothermal Collector Systems. Geosciences 2022, 12, 162. [Google Scholar] [CrossRef]
- DIN EN ISO 17892-4; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 4: Determination of Particle Size Distribution (ISO 17892-4:2016); German Version EN ISO 17892-4:2016. Beuth Verlag GmbH: Berlin, Germany, 2017.
- Beyer, W. Zur Bestimmung der Wasserdurchlässigkeit von Kiesen und Sanden aus der Kornverteilungskurve. WWT 1964, 14, 165–168. [Google Scholar]
- Hazen, A. Some physical properties of sands and gravels with special reverence to their use in filtration. In Massachusetts State Board of Health 24th Annual Report; Massachusetts State Board of Health: Boston, MA, USA, 1892; pp. 539–556. [Google Scholar]
- Kaubisch, M. Zur Indirekten Ermittlung Hydrogeologischer Kennwerte von Kippenkomplexen, Dargestellt am Beispiel des Braunkohlenbergbaus. Ph.D. Thesis, Bergakademie Freiberg, Freiberg, Germany, 1986. [Google Scholar]
- Seelheim, F. Methoden zur Bestimmung der Durchlässigkeit des Bodens. Z. Anal. Chem. 1880, 19, 387–418. [Google Scholar] [CrossRef]
- Diersch, H.-J.G. FEFLOW Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: Berlin/Heidelberg, Germany, 2014; p. 996. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. Calculating the Unsaturated Hydraulic Conductivity with a New Closed-Form Analytical Model; Technical report 78-WR-08; Princeton University: Princeton, NJ, USA, 1978. [Google Scholar]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Peters, A.; Durner, W. Simplified evaporation method for determining soil hydraulic properties. J. Hydrol. 2008, 356, 147–162. [Google Scholar] [CrossRef]
- Peters, A.; Iden, S.C.; Durner, W. Revisiting the simplified evaporation method: Identification of hydraulic functions considering vapor, film and corner flow. J. Hydrol. 2015, 527, 531–542. [Google Scholar] [CrossRef]
- Schindler, U. Ein Schnellverfahren zur Messung der Wasserleitfähigkeit im teilgesättigten Boden an Stechzylinderproben. Arch. Acker Pflanzenbau Bodenkd. 1980, 24, 1–7. [Google Scholar]
- KA5. Manual of Soil Mapping, 5th ed.; Bundesanstalt für Geowissenschaften und Rohstoffe: Hannover, Germany, 2005. [Google Scholar]
- Hölting, B.; Coldewey, W.G. Hydrogeology, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2019; p. 357. [Google Scholar]
- Mace, A.; Rudolph, D.L.; Kachanoski, R.G. Suitability of Parametric Models to Describe the Hydraulic Properties of an Unsaturated Coarse Sand and Gravel. Groundwater 1998, 36, 465–475. [Google Scholar] [CrossRef]
- Luckner, L.; Van Genuchten, M.T.; Nielsen, D.R. A consistent set of parametric models for the two-phase flow of immiscible fluids in the subsurface. Water Resour. Res. 1989, 25, 2187–2193. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Improved Prediction of Unsaturated Hydraulic Conductivity with the Mualem-van Genuchten Model. Soil Sci. Soc. Am. J. 2000, 64, 843–851. [Google Scholar] [CrossRef]
- Van Genuchten, M.; Nielsen, D.R. On Describing and Predicting the Hydraulic Properties of Unsaturated Soils. Ann. Geophys. 1985, 3, 615–628. [Google Scholar]
- Allen, R.; Smith, M.; Pereira, L.; Perrier, A. An update for the calculation of reference evaporation. ICID Bull. 1994, 43, 35–93. [Google Scholar]
- ATV-DVWK-M 504:2002-09; Verdunstung in Bezug zu Landnutzung, Bewuchs und Boden. Beuth Verlag GmbH: Hennef, Germany, 2002.
- Monteith, J.L. Evaporation and Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Hydrologie in Hessen, Heft 23. In Gewässerkundlicher Jahresbericht 2020; Hessisches Landesamt für Naturschutz, Umwelt und Geologie: Wiesbaden, Germany, 2021.
- Hydrologie in Hessen, Heft 24. In Gewässerkundlicher Jahresbericht 2021; Hessisches Landesamt für Naturschutz, Umwelt und Geologie: Wiesbaden, Germany, 2022.
- Kopp, B.; Baumeister, C.; Gudera, T.; Hergesell, M.; Kampf, J.; Morhard, A.; Neumann, J. Changes in soil water balance and groundwater recharge in Baden-Wurttemberg, Bavaria, Rhineland-Palatinate and Hesse from 1951 to 2015. HyWa 2018, 62, 62–67. [Google Scholar] [CrossRef]
- Thurner, F. Auswirkung Des Skelettanteils auf Die Thermische Leitfähigkeit von Böden. Master’s Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2022. [Google Scholar]
- Zhao, X.; Zhou, G.; Jiang, X. Measurement of thermal conductivity for frozen soil at temperatures close to 0 °C. Measurement 2019, 140, 504–510. [Google Scholar] [CrossRef]
- Menberg, K.; Steger, H.; Zorn, R.; Reuß, M.; Pröll, M.; Bayer, P.; Blum, P. Bestimmung der Wärmeleitfähigkeit im Untergrund durch Labor- und Feldversuche und anhand theoretischer Modelle. Grundwasser 2013, 18, 103–116. [Google Scholar] [CrossRef]
- Huber, H.; Arslan, U.; Sass, I. Zum Einfluss der Filtergeschwindigkeit des Grundwassers auf die effektive Wärmeleitfähigkeit. Grundwasser 2014, 19, 173–179. [Google Scholar] [CrossRef]



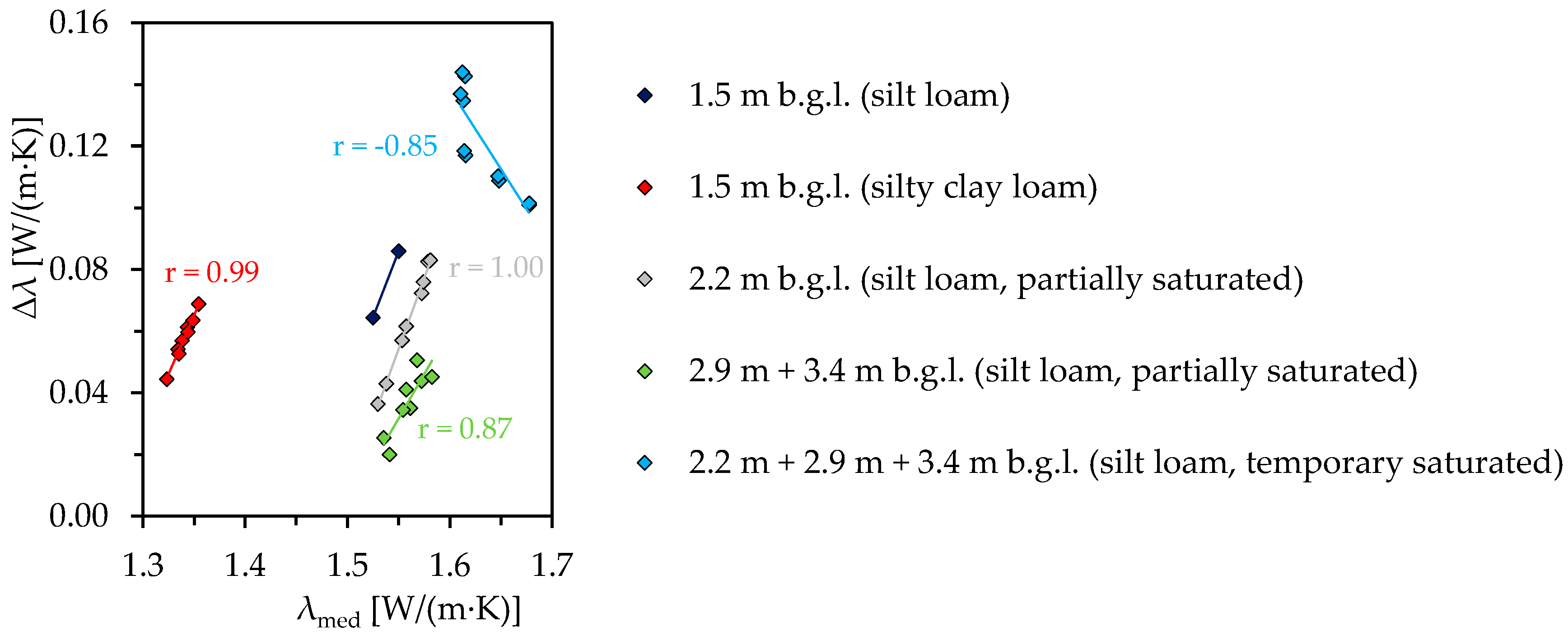
| Domain | Parameter | Sensor | Accuracy | Range |
|---|---|---|---|---|
| Soil | Moisture content | HD3910.1 (DeltaOHM) | ±3% | 0% to 100% |
| Temperature | four-wire Pt1000 (GTF 101 P-OKH) | ±0.4% of the measured value | −25 °C to +70 °C | |
| Groundwater | Temperature | P-Sense320 | ±0.2 °C | 0 °C to 70 °C |
| GWL | ±0.5% | 0 to 1 bar |
| Layer | Reference | mLSC 1 | B1 | B2 | B3 | B4 | B5 |
|---|---|---|---|---|---|---|---|
| Topsoil | 0.20 | 0.30 | 0.25 | 0.40 | 0.35 | 0.25 | 0.25 |
| Silt loam | 1.00 | 0.90 | 0.80 | 0.80 | 0.75 | 1.25 | 0.80 |
| Silty clay loam | 1.80 | 1.65 | 1.30 | 1.60 | 1.80 | 1.85 | 1.85 |
| Silt loam | 2.80 | 4.50 | 6.40 | 4.60 | 4.10 | 3.00 | 3.30 |
| Loam/gravel | 3.20 | 5.25 | 7.00 | 5.70 | 4.80 | 4.40 | 3.60 |
| Gravel | 5.50 | 7.40 | 8.50 | 7.30 | 6.20 | 7.80 | 5.80 |
| Layer | k0 [m/d] | Porosity 1 | Ss 1 | Sr | α [1/m] | n |
|---|---|---|---|---|---|---|
| Topsoil | 0.020 | 0.50 | 1.00 | 0.00 | 0.385 | 1.328 |
| Silt loam | 0.080 | 0.42 | 1.00 | 0.00 | 1.160 | 1.232 |
| Silty clay loam | 0.031 | 0.47 | 1.00 | 0.00 | 0.684 | 1.248 |
| Loam/gravel | 0.625 2 | 0.41 3 | 1.00 | 0.00 4 | 7.010 2 | 1.246 2 |
| Gravel | 43.200 5 | 0.30 6 | 1.00 | 0.00 4 | 24.400 7 | 2.494 7 |
| Scenario | Precipitation Rate [mm/a] | Evapotranspiration Rate [mm/a] | Surface Runoff Rate [mm/a] | Groundwater Recharge Rate [mm/a] |
|---|---|---|---|---|
| A | 569 | 339 | 114 | 116 |
| B | 569 | 339 | 171 | 59 |
| Depth [m b.g.l.] | Layer | ρb [g/cm3] | Calculation Equation |
| 1.5 | Silty clay loam | 1.28 | λ = 1.24∙θ + 0.84 |
| 1.5–3.4 | Silt loam | 1.49 | λ = 1.91∙θ + 0.91 |
| 3.4 | Loam/gravel | 1.81 | λ = −1.13∙S2 + 2.68∙S + 0.81 |
| Layer | k0 [m/d] | Porosity | Ss | Sr | α [1/m] | n |
|---|---|---|---|---|---|---|
| Loam/gravel | 1.366 | 0.41 | 1.00 | 0.00 | 4.000 | 2.189 |
| Influence Factor | Expressed by | Δmax (θ) [cm3/cm3] | Δmax (λ) [W/(m∙K)] |
|---|---|---|---|
| Groundwater | Spatial difference at the same depth for the same fine-grained soil texture class | 0.07 | 0.14 |
| Annual variation in fine-grained soils | 0.08 | 0.14 | |
| Annual variation in loam/gravel layer at 3.4 m b.g.l. | 0.30 | 0.92 | |
| Soil texture | Difference between silt loam and silty clay loam at 1.5 m b.g.l. | 0.09 | 0.21 |
| Difference between silt loam and loam/gravel layer at 3.4 m b.g.l. | 0.17 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rammler, M.; Zeh, R.; Bertermann, D. Influence of Groundwater on the Very Shallow Geothermal Potential (vSGP) in the Area of a Large-Scale Geothermal Collector System (LSC). Geosciences 2023, 13, 251. https://doi.org/10.3390/geosciences13080251
Rammler M, Zeh R, Bertermann D. Influence of Groundwater on the Very Shallow Geothermal Potential (vSGP) in the Area of a Large-Scale Geothermal Collector System (LSC). Geosciences. 2023; 13(8):251. https://doi.org/10.3390/geosciences13080251
Chicago/Turabian StyleRammler, Mario, Robin Zeh, and David Bertermann. 2023. "Influence of Groundwater on the Very Shallow Geothermal Potential (vSGP) in the Area of a Large-Scale Geothermal Collector System (LSC)" Geosciences 13, no. 8: 251. https://doi.org/10.3390/geosciences13080251
APA StyleRammler, M., Zeh, R., & Bertermann, D. (2023). Influence of Groundwater on the Very Shallow Geothermal Potential (vSGP) in the Area of a Large-Scale Geothermal Collector System (LSC). Geosciences, 13(8), 251. https://doi.org/10.3390/geosciences13080251








