Geophysical Subsoil Characterization and Modeling Using Cluster Analysis for Seismic Microzonation Purposes

Abstract

In the municipality of Enna, 80 HVSR measurements were performed, and some of these were combined with MASW seismic measurements, which made it possible to constrain the data inversion and obtain significant shear wave velocity models. A reconstruction of the depth of the seismic bedrock was performed for the whole territory, showing different depths for the higher and lower areas, as evidenced also by the Vseq parameter map. The frequency peaks identified in the H/V curve were analyzed through a cluster analysis algorithm to evaluate similarities that allow these peaks to be divided according to their stratigraphic origin. A non-hierarchical analysis algorithm modified in such a way as to avoid any a priori choice that could influence the partition has been used. The cluster analysis made it possible to divide the frequency peaks into five groupings, each of which was then associated with a seismic discontinuity, according to the geological contacts expected in the subsoil. Finally, the inversion of the data made it possible to reconstruct the geometries of these geological contact surfaces and to reconstruct a 3D model of the subsoil, which agrees well with the surface geology of the area.

1. Introduction

In recent years, the horizontal-to-vertical spectral ratio (HVSR) technique applied to microtremors has acquired increasing importance for the evaluation of the seismic characteristics of a site because the HVSR can aid in identifying areas with similar seismic responses. Theoretical considerations [1] and experimental tests showed that the amplification of horizontal motions between the bottom and the top of a sedimentary cover is related to the ratio between the spectra of the horizontal and vertical components of the ground velocity [1,2]. This ratio is a measure of the ellipticity of Rayleigh wave polarization, overlooking the contribution of Love and body waves. Assuming that subsoil can be represented as a stack of homogeneous horizontal layers and imposing some geometric and/or physical constraints, it is possible to estimate the parameters of the shear wave velocity model [3,4]. Furthermore, the HVSR made it possible, in many cases, to reconstruct the top of the seismic bedrock [5,6]. The integration of data related to the HVSR and active techniques based on the analysis of surface waves can greatly reduce the uncertainties in the interpretation models.

In evaluating the resonance frequencies of the ground, a peak in the HVSR curve is not necessarily related to stratigraphic sources and therefore to a resonant frequency of buried structures. It could depend on the characteristics of the noise sources or complex phenomena of interference and focusing of P and S waves. Cluster analysis constitutes an important contribution to the attempt to identify and group peaks of HVSR curves relating to the same stratigraphic sources, topographical, anthropic or of any other nature. The hypothesis on the knowledge of the sources of the HVSR peaks is fundamental information for data inversion and correct modeling of the subsoil.

Cluster analysis [7] is a statistical procedure that can be used in the exploratory phase of a survey or when there are no a priori hypotheses. This analysis is widely used in different research fields [8,9], being a good tool when there is the need to classify a large amount of information into meaningful and manageable groups. In fact, it allows us to identify within a set of objects of any nature some subsets, called “clusters”, which are mutually exclusive and similar. The dataset is divided into groups according to the level of similarity of data, evaluated starting from the values of a series of pre-selected variables for each cluster. Before proceeding with the analysis, it is very important to know the strengths and weaknesses of the different clustering techniques, hierarchical and non-hierarchical, and to explore the reasons for their analytical differences. Generally, methods that are unconstrained by small variations in the data are preferred, particularly if the clusters are thought to be rather homogeneous. In this case, non-hierarchical analysis techniques are preferred.

Cluster analysis can therefore prove to be very useful both in the statistical processing of the HVSR curves in order to extract stratigraphically interpretable curves [10] and in the interpretation of stratigraphic peaks with one-dimensional modeling.

Because the inversion of HVSR curves implies monodimensional distribution of Vs, before the inversion, the cluster analysis can be applied to the spatial distribution of all the HVSR stratigraphic peaks to group those probably due to the same stratigraphic interface [11,12,13] to define the seismic layers, each characterized by a specific shear wave velocity range. The data of each cluster can be interpreted by imposing conditions of maximum similarity between the 1D models relating to each measurement point. Furthermore, the uncertainty of the solution of the inverse problem in the HVSR can be reduced by using data from other geophysical methods as a priori constraints [14,15,16,17,18,19,20]. In particular, the surveys performed with the Multichannel Analysis of Surface Waves (MASW) method can be utilized to obtain one-dimensional shear wave velocity models that can be used as initial models for the inversion of the HVSR curves [11,21,22,23,24].

The depths of the seismic layers obtained by inverting the HVSR curves, when referring to the same cluster, can then be interpolated to reconstruct the three-dimensional trend of the seismic interface.

This work presents an application of cluster analysis on a dataset of 80 HVSR curves, aimed at the reconstruction of stratigraphic surfaces in the subsoil of Enna (Italy) (Figure 1). Microtremor data processing had previously been performed to extract stratigraphically interpretable curves using a clustering method proposed by [10]. From then, a dataset of HVSR peaks was obtained and analyzed with a non-hierarchical cluster analysis algorithm [6] to subdivide the peaks into clusters, each referring to a specific stratigraphic surface.

The data were inverted by constraining them with 40 MASW models and imposing conditions of maximum similarity for the HVSR inverse models belonging to the same cluster to subsequently be able to reconstruct the three-dimensional trend of the stratigraphic surfaces.

2. Geological Setting of the Studied Area

The study area is located in the central-southern sector of Sicily and is part of the Caltanissetta Basin, a vast structural depression characterized by large syn-tectonic sedimentation from the Upper Tortonian to the Plio-Quaternary. This basin was the ancient foredeep basin of the Apennine-Maghrebi chain (Late Miocene) and is currently part of the chain since it was incorporated into the accretionary prism [25].

In particular, the formations outcropping in the study area (Figure 2), starting from the bottom upwards, are made up of clayey marls of the Terravecchia Formation (Lower Tortonian–Lower Messinian) with maximum thicknesses of about 300–400 m. The gypsum–sulphiferous group follows (Lower Messinian–Upper Messinian) made up of diatomites of the Tripoli Formation (maximum thickness 30 m), the base limestones (about 50 m), the selenitic gypsums (about 50 m), the Cattolica Formation composed of rock salt with intercalation of kaolinite (about 500 m) and the Pasquasia formation (marls and clayey marls less than 100 m thick).

Following upwards is the Trubi, consisting of an alternation of calcareous marls and white marly limestones (maximum thickness of about 100 m). The Enna Formation is found here, characterized by marl and clayey marl (ENNa lower member), which gradually pass upwards to the sands and calcarenites of Capodarso (ENNb upper member). The thickness is about 250 m (Piacenziano).

Finally, there are lacustrine and alluvial Quaternary deposits.

3. Materials and Methods

3.1. HVSR Method

The horizontal-to-vertical spectral ratio (HVSR) technique [1,2], applied to ambient seismic noise, is a method widely used to estimate the resonance frequencies of geological structures and is today one of the most applied methods for expedite microzonation studies of large urban areas [26,27].

A large number of surveys based on this technique were carried out to study site effects in sedimentary basins, near faults or cavities or to estimate the resonance frequency of buildings [28,29,30].

The reliability of the HVSR technique shows some criticalities linked to some assumptions, generally not easily verifiable experimentally, related to the elastic properties of the subsoil, the composition of the microtremor in terms of superposition of surface or body waves and the space–time distribution of the sources.

For example, if the shape of the HVSR curves is mainly controlled by the S-wave transfer function of the shallowest sedimentary layers [1,2,4,31], then both the frequencies and amplitudes of the HVSR curve relative maxima are directly related to subsoil resonance frequencies and site amplification factors. On the other hand, if the shape of the HVSR curves is controlled by the ellipticity of the fundamental mode of Rayleigh wave polarization [32,33,34], then only an indirect correlation between HVSR curve peaks and site amplification may be supposed.

To obtain reliable and geologically interpretable HVSR curves, it is necessary to adopt robust criteria for a correct seismic noise recording and for the choice and analysis of an optimal set of analysis time windows [35]. There are several hypotheses on the choice of these criteria.

Strong transient noise generally depends on nearby sources and therefore should be removed, keeping only the low amplitude part of the recording, for a correct estimation of resonant frequencies [35,36].

The windows selection can be made in both time and frequency domain. In the time domain, windows are selected by visual inspection, while in the frequency domain the spectral ratio is calculated for each time window, and subsequently those HVSR curves which do not deviate too much from the average are selected.

In order to invert the HVSR curves, it is assumed that the subsoil has viscoelastic properties and is horizontally stratified. Furthermore, environmental noise is considered to be composed of the superposition of Rayleigh and Love waves generated by a random distribution of independent sources [3,16,37,38]. The inversion of the HVSR curves can be utilized to obtain 1D layered seismic velocity models. However, to limit the uncertainty, it must be constrained with a priori data achieved from active seismic methods, such as the MASW method [18,23,39,40]. The MASW data, if acquired from multi-station records, can be used to derive the ellipticity of the fundamental mode of Rayleigh waves [41,42] even if the typical frequencies of the sources used, generally higher than those of the microtremor, allow depths of minor investigation.

3.2. MASW Method

The Multichannel Spectral Analysis of Surface Waves (MASW) method [43] is an active investigation technique, based on the analysis of the geometric dispersion of surface waves, that allows the shear wave velocity in the subsoil to be estimated. Surface wave dispersion occurs when the elastic wave velocity varies with depth and, consequently, the spectral components of a surface wave assume different velocities depending on frequency. In the MASW method, an artificial seismic source, usually a sledgehammer, generates a wave front, which is recorded by a linear array of equally spaced geophones placed on the surface. The seismic traces are analyzed in the frequency and wave number domain, obtaining a spectral graph of the oscillation amplitude as a function of phase velocity and frequency. From this, depending on the orientation of the source and the geophones, it is possible to obtain the dispersion curves of the fundamental and higher modes of the Rayleigh and Love waves. The dispersion curves are inverted to achieve stratified one-dimensional models of the shear wave velocities down to investigation depths, which, depending on the analyzed frequency range, generally do not exceed 30 m.

The shear wave velocity models obtained by inverting the MASW data can be used to constrain the topmost part of the inverted HVSR models to ensure their interpretive robustness [23,40].

3.3. The Cluster Analysis

The cluster analysis is the procedure that can identify within a set of objects some subsets, called clusters, that tend to be homogeneous according to some criteria. The statistical units are divided into a number of groups according to their level of similarity (internal cohesion), evaluated from the values that a number of variables chosen takes in each unit. Generally, in the cluster analysis, it is not necessary to have in mind any interpretative model [44]. The partition is successful if the objects within the clusters are closer to each other than other in different clusters [45].

Many clustering algorithms exist [46,47] and can be categorized into two main types: hierarchical clustering (hc) and non-hierarchical clustering (NHC). The HC methods are explorative and are not necessary for defining a priori the number of clusters. The HC methods work with a measure of proximity between the objects to be grouped together. A type of proximity can be chosen which is suited to the subject studied and the nature of the data. One of the results of HC methods is the dendrogram, which shows the progressive grouping of the data. It is then easy to gain an idea of a suitable number of classes into which the data can be grouped.

NHC methods do not have a tree structure and generate new clusters by merging or dividing previous clusters, grouping data in order to maximize or minimize some evaluation criteria. The elements that most influence the results of the cluster analysis are the shape, size and number of clusters; the presence of outliers; the level of overlap between clusters and the type of similarity/dissimilarity measure chosen.

To evaluate the differences between the various clustering techniques, which can also produce results significantly different from each other, the best way is to assess how the different techniques reproduce the structure of known data. These assessments are typically performed on simulated data and are often difficult to interpret and may be contradictory.

Various studies [48,49] suggest that different grouping strategies often lead to not dissimilar results, while others highlight specific cases of strong divergence [44,47]. However, the criteria for choosing between the two types of algorithms (hierarchical and non-hierarchical) have not yet been sufficiently explored, and very different positions can be found in the literature.

Cluster Analysis of HVSR Data

Windows selection for the average HVSR curve estimation is generally performed through visual inspection of the HVSR curves as a function of time. Often it is very difficult to identify the correct time window to be used for the calculation of the mean HVSR. The lack of a not arbitrary selection criteria makes the result clearly operator-dependent and therefore not optimal. To overcome this problem, an agglomerative hierarchical clustering (AHC) algorithm can be used to extract frequency and amplitude of HVSR curves determined in sliding time windows [10].

After identifying the HVSR peaks attributable to site effects, the identification of areas with similar behavior in a seismic perspective involves the simultaneous evaluation of several parameters such as frequency and amplitude of peaks, positions and mutual distances between the measuring points. The task becomes particularly difficult when different peaks on single HVSR curves are identified.

In this regard, we used a procedure proposed by [6], which is based on a centroid-based NHC algorithm. NHC methods are limited by the need to choose a priori the number of clusters. However, the method used here does not fix the number of k clusters, but it chooses automatically for each k value tested the initial centroids from dataset. The parameters considered for the determination of the clusters are the coordinates, the peak frequency and amplitude, and the outcropping lithology at the measurement point. This latter is converted into numerical information by assigning the average density of the corresponding lithology, directly related to the seismic behavior.

The Euclidean normalized distance of each unit from the initial cluster centroid and those obtained after each iteration is calculated as the weighted sum of the distances of all the variables considered.

The choice of the optimal number of clusters and weights is made by testing different values of the number of clusters k and by analyzing for each the trend of the deviance within each cluster and between clusters [6,13].

3.4. Application to the Enna Territory

From October 2014 to February 2015, we performed a passive seismic campaign to determine the resonance frequency of the subsoil, as part of the seismic microzoning studies for the Municipality of Enna (Italy). In this regard, 80 measurement stations distributed throughout the Enna area were chosen (Figure 1). An HVSR analysis was carried out for each measuring station and MASW surveys were carried out at half of these points, aimed at the seismic characterization of the soil and at constraining the inversions of the HVSR curves.

3.4.1. Dataset Acquisition and Elaboration

MASW surveys were performed at half (40) of the 80 HVSR measurement stations. The MASW data were used to obtain an estimate of the shear wave velocities in the surface layers, necessary for a constrained inversion of the HVSR data. The seismic traces had a sampling interval of 256 μs and a recording time of 1024 ms.

For each survey, 24 vertical 4.5 Hz geophones were placed with spacing of 2 m, to investigate the vertical component of Rayleigh waves (ZVF). The source was a 5 kg sledgehammer. Shots were generated at offsets of 2, 4 and 7 m for both sides of the array. Of these shot records, the ones which showed a better signal-to-noise ratio were used for the inversion and interpretation. A stacking process on five shots was set out on all the recordings to increase the signal/noise ratio.

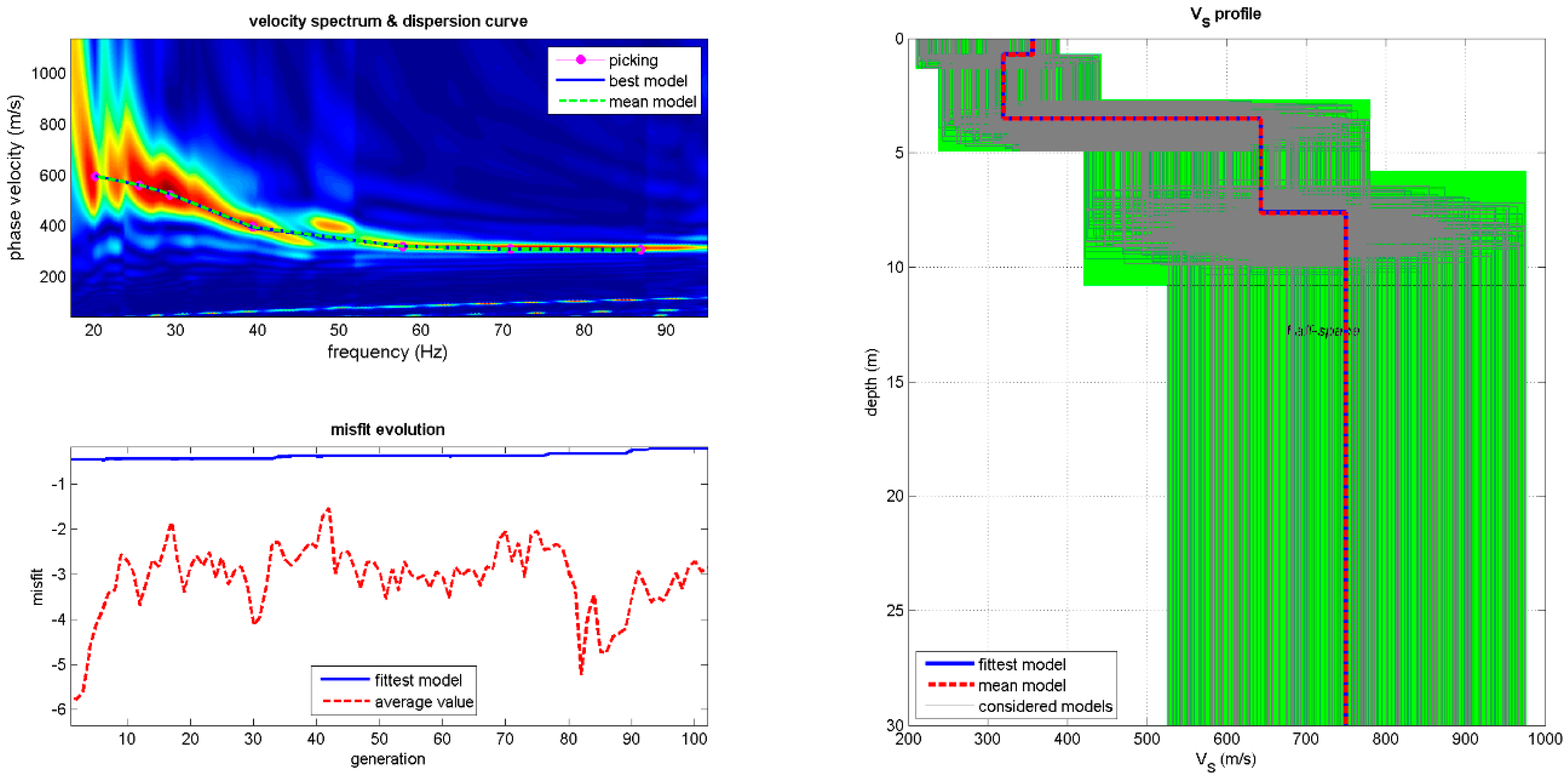
The data were processed and inverted using the winMASW software to obtain from the dispersion curves the vertical profile of the shear wave velocity Vs. Figure 3 shows an example of processing a MASW survey.

The HVSR measurements were performed using the TROMINO^® (Venice, Italy) digital seismic detector from Micromed S.p.A. with a sampling frequency of 256 Hz and a recording duration of 46 min in order to obtain a useful signal of no less than 30 min [35].

The traces were processed using the Micromed S.p.A. Grilla software. For each recorded signal, the choice of the time windows to be analyzed, each lasting 50 s, was made manually, analyzing the graphs of the temporal and azimuth variation of the H/V spectrum and choosing only the noise time windows characterized by temporally stationary spectral estimates and not characterized by clear directional dependence. The effects of spectral directionality were attributed to the characteristics of the subsoil only if they were consistently observed over the 46 min of recording. The frequency domain data were filtered with a triangular window to obtain a smoothing of 10%. The H/V spectral ratios of the microtremors were used to obtain stratified 1D models of the S velocity from each individual environmental vibration record. The inversion of the HVSR curves was performed using the relationship between the amplitude of the observed HV ratio and the ellipticity of the fundamental mode of the Rayleigh waves, assuming that the subsoil can be assimilated to a succession of homogeneous horizontal layers [3,16]. The uncertainty in the solution of the inverse problem was reduced by using the thickness and shear rate parameters of the inverse model related to the corresponding MASW as geometric and/or physical constraints [39,40]. The code used for the calculation of the synthetic H/V curves (Figure 4) is based on the simulation of the surface wave field (Rayleigh and Love waves) in a layered subsoil [23]. The inversion of the H/V curves was performed by choosing the closest MASW as the initial seismic velocity model.

3.4.2. Cluster Analysis of the HVSR Peaks

A modified non-hierarchical algorithm with K-means method [6] was applied to 80 HVSR measurements, acquired in the municipality of Enna. The proposed algorithm has the aim of reducing the units in k classes according to optimization criteria, minimizing the variance within the clusters and maximizing that between the clusters. This modified algorithm avoids any a priori choice of the operator which could influence the partition.

In order to verify the reliability and validity of the different partitions, the ratio between the variance between the clusters and the total variance of the data [6] was used:

$$R^2=\frac{DE{V}_{OUT}}{DE{V}_T}$$

(1)

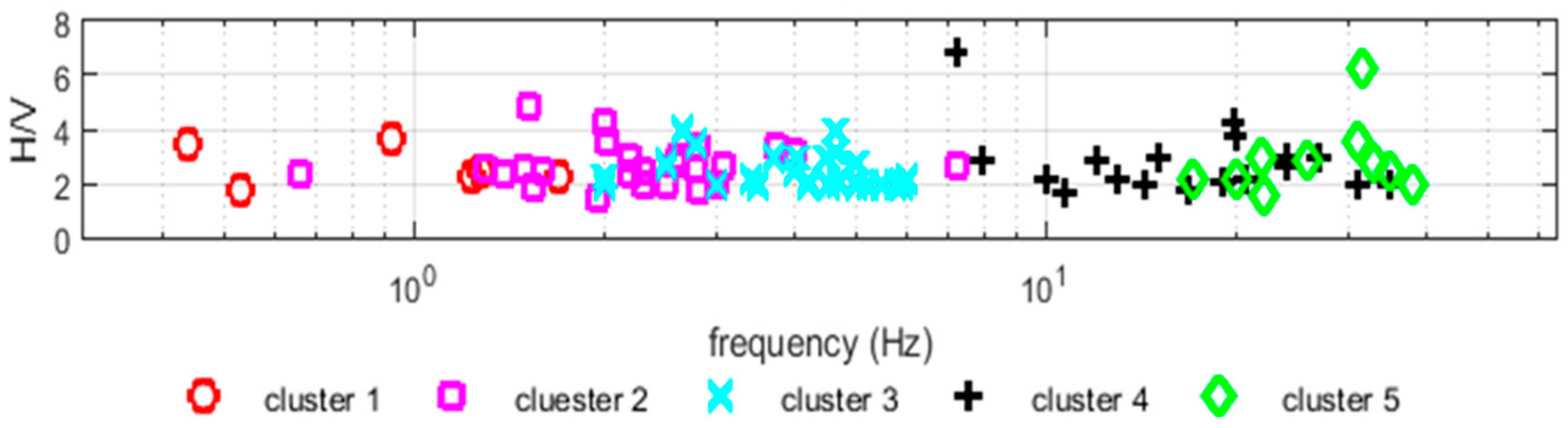
which made it possible to statistically choose a grouping of 5 clusters (Figure 5 and

Table 1. Minimum, average and maximum frequencies of the 5 clusters.

	Freq Min (Hz)	Freq Mean (Hz)	Freq Max (Hz)
cluster 1	0.44	1.02	1.70
cluster 2	0.66	2.46	7.20
cluster 3	2.00	4.14	6.00
cluster 4	7.20	18.19	35.00
cluster 5	17.00	27.58	38.00

). This partitioning of the data was found to be compatible with the number of seismic discontinuities expected in the analyzed area.

4. Results and Discussion

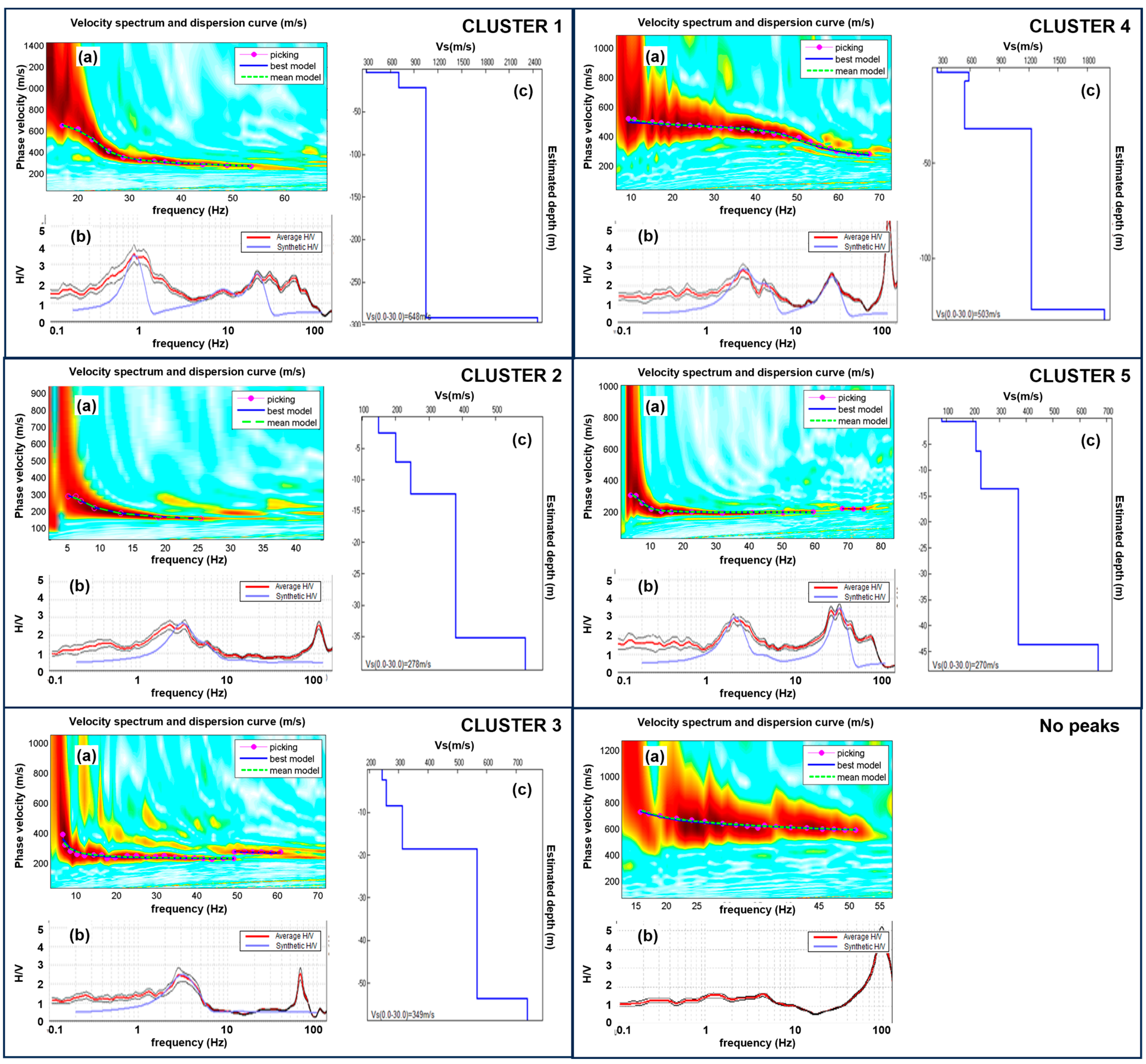
The analysis of the HVSR measurements, linked to the surface seismic velocity data obtained from the MASW measurements, made it possible to obtain the subsoil velocity models at greater depths. Figure 6 shows, for each of the clusters identified, a characteristic example of HVSR inversion, obtained by linking the velocity values of the more superficial layers with those obtained from the corresponding MASW model, together with a case without peaks, in which the corresponding MASW showed values of Vs characteristic of a sub-outcropping seismic bedrock.

By analyzing the inverse models obtained from each single measurement point, the values of the depth of the seismic bedrock were obtained, allowing the pattern of the surface of this subsoil layer to be reconstructed (Figure 7).

Furthermore, for each measurement point, we calculated the equivalent velocity of shear wave propagation V_S,eq defined as:

V_S,eq= H/Σ_i=1…_N(h_i/V_S,i)

(2)

where h_i is the thickness of the i-th layer, V_S,i is the shear wave velocity in the i-th layer, N is the number of layers and H is the depth of the seismic bedrock, defined as that formation, made up of very rigid rock or soil, characterized by a Vs of not less than 800 m/s.

A map of the V_S,eq parameter was reconstructed for the territory (Figure 8) showing higher values of the parameter in the northern part of the territory and low values corresponding to the lower part, which corresponds to the central part of the territory.

The site resonance frequencies grouped into five different clusters were attributed to different geological source. The stratigraphic interpretations were spatially correlated in order to reconstruct a three-dimensional geophysical model of the seismic discontinuities of the subsurface.

The results obtained were compared with the basic geology of the municipal area of Enna. The superimposition between the geological map and the five clusters (Figure 9) shows that, although the spatial limits of the clusters have not been constrained by the known stratigraphic contacts, their distribution seems to agree well, and the reconstructed seismic discontinuities show sub-horizontal geometries and compatible depths with those of the geological contacts present in the outcrop. In particular, cluster 1, characterized by mean frequencies of the centroid of 1.02 Hz and therefore related to a deep interface (greater than 50 m deep), seems to be related to the separation interface between the Enna Formation and the Trubi. Cluster 2, characterized by mean centroid frequencies of 4.14 Hz (less than 50 m deep), seems to be related to a discontinuity below or within the Terravecchia formation. Cluster 3, characterized by mean centroid frequencies of 18.19 Hz (less than 50 m deep), seems to be related to the separation interface between the two members of the Enna Formation, even if the cluster also includes some measurement points external to this formation, which were excluded for the reconstruction of the separation surface, dividing the cluster into cluster 3a and cluster 3b. Cluster 4, characterized by mean centroid frequencies of 18.19 Hz (less than 18 m of depth), and cluster 5, characterized by mean centroid frequencies of 27.58 Hz (less than 13 m of depth), are probably due to seismic interfaces, which delimit the terrains of alteration.

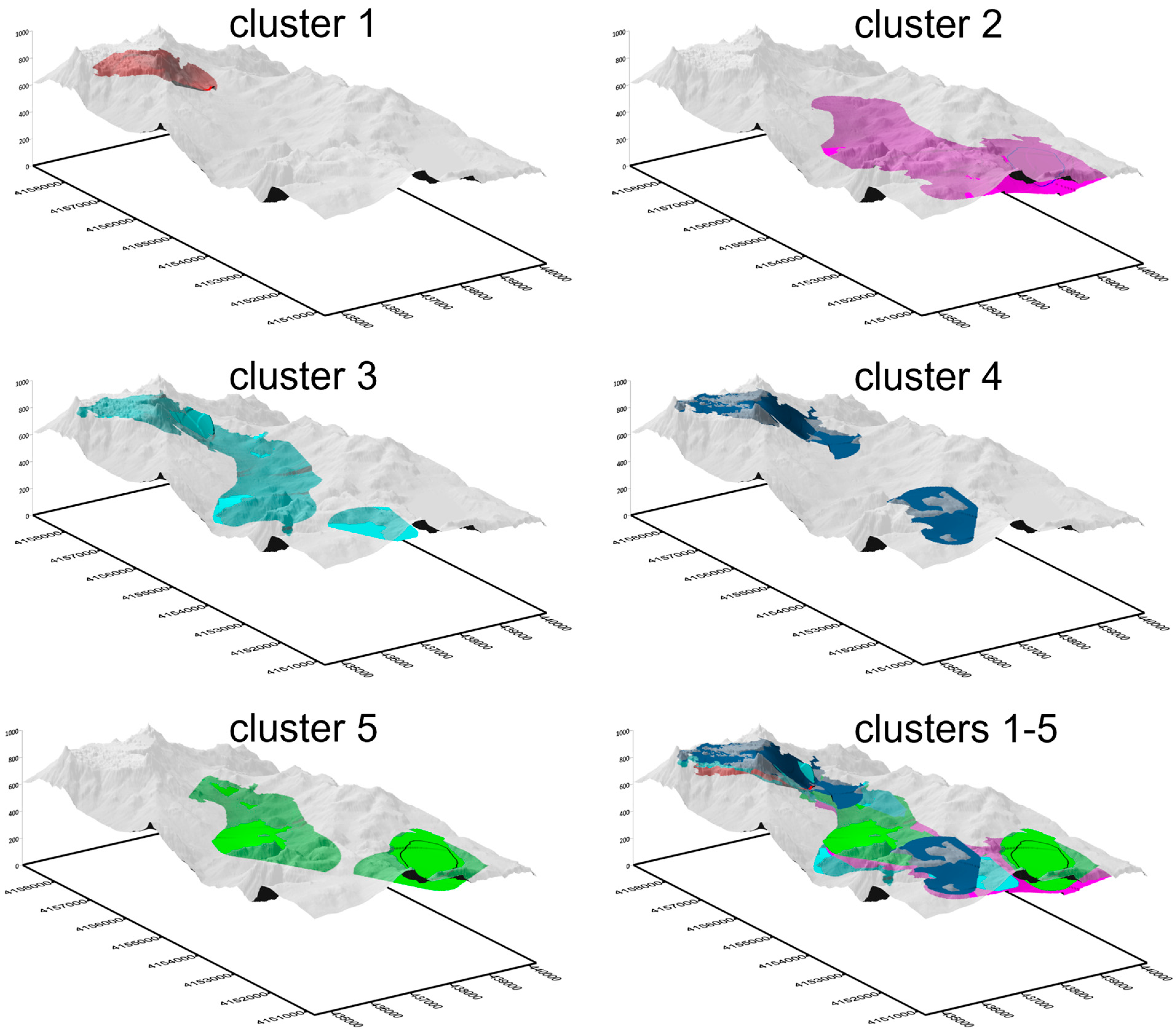
3D Modeling

Except for some measurements that did not show significant resonance peaks, the HVSR data partitioned into five clusters were inverted, assuming that the peaks relating to the same cluster are due to the same seismic generating surface. Therefore, five seismic surfaces were reconstructed, characterized by acoustic impedance contrasts such as being able to generate ground resonance frequency peaks. The surfaces obtained associated with each cluster are shown in Figure 10 together with the topography of the area.

This type of evaluation can be decisive in the study of the seismic microzonation of an area to recognize the local geological and geomorphological conditions that could significantly alter the characteristics of the seismic shaking, generating stresses such as those producing permanent and critical effects.

5. Conclusions

The cluster analysis made it possible to divide the frequency peaks into five groupings, which were correlated to as many seismostratigraphic discontinuities of the subsoil. The inversion of the curves was then performed by extrapolating the depths of these surfaces at the measurement points relating to the cluster of that surface. This procedure made it possible to reconstruct the geometry and shape of these surfaces in the subsoil. However, it should be noted that some of these surfaces have been reconstructed with the few points falling within the relative cluster and that the resolution can therefore only be approximate and simplified. In fact, a reconstruction that is more consistent with reality requires numerous measurement points, especially for surfaces that show irregular trends. In the case of the municipal area of Enna, the trend of the surfaces appears to be sub-horizontal in many cases, as confirmed by the surface geology, so the reconstruction is realistic.

The application of cluster analysis to the analysis of the frequency peaks of the HVSR measurements has therefore shown good potential in the reconstruction of seismic and geological models of the subsoil, especially in the case of geometries that are simple to reconstruct.