Abstract
The permeability of intact geologic media features prominently in many geo-environmental endeavours. The laboratory estimation of permeability is an important adjunct to the field estimation of bulk permeability values, which involves a great deal of supplementary in situ investigations to correctly interpret field data. Laboratory permeability estimation is also a viable method if core samples are recovered from in situ geological mapping of the region under study. The basic methodologies for permeability estimation rely on either steady-state or transient tests of the geologic material depending on the anticipated permeability value. This paper presents a steady flow test conducted on a partially drilled cavity located on the axis of a cylindrical specimen. Certain compact theoretical relationships are proposed for the estimation of steady flow from a cavity of finite dimensions located along the axis of a cylindrical specimen. The relationships are used to estimate the permeability of a cylinder of Lac du Bonnet granite obtained from the western flank of the Canadian Shield. The results from the cavity flow permeability experiments are compared with other estimates for the permeability of granitic rocks reported in the literature.
1. Introduction
Permeability is a key parameter governing many hydro-geological, geoenvironmental and geomechanical endeavours. These can include general problems related to flow and geologic processes in intact, fractured and porous media with random pore networks, groundwater hydrology and estimation of yield, pumping rates in aquifers used as hydrologic basins, ground subsidence due to water and resource extraction, water level fluctuations in geologic formations due to earthquakes and tidal effects, groundwater and geomechanics issues in geologic sequestration groundwater flow in geologic processes and during contaminant transport, coupled processes during glacial advances and ground freezing, geothermal energy and resource extraction, and the use of deep geologic formations for the storage or disposal of hazardous materials and nuclear fuel waste. The articles and texts covering these topics are many and merit a separate review article.
In their natural setting, geologic media are rarely intact, defect-free rock formations. Defects such as fractures, both sparse and high density, intrusions created during the formation of the rocks, fractures created during injection and extraction activities, heterogeneities and other defects at various scales can influence the bulk fluid flow behaviour, particularly in a large-scale geological horizon. In their natural setting, geologic media are rarely intact, defect-free rock formations. Defects such as fractures, both sparse and high density, intrusions created during the formation of the rocks, fractures created during injection and extraction activities, heterogeneities and other defects at various scales can influence the bulk fluid flow behaviour, particularly in a large-scale geological horizon. Typical areas of application are illustrated in Figure 1. With such observations, it is natural to enquire whether the permeability of an intact rock has any relevance to the geosciences. On the contrary, intact permeability can influence the behaviour of fluid transport characteristics at the scale of a fracture where the migration of fluids permeating isolated fracture extremities or stagnant zones can be controlled by the permeability of the intact geologic medium (Figure 2).
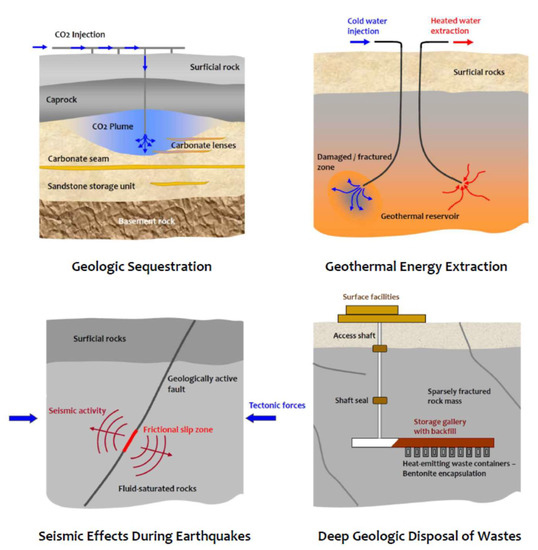
Figure 1.
Geoenvironmental process where fluid transport properties of rocks have a dominant influence (After, Selvadurai and Suvorov [1]).
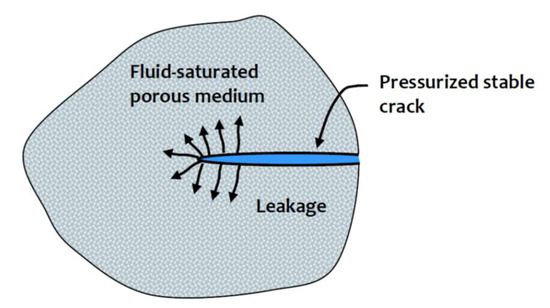
Figure 2.
Fluid transport at extremities of fractures and defects in rocks.
Historically, the estimation of the permeability of soils dates back to the work of Darcy [2], where the permeability is regarded primarily as a rudimentary scalar quantity. In applications with respect to geologic media that possess stratifications, the permeability has directional properties requiring a definition based on a second-order symmetric tensor with six independent components
and the units of permeability are given in L2. The symmetry of the permeability tensor relies on the absence of a rotational or vorticity component in the movement of a particle of fluid through a porous medium. With geological stratifications, the permeability measure reduces to a porous medium with transverse isotropy, which enables the description of permeability by two measures that are applicable to flow along and perpendicular to the stratifications, i.e.,
where KT and KN are, respectively, the permeabilities along and normal to the stratifications. The mechanics of groundwater flow in stratified media modelled as hydraulically transversely isotropic media is described in many studies and further references are given in [3,4,5,6,7,8,9]. In particular, the in situ permeability characteristics of transversely isotropic porous media are determined by considering the flow rates into cased boreholes and the transient rise of water levels within the casing discussed in the above studies. For incompressible steady flow conditions, the fluid mass conservation equation ∇.v(x) = 0, together with the generalised Darcy’s law v(x) = −(Kγw/η) ∇φ(x), where ∇ is the gradient operator, is the reduced Bernoulli potential (units of L), γw is the unit weight of the permeating fluid (with units F/L3), is the dynamic viscosity (with units FT/L2), gives the governing partial differential equation
and this elliptic partial differential equation can be solved for a flow domain by prescribing Dirichlet-, Neumann- or Robin-type boundary conditions [10]. In the case of hydraulic homogeneity of the porous medium and the percolating fluid, the above result reduces to Laplace’s equation for φ(x)
When undisturbed samples of rock can be recovered from the depth at which the permeability is to be measured, laboratory estimation of the isotropic permeability is perhaps the most convenient approach. Two standard types of laboratory permeability tests can be performed on cylindrical samples of rock that can either be cored from block samples or cored directly from the formation. The most straightforward approach is to induce steady-state one-dimensional flow through a saturated cylindrical rock sample under a prescribed hydraulic gradient. To achieve one-dimensional conditions through a cylindrical sample, the cylindrical surface is usually sealed with a membrane and each of the plane surfaces is maintained at a constant potential but with a potential difference to induce flow. These tests are well documented in the geomechanics literature. When the permeability of the rock is sufficiently large and the experimental techniques are capable of maintaining a constant hydraulic gradient across defined surfaces of the test specimen, the constant flow permeability test provides the most efficient method for estimating rock permeability. These techniques have been applied to estimate the permeability of intact cores of rocks such as Indiana limestone, Vosges sandstone, etc. Early attempts to estimate permeability using steady-state tests were performed by Fatt and Davis [11] and Fatt [12], to assess permeability alterations in reservoir rock with confining stress. McLatchie et al. [13] discussed the influence of skeletal compressibility on the permeability of reservoir rock and the correlation between permeability reduction both with confining stresses and with an increase in clay content. Similar studies on sandstone and argillaceous limestone are documented in the bibliography. The concept of localised fluid flow approaches for estimating the permeability of rocks was put forward by Dykstra and Parsons [14] and the experimental techniques were modelled by Goggin et al. [15] The application of steady-state techniques for permeability estimation in large samples of Berea sandstone was discussed by Tidwell and Wilson [16] and the interpretation techniques were improved by Tartakovsky et al. [17]. The concept of an annular patch permeameter was proposed by Selvadurai and Selvadurai [18] and successfully utilised to estimate the permeability distribution on the surface of a 508 mm cuboid of Indiana limestone, using kriging techniques to estimate the interior permeability heterogeneity in the cuboid. Computational procedures were used to estimate the geometric mean of the permeability of the cuboid [18,19]. The geometric mean-based estimate for the permeability of the Indiana limestone was found to be K ≈ 73.75 × 10−15 m2. Rigorous mathematical approaches based on triple integral equations in potential theory were employed to develop an analytical solution, which related the flow rate to the potential difference, and these are documented in the bibliography.
An international benchmarking exercise related to the estimation of the permeability of Grimsel granodiorite and involving 24 research laboratories is documented figure [20,21]. The application of external isotropic compressive stresses to fluid-saturated rocks and their influence on reducing permeability has also been investigated by appeal to steady-state fluid flow tests. The influence of non-isotropic stress states in enhancing permeability derived from steady-state tests has also been discussed in the references cited in the bibliography.
The need for transient flow methods to estimate the fluid transport properties of low permeability rocks was recognised in the pioneering article by Brace et al. [22]. Other contributions relevant to transient tests are also given in [23,24]. Transient techniques are complicated because other properties relevant to the interpretation of the tests have to be determined, including the compressibility of the porous skeleton, the compressibility of the solid material composing the porous skeleton, the compressibility of water, the porosity of the porous medium, the Biot coefficient the air voids that can be present in the fluid region that is pressurised to attain the transient flow, and the appropriate mathematical formulation and modelling (i.e., the diffusion equation approach or a poroelasticity approach) used to interpret the experiments [25,26,27,28,29,30,31,32,33,34,35,36,37]. With the advent of high-precision pumps that can provide flow rates as low as 0.000070 mL/min, steady-state experiments can be performed on low permeability materials such as the Cobourg limestone and the granites from the Canadian Shield. In the case of the Cobourg limestone, the effective permeability of a region measuring 80 mm × 120 mm × 130 mm was estimated using experimental and computational approaches to obtain an isotropic permeability in the range . Similarly, steady-state flow patch permeability tests were performed to determine the effective isotropic permeability of cuboids of Lac du Bonnet granite and Stanstead granite, measuring 300 mm and 280 mm, respectively, from the western and eastern flanks of the Canadian Shield [38]. The geometric mean-based permeability ranged from for the Stanstead granite to for the Lac du Bonnet granite. The brief review presented in this section is not intended to be a comprehensive review of the topic of permeability measurement of rocks; however, the recent key articles that address novel experimental and theoretical developments are instructive.
The development of innovative steady flow techniques for the estimation of permeability of low permeability rocks can benefit the overall utility of permeability testing of intact rocks. This paper deals with the laboratory evaluation of the permeability of the Lac du Bonnet granite using cylindrical samples of the rock with an axisymmetric cylindrical cavity and subjected to steady seepage. The installation of a cylindrical cavity through which steady flow takes place enables the permeability of the interior region of the rock to be estimated, as opposed to surficial tests that only probe a region of the rock close to the surface as achieved by adopting the basic sealed annular patch permeameter [18]. The paper discusses the complexity of the modelling, which involves the purely analytical modelling of the associated potential flow problem and proposes approximate solutions that can be used to estimate the bulk permeability of the granitic rock specimen based on: (i) A combination of radial flow through the cylindrical surface of the cavity and axisymmetric flow through the base of the cylindrical cavity with impermeability constraints on a plane located at the base of the cylindrical cavity. (ii) Flow into an extended rock mass through an oblate hemispheroidal cavity located in a semi-infinite porous medium. The approximate theoretical relationships are used to estimate the permeability of a Lac du Bonnet granite cylinder measuring 150 mm in diameter and 300 mm in length with a central cavity of 10 mm in diameter and a depth of 50 mm. The results of the experiments are compared with values obtained from other investigations reported in the literature.
2. Theoretical Developments
The experimental arrangements involving the initiation of flow from the partially drilled cavity in the granite cylinder are shown in Figure 3. The co-axial nature of the potential flow problem induces a state of axial symmetry. In the experiments conducted, the upper surface of the cylinder is sealed over a finite region as shown in Figure 4.
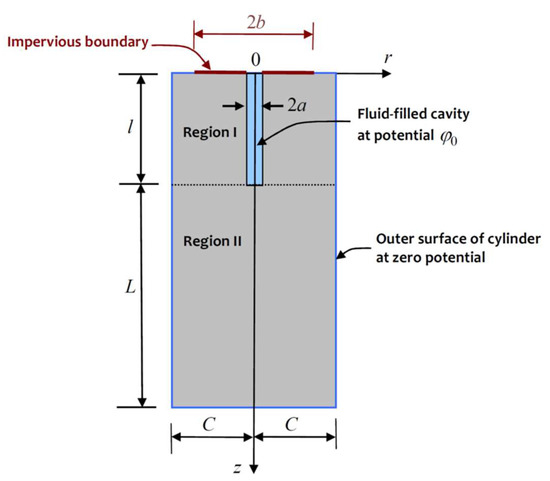
Figure 3.
The flow domain of the experiment involving flow from a cylindrical cavity region in the Lac du Bonnet granite cylinder.

Figure 4.
The sealed region (indicated in red) of the surface of the 150 mm diameter granite cylinder measuring with a cavity diameter of 10 mm.
Considering axial symmetry, the partial differential equation governing steady flow from the cylindrical cavity is governed by Laplace’s equation of the form
The potential can be expressed in units of length. Considering a Hankel transform solution of (1) (see, e.g., [10,39,40,41,42]), the general form of the solution of (1) can be written
where are arbitrary functions and is the zeroth-order Bessel function of the first kind. The arbitrary functions can be identified in relation to the domain (Regions I and II in Figure 3) over which the flow takes place. If a complete mathematical formulation of the problem is contemplated, it is convenient to divide the flow domain into two regions with Region I occupying the domain and Region II occupying the domain . The potential functions applicable to Regions I and II can be defined by the integral forms
where are eight arbitrary functions that need to be determined by satisfying (i) the boundary conditions applicable to the Region I
and (ii) the boundary conditions
applicable to the Region II. The continuity conditions applicable to the common boundary between Region I and Region II are given by
The boundary and continuity conditions (5) to (7) are both necessary and sufficient to uniquely determine a solution to the mixed boundary value problem in potential theory. The research conducted in this area points to the observation that exact solutions of these mixed boundary value problems are not possible; the presence of mixed boundary conditions, where Dirichlet and Neumann boundary conditions are present means that the problem can only be solved in an approximate fashion. Furthermore, the presence of mixed boundary conditions can give rise to solutions where the potential and its derivatives can exhibit singularities, which need to be addressed even if numerical approaches are used to solve the mixed boundary value problem. Computational approaches, such as finite element and boundary element techniques can, of course, be readily applied to solve the porous media flow problem provided special techniques are utilised to accommodate the singularities encountered at a boundary where the boundary conditions change abruptly from a Dirichlet to a Neumann type.
The approach adopted in this study is to obtain approximate solutions that can be used to estimate the flow from the cylindrical cavity that is maintained at a constant potential and where the outer boundary of the cylinder is maintained at zero potential. One approach is to assume that the entire upper surface of the cylinder and the common boundary between Regions I and II are subjected to null Neumann boundary conditions (Figure 5). Invoking this assumption introduces a state of radial symmetry in the potential problem and reduces the partial differential Equation (1) to an ordinary differential equation in , which can be solved, subject to the boundary conditions and . Omitting details, it can be shown that the total flow through the domain can be expressed in the form
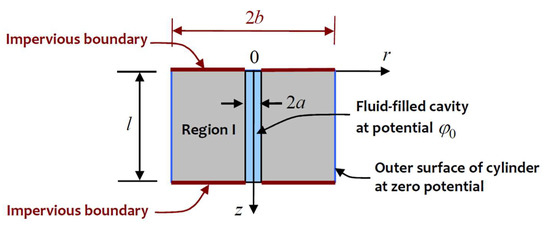
Figure 5.
Purely radial flow in a cylindrical domain.
Implicit in the solution of the radially symmetric flow problem is the requirement that the flow domain is finite and cannot occupy the boundary and, as , the result (8) yields an inadmissible result.
The flow in Region II can be examined by considering the mixed boundary value problem indicated in Figure 6. The mixed boundary value problem applicable to Region II is governed by the boundary conditions
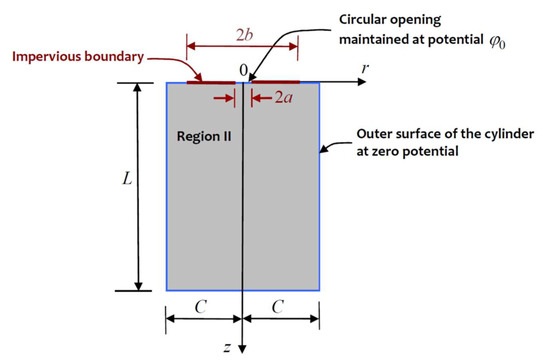
Figure 6.
Axisymmetric flow in flow in Region II.
Again, the analytical solution of the mixed boundary value problem defined by (9) is possible, but the procedures are non-routine. If the flow domain is considered to be semi-infinite (i.e., and ), the mixed boundary value problem can be reduced to a system of triple integral equations for a single unknown function of the form
The system of triple integral equations defined by (10) has been extensively studied [43,44,45,46,47] with applications to problems in elasticity and potential theory. The approximate solution of the system of triple integral equations involves a series approximation of the unknown function in terms of a small non-dimensional parameter . Omitting details, it can be shown that the steady flow rate through the central aperture of a sealed annular region at the surface of the porous halfspace region can be obtained in the form
where
The accuracy of the series approximation solution (12) has been compared with equivalent results derived from finite element computations and the results agree to within 2% of each other, which is sufficient for the purposes of interpretation of permeability test data. In the particular instance when the flow takes place over the central region and the remaining part of the boundary of the halfspace region is sealed, a two-part mixed boundary value problem is obtained for a single unknown function
The solution of the two-part mixed boundary value problem is standard [10,39] and, omitting details, it can be shown that the flow rate is obtained in the exact closed form
which corresponds to the leading term of (12) as . The flow induced in the porous domain due to the cavity subjected to the potential can be obtained using the results obtained from the reduced models with the null Neumann boundary conditions imposed in the critical surfaces. The reduced results given by (8) and (14) for the flow induced in Regions I and II give the following expression for the permeability of the domain
The expression (15) contains both the influence of and , which makes it applicable to only a cylinder with a finite external radius. If the external diameter , or if , flow is restricted to the surface-sealed halfspace region, and we recover the exact solution
A further procedure for estimating the steady flow from the cylindrical cavity maintained at a constant potential assumes that the cylindrical cavity region can be represented by a prolate spheroidal cavity with suitable dimensions to reflect the flow process. Figure 7 illustrates the flow in a semi-infinite porous medium bounded internally by a prolate hemispheroidal cavity, the boundary of which is subjected to a constant potential . By maintaining the plane as an impervious barrier, the flow problem is equivalent to considering the flow from a complete spheroidal cavity subjected to a constant potential .
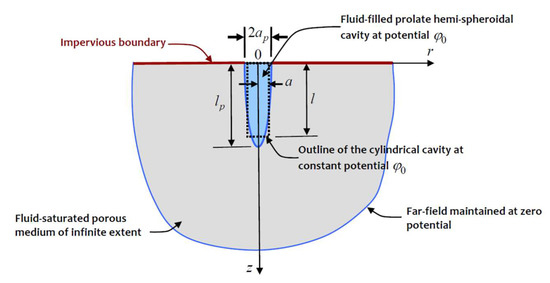
Figure 7.
Flow from a prolate hemispheroidal cavity.
The axisymmetric prolate spheroidal coordinates are related to the cylindrical polar coordinates through the relationships
and cp can be expressed in terms of the dimensions of the semi-major axis and the equatorial radius of the bounding prolate spheroid defined by α = α0 with the semi-major axis lp and semi-minor axis ap with
r = cp sinh α sin β; z = cp cosh α cos β
In prolate spheroidal coordinates, (1) takes the form
The PDE (19) needs to be solved subject to the boundary conditions
and the regularity condition
The types of potential problems defined by (19) to (21) have been discussed in connection with problems in electrostatic potential theory, fluid mechanics and elasticity and authoritative treatises covering these areas are given by [48,49,50,51,52,53,54,55,56] and others. It can be shown that the harmonic function that satisfies the boundary condition (20) and the regularity condition (21) takes the form
where
The velocity vector can be obtained by employing (22) and Darcy’s law and the flow rate from the prolate spheroidal cavity can be obtained from the result
where Sp is the boundary of the prolate spheroidal cavity that is subjected to the constant potential and n is the outward unit normal to Sp. Evaluating the integral (24), we can obtain an expression for the flow rate from the complete prolate spheroidal cavity with semi-minor axis ap and semi-major axis lp subjected to a boundary potential. Since the plane of symmetry corresponds to a null Neumann boundary condition, the results for the flow rate from the complete prolate spheroidal cavity give the flow rate from the prolate hemispheroidal cavity shown in Figure 7, i.e.,
It is now necessary to determine a relationship between the geometry of the cylindrical cavity with radius and length and the geometry of the prolate hemispheroidal cavity with minor radius ap and semi-major radius lp. A very straightforward relationship is to assume that the aspect ratio for the cylindrical cavity is identical to the aspect ratio for the prolate hemispheroidal cavity (i.e., (a/l) = (ap/lp)). A more realistic relationship can be obtained by considering the surface areas over which the flow takes place. If we set a = ap, by equating the surface areas we obtain
Although the equal surface area representation between the cylindrical and hemispheroidal cavities is feasible, the inversion of (26) to obtain an explicit expression for (ap/lp) in terms of (a/l) is not evident. An alternative is to evaluate the expression (26) for a range of values of (ap/lp) and a graph similar to that shown in Figure 8 can be used to determine an aspect ratio (ap/lp) for a specified aspect ratio (a/l) for the cylindrical cavity.
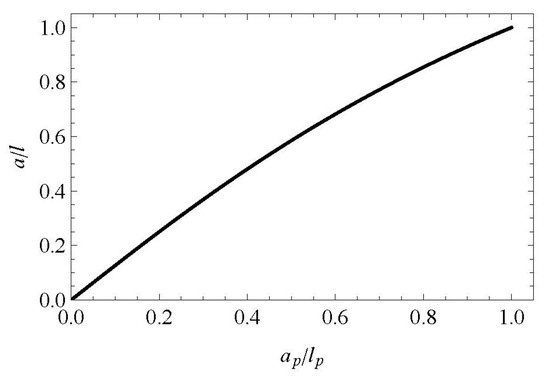
Figure 8.
Comparison of aspect ratios of the cylindrical cavity with that of the prolate hemispheroidal cavity.
In (27), the semi-minor axis of the prolate hemispheroidal cavity is set equal to the radius of the cylindrical cavity; a = ap and the semi-major axis lp is related to the dimension of the cylindrical cavity through (26); i.e., once (a/l) of the cylindrical cavity is specified, the surface area equivalent (ap/lp) is determined from Figure 8. A direct comparison of the results obtained from (15) and (27) is unwarranted because of the explicit dependence of (15) on the outer dimension of the cylindrical region. The result (15) is more suitable for cylindrical cavities that have a small cavity aspect ratio (a/l) →1. The result (27) is a more suitable expression for estimating the permeability of the granite cylinder of finite dimensions that contains a cylindrical cavity. The role of the outer boundary in influencing the estimation of the flow rate was extensively investigated by Selvadurai and Selvadurai [18] in connection with modelling the annular patch permeameter. Referring to Figure 6, for far-field relative dimensions and , the regularity condition is satisfied by the finite domain.
3. Experimental Investigations and Permeability Estimates
The experiments conducted involved the initiation of steady flow from a central cylindrical cavity (diameter 10 mm and length 50 mm) located in a cylinder of Lac du Bonnet granite (150 mm in diameter and 300 mm in length). The granite cylinder was cored from a cuboidal block of Lac du Bonnet granite measuring 500 mm × 500 mm × 350 mm, which was supplied by Cold Spring Granite Ltd., in Pinawa, Manitoba. The plane surfaces of the cylinder were machine polished, allowing for the development of a sealed surface for the placement of the patch permeameter developed by Selvadurai [57]. This type of permeameter was successfully used to measure the effective permeability of an Indiana limestone cuboid measuring 508 mm [18] and a cuboid of Lac du Bonnet granite measuring 300 mm [38]. A schematic view of the experimental configuration is shown in Figure 9.
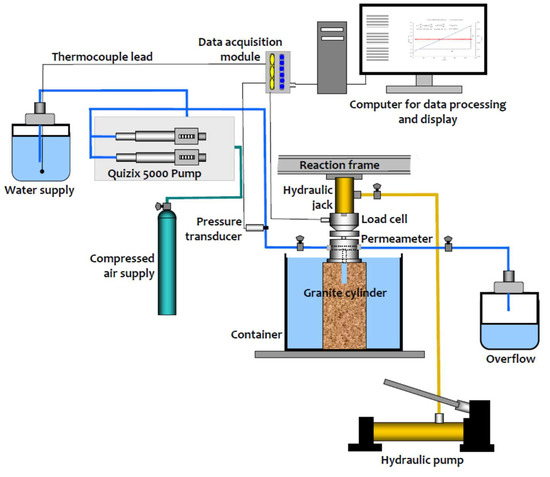
Figure 9.
A schematic view of the experimental configuration adopted for performing steady-state cavity flow permeability tests.
The permeameter provides a cavity radius of 5 mm and sealing is established by applying an axial load to the permeameter; the sealing pressure is 2.5 MPa over an annular region with an internal radius of 12.5 mm and external radius of 50 mm. It is noted that a sealing stress of approximately 2.5 MPa is sufficient to reduce any interface leakage to within 0.1% of the cavity pressure that induces steady flow. It is natural to enquire whether the application of the sealing stress can contribute to the closure of micro-cracks, defects and pores in the Lac du Bonnet granite. To the author’s knowledge, the blocks of the Lac du Bonnet granite supplied were defect-free, although the only way of assessing this is to perform CT scans on the core that was tested. The elastic modulus of the Lac du Bonnet granite was in the range of 70 GPa [33]. Therefore, pore closure during the application of a sealing stress of 2.5 MPa will not be an issue in the current tests. An alternative procedure that involves completely bonding a stainless-steel plate to the plane surface of the cylinder is also a possibility provided that no movement of the location of the annular sealing region is contemplated. The axial sealing load is measured using an Interface Model 1200 Load Cell with a load capacity of 50 kN. The steady flow to the cylindrical cavity region is provided by a Quizix 5000 Precision Pump; flow rates can be varied between 0.000070 mL/min and 30 mL/min. The sample containing the partially drilled central cavity is first saturated using a venturi vacuum saturation technique at −10 kPa, with periodic adjustment of the water level in the saturation chamber to facilitate extraction of air from the unsaturated regions. Periodic weighing of the sample is also conducted to ensure that the saturation procedure is effective. Once the vacuum saturation is complete, the saturation is compared with the porosity estimates. In general saturation levels of approximately 98% can be achieved using the variable height reservoir arrangement. Attainment of 100% saturation requires the application of a greater vacuum, which can also lead to pore compression and alterations to permeability. A 98% level of saturation is considered to be acceptable for steady-state permeability tests and corrections are needed to account for the air void fraction if transient tests are contemplated. The cavity pressure inducing steady flow in the granite cylinder is measured via a Honeywell pressure transducer (Model TJE CP 300 psi). The fluid used in the permeability tests was normal tap water at a room temperature of approximately 24 Deg C. The steady flow rate from the cavity is the important experimental information that enables the estimation of the permeability of the Lac du Bonnet granite. Even though the pumps can supply very low flow rates, the reciprocating action of the pump operation can lead to fluctuations in the recorded pressure. The estimation of the actual flow rate is, however, best achieved by using the volume flow over a prescribed time interval. Since the variation in the cumulative volume with time is steady, this data can be used to estimate the flow rate. Typical examples of the Quizix 5000 Precision Pump records that indicates the cumulative volume with time are shown in Figure 10, Figure 11 and Figure 12 and this information is used to calculate the flow rate under a given inlet pressure. Figure 13 indicates, for purposes of illustration, enlarged views of the flow rates for typical time intervals.
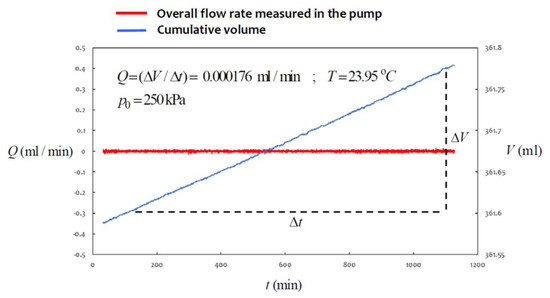
Figure 10.
Estimation of flow rate in a cavity permeability test ().
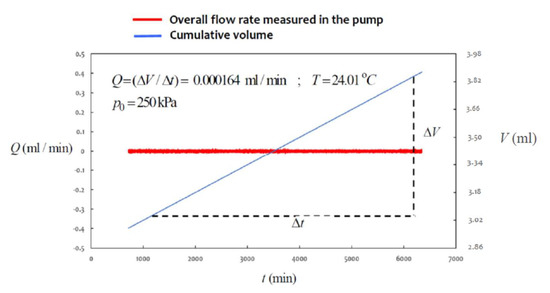
Figure 11.
Estimation of flow rate in a cavity permeability test ().
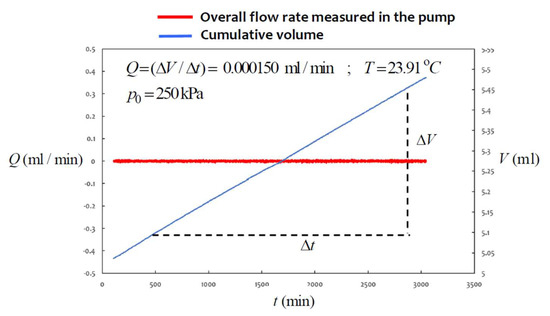
Figure 12.
Estimation of flow rate in a cavity permeability test ().
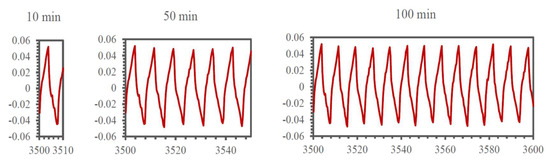
Figure 13.
Typical fluctuations in the flow rate due to reciprocating action of the precision pumps.
The steady-state flow experiments are conducted at a cavity pressure of 250 kPa, which for a fluid unit weight of , corresponds to a potential of φ0 = 25.55 m. All the tests were performed at a laboratory temperature of approximately 24 Deg C. The parameters used in the estimation of the permeability of the Lac du Bonnet granite are as follows:
| Radius of the cylinder | = 0.075 m |
| Radius of the cylindrical cavity | = 0.005 m |
| Depth of the cavity | = 0.050 m |
| Height of the cylinder | = 0.300 m |
| Cavity potential causing steady flow | = 25.55 m |
| Dynamic viscosity of water at 24 Deg C | = 9.11 × 10−1 MPa s |
Prior to performing the cavity flow permeability test, the intact granite cylinder was also subjected to patch permeability testing, where the position of the pressurised patch was moved over the plane surface of the cylinder (Figure 14). In this case, the near-surface permeability of the granite can be determined using the theoretical estimate (14). The results of these tests indicated near-surface permeability estimates in the range (0.43 to 1.00) × 10−19 m2. In the experimental configuration indicated in Figure 9 and Figure 14, it is clear that the sealing action of the upper surface of the cylinder does not extend over the entire surface of the sample as indicated in the last boundary condition in (5), where the sealing extends over the region a < r < b and not a < r < C, where C is the radius of the cylinder. The influence of the unsealed region b < r < C, on the estimated flow rate was extensively investigated computationally by Selvadurai and Selvadurai [18]. It was concluded that the assumption of a perfectly sealed entire upper surface of the cylinder was a satisfactory alternative to the partial sealing experimental technique that would enable the development of a compact analytical result for the interpretation of the test data.

Figure 14.
Arrangement for conducting surface permeability tests on the Lac du Bonnet granite cylinder.
The results of the three cavity permeability tests and the permeability estimates derived from the results (14) and (26) are summarised in Table 1. When using the result (26), it is necessary to obtain an equivalent estimate for in terms of ap/lp. Using the result (25) and Figure 8, it can be shown that for a cavity aspect ratio a/l ≈ 0.10, the aspect ratio ap/lp ≈ 0.08. The development of a stable cumulative volume is attained through the supply of clean de-ionised water and maintaining the laboratory temperatures at a stable value.

Table 1.
Results of cavity flow permeability tests.
4. Concluding Remarks
The estimation of permeability for defect-free granitic rocks has been the subject of extensive investigations conducted over the past five decades. The most conventional approach for estimating permeability is to conduct steady-state one-dimensional flow tests through cylindrical samples. Alternative steady-state permeability tests that involve departures from the one-dimensional require the development of theoretical relationships that can analyse and interpret the steady-state test data accurately. Cavity flow permeability tests involving cavities partially drilled into cylindrical samples of rock provide the opportunity to assess the bulk permeability of the rock when the flow is initiated at the interior of the test specimen. The techniques for interpreting the test results can vary from the hybrid combination of flow that takes place from the surface of the cavity and flow that takes place at the base of the cylindrical cavity. A second approach derives a relationship for the flow rate from a prolate spheroidal cavity maintained at a constant potential. This study provides approximate theoretical relationships that can be used to estimate the permeability of the rock. The results of steady-state flow experiments conducted on a large diameter cylinder installed with a cylindrical cavity are used to estimate the permeability of the rock. The hybrid approach of introducing an impervious barrier between the radial flow region and the sealed halfspace region containing a circular aperture leads to permeability estimates in the range (0.670 to 0.785) × 10−19 m2. The modelling that employs the flow from a prolate hemispheroidal cavity leads to permeability estimates in the range (0.749 to 0.878) × 10−19 m2. The overall range for the permeability of the Lac du Bonnet granite can be assigned by combining the limits in the above results. A comprehensive study of the permeability of the Lac du Bonnet granite was conducted by Selvadurai et al. [38] who performed surface permeability tests on a cuboid measuring 300 mm and used the data to estimate the permeabilities within the block, and with the aid of computational modelling, to arrive at an effective permeability for the granite based on the geometric mean. The results of that investigation gave permeability values in the range (0.840 to 1.090) × 10−19 m2. Other estimates for the permeability of the Lac du Bonnet granite obtained from both laboratory and in situ tests conducted on boreholes give the following values: Stevenson et al. [58] give the following estimates: (0.01 to 0.05) × 10−19 m2, Katsube and Hume [59] indicate a value of (0.90) × 10−19 m2, and Souley et al. [60] give a value of (0.60) × 10−19 m2. The variability of the geomechanical properties of geomaterials is well known and the property of permeability is expected to display a wide statistical variation (Harr [61]). The in situ estimates can be influenced by the methodology adopted for the installation of the borehole, the test procedure and the approach used to interpret the test data. From the results of the laboratory investigations conducted here, the range of permeability for the intact Lac du Bonnet Granite can be assigned values in the range (0.670 to 0.878) × 10−19 m2.
Funding
The work described in this paper was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) through a Discovery Grant [RGPIN-2016-04676] and a Research Tools and Instruments Grant [EQPEQ 337343-07], the Nuclear Waste Management Organization (NWMO) of Canada [NWMO-FORM-FN-0012-R002] and the Distinguished James McGill Research Chairs Program at McGill University.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: www.mcgill.ca/civil/selvadurai/research-repository.
Acknowledgments
The author is grateful to laboratory assistant V. Zasmolin for performing the experiments.
Conflicts of Interest
The author declares no conflict of interest.
References
- Selvadurai, A.P.S.; Suvorov, A.P. Thermo-Poroelasticity and Geomechanics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques De La Ville De Dijon; Dalmont: Paris, France, 1856. [Google Scholar]
- Marcus, H. The permeability of a sample of an anisotropic porous medium. J. Geophys. Res. Atmos. 1962, 67, 5215–5225. [Google Scholar] [CrossRef]
- Payne, L.E.; Rodrigues, J.F.; Straughn, B. Effect of anisotropy on Darcy’s law. Math. Methods Appl. Sci. 2001, 24, 427–438. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. Intake Shape Factors for Entry Points in Porous Media with Transversely Isotropic Hydraulic Conductivity. Int. J. Géoméch. 2003, 3, 152–159. [Google Scholar] [CrossRef][Green Version]
- Selvadurai, A.P. Fluid Intake Cavities in Stratified Porous Media. J. Porous Media 2004, 7, 165–181. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. On the hydraulic intake shape factor for a circular opening located at an impervious boundary: Influence of inclined stratification. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 639–651. [Google Scholar] [CrossRef]
- Morland, L.W. Flow in a Porous Matrix with Anisotropic Structure. Transp. Porous Media 2010, 81, 161–179. [Google Scholar] [CrossRef]
- Bagdassarov, N. Fundamentals of Rock Physics; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. Fundamentals, Laplace’s Equation, Diffusion Equation, Wave Equation. In Partial Differential Equations in Mechanics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1. [Google Scholar]
- Fatt, I.; Davis, D. Reduction in Permeability with Overburden Pressure. Pet. Trans. AIME 1952, 195, 326–329. [Google Scholar] [CrossRef]
- Fatt, I. The Effect of Overburden Pressure on Relative Permeability. Pet. Trans. AIME 1953, 198, 325–326. [Google Scholar] [CrossRef]
- McLatchie, A.; Hemstock, R.; Young, J. The Effective Compressibility of Reservoir Rock and Its Effects on Permeability. J. Pet. Technol. 1958, 10, 49–51. [Google Scholar] [CrossRef]
- Dykstra, H.; Parsons, R.L. The Prediction of Oil Recovery by Waterflooding in Secondary Recovery of Oil in the United States, 2nd ed.; American Petroleum Institute: Washington, DC, USA, 1950. [Google Scholar]
- Goggin, D.J.; Thrasher, R.L.; Lake, L.W. A theoretical and experimental analysis of minipermeameter response including gas slippage and high velocity flow effects. In Situ 1988, 12, 79–116. [Google Scholar]
- Tidwell, V.C.; Wilson, J.L. Laboratory method for investigating permeability upscaling. Water Resour. Res. 1997, 33, 1607–1616. [Google Scholar] [CrossRef]
- Tartakovsky, D.M.; Moulton, J.D.; Zlotnik, V.A. Kinematic structure of minipermeameter flow. Water Resour. Res. 2000, 36, 2433–2442. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Selvadurai, P.A. Surface permeability tests: Experiments and modelling or estimating effective permeability. Proc. R. Soc. A Math. Phys. 2010, 466, 2819–2846. [Google Scholar] [CrossRef]
- Selvadurai, P.A.; Selvadurai, A.P.S. On the effective permeability of a heterogeneous porous medium: The role of the geometric mean. Philos. Mag. 2014, 94, 2318–2338. [Google Scholar] [CrossRef]
- David, C.; David, C.; Wassermann, J.; Amann, F.; Lockner, D.A.; Rutter, E.H.; Vanorio, T.; Amann Hildenbrand, A.; Billiotte, J.; Reuschlé, T.; et al. KG2B: A collaborative benchmarking exercise for estimating the permeability of the Grimsel granodiorite—Part 1: Measurements, pressure-dependence and pore fluid effects. Geophys. J. Int. 2018, 215, 799–824. [Google Scholar] [CrossRef]
- David, C.; Wassermann, J.; Amann, F.; Klaver, J.; Davy, C.; Sarout, J.; Esteban, L.; Rutter, E.H.; Hu, Q.; Louis, L.; et al. KG2B: A collaborative benchmarking exercise for estimating the permeability of the Grimsel granodiorite—Part 2: Modeling, microstructures and complementary data. Geophys. J. Int. 2018, 215, 825–843. [Google Scholar] [CrossRef]
- Brace, W.F.; Walsh, J.B.; Frangos, W.T. Permeability of granite under high pressure. J. Geophys. Res. 1968, 73, 2225–2236. [Google Scholar] [CrossRef]
- Kranzz, R.; Frankel, A.; Engelder, T.; Scholz, C. The permeability of whole and jointed Barre Granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 225–234. [Google Scholar] [CrossRef]
- Bredehoeft, J.D.; Papadopulos, I.S. A method for determining the hydraulic properties of tight formations. Water Resour. Res. 1980, 15, 233–238. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Carnaffan, P. A transient pressure pulse technique for the measurement of permeability of a cement grout. Can. J. Civ. Eng. 1997, 24, 489–502. [Google Scholar] [CrossRef][Green Version]
- Selvadurai, A.P.S.; Boulon, M.J.; Nguyen, T.S. The Permeability of an Intact Granite. Pure Appl. Geophys. 2005, 162, 373–407. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Letendre, A.; Hekimi, B. Axial flow hydraulic pulse testing of an argillaceous limestone. Environ. Earth Sci. 2011, 64, 2047–2058. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. Influence of residual hydraulic gradients on decay curves for one-dimensional hydraulic pulse tests. Geophys. J. Int. 2009, 177, 1357–1365. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Jenner, L. Radial flow permeability testing of an argillaceous limestone. Ground Water 2013, 51, 100–107. [Google Scholar] [CrossRef]
- Selvadurai, A.; Najari, M. Isothermal Permeability of the Argillaceous Cobourg Limestone. Oil Gas Sci. Technol. Rev. L IFP 2016, 71, 53–69. [Google Scholar] [CrossRef]
- Gueguen, Y.; Bouteca, M. Mechanics of Fluid-Saturated Rocks; Elsevier: Amsterdam, The Netherland, 2004. [Google Scholar]
- Cheng, A.H.-D. Poroelasticity; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Selvadurai, A.P.S. On the Poroelastic Biot Coefficient for a Granitic Rock. Geosciences 2021, 11, 219. [Google Scholar] [CrossRef]
- Kasani, H.A.; Selvadurai, A.P.S. A Review of Techniques for Measuring the Biot Coefficient and Other Effective Stress Parameters for Fluid-Saturated Rocks. Appl. Mech. Rev. 2023, 75, 020801. [Google Scholar] [CrossRef]
- Selvadurai, A.; Ichikawa, Y. Some aspects of air-entrainment on decay rates in hydraulic pulse tests. Eng. Geol. 2013, 165, 38–45. [Google Scholar] [CrossRef]
- Selvadurai, A.; Najari, M. On the interpretation of hydraulic pulse tests on rock specimens. Adv. Water Resour. 2013, 53, 139–149. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Najari, M. Laboratory-scale hydraulic pulse testing: Influence of air fraction in the fluid-filled cavity in the estimation of permeability. Geotechnique 2015, 65, 126–134. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Blain-Coallier, A.; Selvadurai, P.A. Estimates for the effective permeability of intact granite obtained from the eastern and western flanks of the Canadian Shield. Mineral 2020, 10, 667. [Google Scholar] [CrossRef]
- Sneddon, I.N. Fourier Transforms; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Sneddon, I.N. The Use of Integral Transforms; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Tranter, C.J. Integral Transforms in Mathematical Physics; John Wiley: New York, NY, USA, 1956. [Google Scholar]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Integral Equations; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Gladwell, G.M.L. Contact Problems in the Classical Theory of Elasticity; Springer: Dordrecht, The Netherland, 1980. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. On the problem of an electrified disc at the central opening of a co-planar sheet. Mech. Res. Commun. 1996, 23, 621–624. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Singh, B.M. On the expansion of a penny-shaped crack by a rigid circular disc inclusion. Int. J. Fract. 1984, 25, 69–77. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Singh, B.M. The Annular Crack Problem for an Isotropic Elastic Solid. Q. J. Mech. Appl. Math. 1985, 38, 233–243. [Google Scholar] [CrossRef]
- Selvadurai, A.; Selvadurai, P.; Suvorov, A. Contact mechanics of a dilatant region located at a compressed elastic interface. Int. J. Eng. Sci. 2018, 133, 144–168. [Google Scholar] [CrossRef]
- Basset, A.B. A Treatise on Hydrodynamics Vol 1; Deighton, Bell and Co.: Cambridge, UK, 1990. [Google Scholar]
- Basset, A.B. A Treatise on Hydrodynamics Vol II, with Numerous Examples; Deighton, Bell and Co.: Cambridge, UK, 1881. [Google Scholar]
- Hobson, E.W. The Theory of Spherical and Ellipsoidal Harmonics; Cambridge University Press: New York, NY, USA, 1931. [Google Scholar]
- Sternberg, W.J.; Smith, T.L. Theory of Potential and Spherical Harmonics; University of Toronto: Toronto, ON, Canada, 1944. [Google Scholar]
- Sternberg, E.; Eubanks, R.A.; Sadowsky, M.A. On the stress function approaches of Boussinesq and Timpe to the axisymmetric problem of elasticity theory. J. Appl. Phys. 1951, 22, 1121–1124. [Google Scholar] [CrossRef]
- Edwards, R.H. Stress Concentrations Around Spheroidal Inclusions and Cavities. J. Appl. Mech. 1951, 18, 19–30. [Google Scholar] [CrossRef]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953; Volume 1–2. [Google Scholar]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Martinus Nijhoff Publishers: The Hague, The Netherlands, 1973. [Google Scholar] [CrossRef]
- Moon, P.; Spencer, D.E. Field Theory Handbook; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Selvadurai, P.A. Permeability of Indiana Limestone: Experiments and Theoretical Concepts for Interpretation of Results. Master’s Thesis, McGill University, Montreal, QC, Canada, 2010. [Google Scholar]
- Stevenson, D.R.; Brown, A.; Davison, C.C.; Gascoyne, M.; McGregor, R.G.; Ophori, D.U.; Schier, N.W.; Stanchell, F.; Thorne, G.A.; Tomsons, D.K. A Revised Conceptual Hydrogeologic Model of a Crystalline Rock Environment, Whiteshell Research Area, Southeastern Manitoba, Canada, AECL-11331, COG-95-271; Atomic Energy of Canada Limited, Whiteshell Laboratories: Pinawa, MB, Canada, 1996. [Google Scholar]
- Katsube, T.J.; Hume, J.P. Permeability determination in crystalline rocks by standard geophysical logs. Geophysics 1987, 52, 342–352. [Google Scholar] [CrossRef]
- Souley, M.; Homand, F.; Pepa, S.; Hoxha, D. Damage-induced permeability changes in granite: A case example at the URL in Canada. Int. J. Rock Mech. Min. Sci. 2001, 38, 297–310. [Google Scholar] [CrossRef]
- Leemis, L.; Harr, M.E. Reliability-Based Design in Civil Engineering; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).