Accuracy of Structure-from-Motion/Multiview Stereo Terrain Models: A Practical Assessment for Applications in Field Geology
Abstract
1. Introduction
2. Background and Methods
2.1. Background
2.2. Methods
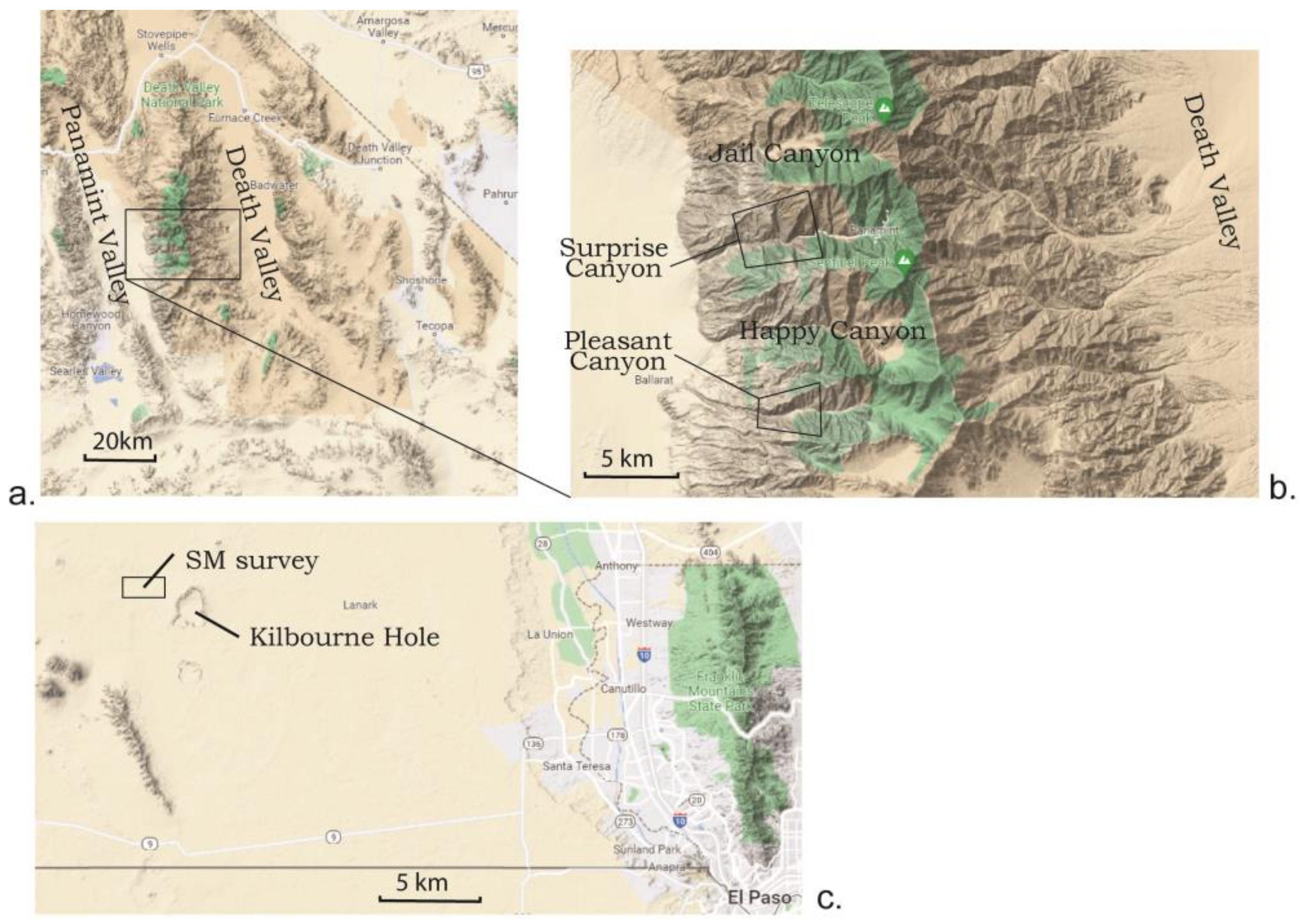
2.2.1. LiDAR Data
2.2.2. SM Data
2.2.3. Data Processing
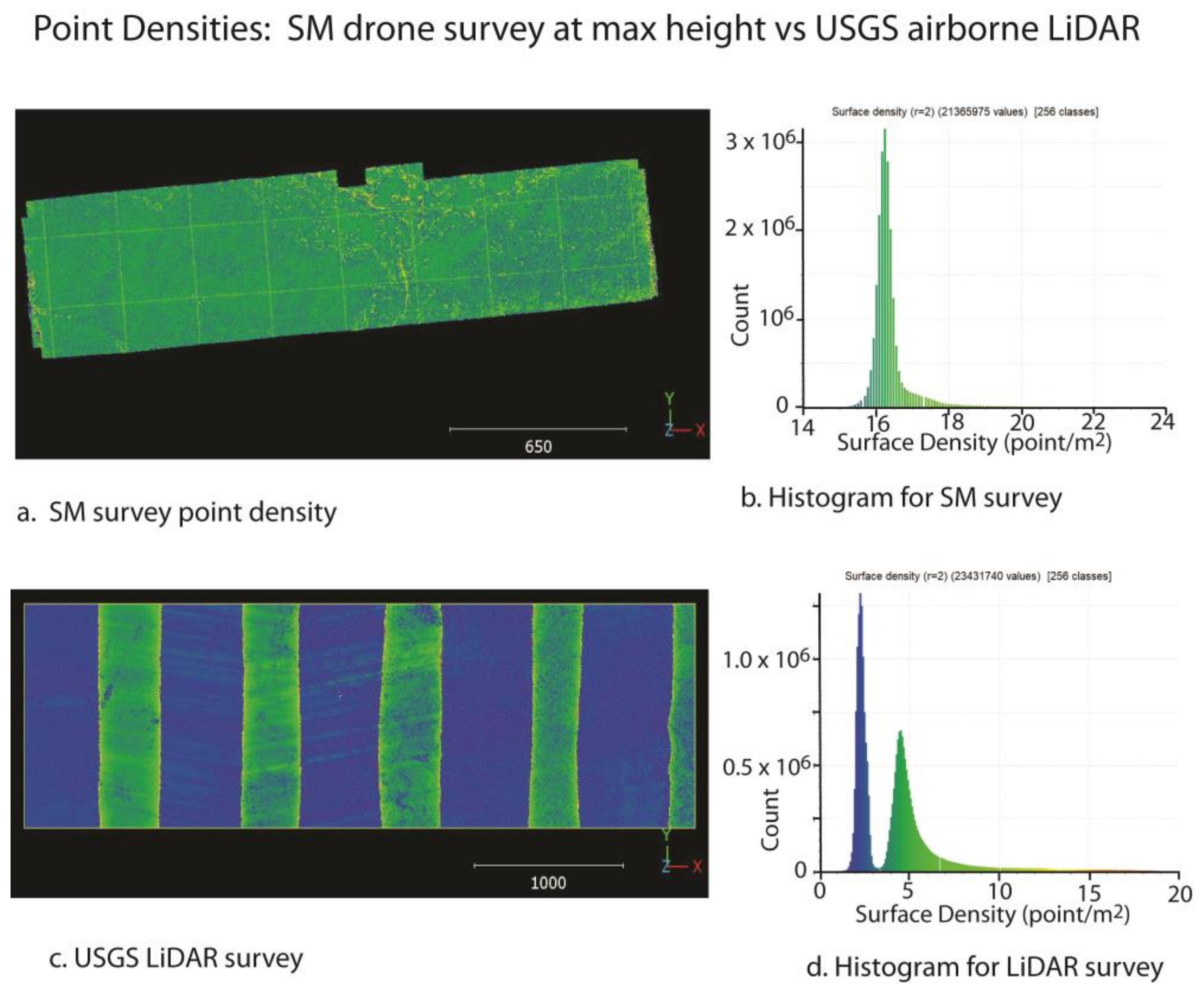
2.2.4. Point Densities and Cloud Mismatch Measurements
3. Results
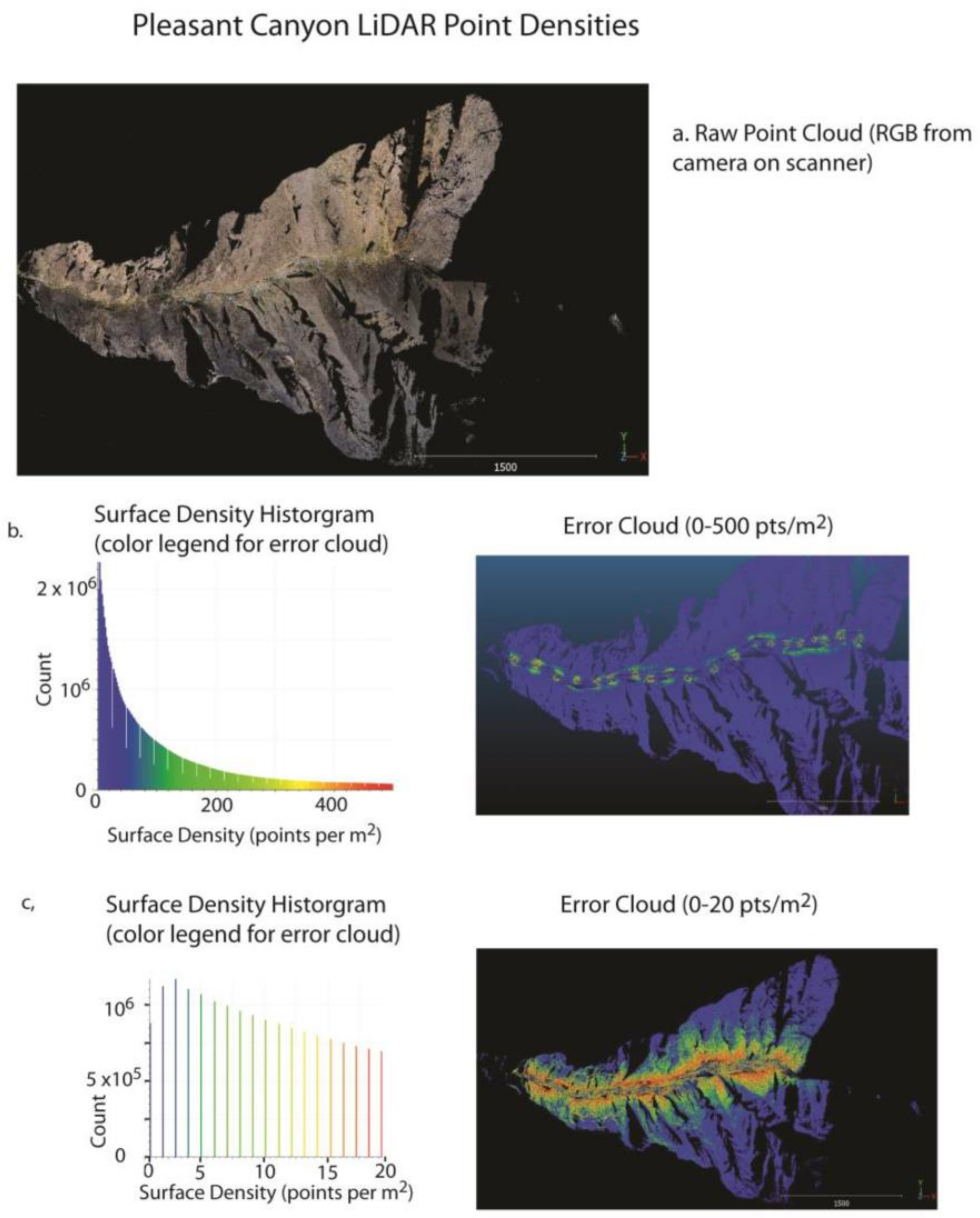
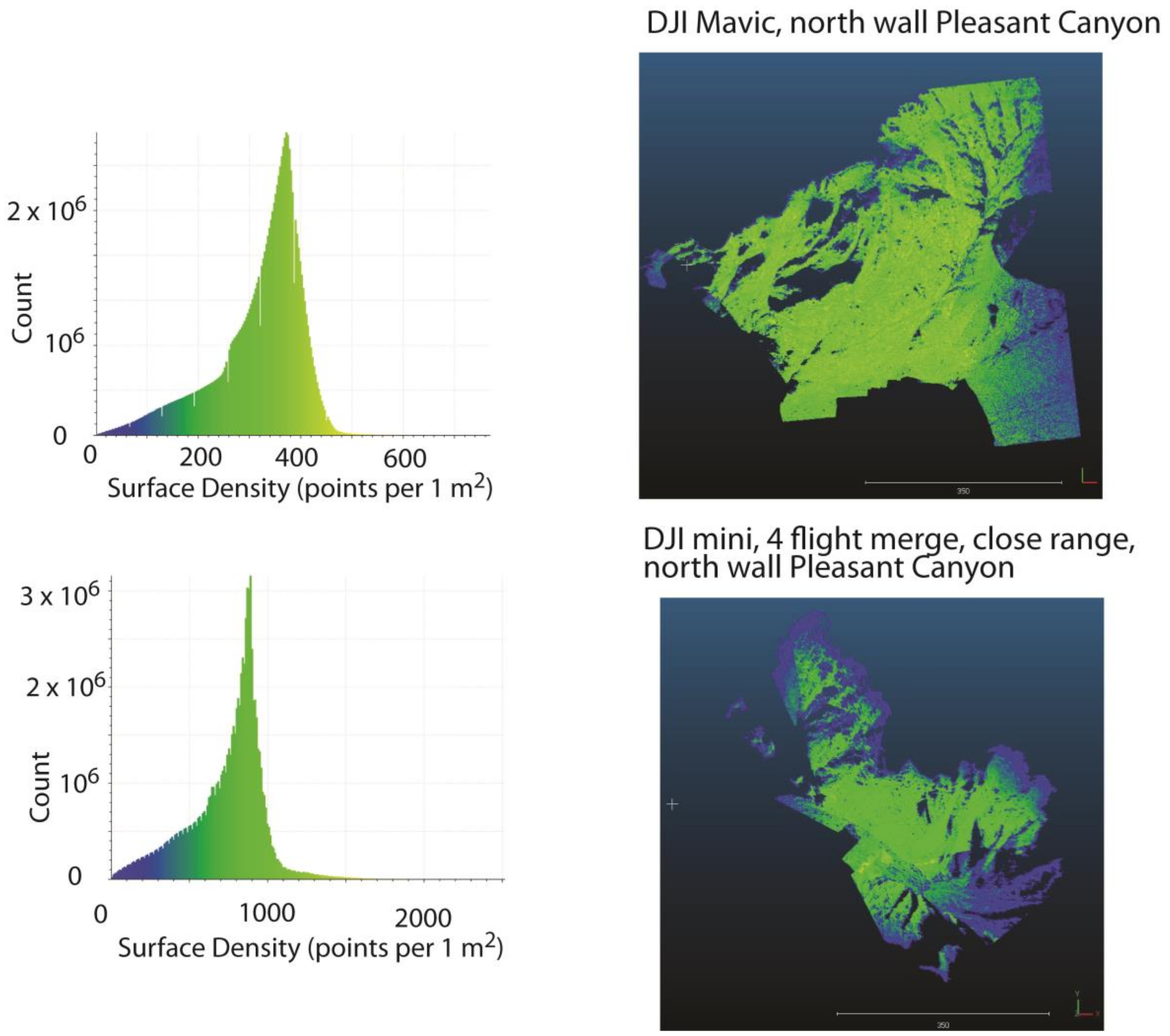
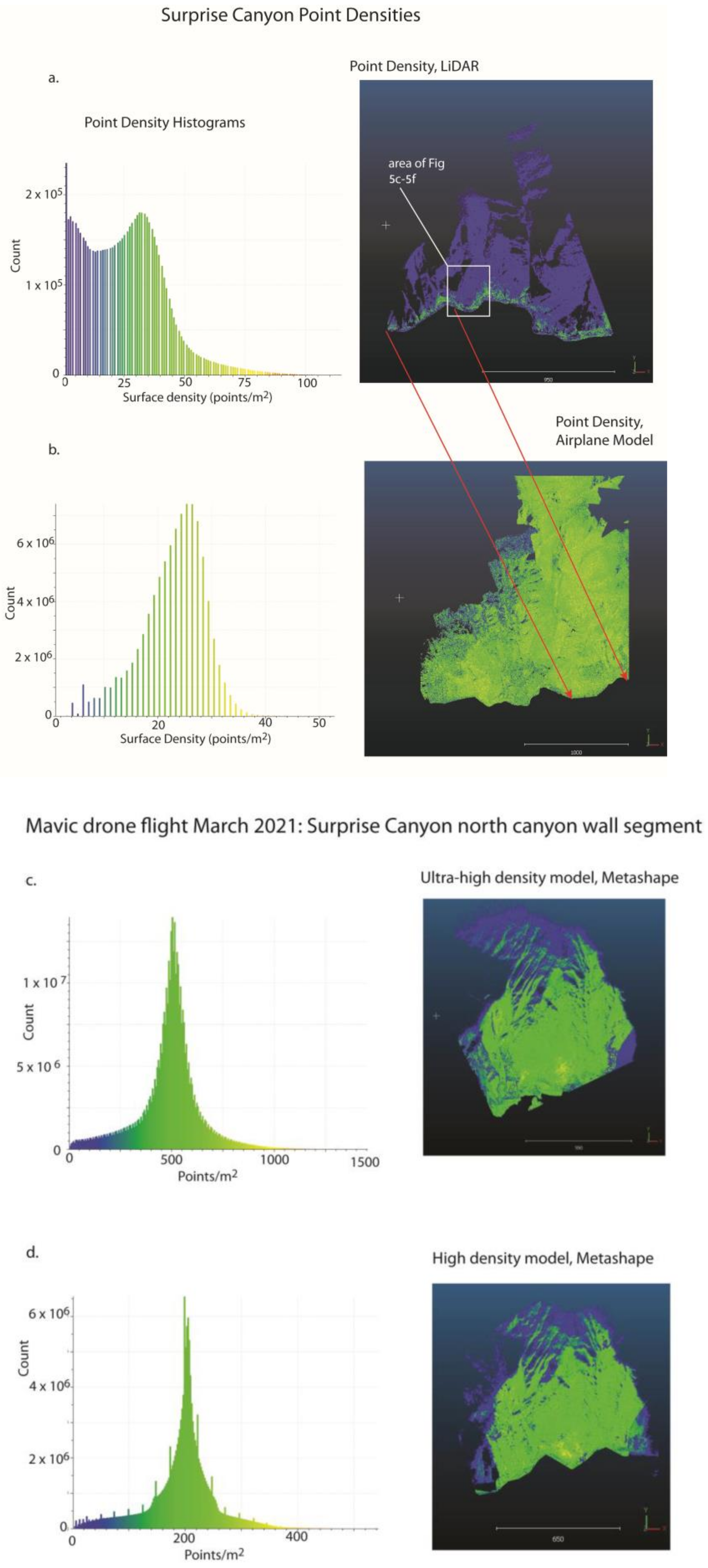
3.1. Point Densities
Animation 1
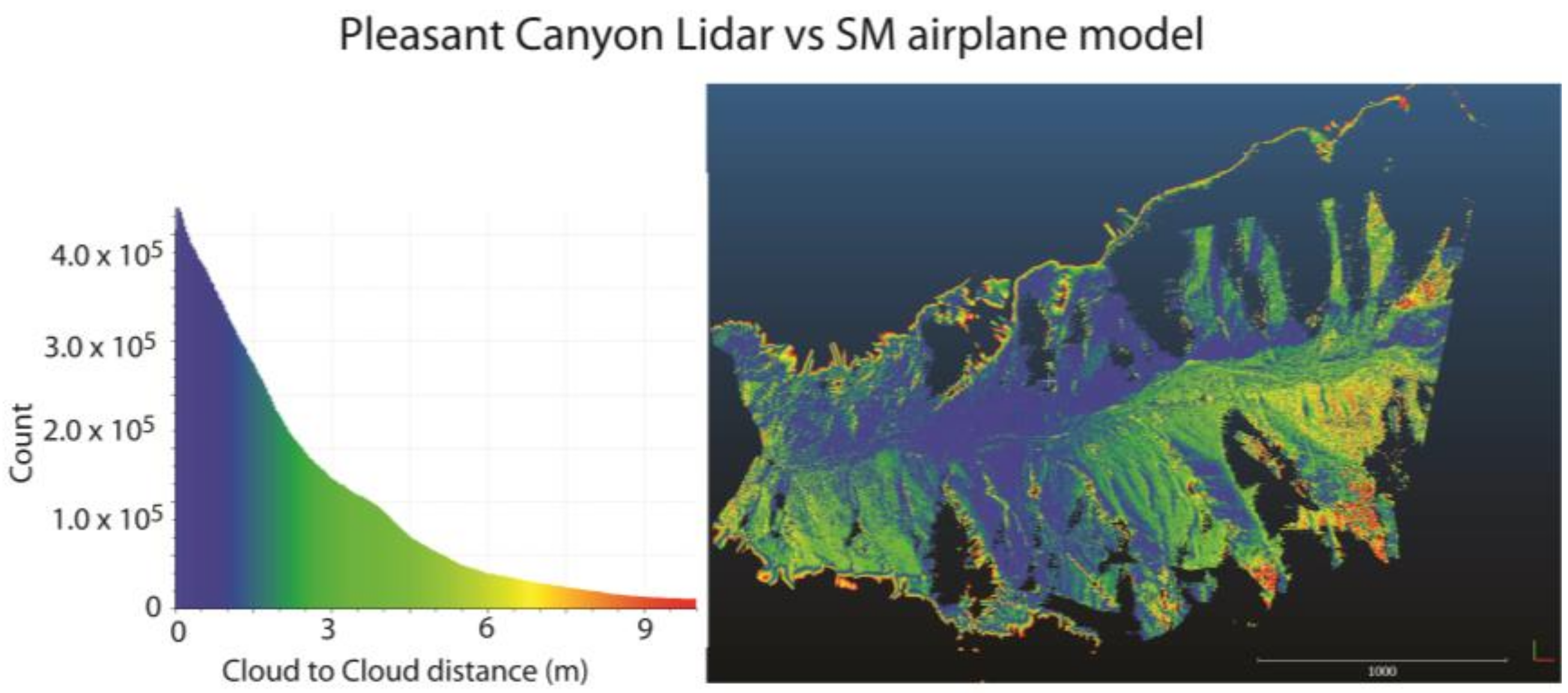
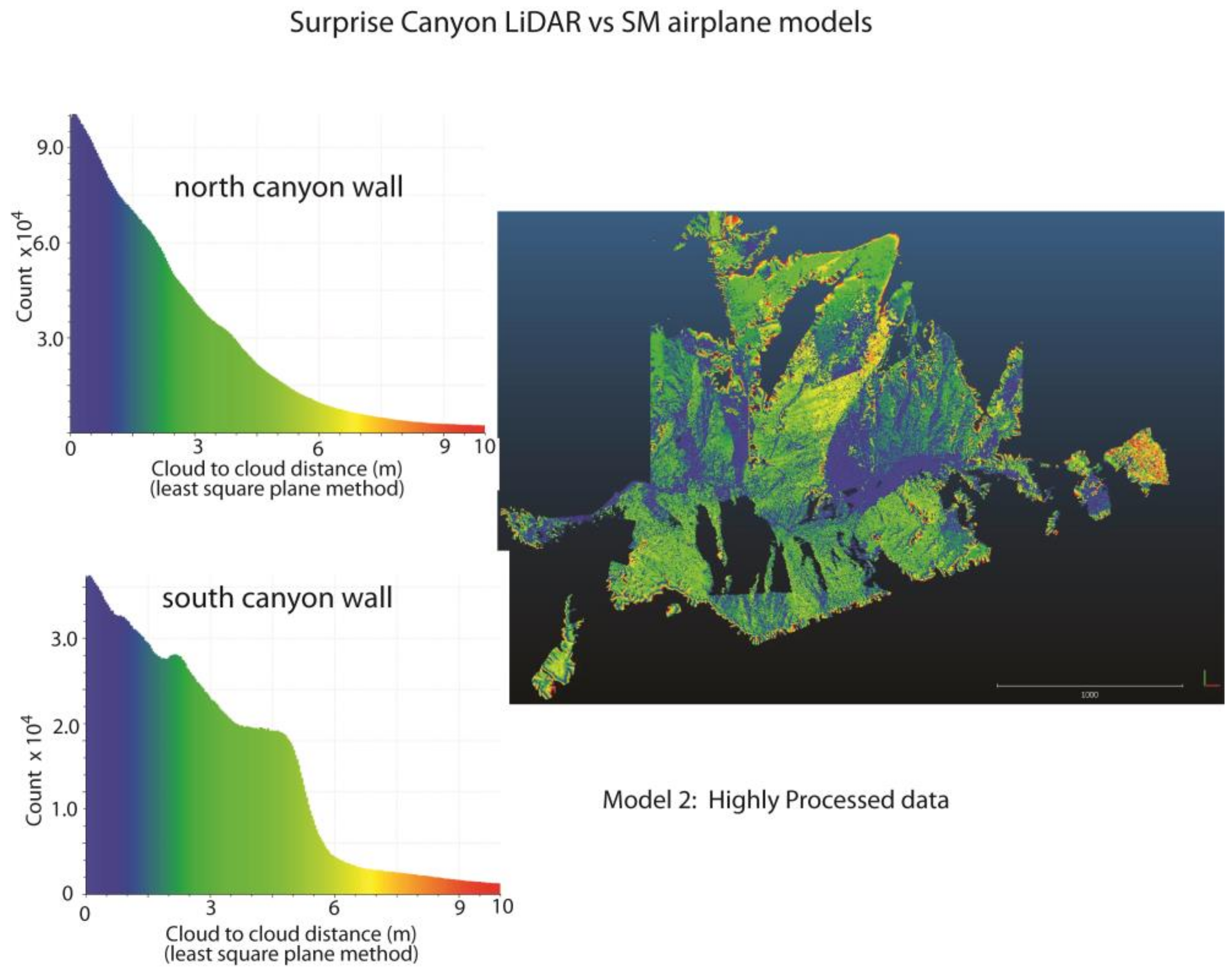
3.2. Cloud–Cloud Distance Measurements
3.2.1. Data Processing Procedure
3.2.2. Analysis of Aircraft Imaging SM vs. LiDAR
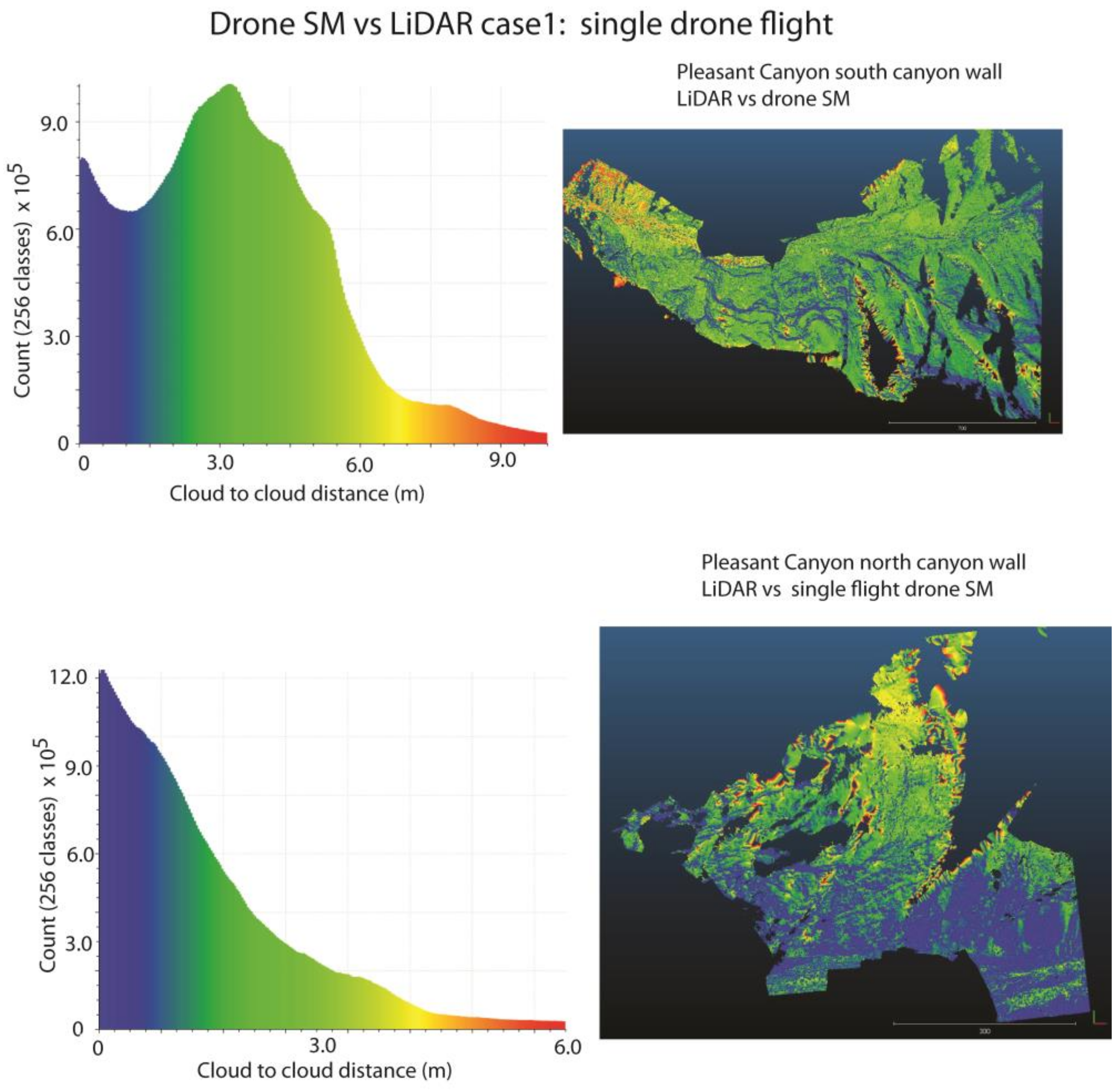
3.2.3. Analysis of Drone Imaging SM vs. LiDAR
4. Discussion
4.1. Resolution and Scale
4.2. Comparison between LiDAR and SM Photogrammetry Model Scale and Absolute Registration
4.3. Camera Quality, Functionality, and Cost
4.4. Significance for Geologic Field Studies
4.5. Suggestions for Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pavlis, T.L.; Langford, R.; Hurtado, J.; Serpa, L. Computer-based data acquisition and visualization systems in field geology: Results from 12 years of experimentation and future potential. Geosphere 2010, 6, 275–294. [Google Scholar] [CrossRef]
- Pavlis, T.L.; Mason, K.A. The new world of 3D geologic mapping. GSA Today 2017, 27, 4–10. [Google Scholar] [CrossRef]
- Brush, J.A.; Pavlis, T.L.; Hurtado, J.M.; Mason, K.A.; Knott, J.R.; Williams, K.E. Evaluation of field methods for 3-D mapping and 3-D visualization of complex metamorphic structure using multiview stereo terrain models from ground-based photography. Geosphere 2018, 15, 188–221. [Google Scholar] [CrossRef]
- Carrivick, J.L.; Smith, M.W.; Quincey, D.J. Structure from Motion in the Geosciences; John Wiley and Sons: West Sussex, UK, 2016; 197p. [Google Scholar]
- Furukawa, Y.; Hernandez, C. Multi-View Stereo: A Tutorial. Found. Trends Comput. Graph. Vis. 2015, 9, 1–148. [Google Scholar] [CrossRef]
- Martinez, V.V.; Serpa, L.F. Introduction to teaching science with three-dimensional images of dinosaur footprints from Cristo Rey, New Mexico. Geosci. Commun. 2022, 5, 1–9. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure from Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Rutkofske, J.E.; Pavlis, T.L.; Ramirez, S. Applications of modern digital mapping systems to Assist inclusion of persons with disabilities in geoscience education and research. J. Struct. Geol. 2022, 161, 104655. [Google Scholar] [CrossRef]
- Svennevig, K.; Guarnieri, P.; Stemmerik, L. From oblique photogrammetry to a 3D model—Structural modeling of Kilen, eastern North Greenland. Comput. Geosci. 2015, 83, 120–126. [Google Scholar] [CrossRef]
- Franceschi Marco Martinelli, M.; Gislimberti, L.; Rizzi, A.; Massironi, M. Integration of 3D modeling, aerial LiDAR and photogrammetry to study a synsedimentary structure in the Early Jurassic Calcari Grigi (Southern Alps, Italy). Eur. J. Remote Sens. 2015, 48, 527–539. [Google Scholar] [CrossRef]
- Johnson, K.; Nissen, E.; Saripalli, S.; Arrowsmith, J.R.; McGarey, P.; Scharer, K.; Williams, P.; Blisniuk, K. Rapid mapping of ultrafine fault zone topography with structure from motion. Geosphere 2014, 10, 969–986. [Google Scholar] [CrossRef]
- Cawood, A.J.; Bond, C.E.; Howell, J.A.; Butler, R.W.H.; Totake, Y. LiDAR, UAV or compass-clinometer? Accuracy, coverage and effects on structural models. J. Struct. Geol. 2017, 98, 67–82. [Google Scholar] [CrossRef]
- Martinez, V.V. Implementation of Structure from Motion (SfM) Technology for Educational Lessons. Ph.D. Thesis, University of Texas, El Paso, TX, USA, 2022; 71p. [Google Scholar]
- Caroti, G.; Martinez-Espejo, Z.; Piemonte, A. Accuracy assessment in structure from motion 3D reconstruction from UAV-born images: The influence of the data processing methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 103–109. [Google Scholar] [CrossRef]
- Paolo, C.; Girelli, V.A.; Mandanici, E. Structure from Motion for aerial thermal imagery at city scale: Pre-procesing, camera calibration, accuracy assessment. ISPRS J. Photogramm. Remote Sens. 2018, 146, 320–333. [Google Scholar] [CrossRef]
- Iheaturu, C.J.; Ayodele, E.G.; Okolie, C.J. An assessment of the accuracy of structure-from-motion (SFM) photogrammetry for 3D terrain mapping. Geomat. Landmanag. Landsc. 2020, 2, 65–82. [Google Scholar] [CrossRef]
- Martinez, J.G.; Albeaino, G.; Gheisari, M.; Volkmann, W.; Alarcon, L.F. UAS Point Cloud Accuracy Assessment Using Structure from Motion–Based Photogrammetry and PPK Georeferencing Technique for Building Surveying Applications. J. Comput. Civ. Eng. 2021, 35, 05020004. [Google Scholar] [CrossRef]
- Deliry, S.D.; Avdan, U. Accuracy of unmanned aerial systems photogrammetry and Structure from Motion in Surveying and Mapping: A review. J. Indian Soc. Remote Sens. 2021, 49, 1997–2017. [Google Scholar] [CrossRef]
- Fleming, Z.; Pavlis, T.L. An orientation based correction method for SfM-MvS point clouds—Implications for field geology. J. Struct. Geol. 2018, 113, 76–89. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A. Elements of Photogrammetry with Applications to GIS, 3rd ed.; McGraw-Hill: Boston, MA, USA, 2000; 608p. [Google Scholar]
- Haugerud, R.A.; Harding, D.J.; Johnson, S.Y.; Harless, J.L.; Weaver, C.S.; Sherrod, B.L. High-resolution LiDAR topography of the Puget Lowland, Washington—A Bonanza for Earth Science. GSA Today 2003, 13, 4–10. [Google Scholar] [CrossRef]
- Höfle, B.; Rutzinger, M. Topographic airborne LiDAR in geomorphology: A technological perspective. Z. Fur Geomorphol. Suppl. 2011, 55, 1. [Google Scholar] [CrossRef]
- Wilkinson, M.W.; Jones, R.R.; Woods, C.E.; Gilment Sr McCaffrey, K.J.W.; Kokkalas, S.; Long, J.J. A comparison of terrestrial laser scanning and structure-from-motion photogrammetry as methods for digital outcrop acquisition. Geosphere 2016, 12, 1865–1880. [Google Scholar] [CrossRef]
- Ramsay, J.G. Folding and Fracturing of Rocks; McGraw-Hill: New York, NY, USA, 1967; 568p. [Google Scholar]
- Ramsay, J.G.; Huber, M.I. The Techniques of Modern Structural Geology, v2: Folds and Fractures; Academic Press: London, UK, 1987; pp. 309–700. [Google Scholar]
- Ramsay, J.G.; Lisle, R.J. The Techniques of Modern Structural Geology, v3: Applications of Continuum Mechanics in Structural Geology; Academic Press: London, UK, 2000; pp. 701–1061. [Google Scholar]




| Location | Acquisition Method | Point Density Range | Point Density at Peak Count | Estimated Resolution at Peak Count |
|---|---|---|---|---|
| LiDAR | (Points/m2) | (Points/m2) | cm | |
| Pleasant Canyon Brush et al. (2018) | TLS | 1–100 at target (spatial dependence) | <20 | >22 |
| Surprise Canyon Brush et al. (2018) | TLS | 1–100 at target (spatial dependence) | <20 | >22 |
| Kilbourne Hole, NM See USGS metadata | USGS airborne LiDAR, low-relief terrain | 2.5 (background) to 5 (overlap areas) | 2.5 | 63 |
| Aircraft | ||||
| Pleasant Canyon-HD Metashape | Manned aircraft, Nikon Df camera, single pass | 1–15 | 10 | 32 |
| Surprise Canyon HD Metashape | Manned aircraft, two cameras | 10–40 | 25 | 20 |
| Handheld Camera | ||||
| Surprise Canyon HD Metashape (Brush et al., 2018) | Ground-based, Nikon D5300 at 200–700 m | 1–500 | 290 | 6 |
| Pleasant Canyon HD Metashape (Brush et al., 2018) | Ground-based, Nikon D5300 at 600–1500 m | 1–80 | 45 | 15 |
| Autonomous Drone flt | ||||
| Kilbourne Hole, NM HD Metashape | DJI Mavic autonomous flight 100 m elevation | 15–18 | 16.2 | 25 |
| UAV (Drone) | ||||
| Pleasant Canyon HD Metashape | DJI Mavic, 100–200 m from target, single flt. | 1–400 | 375 | 5 |
| Pleasant Canyon HD Metashape | DJI mini, close range (10–30 m) | 1–1200 | 850 | 3 |
| Pleasant Canyon HD Metashape | DJI Mavic, 4 flight merge | 1–800 | dual max at ~210 and 390 | 7 and 5 |
| Surprise Canyon HD Metashape | DJI Mavic, single flight | 1–400 | 200 | 7 |
| Surprise Canyon Ultra HD Metashape | DJI Mavic, single flight (same as above) | 1–1000 | 500 | 4 |
| Surprise Canyon Pix4D (optimal) processing | DJI Mavic, single flight (same as above) | 1–200 | 20 | 22 |
| Surprise Canyon HD Pix4D | DJI Mavic, single flight (same as above) | 1–600 | 100 | 10 |
| Surprise Canyon HD Metashape | DJI Mavic, two-flight merge in canyon bend | 1–230 | 170 | 8 |
| Location | Acquisition Method | Georeference Method | Absolute Distance (Range) | Absolute Distance (Histogram Peak Showing Systematic Error) | X (East) Component of Offset | Y (North) Component of Offset | Z (Up) Component of Offset |
|---|---|---|---|---|---|---|---|
| Pleasant Canyon | Handheld camera from chartered airplane | Georeferenced w/Google Earth | 0–9 m. Poorest alignment where camera angles were unfavorable | none | <1 m | <1 m | <1 m, up to 3 m where camera angles were unfavorable |
| Surprise Canyon, Model 1 | Handheld camera from chartered airplane | Quick georeferenced w/Google Earth | 0–60 m. Poorest alignment at east end of model (bad GCP?) | 15–30 m | nd | nd | nd |
| Surprise Canyon, Model 2 | Handheld camera from chartered airplane | Extensive image processing and georeferenced w/Google Earth | 0–5 m. Variance in offsets across canyon and variation with look direction | <1 m | <1 m | <1 m | <1 m |
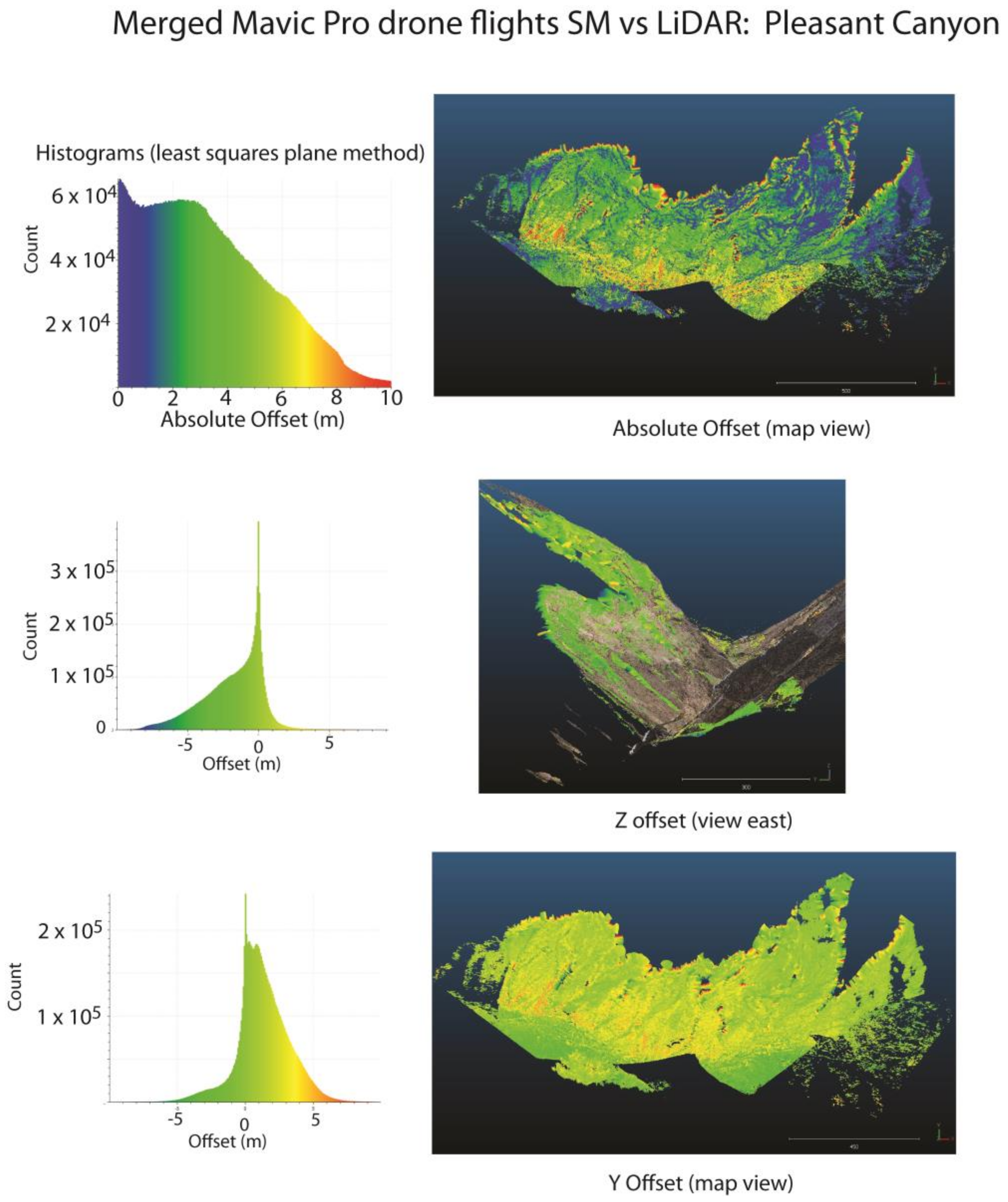
| Pleasant Canyon | single drone flight, DJI Mavic Pro | Standard differential GNSS camera positions | 0–9 m, core data 0–4 m | 4 m | <1 m | <1 m | 3–4 m |
| Pleasant Canyon | single drone flight, DJI Mavic Pro | Standard differential GNSS camera positions | 0–3 m | None, increase error at ridgetop due to sparse LiDAR? | <1 m | <1 m | <1 m |
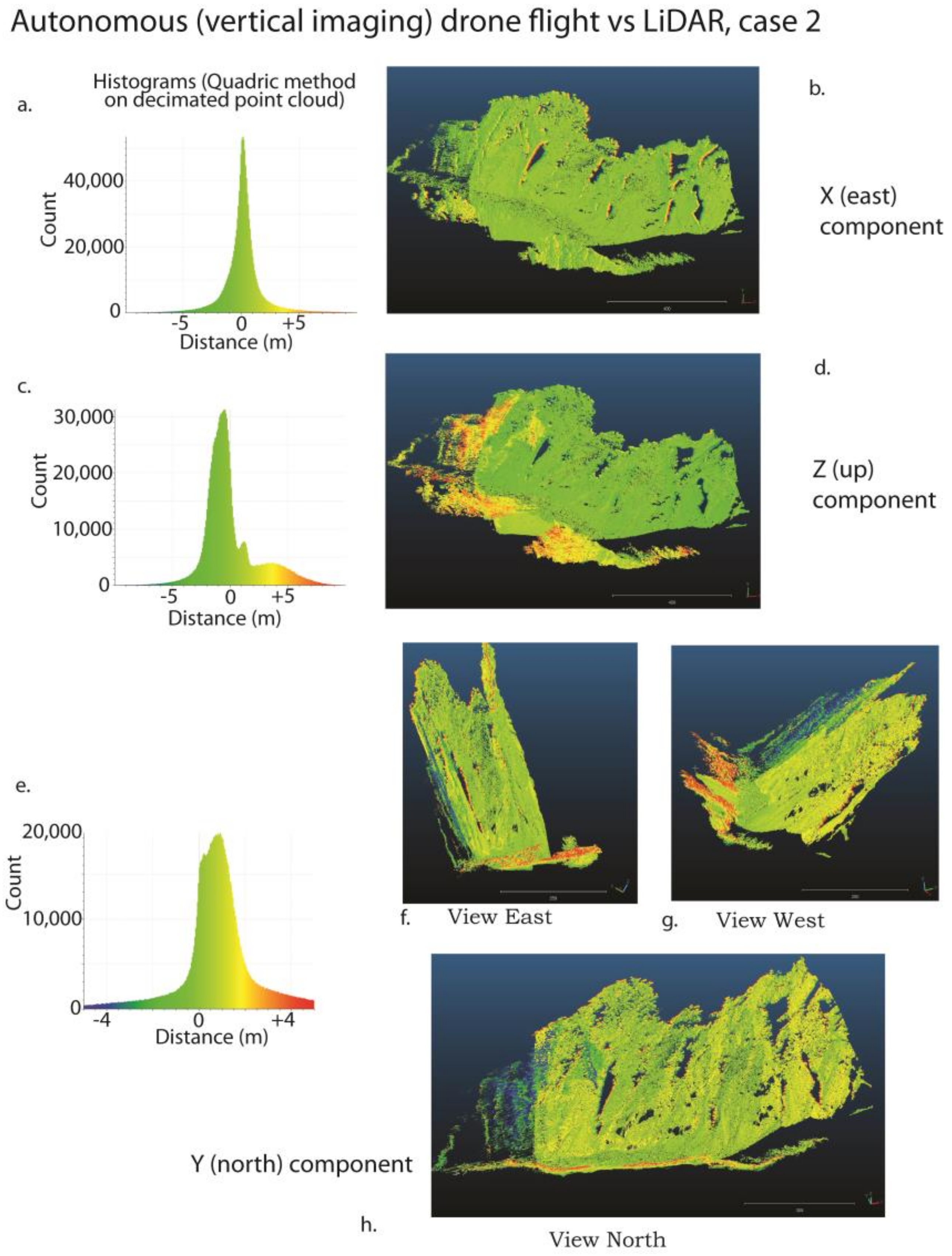
| Pleasant Canyon | Autonomous drone flight, DJI Mavic Pro | Standard differential GNSS camera positions | 0–5 m | ~2 m | <1 m | ~1 m | −2 m |
| Pleasant Canyon | DJI mini 2, single flight | Standard differential GNSS camera positions | 0–8 m | ~4 m | <1 m | <1 m | ~4 m |
| Pleasant Canyon | DJI Mini1, 5 close range flts merged | Standard differential GNSS camera positions | 0–2 m in core model area, larger outside imaging array | <1 m | nd | nd | nd |
| Pleasant Canyon | DJI Mavic Pro, 4 flights, different days, processed in Metashape | Standard differential GNSS camera positions | 0–8m | Peak at 0, secondary peak at 3m | <1 m | Peak at 0, tail to +5 at sites close to scanner | Peak at 0, tail to -5 at sites close to scanner |
| Surprise Canyon, north bank | DJI Mavic Pro, single flight, small variation in Z in flight plan | Standard differential GNSS camera positions | 0–10 m, error systematic across model showing rigid body rotation | ~4 m | <1 m | Peak at 2m, error varies across model showing rigid body rotation | Peak at ~−3m |
| Surprise Canyon, sharp turn in canyon | DJI Mavic Pro, single flight | Standard differential GNSS camera positions | 1–4 m | <1 m | <1 m | <1 m | <1 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlis, T.L.; Serpa, L.F. Accuracy of Structure-from-Motion/Multiview Stereo Terrain Models: A Practical Assessment for Applications in Field Geology. Geosciences 2023, 13, 217. https://doi.org/10.3390/geosciences13070217
Pavlis TL, Serpa LF. Accuracy of Structure-from-Motion/Multiview Stereo Terrain Models: A Practical Assessment for Applications in Field Geology. Geosciences. 2023; 13(7):217. https://doi.org/10.3390/geosciences13070217
Chicago/Turabian StylePavlis, Terry L., and Laura F. Serpa. 2023. "Accuracy of Structure-from-Motion/Multiview Stereo Terrain Models: A Practical Assessment for Applications in Field Geology" Geosciences 13, no. 7: 217. https://doi.org/10.3390/geosciences13070217
APA StylePavlis, T. L., & Serpa, L. F. (2023). Accuracy of Structure-from-Motion/Multiview Stereo Terrain Models: A Practical Assessment for Applications in Field Geology. Geosciences, 13(7), 217. https://doi.org/10.3390/geosciences13070217










