Kinematic and Geometric Characterization of the Vögelsberg Rockslide (Tyrol, Austria) by Means of MT-InSAR Data
Abstract
:1. Introduction
2. Study Site
3. Materials and Methods
3.1. Materials
3.1.1. Ancillary Data
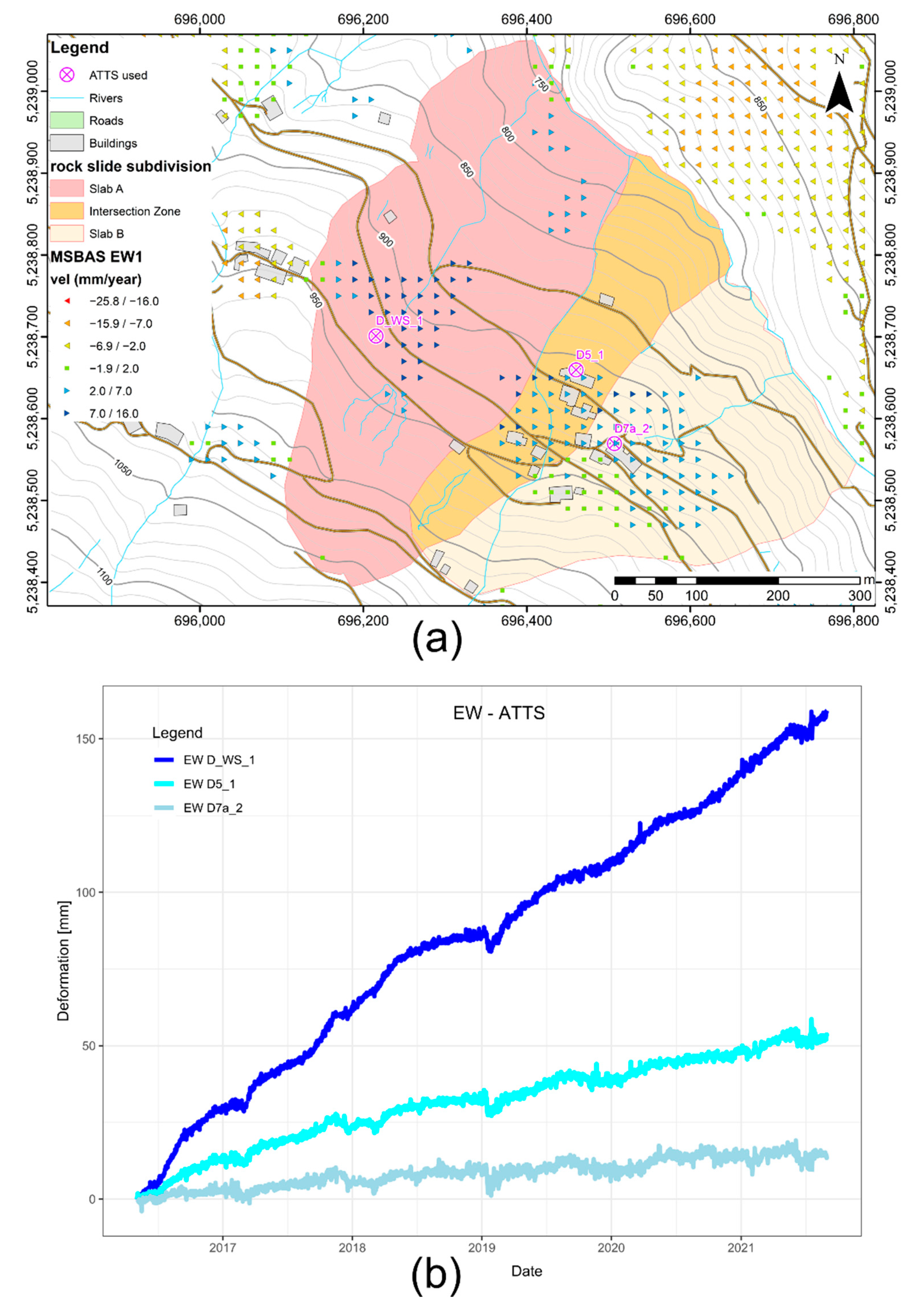
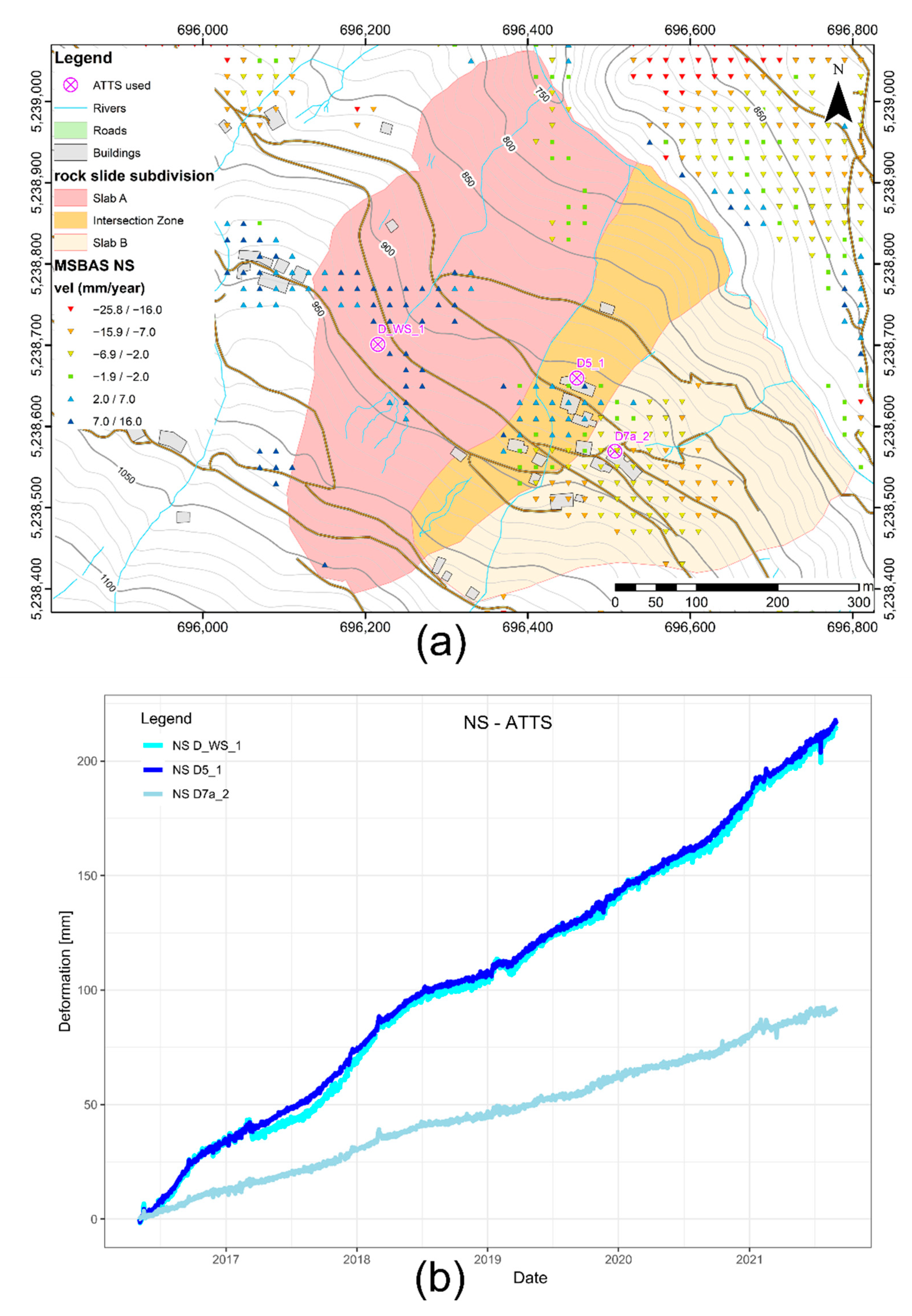
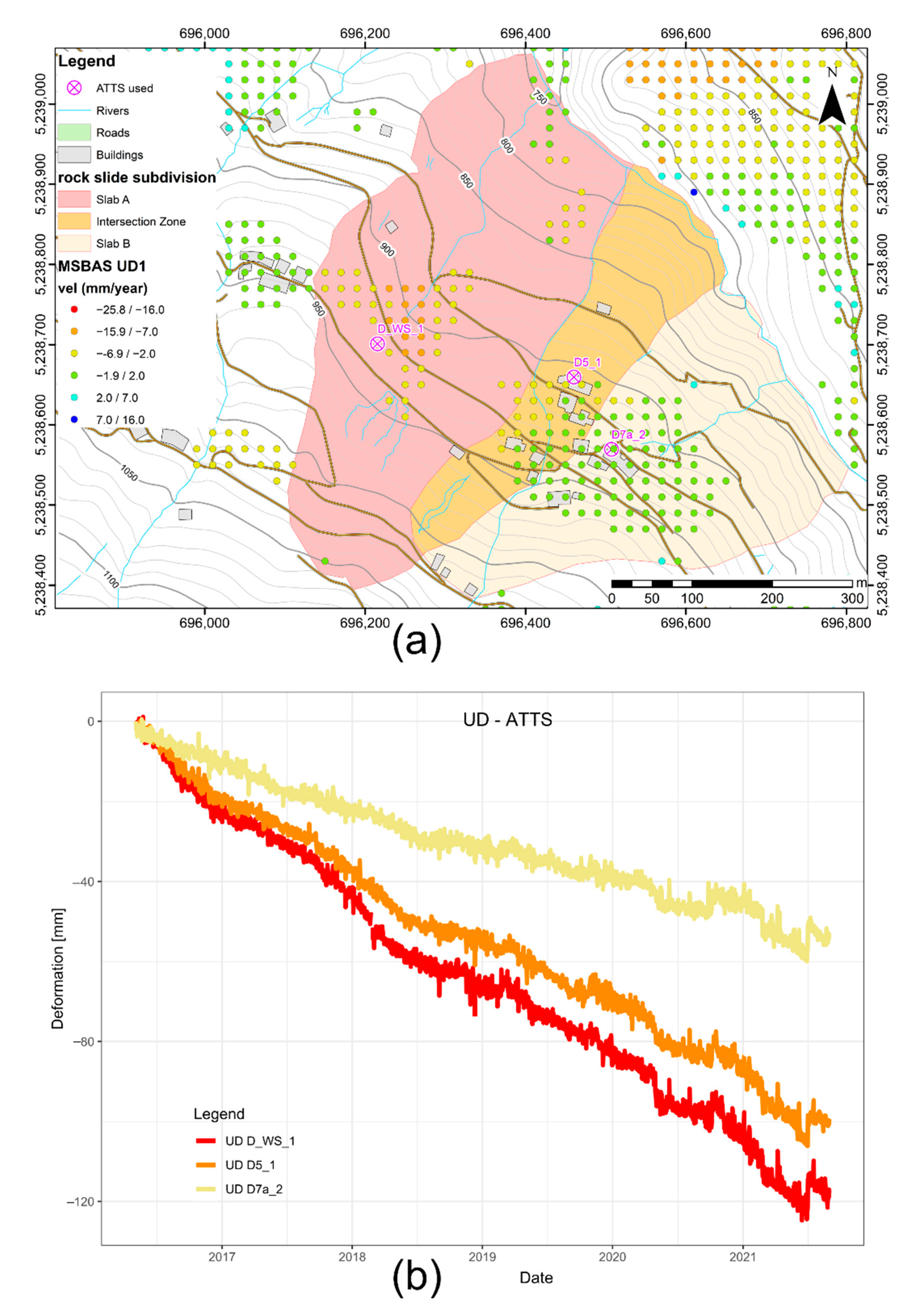
- Slab A: 27.6 cm of horizontal displacement and −11.6 cm of vertical displacement.
- Intersection zone: 22.4 cm horizontal displacement and −10 cm vertical displacement.
- Slab B: 9.2 cm horizontal displacement and −5.2 cm vertical displacement.
- Low damage (green): less visible outside wall cracks; easily eliminated with normal painting works.
- Medium damage (yellow): clearly visible outside wall cracks. It may be necessary to refurbish limited masonry components; locked doors and windows.
- High damage (red): restoration works required, with partial or total removal of the artefact; danger of collapse.
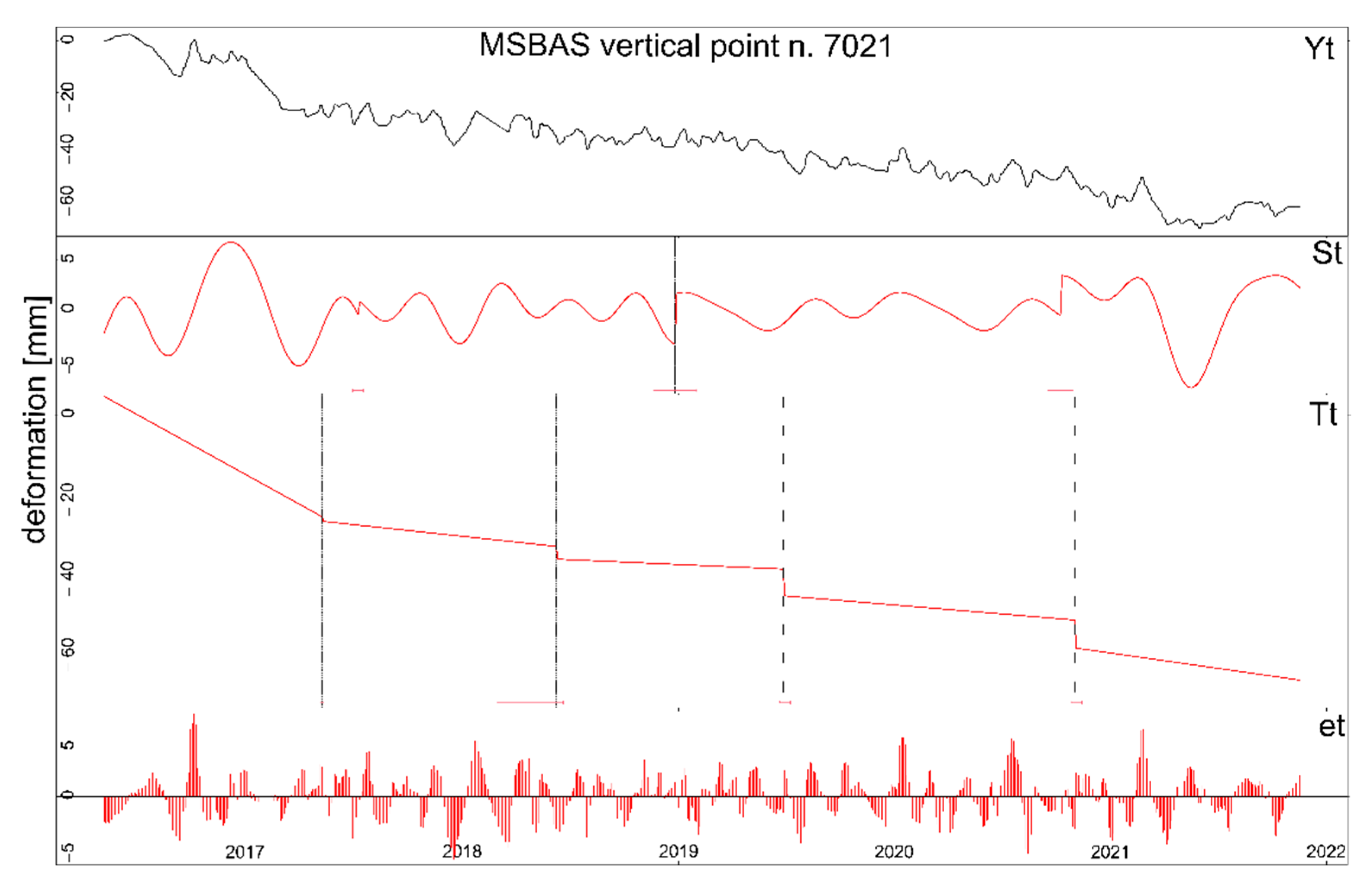
- Event 1: connected to a maximum horizontal displacement rate of 5.71 cm/year and a reactivation phase in August 2016; this event is rain- and snowmelt-dominated and it has a delay-response time varying in the range of 20–60 days.
- Event 2: connected to a second acceleration phase starting in mid-July 2017 and reaching its maximum displacement rate equal to 4.98 cm/year in February 2018; this event is rainfall-dominated and has a delay-response time of 45 days.
- Event 3: connected to a third acceleration phase recorded in March and April 2019 with maximum displacement rate of 3.57 cm/year; this event is mainly snowmelt- dominated and has a delay-response time of 8 days.
3.1.2. Newly Acquired Data
3.2. Methods
3.2.1. MT-InSAR Time Series Decomposition with BFAST
- seasonal changes driven by annual climate variability occur;
- gradual changes such as inter-annual climate variability (e.g., trends in mean annual rainfall) occur;
- abrupt changes, caused by the interaction of long-time and intense precipitation and snow melting that could control ground instabilities activity, are taking place [26];
- extra triggering events are present.
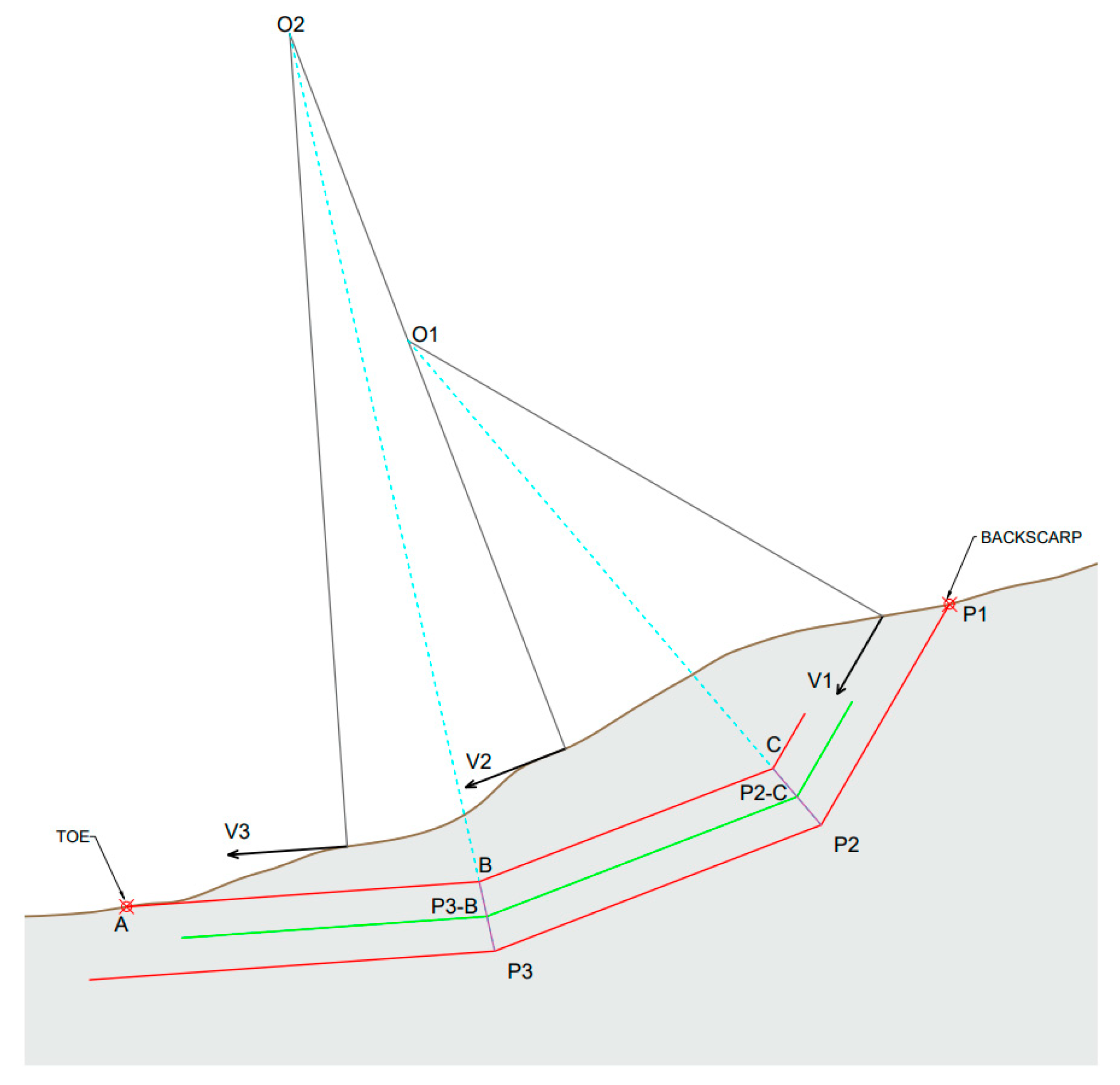
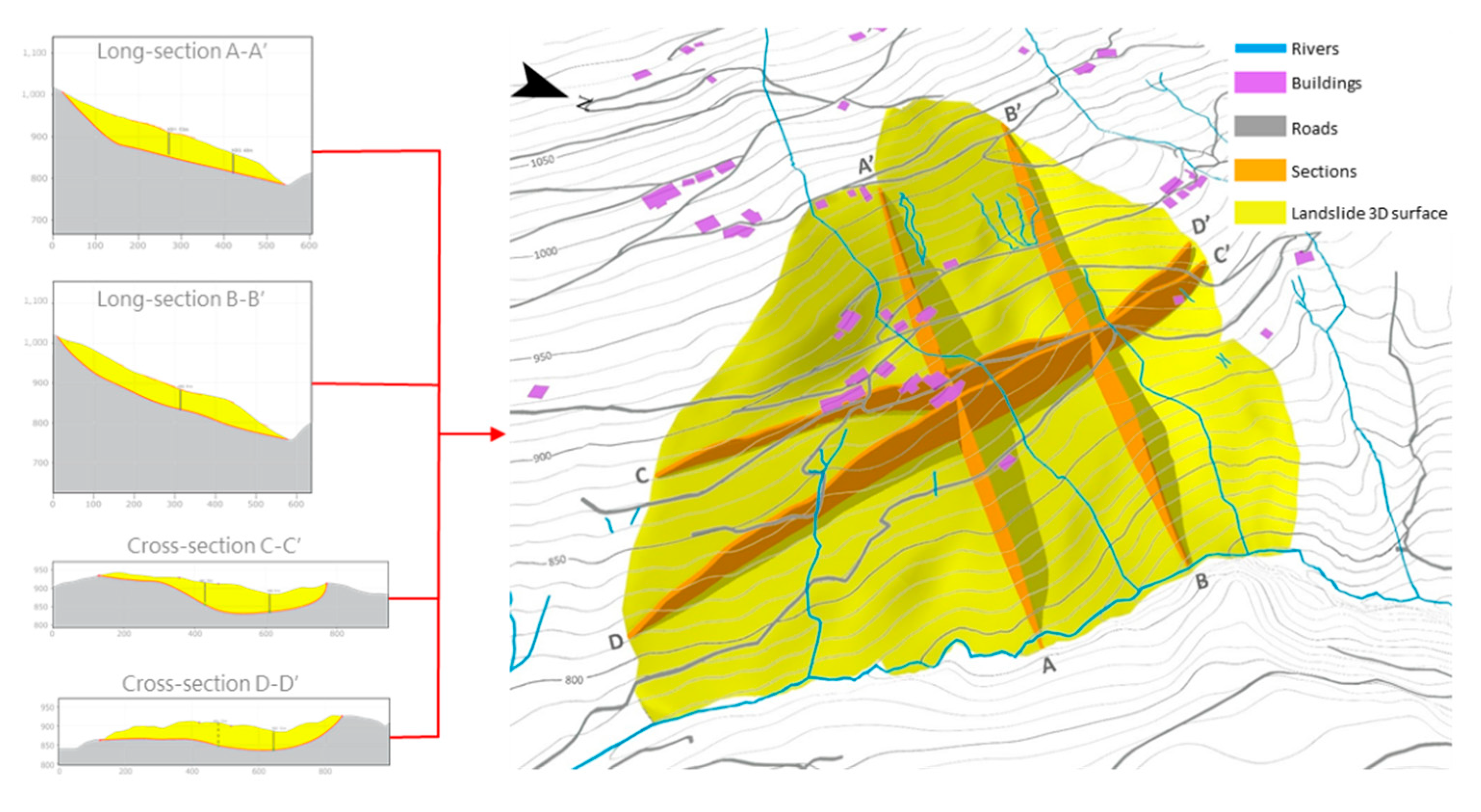
3.2.2. Two- and Three-dimensional Landslide Geometry Reconstruction by Applying the VIM Method
- a single slide surface exists,
- the landslide mass moves as a rigid body,
- a point on the ground will move in a direction that is parallel to the sliding surface beneath.
4. Results
4.1. Kinematic Analysis of Slab A
4.2. Kinematic Analysis of the Intersection Zone
4.3. Kinematic Analysis of Slab B
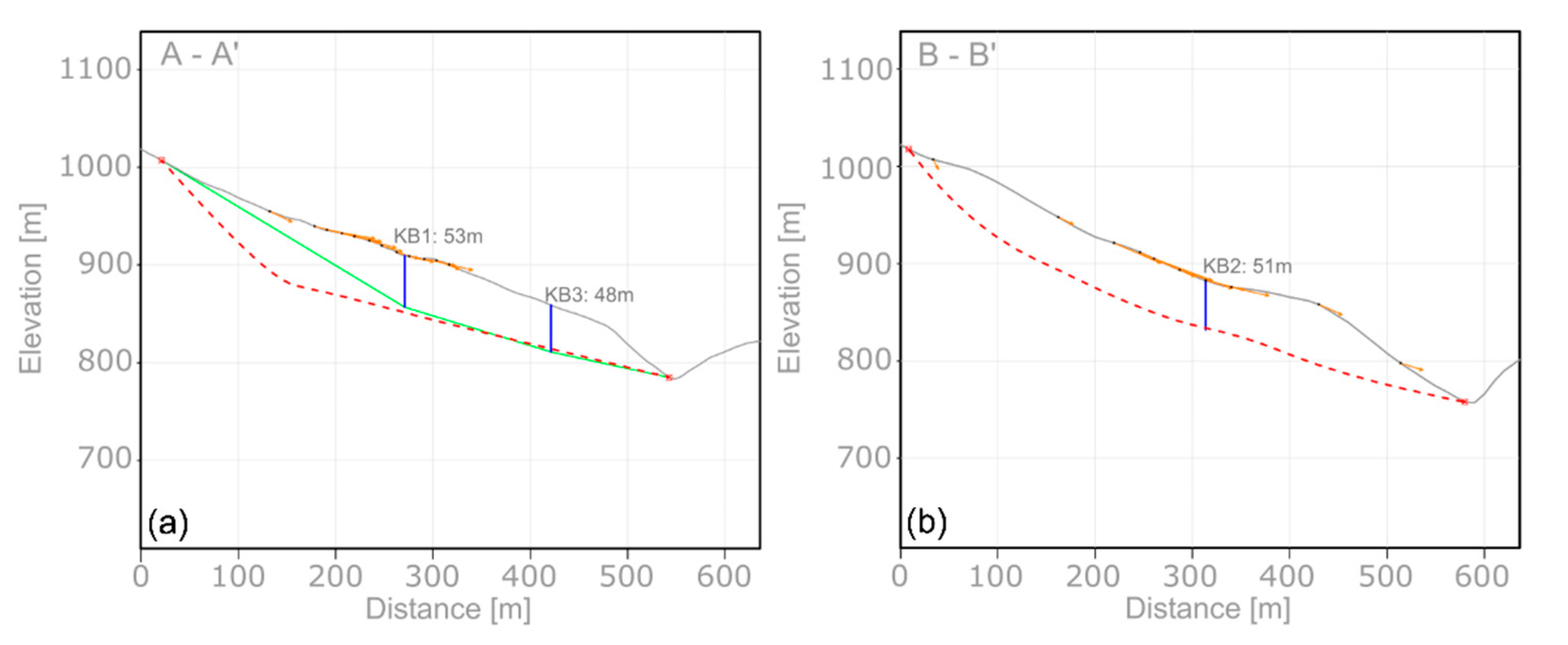
4.4. 3D landslide Reconstruction
- internal inhomogeneous deformation within the landslide;
- the presence of two different slabs.
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crosta, G.B.; Frattini, P.; Agliardi, F. Deep seated gravitational slope deformations in the European Alps. Tectonophysics 2013, 605, 13–33. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslides: Investigation and Mitigation. Chapter 3-Landslide Types and Processes; Transportation Research Board Special Report; National Academy Press: Washington, DC, USA, 1996. [Google Scholar]
- Zangerl, C.; Eberhardt, E.; Perzlmaier, S. Kinematic behaviour and velocity characteristics of a complex deep-seated crystalline rockslide system in relation to its interaction with a dam reservoir. Eng. Geol. 2010, 112, 53–67. [Google Scholar] [CrossRef]
- Crosta, G.B.; Di Prisco, C.; Frattini, P.; Frigerio, G.; Castellanza, R.; Agliardi, F. Chasing a complete understanding of the triggering mechanisms of a large rapidly evolving rockslide. Landslides 2014, 11, 747–764. [Google Scholar] [CrossRef]
- Zangerl, C.; Holzmann, M.; Perzlmaier, S.; Engl, D.; Strauhal, T.; Prager, C.; Steinacher, R.; Molterer, S. Characterisation and Kinematics of Deep-Seated Rockslides in Foliated Metamorphic Rock Masses; Springer: Berlin/Heidelberg, Germany, 2015; pp. 571–575. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Coggan, J.S. Numerical analysis of initiation and progressive failure in natural rock slopes—The 1991 Randa rockslide. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B.; Frattini, P. Slow rock-slope deformation. Landslides Types Mech. Modeling 2012, 23, 207. [Google Scholar]
- Stead, D.; Eberhardt, E. Understanding the mechanics of large landslides. Ital. J. Eng. Geol. Environ. Book Ser. 2013, 6, 85–112. [Google Scholar]
- Riva, F.; Agliardi, F.; Amitrano, D.; Crosta, G.B. Damage-based time-dependent modeling of paraglacial to postglacial progressive failure of large rock slopes. J. Geophys. Res. Earth Surf. 2018, 123, 124–141. [Google Scholar] [CrossRef] [Green Version]
- Hutchinson, J.N. General report: Morphological and geotechnical parameters of landslides in relation to geology and hydrogeology. In Proceedings of the 5th International Symposium on Landslides, Lausanne, Switzerland, 10–15 July 1988; Bonnard, C., Ed.; pp. 3–35. [Google Scholar]
- Cody, E.; Draebing, D.; McColl, S.; Cook, S.; Brideau, M.A. Geomorphology and geological controls of an active paraglacial rockslide in the New Zealand Southern Alps. Landslides 2019, 17, 775–776. [Google Scholar] [CrossRef]
- Vick, M.; Böhme, M.; Rouyet, L.; Bergh, S.G.; Corner, G.D.; Lauknes, T.R. Structurally controlled rock slope deformation in northern Norway. Landslides 2020, 17, 1745–1776. [Google Scholar] [CrossRef]
- Strauhal, T.; Zangerl, C.; Fellin, W.; Holzmann, M.; Engl, D.; Brandner, R.; Tropper, P.; Tessadri, R. Structure, mineralogy and geomechanical properties of shear zones of deep-seated rockslides in metamorphic rocks (Tyrol, Austria). Rock Mech. Rock. Eng. 2017, 50, 419–438. [Google Scholar] [CrossRef]
- Zangerl, C.; Fey, C.; Prager, C. Deformation characteristics and multi-slab formation of a deep-seated rock slide in a high alpine environment (Bliggspitze, Austria). Bull. Eng. Geol. Environ. 2019, 78, 6111–6130. [Google Scholar] [CrossRef] [Green Version]
- Samsonov, S.; d’Oreye, N. Multidimensional time series analysis of ground deformation from multiple InSAR data sets applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar]
- Samsonov, S.; d’Oreye, N. Multidimensional Small Baseline Subset (MSBAS) for Two-Dimensional Deformation Analysis: Case Study Mexico City. Can. J. Remote Sens. 2017, 43, 318–329. [Google Scholar] [CrossRef]
- Samsonov, S.; Dille, A.; Dewitte, O.; Kervyn, F.; d’Oreyede, N. Satellite interferometry for mapping surface deformation time series in one, two and three dimensions: A new method illustrated on a slow-moving landslide. Eng. Geol. 2020, 266, 105471. [Google Scholar] [CrossRef]
- Intrieri, E.; Frodella, W.; Raspini, F.; Bardi, F.; Tofani, V. Using Satellite Interferometry to Infer Landslide Sliding Surface Depth and Geometry. Remote Sens. 2020, 12, 1462. [Google Scholar] [CrossRef]
- Pfeiffer, J.; Zieher, T.; Schmieder, J.; Rutzinger, M.; Strasser, U. Spatio-temporal assessment of the Hydrological drivers of an active deep-seated gravitational slope deformation: The Voegelsberg landlslide in Tyrol (Austria). Earth Surf. Process. Landf. 2021, 46, 1865–1881. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef] [Green Version]
- Rockenschaub, M.; Kolenprat, B.; Nowotny, A. Innsbrucker quarzphyllitkomplex, tarntaler mesozoikum, patscherkofelkristallin. Geologische Bundesanstalt—Arbeitstagung 2003, Blatt 148 Brenner, pp. 41–58. unpublished report.
- Engl, D. Aktueller Kenntnisstand Hangbewegung Vögelsberg, Gemeinde Wattens Forsttechnischer Dienst für Wildbach- und Lawinenverbauung. Innsbruck. 2018. Not published geological report from the Torrent and Avalanches Control (WLV).
- Ludwig, T.; Außerlechner, R. Hangbewegungen und deren Auswirkungen auf Wohn- und Wirtschaftsgebäude im Alpenraum am Beispiel Vögelsberg. 23. Geoforum Umhausen Tirol, 14–15 October 2021. Online Resource. Available online: https://atnastablobgeoforumarc01.blob.core.windows.net/geoforumarchive001/Tagungsband%2023%20Geoforum%20Umhausen%202021.pdf (accessed on 18 May 2022).
- Derauw, D.; d’Oreye, N.; Jaspard, M.; Caselli, A.; Samsonov, S. Ongoing automated ground deformation monitoring of Domuyo —Laguna del Maule area (Argentina) using Sentinel-1 MSBAS time series: Methodology description and first observations for the period 2015–2020. J. South Am. Earth Sci. 2020, 104, 102850. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–111. [Google Scholar] [CrossRef]
- Masiliunas, D.; Tsendbazar, N.-E.; Herold, M.; Verbesselt, J. BFAST Lite: A Lightweight Break Detection Method for Time Series Analysis. Remote Sens. 2021, 13, 3308. [Google Scholar] [CrossRef]
- Saatchi, S.; Asefi-Najafabady, S.; Malhi, Y.; Aragão, L.E.O.C.; Anderson, L.O.; Myneni, R.B.; Nemani, R. Persistent effects of a severe drought on Amazonian forest canopy. Proc. Natl. Acad. Sci. USA 2012, 110, 565–570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watts, L.M.; Laffan, S.W. Effectiveness of the BFAST algorithm for detecting vegetation response patterns in a semi-arid region. Remote Sens. Environ. 2014, 154, 234–245. [Google Scholar] [CrossRef]
- Hamunyela, E.; Verbesselt, J.; Herold, M. Using spatial context to improve early detection of deforestation from Landsat time series. Remote Sens. Environ. 2016, 172, 126–138. [Google Scholar] [CrossRef]
- Tsutsumida, N.; Saizen, I.; Matsuoka, M.; Ishii, R. Land Cover Change Detection in Ulaanbaatar Using the Breaks for Additive Seasonal and Trend Method. Land 2013, 2, 534–549. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y. Using the BFAST Algorithm and Multitemporal AIRS Data to Investigate Variation of Atmospheric Methane Concentration over Zoige Wetland of China. Remote Sens. 2020, 12, 3199. [Google Scholar] [CrossRef]
- Zhu, M.; Wan, X.; Fei, B.; Qiao, Z.; Ge, C.; Minati, F.; Vecchioli, F.; Li, J.; Costantini, M. Detection of Building and Infrastructure Instabilities by Automatic Spatiotemporal Analysis of Satellite SAR Interferometry Measurements. Remote Sens. 2018, 10, 1816. [Google Scholar] [CrossRef] [Green Version]
- Carter, M.; Bentley, S.P. The geometry of slip surfaces beneath landslides: Predictions from surface measurements. Can. Geotech. J. 1985, 22, 234–238. [Google Scholar] [CrossRef]
- Cruden, D.M. The geometry of slip surfaces beneath landslides: Predictions from surface measurements: Discussion. Can. Geotech. J. 1986, 23, 94. [Google Scholar] [CrossRef]
- Cascini, L.; Peduto, D.; Pisciotta, G.; Arena, L.; Ferlisi, S.; Fornaro, G. The combination of DInSAR and facility damage data for the updating of slow-moving landslide inventory maps at medium scale. Nat. Hazards Earth Syst. Sci. 2013, 13, 1527–1549. [Google Scholar] [CrossRef]


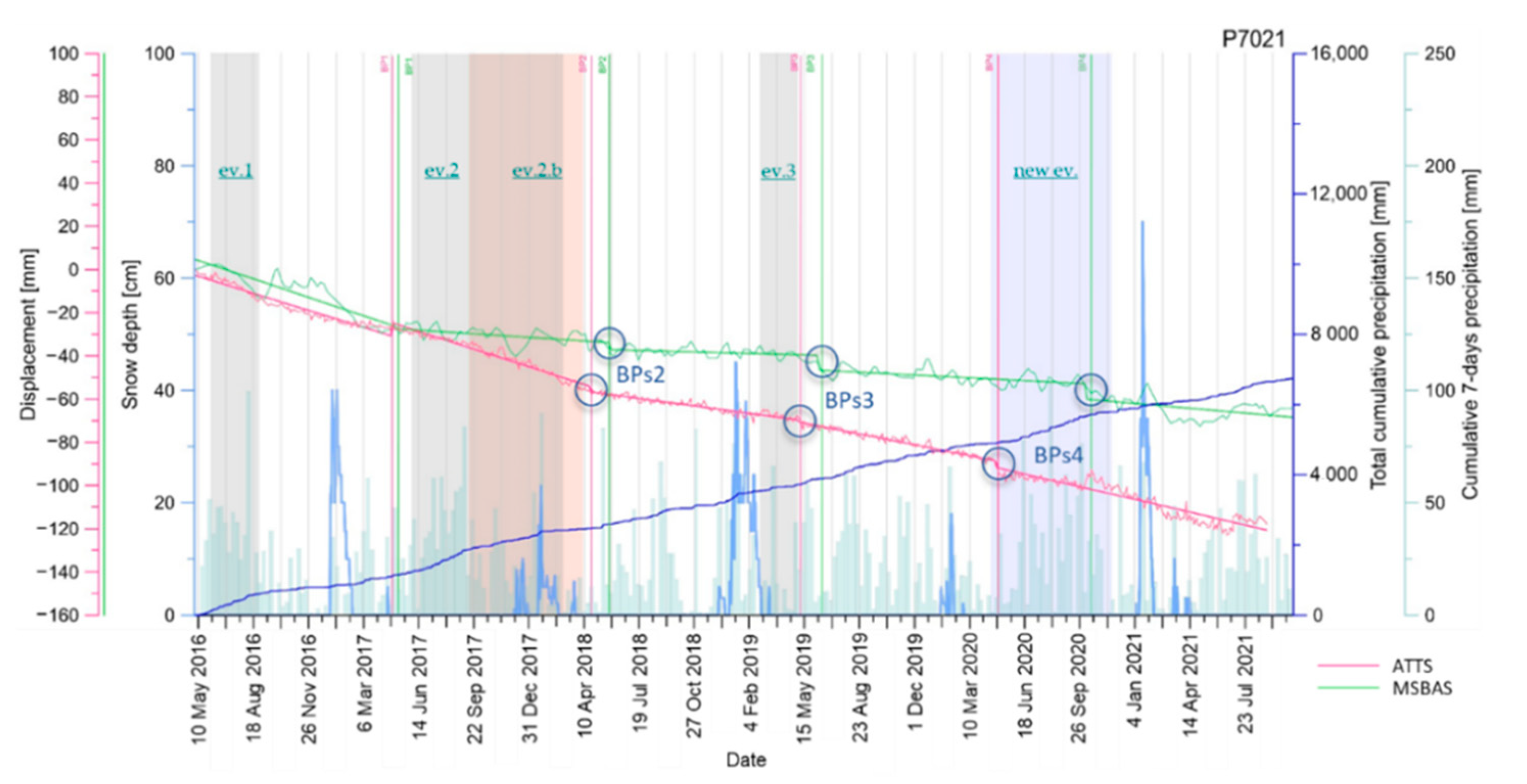



| Event | Period | Main Trigger Factor | Source |
|---|---|---|---|
| 1 | August 2016 | snow and rainfall | Pfeiffer et al., 2020 [21] |
| 2 | June 2017–February 2018 | rainfall | Pfeiffer et al., 2020 [21] |
| 2.b | September 2017–April 2018 | snow and rainfall | Engl, 2018 [24] |
| 3 | March 2019–April 2019 | snow melting | Pfeiffer et al., 2020 [21] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vecchiotti, F.; Amabile, A.S.; Clemente, S.; Ostermann, M.; Nicodemo, G.; Peduto, D. Kinematic and Geometric Characterization of the Vögelsberg Rockslide (Tyrol, Austria) by Means of MT-InSAR Data. Geosciences 2022, 12, 256. https://doi.org/10.3390/geosciences12070256
Vecchiotti F, Amabile AS, Clemente S, Ostermann M, Nicodemo G, Peduto D. Kinematic and Geometric Characterization of the Vögelsberg Rockslide (Tyrol, Austria) by Means of MT-InSAR Data. Geosciences. 2022; 12(7):256. https://doi.org/10.3390/geosciences12070256
Chicago/Turabian StyleVecchiotti, Filippo, Anna Sara Amabile, Salvatore Clemente, Marc Ostermann, Gianfranco Nicodemo, and Dario Peduto. 2022. "Kinematic and Geometric Characterization of the Vögelsberg Rockslide (Tyrol, Austria) by Means of MT-InSAR Data" Geosciences 12, no. 7: 256. https://doi.org/10.3390/geosciences12070256
APA StyleVecchiotti, F., Amabile, A. S., Clemente, S., Ostermann, M., Nicodemo, G., & Peduto, D. (2022). Kinematic and Geometric Characterization of the Vögelsberg Rockslide (Tyrol, Austria) by Means of MT-InSAR Data. Geosciences, 12(7), 256. https://doi.org/10.3390/geosciences12070256






