Abstract
Ripples made from unimodal fine sands can grow much larger on Mars than on Earth, reaching wavelengths of 1–3 m and heights exceeding 1 dm. Smaller decimeter-wavelength ripples can be superimposed on them. Classification and origins of these bedforms have been debated. They have been interpreted as analogous to subaqueous ripples on Earth, or as aeolian impact ripples with a range of grain sizes that reach large maximum sizes on Mars. This study uses a mathematical model to evaluate the formation of large Martian ripples as aeolian impact ripples to further investigate this hypothesis. The model parameters were computed using COMSALT for 100 µm grains under shear velocity of 0.65 m/s, which is a reasonable shear velocity for sand transport on Mars according to recent estimations of threshold Martian winds. The numerical experiments utilize a large grid 8 m long. Experiments also evaluate the development of secondary small ripples between the large ripples from random perturbations. The numerical simulations show the evolution of ripple wavelength and height. According to the results, the time scale for the formation of the large ripples is about 2–3 years, which is a much longer time scale compared to terrestrial impact ripples. Small secondary ripples develop only if the space between the large ripples is sufficiently large.
Keywords:
Mars; large ripples; reptation; COMSALT; shear velocity; fluid drag ripples; impact ripples 1. Introduction
Aeolian sand ripples form due to the interaction between wind and loose sand, and they are ubiquitous both on Earth and Mars [1,2,3,4,5,6,7]. Terrestrial aeolian normal ripples forming in unimodal fine sand are quite small with wavelength <30 cm and height ~1 cm or less [2]. On Mars, these ripples can grow much larger, to wavelengths of 1–3 m and heights exceeding 1 dm with a smaller decimeter-wavelength superimposed (Figure 1; [3,7]). The origins of these large ripples have been debated, and two main theories have been suggested to explain their formation. In one view, the larger Martian ripples are aeolian impact ripples that form by conventional saltation impact splash, similar to normal aeolian ripples on Earth, but growth to larger sizes on Mars is enabled by less interference with crest growth due to lower wind dynamic pressures of the Martian boundary layer [4,7]. Computational fluid dynamics (CFD) experiments simulating atmospheric flow over large ripples under typical Martian atmospheric conditions indicate that shear stress at crests is lower than the fluid threshold needed to dislodge grains, thus enabling further growth of the ripples [8,9]. As the spaces between the primary ripples become large enough, smaller ripples can develop between them and migrate over windward slopes of the large ripples [7]. This hypothesis can explain the observed coexistence of small and large ripples. Within this framework, large Martian ripples result from the process of smaller ripples coalescing to form larger ripples (familiar from the early stages of ripple development on Earth), but on Mars this process can continue to produce greater coalesced ripple sizes as a consequence of delayed interference from lower wind dynamic pressure.
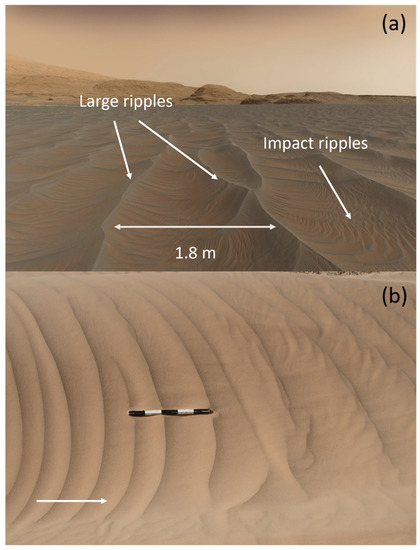
Figure 1.
(a) Multiple ripple sizes at the Sands of Forvie ripple field in Gale Crater, imaged by the NASA MSL Curiosity rover. The wavelength of the largest ripples varies, but 2–3 m is common with smaller impact ripples between them. This picture shows the amazing complexity of the patterns that incorporate multiple ripple scales, probably due to multidirectional winds combined with medium and larger crests shielding parts of troughs from typically low-angle descents of saltating grains. For more information on this picture, see Figure 7 in [10]. Mastcam camera mosaic, sol 2991, NASA/JPL-Caltech/MSSS. (b) Large impact ripples near Merzuga dune field in Morocco during sand transport (from left to right indicated by the white arrow). The length of the scale bar is 0.5 m.
An alternative theory explains the large Martian ripples as fluid/wind-drag ripples or hydrodynamic ripples, like subaqueous ripples on Earth. This hypothesis was motivated by claims that a 20–80 cm wavelength gap exists among Martian ripples, therefore if <20 cm ripples form by conventional impact splash, a second, different mechanism would explain the ripples >80 cm [1,5]. However, subsequent observations have revealed ripples with wavelengths between 20 and 80 cm as part of a continuum from the smallest to the largest ripple sizes [7,10].
Figure 2 shows the wavelength scaling the of large Martian ripples as a function of the atmospheric density based on previous published data (see also [5]). The scaling can be written as a power law with which is different from , the suggested prediction of Lorenz (2014) [11], or suggested by Lapotre et al. [5]. According to the theory of Durán Vinent et al. 2019 [12,13], the large ripples form due to hydrodynamic instability and their size scale with the thickness of viscous sublayer where is the kinematic viscosity and is the shear velocity. This model predicts a wavelength gap, 20–80 cm, between smaller impact ripples and larger meter-scale ripples. It’s important to note that these large meter-scale ripples do not have crests covered with very coarse grains (1–2 mm), thus are not like known terrestrial or Martian megaripples wherein formation is attributed to the sorting mechanism and to the development of an armoring layer at the crests [2,14]. However, in a recent study [6] it was found that the grain size distributions of the small and large ripples differ, indicating that some degree of aeolian sorting is also involved in their formation. Large ripples observed by Curiosity in Gale Crater have larger sand grains than the smaller ripples. The author’s conclusion was that that the large Martian ripples are more similar to terrestrial megaripples [6]. This recent work indicates that we still lack a full understanding of the formation of the large Martian ripples.
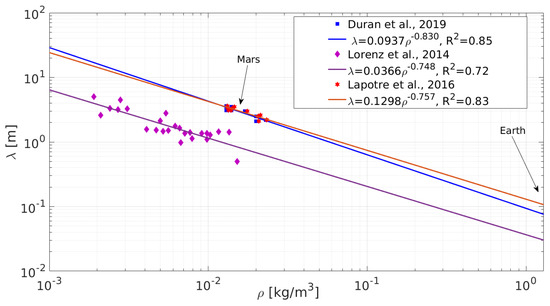
Figure 2.
The scaling of the large Martian ripples’ wavelength with the atmospheric density based on previous published data [1,12,13]. The wavelength of the large ripples increases in lower atmospheric pressure conditions.
The different morphological features of the large Martian ripples predicted by the two hypotheses are summarized in Table 1.

Table 1.
Morphological characteristics of large ripples according to impact ripples and fluid drag ripple theories.
Although the formation of the large Martian ripples is still uncertain, their large size, detectable in orbital images, can inform about the wind flow patterns over Martian dunes [16]. Hood et al. (2021) [17] analyzed the ripple pattern and migration rate in the Nili Patera dune field, one of the most active dune fields on Mars [18]. One of their findings was that changes in ripple patterns and migration rates in dune wakes indicate reattachment lengths of four to seven brink heights. Despite observations in wind tunnel experiments [19,20,21], it is still unknown why large Martian-like ripples do not exist naturally (or are very rare) on Earth although they should form in fine sand grain beds (~100 µm) under terrestrial gravity and shear stress conditions. In addition to the unexplained large ripples, the physics of sand transport on Mars is not fully understood, which makes the interpretation of the meter-scale ripples more difficult.
In the current work, a mathematical model for aeolian ripples, based on the model of Anderson [22,23], was utilized under Martian conditions to study large ripple development. The shear velocity was m/s, with saltation and boundary-layer parameters calculated using COMSALT [7,9,23]. Compared to previous work [7], the grid length was doubled to 8 m for 100 µm sand grains. The larger grid improves the statistics of the results and allows modelling ripples with larger wavelengths. The simulations show that large ripples can reach maximum size in a few years, depending on the grain size and wind speed. In addition, the model was also utilized to study the dynamics of small secondary ripples that are superimposed on the larger ripples. The numerical results support the idea that large Martian ripples can be explained by the impact mechanism. However, the results cannot exclude that large Martian ripples are wind drag ripples or hydrodynamic ripples and it is plausible that on Mars, both mechanisms can be active.
2. Materials and Methods
The main goal of the numerical simulations was to estimate the characteristic formation time and morphological properties (wavelength and height) of large Martian ripples composed of 100 µm sand developing under conditions of m/s. This value is a reasonable estimation for the fluid threshold of 100 µm grains (see Figure 5 in [24]). A second goal of the study was to evaluate the development of secondary small ripples. The choice of 100 µm grains is in accordance with the mean grain size of transverse large ripples at Bagnold Dune Field (Figure 1f in [3]). Modelling of superimposed small impact ripples was carried out by studying their development from small random perturbations on the large well-developed ripples. Another experiment goal was to compare between the modeled reptation flux and reptation flux calculated from observed Martian ripple migration [25]. This time scale is important for understanding the origin of large ripples in the framework of the impact ripple hypothesis. The experiment approach utilized the COMSALT model for saltation [26] together with a spatiotemporal 2D model for aeolian sand ripples [26] in a method similar to Yizhaq et al., 2014 [23] and Sullivan et al., 2020 [7]. COMSALT includes many of the advances made by previous saltation models including: (1) a physically based parameterization of the splash function [26], (2) a generalization of this splash function to beds composed of polydisperse particles (this option was not used in the current study), and (3) a detailed consideration of the effect of turbulence in the boundary layer on particle trajectories, which aligns with wind tunnel experiments. Results of numerical model simulations under Martian conditions indicate that saltation can be maintained on Mars by wind speeds less than those required to initiate saltation (this behavior is known as hysteresis), mainly due to the low-density Martian atmosphere [27].
Specifically, COMSALT supplies three parameters to the ripple model (Figure 3): the average number of reptating grains per impact of one saltating grain , the number density of saltator impacts on a flat surface, and the probability distribution of reptation lengths. The ripple model is based on the mathematical approach developed by Anderson [22] and includes a modification to the reptation flux that depends on the local bed slope [28]. The two-dimensional model of sand transport is based on the 1D Exner equation [22,23] which expresses the mass conservation:
where h(x,t) is the local height of the bed at point x and time t, is the porosity of the bed (assumed here as 0.35), is the grain density and Q(x,t) is the sand flux per unit width perpendicular to flow, which includes both saltation () and reptation () flux. We assume that saltation flux can be taken as uniform and homogenous in the downwind direction, thus the saltation flux does not contribute to ripple formation (i.e., ); for a different view of this assumption, see the referenced study [29]). The reptation flux at a certain point and time is expressed by the sum of all the reptating grains that pass through that point at that time. The ejected grains have a probability distribution of reptation lengths which mainly depend on the grain size and very weakly on the shear velocity [23]. The reptation flux is described by a double integral term that turns Equation (1) into a complex integro-differential equation [2]:
where m is the mass of one sand grain. Because saltation flux is assumed to be spatially uniform and the impact angle (set to 10°) is constant, the number density of impacting grains varies only due to changes in the bed slope. Based on geometrical considerations [26]:
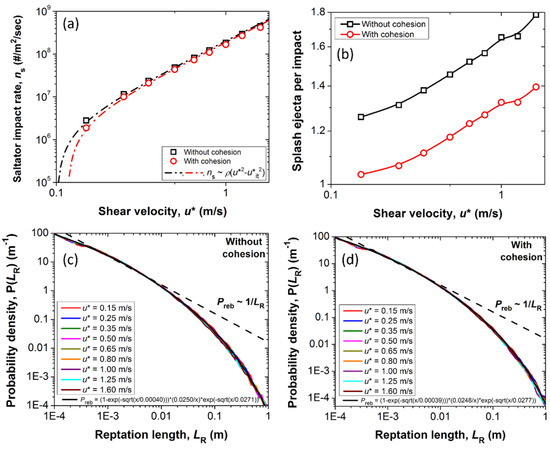
Figure 3.
The parameters supplied to the model from COMSALT calculations. (a) The saltator impact rate on a flat surface for different shear velocities and for 100 μm grain diameter calculated using COMSALT with and without cohesion. The impact rate increases with the shear velocity. (b) The average number of ejected particles per impact of saltating grains () for different shear velocities. COMSALT simulations for the probability distribution of reptation lengths for transport of 100 µm particles at different shear velocities without cohesion (c) and with cohesion (d). The probability distribution of reptation lengths depends very weakly on the shear velocity.
Equation (3) breaks down when the lee slope of the ripple exceeds the impact angle of the impinging saltating particles (i.e., when ), since the ratio becomes negative which is unphysical. In these cases, the constraint that the impact flux is zero was added. The model also uses a complete shadowing effect [30,31] below the line defined by the saltation path of a grain which touches the crest. Equation (2) was modified to include a correction of the reptation flux which is smaller at the stoss slope and larger at the lee slope of the ripple [27]. The physical explanation for this modification is that part of the kinetic energy of the impacting saltator is imparted to surface grains, which vibrate rapidly, and as a result can creep down the slope. This flow of particles is known as “impact-induced gravity flow” [32]. This mechanism acts to reduce the flux on the windward slope and increase it on the lee face due to the addition of rolling grains [30]. The full model which includes the reptation flux modification is demonstrated by:
where the parameter, , heuristically includes the correction to reptation flux discussed above, and. The basic parameters used in the model are calculated using COMSALT, which simulates Martian environments for different shear velocities and grain diameters [7,23]. The computed probability distribution of reptation lengths is demonstrated by
where s, a, b, c are numerical constants (e.g., [9,26]) so that . Figure 3a,b show the rate of impinging saltating grains on a flat surface and the number of ejected reptation particles with cohesion and without cohesion. Figure 3c,d show modelled reptation behavior of 100 µm basaltic grains for different shear velocities. Note that in the current study, only the parameters without cohesion were used. Using the parameters with cohesion will slow down the ripple development (see [23]). Interestingly, the probability distribution of the reptation lengths does not depend on the shear velocity, in concurrence with experimental and theoretical studies.
Equation (4) was solved numerically using the method developed by Yizhaq et al. 2014 [27] in which an explicit second-order finite difference scheme was utilized with periodic boundary conditions. Integral terms of Equation (4) were calculated using the composite trapezoid rule, and time integration was performed by the second-order Adams-Bashforth rule [33]. The number of grid points was 8192, and dt = 0.02 s. Because of the large number of grid points and the integral terms, the code was slow, and more than a year and a half of simulation time on a strong workstation was required to obtain the results presented in the next section. The initial condition was random small perturbation of the flat bed. To simulate the superimposed ripples, random perturbations with an amplitude of 6 mm were added every 4 min to the mature ripple surface (a small amplitude compared with ripples of mean height 10–15 cm).
3. Results
Here we present the main results of the numerical simulations for the evolution of impact ripples under Martian conditions of continuous unidirectional wind of = 0.65 m/s [22] and for 100 µm basaltic sand in an 8 m long experiment grid.
3.1. Ripples Developed from Random Initial Conditions
Figure 4 shows that the evolution of ripples started from very small random initial perturbations of the bed. The ripples grow both in height and wavelength by the merging of small ripples. After 960 min of continuous wind, the mean wavelength is 2.67 m and the mean height is 16.9 cm. Figure 5 shows sand flux along the bed after 264 and 960 min. It is clear that when ripples grow high enough, the shadowing effect becomes more significant and the sand flux at intervals between the ripples is zero.
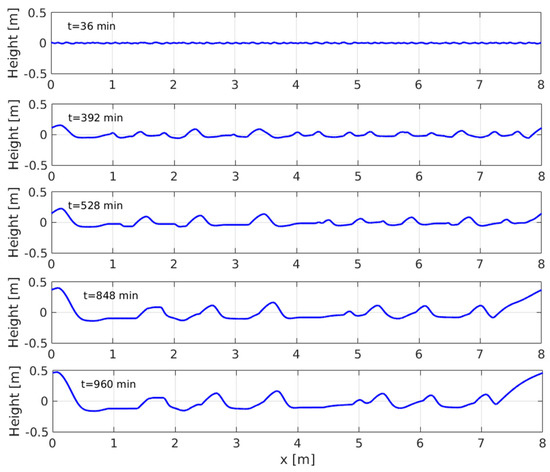
Figure 4.
Evolution of ripples started from random initial condition for 100 µm sand. The wind direction is from left to right and it is constant during the simulation.
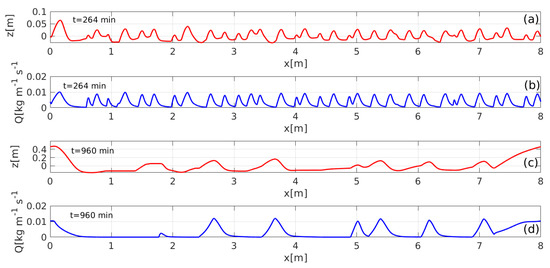
Figure 5.
The sand flux over the ripples at t = 264 min (panels (a,b)) and at t = 960 min (panels (c,d)). The shadowing effect of the large ripples is clear in the segments with zero flux.
Figure 6 shows the coarsening process of ripples due to differences in ripple migration rate (celerity) which depends on their height. The smaller ripples move faster than the larger ripples, so they catch up with and merge into the larger ones. Thus, the number of ripples decreases over time while their wavelengths and heights increase over time as summarized in Figure 7. The abrupt increase in the wavelength is due to the decrease in the number of crests because of the coalescence of smaller ripples. This coarsening process causes the number of crests to decrease sharply during the first stage of the ripple development, after which it changes much more slowly. Thus, after 500 min of simulations, the ripple growth is quite slow. In contrast, the mean height development is a more continuous growth process (see also [23]).
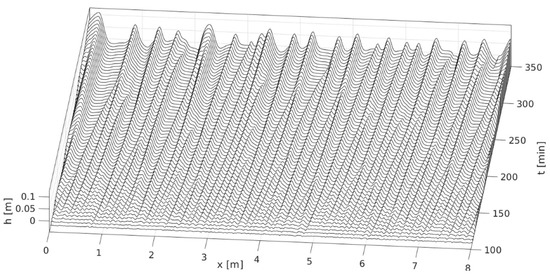
Figure 6.
Bedform evolution due to the coarsening process during 250 min of numerical simulation. Smaller ripples move faster than larger ripples, resulting in collisional merging that cause average ripple size to increase with time.
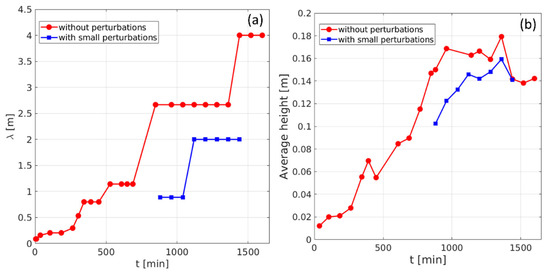
Figure 7.
(a) Evolution of mean wavelength, with and without small perturbations applied after 880 min of simulations. (b) The mean height of the ripples as a function of time in minutes. After a linear growth stage, ripple height grows more slowly and time gaps between each change in the wavelength increases for the mature ripples.
Figure 8 shows the downwind migration of small and large ripples. The calculated migration speeds are 0.125 cm/min and 0.0625 cm/min for the smaller and larger ripples, respectively, or large ripple migration of 328.5 m per year, assuming continuous unidirectional wind of m/s.
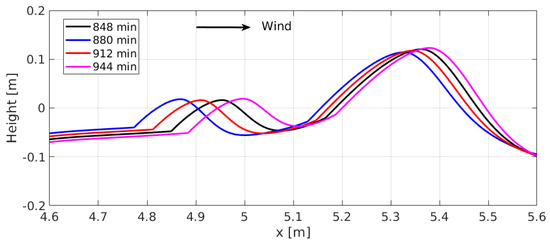
Figure 8.
Small and large ripple migration between t = 848 min and t = 944 min. The small ripple moves downwind faster than the larger ripple due to its smaller volume.
3.2. Modeling Secondary Imposed Ripples
The superposition of ~10 cm ripples over larger 1–2 m ripples is one of the characteristics discovered by Curiosity [1]. According to the impact ripple hypothesis, small ripples can develop between the large ripples when the latter are large enough [7]. Thus, small random perturbations have been added to the large ripples with an amplitude of 6 mm every 4 min along the ripple profile to study the difference between the evolution of ripples with and without small perturbations (Figure 9).
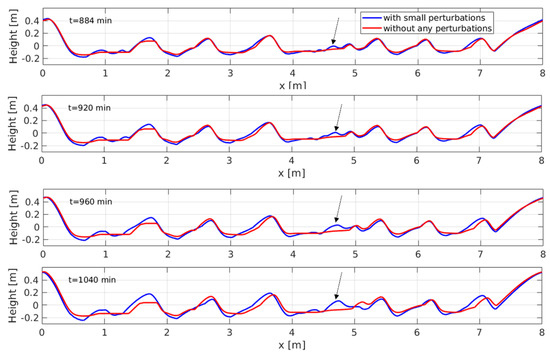
Figure 9.
The effect of adding small random perturbations on the evolution of the large impact ripples. The black arrows indicate development of small ripples between the large matured ripples.
It is important to note that the small ripples developed where the inter-space between the large ripples was large enough, as was suggested by Sullivan et al., 2020 [7]. Small secondary ripples did not develop on the lee slope of the large ripples because of the shadowing effect of the crest; the sand flux is zero there, and they quickly eroded as shown in Figure 10. The real situation is more complex, since small ripples oriented perpendicularly to the large ones have been observed on both the stoss and lee sides of longitudinal ripples in Gale (Figure 1a). However, these patterns require a 3D model which is beyond the scope of the 2D modeling approach used in the current work.
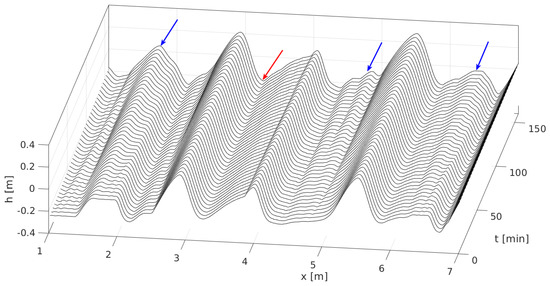
Figure 10.
Development of superimposed ripples between the large ripples during 160 min of numerical simulation. The blue arrows indicate the locations where small ripples developed, whereas the red arrow indicates a location where the space between the two adjacent large ripples was insufficient for the development of small ripples.
4. Discussion
Evaluating origins for large Martian ripples is complicated by the lack of a clear terrestrial analog. In the current work, we tested the impact ripple hypothesis using numerical simulations of ripple growth and migration under Martian conditions. The current version of the model has no provision for increased wind flow to limit growth of ripple crests (compare with [30]), so ripple growth is unconstrained by the boundary layer in the model. However, ripple growth still slows with time in the experiments for other reasons. Ripple merging leads to fewer, larger ripples that take longer to catch up with one another for additional merging events and growth. This is partly because larger ripples move at slower speeds, and partly because larger average spacing between them takes more time to close for additional merging events to occur (e.g., [23,34]; in [27] the mean wavelength grows as a power-law . Still, the model can be used to study the rate of ripple development and the formation of secondary ripples. The wind in the simulations was unidirectional and constant with m/s, saltating 100 µm grains. This shear velocity was chosen as a representative wind velocity when saltation is likely occurring. Kruss et al. [35] found in wind tunnel experiments with 100 μm Mojave Mars simulant sand that threshold velocity was m/s under simulated Martian environmental conditions. Swan et al. (Figure 2 in [36]) predicted shear velocity of 0.5 m/s for 100 µm in regards to non-cohesive grains and 1 m/s for cohesive grains. Fu [24] found, using numerical calculations, that for 50–150 µm, the minimum fluid velocity is between 0.6–0.7 m/s. These recent works justify using m/s as a reasonable velocity for 100 μm grains.
The average reptation flux for the mature ripples is 0.002 kg m−1 s−1; using a bulk density of 1950 kg/m3 [7] yields a flux of 32.34 m3 m−1 yr−1 (assuming a constant wind during the whole year), which is much higher than the reptation flux reported for the ripples at Nili Patera (1.4 m3 m−1 yr−1), one of the most active aeolian sites on Mars [18]. Recently, it was shown that impact ripples at Gale Crater migrate mainly at night as a result of sporadic low-flux saltation events [37]. At Gale Crater, the MarsWRF numerical climate model experiments predict nighttime exceeds 0.65 m/s only 9% of the time, and only 3% during daytime, yielding an average of 6% [37].
Shear velocity of 0.65 m/s is a reasonable velocity needed for impact ripple migration at night when the wind turbulence intensity and atmosphere density are higher compared to daytime [37]. Thus, using this average of 6%, 32.34 · 0.06 = 1.94 m3 m−1 yr−1 is a reasonable estimation of the average annual sand flux predicted by the model.
The simulations can help to estimate the time scale of the formation of the large ripples, assuming that they are impact ripples. According to Figure 8, the large ripple celerity is 0.0625 cm/s, which is 328.5 m/yr assuming a constant and unidirectional yearly wind of m/s. Silvestro et al. (2013) [38] reported that large ripples at Gale Crater with average λ = 2.7 m migrated SW at 0.66 m/yr across the Bagnold Dunes (note that we do not know the celerity in cm/s for the Martian ripples), which gives a factor of 547.5 between the model’s ripples and the large ripple at Gale Crater. Thus, the ripples in the model developed 547.5 faster than the real ripples at Bagnold Dunes because the model assumes a constant and unidirectional wind speed. Using this factor to estimate the formation time of the large ripples (547.5 times 1500 min), the outcome is 1.56 years. This is only a crude estimate since the model does not include feedback between the ripples and the wind velocity, and we used ripples with 2 m (Figure 7a) wavelength instead of the 2.7 m ripples reported by [38]. Thus, the estimated minimum development time for the Bagnold ripples is ~2–3 years compared to the estimated of 8 years based on numerical simulations of 200 µm grains [7]. This value is also consistent with the observation of large ripples with a wavelength of ~1 m forming within 2 years over the largest gully’s apron in Matara Crater’s dune field [39]. The importance of this estimate is that the formation time of large Martian impact ripples is probably years compared to minutes or hours for the largest terrestrial impact ripples (in fine sand) with a wavelength of up to 30 cm [40,41]. Interestingly, the time scale of the large Martian ripples is more similar to the characteristic time scale of terrestrial megaripple formation [2,14]. Like terrestrial megaripples, large Martian ripples are relatively stable depending on the intensity and duration of sand-moving winds [6].
The model was also used to study the development of secondary ripples between the large ripples. As shown in Figure 10, small ripples can develop only if the distance between the large ripples is sufficiently large. As was already shown in [7], the impact ripples hypothesis can explain the coexistence of small and large ripples. The phenomenon of multiscale aeolian patterns is common in nature, but it is still not fully understood. Two main mechanisms can explain the coexistence of two bedform scales. The first is due to two instabilities that developed separately, each one with a different unstable mode such as ripples superimposed on dunes. The second mechanism is the basic instability of a flat, cohesionless surface under saltation bombardment leading to incipient ripple formation (also called a screening instability [29]), a process that exploits any exposed surface that has sufficient fetch to show ripple growth during migration ([19], pp. 146–147 therein). For example, as ripples grow in wavelength during migration downwind, trough surfaces between these crests might become large enough for the same mechanism to initiate another set of incipient, secondary ripples in between. This mechanism can lead to the formation of secondary ripples parallel to the large ripples or perpendicular to them depending on wind direction (Figure 11). Thus, the development of the small, superimposed ripples can be explained by both theories. According to the fluid drag hypothesis, the small ripples are impact ripples and the large ripples develop due to a hydrodynamic instability. According to the impact ripples hypothesis, both ripples are impact ripples and there is no restriction on the wavelength of the small ripples.

Figure 11.
Multiscale impact ripples in fine sand at a lee slope of a small dune near Merzuga Morocco. The white arrows indicate secondary ripples developed by winds perpendicular and oblique to the large ripples. In some places, small ripples have developed parallel to the dominant direction of the large ripples.
The results of this study pertain to the impact ripple hypothesis for the large Martian ripples, therefore do not refute the fluid drag ripples hypothesis. The numerical simulations reported here can provide some insights about large ripple development, assuming that they are impact ripples. Because our current knowledge of aeolian processes is based on what we observe under Earth’s atmospheric conditions, the amazing discoveries of Martian aeolian patterns open new questions and raise new challenges in our understanding of the physics of sand transport. In particular, the presence of these unexplained extraterrestrial patterns calls into question our understanding on how the wind is sculpting and shaping the landscape not only on Mars, but even on Earth [42,43].
5. Conclusions
Numerical simulations of impact ripple development and migration were utilized to study the origins of large Martian ripples composed of 100 µm grains with m/s. According to recent works on the sand transport initiation under Martian conditions, is a good representation of saltation for 100 µm grains. The parameter values used by the model were calculated using the COMSALT model. COMSALT saltation results serve as inputs to the main ripple evolution code, which simulates how a flat sandy bed with initial small random perturbations evolves into a field of growing, migrating aeolian ripples under Martian saltation conditions. During evolution of the ripple bed, smaller ripples move faster than larger ripples, so that smaller, faster ripples tend to catch up to and merge with larger, slower ripples, making them even larger (and slower). In this way, the numerical technique simulates how many smaller ripples on a sandy bed consolidate into fewer larger ripples, as has been observed and documented in field studies and in wind tunnel experiments under Earth and low-pressure conditions. The simulations show that impact ripple growth by coalescence can create large ripples similar in scale to those observed on Mars. Small secondary ripples can develop from random perturbations between the large ripples if the space between them is large enough. The sand flux calculated by the model, 1.94 m3 m−1, is also in the range of estimated sand flux calculated from migration of large Martian ripples. Under the hypothesis of impact ripples which can grow larger due to the low pressure Martian atmosphere, and using data from Gale Crater on the migration of large ripples, we estimate that their characteristic formation time scale is 2–3 years compared to minutes or hours for terrestrial impact ripples in fine sand. The results contribute to the current scientific debate on the origin of large Martian ripples.
Author Contributions
Conceptualization, H.Y. and I.K.; methodology, H.Y. and J.F.K.; software, H.Y. and J.F.K.; formal analysis, H.Y., J.F.K. and L.S.; writing—original draft preparation, H.Y. and S.S.; writing—review and editing, H.Y. and S.S.; supervision, I.K.; project administration, I.K.; funding acquisition, I.K. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Israel Science Foundation (grant No. 1270/20).
Data Availability Statement
The code that integrates the equations of the model used in this study can be made available upon request from the corresponding author.
Acknowledgments
The authors acknowledge two anonymous reviewers, whose comments helped to significantly improve this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lapotre, M.G.A.; Ewing, R.C.; Lamb, M.P.; Fischer, W.W.; Grotzinger, J.P.; Rubin, D.M.; Lewis, K.W.; Ballard, M.J.; Day, M.; Gupta, S.; et al. Large wind ripples on Mars: A record of atmospheric evolution. Science 2016, 353, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Lämmel, M.; Meiwald, A.; Yizhaq, H.; Tsoar, H.; Katra, I.; Kroy, K. Aeolian sand sorting and megaripple formation. Nat. Phys. 2018, 14, 759–765. [Google Scholar] [CrossRef]
- Lapotre, M.G.A.; Ewing, R.C.; Weitz, C.M.; Lewis, K.W.; Lamb, M.P.; Ehlmann, B.L.; Rubin, D.M. Morphologic diversity of Martian ripples: Implications for large-ripple formation. JGR 2018, 45, 229–239. [Google Scholar] [CrossRef]
- Lorenz, R.D. Martian Ripples Making a Splash. J. Geophys. Res. Planets 2020, 125, 12–15. [Google Scholar] [CrossRef]
- Lapotre, M.G.A.; Ewing, R.C.; Lamb, M.P. An evolving understanding of enigmatic large ripples on Mars. JGR Planets 2021, 126, e2020JE006729. [Google Scholar] [CrossRef]
- Gough, T.R.; Hugenholtz, C.H.; Barchyn, E.T. Re-evaluation of large martian ripples in Gale Crater: Granulometric evidence for an impact mechanism and terrestrial analogues. JGR Planets 2021, 126, e2021JE007011. [Google Scholar] [CrossRef]
- Sullivan, R.; Kok, J.; Katra, I.; Yizhaq, H. A broad continuum of aeolian impact ripple morphologies on Mars is enabled by low wind dynamic pressures. JGR Planets 2020, 125, e2020JE006485. [Google Scholar] [CrossRef]
- Siminovich, A.; Elperin, T.; Katra, I.; Kok, J.F.; Sullivan, R.; Silvestro, S.; Yizhaq, H. Numerical study of shear stress distribution over sand ripples under terrestrial and Martian conditions. JGR Planets 2019, 124, 175–185. [Google Scholar] [CrossRef]
- Yizhaq, H.; Siminovich, A.; Katra, I.; Levi, A.; Sullivan, R.; Silvestro, S.; Yakhot, A. Turbulent shear flow over large Martian ripples. JGR Planets 2021, 126, e2020JE006515. [Google Scholar] [CrossRef]
- Sullivan, R.; Baker, M.; Newman, C.; Turner, M.; Schieber, J.; Weitz, C.; Hallet, B.; Ellison, D.; Minitti, M. The aeolian environment in Glen Torridon, Gale crater, Mars. J. Geophys. Res. Planets 2022, 127, e2021JE007174. [Google Scholar] [CrossRef]
- Ewing, R.C.; Lapotre, M.G.A.; Lewis, K.W.; Day, M.; Stein, N.; Rubin, D.M.; Sullivan, R.; Banham, S.; Lamb, M.P.; Bridges, N.T.; et al. Sedimentary processes of the Bagnold Dunes: Implications for the eolian rock record of Mars. JGR Planets 2017, 122, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, R.D.; Bridges, N.T.; Rosenthal, A.A.; Donkor, E. Elevation dependence of bedform wavelength on Tharsis Montes, Mars: Atmospheric density as a controlling parameter. Icarus 2014, 230, 77–80. [Google Scholar] [CrossRef]
- Durán Vinent, O.; Andreotti, B.; Claudin, P.; Winter, C. A unified model of ripples and dunes in water and planetary environments. Nat. Geosci. 2019, 12, 345–350. [Google Scholar] [CrossRef]
- Tholen, K.; Pähtz, T.; Yizhaq, H.; Katra, I.; Kroy, K. Megaripple mechanics: Bimodal transport ingrained in bimodal sands. Nat. Commun. 2022, 13, 162. [Google Scholar] [CrossRef] [PubMed]
- Weitz, C.M.; Sullivan, R.J.; Lapotre, M.G.A.; Rowland, S.K.; Grant, J.A.; Baker, M.; Yingst, R.A. Sand grain sizes and shapes in eolian bedforms at Gale crater, Mars. Geophys. Res. Lett. 2018, 45, 9471–9479. [Google Scholar] [CrossRef]
- Day, M.; Zimbelman, J. Ripples, Megaripples, and TARs, Oh, My! Recommendations Regarding Mars Aeolian Bedform Terminology. Icarus 2021, 369, 114647. [Google Scholar] [CrossRef]
- Hood, D.R.; Ewing, R.C.; Roback, K.P.; Runyon, K.; Avouac, J.-P.; McEnroe, M. Inferring Airflow across martian dunes from ripple patterns and dynamics. Front. Earth Sci. 2021, 9, 702828. [Google Scholar] [CrossRef]
- Bridges, N.T.; Ayoub, F.; Leprince, S.; Lucas, A.; Mattson, S. Earth-like sand fluxes on Mars. Nature 2012, 485, 339–342. [Google Scholar] [CrossRef]
- Bagnold, R.A. The Physics of Blown Sand and Desert Dunes; Methuen: London, UK, 1941; pp. 165–166. [Google Scholar]
- Bagnold, R.A. The flow pf cohesionless grains in fluids. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1956, 249, 235–297. [Google Scholar]
- Greeley, R.; Iversen, J.D. Wind as a Geological Process: Earth, Mars, Venus, and Titan; Cambridge University Press: New York, NY, USA, 1985; p. 333. [Google Scholar]
- Anderson, R.S. A theoretical model for aeolian impact ripples. Sedimentology 1987, 34, 943–956. [Google Scholar] [CrossRef]
- Yizhaq, H.; Kok, J.F.; Katra, I. Basaltic sand ripples at Eagle crater as indirect evidence for the hysteresis effect in Martian saltation. Icarus 2014, 230, 143–150. [Google Scholar] [CrossRef]
- Fu, L.T. Grain size ratio may be crucial for the fluid initiation of martian sand grains. Icarus 2020, 358, 114225. [Google Scholar] [CrossRef]
- Chojnacki, M.; Banks, M.B.; Fenton, L.K.; Urso, A.C. Boundary condition controls on the high-sand-flux regions of Mars. Geology 2019, 47, 427–430. [Google Scholar] [CrossRef] [PubMed]
- Kok, J.F.; Renno, N.O. A comprehensive numerical model of steady state saltation (COMSALT). J. Geophys. Res. 2009, 114, D17204. [Google Scholar] [CrossRef]
- Kok, J.F. Differences in the wind speeds required for initiation versus continuation of sand transport on Mars: Implications for dunes and sand storms. Phys. Rev. Lett. 2010, 104, 074502. [Google Scholar] [CrossRef] [PubMed]
- Yizhaq, H.; Balmforth, N.J.; Provenzale, A. Blown by wind: Nonlinear dynamics of aeolian sand ripples. Phys. D 2004, 195, 207–228. [Google Scholar] [CrossRef]
- Durán, O.; Claudin, P.; Andreotti, B. Direct numerical simulations of aeolian sand ripples. Proc. Natl. Acad. Sci. USA 2014, 111, 665–668. [Google Scholar] [CrossRef] [PubMed]
- Manukyan, E.; Prigozhin, L. Formation of aeolian ripples and sand sorting. PRE 2009, 79, 031303. [Google Scholar] [CrossRef] [PubMed]
- Prigozhin, L. Nonlinear dynamics of aeolian sand ripples. PRE 1999, 60, 729–733. [Google Scholar] [CrossRef]
- Hardisty, R.J.S.; Whitehouse, J. Evidence for a new sand transport process from experiments on Saharan dunes. Nature 1988, 332, 532–534. [Google Scholar] [CrossRef]
- Fausett, L.V. Applied Numerical Analysis Using MATLAB; Prentice-Hall: Upper Saddle River, NJ, USA, 1999; pp. 423–424. [Google Scholar]
- Anderson, R.S. Eolian ripples as examples of self-organization in geomorphological systems. Earth Sci. Rev. 1990, 29, 77–96. [Google Scholar] [CrossRef]
- Kruss, M.; Musiolik, G.; Demirci, T.; Wurm, G.; Teiser, J. Wind erosion on Mars and other small terrestrial planets. Icarus 2020, 337, 113438. [Google Scholar] [CrossRef]
- Swann, C.; Sherman, D.J.; Ewing, R.C. Experimentally derived thresholds for windblown sand on Mars. Geophys. Res. Lett. 2020, 47, e2019GL084484. [Google Scholar] [CrossRef]
- Baker, M.M.; Newman, C.E.; Sullivan, R.; Minitti, M.E.; Edgett, K.; Fey, D.; Ellison, D.; Lewis, K.W. Diurnal variability in aeolian sediment transport at Gale crater, Mars. JGR Planets 2022, 127, e2020JE006734. 1101. [Google Scholar] [CrossRef]
- Silvestro, S.; Vaz, D.A.; Ewing, R.C.; Rossi, A.P.; Fenton, L.K.; Michaels, T.I.; Flahaut, J.; Geissler, P.E. Pervasive aeolian activity along rover Curiosity’s traverse in Gale Crater, Mars. Geology 2013, 41, 483–486. [Google Scholar] [CrossRef]
- Diniega, S. Interplay between seasonal frost and aeolian processes on Matara crater dunes (Mars). In AGU Fall Meeting Abstracts, Proceedings of the AGU Fall Meeting 2012, San Francisco, CA, USA, 3–7 December 2012; American Geophysical Union: Washington, DC, USA, 2012; abstract id.P21C-1852. [Google Scholar]
- Andreotti, B.; Claudin, B.; Pouliquen, O. Aeolian sand ripples: Experimental study of fully developed states. Phys. Rev. Lett. 2006, 96, 028001. [Google Scholar] [CrossRef]
- Rasmussen, K.R.; Valance, A.; Merrison, J. Laboratory studies of aeolian sediment transport processes on planetary surfaces. Geomorphology 2015, 244, 74–94. [Google Scholar] [CrossRef]
- Yizhaq, Y.; Silvestro, S. Editorial: Physics and Geomorphology of Sand Ripples on Earth and in the Solar System. Front. Earth Sci. 2021, 9, 1–3. [Google Scholar] [CrossRef]
- Silvestro, S.; Titus, T. Planetary Aeolian Landforms: An Introduction to the Fifth Planetary Dunes Workshop Special Issue. J. Geophys. Res. Planets 2021, 127, e2022JE007198. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).