1. Introduction
Analysis of underground flows in fractured media is relevant in several engineering fields, e.g., in oil and gas extraction, in geothermal energy production, or in the prevention of geological or water-pollution risk, to mention a few. Many possible approaches exist for modeling fractured media, and among the most used is the Discrete Fracture Network (DFN) model [
1,
2,
3]. In this model, fractures in the rock matrix are represented as planar polygons in a three-dimensional domain that intersect each other; through the intersection segments (called “traces”), a flux exchange between fractures occurs while the 3D domain representing the surrounding rock matrix is assumed to be impermeable. On each fracture, the Darcy law is assumed to characterize the flux and head continuity and flux balance are assumed to characterize all traces.
Underground flow simulations using DFNs can be, however, a quite challenging problem in the case of realistic networks, where the computational domain is often characterized by a high geometrical complexity; in particular, fractures and traces can intersect, forming very narrow angles, or can be very close to each other. These complex geometrical characteristics make the creation of the mesh a difficult task, especially for numerical methods requiring conforming meshes. Therefore, new methods using different strategies have been proposed in the literature to avoid these meshing problems. In particular, in [
4,
5,
6,
7], the mortar method is used, eventually together with geometry modifications, while in [
8,
9,
10], lower-dimensional problems are introduced in order to reduce the complexity. Alternatively, a new method that allowed the meshing process be considered an easy task was illustrated in [
11,
12,
13,
14,
15,
16,
17]; in this case, the problem was reformulated as a Partial Differential Equation (PDE) constrained optimization one; thanks to this reformulation, totally non-conforming meshes are allowed on different fractures and the meshing process can be independently performed on each fracture. The simulations used in this study are performed with this approach. Other approaches can be found in [
18,
19,
20,
21].
In real-world problems, full deterministic knowledge of the hydrogeological and geometric properties of an underground network of fractures is rarely available. Therefore, these characteristics are often described through probability distributions, inferred by geological analyses of the basin [
22,
23,
24,
25]. This uncertainty about the subsurface network of fractures implies a stochastic creation of DFNs, sampling the geometric features (position, size, orientation, etc.) and hydrogeological features from the given distributions; then, the flux and transport phenomena are analyzed from a statistical point of view. For this reason, Uncertainty Quantification (UQ) analyses are required to compute the expected values and variances (i.e., the momentums) of the Quantity of Interests (QoI), e.g., the flux flowing through a section of the network. However, UQ analyses typically involve thousands of DFN simulations to obtain trustworthy values of the QoI momentums [
26,
27] and each simulation may have a relevant computational cost (both in terms of time and memory). Then, it is worth considering some sort of complexity reduction techniques, e.g., in order to speed up the statistical analyses, such as the multi-fidelity approach [
28] or graph-based reduction techniques [
29].
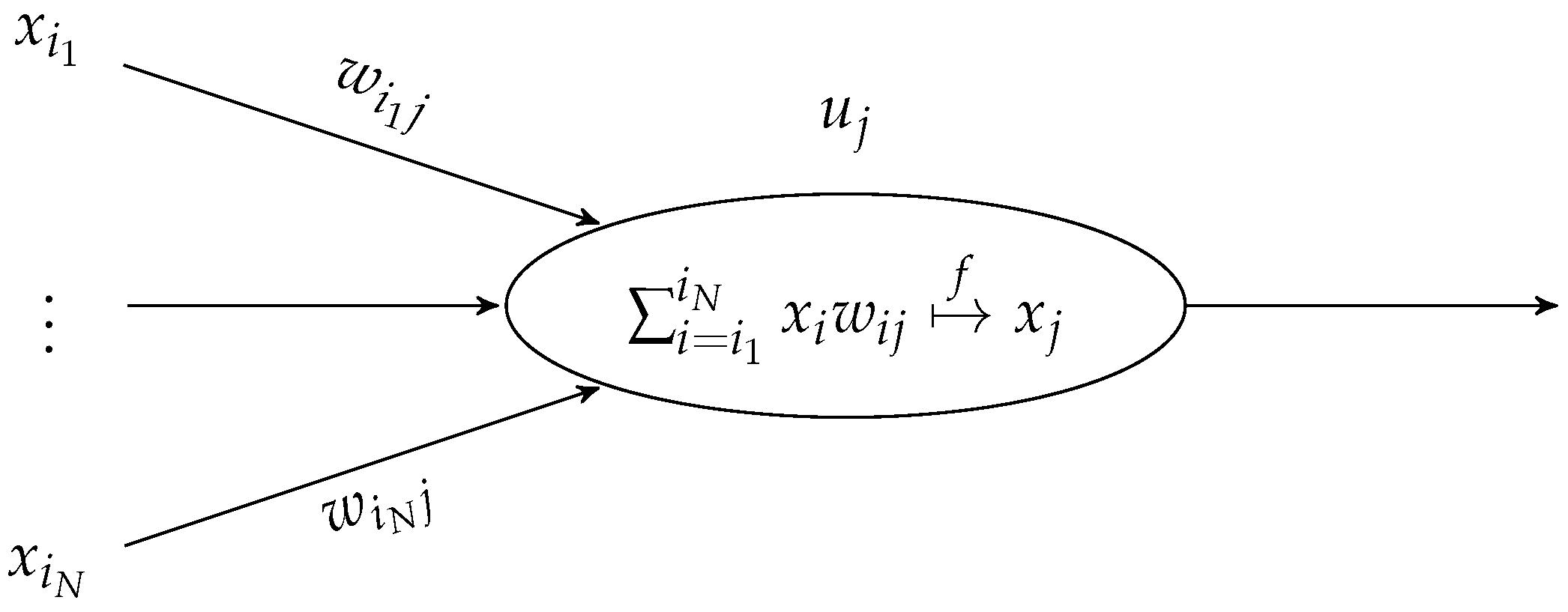
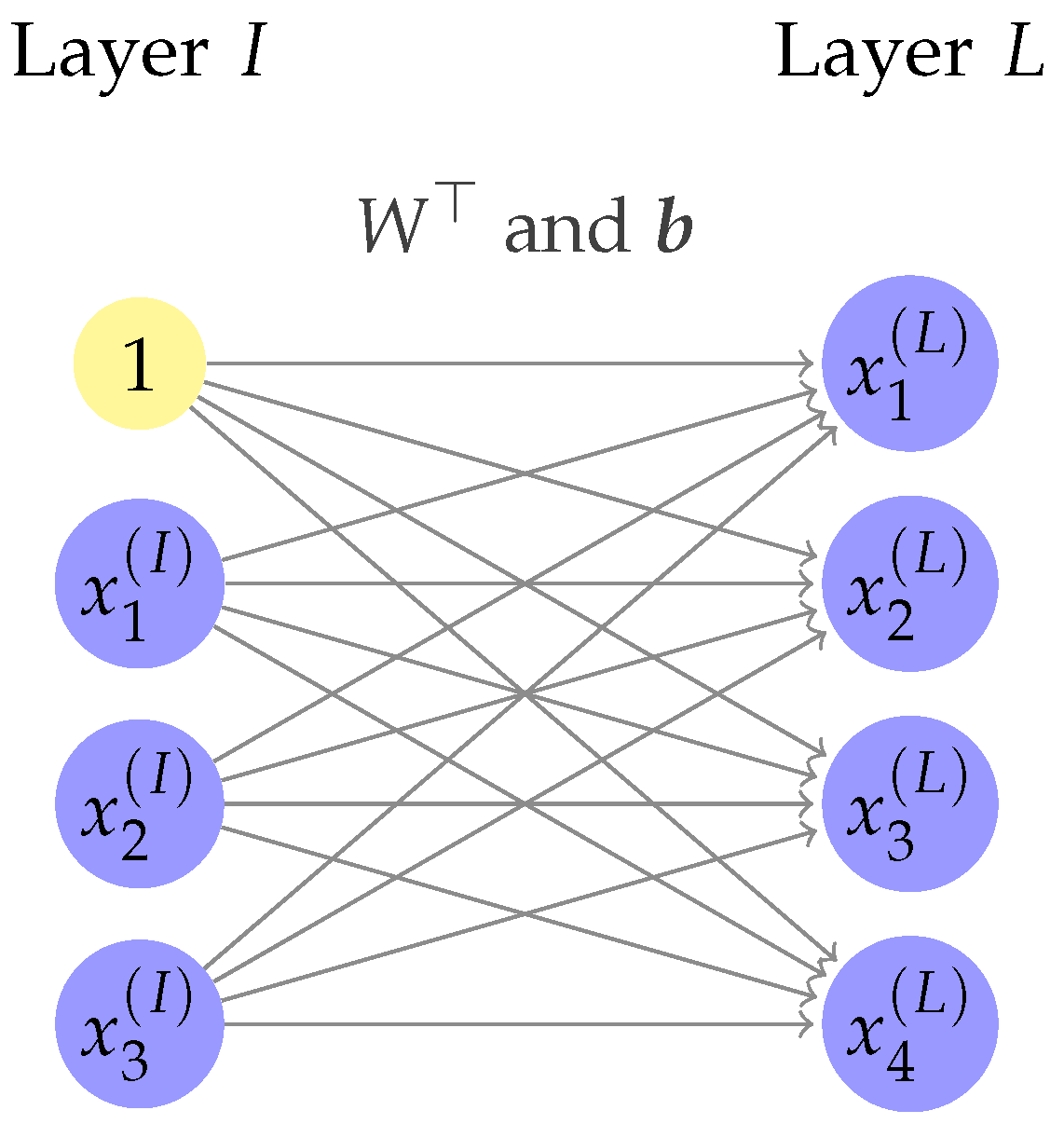
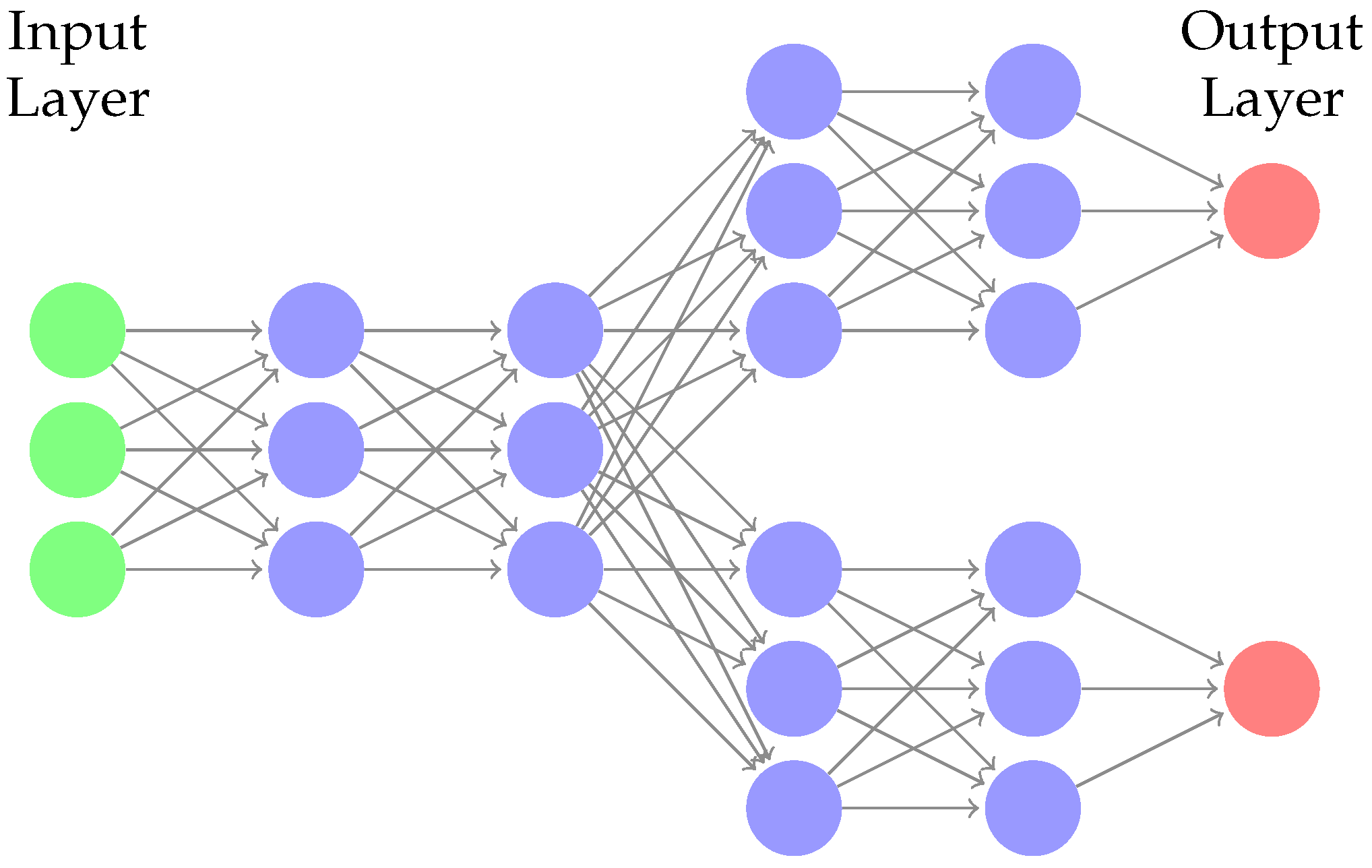
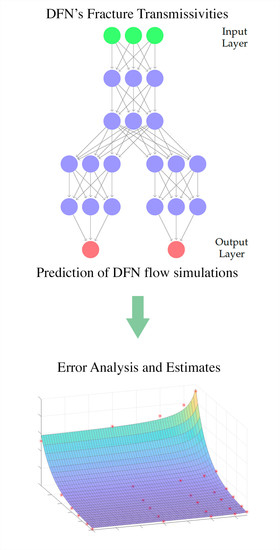
Machine Learning (ML), and in particular Neural Networks (NNs), in recent years has been proven to be a potential useful instrument for frameworks related to complexity reduction due to their negligible computational cost in making predictions. Some recent contributions involving ML and NNs applied to DFN flow simulations or UQ analysis are proposed in [
30,
31,
32,
33,
34,
35]. To the best of the authors’ knowledge, other than [
35,
36,
37] there are no works in the literature that involve the use of NNs as a model reduction method for DFN simulations. In particular, in [
35], multi-task deep neural networks are trained to predict the fluxes of DFNs with fixed geometry, given the fracture transmissivities. A well-trained Deep Learning (DL) model can predict the results of thousands of DFN simulations in the order of a second and, therefore, lets a user estimate the entire distribution (not only momentums) of the chosen QoI; the simulations that must be run to generate the training data are the actual computational cost. The results of [
35] showed not only that NNs can be useful tools for predicting the flux values in a UQ framework but also that the quality of the flux approximation is very sensitive to some training hyperparameters. In particular, a strong dependence of the performance was observed when the training set size varied.
In this paper, we deeply investigate the dependence of the performances of a trained NN and the size of the training set required for good flux prediction on variance in the stochastic parameter of fracture transmissivities. When variability in the phenomenon increases, good training of an NN requires more and more data. If the data are generated by numerical models, a large number of simulations are necessary for the creation of the dataset involved in training the NN. Then, it can be useful to have a tool that provides an estimate of NN performances for different amounts of training data and for different values of variance in the stochastic input parameters. This issue is relevant to predict the convenience of the approach in real-world applicative situations. Indeed, we recall that the DFN simulations required to generate the training data are the only nonnegligible cost for training NNs on these problems. Therefore, it is important to provide a rule that estimates the number of simulations needed to train an NN model with good performances: if the number of simulations for NN training is less than the number required by a standard UQ analysis, it is convenient to use an NN reduced model; otherwise, other approaches can be considered.
In this work, we take into account the same flux regression problem described in [
35] and we explicitly analyze the performance behavior of the NNs trained for DFN flux regression. The analysis is applied to a pair of DFN geometries and to multiple NNs with different architectures and training configurations, showing interesting behaviors that let us characterize the relationship between the number of training data, the transmissivity standard deviation, and the NN performances. From this relationship, we determine a “UQ rule” that provides an estimate of the minimum number of simulations required for training an NN with a flux approximation error less than an arbitrary
. The rule is validated on a third DFN, proving concrete efficiency and applicability to real-world problems.
The paper is organized as follows. In
Section 2, we start with a brief description of the DFN numerical models and their characterization for the analyses of this work; then, we continue with a short introduction on the framework of NNs in order to better describe the concepts discussed in
Section 2.2.3 that concerns the application of deep learning models for flux regression in DFNs. In
Section 2.3, the performance analysis procedure used in this work is described step by step. In
Section 3, we show the application of the analysis described in the previous section and the results obtained for the two test cases considered; in particular, here, we introduce interesting rules that characterize the error behaviors and that are useful for estimating the minimum number of data required for good NN training. We conclude the work with
Section 4 and
Section 5, where the main aspects of the obtained results are commented upon and discussed.
3. Results
Here, we show the application of the performance analysis method described in
Section 2.3 on two test cases. In particular, we consider two DFNs, DFN158, and DFN395, generated with respect to the characterization of
Section 2.1.2; the total number of fractures
n is equal to 158 and 395 for DFN158 and DFN395, respectively, and the number of outflux fracture
m is equal to 7 and 13 for DFN158 and DFN395, respectively.
For each of these two DFNs, we train three different NNs with architectures
(see
Section 2.2.3) for each
and with respect to the two training configurations
and
(see
Section 2.3.2); then, we have a total number of six trained NNs, one for each
combination, for both DFN158 and DFN395. Moreover, we fixed the values
for the test set cardinality and the set
of training-validation set cardinalities
. For the two DFNs considered, we define the set of distribution parameters
such that
DFN158:.
DFN395:
In total, for the following analyses, we trained 180 NNs for DFN158 (30 for each
case) and 90 NNs for DFN395 (15 for each
case); the reason for the smaller set
and, therefore, a smaller number of trainings for DFN395 depends on the more expensive DFN simulations (with respect to the ones of DFN158) that are needed for the creation of the dataset
(see step 5 of the method in
Section 2.3). The results found for the two DFNs are in very good agreement.
The analysis was performed for different combinations of the parameters
and
in order to show that the results found are general for the family of NNs. After these performance analyses, in
Section 3.3, we describe the rules for the best choice of
value given a
value.
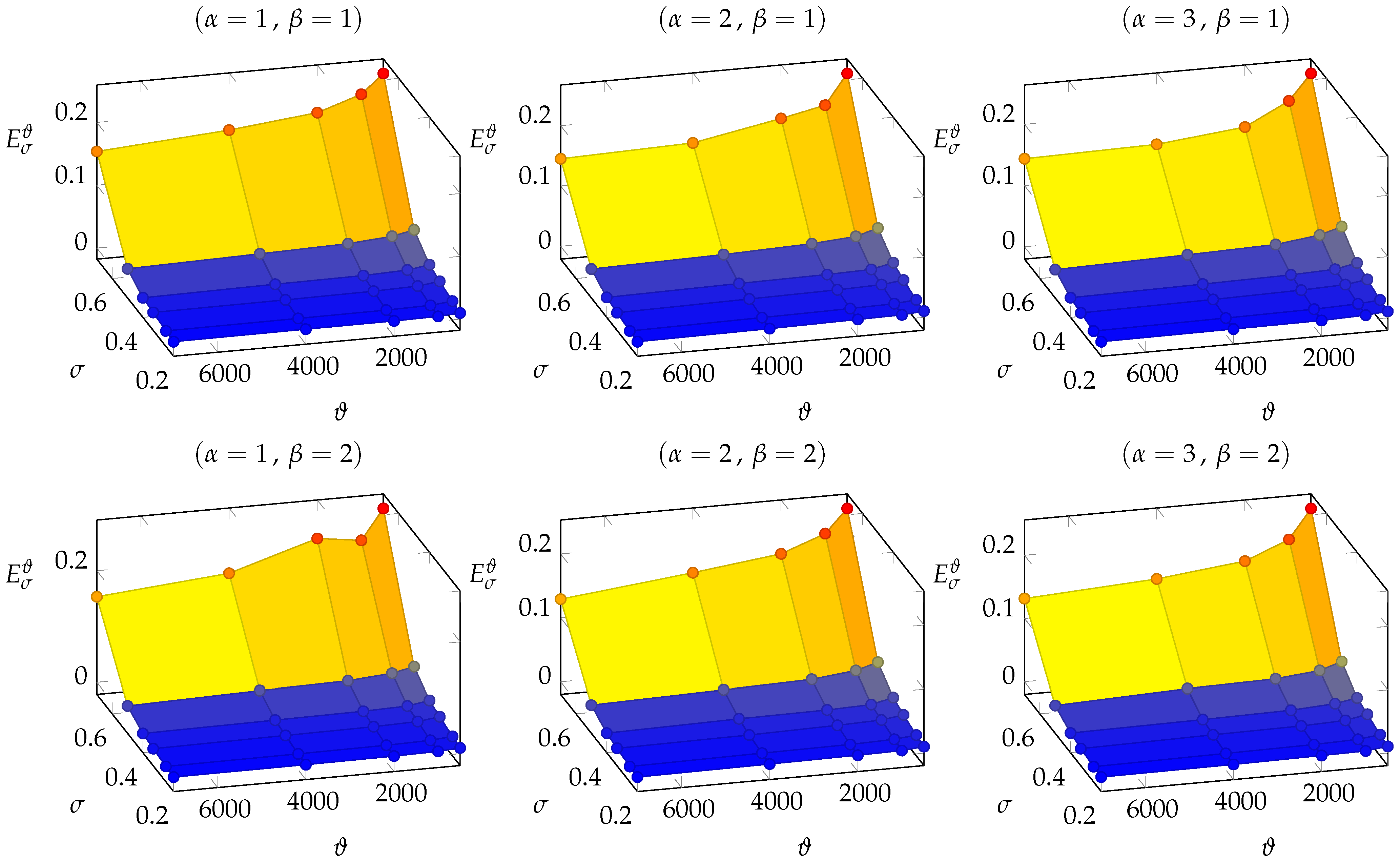
3.1. DFN158
Given the 180 trained NNs with respect to the datasets
and
of DFN158, we analyzed the set of points
(see (
16)) for any fixed combination
; this set of points is described in
Table 1 and illustrated in
Figure 5.
For the average errors , we observed the following behavior characteristics:
The general trend of decreases with respect to and increases with respect to . Indeed, higher values of provide more data for better training the NN whereas higher values for mean a larger variance for input data and, therefore, a more difficult target function to be learned.
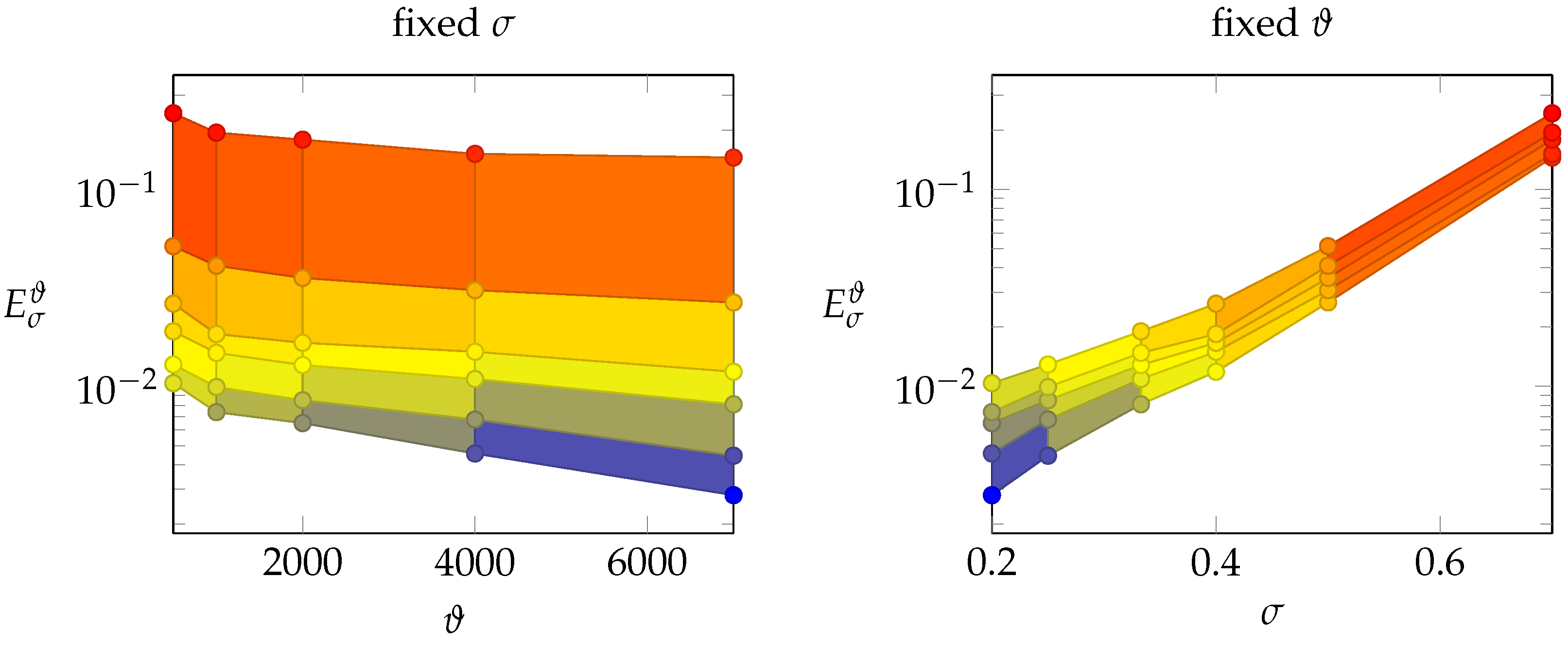
Keeping the value of
fixed, we observed that, in the logarithmic scale, the values of
are inversely proportional to
(see
Figure 6-left).
Keeping the value of
fixed, we observe that, in the logarithmic scale, the values of
increase with respect to
(see
Figure 6-right), with an almost quadratic behavior with respect to
.
The numerical results and these observations actually suggest that the performances of an NN for flux regression seem to be characterized by well-defined hidden rules. Therefore, as proposed at the end of step 11 of the method, we sought a function
such that
for each
.
Taking into account the observations at items 2 and 3, we decided to look for
among the set of exponential functions characterized by exponents inversely proportional to
and proportional to
with linear or quadratic behavior, i.e., functions with the following expressions:
where
and
are parameters of the functions.
Through a least square error minimization process, we found the best-fitting coefficients for the functions (
18) with respect to the data points
(see
Table 2). Looking at the results, we see that the observation made at item 3 concerning the quadratic behavior of
with respect to
is confirmed; indeed, the approximation error of
is always smaller than the one of
(with a nonzero coefficient
). Then, we have that a good function
for the characterization of the average errors is
where
are the fixed parameters obtained with the least square minimization.
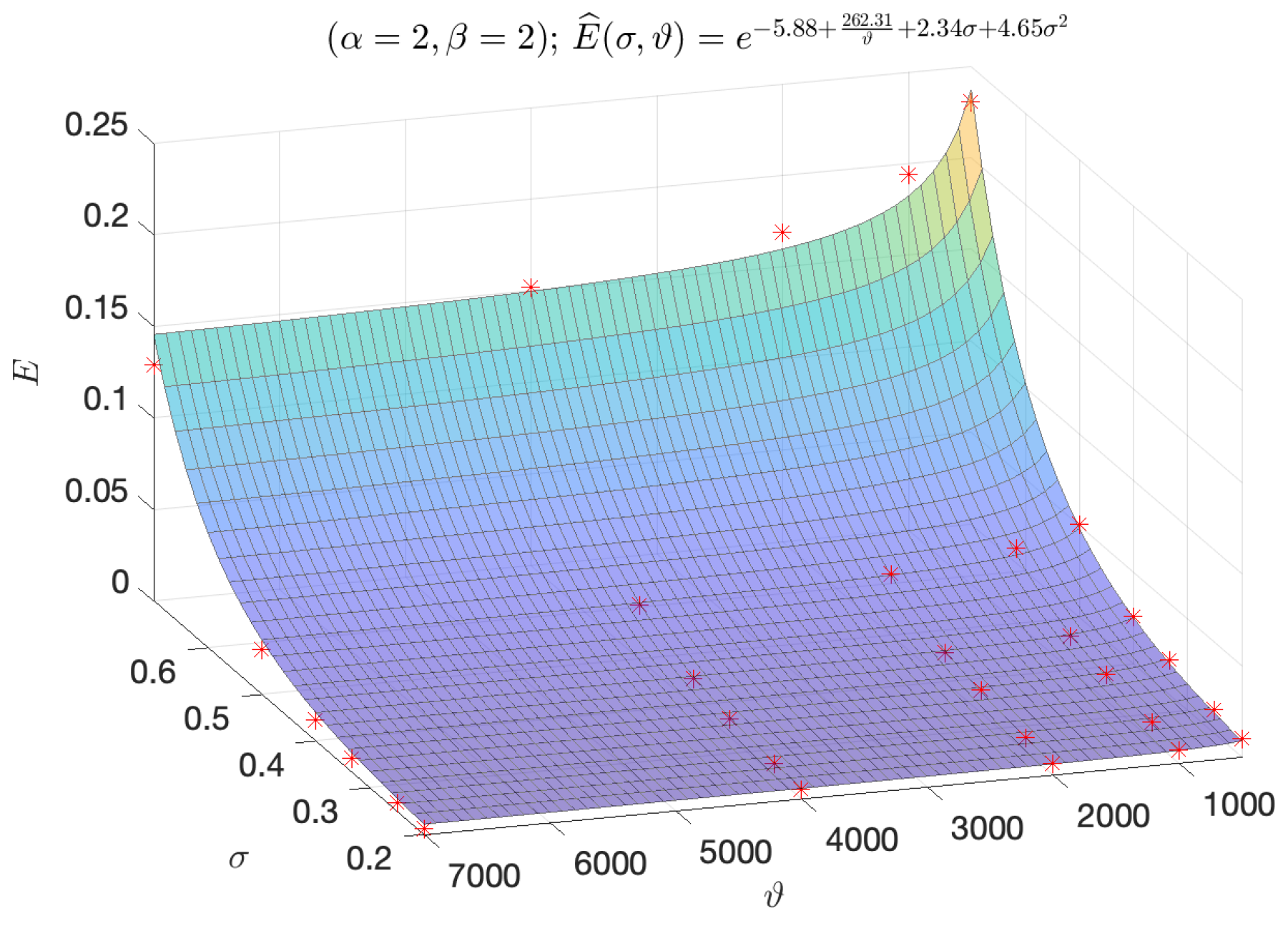
We conclude this section with a visual example (
Figure 7) of the fitting quality of
for the values
of the case
.
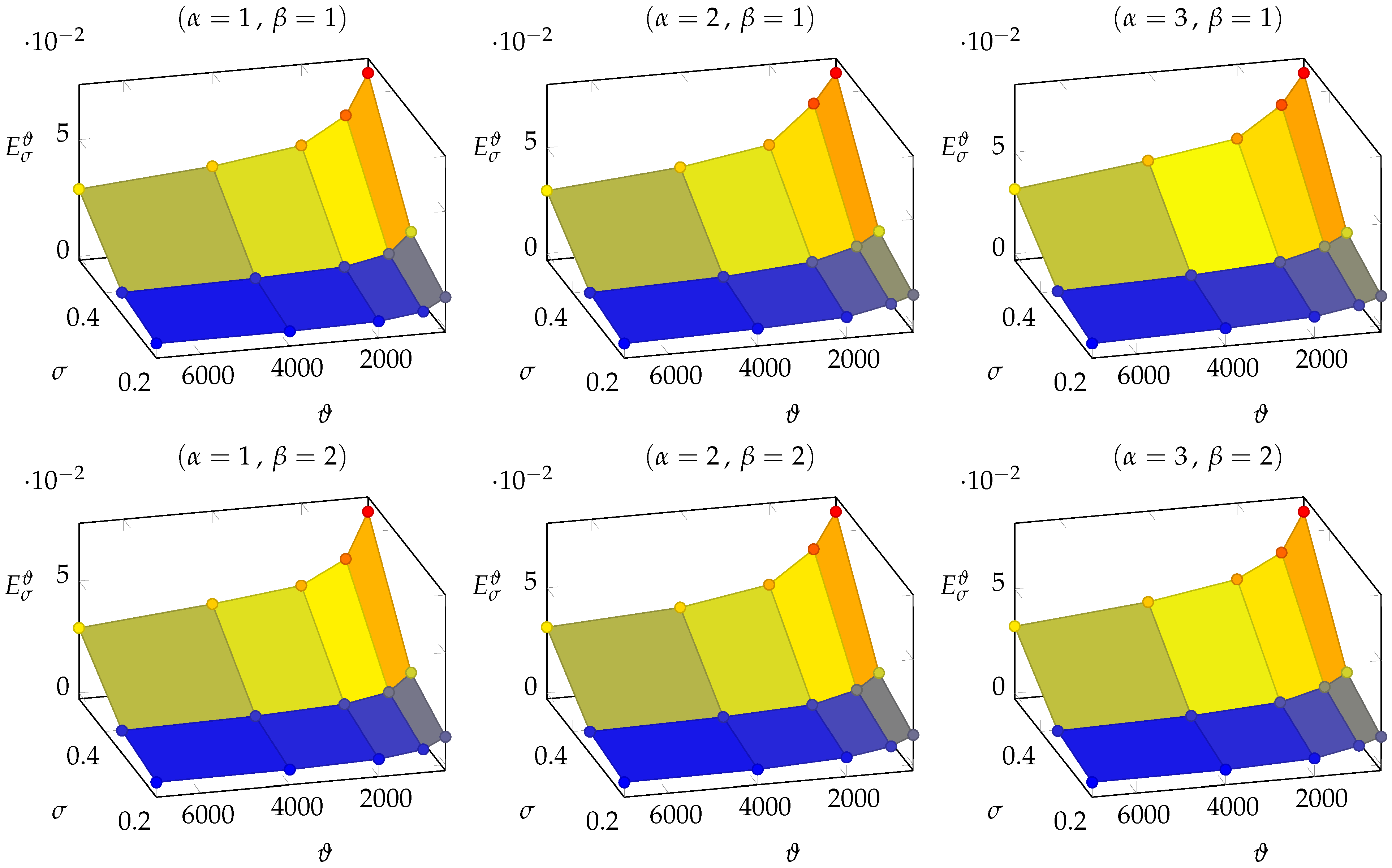
3.2. DFN395
Given the 90 trained NNs with respect to the datasets
and
of DFN395, we analyzed the set of points
for any fixed combination
. This set of points is described in
Table 3 and illustrated in
Figure 8.
Looking at the results in
Table 4, it is very interesting to observe that the average errors
are characterized by the same behaviors observed for DFN158 and, therefore, they can be described by a functions
with the same expressions deduced for DFN158.
We remark that the values of
increase faster with respect to
than in
Section 3.1.
3.3. Error Characterization with Training Data
In Proposition 1 of this section, assuming that the average error of an untrained NN is characterized by the function
described in (
19), we can identify the minimum value of
(i.e., the minimum number of training data) required to obtain an average error smaller than an arbitrary quantity
for each fixed
; in brief, for each fixed
, the proposition tells which is the minimum
such that
.
We conclude this introduction to Proposition 1 by making a few remarks to its assumption on the coefficients
. By construction, it holds that
and
but, looking at the coefficients in
Table 2 and
Table 4, we observe that
is always negative,
is always positive, and
is always nonnegative; then, in the proposition, we assume
,
and
.
Proposition 1. Let be a function defined as in (19), such that , and . Then, for each and , the set of natural solutions of the inequalityis characterized by the following: - 1.
any such thatif , where ; - 2.
no (i.e., ), if .
Proof. Inequality (
20) has the same solutions as inequality
that can be rewritten as
. Therefore, (
22) has no solutions if
and solution
if
; then, both the assertions of Proposition 1 are proven. □
The threshold value
of Proposition 1 is actually the infimum of
, assuming a fixed
:
Thanks to Proposition 1, we can define a rule-of-thumb “
UQ rule” for users who need to perform UQ on a DFN, with a number of fractures
n in the order of magnitude around 158–395 generated by similar laws (
Section 2.1.2) and who want to understand whether it is convenient to train an NN as a reduced model. This rule is based on the regular behavior characterizing the coefficients
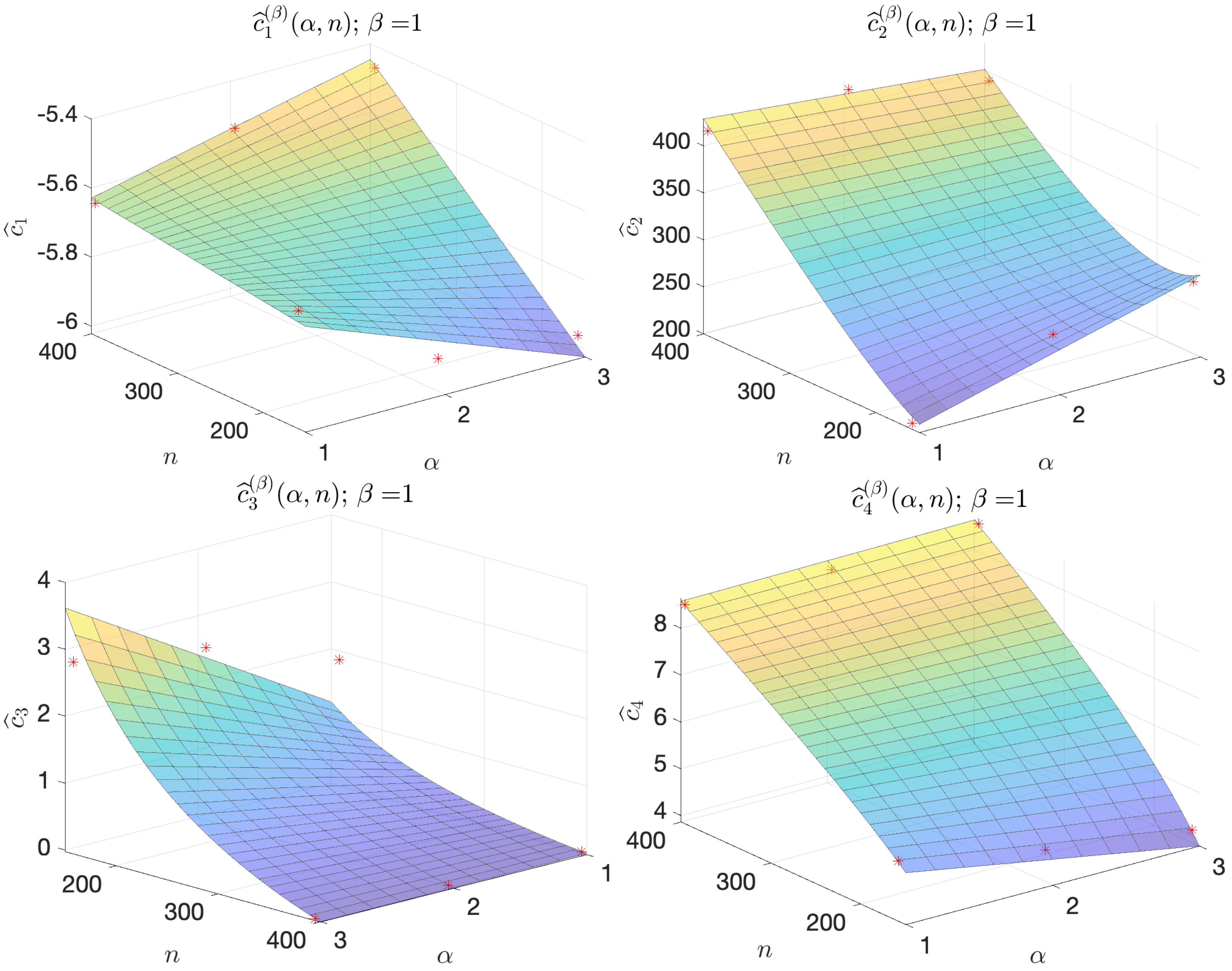
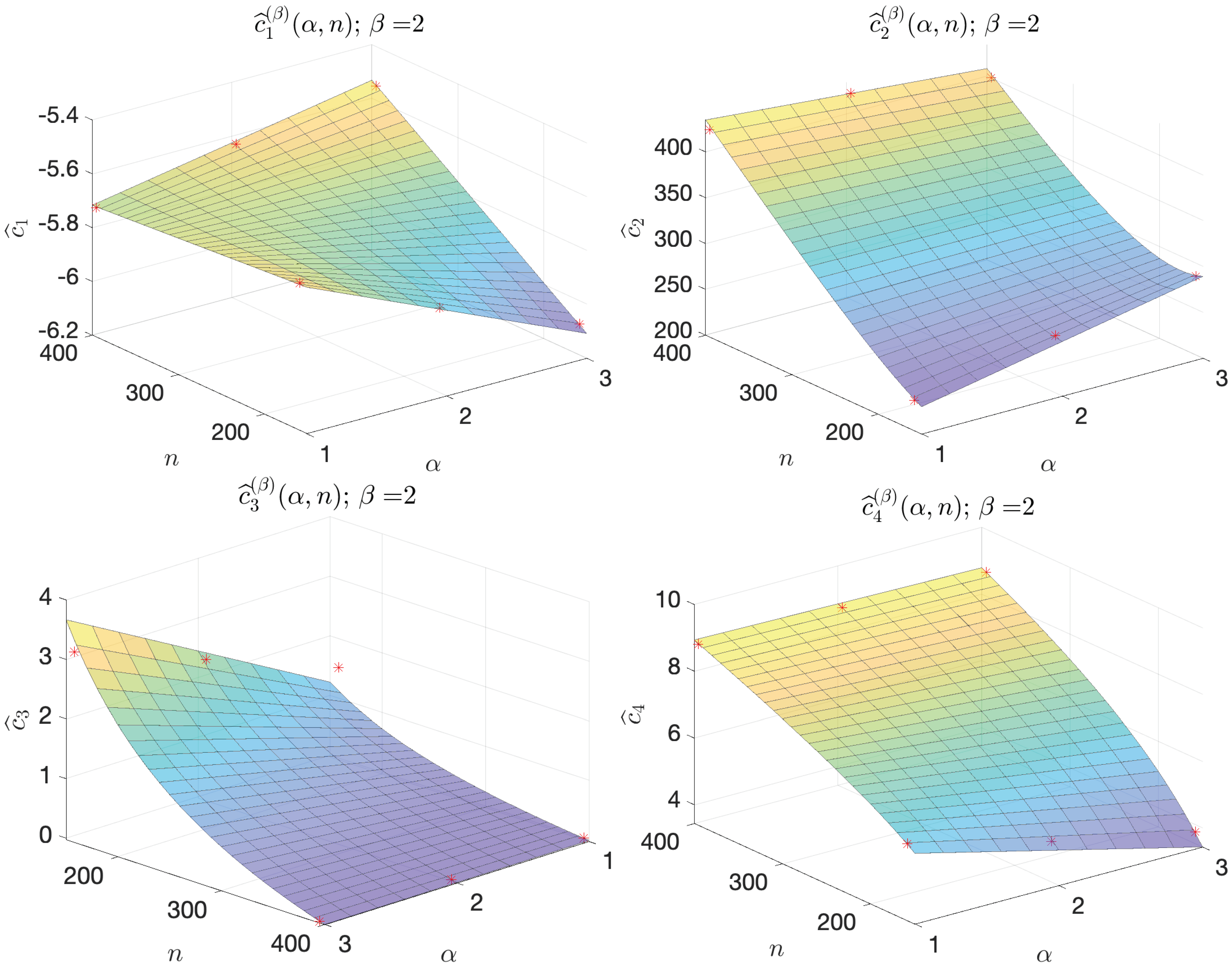
of
, varying the hyperparamenters
and
n for each fixed
. Indeed, for each fixed
and
, we observe that the values of the coefficient
with respect to
are well-approximated by the function
defined in
Table 5 and
Table 6 and illustrated in
Figure 9 and
Figure 10. The expression of the function
was chosen by looking at the positions of the points
in the space
, for each
and each
; future analyses, involving more DFNs (i.e., more cases for
n), may surely help find better-fitting functions to describe the behavior of the coefficients
.
Given the functions
, for each fixed
, we can define a function
that returns estimates of the average errors
for any NN with architecture
trained with respect to a number
of simulations (and configuration
) to approximate the fluxes of a DFN with
n fractures (see
Section 2.1.2) and transmissivity variation characterized by
. Then, the UQ rule exploits (
23) and Proposition 1, and it is outlined by the following steps:
Let
be the number of fractures of a given DFN with fixed geometry generated with respect to the characterization of
Section 2.1.2, and let
be the parameter characterizing the standard deviation of the transmissivity distribution (see (
1));
For each
and each arbitrary
, following the results of Proposition 1, compute the values
where
. Then, the values
represent the estimates of the minimum number of simulations required by the NNs
, trained with respect to configuration
, in order to return an average error
less than or equal to
.
The reliability of the values depends strictly on the reliability of representing the values and on the reliability of the functions representing the coefficients . Therefore, we conclude this section by testing the efficiency of the UQ rule and, consequently, the reliability of the expressions chosen in this work for the functions .
We validate and test the UQ rule with respect to DFN202, a DFN with
fracture (
outflow fractures) and transmissivity distribution characterized by
. We train an NN
with configuration
on a number of simulations
equal to (
24) rounded up to the nearest multiple of five for each
and each
. For the case
, we do not use a value
but a value
because
is too close to the infimum error value
and, indeed, in this case,
is approximately equal to
; since we do not have enough simulations available to test
, we adopt
.
The average errors obtained for the test on DFN202 are reported in
Table 7. For each
, we report the minimum error value
, the chosen target error
, the estimated minimum number of simulations
, the number of simulations
performed for the training of the NN, and the final average error
returned by the trained NN on a test set
(with
). In all the cases, with
, the error
is very close to the target error
.
4. Discussion
Some examples concerning the use of deep learning models to speed up UQ analysis can be found in [
33,
34]. The use of DNNs as surrogate models for UQ is still a novel approach that requires deep investigations but is very promising. To the best of the authors’ knowledge, other than [
35,
36,
37], there are no works in the literature that train DNNs to perform flux regression tasks on DFNs and, in particular, that use these NNs in the context of UQ as in [
35]. While the results illustrated in [
35] are very promising, the ones presented in
Section 3 of this work concerns the use of NN reduced models as a practical possibility in the UQ framework for flow analyses of a subsurface network of fractures.
Let us assume that we deal with a natural fractured basin that can be described by a number of principal fractures in the order of
and probability distributions for fractures and hydrogeological properties as in
Section 2.1.2, with a fixed value
. The stochastic flow analysis can be very relevant for geothermal energy exploitation and for enhanced oil and gas exploitation. Flux investigations can also be relevant in risk assessment for geological storage of nuclear waste. The approach could be extended to different situations, for example, to provide a statistical analysis of the effects of different fracturing approaches [
46,
47,
48].
Uncertainty in fractures and hydrogeological properties requires the generation of an ensemble of DFNs describing the principal flow properties of the basin, and consequently, a UQ analysis of the flow properties is required. The results presented in
Section 3.3 can be useful for deciding if the training of a DNN is convenient with respect to a Monte Carlo approach or the use of a different surrogate flow model. Thanks to the results in
Section 3.3, we have the possibility to fix an approximation tolerance
such that an NN trained on
simulations fits the target tolerance.
Let us provide an example with DFN202, the validation DFN of
Section 3.3 (
). During a UQ analysis for this DFN, a standard approach may need thousands of simulations to obtain good estimations of the mean value and the standard deviation of the flux exiting from the DFN. Nevertheless, the UQ rule tells us that we can train an NN with approximately
or
average error with less than 300 simulations or approximately 1000 simulations, respectively (see
Table 7,
case). Then, once that has been trained, a NN can return virtually infinite reliable predictions (i.e., approximations) of the DFN exiting fluxes, varying the fracture transmissivities, in the order of seconds; therefore, we can estimate the exiting flux’s momentum using the NN predictions with a total cost of only the
DFN simulations used to train the NN. If we repeat the procedure for each geometry of DFN generated for the study, the advantages are significant.
A possible drawback of our method is that a UQ rule must be defined for the family of problems and NN architectures considered. Indeed, the UQ rule defined in
Section 3.3 is tailored on the multi-task architecture described in
Section 2.2.3, applied to the family of DFNs defined by the probability distributions in
Section 2.1.2. Moreover, the UQ rule of this work can be considered reliable at most for DFNs with few hundreds of fractures. The analysis performed here can be extended to larger DFNs and can provide useful information to wider applications.
The approach presented here is not immediately extensible to the case of DFNs with a stochastic geometry (see [
49]) due to the continuous change in inflow and outflow fractures. Nevertheless, a similar approach could be extended to the case of analysis of flows through the DFN that occurs between a fixed set of wells. In that case, the NN can provide flow through fixed wells varying the DFN geometry and the hydraulic properties of the fractures. In that case, we expect that the number of training simulations increases but the proposed approach could provide information correlating the target error tolerance with the variance in the stochastic distributions and the number of fractures.
5. Conclusions
With this work, we proposed an analysis for the characterization of a family of DNNs with multi-task architecture
trained to predict the exiting fluxes of a DFN given the fracture transmissivities. The novelty of this analysis consists in characterizing these NNs, searching for rules that describe the performances, varying the available training data (
) and the standard deviation of the inputs (
). The results of our study show interesting common behaviors for all the trained NNs, providing characterization of the average error with the functions
and
(see (
19) and (
23)). This result is interesting, since it shows that common characterizing formulas for NN performances exist, despite the stochastic nature of the NN training processes; thanks to these regularities, we are able to define a “
UQ rule” that returns an estimate of the minimum number of simulations required for training an NN with an average error less than or equal to an arbitrary value
.
This estimate can be fruitfully exploited in real-world problems. Indeed, in the framework of UQ, it suggests whether it is convenient to train an NN as a reduced model and that a user can choose the best strategy between the use of an NN or direct simulations. In particular, the estimate returned by the UQ rule can be exploited in all “real-world” applications in which flow through a DFN with stochastic trasmissivities is recommended. The fields of interest could be oil and gas extraction, where flows through a fractured medium that occur between a fixed set of wells need to be analyzed and the possible effects of phenomena that can impact the fracture transmissivities (for example clogging) should be foreseen. Similar needs could occur in designing geothermal sites for which the performances strongly depend on the flow properties. Other application examples could be flow analysis for geological risk assessments of geological carbon dioxide or nuclear waste storage or water prevention close to other pollutant storage sites. The usage of NNs as reduced models for DFN flow simulations, optimizing the number of required numerical simulations for training through the UQ rule, can save precious time when computing an estimate of the risks and, therefore, deciding how to intervene when preventing or managing a calamity.
In general, we believe that many approaches for underground flow analysis through DFNs can be endowed with a tailored version of the method proposed in this paper; then, the method can speed up the simulation process, which is often slow and expensive, granting considerable advantages in many real-world geophysical applications.